2019秋九年级数学上册 第一章 特殊平行四边形 1.2 第2课时 矩形的判定习题课件(新版)北师大
1.2《矩形的性质与判定》北师大版数学九年级上册教学课件(第2课时)

探究新知
议一议:你有什么方法检查你家(或教室)刚安装的门框是不是矩形? 如果仅有一根较长的绳子,你怎样检查?请说明检查方法的合理性.
答:可以用直角尺检查安装的门框的四个角是否为直角.如果有三个角 是直角,那么刚安装的门框一定是矩形.也可以用直尺(或皮尺)分别量出 门框两组对边的长度,如果两组对边长度分别相等,则门框一定是平行四边 形,再测量门框的对角线的长度,如果两条对角线的长度相等,那么刚安装 的门框一定是矩形.
课堂练习
3.已知:如图,在□ABCD中,M是AD边的中点,且MB=MC.
求证:四边形ABCD是矩形.
A
M
D
B
C
课堂练习
证明:∵四边形ABCD是平行四边形,
∴AB=DC.
∵M是AD边的中点,
∴AM=DM.
又∵MB=MC,
∴△ABM≌△DCM(SSS)
∴∠A=∠D.
∴∠A=∠D=90°.
又∵AB∥DC,
探究新知
如果仅有一根较长的绳子,可以先用绳子分别测量出门框的两 组对边的长度,做上记号.如果两组对边的长度分别相等,那么这 个门框一定是平行四边形,再用绳子量出门框的对角线的长度.如 果这两条对角线的长度相等,那么这个刚安装的门框一定是矩形, 否则不是矩形.理由是对角线相等的平行四边形是矩形.
典例精析
A.对角线相等且互相平分的四边形是矩形 B.对角互补的平行四边形是矩形 C.对角线相等且有一个角是直角的四边形是矩形 D.四个角都相等的四边形是矩形
课堂练习
2.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E, F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则 四边形EFGH的面积为____1_2_____.
九年级数学(北师大版)上册教案:1.2矩形的性质与判定(1)

第一章特殊平行四边形1.2 矩形的性质与判定(一)教学目标知识与技能:了解矩形的有关概念,理解并掌握矩形的有关性质.过程与方法:经过探索矩形的概念和性质的过程,发展学生合情推理意识;掌握几何思维方法.情感态度与价值观:培养严谨的推理能力,以及自主合作精神;体会逻辑推理的思维价值.重难点、关键重点:掌握矩形的性质,并学会应用.难点:理解矩形的特殊性.关键:把握平行四边形的演变过程,迁移到矩形概念与性质上来,明确矩形是特殊的平行四边形.教学准备教师准备:投影仪,收集有关矩形的图片,制作教具.学生准备:复习平行四边形性质,预习矩形这节内容.学法解析1.认知起点:已经学习了三角形、平行四边形、菱形,•积累了一定的经验的基础上学习本节课内容.2.知识线索:情境与操作→平行四边形→矩形→矩形性质.3.学习方式:观察、操作、感知其演变,以合作交流的学习方式突破难点.教学过程一、联系生活,形象感知【显示投影片】教师活动:将收集来的有关长方形图片,播放出来,让学生进行感性认识,然后定义出矩形的概念.矩形定义:有一个角是直角的平行四边形叫做矩形.(也就是小学学习过的长方形).教师活动:介绍完矩形概念后,为了加深理解,也为了继续研究矩形的性质,拿出教具.同学生一起探究下面问题:问题1:改变平行四边形活动框架,将框架夹角∠α变为90°,•平行四边形成为一个矩形,这说明平行四边形与矩形具有怎样的从属关系?(教师提问)[来源:21世纪教育网学生活动:观察教师的教具,研究其变化情况,可以发现:矩形是平行四边形的特例,属于平行四边形,因此它具有平行四边形的所有性质.[来源:学*科*网Z*X*问题2:既然它具有平行四边形的所有性质,•那么矩形是否具有它独特的性质呢?(教师提问)学生活动:由平行四边形对边平行以及刚才∠α变为90°,可以得到∠α的补角也是90°,从而得到:矩形的四个角都是直角.评析:实际上,在小学学生已经学过长方形四个角都是90°,这里学生不难理解.教师活动:用橡皮筋做出两条对角线,让学生观察这两条对角线的关系,并要求学生证明(口述).学生活动:观察发现:矩形的两条对角线相等。
北师大版九年级数学上册1.2.1矩形的性质与判定课件(共23张PPT)

矩形的定义:
有一个角是直角的平行四边形是矩形
平行四边形
有一个角 是直角
矩形
矩形是特殊的平行四边形
生活中的实例
分组讨论 探究新知
问题1: 既然矩形是平行四边形,那么它具有平行四 边形的哪些性质?
性质
边
角
对角线 对称性
矩形
对边平行 且相等
对角相等
对角线互相 中心对称 平分 图形
问题2
例1:如图,在矩形ABCD中,两条对角线相交于点O, ∠AOD=120°,AB=2.5cm,求矩形对角线的长。
A
D
O
B
C
你还有其他解法吗?
反馈练习二
1. 下面性质中,矩形不一定具有的是 [ D ]
A.对角线相等 C.是轴对称图形
B.四个角都相等 D.对角线垂直
2. 如图,在矩形ABCD中,两条对角线AC与 BD相交于点O,AB=6,OA=4.求BD与AD的长.
矩形是特殊的平行四边形
公平,因为OA=OC=OB=OD
当矩形的大小不断变化时,发现的结论是否仍然成立?
(2)AC = BD
公平,因为OA=OC=OB=OD (2)在运动过程中四边形不变的是什么?
这是矩形所
矩形的四个角都是直角.
O
特有的性质
生活链接---投圈游戏
四个学生正在做投圈游戏,他们分别站在一
B
C
O
B
C
直角三角形斜边上的中线等于斜边的一半。这个结 论对于所有直角三角形都成立。
反馈练习一
已知△ABC是Rt△,∠ABC=90°,BD是斜边AC上的中线. (1)若BD=3㎝,则AC=_6____㎝; (2)若∠C=30°,AB=5㎝,则AC=__1_0__㎝,BD=__5___ ㎝.
北师版九年级数学上册第1章2矩形的性质与判定

称
性 是中心对称图形,对称中心是对角线
的交点
矩形的任意一条对角线都把矩形分成两个全等的直角三角形,
如Rt △ ADB ≌Rt△CBD,Rt△ ABC ≌Rt △ CDA.
2.矩形的两条对角线把矩形分成四个面积相等的等腰三角形,
并且相对的两个等腰三角形全等,如S△ AOB=S △ AOD=
解题秘方:紧扣矩形定义的“两个条件”进行证明.
解题通法:根据矩形的定义判定矩形的方法
知1-练
知1-练
证明:∵ O 为AB 的中点,∴ OB=OA. 又∵ OE=OD,∴四边形AEBD 是平行四边形. ∵ AB=AC,AD 是△ABC 的角平分线,∴ AD⊥ BC. ∴∠ ADB=90°. ∴四边形AEBD 是矩形.
AB∥CD,AD∥BC AB=CD,AD=BC
角
矩形的四个 角都是直角
∵四边形ABCD 是矩形, ∴∠ DAB= ∠ DCB= ∠ ADC=∠ ABC =90°
知2-讲
图形
性质
数学表达式
对 角 线
矩形的对角 ∵四边形ABCD 是矩形,
线相等
∴ AC=BD
对
是轴对称图形,它有两条对称轴,过 每组对边中点的直线是其对称轴
第一章 特殊平行四边形
2 矩形的性质与判定
1 课时讲解 矩形的定义
矩形的性质 直角三角形斜边上中线的性质
2 课时流程 矩形的判定
逐点 导讲练
课堂 小结
作业 提升
知识点 1 矩形的定义
定义
有一个角是 直角的平行 四边形叫做
矩形
图示
知1-讲
数学表达式 ∵在ABCD 中,∠ A=90°(或∠ B=90° 或∠ C=90°或∠ D=90°),∴ ABCD 是 矩形
九年级数学 第一章 特殊平行四边形2 矩形的性质与判定第2课时 矩形的判定作业

A.4 B.4.8 C.5.2 D.6
第10题图
11.如图,在△ABC 中,AC 的垂直平分线分别交 AC,AB 于点 D, F,BE⊥DF 交 DF 的延长线于点 E,已知∠A=30°,BC=2,AF=BF, 则四边形 BCDE 的面积是_2___3____.
第11题图
12.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F 作FG⊥EF交BC于点G,连接GH,当AD,AB满足______A__B_=__A(D关系)时, 四边形EFGH为矩形.
第12题图
13.如图,AB∥CD,PM,PN,QM,QN分别为∠APQ,∠BPQ,∠CQP, ∠DQP的平分线.求证:四边形PMQN是矩形.
证明:∵PM,PN,QM 分别平分∠APQ,∠BPQ,∠CQP,∴∠MPQ
=21 ∠APQ,∠NPQ=21 ∠BPQ,∠MQP=21 ∠CQP.∵∠APQ+∠BPQ =180°,∴∠MPQ+∠NPQ=90°,即∠MPN=90°.同理可证∠MQN =90°.∵AB∥CD,∴∠APQ+∠CQP=180°,∴∠MPQ+∠MQP=90 °,即∠PMQ=90°,∴四边形 PMQN 是矩形
9.如图,顺次连接四边形ABCD各边的中点,得到四边形EFGH,在下列
条件中,能使四边形EFGH为矩形的是( C)
A.AB=CD B.AC=BD C.AC⊥BD D.AD∥BC
第9题图
10.如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且 点P不与点B,C重合),PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为
第5题图
6.(2019·江西)如图,四边形ABCD中,AB=CD,AD=BC,对角线AC, BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
2018-2019学年九年级数学上册 第一章 特殊平行四边形 1.2 矩形的性质与判定作业设计 (新版)北师大版
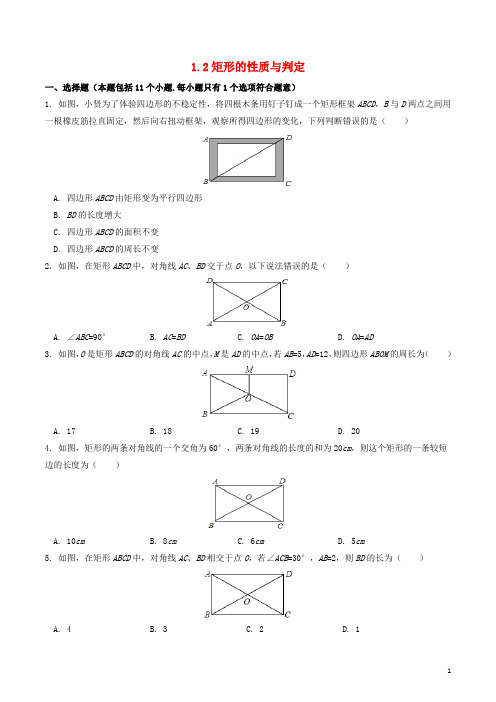
1.2矩形的性质与判定一、选择题(本题包括11个小题.每小题只有1个选项符合题意)1. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是()A. 四边形ABCD由矩形变为平行四边形B. BD的长度增大C. 四边形ABCD的面积不变D. 四边形ABCD的周长不变2. 如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是()A. ∠ABC=90°B. AC=BDC. OA=OBD. OA=AD3. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为()A. 17B. 18C. 19D. 204. 如图,矩形的两条对角线的一个交角为60°,两条对角线的长度的和为20cm,则这个矩形的一条较短边的长度为()A. 10cmB. 8cmC. 6cmD. 5cm5. 如图,在矩形ABCD中,对角线AC、BD相交于点O,若∠ACB=30°,AB=2,则BD的长为()A. 4B. 3C. 2D. 16. 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是212,则该矩形的面积为()A. 602B. 702C. 1202D. 14027. 如图,矩形ABCD中,AC交BD于点O,∠AOD=60°,OE⊥AC.若AD=,则OE=()A. 1B. 2C. 3D. 48. 矩形具有而菱形不具有的性质是()A. 对角线相等B. 两组对边分别平行C. 对角线互相平分D. 两组对角分别相等9. 矩形的一内角平分线把矩形的一条边分成3cm和5cm的两部分,则此矩形的周长为()A. 16cmB. 22cmC. 26cmD. 22cm或26cm10. 矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是()A. 57.5°B. 32.5°C. 57.5°,23.5°D. 57.5°,32.5°11. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是()A. 对角线相等的四边形B. 对角线垂直的四边形C. 对角线互相平分且相等的四边形D. 对角线互相垂直平分的四边形二、填空题(本题包括3个小题)12. 如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件__________(只添一个即可),使平行四边形ABCD是矩形.13. 平行四边形ABCD的对角线相交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC 平分∠BAD;⑤AO=DO.使得四边形ABCD是矩形的条件有________14. 木工做一个长方形桌面,量得桌面的长为15cm,宽为8cm,对角线为17cm,这个桌面_________(填”合格”或”不合格”)三、解答题(本题包括5个小题)15. 如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.(1)求证:四边形EFGH是平行四边形;(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形16. 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积17. 如图,在平行四边形ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.求证:四边形ABCD是矩形18. 有一块形状如图所示的玻璃,不小心把DEF部分打碎,现在只测得AB=60cm,BC=80cm,∠A=120°,∠B=60°,∠C=150°,你能设计一个方案,根据测得的数据求出AD的长吗?19. 如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE答案一、选择题1. 【答案】C【解析】由题意可知,当向右扭动框架时,BD可伸长,故BD的长度变大,四边形ABCD由矩形变为平行四边形,因为四条边的长度不变,所以四边形ABCD的周长不变.原来矩形ABCD的面积等于BC乘以AB,变化后平行四边形ABCD的面积等于底乘以高,即BC乘以BC边上的高,BC边上的高小于AB,所以四边形ABCD 的面积变小了,故A,B,D说法正确,C说法错误.故正确的选项是C.考点:1.四边形面积计算;2.四边形的不稳定性.2. 【答案】D【解析】本题考查了矩形的性质;熟练掌握矩形的性质是解决问题的关键.矩形的性质:四个角都是直角,对角线互相平分且相等;由矩形的性质容易得出结论.∵四边形ABCD是矩形,∴∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,OA=AC,OB=BD,∴OA=OB,∴A、B、C正确,D错误考点:矩形的性质3. 【答案】D【解析】∵O是矩形ABCD的对角线AC的中点,M是AD的中点,∴∠ABC=∠D=90°,CD=AB=5,BC=AD=12,OA=OB,OM为△ACD的中位线,∴OM=CD=2.5,AC==13,∵O是矩形ABCD的对角线AC的中点,∴BO=AC=6.5,∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20,故选D.考点:矩形的性质.4. 【答案】D【解析】∵四边形ABCD是矩形,∴OA=OC=AC,OD=OB=BD,AC=BD,∴OA=OB,∵AC+BD=20,∴AC=BD=10cm,∴OA=O B=5cm,∵OA=OB,∠AOB=60°,∴△OAB是等边三角形,∴AB=OA=5cm,故选D.考点:1.矩形的性质;2.等边三角形的判定与性质.5. 【答案】A【解析】在矩形ABCD中,∠ABC=90°,∵∠ACB=30°,AB=2,∴AC=2AB=2×2=4,∵四边形ABCD是矩形,∴BD=AC=4.故选A.6. 【答案】A【解析】黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的(50%-15%)=35%,已知黄色三角形面积是21平方厘米,故矩形的面积=21÷(50%-15%)=21÷35%=60(cm2).故选A.考点:矩形的性质.7.【答案】A【解析】∵四边形ABCD是矩形,∠AOD=60°,∴△ADO是等边三角形,∴OA=,∠OAD=60°,∴∠OAE= 30°,∵OE⊥AC,∴△OAE是一个含30°的直角三角形,∴OE=1,故选A.8.【答案】A【解析】∵矩形具有的性质是:对角线相等且互相平分,两组对边分别平行,两组对角分别相等;菱形具有的性质是:两组对边分别平行,对角线互相平分,两组对角分别相等;∴矩形具有而菱形不具有的性质是:对角线相等.故选A.9. 【答案】D【解析】∵四边形ABCD是矩形,∴AD=BC,AB=CD,AD∥BC,∴∠AEB=∠CBE,∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠AEB=∠ABE,∴AB=AE,当AE=3cm时,AB=AE=3=CD,AD=3cm+5cm=8cm=BC,∴此时矩形ABCD的周长是AB+BC+CD+AD=3cm+8cm+3cm+8cm=22cm;当AE=5cm时,AB=AE=5cm=CD,AD=3cm+5cm=8cm=BC,∴此时矩形ABCD的周长是AB+BC+CD+AD=5cm+8cm+5cm+8cm=26cm;故选D.考点:矩形的性质.10. 【答案】D【解析】∵四边形ABCD是矩形,∴∠ABC=90°,AD∥BC,AB∥CD,AC=BD,AO=OC,OB=OD,∴OB=OA=OC=OD,∠OAB=∠OCD,∠DAO=∠OCB,∴∠OAD=∠ODA,∠OCB=∠OBC,∠ODC=∠OCD,∠OAB=∠OBA=×(180°﹣∠AOB)=×(180°﹣65°)=57.5°,∵∠ABC=90°,∴∠ACB=90°﹣57.5°=32.5°,即∠OAD=∠ODA=∠OBC=∠OCB=32.5°,∠OAB=∠OBA=∠ODC=∠OCD=57.5°,对角线与各边所成的角度是57.5°和32.5°,故选D.点睛:本题考查了矩形的性质,三角形的内角和定理,等腰三角形的性质的应用,能正确运用矩形的性质进行推理是解此题的关键,注意:矩形的对角线相等且互相平分.11. 【答案】B【解析】∵四边形EFGH是矩形,∴∠E=90°,∵EF∥AC,EH∥BD,∴∠E+∠EAG=180°,∠E+∠EBO=180°,∴∠EAO=∠EBO=90°,∴四边形AEBO是矩形,∴∠AOB=90°,∴AC⊥BD,故选B.二、填空题12. 【答案】AC=BD.答案不唯一【解析】添加的条件是AC=BD,理由是:∵AC=BD,四边形ABCD是平行四边形,∴平行四边形ABCD是矩形,故答案为:AC=BD.答案不唯一.点睛:本题考查了矩形的判定定理的应用,注意:对角线相等的平行四边形是矩形,此题是一道开放型的题目,答案不唯一.13.【答案】①⑤【解析】要使得平行四边形ABCD为矩形添加:①∠ABC=90°;⑤AO=DO2个即可;故答案为:①⑤.14. 【答案】合格【解析】勾股定理的逆定理:若一个三角形的两边长的平方和等于第三边的平方,则这个三角形的直角三角形.∵∴这个桌面合格.考点:勾股定理的逆定理点评:本题属于基础应用题,只需学生熟练掌握勾股定理的逆定理,即可完成.三、解答题15. 【答案】(1)证明见解析;(2)证明见解析.【解析】(1)易证得△AEH≌△CGF,从而证得BE=DG,DH=BF.故有,△BEF≌△DGH,根据两组对边分别相等的四边形是平行四边形而得证.(2)由题意知,平行四边形ABCD是菱形,连接AC,BD,则有AC⊥B D,由AB=AD,且AH=AE可证得HE∥BD,同理可得到HG∥AC,故HG⊥HE,又由(1)知四边形HGFE是平行四边形,故四边形HGFE是矩形.证明:(1)在平行四边形ABCD中,∠A=∠C,又∵AE=CG,AH=CF,∴△AEH≌△CGF.∴EH=GF.在平行四边形ABCD中,AB=CD,AD=BC,∴AB-AE=CD-CG,AD-AH=BC-CF,即BE=DG,DH=BF.又∵在平行四边形ABCD中,∠B=∠D,∴△BEF≌△DGH.∴GH=EF.∴四边形EFGH是平行四边形.(2)在平行四边形ABCD中,AB∥CD,AB=CD.设∠A=α,则∠D=180°-α.∵AE=AH,∴∠AHE=∠AEH=.∵AD=AB=CD,AH=AE=CG,∴AD-AH=CD-CG,即DH=DG.∴∠DHG=∠DGH=.∴∠EHG=180°-∠DHG-∠AHE=90°.又∵四边形EFGH是平行四边形,∴四边形EFGH是矩形.考点:1.矩形的判定与性质;2.全等三角形的判定与性质;3.平行四边形的判定与性质.16. 【答案】12.【解析】利用平行四边形的性质和矩形的判定定理推知平行四边形AEBD是矩形.在Rt△ADC中,由勾股定理可以求得AD的长度,由等腰三角形的性质求得CD(或BD)的长度,则矩形的面积=长×宽=AD•BD=AD•CD.解:∵AE∥BC,BE∥AC,∴四边形AEDC是平行四边形,∴AE=CD.在△ABC中,AB=AC,AD为BC边上的高,∴∠ADB=90°,BD=CD,∴BD=AE,∴平行四边形AEBD是矩形.在Rt△ADC中,∠ADB=90°,AC=5,CD=BC=3,∴AD==4,∴四边形AEBD的面积为:BD•AD=CD•AD=3×4=12.点睛:本题考查了矩形的判定与性质和勾股定理,根据“等腰三角形的性质和有一内角为直角的平行四边形为矩形”推知平行四边形AEBD是矩形是解题的难点.17. 【答案】证明见解析.【解析】欲证明四边形ABCD是矩形,只需推知∠DAB是直角.证明:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAF=∠F.∵∠F=45°,∴∠DAE=45°.∵AF是∠BAD的平分线,∴∠EAB=∠DAE=45°,∴∠DAB=90°.又∵四边形ABCD是平行四边形,∴四边形ABCD是矩形.18. 【答案】AD=140cm.【解析】过C作CM∥AB,交AD于M,推出平行四边形ABCM,推出AM=BC=80cm,AB=CM=60cm,∠B=∠AMC,求出∠D=∠MCD,求出CM=DM=60cm,代入AD=AM+DM求出即可.解:过C作CM∥AB,交AD于M,∵∠A=120°,∠B=60°,∴∠A+∠B=180°,∴AM∥BC,∵AB∥CM,∴四边形ABCM是平行四边形,∴AB=CM=60cm,BC=AM=80cm,∠B=∠AMC=60°,∵AD∥BC,∠C=150°,∴∠D=180°﹣150°=30°,∴∠MCD=60°﹣30°=30°=∠D,∴CM=DM=60cm,∴AD=60cm+80cm=140cm.19. 【答案】证明见解析.【解析】先由角平分线和等腰三角形的性质证明AE∥BD,再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE,可得AD∥BE,可证得四边形ADBE为矩形,可得结论.证明:∵AD、AE分别是∠BAC与∠BAC的外角的平分线,∴∠BAD+∠EAB=(∠BAC+∠FAB)=90°,∵BE⊥AE,∴DA∥BE,∵AB=AC,∴∠ABC=∠ACB,∵∠FAB=∠ABC+∠ACB=2∠ABC,且∠FAB=2∠EAB,∴∠ABC=∠EAB,∴AE∥BD,∴四边形AEBD为平行四边形,且∠BEA=90°,∴四边形AEBD为矩形,∴AB=DE.点睛:本题主要考查矩形的判定和性质,由角平分线及等腰三角形的性质证明AE∥BD是解题的关键.。
1.2.2 矩形的判定-北京师范大学出版社九年级数学上册

2 下列关于矩形的说法中正确的是( B ) A.对角线相等的四边形是矩形 B.矩形的对角线相等且互相平分 C.对角线互相平分的四边形是矩形 D.矩形的对角线互相垂直且平分
知1-练
知1-练
3 已知四边形ABCD是平行四边形,对角线AC与BD 相交于点O,下列结论中不正确的是( D ) A.当AB=BC时,四边形ABCD是菱形 B.当AC⊥BD时,四边形ABCD是菱形 C.当OA=OB时,四边形ABCD是矩形 D.当∠ABD=∠CBD时,四边形ABCD是矩形
∴OA=OC,OB=OD. 又∵△ABO是等边三角形, ∴OA=OB=AB=4,∠BAC=60°. ∴OA=OB=OC=OD=4. ∴AC=BD=2OA=2×4=8. ∴ ABCD是矩形(对角线相等的平行四边形是矩形).
知1-练
1 如图,四边形ABCD的对角线互相平分,要使它变 为矩形,需要添加的条件是( D )
证明:∵AD平分∠BAC,AN平分∠CAM, ∴∠CAD= 12∠BAC,∠CAN= 12∠CAM. ∴∠DAE=∠CAD+∠CAN= 12(∵AB=AC,AD为∠BAC的平分线, ∴AD⊥BC.∴∠ADC=90°. 又∵CE⊥AN,∴∠CEA=90°. ∴四边形ADCE是矩形(有三个角是直角的四边形是矩形).
你能得到一个怎样的猜想?
知识点 1 由对角线的关系判定矩形
知1-讲
判定定理1:对角线相等的平行四边形是矩形. 请完成该定理的证明:
知1-讲
例知1 识如点图,在 ABCD中,对角线AC与BD相交于点O,
△ABO是等边三角形,AB=4,求 ABCD是矩形.
知1-讲
解:∵四知边识形点ABCD是平行四边形,
1.2.2 矩形的判定 公开课课件

解:(1)证明:∵CF 平分∠ACD,且 MN∥BD,∴∠ACF =∠FCD=∠CFO.∴OF=OC.同理可证:OC=OE.∴OE=OF (2)由(1)知:OF=OC,OC=OE,∴∠OCF=∠OFC,∠OCE= ∠OEC.∴∠OCF+∠OCE=∠OFC+∠OEC.而∠OCF+∠OCE +∠OFC+∠OEC=180°,∴∠ECF=∠OCF+∠OCE=90°,
•
蔡琰(作者有待考证)的《胡笳十八拍》
郭璞的《游仙诗》
鲍照的《拟行路难》
庾信的《拟咏怀》
都特别喜欢。不过都是组诗,太长了,就不贴了orz。
最后还想推一下萧绎的《幽逼诗》四首:
【南史曰:元帝避建邺则都江陵,外迫强敌,内失人和。魏师至,方征兵四方,未至而城见克。在幽逼求酒,饮之,制诗四绝。后为梁王詧所害。】 南风且绝唱,西陵最可悲。今日还蒿里,终非封禅时。 人世逢百六,天道异贞恒。何言异蝼蚁,一旦损鲲鹏。 松风侵晓哀,霜雰当夜来。寂寥千载后,谁畏轩辕台。 夜长无岁月,安知秋与春。原陵五树杏,空得动耕人。
9.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点, PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件
BC=2AB 时,四边形PEMF为矩形.
第8题图
第9题图
10.已知▱ABCD的对角线交于点O,分别添加下列条件:① ∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.使▱ABCD 是矩形的条件的序号是 ①③④ .
OA=12BD,OA=12AC,∴BD=AC,∴▱ABCD 是矩形
13.如图,AB=AC,AD=AE,DE=BC且∠BAD=∠CAE, 求证:四边形BCDE是矩形.
解 : 证 明 : ∵ AC = AB , AD = AE , ∠ BAD = ∠ CAE , ∴ ∠ CAD = ∠ BAD - ∠ CAB = ∠ CAE - ∠ CAB = ∠ BAE.∴△ADC≌△AEB.∴DC = BE , ∠ ABE = ∠ ACD. 又 ∵ DE = BC , ∴ 四 边 形 BCDE 为 平 行 四 边 形 . ∵ AB = AC , ∴ ∠ ABC = ACB , ∴ ∠ ABC + ∠ ABE = ∠ ACB + ∠ ACD , 即 ∠EBC=∠DCB=90°.∴四边形BCED为矩形
