第01讲 集合的概念与运算(原卷版)
第1章 第1节 集合的概念与运算
B＝{x|－2≤x≤2}，则如图所表示阴影部分所示的集合为( )
A．{x|－2≤x<4}
B．{x|x≤2 或 x≥4}
C．{x|－2≤x≤－1}
D．{x|－1≤x≤2}
解析： 依题意得 A＝{x|x<－1 或 x>4}，因为∁RA＝{x|－1≤x≤4}，题中的
阴影部分所表示的集合为(∁RA)∩B＝{x|－1≤x≤2}． 答案： D
返回
[同类练]
1．(2017·天津卷)设集合 A＝{1,2,6}，B＝{2,4}，C＝{x∈R|－1≤x≤5}，则(A
∪B)∩C＝( )
A．{2}
B．{1,2,4}
C．{1,2,4,6}
D．{x∈R|－1≤x≤5}
解析： 因为 A＝{1,2,6}，B＝{2,4}，所以 A∪B＝{1,2,4,6}，又 C＝{x∈R| －1≤x≤5}，所以(A∪B)∩C＝{1,2,4}．
返回
2．判断集合关系的三种方法 (1)一一列举观察． (2)集合元素特征法：首先确定集合的元素是什么，弄清集合元素的特征，再 利用集合元素的特征判断集合关系． (3)数形结合法：利用数轴或 Venn 图．
返回
考向·分层突破
考向一 集合的基本概念 自主练透型
1．已知集合 A＝{0,1,2}，则集合 B＝{(x，y)|x≥y，x∈A，y∈A}中元素的个
(2)∵B⊆A，
∴①若 B＝∅，则 2m－1<m＋1，此时 m<2.
②若 B≠∅，则2mm＋－11≥≥－m2＋，1， 2m－1≤5.
注意集合的分类 讨论问题
解得 2≤m≤3.
由①、②可得，符合题意的实数 m 的取值范围为 m≤3.
答案： (1)D (2)(－∞，3]
第一章 集合的概念及运算(集合论讲义)
(5) 德·摩根律 A ∪ B = A ∩ B ， A ∩ B = A ∪ B
A − (B ∪ C) = (A − B) ∩ (A − C) ， A − (B ∩ C) = (A − B) ∪ (A − C)
4
|
A1
|=
⎢ 250 ⎥ ⎢⎣ 2 ⎥⎦
=
125
，|
A2
|=
⎢ 250 ⎢⎣ 3
⎥ ⎥⎦
=
83
，|
A3
|=
⎢ 250 ⎥ ⎢⎣ 5 ⎥⎦
=
50
，|
A4
|=
⎢ ⎢⎣
250 ⎥ 7 ⎥⎦
=
35
，
|
A1
∩
A2
|=
⎢ ⎢⎣
250 ⎥ 2× 3⎥⎦
=
41
，|
A1
∩
A3
|=
⎢ 250 ⎥ ⎢⎣2× 5⎥⎦
=
(6) 吸收律 A ∪ ( A ∩ B) = A ， A ∩ ( A ∪ B) = A (7) 零律 A ∪ E = E ， A ∩ ∅ = ∅ (8) 同一律 A ∪ ∅ = A ， A ∩ E = A (9) 排中律 A ∪ A = E
5
(10) 矛盾律 A ∩ A = ∅ (11) 全补律 ∅ = E ， E = ∅ (12) 双重否定律 A = A (13) 补交转换律 A − B = A ∩ B
3
还可以将交，并运算推广到集族上。
∪ 定义 2.3 设 A 为一个集族，称由 A 中全体集合的元素组成的集合为 A 的广义并集，记作 A ， ∪ 称 ∪ 为广义并运算符， A 可描述为
01集合的概念及运算
251 16, 261 32, 271 64, 281 128,
且1 4 16 64 128 211,
i1 1, i2 2, i3 5, i4 7, i5 8.
走进高考
综上知，当A⊆B时，a<-8或a≥2.
(2)当 a=0 时，显然 B ⊆A；
当 则 又当∵ 当a则则 又则又<a－ 4aaa∵<0≤∵<>1a0－4a－0时 0a4a－－ 时4aa≤， 时<≤1a≥>1a<， 0≤1a2，－20∴ ，，2－>，若－12>2∴－ 若若12212∴， B－12BB⊆ ，<－⊆⊆∴ 12a，，<∴AA1<2a∴，，<0<∴－ － .a0－ －如如如 <.00128<<1208≤ <－－图图图 <≤aa. a≤ ≤a128a，，a<，<<≤<22<0000aa.<<0.0.
走进高考
【2】（10 湖南文 15）若规定 E={a1,a2 ,..., a10}的子集{ai1 ai2 ,..., ain }
为 E 的第 k 个子集，其中 k 2i11 2i2 1 2in 1 ，则
（1）{a1, a3} 是 E 的第_____5____个子集；
（2）E 的第 211 个子集是_{__a_1_,__a_2_,__a_5_,__a_7__,_a_8_}___．
(4)常用数集的记法
数集
自然 数集
正整数集
整数 集
有理 数集
实数 集
复数 集
记法 N N(或N ) Z Q R C
第01讲-集合(讲义版)
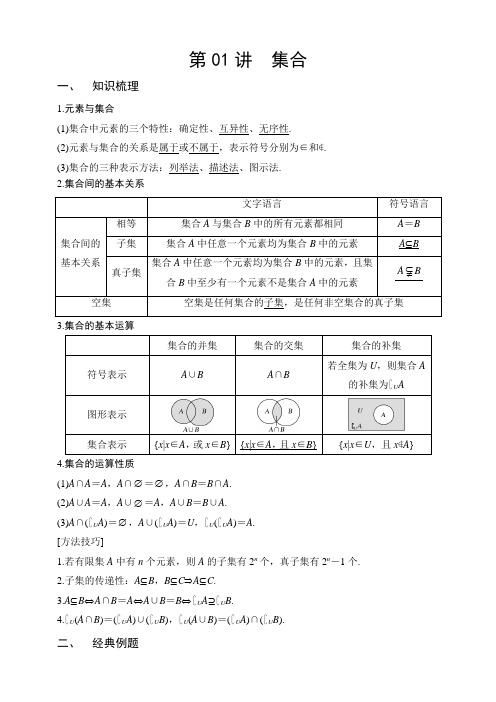
第01讲集合一、知识梳理1.元素与集合(1)集合中元素的三个特性：确定性、互异性、无序性.(2)元素与集合的关系是属于或不属于，表示符号分别为∈和∉.(3)集合的三种表示方法：列举法、描述法、图示法.2.集合间的基本关系文字语言符号语言集合间的基本关系相等集合A与集合B中的所有元素都相同A＝B 子集集合A中任意一个元素均为集合B中的元素A⊆B 真子集集合A中任意一个元素均为集合B中的元素，且集合B中至少有一个元素不是集合A中的元素BA⊂≠空集空集是任何集合的子集，是任何非空集合的真子集3.集合的基本运算集合的并集集合的交集集合的补集符号表示A∪B A∩B 若全集为U，则集合A 的补集为∁U A图形表示集合表示{x|x∈A，或x∈B}{x|x∈A，且x∈B}{x|x∈U，且x∉A} 4.集合的运算性质(1)A∩A＝A，A∩∅＝∅，A∩B＝B∩A.(2)A∪A＝A，A∪∅＝A，A∪B＝B∪A.(3)A∩(∁U A)＝∅，A∪(∁U A)＝U，∁U(∁U A)＝A.[方法技巧]1.若有限集A中有n个元素，则A的子集有2n个，真子集有2n－1个.2.子集的传递性：A⊆B，B⊆C⇒A⊆C.3.A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁U A⊇∁U B.4.∁U(A∩B)＝(∁U A)∪(∁U B)，∁U(A∪B)＝(∁U A)∩(∁U B).二、经典例题考点一 集合的基本概念【例1-1】（2020·海南省海南中学高三月考）若S 是由“我和我的祖国”中的所有字组成的集合，则S 的非空真子集个数是（ ） A ．62B ．32C ．64D ．30规律方法 1.研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义.2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合中的元素是否满足互异性. 考点二 集合间的基本关系【例2-1】（2020·天津市滨海新区塘沽第一中学高三二模）已知集合|03x A x Z x ⎧⎫=∈≤⎨⎬+⎩⎭，则集合A 真子集的个数为（ ） A ．3B ．4C ．7D ．8规律方法 1.若B ⊆A ，应分B ＝∅和B ≠∅两种情况讨论.2.已知两个集合间的关系求参数时，关键是将两个集合间的关系转化为元素或区间端点间的关系，进而转化为参数满足的关系.解决这类问题常常要合理利用数轴、Venn 图，化抽象为直观进行求解. 考点三 集合的运算【例3-1】（2020·全国高三一模（文））已知集合{}|15A x x =-≤≤，{}2|23B x x x =->，则A B =（ ）A ．5}|3{x x <≤B ．{|15}x x -≤≤C ．{|1x x <-或3}x >D ．R【例3-2】（2020·安徽省六安一中高一月考）已知集合{}2230A x x x =-->，(){}lg 11B x x =+≤，则()R A B =（ ）A ．{}13x x -≤< B ．{}19x x -≤≤ C ．{}13x x -<≤D ．{}19x x -<<规律方法 1.进行集合运算时，首先看集合能否化简，能化简的先化简，再研究其关系并进行运算.2.注意数形结合思想的应用.(1)离散型数集或抽象集合间的运算，常借助Venn图求解.(2)连续型数集的运算，常借助数轴求解，运用数轴时要特别注意端点是实心还是空心.(3)集合的新定义问题：耐心阅读，分析含义，准确提取信息是解决这类问题的前提，剥去新定义、新法则、新运算的外表，利用所学的集合性质等知识将陌生的集合转化为我们熟悉的集合，是解决这类问题的突破口.[思维升华]1.集合中的元素的三个特征，特别是无序性和互异性在解题时经常用到.解题后要进行检验，要重视符号语言与文字语言之间的相互转化.2.对连续数集间的运算，借助数轴的直观性，进行合理转化；对已知连续数集间的关系，求其中参数的取值范围时，要注意单独考察等号能否取到.3.对离散的数集间的运算，或抽象集合间的运算，可借助Venn图.这是数形结合思想的又一体现.[易错防范]1.集合问题解题中要认清集合中元素的属性(是数集、点集还是其他类型集合)，要对集合进行化简.2.空集是任何集合的子集，是任何非空集合的真子集，时刻关注对空集的讨论，防止漏解.3.解题时注意区分两大关系：一是元素与集合的从属关系；二是集合与集合的包含关系.4.Venn图图示法和数轴图示法是进行集合交、并、补运算的常用方法，其中运用数轴图示法时要特别注意端点是实心还是空心.。
2021最新版新高一暑假预习讲义《专题01 集合的概念》(原卷版)
这些符号是我们学习高中数学的基础，它大大简化了数集的表示方法，应当熟练掌握．
2．判断一个元素是不是某个集合的元素，关键是判断这个元素是否具有这个集合的元素的共同特征．
重要考点三：用列举法表示集合
【典型例题】方程组
2
− +
==36的解构成的集合为（
）
A． = 3, = 0
B． 3,0
C． 3,0
D． 0,3
合 A 中所有元素之积为_______.
17．【广东省广州市真光中学 2019-2020 学年高一上学期第一次月考】已知 ∈ {1, }，则实数 的值为______. 18．【山东省新高考 2018-2019 学年高一上学期 10 月阶段性考试】设 , , 为非零实数,m=| |+ + + ，则 的所有值组成的集合为____ 19．【必修第一册 逆袭之路】用列举法表示下列集合： （1）小于 10 的所有自然数组成的集合； （2）方程 2 = 的所有实数根组成的集合.
组成的集合.
【名师点睛】
1．用描述法表示相应集合时，首先明确代表元素是点集还是数集，在此基础上，结合描述的定义给出集合 的表示．
2．用描述法表示集合时，其代表元素的范围务必明确，如果省略不写，则默认为 x∈R.
重要考点五：忽略集合中元素的互异性
【典型例题】若−1 ∈ 3, 2 − − 1, 2 − 1 ，则 a=（ ）
重要考点六：解决集合的新定义问题的基本方法
【典型例题】定义集合运算： ※ = ︳ = − , ∈ , ∈ ，设集合 = 1,2 ， = 2,3 ，则集
合 ※ 的所有元素个数为（ ）
A．2
B．3
C．4
D．5
【题型强化】1.已知：集合 = 0，2，3 ，定义集合运算 ※ = { | = + , ∈ , ∈ }，则
第1讲 集合的概念和运算
第一章集合与常用逻辑用语第1讲集合的概念和运算一、选择题1. 已知集合P＝{x|x2≤1}，M＝{a}．若P∪M＝P，则a的取值范围是()A．(－∞，－1] B．[1，＋∞)C．[－1,1] D．(－∞，－1]∪[1，＋∞)解析因为P∪M＝P，所以M⊆P，即a∈P，得a2≤1，解得－1≤a≤1，所以a的取值范围是[－1,1]．答案 C2．已知集合M＝{0,1,2,3,4}，N＝{1,3，5}，P＝M∩N，则P的子集共有() A．2个B．4个C．6个D．8个解析因为M＝{0,1,2,3,4}，N＝{1,3,5}，所以P＝M∩N＝{1,3}，所以集合P的子集共有∅，{1}，{3}，{1,3}4个．答案B3．设集合U＝{x|x<5，x∈N*}，M＝{x|x2－5x＋6＝0}，则∁U M＝()．A．{1,4} B．{1,5} C．{2,3} D．{3,4}解析U＝{1,2,3,4}，M＝{x|x2－5x＋6＝0}＝{2,3}，∴∁U M＝{1,4}．答案 A4．若A＝{2,3,4}，B＝{x|x＝n·m，m，n∈A，m≠n}，则集合B中的元素个数是()．A．2 B．3 C．4 D．5解析B＝{x|x＝n·m，m，n∈A，m≠n}＝{6,8,12}．答案 B5．设集合M＝{1,2}，N＝{a2}，则“a＝1”是“N⊆M”的()．A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分又不必要条件解析若N⊆M，则需满足a2＝1或a2＝2，解得a＝±1或a＝±2.故“a＝1”是“N⊆M”的充分不必要条件．答案 A6．设A、B是两个集合，定义M*N＝{x|x∈M且x∉N}．若M＝{y|y＝log2(－x2－2x＋3)}，N＝{y|y＝x，x∈【0,9】}，则M*N＝()A．(－∞，0】B．(－∞，0)C．【0,2】D．(－∞，0)∪(2,3】解析y＝log2(－x2－2x＋3)＝log2【－(x＋1)2＋4】∈(－∞，2】，N中，∵x∈【0,9】，∴y ＝x∈【0,3】．结合定义得：M*N＝(－∞，0)．答案B二、填空题7．已知集合A＝{x∈R||x－1|<2}，Z为整数集，则集合A∩Z中所有元素的和等于________．解析A＝{x∈R||x－1|<2}＝{x|－1<x<3}．∴A∩Z＝{0,1,2}，即0＋1＋2＝3.答案38．已知集合A＝{0,2，a2}，B＝{1，a}，若A∪B＝{0,1,2,4}，则实数a的值为________．解析若a＝4，则a2＝16∉(A∪B)，所以a＝4不符合要求，若a2＝4，则a＝±2，又－2∉(A ∪B)，∴a＝2.答案 29．已知集合A＝{(0,1)，(1,1)，(－1,2)}，B＝{(x，y)|x＋y－1＝0，x，y∈Z}，则A∩B＝________.解析A、B都表示点集，A∩B即是由A中在直线x＋y－1＝0上的所有点组成的集合，代入验证即可．答案{(0,1)，(－1,2)}10．设A，B是非空集合，定义A*B＝{x|x∈A∪B且x∉A∩B}，已知A＝{x|0≤x≤3}，B＝{y|y≥1}，则A*B＝____________________.解析由题意知，A∪B＝[0，＋∞)，A∩B＝[1,3]，∴A*B＝[0,1)∪(3，＋∞)．答案[0,1)∪(3，＋∞)三、解答题11．若集合A＝{－1,3}，集合B＝{x|x2＋ax＋b＝0}，且A＝B，求实数a，b.解∵A＝B，∴B＝{x|x2＋ax＋b＝0}＝{－1,3}．∴⎩⎨⎧ －a ＝－1＋3＝2，b ＝(－1)×3＝－3，∴a ＝－2，b ＝－3. 12．已知集合A ＝{－4,2a －1，a 2}，B ＝{a －5,1－a,9}，分别求适合下列条件的a 的值．(1)9∈(A ∩B )；(2){9}＝A ∩B .解 (1)∵9∈(A ∩B )，∴9∈A 且9∈B ，∴2a －1＝9或a 2＝9，∴a ＝5或a ＝－3或a ＝3，经检验a ＝5或a ＝－3符合题意．∴a ＝5或a ＝－3.(2)∵{9}＝A ∩B ，∴9∈A 且9∈B ，由(1)知a ＝5或a ＝－3.当a ＝－3时，A ＝{－4，－7,9}，B ＝{－8,4,9}，此时A ∩B ＝{9}，当a ＝5时，A ＝{－4,9,25}，B ＝{0，－4,9}，此时A ∩B ＝{－4,9}，不合题意．∴a ＝－3.13．已知集合A ＝{x|x2－2x －3≤0，x ∈R}，B ＝{x|m －2≤x≤m ＋2}．(1)若A∩B ＝[1,3]，求实数m 的值；(2)若A ⊆∁RB ，求实数m 的取值范围．解 A ＝{x|－1≤x≤3}，B ＝{x|m －2≤x≤m ＋2}．(1)∵A∩B ＝[1,3]，∴⎩⎨⎧ m －2＝1，m ＋2≥3，得m ＝3. (2)∁RB ＝{x|x ＜m －2或x ＞m ＋2}．∵A ⊆∁RB ，∴m －2＞3或m ＋2＜－1.14．已知集合A ＝{x ∈R|ax2－3x ＋2＝0，a ∈R}．(1)若A 是空集，求a 的取值范围；(2)若A 中只有一个元素，求a 的值，并把这个元素写出来；解 集合A 是方程ax2－3x ＋2＝0在实数范围内的解组成的集合．(1)A 是空集，即方程ax2－3x ＋2＝0无解，得⎩⎨⎧ a≠0，Δ＝－32－8a<0，∴a>98.即实数a 的取值范围是(98，＋∞)．(2)当a ＝0时，方程只有一解，方程的解为x ＝23；当a≠0且Δ＝0，即a ＝98时，方程有两个相等的实数根，A 中只有一个元素43. ∴当a ＝0或a ＝98时，A 中只有一个元素，分别是23和43.。
高中数学高考第1讲 集合的概念与运算
第一章 集合与常用逻辑用语
20
(1)已知集合 A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0<x<5，x∈N}，则满足条件
A⊆C⊆B 的集合 C 的个数为
()
A．1
B．2
C．3
D．4
(2)已知集合 A＝{x|－1＜x＜3}，B＝{x|－m<x<m}，若 B⊆A，则 m 的取值范围为______．
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
24
2．已知集合 A＝{x|x2－2x－3≤0，x∈N*}，则集合 A 的真子集的个数为
()
A．7
B．8
C．15
D．16
解析：选 A．法一：A＝{x|－1≤x≤3，x∈N*}＝{1，2，3}，其真子集有：∅，{1}，{2}，
{3}，{1，2}，{1，3}，{2，3}共 7 个．
下一页
第一章 集合与常用逻辑用语
8
2．设集合 A＝{x|－2≤x≤2}，Z 为整数集，则集合 A∩Z 中元素的个数是 ( )
A．3
B．4
C．5
D．6
解析：选 C．A 中包含的整数元素有－2，－1，0，1，2，共 5 个，所以 A∩Z 中的元
素个数为 5.
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
上一页
返回导航
下一页
第一章 集合与常用逻辑用语
11
2．已知集合 A＝{x|(x－1)(x－3)<0}，B＝{x|2<x<4}，则 A∩B＝________，A∪B＝ ________，(∁RA)∪B＝________. 解析：由已知得 A＝{x|1<x<3}，B＝{x|2<x<4}， 所以 A∩B＝{x|2<x<3}，A∪B＝{x|1<x<4}，(∁RA)∪B＝{x|x≤1 或 x>2}． 答案：(2，3) (1，4) (－∞，1]∪(2，＋∞)
集合与常用逻辑语言(期中考-考点精讲)-【金典数学】复习数学考点提分课堂系列(人教版)(原卷版)
第1章集合与常用逻辑语言（考点精讲）第1章 集合与常用逻辑用语§1.1集合的概念1.集合定义：把研究的对象统称为元素，把一些元素组成的总体叫做集合. 集合三要素：确定性.互异性.无序性.2.集合的相等：只要构成两个集合的元素是一样的，就称这两个集合相等.3.元素和集合的关系：属于（a A ∈）和不属于（a A ∉）.4.常见数集：自然数集：N ，正整数集：*N 或+N ，整数集：Z ，有理数集：Q ,实数集R .5.集合的表示方法：（1）列举法：把集合的所有元素一一列举出来，并用花括号“{} ”括起来表示集合的方法叫列举法.（2）描述法：设A 是一个集合，我们把集合A 中所有具有共同特征()P x 的元素x 所组成的集合表示为{}()x A P x ∈，这种表示集合的方法称为描述法.【对点训练1】 （2021秋•福清市期中）若2{1a +∈，3，2}a ，则a 的值为( ) A ．1-或1或2B ．1-或1C ．1-或2D ．2【对点训练2】 （2021秋•福州期中）下列关系中，正确的有( ) A ．{0}∅⊆B ．{0，1}{(0,1)}=C ．Q Z ∈D ．{0}{0∈，1，2}【对点训练3】 （2021秋•仓山区校级月考）下列表示正确的个数是( )（1）0∉∅；（2）{1∅⊆，2}；（3）210{(,)|{335x y x y x y +=⎧⎫=⎨⎬-=⎩⎭，4}；（4）若A B ⊆，则A B A =．A ．0B ．1C ．2D ．3【对点训练4】 （2021秋•鼓楼区校级月考）下列集合中，表示方程组31x y x y +=⎧⎨-=⎩的解集的是( )A ．{2，1}B ．{2x =，1}y =C ．{(2,1)}D ．{(1,2)}【对点训练5】 （多选题）（2021秋•福清市校级月考）已知集合2{|1}A y y x ==+，集合2{(,)|1}B x y y x ==+，下列关系正确的是( ) A ．(1,2)B ∈B ．A B =C ．0A ∉D ．(0,0)B ∉【对点训练6】 （2021•鼓楼区校级开学）用列举法表示集合|||,0||a bx x ab a b ⎧⎫=+≠⎨⎬⎩⎭为： ．§1.2集合间的基本关系1.子集：对于两个集合A ，B ，如果集合A 中任意一个元素都是集合B 中的元素，则称集合A 是集合B 的子集，记作B A ⊆.2.真子集：如果集合B A ⊆，但存在元素B x ∈，且A x ∉，则称集合A 是集合B 的真子集.记作：集合AB(或BA ).3.空集：把不含任何元素的集合叫做空集.记作：∅.并规定：空集合是任何集合的子集.4.子集个数：如果集合A 中含有n 个元素，则集合A 有n 2个子集，21n -个真子集.【对点训练1】 （2021秋•鼓楼区校级月考）已知集合{0A =，1}，22{|1B y x y =+=，}x A ∈，则集合A 、B 的关系是( )A ．AB =B ．A B ⊆C ．B A ⊂D ．B A ⊆【对点训练2】 （2021秋•台江区校级期中）已知集合{(A x =，2)||1|(2)0y x y ++-=，x R ∈，}y R ∈，{(,)|0B x y xy =，x R ∈，}y R ∈，则( )A ．AB ∈ B ．A B ⊆C ．A B ⊇D ．A B =∅【对点训练3】 （2021春•台江区校级期末）设集合{|(3)}M x y ln x ==+，{|2}N x x =，则( ) A ．M N =B ．M N ⊆C ．N M ⊆D ．MN =∅【对点训练4】 （2021•晋安区校级开学）已知集合{1A =，2，3，4}，{2B =，4，6，8}，则A B 的真子集个数为( ) A ．1B ．2C ．3D ．4【对点训练5】 （2021秋•鼓楼区校级期中）已知a ，b R ∈，若{}2,,1,,0b a a a b a ⎧⎫=+⎨⎬⎩⎭，则20212021a b +的值为( ) A ．1-B ．0C ．1D ．1-或0【对点训练6】 （2020秋•福州期末）下列集合与集合{2A =，3}相等的是( ) A ．{(2,3)}B ．{(,)|2x y x =，3}y =C ．2{|560}x x x -+=D ．2{|90}x N x ∈-【对点训练7】 （多选题）（2021秋•连江县期中）已知集合{2M =，4}，集合{1M N ⊆，2，3，4，5}，则集合N 可以是( ) A ．{2，4}B ．{2，3，4}C ．{1，2，3，4}D ．{1，2，3，4，5}【对点训练8】 （多选题）（2021秋•鼓楼区校级期中）若集合2{|60}P x x x =+-=，{|10}S x ax =-=，且S P ⊆，则实数a 的可能取值为( ) A ．0B ．13-C ．4D ．12【对点训练9】 （2021•鼓楼区校级开学）已知集合22{|(1)7340}A a R x a ax x x =∈-+++-=，{0}A ⊆，则x 的值为 ．【对点训练10】 （2021秋•台江区校级期中）设集合{|0A x x =<或1}x ，{|}B x x a =，若B A ⊆，则实数a 的取值范围是 ．§1.3集合的基本运算1.并集：由所有属于集合A 或集合B 的元素组成的集合，称为集合集合A 是集合B 与B 的并集.记作：B A .即{},AB x x A x B =∈∈或.2.交集：由属于集合A 且属于集合B 的所有元素组成的集合，称为集合A 是集合B 与B 的交集.记作：B A .即{},AB x x A x B =∈∈且.3.补集：对于集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集， 记作:UA ,即{|,}UA x x U x U =∈∉且.【对点训练1】 （2022春•鼓楼区校级期末）已知全集U R =，集合{|112}M x Z x =∈--和{|21N x x k ==+，*}k N ∈的关系如图所示，则阴影部分表示的集合的元素共有( )A ．2个B ．3个C ．4个D ．无穷多个【对点训练2】 （2022春•福州期末）设集合{}1|11,|214x M x x N x ⎧⎫=-=<<⎨⎬⎩⎭，则(MN = )A ．{|10}x x -<B ．{|21}x x -<C ．{|11}x x -<D ．{|20}x x -<<【对点训练3】 （2022春•鼓楼区校级期末）已知集合{}2{|1},|2,A x y x B y y x x R =-==-+∈，则(AB = )A ．(-∞，2]B ．[1，2]C ．[1，2)D ．[1，)+∞【对点训练4】 （2022春•鼓楼区校级期末）已知集合{|(1)(3)0}A x Z x x =∈+-<，2{|0}B x x =>，则(AB = )A ．{0，1，2}B ．{1-，0，1，2}C ．{1-，1，2}D ．{1，2}【对点训练5】 （2022•鼓楼区校级三模）已知集合M ，N 是R 的子集，且M N ⊆，则()(RMN =⋂) A ．MB ．NC ．∅D ．R【对点训练6】 （2022•鼓楼区校级模拟）已知全集为R ，集合2{|log (1)}A x y x ==+，1|1B x x ⎧⎫=⎨⎬⎩⎭，则(RAB = )A ．{|1}x x >B ．{|01}x x <C ．{|10x x -<或1}x >D ．{|10x x -<<或1}x >【对点训练7】 （2022春•福州期末）集合{2M =，4，6，8，10}，{|16}N x x =-<<，则(MN =)A ．{2，4}B ．{2，4，6}C ．{2，4，6，8}D ．{2，4，6，8，10}【对点训练8】 （2021秋•福州期末）设集合2{|340}A x x x =--<，{|3}B x x =<，则(A B = )A ．{|1}x x <-B ．{|4}x x <C ．{|41}x x -<<D ．{|13}x x -<<【对点训练9】 （2022春•台江区校级期末）已知集合2{|0}1x A x x -=>+，3{|log 1}B x x =，则(A B =)A ．(-∞，1)(2-⋃，3]B ．(2，3]C ．(0,2)D ．(,2)-∞【对点训练10】 （2021秋•福州期末）已知集合{2A =-，1}-，2{*|20}B x N x x =∈--，则(AB =) A ．∅B ．{2-，1-，1}C ．{2-，1-，1，2}D ．{2-，1-，0，1，2}【对点训练11】 （2022春•福州期末）设集合{|24}x A x =，集合{|(1)}B x y lg x ==-，则AB 等于()A ．(1,2)B ．[2，)+∞C ．(1,)+∞D ．[1，2]【对点训练12】 （2022春•福州期末）已知集合{|2}M x y x ==-，{|23}N x x =-<<，则(MN =)A ．{|32}x x -<B ．{|32}x x -<<C ．{|22}x x -<D ．{|22}x x -<< 【对点训练13】 （2021秋•仓山区校级期中）已知集合{|}12xA x y ==-，{||3|2}B y y x ==---，则(AB = )A ．[2-，0)B ．(-∞，2]-C ．(-∞，0]D ．(,0)-∞【对点训练14】 （2021秋•鼓楼区校级期中）设全集{1U =，2，3，4，5，6，7}，{2A =，3}，{3B =，4}，则()(U A B =⋂ )A ．{1，2，5，6，7}B ．{2}C ．{3}D ．{1，4，5，6，7}【对点训练15】 （2021秋•福州期中）设全集U Z =，集合{|17A x x =<，}x Z ∈，{|21B x x k ==-，}k Z ∈，则()(U A B =⋂ ) A ．{1，2，3，4，5，6}B ．{1，3，5}C ．{2，4，6}D ．∅【提分变式1】 （2021春•福州期末）已知集合2{|2}A x x x =<，集合{|13}B x x =<<，则(AB =)A ．{|23}x x <<B ．{|12}x x <<C ．{|03}x x <<D ．{|02}x x <<【提分变式2】 （2021•鼓楼区校级模拟）集合1{|28}4xA x =，2{|log ()1}B x x a =->，若A B =∅，则a 的取值范围为( ) A ．[1-，)+∞B ．(1,)-+∞C ．[1，)+∞D ．(1,)+∞【提分变式3】 （2021春•鼓楼区校级期中）设集合{2A =，3，5}，2{|60}B x Z x x m =∈-+<，{3}A B =，则(AB = )A ．{2，3，4}B ．{1，2，3，4，5}C ．{2，3，5}D ．{2，3，4，5}【提分变式4】 （2020秋•福州期末）已知全集*{|4}U x N x =∈，集合{1A =，2}，{2B =，4}，则()(U A B =⋃ )A ．{1}B ．{1，3}C ．{1，2，3}D ．{0，1，2，3}【提分变式5】 （2021春•台江区校级期中）集合{|(1)}A x y ln x ==-，{|0}B x x =>，则(A B = )A ．(0,1)B ．(0,)+∞C ．[0，)+∞D ．(1,)+∞【提分变式6】 （2021•鼓楼区校级模拟）已知集合2{|0}A x x x =-<，{|1B x x =>或0}x <，则( ) A ．B A ⊆B ．A B ⊆C ．AB R =D ．A B =∅【提分变式7】 （2021秋•鼓楼区校级期中）已知集合{|14}A x N x =∈-，{|23}B x x =-，则(A B =)A ．[1-，3]B ．[2-，4]C ．{0，1，2，3}D ．{1，2，3}【提分变式8】 （2021秋•鼓楼区校级月考）已知全集{1U =，3，5，7，9}，集合{5A =，7}，{1U A =，2a ，||}a ，则a 的值为( )A ．3B ．3-C ．3±D ．9±【提分变式9】 （2021秋•鼓楼区校级月考）已知集合{(,)|22}M x y x y =+=，集合{(,)|4}N x y x y =-=，则MN 是( )A ．2x =，2y =-B ．(2,2)-C ．{2，2}-D ．{(2,2)}-【提分变式10】 （2021春•鼓楼区校级期中）已知集合2{|20}A x x x =-<，{|10}B x x =-，则集合(AB = )A ．{|02}x x <<B ．{|01}x x <C ．{|1}x xD ．{|12}x x <【提分变式11】 （2021秋•鼓楼区校级期中）设全集{1U =，2，3，4，5，6}，集合{2A =，3，5}，{3B =，4，6}，则()(U A B = )A ．{3}B ．{4，6}C ．{1，3，4，6}D ．{2，3，4，5，6}【提分变式12】 （2020秋•台江区校级期末）已知集合{|34}M x x =-<，2{|280}N x x x =--，则() A ．M N R =B ．{|34}MN x x =-<C ．{|24}MN x x =-D ．{|24}MN x x =-<【提分变式13】 （多选题）（2021秋•福州期中）已知全集{0U =，1，2，3，4，5，6，7}，集合{|5}A x N x =∈<，{1B =，3，5，7}，则图中阴影部分所表示的集合为( )A ．{0，2，4}B ．{2，4}C ．()U ABD ．()()U U A B【提分变式14】 （多选题）（2021秋•鼓楼区校级月考）已知全集U R =，集合A ，B 满足A B ，则下列选项正确的有 A ．AB B =B ．A B B =C ．()U A B =∅ D ．()U AB =∅【提分变式15】 （2021秋•鼓楼区校级期中）已知全集U R =，集合2{|log |2|1}A x x a =-，{|3327}x B x =<<． （1）当3a =时，求A B ；（2）在①B A ⊆；①AB ≠∅；①()A B A =⋃⋃，任选一个条件，求实数a 的取值范围．【提分变式16】 （2021秋•鼓楼区校级期中）已知集合{|28}x A x R =∈<，{|0.25x B y R y =∈=+，}x R ∈． （1）求AB ；（2）集合{|11}C x m x m =--，若集合()C AB ⊆，求实数m 的取值范围．【提分变式17】 （2021•鼓楼区校级开学）已知集合2{|32}A x y x x ==--，22{|210}B x x x m =-+-． （1）若3m =，求AB ；（2）若0m >，A B ⊆，求m 的取值范围．【提分变式18】 （2022春•福州期末）已知集合{|(2)}1A x y ln x x ==-+，{|21}B x a x a =<<+．（1）若1a =，求A B ；（2）若AB B =，求实数a 的取值范围．【提分变式19】 （2021秋•鼓楼区校级月考）设全集U R =，已知集合{|25}A x x =-，{|08}B x x =<<，{|C x x a =<或10}x >．（1）求A B ； （2）求UAB ；（3）若A C =∅，求a 的取值范围．【提分变式20】 （2021秋•鼓楼区校级月考）已知集合{|211}A x a x a =-<<+，2{|0}B x x x =-． （1）若1a =，求A B ；（2）若AB =∅，求实数a 的取值范围．【提分变式21】 （2021秋•闽侯县校级月考）已知集合3|01x A x x -⎧⎫=⎨⎬-⎩⎭，{|21}B x m x m =<<-．（1）当1m =-时，求A B ；（2）若AB A =，求实数m 的取值集合．【提分变式22】 （2020秋•福州期末）已知集合2{|(6)}A x y lg x x ==-++，集合2{|0}B x x ax =-<，(0)a >．（1）当5a =时，求A B ；（2）若AB B =，求实数a 的取值范围．【提分变式23】 （2021•晋安区校级开学）已知全集U R =，函数()3(10)f x x lg x =-+-的定义域为集合A ，集合{|57}B x x =<． （1）求集合A ； （2）求()U B A ．【提分变式24】 （2021秋•仓山区校级期中）已知集合{|17}A x x =<，{|210}B x x =<<，{|}C x x a =<，全集为实数集R ． （1）求A B ，()R A B ；（2）如果AC ≠∅，求a 的取值范围．§1.4充分条件与必要条件1.命题：可以判断真假的陈述句叫命题；2.充分条件.必要条件与充要条件如果“若p ，则q ”为真命题，是指由p 通过推理可以得出q ，我们就说由p 可以推出q ，记作p q ⇒，并且说p 是q 的充分条件，q 是p 的必要条件；如果“若p ，则q ”为假命题，那么由条件p 不能提出结论q ，记作p q ⇒/，我们就说p 不是q 的充分条件，q 不是p 的必要条件；如果“若p ，则q ”和它的逆命题“若q ，则p ”均是真命题，即既有p q ⇒，又有q p ⇒，就记作p q ⇔ 此时则p 是q 的充分条件，也是q 的必要条件，我们就说p 是q 的充分必要条件，简称为充要条件． 如果p q ⇔，那么p 与q 互为充要条件.【对点训练1】 （2022春•福州期末）“0m n >>”是22m n >的( ) A ．充分不必要条件 B ．充要条件C ．必要不充分条件D ．既不充分又不必要条件【对点训练2】 （2022春•福州期末）设a ，b R ∈，则使a b >成立的一个必要不充分条件为( ) A ．lna lnb >B ．22a b >C ．1a b >-D ．1a b >+【对点训练3】 （2022春•福州期末）“2log 5x >”的一个必要不充分条件是( ) A ．2log 10x <B ．0.5log 0.2x >C ．2x >D ．4log 35x >【对点训练4】 （2022春•台江区校级期末）设x R ∈，则“02x <<”是“230x x -<”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【对点训练5】 （2022•福州模拟）“0a b <<”是“11a b a b-<-”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件【对点训练6】 （2021秋•福州期末）“四边形是菱形”是“四边形是平行四边形”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【对点训练7】 （2019秋•福州期末）实数1a >，1b >是2a b +>的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【对点训练8】 （2021秋•台江区校级月考）已知p ：“01a <<，1b >”， q ：“()(0,1)x f x a b a a =->≠的图象不过第一象限”，则p 是q 的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件【对点训练9】 （2020秋•福州期末）设a R ∈，则“1a >”是“2a a >”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件【对点训练10】 （2020秋•福清市校级月考）已知1:12p x -，:||2q x a -<，若p 是q 的充分不必要条件，则实数a 的取值范围为( ) A ．(-∞，4]B ．[1，4]C ．(1，4]D ．(1,4)【对点训练11】 （2020秋•福州期中）24x >成立的一个充分非必要条件是( ) A ．23x >B ．||2x >C ．2xD ．3x >【对点训练12】 （2021秋•鼓楼区校级月考）已知:13p x -，22:210(0)q x x a a -+->，若p 是q ⌝的必要不充分条件，则实数a 的取值范围是 ．【对点训练13】 （2021秋•仓山区校级期中）已知集合22{|240}A x x ax a =-+-，{||25|3}B x x =->． （1）当3a =时，求AB ；（2）若“R x B ∈”是“x A ∈”的充分不必要条件，求实数a 的取值范围．【对点训练14】 （2021秋•福州期中）已知全集为R ，集合{|5}A x m x m =-<<，{|210}B x x =<． （1）若6m =，求AB ，()R A B ；（2）若“x B ∈”是“x A ∈”的充分条件，求实数m 的取值范围．【对点训练15】 （2021秋•台江区校级期中）已知函数()43f x x x -++的定义域为A ，集合{|11}B x a x a =-<<+．（1）求集合A ；（2）若全集{|5}U x x =，2a =，求UAB ；（3）若x B ∈是x A ∈的充分条件，求a 的取值范围．§1.5全称量词与存在量词1.全称量词与存在量词 （1）全称量词与全称量词命题短语“所有的”“任意一个”在逻辑中通常叫做全称量词，并用符号“∀”表示. 含有全称量词的命题，叫做全称量词命题.记为,()x p x ∀∈M .（2）存在量词与存在量词命题短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词，并用符号“∃”表示. 含有存在量词的命题，叫做存在量词命题.记为,()x p x ∃∈M . 2.全称量词命题与存在量词命题的否定（1）全称量词命题p ：,()x p x ∀∈M ，它的否定p ⌝：,().x p x ∃∈M ⌝ （2）存在量词命题p ：,()x p x ∃∈M ，它的否定p ⌝：【对点训练1】 （2021秋•福州期末）命题“0x ∀>，210x -”的否定是( ) A ．0x ∃，210x -> B ．0x ∀>，210x -> C ．0x ∃>，210x -> D ．0x ∀，210x ->【对点训练2】 （2021秋•福州期中）命题“0x ∃>，13x x+”的否定是( ) A ．0x ∃>，13x x +> B ．0x ∃，13x x + C ．0x ∀，13x x +> D ．0x ∀>，13x x+> 【对点训练3】 （2021秋•鼓楼区校级期中）命题“x Q ∀∈，210x x ++>”的否定为( ) A ．x Q ∃∈，210x x ++> B ．x Q ∀∈，210x x ++ C ．x Q ∃∈，210x x ++D ．x Q ∃∉，210x x ++【对点训练4】 （2021春•福州期末）已知命题:0P a ∃<，使得102021a +>，则命题p ⌝为( )A ．0a ∃，使得102021a + B ．0a ∀<，都有102021a +<C ．0a ∃<，使得102021a +D ．0a ∀<，都有102021a +【对点训练5】 （2020秋•福州期末）若命题0:1p x ∃<，21x <，则p ⌝为( ) A ．1x ∀<，21x B ．1x ∀<，21x <C ．01x ∃<，201x D ．01x ∃，21x < 【对点训练6】 （2021春•仓山区校级期末）已知命题:p x R ∀∈，2230ax x ++>的否定是真命题，那么实数a 的取值范围是( ) A ．13a <B ．103a< C ．13aD ．13a【对点训练7】 （2021•鼓楼区校级模拟）命题“[2x ∀∈-，)+∞，31x +”的否定为( ) A ．0[2x ∃∈-，)+∞，031x +< B ．0[2x ∃∈-，)+∞，031x +C ．0[2∀∈-，)+∞，031x +<D ．0(,2)x ∀∈-∞-，031x +【对点训练8】 （2021秋•鼓楼区校级月考）已知命题:[1p x ∀∈，)+∞，22x >，则p 的否定是 ．。
1集合的概念与运算【讲义】
第一章 集合集合是高中数学中最原始、最基础的概念，也是高中数学的起始单元，是整个高中数学的基础.它的基础性体现在：集合思想、集合语言和集合的符号在高中数学的很多章节如函数、数列、方程与不等式、立体几何与解析几何中都被广泛地使用.在高考试题和数学竞赛中，很多问题可以用集合的语言加以叙述.集合不仅是中学数学的基础，也是支撑现代数学大厦的基石之一，本章主要介绍集合思想在数学竞赛中出现的问题.§1.1 集合的概念与运算【基础知识】一．集合的有关概念1．集合：具有某些共同属性的对象的全体，称为集合.组成集合的对象叫做这个集合的元素.2．集合中元素的三个特征：确定性、互异性、无序性.3．集合的分类：无限集、有限集、空集φ.4. 集合间的关系：二．集合的运算1．交集、并集、补集和差集差集：记A 、B 是两个集合，则所有属于A 且不属于B 的元素构成的集合记作B A \.即A x B A ∈={\且}B x ∉.2.集合的运算性质(1)A A A = ,A A A = (幂等律);(2)A B B A =, A B B A =(交换律);(3))()(C B A C B A =, )()(C B A C B A =(结合律);(4))()()(C A B A C B A =,)()()(C A B A C B A =(分配律);(5)A A B A =)( ,A B A A =)( (吸收律);(6)A A C C U U =)((对合律);(7))()()(B C A C B A C U U U =, )()()(B C A C B A C U U U =(摩根律)(8))\()\()(\C A B A C B A =,)\()\()(\C A B A C B A =.3.集合的相等(1)两个集合中元素相同,即两个集合中各元素对应相等;(2)利用定义,证明两个集合互为子集;(3)若用描述法表示集合,则两个集合的属性能够相互推出(互为充要条件),即等价;(4)对于有限个元素的集合,则元素个数相等、各元素的和相等、各元素之积相等是两集合相等的必要条件.【典例精析】【例1】在集合},,2,1{n 中,任意取出一个子集,计算它的各元素之和.则所有子集的元素之和是 .〖分析〗已知},,2,1{n 的所有的子集共有n 2个.而对于},,2,1{n i ∈∀,显然},,2,1{n 中包含i 的子集与集合},,1,1,,2,1{n i i +-的子集个数相等.这就说明i 在集合},,2,1{n 的所有子集中一共出现12-n 次,即对所有的i 求和,可得).(211∑=-=n i n n i S 【解】集合},,2,1{n 的所有子集的元素之和为2)1(2)21(211+⋅=+++--n n n n n =.2)1(1-⋅+⋅n n n 〖说明〗本题的关键在于得出},,2,1{n 中包含i 的子集与集合},,1,1,,2,1{n i i +-的子集个数相等.这种一一对应的方法在集合问题以及以后的组合总是中应用非常广泛.【例2】已知集合}034|{},023|{222<+-=<++=a ax x x B x x x A 且B A ⊆,求参数a 的取值范围.〖分析〗首先确定集合A 、B,再利用B A ⊆的关系进行分类讨论.【解】由已知易求得}0)3)((|{},12|{<--=-<<-=a x a x x B x x A当0>a 时,}3|{a x a x B <<=,由B A ⊆知无解;当0=a 时,φ=B ,显然无解;当0<a 时, }3|{a x a x B <<=,由B A ⊆解得.321≤≤-a 综上知,参数a 的取值范围是]32,1[-.〖说明〗本题中,集合的定义是一个二次三项式,那么寻于集合B 要分类讨论使其取值范围数字化,才能通过条件求出参数的取值范围.【例3】已知+∈∈R y R x ,,集合}1,2,{},1,,1{2+--=---++=y y y B x x x x A .若B A =,则22y x +的值是( )A.5B.4C.25D.10【解】0)1(2≥+x ,x x x -≥++∴12,且012>++x x 及集合中元素的互异性知 x x x -≠++12,即1-≠x ,此时应有.112-->->++x x x x而+∈R y ,从而在集合B 中,.21y y y ->->+ 由B A =,得)3()2()1(12112⎪⎪⎩⎪⎪⎨⎧-=---=-+=++yx y x y x x 由(2)(3)解得2,1==y x ,代入(1)式知2,1==y x 也满足(1)式..5212222=+=+∴y x〖说明〗本题主要考查集合相等的的概念,如果两个集合中的元素个数相等,那么两个集合中对应的元素应分别相等才能保证两个集合相等.而找到这种对应关系往往是解决此类题目的关键.【例4】已知集合}|,|,0{)},lg(,,{y x B xy y x A ==.若B A =,求++++)1()1(22y x y x ……+)1(20082008y x +的值.〖分析〗从集合A=B 的关系入手,则易于解决.【解】B A = ,⎩⎨⎧=⋅⋅+=++∴0)lg(||)lg(xy xy x y x xy xy x ,根据元素的互异性,由B 知0,0≠≠y x . B ∈0 且B A =,A ∈∴0,故只有0)lg(=xy ,从而.1=xy又由A ∈1及B A =,得.1B ∈所以⎩⎨⎧==1||1x xy 或⎩⎨⎧==11y xy ,其中1==y x 与元素的互异性矛盾! 所以,1-=y x 代入得:++++)1()1(22y x y x ……+)1(20082008yx +=(2-)+2+(2-)+2+……+(2-)+2=0. 〖说明〗本题是例4的拓展,也是考查集合相等的概念,所不同的是本题利用的是集合相等的必要条件,即两个集合相等,则两个集合中,各元素之和、各元素之积及元素个数相等.这是解决本题的关键.【例5】已知A 为有限集,且*N A ⊆,满足集合A 中的所有元素之和与所有元素之积相等,写出所有这样的集合A.【解】设集合A=)1}(,,,{21>n a a a n 且n a a a <<≤211,由=+++n a a a 21n a a a ⋅⋅⋅ 21, *)(N n n a n ∈≥,得≥n na =+++n a a a 21n a a a ⋅⋅⋅ 21)!1(-≥n a n ,即)!1(-≥n n2=∴n 或3=n (事实上,当3>n 时,有)2)1()2)(1()!1(n n n n n >⋅-≥--≥-. 当2=n 时,1,2,21122121=∴<∴<+=⋅a a a a a a a ,而.2,1122≠∴+≠⋅n a a 当3=n 时,3,3213321321<⋅∴<++=⋅⋅a a a a a a a a a ,.2,121==∴a a由3332a a +=,解得.33=a综上可知,}.3,2,1{=A〖说明〗本题根据集合中元素之间的关系找到等式,从而求得集合A.在解决问题时,应注意分析题设条件中所给出的信息,根据条件建立方程或不等式进行求解.【例6】已知集合}02|{},023|{22≤+-=≤+-=a ax x x S x x x P ,若P S ⊆,求实数a 的取值组成的集合A.【解】}21|{≤≤=x x P ,设a ax x x f +-=2)(2.①当04)2(2<--=∆a a ,即10<<a 时,φ=S ,满足P S ⊆;②当04)2(2=--=∆a a ,即0=a 或1=a 时,若0=a ,则}0{=S ,不满足P S ⊆,故舍去;若1=a 时,则}1{=S ,满足P S ⊆.③当04)2(2>--=∆a a 时,满足P S ⊆等价于方程022=+-a ax x 的根介于1和2之间. 即⎪⎪⎩⎪⎪⎨⎧≥-≥-<<><⇔⎪⎪⎩⎪⎪⎨⎧≥≥<--<>∆0340121100)2(0)1(22)2(10a a a a a f f a 或φ∈⇔a . 综合①②③得10≤<a ,即所求集合A }10|{≤<=a a .〖说明〗先讨论特殊情形(S=φ),再讨论一般情形.解决本题的关键在于对∆分类讨论,确定a 的取值范围.本题可以利用数形结合的方法讨论.0>∆【例7】(2005年江苏预赛)已知平面上两个点集{(,)||1|,M x y x y x y =++≥∈R },{(,)||||1|1,,N x y x a y x y =-+-≤∈R }. 若 M N ≠∅ , 则 a 的取值范围是．【解】由题意知 M 是以原点为焦点、直线 10x y ++= 为准线的抛物线上及其凹口内侧的点集，N 是以 (,1)a 为中心的正方形及其内部的点集(如图)．考察 M N =∅ 时, a 的取值范围:令 1y =,代入方程|1|x y ++=, 得 2420x x --=，解出得2x = 所以，当211a <= 时, M N =∅ ． ………… ③令 2y =，代入方程|1|x y ++=得 2610x x --=. 解出得3x =3a >时, M N =∅ ． ………… ④因此, 综合 ③ 与 ④ 可知，当13a ≤≤，即[13a ∈ 时, M N ≠∅ ．故填[1.【例8】已知集合},,,{4321a a a a A =,},,,{24232221a a a a B =,其中4321a a a a <<<,N a a a a ∈4321,,,.若},{41a a B A = ,1041=+a a .且B A 中的所有元素之和为124,求集合A 、B.【解】 4321a a a a <<<,且},{41a a B A = ,∴211a a =,又N a ∈1,所以.11=a又1041=+a a ,可得94=a ,并且422a a =或.423a a =若922=a ,即32=a ,则有,12481931233=+++++a a 解得53=a 或63-=a (舍) 此时有}.81,25,9,1{},9,5,3,1{==B A 若923=a ,即33=a ,此时应有22=a ,则B A 中的所有元素之和为100≠124.不合题意.综上可得, }.81,25,9,1{},9,5,3,1{==B A 〖说明〗本题的难点在于依据已知条件推断集合A 、B 中元素的特征.同时上述解答中使用发分类讨论的思想.分类讨论是我们解决问题的基本手段之一,将问题分为多个部分,每一部分的难度比整体都要低,这样就使问题变得简单明了.【例9】满足条件||4|)()(|2121x x x g x g -≤-的函数)(x g 形成了一个集合M,其中R x x ∈21,,并且1,2221≤x x ,求函数)(23)(2R x x x x f y ∈-+==与集合M 的关系.〖分析〗求函数23)(2-+=x x x f 集合M 的关系,即求该函数是否属于集合M,也就是判断该函数是否满足集合M 的属性.【解】|3||||)23()23(||)()(|212122212121++⋅-=++-++=-x x x x x x x x x f x f 取65,6421==x x 时, .||4||29|)()(|212121x x x x x f x f ->-=- 由此可见,.)(M x f ∉〖说明〗本题中M 是一个关于函数的集合.判断一个函数)(x f 是否属于M,只要找至一个或几个特殊的i x 使得)(i x f 不符合M 中的条件即可证明.)(M x f ∉【例10】对集合}2008,,2,1{ 及每一个非空子集定义唯一“交替和”如下:把子集中的数按递减顺序排列,然后从最大数开始,交替地加减相继各数,如}9,6,4,2,1{的“交替和”是612469=+-+-,集合}10,7{的“交替和”是10－7=3,集合}5{的“交替和”是5等等.试求A 的所有的“交替和”的总和.并针对于集合},,2,1{n 求出所有的“交替和”.〖分析〗集合A 的非空子集共有122008-个,显然,要想逐个计算“交替和”然后相加是不可能的.必须分析“交替和”的特点,故可采用从一般到特殊的方法.如{1,2,3,4}的非空子集共有15个,共“交替和”分别为:{1} 1;{2} 2 ;{3} 3;{4} 4;{1,2} 2-1; {1,3} 3-1; {1,4} 4-1;{2,3} 3-2;{2,4} 4-2;{3,4} 4-3;{1,2,3} 3-2+1;{1,2,4} 4-2+1;{1,3,4} 4-3=1;{2,3,4} 4-3+2;{1,2,3,4} 4-3+2-1.从以上写出的“交替和”可以发现,除{4}以外,可以把{1,2,3,4}的子集分为两类:一类中包含4,另一类不包含4,并且构成这样的对应:设i A 是{1,2,3,4}中一个不含有的子集,令i A 与i A }4{相对应,显然这两个集合的“交替和”的和为4,由于这样的对应应有7对,再加上{4}的“交替和”为4,即{1,2,3.4}的所有子集的“交替和”为32.【解】集合}2008,,2,1{ 的子集中,除了集合}2008{,还有222008-个非空子集.将其分为两类:第一类是含2008的子集,第二类是不含2008的子集,这两类所含的子集个数相同.因为如果i A 是第二类的,则必有}2008{ i A 是第一类的集合;如果j B 是第一类中的集合,则j B 中除2008外,还应用1,2,……,2007中的数做其元素,即j B 中去掉2008后不是空集,且是第二类中的.于是把“成对的”集合的“交替和”求出来,都有2008,从而可得A 的所有子集的“交替和”为.2008220082008)22(2120072008⨯=+⨯- 同样可以分析},,2,1{n ,因为n 个元素集合的子集总数为n 2个(含φ,定义其“交替和”为0),其中包括最大元素n 的子集有12-n 个,不包括n 的子集的个数也是12-n 个,将两类子集一一对应(相对应的子集只差一个元素n ),设不含n 的子集“交替和”为S,则对应的含n 子集的“交替和”为S n -,两者相加和为n .故所有子集的“交替和”为.21n n ⋅-〖说明〗本题中＂退到最简＂,从特殊到一般的思想及分类讨论思想、对应思想都有所体现,这种方法在数学竞赛中是常用的方法,在学习的过程中应注意强化.【例11】一支人数是5的倍数的且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人，求这支游行队伍的人数最少是多少？〖分析〗已知游行队伍的总人数是5的倍数，那么可设总人数为n 5.“按每横排4人编队，最后差3人”，从它的反面去考虑，可理解为多1人，同样按3人、2人编队都可理解为“多1人”，显然问题转化为同余问题.n 5被4、3、2除时都余地，即15-n 是12的倍数，再由总人数不少于1000人的条件，即可求得问题的解.【解】设游行队伍的总人数为)(5+∈N n n ，则由题意知n 5分别被4、3、2除时均余1，即15-n 是4、3、2的公倍数，于是可令)(1215+∈=-N m m n ，由此可得：5112+=m n ①要使游行队伍人数最少，则式①中的m 应为最少正整数且112+m 为5的倍数，应为2.于是可令)(25+∈+=N p q m ，由此可得：512]1)25(12[51+=++⋅=p p n ，25605+≥p n ② 所以10002560≥+p ，4116≥p . 取17=p 代入②式，得10452517605=+⨯=n故游行队伍的人数最少是1045人.〖说明〗本题利用了补集思想进行求解，对于题目中含有“至少”、“至多”、“最少”、“不都”、“都”等词语，可以根据补集思想方法，从词义气反面（反义词）考虑，对原命题做部分或全部的否定，用这种方法转化命题，常常能起到化繁为简、化难为易的作用，使之寻求到解题思想或方法，实现解题的目的.【例12】设n N ∈且n ≥15，B A ,都是{1，2，3，…，n }真子集，A B φ= ，且A B ={1，2，3，…，n }.证明：A 或者B 中必有两个不同数的和为完全平方数.【证明】由题设，{1，2，3，…，n }的任何元素必属于且只属于它的真子集B A ,之一. 假设结论不真，则存在如题设的{1，2，3，…，n }的真子集B A ,，使得无论是A 还是B 中的任两个不同的数的和都不是完全平方数.不妨设1∈A ，则3∉A ，否则1+3=22，与假设矛盾，所以3∈B .同样6∉B ，所以6∈A ，这时10∉A ，，即10∈B .因n ≥15，而15或者在A 中，或者在B 中，但当15∈A 时，因1∈A ，1+15=24，矛盾；当15∈B 时，因10∈B ，于是有10+15=25，仍然矛盾.因此假设不真,即结论成立.【赛向点拨】1.高中数学的第一个内容就是集合，而集合又是数学的基础.因此，深刻理解集合的概念,熟练地进行集合运算是非常重要的.由于本节中涉及的内容较多,所以抓好概念的理解和应用尤其重要.2.集合内容几乎是每年的高考与竞赛的必考内容.一般而言,一是考查集合本身的知识;二是考查集合语言和集合思想的应用.3.对于给定的集合,要正确理解其含义,弄清元素是什么,具有怎样的性质?这是解决集合问题的前提.4.集合语言涉及数学的各个领域,所以在竞赛中,集合题是普遍而又基本的题型之一.【针对练习】(A 组)1.(2006年江苏预赛) 设在xOy 平面上，20x y ≤<，10≤≤x 所围成图形的面积为31，则集合},1),{(≤-=x y y x M }1),{(2+≥=x y y x N 的交集N M 所表示的图形面积为( ) A.31 B.32 C.1 D.34 2. (2006年陕西预赛)b a ,为实数,集合M=x x f a P ab →=:},0,{},1,{表示把集合M 中的元素x 映射到集合P 中仍为x ,则b a +的值等于( )A.1-B.0C.1D.1± 3. (2004年全国联赛)已知M={}32|),(22=+y x y x ，N={}b mx y y x +=|),(，若对于所有的R m ∈，均有,φ≠⋂N M 则b 的取值范围是 A ．[26,26-] B.（26,26-）C.（332,332-） D.[332,332-] 4. (2005年全国联赛) 记集合},6,5,4,3,2,1,0{=T },4,3,2,1,|7777{4433221=∈+++=i T a a a a a M i 将M 中的元素按从大到小的顺序排列，则第2005个数是（ ）A ．43273767575+++ B ．43272767575+++ C ．43274707171+++ D ．43273707171+++ 5. 集合A,B 的并集A ∪B={a 1,a 2,a 3}，当且仅当A≠B 时，(A,B)与(B,A)视为不同的对，则这样的(A,B)对的个数有( )A.27B.28.C.26D.256.设A={n |100≤n ≤600,n ∈N }，则集合A 中被7除余2且不能被57整除的数的个数为______________.7. 已知2{430,}A x x x x R =-+<∈,12{20,2(7)50,}x B x a x a x x R -=+-++∈且≤≤.若A B ⊆,则实数a 的取值范围是 .8. 设M={1,2,3,…,1995}，A 是M 的子集且满足条件: 当x ∈A 时,15x ∉A ，则A 中元素的个数最多是_______________.9. (2006年集训试题)设n 是正整数，集合M={1，2，…，2n }．求最小的正整数k ，使得对于M 的任何一个k 元子集，其中必有4个互不相同的元素之和等于10. 设A ＝{a |a ＝22x y -,,x y Z ∈}，求证：⑴21k -∈A (k Z ∈)； ⑵42 ()k A k Z -∉∈.11.（2006年江苏）设集合()12log 32A x x ⎧⎫⎪⎪=-≥-⎨⎬⎪⎪⎩⎭，21a B x x a ⎧⎫=>⎨⎬-⎩⎭．若A B ≠∅ ，求实数a 的取值范围．12. 以某些整数为元素的集合P 具有下列性质：①P 中的元素有正数，有负数；②P 中的元素有奇数,有偶数；③－1∉P ；④若x ，y ∈P ,则x ＋y ∈P 试判断实数0和2与集合P 的关系.(B 组)1. 设S 为满足下列条件的有理数的集合：①若a ∈S ，b ∈S ，则a +b ∈S ， S ab ∈；②对任一个有理数r ，三个关系r ∈S ，－r ∈S ，r ＝0有且仅有一个成立.证明：S 是由全体正有理数组成的集合.2．321,,S S S 为非空集合，对于1，2，3的任意一个排列k j i ,,，若j i S y S x ∈∈,，则k S y x ∈- （1）证明：三个集合中至少有两个相等.（2）三个集合中是否可能有两个集无公共元素？3．已知集合：}1|),{(},1|),{(},1|),{(22=+==+==+=y x y x C ay x y x B y ax y x A 问（1）当a 取何值时，C B A )(为含有两个元素的集合？（2）当a 取何值时，C B A )(为含有三个元素的集合？4．已知{}22(,)4470,,A x y x y x y x y R =++++=∈, {}(,)10,,B x y xy x y R ==-∈.⑴请根据自己对点到直线的距离,两条异面直线的距离中 “距离”的认识,给集合A 与B 的距离定义;⑵依据⑴中的定义求出A 与B 的距离.5.设集合=P ｛不小于３的正整数｝，定义Ｐ上的函数如下：若P n ∈，定义)(n f 为不是n 的约数的最小正整数，例如5)12(,2)7(==f f .记函数f 的值域为Ｍ.证明：.99,19M M ∉∈6．为了搞好学校的工作，全校各班级一共提了P )(+∈N P 条建议.已知有些班级提出了相同的建议，且任何两个班级都至少有一条建议相同，但没有两个班提出全部相同的建议.求证2 P个.该校的班级数不多于1。
重难点01 集合的概念与运算—2023年高考数学(原卷版)
重难点01 集合概念与运算1．集合的有关概念(1)集合中元素的三个特性：确定性、互异性、无序性。
(2)集合与元素的关系：若a属于集合A，记作a∈A；若b不属于集合A，记作b∉A。
(3)集合的表示方法：列举法、描述法、图示法。
(4)五个特定的集合：集合非负整数集(或自然数集) 正整数集整数集有理数集实数集符号N N*或N＋Z Q R 2.集合间的基本关系表示关系文字语言记法集合间的基本关系子集集合A中任意一个元素都是集合B中的元素A⊆B或B⊇A 真子集集合A是集合B的子集，并且B中至少有一个元素不属于AA⊂B或B⊃A 相等集合A中的每一个元素都是集合B中的元素，集合B中的每一个元素也都是集合A中的元素A⊆B且B⊆A⇔A＝B 空集空集是任何集合的子集∅⊆A空集是任何非空集合的真子集∅⊂B且B≠∅3.集合的三种基本运算符号表示图形表示符号语言集合的并集A∪B A∪B＝{x|x∈A，或x∈B}集合的交集 A ∩ BA ∩B ＝{x |x ∈A ，且x ∈B }集合的补集若全集为U ，则集合A 的补集为∁U A∁U A ＝{x |x ∈U ，且x ∉A }4.集合基本运算的性质 (1)A ∩A ＝A ，A ∩∅＝∅。
(2)A ∪A ＝A ，A ∪∅＝A 。
(3)A ∩(∁U A )＝∅，A ∪(∁U A )＝U ，∁U (∁U A )＝A 。
(4)A ⊆B ⇔A ∩B ＝A ⇔A ∪B ＝B ⇔∁U A ⊇∁U B ⇔A ∩(∁U B )＝∅。
2023年高考中仍将与一元二次不等式解法、一元一次不等式解法、指数、对数不等式解法结合重点考查集合的交集运算，也可能考查集合的并集、补集运算，依然放在前2题位置，难度为基础题.（建议用时：20分钟）一、单选题1.设集合{1,3,5,7}A =，{|25}B x x =≤≤，则A B =（ ）（A ）{1,3}（B ）{3,5}（C ）{5,7}（D ）{1,7}2.已知集合{}{}{}1,2,3,4,5,6,72,3,4,52,3,6,7U A B ===，，，则C U B A =（ ）A. {}1,6B. {}1,7C. {}6,7D. {}1,6,73.已知全集{}1,2,3,4,5,6,7,8U =，集合{}2,3,5,6A =，集合{}1,3,4,6,7B =，则集合UAB =A ．{}2,5B ．{}3,6C ．{}2,5,6D ．{}2,3,5,6,8 4.设集合},]2,0[,2{},21{∈==<-=x y y B x x A x 则=B A A ． [0,2] B ．(1,3) C ． [1,3) D ． (1,4)5.设集合{|(1)(2)0}A=x x x +-<,集合{|13}B x x =<<,则A BA ．{|13}x x -<<B ．{|11}x x -<<C ．{|12}x x <<D ．{|23}x x <<6.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R ，则()A C B =A.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,4 7.设集合}034|{2<+-=x x x A ，}032|{>-=x x B ，则B A = A.3(3,)2-- B.3(3,)2- C.3(1,)2 D.3(,3)28.已知集合A ={1,2,3,4,5}，B ={(x ,y )|x ∈A ,y ∈A ,x y -∈A }，则B 中所含元素的个数为A .3B .6C .8D .109.已知集合B A 、均为全集}4,3,2,1{=U 的子集，且(){4}UA B =,{1,2}B =,则UAB =A ．{3}B ．{4}C ．{3,4}D ．∅10.设集合{}1,2,4A =，{}240x x x m B =-+=．若{}1AB =，则B =A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,5 11.已知集合{}}242{60M x x N x x x =-<<=--<，，则M N ⋂=（ ）A. }{43x x -<<B. }{42x x -<<-C. }{22x x -<<D. }{23x x <<12.已知全集为R ，集合112xA x ⎧⎫⎪⎪⎛⎫=≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭，{}2|680B x x x =-+≤，则R A C B =A ．{}|0x x ≤B ．{}|24x x ≤≤C ． {}|024x x x ≤<>或D ．{}|024x x x <≤≥或13.集合{}R 25A x x =∈-≤中的最小整数为_______.14.已知集合A ＝{x |y ＝x 2}，B ＝{y |y ＝x 2}，C ＝{(x ，y )|y ＝x 2}，则A ∩B ＝________，A ∩C ＝________。
第01讲 集合(原卷版)备战2023年高考数学一轮复习精讲精练(全国通用版)
第01讲集合(精讲+精练）目录第一部分：思维导图（总览全局）第二部分：知识点精准记忆第三部分：课前自我评估测试第四部分：典型例题剖析高频考点一：集合的基本概念高频考点二：集合的基本关系高频考点三：集合的运算高频考点四：venn图的应用高频考点五：集合新定义问题第五部分：高考真题感悟第六部分：集合(精练）1、元素与集合（1）集合中元素的三个特性：确定性、互异性、无序性.（2）元素与集合的关系：属于 或 不属于，数学符号分别记为：∈和∉.（3）集合的表示方法：列举法、描述法、韦恩图（venn 图）.（4）常见数集和数学符号①确定性：给定的集合，它的元素必须是确定的；也就是说，给定一个集合，那么任何一个元素在不在这个集合中就确定了.给定集合{1,2,3,4,5}A =，可知1A ∈,在该集合中，6A ∉,不在该集合中；②互异性：一个给定集合中的元素是互不相同的；也就是说，集合中的元素是不重复出现的.集合{,,}A a b c =应满足a b c ≠≠.③无序性：组成集合的元素间没有顺序之分。
集合{1,2,3,4,5}A =和{1,3,5,2,4}B =是同一个集合. ④列举法把集合的元素一一列举出来，并用花括号“{}”括起来表示集合的方法叫做列举法.⑤描述法用集合所含元素的共同特征表示集合的方法称为描述法.具体方法是：在花括号内先写上表示这个集合元素的一般符号及取值（或变化）范围，再画一条竖线，在竖线后写出这个集合中元素所具有的共同特征.2、集合间的基本关系（1）子集（subset ）：一般地，对于两个集合A 、B ，如果集合A 中任意一个元素都是集合B 中的元素，我们就说这两个集合有包含关系，称集合A 为集合B 的子集 ，记作A B ⊆（或B A ⊇），读作“A 包含于B ”（或“B 包含A ”）.（2）真子集（proper subset ）：如果集合A B ⊆，但存在元素x B ∈，且x A ∉，我们称集合A 是集合B 的真子集，记作A B （或B A ⊃≠）.读作“A 真包含于B ”或“B 真包含A ”.（3）相等：如果集合A 是集合B 的子集（A B ⊆，且集合B 是集合A 的子集（B A ⊆），此时，集合A 与集合B 中的元素是一样的，因此，集合A 与集合B 相等，记作A B =.（4）空集的性质： 我们把不含任何元素的集合叫做空集，记作∅；∅是任何集合的子集，是任何非空集合的真子集.3、集合的基本运算（1）交集：一般地，由属于集合A 且属于集合B 的所有元素组成的集合，称为A 与B 的交集，记作A B ，即{|,}A B x x A x B =∈∈且．（2）并集：一般地，由所有属于集合A 或属于集合B 的元素组成的集合，称为A 与B 的并集，记作A B ，即{|,}A B x x A x B =∈∈或．（3）补集：对于一个集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，简称为集合A 的补集，记作U C A ，即{|,}U C A x x U x A =∈∉且．4、集合的运算性质（1）AA A =，A ∅=∅，AB B A =． （2）AA A =，A A ∅=，AB B A =． （3）()U AC A =∅，()U A C A U =，()U U C C A A =．5、高频考点结论（1）若有限集A 中有n 个元素，则A 的子集有2n 个，真子集有21n -个，非空子集有21n -个，非空真子集有22n -个．（2）空集是任何集合A 的子集，是任何非空集合B 的真子集．（3）U U A B AB A A B BC B C A ⊆⇔=⇔=⇔⊆． （4）()()()U U U C A B C A C B =,()()()U U U C A B C A C B =．一、判断题1．（2022·江西·贵溪市实验中学高二期末）集合{},,,A a b c d =的子集共有8个 ( )2．（2021·江西·贵溪市实验中学高二阶段练习）集合{}1,2,3,4,5和{}5,4,3,2,1表示同一个集合( ) 3．（2021·江西·贵溪市实验中学高三阶段练习）满足条件{}{}11,2,3M ⋃=的集合M 的个数是2个.( )4．（2021·江西·贵溪市实验中学高三阶段练习）已知集合{}20M x x x =+=∣，则1M -∈.( ) 5．（2021·江西·贵溪市实验中学高二阶段练习）满足条件{}{}11,2,3M ⋃=的集合M 的个数是3 ( )二、单选题1．（2022·广东茂名·高一期末）已知集合{}21A x y x ==+，集合{}21B y y x ==+，则A B =（ ）A ．0B ．{}|1x x ≥C ．{}|1x x ≤D ．R2．（2021·广东·佛山一中高一阶段练习）已知集合{}22,531,=-+A a a ，，{}5,9,1,4=+-B a a ，若{}4A B ⋂=，则实数a 的取值的集合为（ ）A ．{}1,2,2-B ．{}1,2C ．{}1,2-D ．{}13．（2022·河南平顶山·高三阶段练习（文））已知集合{}1A x x =>，{}260B x x x =--<，则()R A B ⋂=（ ） A ．{}13x x << B ．{}12x x << C ．{}3x x ≥ D ．{}2x x ≥4．（2022·湖南·沅陵县第一中学高二开学考试）如图所示，阴影部分表示的集合是（ ）A ．(UB ⋂)A B ．(U A ⋂)BC ．() U A B ⋂D ．(U A B )高频考点一：集合的基本概念1．（2020·重庆·一模（理））已知集合{}2|280,A x Z x x =∈+-<{}2|B x x A =∈，则B 中元素个数为 A ．4 B ．5 C ．6 D ．72．（2021·上海黄浦·一模）已知集合{}2,(R)A x x x =∈，若1A ∈，则x =___________.3．（2012·全国·一模（理））集合中含有的元素个数为 A ．4 B ．6 C ．8 D ．124．（2017·河北·武邑宏达学校模拟预测（理））集合{}2*|70,A x x x x N =-<∈，则*6|,B y N y A y ⎧⎫=∈∈⎨⎬⎩⎭中元素的个数为A ．1个B ．2个C ．3个D ．4个5．（2020·湖南·邵东市第十中学模拟预测（理））已知集合{}1,0,1A =-，(),|,,x B x y x A y A y ⎧⎫=∈∈∈⎨⎬⎩⎭N ，则集合B 中所含元素的个数为（ ）A ．3B ．4C ．6D ．96．（2021·全国·二模（理））定义集合运算：{},,A B z z xy x A y B *==∈∈，设{1,2}A =，{1,2,3}B =，则集合A B *的所有元素之和为（ ）A ．16B ．18C ．14D ．8高频考点二：集合的基本关系1．（2021·广东肇庆·模拟预测）已知集合{}3P x x =<，{}2Q x Z x =∈<，则（ ）A ．P Q ⊆B ．Q P ⊆C ．P Q P =D ．P Q Q ⋃= 2．（2020·山东·模拟预测）已知集合==2{1,},{}M x N x ，若N M ⊆，则x =__.3．（2020·江苏省如皋中学二模）设{,2}M m =，{2,2}N m m =+，且M N ，则实数m 的值是________. 4．（2021·辽宁·东北育才学校一模）所有满足{}{},,,a M a b c d ⊆的集合M 的个数为________；5．（2022·全国·模拟预测）已知集合{}213M x x =+<，{}N x x a =<，若N M ⊆，则实数a 的取值范围为（ ）A ．[)1,+∞B ．[)2,+∞C ．(],1-∞D ．(),1-∞6．（2020·广西·模拟预测）已知集合{|15}A x x =<≤，{}|04B x x =<<，{}|121C x m x m =+<<-. （1）求A B ，()R A B ⋂：（2）若B C C =，求实数m 的取值范围.7．（2020·广西·模拟预测）已知集合{|121}A x a x a =+≤≤-，{|3B x x =≤或5}x >.（1）若4a =，求A B ； （2）若A B ⊆，求a 的取值范围.高频考点三：集合的运算1．（2022·甘肃陇南·模拟预测（理））已知集合{}|321A x x =->，{}260B x x x =--<，则A B =（ ） A ．{}13x x <<B ．{}12x x <<C ．{}21x x -<<D ．{}31x x -<<2．（2022·北京丰台·一模）已知集合{|12}A x x =-<≤，{|21}B x x =-<≤，则A B ⋃=（ ）A ．{|11}x x -<<B ．{|11}x x -<≤C ．{|22}x x -<<D ．{|22}x x -<≤3．（2022·河南·模拟预测（理））已知集合{}14A x x =≤≤，(){}214B x x =-≥，则()A B =R （ ） A ．[]3,4 B ．[]1,4 C ．[)1,3 D ．[)3,+∞4．（2022·全国·模拟预测（理））设全集U =R ，集合102x A x x ⎧⎫+=≤⎨⎬-⎩⎭，集合{}ln 1B x x =≤，则A B 是（ ）A ．(]0,2B ．()2,eC ．()0,2D ．[)1,e -5．（2022·江西赣州·一模（理））设集合{}1,0,A n =-，{},,B x x a b a A b A ==⋅∈∈.若A B A =，则实数n 的值为（ ）A ．1-B ．0C ．1D ．26．（2021·江西·模拟预测）2021年是中国共产党成立100周年，电影频道推出“经典频传：看电影，学党史”系列短视频，传扬中国共产党的伟大精神，为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频，某大学社团有50人，观看了《青春之歌》的有21人，观看了《建党伟业》的有23人，观看了《开国大典》的有26人.其中，只观看了《青春之歌》和《建党伟业》的有4人，只观看了《建党伟业》和《开国大典》的有7人，只观看了《青春之歌》和《开国大典》的有6人，三支短视频全观看了的有3人，则没有观看任何一支短视频的人数为________.7．（2021·上海·模拟预测）已知集合{}2890,U x x x x Z =--≤∈，{}A y y y Z ==∈，则U A__________.高频考点四：venn 图的应用1．（2022·贵州贵阳·一模（理））若全集U 和集合A ，B 的关系如图所示，则图中阴影部分表示的集合为（ ）A ．()U AB ⋂B ．()U B AC ．()U A BD ．()U A B2．（2021·广东·模拟预测）已知全集U =R ，集合{}2,20A x yB x x x ⎧==--<⎨⎩∣∣，它们的关系如图（Venn 图）所示，则阴影部分表示的集合为（ ）A ．{12}x x -≤<∣B ．{12}xx -<<∣ C ．{12}xx ≤<∣ D ．{12}x x <<∣ 3．（2021·黑龙江·哈九中三模（理））如图，U 是全集，,,M P S 是U 的子集，则阴影部分表示的集合是（ ）A ．()M P SB ．()M P SC ．()U M P S ⋂⋂D ．()U M P S ⋂⋃4．（2021·江苏徐州·二模）某班45名学生参加“3·12”植树节活动，每位学生都参加除草､植树两项劳动.依据劳动表现，评定为“优秀”､“合格”2个等级，结果如下表：若在两个项目中都“合格”的学生最多有10人，则在两个项目中都“优秀”的人数最多为（ ）A ．5B ．10C ．15D ．205．（2020·北京市第五中学模拟预测）高二一班共有学生50人，每名学生要从物理、化学、生物、历史、地理、政治这六门课程中选择三门课程进行学习.已知选择物理、化学、生物的学生各有至少20人，这三门课程都不选的有10人，这三门课程都选的有10人，在这三门课程中选择任意两门课程的都至少有13人，物理、化学只选一科的学生都至少6人，那么选择物理和化学这两门课程的学生人数至多（ ） A ．16 B ．17 C ．18 D ．19高频考点五：集合新定义问题1．定义集合{|A B x x A -=∈ 且}x B ∉.己知集合{}Z 26U x x =∈-<<，{}0,2,4,5A =，{}1,0,3B =-，则()U A B -中元素的个数为（ ）A ．3B ．4C ．5D ．6 2．设A 、B 是非空集合，定义：{|A B x x A B ⨯=∈且}x A B ∉．已知{|A x y =，{|1}B x x =>，则A B ⨯等于（ ）A ．[0,1](2,)+∞B ．[0,1)(2,)⋃+∞C ．[0,1]D ．[0,2]3．已知集合{}1,2,3M =，(){},,,N x y x M y M x y M =∈∈+∈，则集合N 中的元素个数为（ ） A ．2 B ．3 C ．8 D ．94．已知非空集合A 、B 满足以下两个条件：（1）{}1,2,3,4,5A B =，A B =∅；（2）A 的元素个数不是A 中的元素，B 的元素个数不是B 中的元素.则有序集合对(),A B 的个数为（ ）A ．4B ．6C ．8D ．165．（多选）在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[k ]，即{}[]5k n k n Z =+∈，0,1,2,3,4k =.则下列结论正确的是（ ）A ．2011[1]∈；B ．[0][1][2][3][4]Z =⋃⋃⋃⋃；C ．3[3]-∈；D ．整数a ，b 属于同一“类”的充要条件是“[0]a b -∈”.1．（2021·山东·高考真题）假设集合{}1,2,3A =，{}1,3B =，那么A B 等于（ ）A ．{}1,2,3B ．{}1,3C ．{}1,2D ．{}22．（2021·湖南·高考真题）已知集合{}13,5A =,，{}1,2,3,4B =，且A B =（ ） A ．{}1,3B ．{}1,3,5C ．{}1,2,3,4D ．{}1,2,3,4,53．（2021·江苏·高考真题）已知集合{}1,3M =，{}1,3N a =-，若{}1,2,3MN =，则a 的值是（ ） A ．-2 B ．-1 C ．0 D ．14．（2021·天津·高考真题）设集合{}{}{}1,0,11,3,5,0,2,4A B C =-==，，则()A B C ⋂⋃=（ ） A ．{}0 B ．{0,1,3,5} C ．{0,1,2,4} D ．{0,2,3,4} 5．（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()U A B =（ ） A ．{3} B ．{1,6} C ．{5,6} D ．{1,3} 6．（2021·浙江·高考真题）设集合{}1A x x =≥，{}12B x x =-<<，则A B =（ ） A ．{}1x x >- B ．{}1x x ≥ C ．{}11x x -<< D ．{}12x x ≤<7．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （ ）A ．∅B ．SC ．TD ．Z一、单选题1．（2021·北大附中云南实验学校高一阶段练习）下列各对象可以组成集合的是（ ）A ．与1非常接近的全体实数B ．北大附中云南实验学校20202021-学年度第二学期全体高一学生C ．高一年级视力比较好的同学D ．高一年级很有才华的老师2．（2022··模拟预测（理））已知集合A ={}250x x x -≤，B ={}21,x x k k Z =-∈，则A B 中元素的个数为（ ）A ．2B ．3C ．4D ．53．（2022·贵州毕节·模拟预测（理））已知集合(){}10A x x x =-=，{}20,,B m m =，若A B B ⋃=，则m =（ ）A ．1-B ．0C ．1D ．±14．（2022·全国·模拟预测）已知集合{}1,2,3,4,5,6A =，6,1B x x A x ⎧⎫=∈∈⎨⎬-⎩⎭N ，则集合B 的子集的个数是（ ）A ．3B ．4C ．8D ．165．（2022·湖南·长沙一中高三阶段练习）集合1,36n M x x n Z ⎧⎫==+∈⎨⎬⎩⎭，1,63n N x x n Z ⎧⎫==+∈⎨⎬⎩⎭，则M N =（ ）A ．MB ．NC ．∅D ．,6n x x n Z ⎧⎫=∈⎨⎬⎩⎭6．（2022·广东·高二期末）集合{}2230A x x x =--=，{}10B x mx =+=，A B A ⋃=，则m 的取值范围是（ ）A ．11,3⎧⎫-⎨⎬⎩⎭B ．{}1,3-C ．10,3⎧⎫-⎨⎬⎩⎭D ．10,1,3⎧⎫-⎨⎬⎩⎭7．（2022·湖南·长郡中学高二阶段练习）已知集合(){}2ln 4A x y x ==-，{B y x =，则A B =（ ） A ．()2,3B ．()(],22,3-∞-C ．()0,3D ．(]2,3 8．（2022·河南·温县第一高级中学高三阶段练习（理））已知集合102x A x x ⎧⎫-=≤⎨⎬+⎩⎭，B ={-2，-1，0，1}，则A ∩B =（ ）A ．{-2，-1，0，1}B ．{-1，0，1}C ．{-1，0}D ．{-2，-1，0}二、填空题9．（2022·四川·雅安中学高一阶段练习）集合{|13},{|25}A x x B x x =∈<≤=∈<<Z Z ，则A B 的子集的个数为___________.10．（2022·上海金山·高一期末）满足条件：{}a {},,,M a b c d ⊆的集合M 的个数为______.11．（2022·全国·高三专题练习）已知集合{}2{123},280A x a x a B x x x =-<<+=--≤，若()R A B A ⋂=，求实数a 的取值范围是___________.12．（2022·全国·高三专题练习）设集合{}2280A x x x =-->，{B x x a =≤或}5x a ≥+，若()R A B ⋂=∅，则a 的取值范围是___________.三、解答题13．（2022·山西·榆次一中高一开学考试）已知集合{}22150M x x x =--≤，{}N x m x m =-≤≤．(1)当1m =时，求M N ⋂以及()()R R M N ⋃；(2)若M N ，求实数m 的取值范围．14．（2022·江苏省天一中学高一期末）集合1121x A x x +⎧⎫=>⎨⎬-⎩⎭，{}22240B x x ax a =-+-<. (1)若{}23,4,23C a a =+-，()0B C ∈，求实数a 的值；(2)从条件①②③这三个条件中选择一个作为已知条件，求实数a 的取值范围.条件：①A B A =；②()R A B ⋂=∅；③()R B A R ⋃=.（注：答题前先说明选择哪个条件，如果选择多于一条件分别解答，按第一个解答计分）.15．（2022·江西·赣州市赣县第三中学高一开学考试）已知集合{}2430A x x x =++=，{}22230B x x ax a a =-+--=. (1)若1a =，求A B ；(2)若A B A ⋃=，求a 的取值集合.16．（2022·江苏·高一）已知集合A 为非空数集，定义：{},,S x x a b a b A ==+∈，{},,T x x a b a b A ==-∈.(1)若集合{}1,3A =，直接写出集合S 、T ；(2)若集合{}1234,,,A x x x x =，且T A =，写出一个满足条件的集合A ，并说明理由；(3)若集合{}02020,A x x x N ⊆≤≤∈，S T ⋂=∅，记A 为集合A 中元素的个数，求A 的最大值.。
(复习指导)第一章第一讲 集合的概念与运算含答案
第一章集合与常用逻辑用语第一讲集合的概念与运算知识梳理·双基自测ZHI SHI SHU LI SHUANG JI ZI CE知识梳理知识点一集合的基本概念一组对象的总体构成一个集合．(1)集合中元素的三大特征：确定性、互异性、无序性．(2)集合中元素与集合的关系：对于元素a与集合A，a∈A或a∉A，二者必居其一．(3)常见集合的符号表示.数集自然数集正整数集整数集有理数集实数集符号N N*Z Q R(4)集合的表示法：列举法、描述法、Venn图法、区间表示法．(5)集合的分类：集合按元素个数的多少分为有限集、无限集，有限集常用列举法表示，无限集常用描述法表示．知识点二集合之间的基本关系关系定义表示相等集合A与集合B中的所有元素都相同A＝B子集A中的任意一个元素都是B中的元素A⊆B真子集A是B的子集，且B中至少有一个元素不属于A A B注意：(1)空集用∅表示．(2)若集合A中含有n个元素，则其子集个数为2n，真子集个数为2n－1，非空真子集的个数为2n－2．(3)空集是任何集合的子集，是任何非空集合的真子集．(4)若A⊆B，B⊆C，则A⊆C．知识点三集合的基本运算符号语言交集A∩B 并集A∪B 补集∁U A图形语言意义A∩B＝{x|x∈A且x∈B}A∪B＝{x|x∈A或x∈B}∁U A＝{x|x∈U且x∉A}重要结论1．A∩A＝A，A∩∅＝∅.2．A∪A＝A，A∪∅＝A．3．A∩(∁U A)＝∅，A∪(∁U A)＝U，∁U(∁U A)＝A．4．A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁U A⊇∁U B⇔A∩(∁U B)＝∅.双基自测题组一走出误区1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)集合A中含有三个元素0，1，x，且x2∈A，则实数x的值为1或－1或0.(×)(2){x|y＝x2}＝{y|y＝x2}＝{(x，y)|y＝x2}．(×)(3)方程x －2 022＋(y＋2 023)2＝0的解集为{2 022，－2 023}．(×)(4)若A∩B＝A∩C，则B＝C．(×)(5)设U＝R，A＝{x|lg x<1}，则∁U A＝{x|lg x≥1}＝{x|x≥10}．(×)题组二走进教材2．(必修1P 5B1改编)若集合P＝{x∈N|x≤ 2 022}，a＝45，则(D)A．a∈P B．{a}∈PC．{a}⊆P D．a∉P[解析]452＝2 025>2 022，∴a∉P，故选D．3．(必修1P7T3(2)改编)若A＝{x|x＝4k－1，k∈Z}，B＝{x＝2k－1，k∈Z}，则集合A与B 的关系是(B)A．A＝B B．A BC．A B D．B⊆A[解析]因为集合B＝{x|x＝2k－1，k∈Z}，A＝{x|x＝4k－1，k∈Z}＝{x|x＝2(2k)－1，k∈Z}，集合B表示2与整数的积减1的集合，集合A表示2与偶数的积减1的集合，所以A B，故选B．题组三走向高考4．(2020·新高考Ⅱ，1，5分)设集合A＝{2，3，5，7}，B＝{1，2，3，5，8}，则A∩B ＝(C)A．{1，8} B．{2，5}C．{2，3，5} D．{1，2，3，5，7，8}[解析]∵A＝{2，3，5，7}，B＝{1，2，3，5，8}，∴A∩B＝{2，3，5}，故选C．5．(2020·新高考Ⅰ，1，5分)设集合A ＝{x |1≤x ≤3}，B ＝{x |2<x <4}，则A ∪B ＝( C ) A ．{x |2<x ≤3} B ．{x |2≤x ≤3} C ．{x |1≤x <4}D ．{x |1<x <4}[解析] 已知A ＝{x |1≤x ≤3}，B ＝{x |2<x <4}，在数轴上表示出两个集合，由图易知A ∪B ＝{x |1≤x <4}．故选C ．6．(2020·天津，1，5分)设全集U ＝{－3，－2，－1，0，1，2，3}，集合A ＝{－1，0，1，2}，B ＝{－3，0，2，3}，则A ∩(∁U B )＝( C )A ．{－3，3}B ．{0，2}C ．{－1，1}D ．{－3，－2，－1，1，3}[解析] 因为U ＝{－3，－2，－1，0，1，2，3}，B ＝{－3，0，2，3}，所以∁U B ＝{－2，－1，1}，又A ＝{－1，0，1，2}，所以A ∩(∁U B )＝{－1，1}，故选C ．考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU 考点一 集合的基本概念——自主练透例1 (1)(多选题)已知集合A ＝{x |x ＝3k ＋1，k ∈Z }，则下列表示正确的是( ABD )A ．－2∈AB ．2 022∉AC ．3k 2＋1∉AD ．－35∈A(2)已知集合A ＝{0，1，2}，则集合B ＝{(x ，y )|x ≥y ，x ∈A ，y ∈A }中元素的个数是( C ) A ．1 B ．3 C ．6D ．9(3)已知集合A ＝{a ＋2，(a ＋1)2，a 2＋3a ＋3}，若1∈A ，则2 020a 的值为1；若1∉A ，则a 不可能取得的值为－2，－1，0，－1＋52，－1－52．[解析] (1)当－2＝3k ＋1时，k ＝－1∈Z ，故A 正确；当2 022＝3k ＋1时，k ＝67323∉Z ，故B 正确；∵k ∈Z ，∴k 2∈Z ，显然3k 2＋1∈A ，当－35＝3k ＋1时，k ＝－12∈Z ，故D 正确．故选A 、B 、D ．(2)当x ＝0时，y ＝0；当x ＝1时，y ＝0或y ＝1； 当x ＝2时，y ＝0，1，2.故集合B ＝{(0，0)，(1，0)，(1，1)，(2，0)，(2，1)，(2，2)}， 即集合B 中有6个元素．(3)若a ＋2＝1，则a ＝－1，A ＝{1，0，1}，不合题意；若(a ＋1)2＝1，则a ＝0或－2，当a ＝0时，A ＝{2，1，3}，当a ＝－2时，A ＝{0，1，1}，不合题意；若a 2＋3a ＋3＝1，则a ＝－1或－2，显然都不合题意；因此a ＝0，所以2 0200＝1.∵1∉A ，∴a ＋2≠1，∴a ≠－1；(a ＋1)2≠1，解得a ≠0，－2；a 2＋3a ＋3≠1解得a ≠－1，－2.又∵a ＋2、(a ＋1)2、a 2＋3a ＋3互不相等，∴a ＋2≠(a ＋1)2得a ≠－1±52；a ＋2≠a 2＋3a＋3得a ≠－1；(a ＋1)2≠a 2＋3a ＋3得a ≠－2；综上a 的值不可以为－2，－1，0，－1＋52，－1－52.名师点拨 MING SHI DIAN BO(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集还是其他类型的集合．(2)集合中元素的互异性常常容易忽略，特别是含有字母的集合，在求出字母的值后，要注意检验集合中元素是否满足互异性．分类讨论的思想方法常用于解决集合问题．考点二 集合之间的基本关系——师生共研例2 (1)(2021·新高考八省联考)已知M ，N 均为R 的子集，且∁R M ⊆N ，则M ∪(∁R N )＝( B )A ．∅B ．MC ．ND ．R(2)(多选题)已知集合A ＝⎩⎨⎧⎭⎬⎫－13，12，B ＝{x |ax ＋1＝0}，且B ⊆A ，则实数a 的可能取值为( BCD )A ．－3B ．－2C ．0D ．3(3)设集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝k 3＋16，k ∈Z ，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k 6＋23，k ∈Z ，则下面正确的是( B ) A ．M ＝N B ．MNC ．NMD ．M ∩N ＝∅[解析] (1)如图，∁R M ⊆N ，显然(∁R N )⊆M ，∴M ∪(∁R N )＝M ，故选B ．(2)本题考查集合之间的关系．由题知B ⊆A ，B ＝{x |ax ＋1＝0}，所以B ＝⎩⎨⎧⎭⎬⎫－13，⎩⎨⎧⎭⎬⎫12，∅.当B ＝⎩⎨⎧⎭⎬⎫－13时，－13a ＋1＝0，解得a ＝3；当B ＝⎩⎨⎧⎭⎬⎫12时，12a ＋1＝0，解得a ＝－2；当B ＝∅时，a ＝0.综上可得实数a 的可能取值为3，0，－2，故选B 、C 、D ．(3)解法一：(列举法)，由题意知 M ＝⎩⎨⎧⎭⎬⎫…，－12，－16，16，12，56，76，…N ＝⎩⎨⎧⎭⎬⎫…，－16，0，16，13，12，23，56，…显然M N ，故选B ．解法二：(描述法) M ＝⎩⎨⎧⎭⎬⎫x |x ＝2k ＋16，k ∈Z ，N ＝⎩⎨⎧⎭⎬⎫x |x ＝k ＋46，k ∈Z∵2k ＋1表示所有奇数，而k ＋4表示所有整数(k ∈Z ) ∴MN ，故选B ．名师点拨 MING SHI DIAN BO 判断集合间关系的3种方法 列举法根据题中限定条件把集合元素表示出来，然后比较集合元素的异同，从而找出集合之间的关系．(如第(3)题解法一)结构法从元素的结构特点入手，结合通分、化简、变形等技巧，从元素结构上找差异进行判断．(如第(3)题解法二)数轴法在同一个数轴上表示出两个集合，比较端点之间的大小关系，从而确定集合与集合之间的关系.(1)集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝n 2＋1，n ∈Z ，N ＝⎩⎨⎧⎭⎬⎫y |y ＝m ＋12，m ∈Z ，则两集合M ，N 的关系为( D )A ．M ∩N ＝∅B ．M ＝NC ．M ⊆ND ．N ⊆M(2)(多选题)(2020·湖南长郡中学模拟改编)已知集合M ＝{y |y ＝x －|x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫y |y ＝⎝⎛⎭⎫12x ，x ∈R ，则下列结论不正确的是( ABD ) A ．M ＝N B ．N ⊆M C ．M ＝∁R ND ．(∁R N )∩M ＝∅(3)已知集合A ＝{x ∈R |x 2－3x ＋2＝0}，B ＝{x ∈N |0<x <5}，则满足条件A ⊆C ⊆B 的集合C 的个数为4．(4)已知集合A ＝{x |x 2－2 023x ＋2 022<0}，B ＝{x |x <a }，若A ⊆B ，则实数a 的取值范围是[2_022，＋∞)．[解析] (1)由题意，对于集合M ，当n 为偶数时，设n ＝2k (k ∈Z )，则x ＝k ＋1(k ∈Z )，当n 为奇数时，设n ＝2k ＋1(k ∈Z )，则x ＝k ＋1＋12(k ∈Z )，∴N ⊆M ，故选D ．(2)由题意得y ＝x －|x |＝⎩⎪⎨⎪⎧0，x ≥0，2x ，x <0，∴M ＝(－∞，0]，N ＝(0，＋∞)，∴M ＝∁R N .故选A 、B 、D ． (3)由题意可得，A ＝{1，2}，B ＝{1，2，3，4}．又∵A ⊆C ⊆B ，∴C ＝{1，2}或{1，2，3}或{1，2，4}或{1，2，3，4}，∴有4个． (4)由x 2－2 023x ＋2 022<0，解得1<x <2 022， 故A ＝{x |1<x <2 022}．又B ＝{x |x <a }，A ⊆B ，如图所示，可得a ≥2 022.考点三 集合的基本运算——多维探究 角度1 集合的运算例3 (1)(2020·课标Ⅱ)已知集合U ＝{－2，－1，0，1，2，3}，A ＝{－1，0，1}，B ＝{1，2}，则∁U (A ∪B )＝( A )A ．{－2，3}B ．{－2，2，3}C ．{－2，－1，0，3}D ．{－2，－1，0，2，3}(2)(2020·课标Ⅱ)已知集合A ＝{x ||x |<3，x ∈Z }，B ＝{x ||x |>1，x ∈Z }，则A ∩B ＝( D ) A ．∅B ．{－3，－2，2，3}C ．{－2，0，2}D ．{－2，2}(3)(2021·浙江杭州模拟)已知全集U ＝R ，集合A ＝{x |x 2－3x ＋2<0}，集合B ＝ {x |log 3(x ＋1) <1}，则A ∪B ＝(－1，2)，( ∁R A )∩B ＝(－1，1]．[解析] (1)∵A ＝{－1，0，1}，B ＝{1，2}，∴A ∪B ＝{－1，0，1，2}，又∵集合U ＝{－2，－1，0，1，2，3}，∴∁U (A ∪B )＝{－2，3}．故选A ．(2)由已知得A ＝{x |－3<x <3，x ∈Z }＝{－2，－1，0，1，2}，B ＝{x |x <－1或x >1，x ∈Z }，∴A ∩B ＝{－2，2}．故选D ．(3)依题意可知，A ＝{x |1<x <2}，B ＝{x |0<x ＋1<3}＝{x |－1<x <2}，所以A ∪B ＝(－1，2)，∁R A ＝{x |x ≤1或x ≥2}，所以(∁R A )∩B ＝(－1，1]．角度2 利用集合的运算求参数例4 (1)已知集合A ＝{x |x 2－3x <0)，B ＝{1，a }，且A ∩B 有4个子集，则实数a的取值范围是( B )A ．(0，3)B ．(0，1)∪(1，3)C ．(0，1)D ．(－∞，1)∪(3，＋∞)(2)已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}≠∅，若A ∩B ＝B ，则实数m 的取值范围为[2，3]．[解析] (1)因为A ∩B 有4个子集，所以A ∩B 中有2个不同的元素，所以a ∈A ，所以a 2－3a <0，解得0<a <3.又a ≠1，所以实数a 的取值范围是(0，1)∪(1，3)，故选B ．(2)由A ∩B ＝B 知，B ⊆A ．又B ≠∅，则⎩⎪⎨⎪⎧2m －1≥m ＋1，m ＋1≥－2，2m －1≤5.解得2≤m ≤3，则实数m 的取值范围为[2，3]．[引申1]本例(2)中若B ＝{x |m ＋1≤x ≤2m －1}情况又如何？ [解析] 应对B ＝∅和B ≠∅进行分类． ①若B ＝∅，则2m －1<m ＋1，此时m <2. ②若B ≠∅，由例得2≤m ≤3.由①②可得，符合题意的实数m 的取值范围为(－∞，3]．[引申2]本例(2)中是否存在实数m ，使A ∪B ＝B ？若存在，求实数m 的取值范围；若不存在，请说明理由．[解析] 由A ∪B ＝B ，即A ⊆B 得⎩⎪⎨⎪⎧m ＋1≤－2，2m －1≥5，即⎩⎪⎨⎪⎧m ≤－3，m ≥3，不等式组无解，故不存在实数m ，使A ∪B ＝B ． [引申3]本例(2)中，若B ＝{x |m ＋1≤x ≤1－2m }，AB ，则m 的取值范围为(－∞，－3]．[解析] 由题意可知⎩⎪⎨⎪⎧m ＋1≤－2，1－2m ≥5，解得m ≤－3.名师点拨 MING SHI DIAN BO集合的基本运算的关注点1．集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的前提． 2．有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了，易于解决．3．注意数形结合思想的应用，常用的数形结合形式有数轴、坐标系和Venn 图． 4．根据集合运算结果求参数，先把符号语言译成文字语言，然后应用数形结合求解． 〔变式训练2〕(1)(角度1)(2020·北京，1，4分)已知集合A ＝{－1，0，1，2}，B ＝{x |0<x <3}，则A ∩B ＝( D )A ．{－1，0，1}B ．{0，1}C ．{－1，1，2}D ．{1，2}(2)(角度1)设全集U ＝R ，集合A ＝{x |0≤x ≤2}，B ＝{y |1≤y ≤3}，则(∁U A )∪B ＝( D ) A ．(2，3] B ．(－∞，1]∪(2，＋∞) C ．[1，2)D ．(－∞，0)∪[1，＋∞)(3)(角度2)已知集合A ＝{x |x <a }，B ＝{x |x 2－3x ＋2<0}，若A ∩B ＝B ，则实数a 的取值范围是( D )A ．a <1B ．a ≤1C ．a >2D ．a ≥2[解析] (1)集合A 与集合B 的公共元素为1，2，由交集的定义知A ∩B ＝{1，2}，故选D ． (2)∁U A ＝{x |x <0或x >2}，则(∁U A )∪B ＝{x |x <0或x ≥1}，故选D ．(3)集合B ＝{x |x 2－3x ＋2<0}＝{x |1<x <2}，由A ∩B ＝B 可得B ⊆A ，作出数轴如图，可知a ≥2.名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG集合中的新定义问题例5 定义集合的商集运算为A B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝m n ，m ∈A ，n ∈B ，已知集合A ＝{2，4，6}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k 2－1，k ∈A ，则集合⎝⎛⎭⎫B A ∪B 中的元素个数为( B ) A ．6 B ．7 C ．8D ．9[解析] 由题意知，B ＝{0，1，2}，B A ＝⎩⎨⎧⎭⎬⎫0，16，14，13，12，1，则⎝⎛⎭⎫B A ∪B ＝⎩⎨⎧⎭⎬⎫0，16，14，13，12，1，2，共有7个元素．名师点拨 MING SHI DIAN BO集合新定义问题的“3定”(1)定元素：确定已知集合中所含的元素，利用列举法写出所有元素．(2)定运算：根据要求及新定义运算，将所求解集合的运算问题转化为集合的交集、并集与补集的基本运算问题，或转化为数的有关运算问题．(3)定结果：根据定义的运算进行求解，利用列举法或描述法写出所求集合中的所有元素． 〔变式训练3〕(2021·江西九江联)设A ，B 是非空集合，定义A ⊗B ＝{x |x ∈(A ∪B )且x ∉(A ∩B )}．已知M ＝{y |y ＝－x 2＋2x ，0<x <2}，N ＝{y |y ＝2x －1，x >0}，则M ⊗N ＝⎝⎛⎦⎤0，12∪(1，＋∞) [解析] M ＝{y |y ＝－x 2＋2x ，0<x <2}＝(0，1]，N ＝{y |y ＝2x －1，x >0}＝⎝⎛⎭⎫12，＋∞，则M ∪N ＝(0，＋∞)，M ∩N ＝⎝⎛⎦⎤12，1，所以M ⊗N ＝⎝⎛⎦⎤0，12∪(1，＋∞)．。
01第一讲：集合的概念与运算
第一讲：集合的概念与运算一、知识梳理：1． 集合的含义与表示：（1） 一般地，我们把研究对象统称为__________，把一些元素组成的总体叫做____________（简称______）.（2） 集合中元素的三个性质：____________,__________,___________. （3）集合中元素与集合的关系分为____________和____________两种，分别用__________和_________表示. （4） 几种常用集合的表示法：数集 自然数集正整数集整数集有理数集 实数集 表示（5） 集合的三种表示法：___________,____________,_______________. 2． 集合间的基本关系：（1）B ⊆的含义是：__________________________________________. （2）若集合B A ⊆且A B ⊆，我们就说____________________________. （3）若集合B A ⊆且B A ≠，则称__________________记着___________. 即若B A ⊆，但存在B x ∈0，且A x ∉0。
（4）不含任何元素的集合叫做________，记为_______，并规定：空集是任何集合的子集，空集是任何非空集合的真子集。
3．集合的基本运算：（1）B A ⋃的含义是__________________________________________. （2）B A ⋂的含义是_______ _____________________________. （3）如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为__________________，通常记作________________.（4）对于一个集合A ，由全集U 中___________________的所有元素组成的集合称为集合A 相对于全集U 的补集，记作________________. 即________________________________=C U 。
第1讲 集合的概念与运算学生(新高一培优十六讲系列)
第1讲 集合的概念与运算[玩前必备]1.元素与集合的概念(1)集合：研究的对象统称为元素，把一些元素组成的总体叫作集合. (2)集合元素的特性：确定性、互异性. 2.元素与集合的关系(1)空集：不含任何元素的集合，记作∅.(2)非空集合：①有限集：含有有限个元素的集合. ②无限集：含有无限个元素的集合. 4.常用数集的表示符号 把有限集合中的所有元素都列举出来，写在花括号“{__}”内表示这个集合的方法. 6.描述法(1)集合的特征性质如果在集合I 中，属于集合A 的任意一个元素x 都具有性质p (x )，而不属于集合A 的元素都不具有性质p (x )，则性质p (x )叫做集合A 的一个特征性质. (2)特征性质描述法集合A 可以用它的特征性质p (x )描述为{x ∈I |p(x )}，它表示集合A 是由集合I 中具有性质p (x )的所有元素构成的.这种表示集合的方法，叫做特征性质描述法，简称描述法. 7.集合间的基本关系A B(或B A)8.集合的运算(1)如果一个集合包含了我们所要研究的各个集合的全部元素，这样的集合就称为全集，全集通常用字母U表示；[玩转典例]题型一集合的基本概念例1(大纲全国，1) 设集合A＝{1，2，3}，B＝{4，5}，M＝{x|x＝a＋b，a∈A，b∈B}，则M中元素的个数为()A.3B.4C.5D.6例2 已知集合A＝{m＋2,2m2＋m}，若3∈A，则m的值为________．[玩转跟踪]1.(新课标全国，1)已知集合A＝{1，2，3，4，5}，B＝{(x，y)|x∈A，y∈A，x－y∈A}，则B 中所含元素的个数为()A.3B.6C.8D.102.已知集合A是由a－2,2a2＋5a,12三个元素组成的，且－3∈A，求实数a.3.(探究与创新)设A 为实数集，且满足条件：若a ∈A ，则11－a∈A (a ≠1).求证： (1)若2∈A ，则A 中必还有另外两个元素； (2)集合A 不可能是单元素集.题型二 集合的表示方法例3 下面三个集合：A ＝{x |y ＝x 2＋1}；B ＝{y |y ＝x 2＋1}；C ＝{(x ，y )|y ＝x 2＋1}. 问：(1)它们是不是相同的集合？ (2)它们各自的含义是什么？例4 已知集合A ＝{x ∈R |ax 2＋2x ＋1＝0}，其中a ∈R .若1是集合A 中的一个元素，请用列举法表示集合A .[玩转跟踪]1.已知x ，y 为非零实数，则集合M ＝⎩⎨⎧m |m ＝x |x |＋y |y |＋⎭⎬⎫xy |xy |为( )A.{0,3}B.{1,3}C.{－1,3}D.{1，－3}2.(探究与创新)已知集合A ＝{x |ax 2－3x －4＝0，x ∈R }： (1)若A 中有两个元素，求实数a 的取值范围； (2)若A 中至多有一个元素，求实数a 的取值范围.题型三 集合间的基本关系例5 (2013·江苏，4)集合{－1，0，1}共有________个子集.例6 设集合⎭⎬⎫⎩⎨⎧∈+==Z k k x x M ，412|，⎭⎬⎫⎩⎨⎧∈+==Z k k x x N ，421|，则( ) A ．N M =B ．NM C ．MN D ．=N M I例7 已知集合A ＝{x |－3≤x ≤4}，B ＝{x |2m －1＜x ＜m ＋1}，且B ⊆A . 求实数m 的取值范围.[玩转跟踪]1.设M 为非空的数集，M ⊆{1,2,3}，且M 中至少含有一个奇数元素，则这样的集合M 共有( ) A ．6个B ．5个C ．4个D ．3个2.(2016·山东北镇中学、莱芜一中、德州一中4月联考)定义集合A －B ＝{x |x ∈A 且x ∉B },若集合M ＝{1,2,3,4,5},集合N ＝{x |x ＝2k －1,k ∈Z },则集合M －N 的子集个数为( ) A.2 B.3C.4D.无数个3.已有集合A ＝{x |x 2－4x ＋3＝0}，B ＝{x |mx －3＝0}，且B ⊆A ，求实数m 的集合.题型四 集合的基本运算例8 (2016·全国Ⅰ,1)设集合A ＝{x |x 2－4x ＋3<0},B ＝{x |2x －3>0},则A ∩B ＝( ) A.⎝⎛⎭⎫－3，－32 B.⎝⎛⎭⎫－3，32 C.⎝⎛⎭⎫1，32 D.⎝⎛⎭⎫32，3 例9 (2015·四川,1)设集合A ＝{x |(x ＋1)(x －2)＜0},集合B ＝{x |1＜x ＜3},则A ∪B ＝( ) A ．{x |－1＜x ＜3} B ．{x |－1＜x ＜1} C ．{x |1＜x ＜2} D ．{x |2＜x ＜3} 例10 (1)设全集U ＝R ，A ＝{x |x (x ＋3)<0}，B ＝{x |x <－1}，则图中阴影部分表示的集合为( )A ．{x |－3<x <－1}B ．{x |－3<x <0}C ．{x |－1≤x ＜0}D ．{x |x <－3}(2).(2011·江西，2)若集合A ＝{x |－1≤2x ＋1≤3}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x －2x ≤0，则A ∩B ＝( )A.{x |－1≤x ＜0}B.{x |0<x ≤1}∅C.{x |0≤x ≤2}D.{x |0≤x ≤1}例11 已知A ＝{x |2a ≤x ≤a ＋3}，B ＝{x |x ＜－1，或x ＞5}，若A ∩B ＝∅，求实数a 的取值范围.[玩转跟踪]1.(2016·安徽安庆市第二次模拟)若集合P ＝{x ||x |＜3,且x ∈Z },Q ＝{x |x (x －3)≤0,且x ∈N },则P ∩Q 等于( )A.{0,1,2}B.{1,2,3}C.{1,2}D.{0,1,2,3}2.如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是( )A.(M ∩P )∩SB.(M ∩P )∪SC.(M ∩P )∩(∁I S )D.(M ∩P )∪(∁I S )3.(探究与创新)已知集合A ＝{x |－2≤x ≤5}，B ＝{x |2a ≤x ≤a ＋3}，若A ∪B ＝A ，求实数a 的取值范围.[玩转练习]1．已知集合A ＝{y |y ＝|x |－1，x ∈R }，B ＝{x |x ≥2}，则下列结论正确的是( ) A ．－3∈A B ．3∉B C ．A ∩B ＝BD ．A ∪B ＝B2．设集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪1x<2，则下列结论中正确的是( ) A ．N M B ．M N C ．N ∩M ＝∅D ．M ∪N ＝R3．(2018·全国Ⅱ)已知集合A ＝{(x ，y )|x 2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为() A ．9 B ．8 C ．5 D ．44.(2018·济南模拟)设全集U ＝R ，集合A ＝{x |x －1≤0}，集合B ＝{x |x 2－x －6<0}，则右图中阴影部分表示的集合为( )A ．{x |x <3}B ．{x |－3<x ≤1}C ．{x |x <2}D ．{x |－2<x ≤1}5．(2018·潍坊模拟)设集合A ＝N ，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x x －3≤0，则A ∩B 等于( )A ．[0,3)B ．{1,2}C ．{0,1,2}D ．{0,1,2,3}6．(2017·全国Ⅱ)设集合A ＝{1,2,4}，B ＝{x |x 2－4x ＋m ＝0}．若A ∩B ＝{1}，则B 等于( ) A ．{1，－3} B ．{1,0} C ．{1,3} D ．{1,5}7．已知集合A ＝{x |－1<x <0}，B ＝{x |x ≤a }，若A ⊆B ，则a 的取值范围为( ) A ．(－∞，0] B ．[0，＋∞) C ．(－∞，0)D ．(0，＋∞)8.满足{a ，b }∪B ＝{a ，b ，c }的集合B 的个数是________.9.设集合A ＝{－1,1,3}，B ＝{a ＋2，a 2＋4}，A ∩B ＝{3}，则实数a 的值为________. 10.已知集合M ＝{－2,3x 2＋3x －4，x 2＋x －4}，若2∈M ，则满足条件的实数x 组成的集合为________.11.已知全集I ＝{2,3，a 2＋2a －3}，若A ＝{b,2}，∁I A ＝{5}，求实数a ，b .12.已知A ＝{x |x 2－3x ＋2＝0}，B ＝{x |ax －2＝0}，且A ∪B ＝A ，求实数a 组成的集合C .13.设全集为R ，集合A ＝{x |3≤x ＜6}，B ＝{x |2＜x ＜9}. (1)分别求A ∩B ，(∁R B )∪A ；(2)已知C ＝{x |a ＜x ＜a ＋1}，若C ⊆B ，求实数a 的取值构成的集合.14.已知集合A ＝{x |0＜x －a ≤5}，B ＝{x |－a2＜x ≤6}.(1)若A∩B＝A，求a的取值范围；(2)若A∪B＝A，求a的取值范围.。
第1讲集合的概念及运算
（2）设I为全集，S1,S2,S3是I的三个非空 子集，且S1∪S2∪S3=I,则下面论断正确 的是( C )
A. IS1∩(S2∪S3) B.S1 ( IS2∩ IS3) C IS1∩ IS2 ∩ IS3= D.S1 ( IS2∪ IS3)
分析
集合的运算→优先化简→数形结合， 按交、并、补、子集概念依次进行.
A B(或B A).
A A; A; 若A B,B C, 则A C;
有n个元素的集合 的子集的个数是
⑥ 2n .
定义
性质与说明
如果A是B的子集，且B中 空集是任何非空集合的
至少有一个元素不属于A， 真子集；
那么集合A是集合B的真子
真 子
集，记为A B(或B A).
集
若A B,B C,则A C;
补集等于两个集合的补集的并集，可 利用这个知识点直接解决本题.
(2)元素与集合的关系有两种：
① 属于“∈” ,
②
.
(3)集合中元素的性质： ③ 确定性、互异性、无序性 .
(4)集合的表示法： ④ 列举法、描述法、图示法、区；间法
(5)集合的分类：按元素个数可分为 ⑤ 空集、有限集、无限集； .
(6)两个集合A与B之间的关系：
定义
性质与说明
子集
如果集合A的任何一 个元素都是集合B的 元素，那么集合A叫 集合B的子集，记为
第1讲
集合的概念及运算
理解集合、子集、真子集、交集、 并集、补集的概念，了解全集、空集、 属于、包含、相等关系的意义，掌握有 关的术语和符号，能使用韦恩图表达集 合的关系及运算.
知识要点
1.集合的有关概念
(1)一般的，某些指定的对象集中在一起 就构成了一个集合，集合中的每个对 象叫这个集合的元素.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第 1 讲：集合的概念与运算一、课程标准1、通过实例，了解集合的含义，体会元素与集合的“属于”关系．2、.理解集合之间包含与相等的含义，能识别给定集合的子集．了解全集与空集的含义．3、.理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集．4、.理解在给定集合中一个子集的补集的含义，会求给定子集的补集．二、基础知识回顾1、元素与集合(1)集合中元素的三个特性：确定性、互异性、无序性。
(2)元素与集合的关系是属于或不属于，表示符号分别为∈和∉。
2、集合间的基本关系(1)子集：若对任意x∈A，都有x∈B，则A⊆B或B⊇A。
(2)真子集：若A⊆B，且集合B中至少有一个元素不属于集合A，则A B或B A。
(3)相等：若A⊆B，且B⊆A，则A＝B。
(4)空集的性质：∅是任何集合的子集，是任何非空集合的真子集。
3、集合的基本运算(1)交集：一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集，记作A∩B，即A∩B＝{x|x∈A，且x∈B}．(2)并集：一般地，由所有属于集合A或属于集合B的元素组成的集合，称为A与B的并集，记作A∪B，即A∪B＝{x|x∈A，或x∈B}．(3)补集：对于一个集合A，由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集，简称为集合A的补集，记作∁U A，即∁U A＝{x|x∈U，且x∉A}．4、集合的运算性质(1)A∩A＝A，A∩∅＝∅，A∩B＝B∩A。
(2)A∪A＝A，A∪∅＝A，A∪B＝B∪A。
A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁U A⊇∁U B(3)A∩(∁U A)＝∅，A∪(∁U A)＝U，∁U(∁U A)＝A。
（4）∁U(A∩B)＝(∁U A)∪(∁U B)，∁U(A∪B)＝(∁U A)∩(∁U B)。
5、相关结论：(1)若有限集A 中有n 个元素，则A 的子集有2n 个，真子集有2n －1个。
(2)不含任何元素的集合．空集是任何集合A 的子集，是任何非空集合B 的真子集．记作∅.三、自主热身、归纳总结1、已知集合A ＝{1,3,5,7}，B ＝{2,3，4,5}，则A ∩B ＝( )A ．{3}B ．{5}C ．{3,5}D ．{1,2,3,4,5,7}2、已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝( )A.{x |x ≥0}B.{x |x ≤1}C.{x |0≤x ≤1}D.{x |0<x <1}3、已知集合A ＝{x |x 2－2x －3≤0}，B ＝{x |0<x ≤4}，则A ∪B ＝( )A ．[－1,4]B ．(0,3]C ．(－1,0]∪(1,4]D ．[－1,0]∪(1,4]4、已知集合A ＝{1，2，3}，B ＝{y |y ＝2x －1，x ∈A }，则A ∩B ＝________.5、已知集合A ＝{x |x 2－2x ＋a >0}，且1∉A ，则实数a 的取值范围是________.6、（多选题）已知全集U R =，集合A ，B 满足A B ，则下列选项正确的有( ) A ．A B B = B ．A B B = C ．()U A B =∅ D ．()U A B =∅7、（多选题）已知集合[2A =，5)，(,)B a =+∞．若A B ⊆，则实数a 的值可能是( )A ．3-B ．1C ．2D ．5四、例题选讲、变式突破考点一 集合的基本概念例1、已知集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈Z ⎪⎪⎪ x ＋1x －2≤0，则集合A 的子集的个数为( ) A ． 7 B ． 8 C ． 15 D ．16【变式1】若集合A ＝{x ∈R |ax 2－3x ＋2＝0}中只有一个元素，则a ＝( )A.92 B.98 C.0 D.0或98【变式2】设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝( )A ．1B ．－1C ．2D ．－2【变式3】已知P ＝{x |2<x <k ，x ∈N }，若集合P 中恰有3个元素，则k 的取值范围为________． 方法总结：1.研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义。
2.利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合中的元素是否满足互异性。
特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性考点2、集合间的基本关系例2、已知集合M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ x ＝k π4＋π4，k ∈Z ，集合N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k π8－π4，k ∈Z ，则( ) A ．M ∩N ＝∅B ．M ⊆NC ．N ⊆MD ．M ∪N ＝M例3、已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1<x <2m －1}，若B ⊆A ，则实数m 的取值范围是________.【变式】已知集合A ＝{x |－1<x <3}，B ＝{x |－m <x <m }，若B ⊆A ，则m 的取值范围为________．方法总结(1)若B ⊆A ，应分B ＝∅和B ≠∅两种情况讨论.(2)已知两个集合间的关系求参数时，关键是将两个集合间的关系转化为元素或区间端点间的关系，进而转化为参数满足的关系.解决这类问题常常要合理利用数轴、Venn 图，化抽象为直观进行求解.考点三：集合的运算例4、若集合A ＝{x |2x 2－9x ＞0}，B ＝{y |y ≥2}，则A ∩B ＝________，(∁R A )∪B ＝________.【变式1】设集合A ＝⎩⎨⎧⎭⎬⎫x ∈N |14≤2x ≤16，B ＝{x |y ＝ln(x 2－3x )}，则A ∩B 中元素的个数是________.【变式2】已知集合M ＝{x |－4<x <2}，N ＝{x |x 2－x －6<0}，则M ∩N ＝( )A ．{x |－4<x <3}B ．{x |－4<x <－2}C ．{x |－2<x <2}D ．{x |2<x <3}【变式3】已知集合A ＝{x |x 2－x －2>0}，则∁R A ＝( )A ．{x |－1<x <2}B ．{x |－1≤x ≤2}C ．{x |x <－1}∪{x |x >2}D ．{x |x ≤－1}∪{x |x ≥2}方法总结：集合运算的常用方法①若集合中的元素是离散的，常用Venn 图求解；②若集合中的元素是连续的实数，则用数轴表示，此时要注意端点的情况．例5、设集合A ＝{0，－4}，B ＝{x |x 2＋2(a ＋1)x ＋a 2－1＝0，x ∈R}．若A ∩B ＝B ，则实数a 的取值范围是________．【变式】已知集合A ＝{1,2}，B ＝{x |x 2＋mx ＋1＝0，x ∈R }，若B ⊆A ，则实数m 的取值范围为________． 方法总结：利用集合的运算求参数的值或取值范围的方法①与不等式有关的集合，一般利用数轴解决，要注意端点值能否取到；②若集合能一一列举，则一般先用观察法得到不同集合中元素之间的关系，再列方程(组)求解．考点五：集合的新定义问题例6、.若x ∈A ，则1x ∈A ，就称A 是伙伴关系集合，集合M ＝⎩⎨⎧⎭⎬⎫－1，0，12，2，3的所有非空子集中具有伙伴关系的集合的个数是( )A.1B.3C.7D.31【变式】．给定集合A ，若对于任意a ，b ∈A ，有a ＋b ∈A ，且a －b ∈A ，则称集合A 为闭集合，给出如下三个结论：①集合A ＝{－4，－2,0,2,4}为闭集合；②集合A ＝{n |n ＝3k ，k ∈Z }为闭集合；③若集合A 1，A 2为闭集合，则A 1∪A 2为闭集合．其中正确结论的序号是________．方法总结：正确理解新定义：耐心阅读，分析含义，准确提取信息是解决这类问题的前提，剥去新定义、新法则、新运算的外表，利用所学的集合性质等知识将陌生的集合转化为我们熟悉的集合，是解决这类问题的突破口。
五、优化提升与真题演练1、设集合A ＝{x |x 2－4x ＋3<0}，B ＝{x |2x －3>0}，则A ∩B ＝________.A.⎝⎛⎭⎫－3，－32B.⎝⎛⎭⎫－3，32C.⎝⎛⎭⎫1，32D.⎝⎛⎭⎫32，32、设全集U ＝{x |x ∈N *，x <6}，集合A ＝{1，3}，B ＝{3，5}，则∁U (A ∪B )等于( )A.{1，4}B.{1，5}C.{2，5}D.{2，4}3、已知集合，，则（ ）A ．B ．C ．D ．4、若全集0，1，，，则A ．B ．C ．D ．1，5、已知集合，则（ ）A ．B ．C ．D ．6、设集合，则(A ∩C )∪B ＝（ ） A ． B ．C ．D ．7、已知集合A ＝{x |x －1≥0}，B ＝{0，1，2}，则A ∩B ＝( )A.{0}B.{1}C.{1，2}D.{0，1，2}8、已知集合M ＝{(x ，y )|y ＝f (x )}，若对于任意实数对(x 1，y 1)∈M ，都存在(x 2，y 2)∈M ，使得x 1x 2＋y 1y 2＝0成立，则称集合M 是“垂直对点集”．给出下列四个集合：①M ＝⎩⎨⎧⎭⎬⎫x ，y b\lc|\rc (a\vs4al\co1(y ＝1x ))；②M ＝{(x ，y )|y ＝log 2x }；③M ＝{(x ，y )|y ＝e x －2}；④M ＝{(x ，y )|y ＝sin x ＋1}．其中是“垂直对点集”的序号是( )A ．①④B ．②③C ．③④D ．②④9、（多选题）已知{A =第一象限角}，{B =锐角}，{C =小于90︒的角}，那么A 、B 、C 关系是( )2{2}A x x x =5{|1}3B x x =+<A B =20,3⎛⎫⎪⎝⎭(,2)-∞(0.)+∞2,23⎛⎫ ⎪⎝⎭2{1,0,1,2},{|1}A B x x =-=≤A B ⋂={}1,0,1-{}0,1{}1,1-{}0,1,2{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R {}2{}2,3{}1,2,3-{}1,2,3,4A ．B AC = B ．B C C = C ．B A B =D ．A B C ==10、已知集合A ＝{(x ，y )|x ，y ∈R ，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y ∈R ，且y ＝x }，则A ∩B 的元素个数为________.11、.集合A ＝{x |x <0}，B ＝{x |y ＝lg[x (x ＋1)]}，若A －B ＝{x |x ∈A ，且x ∉B }，则A －B ＝________. 12、已知集合A ＝{x ∈R ||x ＋2|<3}，集合B ＝{x ∈R |(x －m )(x －2)<0}，且A ∩B ＝(－1，n )，则m ＋n ＝________. 13（2019年江苏高考）、已知集合{1,0,1,6}A =-，{|0,}B x x x =>∈R ，则A B =_____. 14（2018年江苏高考）、.已知集合{}0,1,2,8A =，{}1,1,6,8B =-，那么A B ⋂=________．。