点击2010年江苏高考数学卷第12题
2010江苏高考数学试卷(完整版)
①设动点P满足 ,求点P的轨迹
②设 ，求点T的坐标
③设 ,求证：直线MN必过x轴上的一定点
（其坐标与m无关）
点评人： 刘新春 （江苏省扬中高级中学 教授级高级教师 特级教师） 王宛璐 俞银娟
19．（16分）设各项均为正数的数列 的前n项和为 ，已知 ，数列 是公差为 的等差数列.
①求数列 的通项公式（用 表示）
②设 为实数，对满足 的任意正整数 ，不等式 都成立。求证： 的最大值为
20.（16分）设 使定义在区间 上的函数，其导函数为 .如果存在实数 和函数 ，其中 对任意的 都有 >0，使得 ，则称函数 具有性质 .
新华网：2010江苏高考首日回顾：语文有陷阱 数学都说难
区分度高：有考生哭着出来
■考生的话：很难很棘手
考生们对今年数学考题的评价，集中为一个字，就是：难！甚至有考生是哭着走出考场的。
“看起来似乎简单，但要下手得分却很难。”29中的魏同学连连叹气。梅园中学的杨同学告诉记者：“第19、20题把大家都难住了。很多同学连这两题的题目都来不及看清楚。”题目难，时间也不够。“最后一题根本就来不及看，更别谈做了。”南京田家炳中学的陈同学告诉记者。至于附加题，考生们却反映和前面的大题相比，难度反而小了。
三、立意高远，注重创新。
许多试题立意高远，情境新颖，设问灵活，层次清晰，注重创新。如第8题将函数、导数、数列结合在知识交汇点命题。第10题将正弦、余弦、正切函数的图像结合，求交点间的距离。第12题条件设置类似线性规划，运用不等式性质求最大值。第14、17、18、20题构思巧妙，采取结论开放、探究发现、自主定义概念等方式表述条件与结论。
江苏2010年高考数学试卷(含答案、解析)
h(x) >0， 使得 f '(x) = h(x)(x 2 − ax + 1) ，则称函数 f (x) 具有性质 P(a) . (1)设函数 f (x) = h(x) + b + 2 (x > 1) ，其中 b 为实数
x +1 ①求证：函数 f (x) 具有性质 P(b)
求函数 f (x) 的单调区间
（1）估计该问题目有错，似乎为 f (x) = ln x + b + 2 (x > 1) ，则有如下解答： x +1
①
f
'( x)
=
1 x
−
b+2 (x + 1)2
=
1 x(x +1)2
(x2
− bx +1)
∵
x
> 1 时， h(x) =
1 x(x + 1)2
> 0 恒成立，
∴函数 f (x) 具有性质 P(b) ；
20)
(x
−
3(m2 − 20) )
m2 + 20
,
m2 + 80 m2 + 20
化简得
y
+
20 m2 + 20
=
−
10 m2 − 40
(x
−
3(m2 − 20) m2 + 20 )
令 y = 0 ，解得 x = 1 ，即直线 MN 过 x 轴上定点 (1,0) 。
{ } 19．（16 分）设各项均为正数的数列 {an }的前 n 项和为 Sn ，已知 2a2 = a1 + a3 ，数列 Sn 是公差为 d 的等差数列.
2010年高考江苏省数学卷试题解法集锦
tan A = 2 . t an C = - t an( A + B ) = - t an 2 A 图1 = - 2t an A = 2 2. 1 - t an2 A 所以 t an C + t an C = 4. t an A t an B 解法 2 ( 将角 全部化 归为边 ) 将 co s C = a2 + b2 - c2 代入 b + a = 6co s C, 并变形得 2( a2 2ab a b 2 2 + b ) = 3c . tan C tan C sin C co s A sin Ccos B + = + t an A t an B sin A co s C sin B co s C 2 2 2 2 2 2 c b + c - a c c + a - b 2 bc 2ca = + a 2 + b 2 - c2 a 2 + b2 - c2 a b 2 ab 2ab 2 2 2 c 2 c = 2 = 4. 2 2 = a + b - c 3 c2 - c2 2 解法 3 ( 将边全部化归为角) 因为 6cos C = 2 2 b + a = sin B + sin A = sin A + sin B , a b sin A sin B sin A sin B 于是 6sin A sin B cos C = sin2 A + sin2 B . 因 a 2 + b 2 = c2 + 2 ab cos C, 故 sin 2 A + sin2 B 2 = sin C + 2sin A sin B co s C, 2 于是 sin C = 4sin A sin B co s C. tan C + t an C = sin C ( cos A + cos B ) = tan B cos C sin A sin B t an A 2 sin C sin( A + B) = sin C = 4. cos C sin A sin B sin A sin B cos C b a 解法 4 ( 将边与角部分进行转化) 因 + a b = 6co s C, 故 a2 + b2 = 6ab cos C. 2 2 2 2 因 a + b = c + 2 ab cos C, 故 c = 4ab cos C. 1 ( sin C cos A + 则 t an C + t an C = t an A t an B co s C sin A sin C 1 c b2 + c2 - a 2 c cos B ) = ( + sin B cos C a 2 bc b 2 2 2 2 c + a - b ) = c = 4. 2ca ab co s C 解法 5 如图 2, 作 A D ∃ BC 交 BC 于 D , 则 a = BD + DC = ccos B + bcos C, 于是 a = c b b cos B + cos C.
2010年普通高等学校招生全国统一考试数学试题(江苏卷)(含答案)
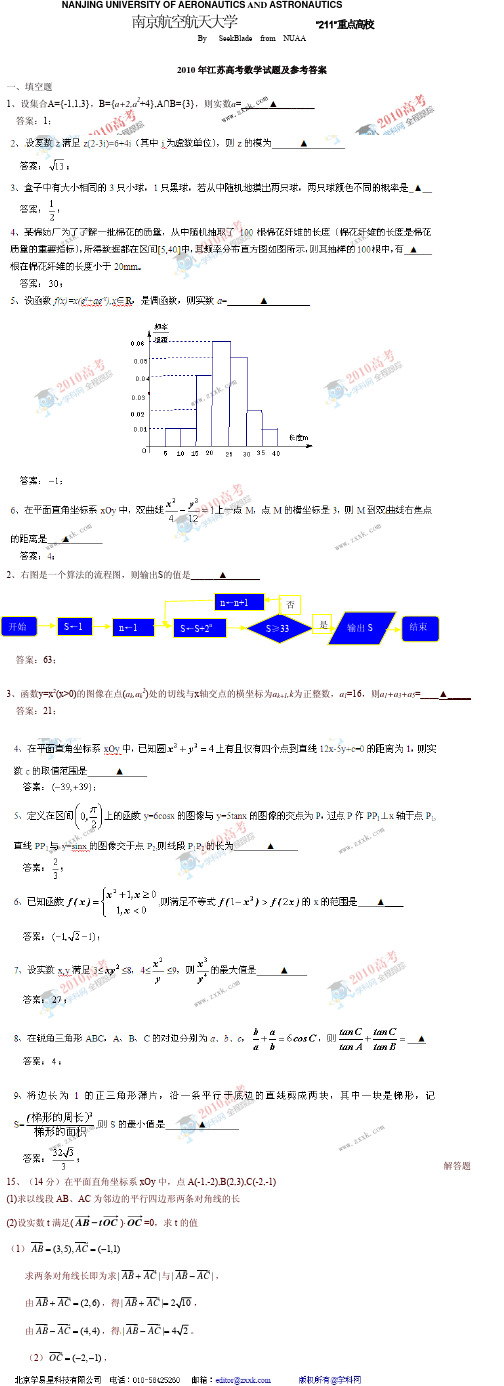
2010年江苏高考数学试题及参考答案一、填空题1、设集合A={-1,1,3}，B={a+2,a2+4},A∩B={3}，则实数a=______▲________ 答案：1；2、右图是一个算法的流程图，则输出S的值是______▲_______答案：63；3、函数y=x 2(x>0)的图像在点(a k ,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数，a 1=16，则a 1+a 3+a 5=____▲_____答案：21；解答题15、（14分）在平面直角坐标系xOy 中，点A(-1,-2),B(2,3),C(-2,-1)(1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长(2)设实数t 满足(OC t AB -)·OC =0，求t 的值（1）(3,5),(1,1)AB AC ==-求两条对角线长即为求||AB AC + 与||AB AC - ，由(2,6)AB AC +=，得||AB AC +=由(4,4)AB AC -=，得||AB AC -=（2）(2,1)O C =-- ，∵(OC t AB -)·OC 2AB OC tOC =- ，易求11AB OC =- ，25OC = ， 所以由(OC t AB -)·OC =0得115t =-。
16、（14分）如图，四棱锥P-ABCD 中，PD⊥平面ABCD ，PD=DC=BC=1,AB=2,AB∥DC，∠BCD=900(1)求证：PC⊥BC(2)求点A 到平面PBC 的距离D CB APE（1）∵PD⊥平面ABCD ，∴PD BC ⊥，又BC C D ⊥，∴B C ⊥面P C D ，∴BC PC ⊥。
（2）设点A 到平面PBC 的距离为h ，∵A PBC P ABC V V --=,∴1133PBC ABC S h S PD ⋅=容易求出h =17、（14分）某兴趣小组测量电视塔AE 的高度H(单位m ），如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=α，∠ADE=β(1)该小组已经测得一组α、β的值，tan α=1.24,tan β=1.20,,请据此算出H 的值(2)该小组分析若干测得的数据后，发现适当调整标杆到电视塔的距离d （单位m ），使α与β之差较大，可以提高测量精确度，若电视塔实际高度为125m ，问d 为多少时，α-β最大（1）∵tan AE AB α=，tan AE AD β=，∴tan 31tan 30A D A B αβ== （2）。
2010年江苏高考数学试题 参考答案
2010 年江苏高考数学试题
参考答案
第 4 页 共 5 页
（2）依题意，至少需要生产 3 件一等品
3 P C4 0.83 0.2 0.84 0.8192
答：利润不少于 10 万元的概率是 0.8192.
23、 （1）设三边长分别为 a , b, c ， cos A 为
b2 c2 a 2 ，∵ a , b, c 是有理数， a , b, c 均可表示 2bc
1 cos(n 1) Acos A {cos[(n 1) A A] cos[(n 1) A A]} 2 ∴ cos nA 2cos(n 1) A cos A cos(n 2) A ，
∵cosA， cos 2 A 是有理数，∴ cos 3 A 是有理数，∴ cos 4 A 是有理数，……，依次类推， 当 cos(n 1) A,cos(n 2) A 为有理数时， cos nA 必为有理数。
b2 c2 a 2 q q （ p, q 为互质的整数）形式∴ 必能表示为 （ p, q 为互质的整数）形式， 2bc p p
∴cosA 是有理数 （2）∵ cos 2 A 2cos 2 A 1 ，∴ cos 2 A 也是有理数， 当 n 3 时，∵ cos nA cos(n 1) A cos A sin(n 1) A sin A
2010 年江苏高考数学试题
1、1 2、 3、 10、 4、30 11、 5、-1
参考答案
6、4 12、27 7、63 13、4 8、21 14、
9、 （+39，-39）
15、 （1） AB (3,5), AC (1,1) 求两条对角线长即为求 | AB AC | 与 | AB AC | ， 由 AB AC (2,6) ，得 | AB AC | 2 10 ， 由 AB AC (4,4) ，得 | AB AC | 4 2 。 （2） OC (2, 1) ， ∵( AB t OC )· OC AB OC tOC ，
2010年江苏高考数学试题(含答案详解
2010 年普通高等学校招生全国统一考试江苏卷数学全解全析数学Ⅰ试题注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共 4 页，包含填空题（第 1 题——第14 题）、解答题（第15 题——第20 题）。
本卷满分160 分，考试时间为120 分钟。
考试结束后，请将本卷和答题卡一并交回。
2.答题前，请您务必将自己的姓名、准考证号用0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4.请在答题卡上按照晤顺序在对应的答题区域内作答，在其他位置作答一律无效。
作答必须用0.5毫米黑色墨水的签字笔。
请注意字体工整，笔迹清楚。
5.如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗。
6.请保持答题卡卡面清洁，不要折叠、破损。
参考公式：锥体的体积公式 : V1h 是高。
锥体= Sh，其中 S 是锥体的底面积，3一、填空题：本大题共14 小题，每小题 5 分，共 70分。
请把答案填写在答题卡相应的位．．．．．．．置上 .．．1、设集合 A={-1,1,3}，B={a+2,a 2+4},A ∩ B={3} ，则实数 a=______▲ _____.[ 解析 ] 考查集合的运算推理。
3B, a+2=3, a=1.2、设复数 z 满足 z(2-3i)=6+4i （其中 i 为虚数单位），则 z 的模为 ______ ▲_____.[ 解析 ] 考查复数运算、模的性质。
z(2-3i)=2(3+2 i), 2-3i与 3+2 i 的模相等， z 的模为 2。
3、盒子中有大小相同的 3 只白球， 1 只黑球，若从中随机地摸出两只球，两只球颜色不同的概率是 _ ▲ __.[ 解析 ] 考查古典概型知识。
p316 24、某棉纺厂为了了解一批棉花的质量，从中随机抽取了 100 根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标），所得数据都在区间[5,40] 中，其频率分布直方图如图所示，则其抽样的100 根中，有 _▲ ___根在棉花纤维的长度小于20mm。
2010年普通高等学校招生全国统一考试数学（江苏卷）（附答案-完全）
2010年普通高等学校招生全国统一考试（江苏卷）数学Ⅰ试题参考公式：锥体的体积公式：13V Sh 锥体，其中S 是锥体的底面面积，h 是高.一、填空题：本大题共14小题，每小题5分，共计70分.请把答案填写在答题卡相应位置上．．．．．．．．.1.设集合{1,1,3}A，4,22aa B ，3BA ，则实数a 的值为____▲____.1.【答案】1.【命题意图】本题考查交集的定义，对求得的集合中的元素要进行检验.【解析】由题意得1,32a a .又由342a不符合题意.经检验得1a.2.设复数z 满足(23)64z i i （i 为虚数单位），则z 的模为____▲____.2.【答案】2.【命题意图】本题考查复数有关运算及复数模的计算.【解析】由i i z 46)32(得,2)32)(32()32)(46(3246i i i i i ii z即2,2z i z.3.盒子里共有大小相同的3只白球，1只黑球.若从中随机摸出两只球，则它们颜色不同的概率是_ ▲__.3.【答案】21.【命题意图】本题考查古典概型知识.【解析】31.62p4.某棉纺厂为了解一批棉花的质量，从中随机抽测了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标).所得数据均在区间[5,40]中，其频率分布直方图如图所示，则在抽测的100根中，有_ ▲__ 根棉花纤维的长度小于20mm.4.【答案】30.【命题意图】本题考查概率统计中频率分布直方图的有关运用,注意纵坐标是频率/组距.【解析】由频率分布直方图得棉花纤维长度小于mm 20的根数为(0.01+0.01+0.04)301005.5.设函数()()xxf x x eae (x R )是偶函数，则实数a 的值为____▲____.5.【答案】1.【命题意图】本题考查函数的奇偶性.【解析】设R xae e x g x x ,)(,由题意分析)(x g 应为奇函数(奇函数奇函数=偶函数),又R x ，0)0(g ，则,01a 所以1a .6.在平面直角坐标系xOy 中，已知双曲线221412xy上一点M 的横坐标为3，则点M 到此双曲线的右焦点的距离为____▲____. 6.【答案】4.【命题意图】本题考查求曲线上点的坐标、双曲线的焦点坐标、两点间距离公式的运用.【解析】由题意得点15,3(M ),双曲线的右焦点的坐标为(4,0)，2MF 22)015()43(=4.或用第二定义：2MF ed，2d，4MF .7.右图是一个算法流程图，则输出的S 的值是____▲____.7.【答案】63.【命题意图】本题考查算法流程图,由流程图得出S 的关系式,比较得出S 的值.【解析】由流程图得12345122222S =1+2+48+16+32=6333,即.63S 8.函数2(0)y x x的图象在点2(,)k ka a 处的切线与x 轴的交点的横坐标为1k a ，其中kN *.若116a ，则123a a a 的值是____▲____.8.【答案】21.【命题意图】考查函数的切线方程、数列的通项.【解析】在点2(,)k k a a 处的切线方程为22(),k k k y a a xa 当0y时，解得2k a x，所以1135,1641212kka a a a a .9.在平面直角坐标系xOy 中，已知圆224x y上有且只有四个点到直线1250x y c 的距离为1，则实数c 的取值范围是____▲____. 9.【答案】(13,13).【命题意图】本题考查直线与圆的位置关系.【解析】如图,圆422yx的半径为2,圆上有且仅有四个点到直线的距离为1,问题转化为原点(0,0)到直线0512cyx 的距离小于1,即1313,13,151222c c c .10.设定义在区间(0,)2上的函数y=6cosx 的图象与y=5tanx 的图象交于点P ，过点P 作x 轴的垂线，垂足为P 1，直线PP 1与函数y=sinx 的图像交于点P 2，则线段P 1P 2的长为____▲____.10.【答案】.32【命题意图】本题考查三角函数问题,由图象相交,即三角函数值相等,建立关系式,求出,32sin x结合图象,数形结合分析P 1P 2的值.xyO 0512cyx1 11【解析】由题意得x x tan 5cos 6，即x x xx xsin 5cos 6,cos sin 5cos 62，226(1sin )5sin ,6sin 5sin 60x x x x 得,32sin x结合图象分析得32sin 21P P x.11.已知函数21,0,()1,0,xx f x x则满足不等式2(1)(2)f x f x 的x 的取值范围是____▲____.11.【答案】).12,1(【命题意图】本题考查分段函数的单调性.【解析】2212,10,x x x解得121x ，所以x 的取值范围是).12,1(12.设x,y 为实数，满足3≤2xy ≤8，4≤2xy≤9，则34xy 的最大值是____▲____. 12.【答案】27.【命题意图】考查不等式的基本性质，等价转化思想.【解析】22()[16,81]xy，2111[,]83xy，322421()[2,27]xxyyxy，43yx 的最大值是27.13.在锐角△ABC 中,角A 、B 、C 的对边分别为a 、b 、c.若6cos b a C ab,则tan tan tan tan C C AB的值是▲.【答案】4.【解析】考查三角函数知识，三角形中的正、余弦定理的应用，等价转化思想.（方法一）考虑已知条件和所求结论对于角A 、B 和边a 、b 具有轮换性.当A=B 或a=b 时满足题意，此时有1cos 3C，21cos 1tan21cos 2C C C ，2tan22C .等腰三角形中，1tan tan 2tan2A BC ，tan tan tan tan C C AB=4.（方法二）226cos 6cos b a C ab Cab ab，2222222236,22a bccabab abab.2tan tan sin cos sin sin cos sin sin()1sin tan tan cos sin sin cos sin sin cos sin sin C C C B A B A C A B CABCA B C A B C A B,由正弦定理，得上式22222214113cos ()662cc cc C abab .14.将边长为1m 的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记2(s梯形的周长）梯形的面积,则s 的最小值是____▲____.【答案】3233.【解析】考查函数中的建模应用，等价转化思想.设剪成的小正三角形的边长为x ，则222(3)4(3)(01)1133(1)(1)22x x sx xx x .（方法一）利用导数求函数最小值.224(3)()13x S x x，22224(26)(1)(3)(2)()(1)3x x x x S x x 2242(31)(3)(1)3x x x 1()0,01,3S x xx.当1(0,]3x时，()0,S x 递减；当1[,1)3x 时，()0,S x 递增.故当13x时，S 取最小值3233.（方法二）利用函数的方法求最小值.令1113,(2,3),(,)32x t t t ，则2224418668331tS tttt .故当131,83xt时，S 取最小值3233.二、解答题：本大题共6小题，共计90分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤.15.（本小题满分14分）在平面直角坐标系xOy 中，已知点(1,2)A ，(2,3)B ，(2,1).C (1)求以线段AB 、AC 为邻边的平行四边形的两条对角线的长；(2)设实数t 满足(OC t AB)·OC =0，求t 的值.【解析】本小题主要考查平面向量的几何意义、线性运算、数量积，考查运算求解能力.满分14分.解：（1）由题设知(3,5)AB，(1,1)AC，则(2,6)A B A C ，(4,4).AB AC所以||210AB AC ，||4 2.ABAC 故所求的两条对角线长分别为42，210.（2）由题设知(2,1)OC，(32,5).ABtOCt t由()0AB tOC OC ，得(32,5)(2,1)0t t ，从而511t ，所以11.5t16.（本小题满分14分）如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，PD=DC=BC=1，AB=2，AB ∥DC ，∠BCD=900.(1)求证：PC ⊥BC ；(2)求点A 到平面PBC 的距离.【解析】本小题主要考查直线与平面、平面与平面的位置关系，考查几何体的体积，考查空间想象能力、推理论证能力和运算能力.满分14分. 解：（1）因为PD ⊥平面ABCD ，BC 平面ABCD ，所以PD ⊥BC. 由∠BCD=900，得BC ⊥DC. 又PD DC D ，PD平面PCD ，DC平面PCD ，所以BC ⊥平面PCD.因为PC平面PCD ，所以PC ⊥BC.（2）（方法一）分别取AB 、PC 的中点E 、F ，连DE 、DF.则易证DE ∥CB ，DE ∥平面PBC ，点D 、E 到平面PBC 的距离相等. 由（1）知BC ⊥平面PCD ，所以平面PBC ⊥平面PCD.因为PD=DC ，PF=FC ，所以DF ⊥PC ，所以DF ⊥平面PBC 于F. 易知DF=22.又点A 到平面PBC 的距离等于E 到平面PBC 的距离的2倍，故点A 到平面PBC 的距离等于2.（方法二）连结AC.设点A 到平面PBC 的距离h.因为AB ∥DC ，∠BCD=900，所以∠ABC=900. 从而由AB=2，BC=1，得ABC 的面积1ABCS.由PD ⊥平面ABCD 及PD=1，得三棱锥PABC 的体积11.33ABCVSPD因为PD ⊥平面ABCD ，DC 平面ABCD ，所以PD ⊥DC.又PD=DC=1，所以222.PC PDDC由PC ⊥BC ，BC=1，得PBC 的面积2.2PBCS 由11213323PBCVShh ，得2h .因此，点A 到平面PBC 的距离为2.17.（本小题满分14分）某兴趣小组要测量电视塔AE 的高度H(单位：m).如示意图，垂直放置的标杆BC 高度h=4m ，仰角∠ABE=，∠ADE=.（1）该小组已测得一组，的值，算出了tan =1.24，tan =1.20，请据此算出H 的值；。
2010江苏省高考数学真题(含答案)
62
4、[解析]考查频率分布直方图的知识。 100×（0.001+0.001+0.004）×5=30
6
5、[解析]考查函数的奇偶性的知识。g(x)=ex+ae-x为奇函数，由 g(0)=0，得 a=－1。
6、[解析]考查双曲线的定义。 MF e 4 2 ， d 为点 M 到右准线 x 1 的距离， d
2、设复数 z 满足 z(2-3i)=6+4i（其中 i 为虚数单位），则 z 的模为______▲_____.
3、盒子中有大小相同的 3 只白球，1 只黑球，若从中随机地摸出两只球，两只球颜色不 同的概率是_ ▲__.
4、某棉纺厂为了了解一批棉花的质量，从中随机抽 取了 100根棉花纤维的长度（棉花纤维的长度是棉 花质量的重要指标），所得数据都在区间[5,40]中， 其频率分布直方图如图所示，则其抽样的 100根 中，有_▲___根在棉花纤维的长度小于 20mm。
23、（本小题满分 10分）
5
已知△ABC的三边长都是有理数。 （1）求证 cosA是有理数；（2）求证：对任意正整数 n，cosnA是有理数。
2010年答案 填空题 1、[解析] 考查集合的运算推理。3 B, a+2=3, a=1 2、[解析] 考查复数运算、模的性质。z(2-3i)=2(3+2 i), 2-3i与 3+2 i 的模相等，z 的 模为 2。
3
（1）设动点 P 满足 PF PB 4 ,求点 P 的轨迹；
（2）设 x1
2, x2
1
2
，求点
2
T
的坐标；
3
（3）设t 9 ,求证：直线 MN必过 x 轴上的一定点（其坐标与 m 无关）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（
）
（ ） 收稿日期 ： ２ ０ １ ０－ ０ ７－ ０ ７
４ ６ 解法１ 因为 所以 ２≤ ８ １，
中学数学教学
２ ｘ １ １ １ １ ６≤ ≤ ２≤ ， ８ ｘ ３ ｙ ｙ ２ ２ ３
２ ０ １ ０ 年第 ５ 期
（）
４
２
≤
两边取对数 ， 目的是把幂 与 乘 除 的 运 算 转 化 为 加 减运算 ， 实 现 问 题 的 转 化， 最终通过不等式的性 质解决问题 ．
ｒ ｓ 题 的 通 法！ 用 这 种 方 法 还 可 求 出 ｘ ｙ ＝
２ ｌ ２ ｋ ｘ （ （ ）的取值范围 （ 必须对ｋ、 ｘ ｋ、 ｌ∈ Ｚ ｌ是 ｙ） ｙ 正数 、 零、 负数进行分类讨论） 这里就不再讨论！ ．
（）
｛
这是线性规划的基本题 ， 作出可行 ４ Ｙ 的最大值 ． ３ １ 经过点 ） ， ： 域（ 如图 １ 易知直线ｌ Ｙ ＝ Ｘ － Ｚ， ４ ４ ） 时， 此 Ａ（ ｌ ３， ０ Ｚ ＝３ Ｘ －４ Ｙ 取得最大值是ｌ ２ ７， ｇ ｇ ３ ｘ ＝ ３， ｘ 时， 故 ４ 的最大值是 ２ ７． ｙ ＝ １， ｙ
２ ｘ ２ 原 题 设实数ｘ、 ４≤ ｙ 满足３≤ｘ ｙ ≤８， ｙ ３
分析 １ 直接解不等 式 ， 再求最大值非常困 难， 我们细细观察 ， 发现 ：
２ ｘ ｘ３ ２ ｘ ｙ 的倒数与 的平方的乘积正好等于 ４ ， ｙ ｙ 利 用不等式的性质 ： 则ａ ａ ＞ｂ＞０且ｃ＞ｄ ＞０， ｃ
可得解法 １： ｄ． ＞ｂ
所以 ｌ ｇ ｙ 都成立，
３
３
｛
， ， ｍ ＋２ ｎ ＝３ ｍ ＝－１ 解得 ， ２ ｍ －ｎ ＝－４ ｎ ＝２ ．
｛
｛
１ ≤ ｘ ＋ｙ ≤ ３
， 求４ ｘ ＋２ ｙ 的取值 －１ ≤ ｘ －ｙ ≤ １
ｘ 则ｌ ｌ ｘ－４ ｌ ｌ ｘ＋２ ｌ ＋ ｇ ４ ＝３ ｇ ｇ ｇ ｇ ｙ ＝－ （ ｙ） ｙ （ ， ２ ２ ｌ ｘ－ｌ ｇ ｇ ｙ）
Ｆ１ 和 Ｐ Ｆ２ 的斜率分 别 为 ｋ （ Ⅱ ）设直线 Ｐ １、 ， ： ； ｋ ｋ ２ 证明 ｋ １· ２ ＝１ （ 使得｜Ａ Ｂ｜ Ｃ Ｄ｜＝ ＋ ｜ Ⅲ ）是否存在常数λ， 若存在 ． 求λ 的值 ； 若不 · Ｂ｜ Ｄ ｜ 恒成立？ ｜Ｃ λ｜Ａ 存在 ， 请说明理由 ． 注 第二个问涉及到了双曲线上三个点 、 其中 Ｆ 求证 Ｐ Ｆ１ Ｆ２ 、 Ｐ， Ｆ２ 关 于 原 点 对 称 ， Ｆ１ １、 和Ｐ Ｆ２ 的斜率积为定值 １．
则ｘ 的最大值是 ． ≤ ９， ４ ｙ 檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹檹 １ → ３ → ； Ｐ → Ａ＋ Ｏ Ｂ ② Ｏ ＝ Ｏ ３ ４ １ → １ → ； Ｐ → Ａ＋ Ｏ Ｂ ③Ｏ ＝ Ｏ ３ ２ Ｐ → Ａ → Ｏ → ④Ｏ ＝－Ｏ ＋ Ｂ； １ → → Ｐ → Ａ ＋Ｏ Ｂ． ⑤Ｏ ＝－ Ｏ ２ 解 对于 ① 有 ｘ ＋ｙ ＝ １＋２ ＝ ３ ＞ １， 对 １ ３ １ ３ 所以根据 ② 有 ｘ ＋ｙ ＝ ＋ ＋ ＝ １， ＞ ３ ４ ４ ４ 推论 １、 推论 ２ 以及平 面 向 量 的 基 本 定 理 知 ①② 符合 ， 其余不符合 ． 例９ （ ２ ０ ０ ６年湖南 卷 文 ）如 右 图， Ｏ Ｍ ∥ 点 Ｐ 在由射线ＯＭ 、 Ａ Ｂ， 线段 Ｏ Ｂ 及Ａ Ｂ 的延长 线围成的阴影区域内 Ｐ → （ ，且 Ｏ 不含 边 界） ＝ → → ｘ Ｏ Ａ ＋ｙＯ Ｂ ，则实数对 （ ｘ， ） ｙ）可以是 （ － ， ３ ３） （４ ，４ ） Ｂ．（ １ ３ １ ７ Ｃ． － ， － ， ５ ５） （ ４ ４ ） Ｄ．（ Ａ． １ ３ ２ ２ ２ 则 Ｂ → Ｏ → Ａ → ｔ Ｂ →， ｔ （ ｔ Ｏ ｔ Ｏ ｔ＝ － Ａ） ＝－ ＋ Ｏ － ＝－ ， ３ ２， ２ 从而ｙ ＝ｔ＝ ２ ， 故当 ｘ ＝－ ２ 时 ， ＜ｙ ＜ ３ ３ ３ ３ ５， 故 Ｂ 不符合 ； ３ １ ３ １ 对 于 Ｃ， 故Ｐ 在 ｘ＋ｙ ＝－ ＋ ＝ ＜１， ４ ４ ２ 直线 Ａ 当 ｘ ＝－ １ 时 ， 若 Ｐ 在Ａ Ｂ 左下方 ， Ｂ 上， ４ Ｍ → 故Ｏ Ｍ → Ａ → ｔ 则ｙ ＝ ５， 若 Ｐ 在Ｏ 则Ｏ Ｍ 上， ＝ ∥ Ｂ， ４ １ 故 １ 故 → → Ｂ →， ｔ Ａ Ｂ ＝－ ｔ Ｏ Ａ＋ ｔ Ｏ ｔ＝ ， － ＝－ ， ｙ＝ ４ ４ １ 故当 １ １ ５ 而１ ３ ｔ＝ ． ｘ ＝－ 时 ， ＜ｙ ＜ ， ＜ ４ ４ ４ ４ ４ ４ ５ 故 符合 Ｃ ． ＜ ， ４ 变式 ５ （ ２ ０ ０ ６ 年湖 南卷 理 ）如 右 图 ， Ｏ Ｍ ∥ 点 Ｐ 在由射线ＯＭ 、 Ａ Ｂ， 线段 Ｏ Ｂ 及Ａ Ｂ 的延长线 围成 的 阴 影 区 域 内 （ 不 → 运动 ， 且Ｏ 含边界 ） Ｐ ＝ｘ Ａ → Ｂ →， 则 ｘ 的取值范围是 ； Ｏ ＋ｙＯ 当 ｘ ＝－ １ 时 ， ｙ 的取值范围是 ． ２ ３ （ ） ， １， 答案 ： ０ ． － ∞， ２ ２ 评注 此高考题利 用 三 点 共 线 平 面 向 量 式 及其推论解决 ， 显得比较简便 ．
２ ２ 具体证法为 ： 由（ 可求得双曲线为ｘ －ｙ Ⅰ） ４ ４ ） 、 ） 知Ｆ 设 Ｐ（ 则ｋ ０ Ｆ２（ ２， ０ ． ｘ ＝ １， －２， ｙ １（ ０， ０） １
ｘ ｙ （ ） 的 ２ ＋ ２ ＝ １ ａ ＞ｂ ＞ ０ ａ ｂ
２， 离心率为槡 以该椭圆上的 ２ 右焦点 Ｆ 点和椭 圆 的 左 、 １、
２ ０ １ ０ 年第 ５ 期
中学数学教学
４ ５
点击 ２ ０ １ ０ 年江苏高考数学卷第 １ ２题
） 江苏省东台市第一中学 刘海东 （ 邮编 ： ２ ２ ４ ２ ０ ０
以能力立 意 为 指 导 ， 以考查能力和素质为 “ 导向 ”是 数 学 学 科 高 考 命 题 的 一 条 基 本 原 则 ， 则充分体现 ２ ０ １ ０ 年江苏 省 高 考 数 学 卷 第 １ ２ 题， 了这一命题的基本原则 ．
１· ｘ ２ ｙ ｘ ｙ
ｘ ７， ≤２ （ ） ≤２７，即２≤ｙ
３ 故ｘ 的最大值是 ２ ７． ４ ｙ 点评 解 题 是 需 要 灵 感 的 ， 作为高考填空
ｘ ２ 解法 ３ 由条件 ３ ≤ ｘ ４≤ ｙ ≤ ８， ≤ ９， ｙ 知 ｘ ＞ ０， 在不等式两边同时取对数 ， 得到 ｙ ＞ ０．
２
２
Ｆ２ 为顶 点 的 三 角 形 的 周 长
（ ） ， 为４ 一等轴双曲线的顶点是该椭圆的焦 ２＋１ 槡 点， 设 Ｐ 为该双曲线上异于顶点的 任 一 点． 直线 Ｐ Ｆ１ 和 Ｐ Ｆ２ 与椭圆的交点分别为 Ａ、 Ｂ 和Ｃ、 Ｄ． （ ） ； 求椭圆和双曲线的标准方程 Ⅰ 点评 这种解法虽然 也是两边取对数 ， 但最终解 决的 方 式 与 解 法 ３ 是 不 一 样的 ， 解法 ３ 取对数后用不 等式的性质解决问题 ， 此种 解法 取 对 数 后 通 过 换 元 转 化为 线性规划的常规问题 ，
４ ７
对２ ０ １ ０ 年山东省一道高考题的探究
） 安徽省全椒县城东中学 顾代军 （ 邮编 ： ２ ３ ９ ５ ０ ０
主要 平面解析几何是高考重点考查的内容 ， 是用来考查学生运用数学知识进行推理和运算的 能力 ． 很 多 省 市 把 它 作 为 高 考 的 压 轴 题． 推理繁 琐、 计算量大 ， 要想拿到满分 ， 实属不易 ． 但有许多 试题看似很复杂 ， 其实存在着一定的规律 ． 掌握这 些规律 ， 就能给解题带来意想不到的效果 ． 这就要 靠我们平时注意探究和发掘 ． 下面就 ２ 年山东 ０ １ ０ 省理科数学第 ２ １ 题探究其具有的规律 ． 题 如 图， 已知椭圆
① （ ） ２ｌ ４ ≤ ２ ２ｌ ｘ －ｌ ３ ② ｇ ｇ ｇ ｇ ｙ ≤ ４ｌ ， 所以 ① ＋ ② 得ｌ ２≤３ ｌ ｘ－４ ｌ ２ ７即 ｇ ｇ ｇ ｇ ｙ ≤ｌ ２≤
３ ， ｌ ｘ＋２ ｌ ３ ｇ ｇ ｇ ｙ ＝ｌ ｘ ， 当且仅当 ７ ４ ≤２ ， ｙ ２ ｌ ｘ－ｌ ｌ ３ ｇ ｇ ｇ ｙ ＝２ ３ ， ｌ ｘ ＝ｌ ３ ｘ ＝３ ｇ ｇ 解之 时， 故ｘ 的最大值 即 ４ ， ｙ ｌ ＝１ ｇ ｙ ＝０ ｙ
解 对于 Ａ， 不符合 ； ｘ ＋ｙ ＝ １， １ ７ ６ 对于 Ｄ， 不符合 ； － ＋ ＝ ＞ １， ５ ５ ５ 对于 Ｂ， 故 Ｐ 在Ａ ｘ ＋ｙ ＝ ０ ＜ １， Ｂ 左下方 ，
但当 ｘ ＝－ ２ 时 ， 若 Ｐ 在直线Ａ 则ｙ ＝ ５ ， Ｂ 上， ３ ３ → Ａ →， → ｔ → Ｍ Ｂ Ｍ Ｂ 若 Ｐ 在ＯＭ 上 ， 则因Ｏ 故 Ｏ Ａ ＝ ＝ ∥
而 －３ｌ ２ ≤－ （ ｌ ｘ ＋２ｌ ３ ｇ ｇ ｇ ｇ ｙ）≤－ｌ
（）
ｌ
， 得ｘ ４ ＝ ｙ
３
｛
｛ ｛
是２ ７ ． 点评 实际上当初数学家引入对数的目的之 一就是为了把复杂的幂的运算转化为加减运算 ． 分析４ 解法３告诉我们， 两边取对数， 把幂的 关系与乘除的运算转化为加减运算． 线性规划实际 上就是加减运算， 因此， 我们可以在解法 ３ 的基础 通过换元转化为线性规划问题， 得到解法４ 上， ． 解法 ４ 设 ｌ 则问题转 ｘ ＝ Ｘ， ｌ ｇ ｇ ｙ ＝ Ｙ， 化为 ： 已知 ｌ ３ ≤ Ｘ ＋２ Ｙ ≤ ３ｌ ２， ｇ ｇ 求Ｚ ＝３ Ｘ－ ｌ ４≤２ Ｘ －Ｙ ≤ ２ｌ ３， ｇ ｇ
分析 ３ 实际上很多 学 生 看 到 本 题 ， 首先想 到： 这题 是 不 是 考 查 线 性 规 划 ， 再一思考发现又 不像嘛！ 区别就在于线性 规 划 是 线 性 关 系 即 加 减 运算 ， 而 本 题 是 幂 的 关 系 与 乘 除 运 算． 所以想到
｛
２ ０ １ ０ 年第 ５ 期
中学数学教学
２ ｘ ２ ｌ ３ ≤ｌ ｘ ８， ｌ ４ ≤ｌ ９． ｇ ｇ ｇ ｇ ｇ ≤ｌ ｇ ｙ ≤ｌ ｙ ， 即ｌ ３ ≤ｌ ｘ＋２ ｌ ｌ ２ ｇ ｇ ｇ ｇ ｙ ≤３