追击相遇问题专题总结(完整资料).doc
(完整版)追击相遇问题专题总结,推荐文档
4
“
”
“
”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
追击相遇问题题型汇总

直线运动——追击相遇问题例1.一辆巡逻车最快能在10 s内由静止加速到最大速度50 m/s,并能保持这个速度匀速行驶,问该巡逻车在平直的高速公路上由静止追上前方2000 m处正以35 m/s的速度匀速行驶的汽车,至少需要多少时间?例2.由于某种错误致使两列车相向行驶在同一轨道上,两车司机同时发现了对方,同时刹车,设两车的行驶速度分别为54 km/h和36 km/h,刹车加速度分别为1.5 m/s2和0.5 m/s2,司机需在多远处同时发现对方才不会相碰?例3.一辆轿车违章超车,以108km/h的速度驶人左侧逆行时,猛然发现正前方80m处一辆卡车正以72km/h 的速度迎面驶来,两司机同时刹车,刹车的加速度大小均为10m/s2,两司机的反应时间(即司机发现险情到实施刹车所经历的时间)都是△t,试问△t为何值时才能保证两车不相撞?例4.经检测汽车A的制动性能:以标准速度20m/s在平直公路上行驶时,制动后40s停下来。
现A在平直公路上以20m/s的速度行驶发现前方180m处有一货车B以6m/s的速度同向匀速行驶,司机立即制动,能否发生撞车事故?例5.公共汽车A由停车站从静止出发以2 m/s2的加速度做匀加速运动,这时一辆载重汽车B从后面超过公共汽车,载重汽车以10 m/s的速度匀速前进.问:经过多长时间公共汽车能追上载重汽车?在追上前经过多长时间两车相距最远,相距最远时两车之间的距离是多少?B 总结:讨论追及、相遇的问题,其实质就是分析讨论两物体在相同时间内能否到达相同的空间位置问题.(1)两个关系:即时间关系和位移关系,这两个关系可通过画草图得到.(2)一个条件:即两者速度相等,它往往是物体间能否追上、追不上或(两者)距离最大、最小的临界条件,也是分析判断的切入点.课后作业〈一〉1.一辆客车在平直公路上以30 m/s 的速度行驶,突然发现正前方40 m 处有一货车正以20 m/s 的速度沿同一方向匀速行驶,于是客车立即刹车,以2 m/s 2的加速度做匀减速直线运动,问此后的过程中客车能否会撞到货车上?2.为了安全,在公路上行驶的汽车之间应保持必要的距离.已知某高速公路的最高限速为120 km/h,假设前方车辆突然停止,后车司机从发现这一情况经操纵刹车到汽车开始减速所经历的时间(即反应时间)t =0.5 s,刹车时汽车加速度为4 m/s 2.则该段高速公路上汽车间应保持的最小距离是多少?3.一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s 的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s 后警车发动起来,并以2.5m/s 2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h 以内.问:(1)警车在追赶货车的过程中,两车间的最大距离是多少?(2)警车发动后要多长时间才能追上货车?4.A 、B 两辆汽车在笔直的公路上同向行驶,当B 车在A 车前84 m 处时,B 车速度为4 m/s,且正以2 m/s 2的加速度做匀加速运动;经过一段时间后,B 车加速度突然变为零.A 车一直以20 m/s 的速度做匀速运动,经过12 s 后两车相遇.问B 车加速行驶的时间是多少?5.如图所示,A 、B 两物体相距s =7m ,物体A 以v A =4m/s 的速度向右匀速运动。
追击和相遇问题专题

追击和相遇问题1.速度大者追速度小者:【例1】一列货车以28.8 km/h 的速度在平直铁路上运行,由于调度失误,在后面600 m 处有一列快车以72 km/h 的速度向它靠近。
快车司机发觉后立即合上制动器,但快车要滑行2000 m 才停止。
试判断两车是否会相碰。
★解析:两车速度相等恰追及前车,这是恰不相碰的临界情况,因此只要比较两车等速时的位移关系,即可明确是否相碰。
因快车减速运动的加速度大小为:222/1.020002202s m s v a =⨯==快故快车刹车至两车等速历时: s a v v t 1201.0820=-=-=慢快 该时间内两车位移分别是:m at t v s 16801201.021120202122=⨯⨯-⨯=-=快快 m t v s 9601208=⨯==慢慢因为s 快>s 货+s 0=1560 m ,故两车会发生相撞。
针对训练:火车以速率V 1向前行驶,司机突然发现在前方同一轨道上距车为S 处有另一辆火车,它正沿相同的方向以较小的速率V 2作匀速运动,于是司机立即使车作匀减速运动,加速度大小为a ,要使两车不致相撞,求出a 应满足关式。
★解析:速度相等时,位移也相等则恰好不撞,at 21υυ-= a S a 21221212υυυυυυυ-⋅+=-⋅+ 解得:S a 2)(221υυ-=,则要求Sa 2)(221υυ-≥ 2.速度小者追速度大者:【例2】一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s 的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s 后警车发动起来,并以2.5m/s 2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h 以内.问:(1)警车在追赶货车的过程中,两车间的最大距离是多少?(2)警车发动后要多长时间才能追上货车?★解析:(l )警车在追赶货车的过程中,当两车速度相等时.它们的距离最大,设警车发动后经过t 1时间两车的速度相等.则.11042.5t =s=s s 货=(5.5+4)×10m = 95ms 警22111 2.54m 20m 22=at ==⨯⨯ 所以两车间的最大距离△s =s 货-s 警=75m (2) v 0=90km/h=25m/s ,当警车刚达到最大速度时,运动时间225s 10s 2.5t == s 货’=(5.5+10)×10m=155ms 警’=22211 2.510m 125m 22at ==⨯⨯ 因为s 货’>s 警’,故此时警车尚未赶上货车,且此时两本距离△s’=s 货’-s 警’=30m警车达到最大速度后做匀速运动,设再经过△t 时间迫赶上货车.则:m 2s s't==-∆∆v v所以警车发动后耍经过212s t=t +t=∆才能追上货车。
四年级相遇与追击综合问题知识点总结

相遇和追及综合知识点总结一、基础知识点(相遇和追及):其实相遇和追及最核心的问题就是路程S、速度V和时间T的问题,基本公式就是S÷V=T以及这个公式的变形S÷T=V,V×T=S。
相遇问题:路程和S和------相遇时间T------ 速度和V和⏹S和:一定是甲乙两者共同时间内走过的路程。
如果其中一方提前走了一段路程,这个不算,需要去掉。
⏹T相遇时间:一定是在相遇过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲+ V乙⏹路程和÷速度和=相遇时间路程和÷相遇时间=速度和速度和×相遇时间=路程和追击问题:路程差S差-------追及时间T -------速度差V差⏹S差:有些题没有明确给出路程差,而是隐含在一些条件中,如甲先出发一段时间。
⏹T追及时间:一定是在追及过程中共同经历过的时间。
需要小心题目陷阱,如其中一方休息了一段时间,其中一方提前出发了一段时间都应该剔除。
⏹V和=V甲- V乙路程差÷速度差=追及时间路程差÷追及时间=速度差速速度差×追及时问=路程差二、直线的相遇与追击略三、环形跑道的相遇与追击1、同时同地每次相遇都是合走一圈S和=S甲+S乙=1圈2、同时不同地首次相遇等于初始距离,初始距离需要依据双方的运动方向确定。
每次相遇都是合走一圈S和=S甲+S乙=1圈四、火车过桥火车过杆:S火=车长火车完全过桥:S火=车长+桥长火车完全在桥上:S火= 桥长-车长超人(同向):S差=车长---等效为:人追行人错人(相向):S和=车长---等效为:车尾人与行人相遇超车(同向):S差=车长1+车长2 ---等效为:快车车尾人追慢车车头人错车(相向):S和==车长1+车长2 ---等效为:两个车尾的人相遇五、流水行船静水速度(船速),水速,顺水速度,逆水速度顺水速度=船速+ 水速逆水速度=船速- 水速船速=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2。
相遇追击问题总结

行程问题
基本公式:路程=速度×时间
(1)相遇问题
①、设:题目的问题既是所要设的未知量;
②、分析:根据题意画出相应的横线图
相遇点
甲所行驶路程乙所行驶的里程
③、等量关系:由②得
甲所行驶的路程+乙所行驶的路程=总路程
④、根据③中的等量关系列方程;
⑤、解、验、答。
(2)追击问题
①、设:题目的问题既是所要设的未知量;
②、分析:根据题意画出相应的横线图
甲乙相距距离追击过程中乙的路程及时间
甲乙
追击过程中甲的路程及时间
③、等量关系:一般的,追击者所走的路程=被追击者所走的路程+两者原来的距离
追击者所用时间=被追击者所用时间
④、根据③中的等量关系列方程;
⑤、解、验、答。
第1页共1 页。
高中物理追及相遇问题总结

高中物理追及相遇问题总结
追及相遇问题是高中物理中常见的一类问题,涉及到物体在不同的速度下,相对运动以及相遇时的时间、距离等概念。
下面是关于追及相遇问题的总结:
1.基本概念:
o相对速度:指两个物体之间的相对移动速度。
o追及问题:指两个物体一起出发后,其中一个物体追赶另一个物体,最终相遇的问题。
o相遇时的距离和时间:指在相对运动中,两个物体最终相遇时的距离和花费的时间。
2.追及相遇问题的解题方法:
o建立数学模型:根据问题描述,确定需要求解的变量,设定符号和数学关系。
o列方程:根据物体的运动特点,建立相对速度与距离、时间之间的数学关系。
o解方程:将列出的方程求解,得到未知数的数值。
o验证答案:回到原问题中,用求得的数值重新计算相关参数,验证答案的合理性。
3.常见的追及相遇问题类型:
o同向追及问题:两个物体以相同的方向、不同的速度移动,追及后相遇。
o反向追及问题:两个物体以相反的方向、不同的速
度移动,追及后相遇。
o来回追及问题:一个物体以一定速度往返移动,另一个物体以相同或不同的速度追及后相遇。
4.注意点:
o单位一致:保持问题中涉及的速度、时间、距离等单位统一,并根据需要进行换算。
o确定起点:确定问题中物体的起点位置,并根据需要选择相对位置进行计算。
o考虑时间方面:确保在方程中的时间一致,有时候需要根据问题的描述将时间分割为多个段落。
追及相遇问题需要根据具体的问题情境和要求,学生可以多进行实际问题的练习和实践,熟练掌握解决此类问题的方法和技巧。
追击相遇问题知识点总结

追击相遇问题知识点总结
追击相遇问题是数学中较为常见的几何问题,通常涉及到两个物体在同一直线
上追逐的情况。
以下是追击相遇问题的一些核心知识点总结:
1. 相对速度:追击相遇问题中,我们需要计算追赶者与被追赶者的相对速度。
这可以通过将两者的速度相减得出。
2. 时间关系:追赶者通常会追上被追赶者,因此我们关注的是时间的关系。
如
果我们能够确定他们相遇的时间,就能解决问题。
3. 距离关系:追击相遇问题中,我们通常需要确定两者的初始距离以及相遇时
的距离。
这些信息可以帮助我们计算出相遇的时间。
4. 运动方向:追击相遇问题中,我们需要考虑追赶者和被追赶者的运动方向。
这可以通过正负号来表示,正号表示正向运动,负号表示反向运动。
5. 使用方程:追击相遇问题通常可以通过建立方程来解决。
我们可以利用速度、时间和距离的关系来建立方程,从而求解问题。
总的来说,追击相遇问题要求我们理解速度、时间、距离和运动方向的关系,
并能够灵活运用这些关系来解题。
熟练掌握以上知识点,可以帮助我们解决各种追击相遇问题。
追击相遇问题方法全

v汽aT1m 2/s
s汽12aT2=24m
方法二:图象法
解:画出自行车和汽车的V-t图线,两车之间的距离等于图中矩形的 面积与三角形面积的差,由图得,当t=t0时矩形与三角形的面积之差 最大。
V-t图像的斜率表示物体的加速度
6m/sta na3m/s2
t0
t0
2s
当t=2s时两车的距离最大
xm1226m6m
例1:一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的 加速度开始加速行驶,恰在这时一辆自行车以6m/s的速度匀速驶 来,从后边超过汽车。试求:汽车从路口开动后,在追上自行车之 前经过多长时间两车相距最远?此时距离是多少?
x汽
△x
x自
追击相遇问题方法全
方法一:公式法
当v汽=v自时,两车之间的距 离最大。设经时间t两车之间的
追击相遇问题方法全
在刚开始追车时,由于人的速度大于车的速度, 因此人车间的距离逐渐减小;当车速大于人的速 度时,人车间的距离逐渐增大。因此,当人车速 度相等时,两者间距离最小。
at'=6 t'=6s 在这段时间里,人、车的位移分别为:
x人=v人t=6×6=36m x车=at'2/2=1×62/2=18m Δx=x0+x车-x人=25+18-36=7m
的临界条件。
追击相遇问题方法全
两种典型追及问题——
常见题型一:
同地同时出发,匀加速(速度小)直线运动追及匀速(速 度大)直线运动
开始两者距离增加,直到两者速度相等, 然后两者距离开始减小,直到相遇,最后 距离一直增加。
1)当 v加=v匀 时,A、B距离最大; 2)当两者位移相等时追,击相有遇问题v方加法全=2v匀 且A追上B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此文档下载后即可编辑
追及相遇问题专题总结
一、 解相遇和追及问题的关键
(1)时间关系 :0t t t B A ±= (2)位移关系:0A B x x x =±
(3)速度关系:两者速度相等。
它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
二、追及问题中常用的临界条件:
1、速度小者追速度大者,追上前两个物体速度相等时,有最大距离;
2、速度大者减速追赶速度小者,追上前在两个物体速度相等时,有最小距离.即必须在此之前追上,否则就不能追上:
(1)当两者速度相等时,若追者仍没有追上被追者,则永远追不上,此时两者之间有最小距离。
(2)若两者速度相等时恰能追上,这是两者避免碰撞的临界条件。
(3)若追者追上被追者时,追者速度仍大于被追者的速度,则被追者还有一次追上追者的机会,即会相遇两次。
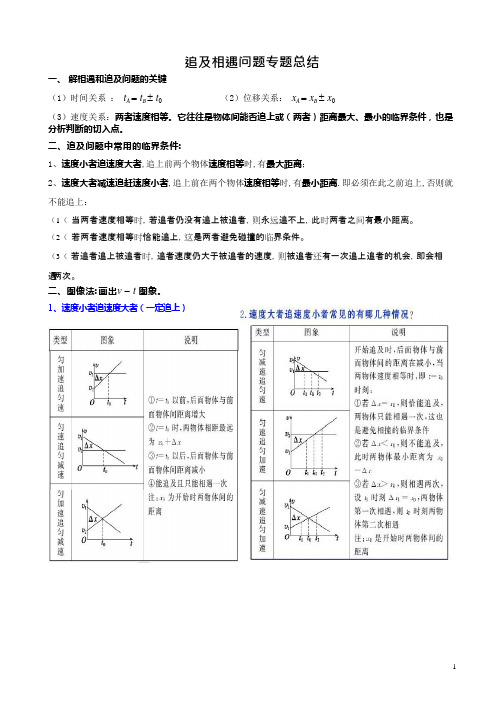
二、图像法:画出v t -图象。
1、速度小者追速度大者(一定追
上)
追击与相遇问题专项典型例题分析
(一).匀加速运动追匀速运动的情况(开始时v1< v2):v1< v2时,两者距离变大;v
时,
2
两者距离最大;v1>v2时,两者距离变小,相遇时满足x1= x2+Δx,全程只相
遇(即追上)一次。
【例1】一小汽车从静止开始以3m/s2的加速度行驶,恰有一自行车以6m/s
的速度从车边匀速驶过.求:(1)小汽车从开动到追上自行车之前经过多长
时间两者相距最远?此时距离是多少?(2)小汽车什么时候追上自行车,此时小汽车的速度是多少?
【针对练习】一辆执勤的警车停在公路边,当警员发现从他旁边驶过的货车(以8m/s的速度匀速行驶)有违章行为时,决定前去追赶,经2.5s将警车发动起来,以2m/s2的加速度匀加速追赶。
求:①发现后经多长时间能追上违章货车?②追上前,两车最大间距是多少?
(二).匀速运动追匀加速运动的情况(开始时v1> v2):v1> v2时,两者距离变小;v1= v2时,①若满足x1< x2+Δx,则永远追不上,此时两者距离最近;②若满足x1=x2+Δx,则恰能追上,全程只相遇一次;③若满足x1> x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
【例2】一辆汽车在十字路口等绿灯,当绿灯亮时汽车以3m/s2的加速度开使行驶,恰在这时一辆自行车在汽车后方相距20m的地方以6m/s的速度匀速行驶,则自行车能否追上汽车?若追不上,两车间的最小间距是多少?
例2中若汽车在自行车前方4m的地方,则自行车能否追上汽车?若能,两车经多长时间相遇?
(三).匀减速运动追匀速运动的情况(开始时v1> v2):v1> v2时,两者距离变小;v1=v2时,①若满足x1<x2+Δx,则永远追不上,此时两者距离最近;②若满足x1= x2+Δx,则恰能追上,全程只相遇一次;③若满足x1> x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
【例3】汽车正以10m/s的速度在平直公路上前进,突然发现正前方有一辆自行车以4m/s 的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小为6 m/s2的匀减速运动,汽车恰好不碰上自行车。
求关闭油门时汽车离自行车多远?
特别注意:若被追者做匀减速直线运动,要注意追上之前是否已经停止运
动
【例4】甲车在前以15m/s的速度匀速行驶,乙车在后以9m/s的速度行驶。
当两车相距32m时,甲车开始刹车,加速度大小为1m/s2。
问(1)两车间的最大距离(2)经多少时间乙车可追上
(四).匀速运动追匀减速运动的情况(开始时v1<v2):v1<v2时,两者距离变大;v1=v2时,两者距离最远;v1>v2时,两者距离变小,相遇时满足x
= x2+Δx,全程只相遇一次。
1
【例5】当汽车B在汽车A前方7m时,A正以v A=4m/s的速度向前做匀速直线运动,而汽车B此时速度v B=10m/s,并关闭油门向前做匀减速直线运动,加速度大小为a=2m/s2。
此时开始计时,则A追上B需要的时间是多少?
【针对训练】在一条平直的公路上,乙车以10m/s的速度匀速行驶,甲车在乙车的后面做初速度为15m/s,加速度大小为0.5m/s2的匀减速运动,则两车初始距离L满足什么条件时可以使(1)两车不相遇;(2)两车只相遇一次;
(3)两车能相遇两次(设两车相遇时互不影响各自的运动).
答案】能追上。
设经过t追上;则有x汽+x0=x
自;
3×t2/2+4=6t
得t=(6±2√3)/3s,二
次相遇。
