正方体的11种展开图
正方体的11种侧面展开图
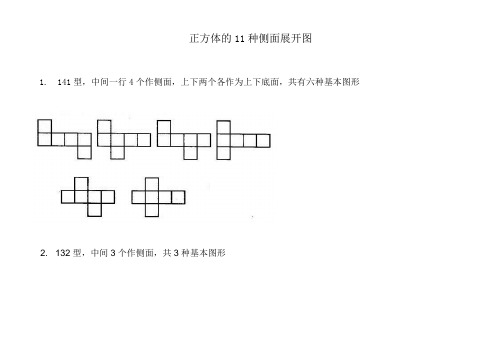
正方体的11种侧面展开图
1. 141型,中间一行4个作侧面,上下两个各作为上下底面,共有六种基本图形
2. 132型,中间3个作侧面,共3种基本图形
3. 222型,两行只能有1个正方形相连
4. 33型,两行只能有一个正方形相连
小结:一四一,都可以;
一三二,二必连;
二成三阶梯;
两排三三连;
田字必舍弃。
正方体的展开图可以按照行进行分类。
主要有以下特点:
1.上中下三行,每两行之间只能有一条边重合。
2.222、33两类是特殊的,为阶梯状。
3.有的看似不属于任一类,旋转后就是其中一类了。
在下面的口诀中,前四行是描述十一种展示图的特点,后两行是描述哪些图形不能构成正方体,哪些面是相对的面,哪些面是相邻的面。
正方体展开图口诀
正方体展有规律,十一种类看仔细;
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;
相间之端是对面,间二拐角面相邻。
正方体的 11 种展开图精品打印附带讲解

正方体的11种展开图打印附带讲解本文章主要带孩子认识11种正方体展开图,家人可以把它打印下来,陪孩子一起制作。
(PS:1、如果A4的纸太软不好固定,可以用纸箱、纸质购物袋等画出对应的图形进行裁剪;2、亦或者可以用包书的纸裁剪出展开图的样子,做成精美的包装纸贴在正方体外面,做一个精美的小礼盒哦)(为了方便打印,文章末尾,把所有资料汇总了一遍,可直接跳转到末尾打印11钟展开图)在正式学习之前,可以将家中的魔方拿出来,看看正方体有几面?每一面都是什么形状?以此区分一下正方体和正方形。
分别有前面、后面、上面、下面、左面、右面这六面。
接着介绍“正方体的展开图”,带着孩子观察展开图的特点,并知道其名称。
(一)首先认识一下1-4-1型,为了更形象的记忆,我把它概括为“1头4身体1脚”(头是由1个正方形组成的,身体是由4个正方形组成的,脚是由1个正方形组成的,)家人可以先把图形制作出来,然后带孩子去观察特点。
打印图纸:1-4-1打印专用:1-4-1共有6种,身体均是4个正方体,头和脚各一个,头和脚的位置可左右移动改变(二)接下来认识2-3-1型,2-3-1共有3种,头2个正方体,身体3个,脚1个。
脚的位置可左右移动改变,以此展开图为例,虽然身体部分较原来少了一个,但是恰好可以由头部多的一个补上。
操作演示时,先把身体折起来,发现身体少了一个,接着把上面脑袋部分拼好,拼好之后脑袋部分多的一个刚好可以补充身体。
2-3-1打印专用:2-3-1共有3种,头2个正方体,身体3个,脚1个。
脚的位置可左右移动改变(三)接下来认识2-2-2型,与3-3型,可以把资料打印下来,通过操作去提升动手以及想象能力。
2-2-2与3-3打印专用。
正方体展开全图11种情况演示

精选2021版课件
38
2、“坚”在下,“就”在后,“胜”、 “利”在哪里?
坚
持就是
胜
“胜”在上,
利
“利”在前!
精选2021版课件
39
精选2021版课件
40
圆 柱
圆 锥
精选2021版课件
41
三 棱 锥
四棱锥 精选2021版课件
五棱锥
42
第一类(6种):中间四连方,两侧各有一个。
展开6
精选2021版课件
11
第二类(3种):中间三连方,两侧各有一、二个。
展开7
精选2021版课件
12
第二类(3种):中间三连方,两侧各有一、二个。
展开8
精选2021版课件
13
第二类(3种):中间三连方,两侧各有一、二个。
展开9
精选2021版课件
14
精选2021版课件
6
第一类(6种):中间四连方,两侧各有一个。
展开2
精选2021版课件
7
第一类(6种):中间四连方,两侧各有一个。
展开3
精选2021版课件
8
第一类(6种):中间四连方,两侧各有一个。
展开4
精选2021版课件
9
第一类(6种):中间四连方,两侧各有一个。
展开5
精选2021版课件
021版课件
31
(12 )
精选2021版课件
32
(13)
精选2021版课件
33
(14)
精选2021版课件
34
(15 )
精选2021版课件
35
(16)
精选2021版课件
36
正方体的11种展开图规律大全

正方体的11种展开图
判断技巧
我们知道,同一个立方体图形,按不同的方式展开得到的平面展开图形一般是不一样的。
常见的正方体平面展开图究竟有几种不同的形状呢?
同学们一定熟悉这样一种操作:把一个正方形纸片平均分成9个小正方形,剪去角上四个小正方形,可以拼成一个无盖的正方体纸盒,其中五个面按习惯不妨记为下、左、右、前、后,如图一。
好啦!现在只要把刚才剪去的一个小正方形作为“上”面,就可拼成一个正方体。
作为正方体平面展开图,这个“上”应该和图1(1)中哪个面拼接在一起呢?观察图1(2),知“上”和前、后、左、右任一个面拼接都行(这四种拼接看作同一种情形),不妨和“后"拼接在一起,如图2.
根据上和下、左和右、前和后相间隔这一规律,现在我们把图2中的“左"或“右"平移,可得图3~图7五种情形.
平移图2中的“前”,可得图8;再平移图8中的“左”,可得图9、图10;
把图10中的“上”向左平移,得图11;若移动图8(或图9、图10)中的“左",又可得图12。
同学们,当你和我一样,把图2~图12这11个图剪下来,动手折一折,得到1 1个漂亮的小正方体时,你一定为我们的收获感到欢欣鼓舞吧!
对正方体表面展开图的11种情况,为加深记忆,可编成如下口诀:一四一呈6种,一三二有3种,二二二与三三各1种,展开图共有11种。
“动手实践,自主探索和合作交流"是新课程标准倡导学习数学的三种重要方法,而实践活动是培养我们进行主动探索与合作交流的重要途径.只要通过自己主动观察、实验、猜想、验证等数学活动,就能使我们“建立空间观念,发展几何直觉",提高思维能力。
正方体11种展开图

展开11
第四类(1种):两排各有三个。
展开4
第一类(6种):中间四连方,两侧各有一个。
展开5
第一类(6种):中间四连方,两侧各有一个。
展开6
第二类(3种):中间三连方,两侧各有一、二个。
展开7
第二类(3种):中间三连方,两侧各有一、二个。
展开8
第二类(3种):中间三连方,两侧各有一、二个。
展开9
展开10
第三类(1种):中间二连方,两侧各有二个。
安 勤 课程标准实验教科书数学(西师版) 全 思 与 与 健 智 康 慧 曾宁 丹山镇中心小学 携 同 QQ:392362826 手 行
正方体共有11种展开图,分为四类:
第一类(6种):中间四连方,两侧各有一个。
图 1 图 2 图 3 图 4 图 5 图 6
第二类(3种):中间三连方,两侧各有一、二个。
图 7 图 8 图 9
第三类(1种):中间二连方,两侧各有二个。
图 10
第四类(1种):两排各有三个。
图 11
第一类(6种):中间四连方,两侧各有一个。
展开1Βιβλιοθήκη 第一类(6种):中间四连方,两侧各有一个。
展开2
第一类(6种):中间四连方,两侧各有一个。
展开3
第一类(6种):中间四连方,两侧各有一个。
正方体的11种展开图形

第1类:中间四方连,两侧各一个(6种)
“一四一 型”
第2类:中间三方连,两侧各一、二个
第2类:中间三方连,两侧各一、二个
第2类:中间三方连,两侧各一、二个
第2类:中间三方连,两侧各一、二个(3种)
“二三一 型”
第3类:中间二方连,两侧各二个
第3类:中间二方连,两侧各二个(1种) “二二二 型”
正方体的11种展开图形
本课件仅供大家学习学习 学习完毕请自觉删除
谢谢 本课件仅供大家学习学习
学习完毕请自觉删除 谢谢
第1类:中间四方连,两侧各一个
第1类:中间四方连,两侧各一个
第1类:中间四方连,两侧各一个
第1类:中间四方连,两侧各一个
第1类:中间四方连,两侧பைடு நூலகம்一个
第1类:中间四方连,两侧各一个
第4类:两排各三个
第1类:中间四方连,两侧各一个(6种)
“一四一 型”
第2类:中间三方连,两侧各一、二个(3种)
“二三一 型”
第3类:中间二方连,两侧各二个(1种) “二二二 型”
第4类:两排各三个(1种) “三三型”
判断下列图形能不能折成正方体?
正方体11种展开图

类型六:十字型
总结词
由两个相同的等腰直角三角形和两个相同的矩形组成的展开图,呈十字形状。
详细描述
这种类型的展开图在正方体的两个相对的面上保留了一个矩形,而其他面则由两个等腰直角三角形组成,整体呈 十字形状。
类型七:二字型
总结词
由两个相同的矩形和两个相同的等腰直角三角形组成的展开图,呈二字形状。
详细描述
正方体11种展开图
• 正方体的基本特性 • 正方体的11种展开图 • 正方体展开图的制作方法 • 正方体展开图的应用场景 • 正方体展开图的挑战与未来发展
01
正方体的基本特性
定义与特性
01
正方体是一种三维几何体,由六 个正方形面组成,每个面都是等 大的正方形。
02
正方体的体对角线、棱和面都是 对称的,具有高度的空间对称性 。
05
正方体展开图的挑战与未来发展
当前面临的挑战
寻找新的展开方式
目前已知的正方体展开图种类有 限,需要探索新的展开方式以丰
富其多样性。
证明无解的存在
对于某些特定条件下的正方体展开 问题,需要证明无解的存在,这需 要深入的数学理论支持。
实际应用中的限制
正方体展开图在实际应用中可能受 到材料、工艺等因素的限制,需要 解决这些实际问题。
正方体的几何属性
正方体的体积是边长的三次方,记作 V=a^3,其中a是正方体的边长。
正方体的表面积是6倍的边长的平方, 记作A=6a^2。
正方体的展开与折叠
正方体的展开是将正方体的表面沿某些边展开成平面的过程,通常用于制作纸盒等 包装材料。
正方体的折叠则是将展开的平面重新折回成立体的过程,常用于制作纸艺模型和玩 具。
详细描述
