第4章习题解答
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
JAVA第四章课后习题解答

txtFl1=new TextField(5); txtFl2=new TextField(5); txtFl3=new TextField(5); btn1=new Button("+"); btn2=new Button("-"); btn3=new Button("*"); btn4=new Button("÷");
public class Test4_9 extends Frame implements ActionListener{ Button btn; public Test4_9(){ super("弹出窗口练习"); setSize(300,200);
5
setVisible(true); setLayout(new BorderLayout());
TextField txtFl1,txtFl2,txtFl3;
2
Button btn; public Test4_6(){
super("简单加法运算器"); setSize(300,200); setVisible(true); setLayout(new FlowLayout());
txtFl1=new TextField(5); txtFl2=new TextField(5); txtFl3=new TextField(10); btn=new Button("=");
光学第四章习题解答

′ s1 = d − s1 = 22 − 2 = 20cm
1 1 1 1 1 1 又∵ − = 即: = − s s f′ s s′ f ′
' 1 1 1 1 1 1
1 1 1 39 ∴ = − =− s1 20 0.5 20
− 20 s′ = − = −0.51 (cm). ɺ 39 ′
1
s′ 20 又∵ β = = − = −39. 0.51 s
∴ Φ= 1 1 1 = − f ′ s′ s 1 1 = − − 1.0 − 0.25 100 = −1 + 25 = +3.0 ( D) = +300 度
需配戴300度的远视眼镜 度的远视眼镜 需配戴
4.3 一照相机对准远物时,底片距物镜 一照相机对准远物时,底片距物镜18cm,当 , 镜头拉至最大长度时,底片与物镜相距20cm ,求目 镜头拉至最大长度时,底片与物镜相距 的物在镜头前的最近距离? 的物在镜头前的最近距离? 解: ∵ 1 − 1 = 1 s′ s f ′
解:(1)将 s = −20cm,f ′ = 15cm 代入高斯公式
s1 f ′ (−20) ×′ −20 + 15
′ s1 60 × 0.5 = −1.5cm (2) y1′ = β1 y1 = y1 = −20 s1
EO 2 (3) u = arctg = arctg = 7°35′40′′ PO 15
(4)将 s2 = −5cm,f ′ = 15cm 代入高斯公式
s2 f ′ ( −5) × 15 ′ s2 = = = −7.5cm s2 + f ′ −5 + 15 ′ s2 −7.5 ′ × 2 = 3cm 出射光瞳的半径 E ′O′ = y2 = y2 = −5 s2
习题参考答案(第4章)
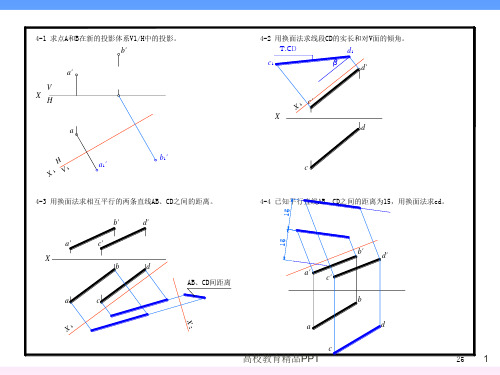
a' V XH
a
4-2 用换面法求线段CD的实长和对V面的倾角。
T.CD
d1
c1 d'
X 1 c' X
d
H X1 V1
a1'
b1'
c
4-3 用换面法求相互平行的两条直线AB、CD之间的距离。
b'
d'
a'
c'
X
b
d
a
c
AB、CD间距离
4-4 已知平行直线AB、CD之间的距离为15,用换面法求cd。
15
15
a' c'
b'
d'
b
X2
பைடு நூலகம்X1
a
d
c
高校教育精品PPT
25 1
4-5 已知直线AB与CD垂直相交,用换面法求c'd'。 b'
a'
c a
b d
4-6 用换面法求点到直线BC距离,并求垂足。
a'
c'
b'
c a
A到BC距离 b
O2
4-7 已知点A到直线BC的距离为15,求a。 a1
R15
b1
c1
O1
a b
c a'1
c'1 c2
a2
b1' b2
高校教育精品PPT
27 3
4-11 已知直线AB与 CDE的距离为10,用换面法求ab。
c' e'
b'
a' X
第4章 习题解答
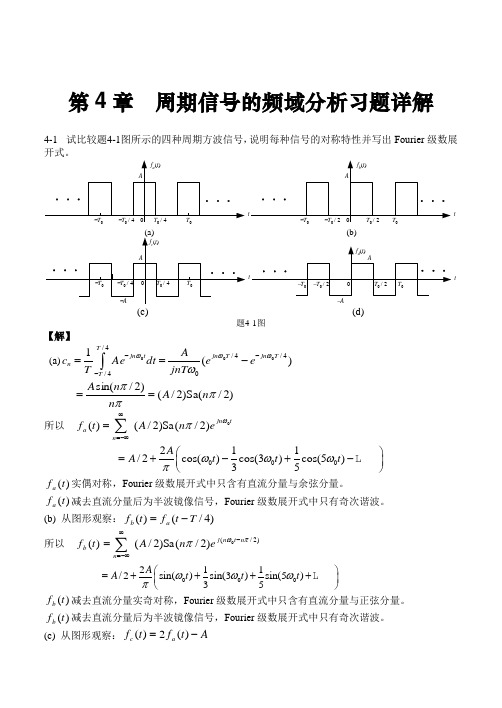
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
第4章 习题答案

50������-2 = 0
������������������������ = -0.5 +
������������
解得 L=10(已舍去负值)
且
������2������������������ ������������2
=
-100������-3<0
所以,当劳动投入量 L=10 时,劳动的
第四章 生产论 3. 已知生产函数 Q=f(L,K)=2KL-0.5L2 -0.5K2, 假定厂商目前处于短期生产,且 K =10。
(1)写出在短期生产中该厂商关于劳动的 总产量 TPL 函数、劳动的平均产量 APL 函数 和劳动的边际产量 MPL 函数。
(2)分别计算当劳动的总产量 TPL、劳动 的平均产量 APL 和劳动的边际产量 MPL 各自 达到最大值时的厂商的劳动投入量。
有 MP=0,于是,有 35+16L-3L2=0。
解得������ = − 5
3
和
L=7。������
=
-
5 3
不合
理,舍去,故取 L=7。
由此可得,生产要素 L 投入量的合理区 间为[4,7]。因此,企业对生产要素 L 的使用 量为 6 是处于短期生产的合理区间的。
11. 已知生产函数 Q=AL1/3K2/3。 判断:(1)在长期生产中,该生产函数的规模 报酬属于哪一种类型?
50 劳动的平均产量函数:
APL=
TPL =20-0.5L- 50
������
������
劳动的边际产量函数:
MPL=
������������������������ ������������
=20-L
(2)关于总产量的最大值:
第4章_组合逻辑电路习题解答
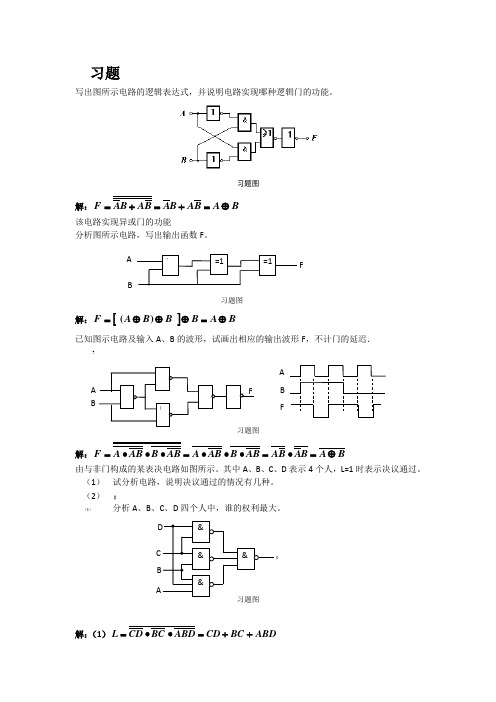
习题写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能分析图所示电路,写出输出函数F 。
习题图 解:[]B A B BB A F ⊕=⊕⊕⊕=)(已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.?解:B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 【 (3) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题图解:(1)ABD BC CD ABD BC CD L ++=••=C & && & D $ L B A " =1=1 =1FFA B[FB A(2)(3)根据真值表可知,四个人当中C 的权利最大。
分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
&习题图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)(3)当S 1S 0=00和S 1S 0=11时,该电路实现两输入或门,当S 1S 0=01时,该电路实现两输入或非门,当S 1S 0=10时,该电路实现两输入与非门。
(2)1¥电路逻辑功能为:“判输入ABC 是否相同”电路。
已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示,试写出F 的最简与或表达式。
习题图:解:(1)根据波形图得到真值表:,(2)由真值表得到逻辑表达式为C AB BC A C B A F ++=、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ,要求用最简单的方法,实现的电路最简单。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
1
×
×
×
1
×
0
1
化简后所得到的MS、ML输出函数最简表达式为
(4)根据化简后所得到的MS、ML输出函数最简表达式画出逻辑电路图即为所求,如下所示:
4.9交通灯的亮与灭的有效组合如图P4.9所示,如果交通灯的控制电路失灵,就可能出现信号灯的亮与灭的无效组合,试设计一个交通控制灯失灵检测电路,检测电路要能检测出任何无效组合。要求用最少与非门实现。
4.2图P4.2是一个多功能逻辑函数发生器电路。试写出当S0、S1、S2、S3为0000~1111共16种不同状态时输出Y的逻辑函数式。
解:
当 为 时 的逻辑函数式如下表:
0 0 0 0
1
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 10 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0 0 0
1
1 0 0
0
0 1 0
0
1 1 0
1
0 0 1
0
1 0 1
0
0 1 1
1
1 1 1
0
据真值表可得:
4.5用与非门设计一个4变量表决电路。其功能是:4个变量中有多数个变量为1时,输出为1,否则为0。
解:设4个逻辑变量分别用 表示,输出变量用 表示。
(1)列真值表:
由电路的功能得真值表:
0 0 0 0
A B C
MSML
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 0
1 0
× ×
0 1
× ×
× ×
× ×
1 1
(3)根据真值表写出输出MS、ML的逻辑表达式并利用卡诺图化为最简表达式,卡诺图如下图所示:
BC
A 00 01 11 10
0
1
0
×
×
×
1
×
0
1
BC
A 00 01 11 10
0
1
1
1
0
1
0
0
0
1
(3)逻辑函数变换:
按பைடு நூலகம்意采用与非门,逻辑函数变换为与非与非式:
(4)画出逻辑电路图:
4.7设计一个路灯控制电路,要求在4个不同的地方都能独立控制路灯的亮和灭。当一个开关动作后灯亮,另一个开关动作后灯灭。设计一个能实现此要求的逻辑电路。
解:设四个开关分别用 四个变量表示,开关动闭合1,断开为0。用变量 表示灯泡的亮灭,灯亮时 为1,否则为0。
(1)列真值表:由电路的功能得真值表
0 0 0 0
0
0 0 0 1
1
0 0 1 0
1
0 0 1 1
0
0 1 0 0
1
0 10 1
0
0 1 1 0
0
0 1 1 1
1
1 0 0 0
1
1 0 0 1
0
1 0 1 0
0
1 0 1 1
1
1 1 0 0
0
1 1 0 1
1
1 1 1 0
1
1 1 1 1
0
(3)化简逻辑函数:由真值表画出卡诺图,得最简与或式:
0
0
0
0
0
0
1
0
0
1
1
1
0
0
1
0
00
01
11
10
(3)逻辑函数变换:
按题意采用与非门,逻辑函数变换为与非与非式:
(4)画出逻辑电路图:
4.6某设备由开关A、B、C控制,要求:只有开关A接通的条件下,开关B才能接通;开关C只有在开关B接通的条件下才能接通。违反这一规程,则发出报警信号。设计一个用与非门组成的能实现这一功能的报警控制电路。
4.10设计一个小汽车尾灯控制电路,小汽车左右两侧各有三个尾灯,要求:
(1)左转弯时,在左转弯开关控制下,左侧3个灯按图P4.10所示周期性地亮与灭;
(2)右转弯时,在右转弯开关控制下,右侧3个灯按图P4.10所示周期性地亮与灭;
习题4
4.1分析图P4.1所示电路,写出Y1、Y2的逻辑表达式,列出真值表,指出电路完成什么逻辑功能。
解:
真值表如下:
0 0 0
0 0
0 0 1
1 0
0 1 0
1 0
0 1 1
0 1
1 0 0
1 0
1 0 1
0 1
1 1 0
0 1
1 1 1
1 1
电路为全加器,其中 分别为被加数、加数和进位输入, 为和, 为进位输出。
0
0 0 0 1
0
0 0 1 0
0
0 0 1 1
0
0 1 0 0
0
0 10 1
0
0 1 1 0
0
0 1 1 1
1
1 0 0 0
0
1 0 0 1
0
1 0 1 0
0
1 0 1 1
1
1 1 0 0
0
1 1 0 1
1
1 1 1 0
1
1 1 1 1
1
(2)划简逻辑函数:由真值表画出卡诺图,得最简与或式:
CD
AB 00 01 11 10
CD
AB 00 01 11 10
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
00
01
11
10
(3)逻辑函数变换:
采用与非门,逻辑函数变换为与非与非式:
(4)画出逻辑电路图:
4.8有一水箱由大小两台水泵ML和MS供水,水箱中设置了3个水位检测元件A、B、C,如图P4.8所示。水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。现要求当水位高于C点时水泵停止工作;水位高于B点而低于C点时MS单独工作;水位低于B点而高于A点ML单独工作;水位低于A点时ML和MS同时工作。试用门电路设计一个控制两台水泵的逻辑电路。
(1)交通灯由红灯A、黄灯B、绿灯C组成,任意时刻只能有一盏灯亮,其他情况为故障状态。若设灯亮为逻辑状态1,灯灭为0;电路输出为Y,故障Y=1非故障为Y=0.
(2)根据以上分析可得真值表:
A
B
C
Y
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
0
1
0
1
1
1
(3)由以上真值表利用卡诺图化简可得
(4)其逻辑电路图如下图所示
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0
4.3分析图P4.3电路的逻辑功能,写出Y1、Y2的逻辑表达式,列出真值表,指出电路完成什么逻辑功能。
解:
4.4已知某组合电路的输入A、B、C和输出Y的波形如图P4.4所示,试写出Y的最简与或表达式。
解:
根据题中所给的波形可得到如下的真值表:
解:设开关 表示三个逻辑变量,开关闭合为1,开关断开为0;用变量 表示报警信号,当报警时 为1,否则为0。
(1)列真值表:
由电路的功能得真值表:
0 0 0
0
0 0 1
1
0 1 0
1
0 1 1
1
1 0 0
0
1 0 1
1
1 1 0
0
1 1 1
0
(2)化简逻辑函数:由真值表画出卡诺图,得最简与或式:
BC
A 00 01 11 10
解:(1)根据逻辑功能要求确定输入,输出变量并进行状态赋值:
设输入变量为A、B、C,采用正逻辑,低电平=0,高电平=1。输出变量为MS、ML,水泵MS、ML不工作时为0,工作时为1。
(2)由题目要求知,ABC组合只有4种情况:000(水面高于C),001(水面高于B),011(水面高于A),111(水面低于A)。因此,真值表为:
