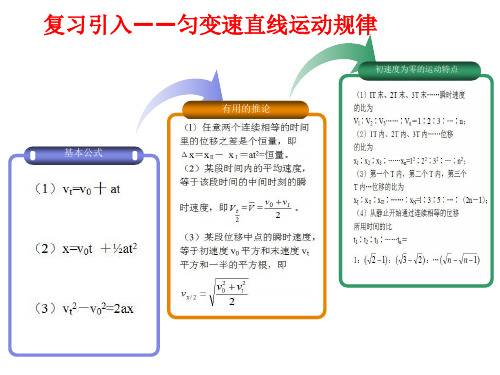
初速度为零的匀加速直线运动的几个比例式

合集下载

2.4推论：初速度为零的匀变速直线运动的比例式推导和应用解析

x
x
x
x
v1
t1
t2
t3
t4
v0=0
v2
v3
v4
v
……
1X末的瞬时速度为
2X末的瞬时速度为
3X末的瞬时速度为
NX末的瞬时速度为
x
x
x
x
v1
t1
t2
t3
t4
v0=0
v2
v3
v4
v
5、一质点做初速度为零的匀加速直线运动，加速度为a，则前1X内、前2X内、前3X内……前nX 内的时间是多少？前1X内、前2X内、前3X内……前nX 内的时间之比是多少？
（ B ）
3.把物体做初速度为零的匀加速直线运动的总位移分成等长的三段,按从开始到最后的顺序,经过这三段位移的平均速度之比为( )
D
思考：一质点做初速度为零的匀加速直线运动，1T秒末、2T秒末、3T秒末……nT秒末的速度比是多少？
1s末的瞬时速度为
2s末的瞬时速度为
3s末的瞬时速度为
… …
… …
v
T
T
T
v0=0
xⅡ
xⅢ
xⅠ
v1
v3
v2
1T末的瞬时速度为
2T末的瞬时速度为
3T末的瞬时速度为
推论一：做初速度为零的匀加速直线运动的物体，在1T秒末、2T秒末、3T秒末……nT秒末的速度比也是 V1：V2：V3：…Vn=1:2:3: … :n。
2、一质点做初速度为零的匀加速直线运动，加速度为a，则1秒内、2秒内、3秒内……n秒内的位移各是多少？1秒内、2秒内、3秒内……n秒内的位移比是多少？
结论二：1s内、2s内、3s内…ns内的位移比 x1﹕x2﹕ x3﹕……x来自=12﹕22 ﹕32 ﹕……n2

06--初速度为零的匀变速直线运动的比例式推导和应用解析

内……第nX 内的时间是多少？第1X内、第
2X内、第3X内……第nX 内的时间之比是多
少？
v
x
x
x
xa
t1
t2
t3
t4
v0=0 v1
v2
v3
v4
推导：设X为等分位移，由公式x 1 at2得
2
通过第1个x所用时间
t1
2x a
通过第2个x所用时间
t2
2 2x a
2x a
2x ( 2 1) a
3、一质点做初速度为零的匀加速直线运动，加速度为a，则第1秒内、第2秒内、第3秒内……第n秒内的位移各是多少？第1秒内、第2秒内、第3秒内……第n秒内的位移之比是多少？
结论三：连续相等时间T内的位移比 xⅠ﹕xⅡ﹕xⅢ﹕……:xN=1﹕3﹕5﹕ ……(2n-1)
思考：做初速度为零的匀加速直线运动，连续相等时间间隔T内的位移比是多少？
2. 解：
A1B 3 5 C 7
1s
2s
9
11 D
3s
4.如右图所示，在水平面上固定着三个完全相同的木块，一
粒子弹以水平速度 v 射入．若子弹在木块中做匀减速直线运
动，当穿透第三个木块时速度恰好为零，则子弹
依次穿入每个木块时的速度之比和穿过每个木块
所用时间之比分别为( D )
A．v1∶v2∶v3＝3∶2∶1 B．v1∶v2∶v3＝ 3∶ 2∶1 C．t1∶t2∶t3＝1∶ 2∶ 3 D．t1∶t2∶t3＝( 3－ 2)∶( 2－1)∶1
at得v∶ 3 v5
3∶5.由x
1 2
at 2
得x∶ 3 x5 32∶52 9∶25, 根据推论xⅠ∶xⅡ∶xⅢ∶xN

2019版步步高高中物理教科版必修一教师用书：第一章运动的描述 8 Word版含答案

8 匀变速直线运动规律的应用[学习目标] 1.会推导匀变速直线运动的速度与位移的关系式，并会用此公式进行分析和相关计算.2.能推导初速度为零的匀加速直线运动的几个比例式．速度与位移的关系式 1．公式：v t 2－v 02＝2ax . 2．推导：速度公式v t ＝v 0＋at . 位移公式x ＝v 0t ＋12at 2.由以上两式可得：v t 2－v 02＝2ax .1．判断下列说法的正误．(1)公式v t 2－v 02＝2ax 适用于所有的直线运动．(×)(2)确定公式v t 2－v 02＝2ax 中的四个物理量的数值时，选取的参考系应该是统一的．(√) (3)因为v t 2－v 02＝2ax ，v t 2＝v 02＋2ax ，所以物体的末速度v t 一定大于初速度v 0.(×) (4)在公式v t 2－v 02＝2ax 中，a 为矢量，与规定的正方向相反时a 取负值．(√)2．汽车以10m/s 的速度行驶，刹车的加速度大小为3 m/s 2，则它向前滑行12.5m 后的瞬时速度为________m/s. 答案 5一、关系式v t 2－v 02＝2ax 的理解和应用如图1所示，一质点做匀加速直线运动，已知质点的初速度为v 0，加速度为a ，质点通过位移x 时的末速度为v t ，试推导：v t 2－v 02＝2ax .图1答案 v t ＝v 0＋at ① x ＝v 0t ＋12at 2②由①得t ＝v t －v 0a ③将③代入②x ＝v 0v t －v 0a ＋12a (v t －v 0a )2＝v t 2－v 022a整理得：v t 2－v 02＝2ax1．适用范围：速度与位移的关系v t 2－v 02＝2ax 仅适用于匀变速直线运动．2．公式的矢量性：v t 2－v 02＝2ax 是矢量式，v 0、v t 、a 、x 都是矢量，应用解题时一定要先设定正方向，取v 0方向为正方向：(1)若加速运动，a 取正值，减速运动，a 取负值．(2)x ＞0，位移的方向与初速度方向相同，x ＜0则为减速到0，又反向运动到计时起点另一侧的位移．(3)v t ＞0，速度的方向与初速度方向相同，v t ＜0则为减速到0，又反向运动的速度．注意：应用此公式时，注意符号关系，必要时对计算结果进行分析，验证其合理性． 3．两种特殊形式(1)当v 0＝0时，v t 2＝2ax .(初速度为零的匀加速直线运动) (2)当v t ＝0时，－v 02＝2ax .(末速度为零的匀减速直线运动)例1 长100m 的列车通过长1000m 的隧道时做匀加速直线运动，列车刚进隧道时的速度是10m/s ，完全出隧道时的速度是12 m/s ，求： (1)列车过隧道时的加速度是多大？ (2)通过隧道所用的时间是多少？答案 (1)0.02m/s 2 (2)100s解析 (1)x ＝1000m ＋100m ＝1100m ，v 1＝10m/s ， v 2＝12m/s ，由v 2－v 02＝2ax 得，加速度a ＝v 22－v 122x ＝0.02m/s 2.(2)由v t ＝v 0＋at 得所用时间为t ＝v 2－v 1a ＝12－100.02s ＝100s.解答匀变速直线运动问题时巧选公式的基本方法1．如果题目中无位移x ，也不让求x ，一般选用速度公式v t ＝v 0＋at ； 2．如果题目中无末速度v t ，也不让求v t ，一般选用位移公式x ＝v 0t ＋12at 2；3．如果题目中无运动时间t ，也不让求t ，一般选用导出公式v t 2－v 02＝2ax .针对训练两个小车在水平面上做加速度相同的匀减速直线运动，若它们的初速度之比为1∶2，它们运动的最大位移之比为( )A ．1∶2B ．1∶4C ．4∶1D ．2∶1 答案 B解析小车的末速度为0，由v t 2－v 02＝2ax 得x 1x 2＝v 012v 022＝14，选项B 正确．例2 物体从斜面顶端由静止开始下滑，到达斜面底端时速度为4m/s ，则物体经过斜面中点时的速度为( )A ．2m/sB ．22m/sC.2m/sD.22m/s 答案 B解析从顶端到底端v 2＝2ax 从顶端到中点22x v ＝2a ·x2得：2x v ＝v 22＝22m/s ，选项B 正确．中间位置的速度与初、末速度的关系：在匀变速直线运动中，某段位移x 的初、末速度分别是v 0和v t ，加速度为a ，中间位置的速度为2x v ，则2x v ＝v 02＋v t 22.(请同学们自己推导) 二、匀变速直线运动的规律总结 1．两个基本公式 v t ＝v 0＋at x ＝v 0t ＋12at 2上两个公式中包括五个物理量，原则上已知其中三个物理量可以求解另外两个物理量，由这两个基本公式可以解决所有的匀变速直线运动问题．解题时要注意公式的矢量性，先根据规定好的正方向确定好所有矢量的正负值． 2．几个导出公式及特点(1)v t 2－v 02＝2ax ，此式不涉及时间，若题目中已知量和未知量都不涉及时间，利用此式往往比较简单．(2)x ＝v t 普遍适用于各种运动，而v ＝v 0＋v t2＝2t v 只适用于匀变速直线运动，两者相结合可以轻松地求出中间时刻的瞬时速度或者初、末速度．(3)x 2－x 1＝aT 2适用于匀变速直线运动，进一步的推论有x m －x n ＝(m －n )aT 2(其中T 为连续相等的时间间隔，x m 为第m 个时间间隔内的位移，x n 为第n 个时间间隔内的位移)．例3 一辆汽车从静止开始做匀加速直线运动，已知途中先后经过相距27m 的A 、B 两点所用时间为2s ，汽车经过B 点时的速度为15m/s.求： (1)汽车经过A 点时的速度大小和加速度大小； (2)汽车从出发点到A 点经过的距离；(3)汽车经过B 点后再经过2s 到达C 点，则BC 间距离为多少？答案 (1)12m/s 1.5 m/s 2 (2)48m (3)33m解析 (1)设汽车初始运动方向为正方向，过A 点时速度为v A ，则AB 段平均速度为v AB ＝v A ＋v B2故由x ＝v t ＝vAB t ＝v A ＋v B2t ，解得v A ＝12m/s. 对AB 段：a ＝v B －v At AB＝1.5m/s 2.(2)对OA 段(v 0＝0)：由v A 2－v 02＝2ax OA 得x OA ＝v A 2－v 022a＝48m.(3)汽车经过BC 段的时间等于经过AB 段的时间，根据公式x 2－x 1＝aT 2对于AC 段有：x BC －x AB ＝aT 2，得x BC ＝x AB ＋aT 2＝27m ＋1.5×22m ＝33m. 三、初速度为零的匀加速直线运动的比例式例4 飞机、火车、汽车等交通工具由静止到稳定运动的过程都可以看做从零开始的匀加速直线运动．若一辆汽车从静止开始做匀加速直线运动，则求汽车： (1)1s 末、2s 末、3s 末瞬时速度之比； (2)1s 内、2s 内、3s 内的位移之比； (3)第1s 内、第2s 内、第3s 内的位移之比；(4)经过连续相等的位移，如经过第一个x 、第二个x 、第三个x 所用时间之比．答案 (1)1∶2∶3 (2)1∶4∶9 (3)1∶3∶5 (4)1∶(2－1)∶(3－2)解析 (1)由v ＝at 知：v 1∶v 2∶v 3＝1∶2∶3(2)由x ＝12at 2得：x 1∶x 2∶x 3＝1∶22∶32＝1∶4∶9(3)第1s 内位移x Ⅰ＝12a ×12第2s 内位移x Ⅱ＝12a ×22－12a ×12＝12a ×3第3s 内位移为x Ⅲ＝12a ×32－12a ×22＝12a ×5故x Ⅰ∶x Ⅱ∶x Ⅲ＝1∶3∶5(4)由x ＝12at Ⅰ2，得第一个x 所用时间t Ⅰ＝2xa .前2x 所用时间t 2＝2×2xa故第二个x 所用时间为t Ⅱ＝t 2－t Ⅰ＝(2－1)2x a同理第三个x 所用时间t Ⅲ＝(3－2)2x a所以有t Ⅰ∶t Ⅱ∶t Ⅲ＝1∶(2－1)∶(3－2)．1．初速度为0的匀加速直线运动，按时间等分(设相等的时间间隔为T )，则： (1)T 末、2T 末、3T 末、…、nT 末的瞬时速度之比为： v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .(2)T 内、2T 内、3T 内、…、nT 内的位移之比为： x 1∶x 2∶x 3∶…∶x n ＝12∶22∶32∶…∶n 2.(3)第一个T 内、第二个T 内、第三个T 内、…、第n 个T 内的位移之比为： x 1′∶x 2′∶x 3′∶…∶x n ′＝1∶3∶5∶…∶(2n －1)． 2．按位移等分(设相等的位移为x )的比例式(1)前x 末、前2x 末、前3x 末、…、前nx 末的瞬时速度之比v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .(2)通过前x 、前2x 、前3x 、…、前nx 的位移所用时间之比t 1∶t 2∶t 3∶…∶t n ＝1∶2∶3∶…∶n .(3)通过连续相同的位移所用时间之比为：t 1′∶t 2′∶t 3′∶…∶t n ′＝1∶(2－1)∶(3－2)∶…∶(n －n －1)．例5 一小球沿斜面由静止开始匀加速滚下(斜面足够长)，已知小球在第4s 末的速度为4m/s.求：(1)第6s 末的速度； (2)前6s 内的位移； (3)第6s 内的位移．答案 (1)6m/s (2)18m (3)5.5m解析 (1)由v 4＝at 4得a ＝v 4t 4＝4m/s 4s ＝1m/s 2.所以第1s 内的位移x 1＝12a ×12m ＝0.5m由于第4s 末与第6s 末的速度之比v 4∶v 6＝4∶6＝2∶3 故第6s 末的速度v 6＝32v 4＝6m/s(2)第1s 内与前6s 内的位移之比x 1∶x 6＝12∶62 故前6s 内小球的位移x 6＝36x 1＝18m (3)第1s 内与第6s 内的位移之比 x Ⅰ∶x Ⅵ＝1∶(2×6－1)＝1∶11 故第6s 内的位移x Ⅵ＝11x Ⅰ＝5.5m.求出第1s 末的速度和第1s 内的位移，然后灵活应用初速度为零的比例式求解会比较简捷．1．(初速度为零的比例式)一个物体从静止开始做匀加速直线运动，它在第1s 内与第2s 内的位移之比为x 1∶x 2，在走完第1 m 时与走完第2 m 时的速度之比为v 1∶v 2.以下说法正确的是( )A ．x 1∶x 2＝1∶3，v 1∶v 2＝1∶2B ．x 1∶x 2＝1∶3，v 1∶v 2＝1∶ 2C ．x 1∶x 2＝1∶4，v 1∶v 2＝1∶2D ．x 1∶x 2＝1∶4，v 1∶v 2＝1∶ 2 答案 B解析由初速度为零的匀变速直线运动的比例关系知x 1∶x 2＝1∶3，由x ＝12at 2知，走完1m与走完2m 所用时间之比为t 1∶t 2＝1∶2，又v ＝at ，可得v 1∶v 2＝1∶2，B 正确． 2．(初速度为零的比例式)一石块从楼房阳台边缘向下做自由落体运动到达地面，把它在空中运动的总时间分为相等的三段，如果它在第一段时间内的位移是1.2m ，那么它在第三段时间内的位移是( ) A ．1.2m B ．3.6m C ．6.0m D ．10.8m答案 C解析该自由落体运动将时间分成了相等的三段，由其规律知：第T 内、第2T 内、第3T 内、…、第nT 内的位移之比为x 1∶x 2∶x 3∶…∶x n ＝1∶3∶5∶…∶(2n －1)，第一段时间内的位移为1.2m ，则第三段时间内的位移为x ＝1.2×5m ＝6.0m ，故选C.。

物理复习：初速度为零的匀变速直线运动的几个比例式推导及应用

物理复习：初速度为零的匀变速直线运动的几个比例式推导及应用1．初速度为0的匀加速直线运动，按时间等分(设相等的时间间隔为T )的比例式(1)T 末、2T 末、3T 末、…nT 末的瞬时速度之比为：v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .T 末的速度： aT v =12T 末的速度： aT T a v 2)2(2==3T 末的速度： aT T a v 3)3(3==……nT 末的速度： naT nT a v n ==)(所以v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .(2)T 内、2T 内、3T 内、…nT 内的位移之比为：x 1∶x 2∶x 3∶…∶x n ＝12∶22∶32∶…∶n 2.T 内（0-T)的位移： 2121aT x = 2T 内（0-2T)的位移： 22224)2(21aT T a x == 3T 内（0-3T)的位移： 22329)3(21aT T a x ==……nT 内（0-nT)的位移： 2222)(21aT n nT a x n == 所以x 1∶x 2∶x 3∶…∶x n ＝12∶22∶32∶…∶n 2.(3)第一个T 内、第二个T 内、第三个T 内、…第n 个T 内的位移之比为：x 1∶x 2∶x 3∶…∶x n ＝1∶3∶5∶…∶(2n －1)．第一个T 内（0-T ）的位移： 21I 21aT x x == 第二个T 内（T-2T ）的位移： 22212II 2321)2(21aT aT T a x x x =-=-= 第三个T 内（2T-3T ）的位移： 22223III 25)2(21)3(21aT T a T a x x x =-=-= ……第n 个T 内[]nT T n --)1(的位移： []2221III 212)1(21)(21aT n T n a nT a x x x n n -=--=-=- 所以x 1∶x 2∶x 3∶…∶x n ＝1∶3∶5∶…∶(2n －1)．2．初速度为0的匀加速直线运动，按位移等分(设相等的位移为x )的比例式(1)通过位置x 、2x 位置、3x 位置…nx 位置时的瞬时速度之比为：v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .当物体位移为x 时： ax v 221= ax v 21=当物体位移为2x 时： ax x a v 4)2(222== ax v 42=当物体位移为3x 时： ax x a v 6)3(223== ax v 63=……当物体位移为nx 时： nax nx a v n 2)(22== nax v n 2=所以v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .(2)通过前x 、前2x 、前3x …前nx 的位移所用时间之比为：t 1∶t 2∶t 3∶…∶t n ＝1∶2∶3∶…∶n .当物体位移为x 时： ax v 221= ax v 21= aax a v t 2011=-= 当物体位移为2x 时： ax x a v 4)2(222== ax v 42= a ax av t 4022=-= 当物体位移为3x 时： ax x a v 6)3(223== ax v 63= a ax a v t 6033=-=……当物体位移为nx 时： nax nx a v n 2)(22== nax v n 2= anax a v t n n 20=-= 所以t 1∶t 2∶t 3∶…∶t n ＝1∶2∶3∶…∶n .(3)通过连续相同的位移所用时间之比为：t 1′∶t 2′∶t 3′∶…∶t n ′＝1∶(2－1)∶(3－2)∶…∶(n －n －1)．当物体通过第1个x 时： ax v 21= aax a v t 2011=-=' 当物体通过第2个x 时： ax v 42= ax v 21= a ax ax av v t 24122-=-=' 当物体通过第3个x 时：axv 63= ax v 42= a ax ax a v v t 46233-=-=' ……当物体通过第n 个x 时：nax v n 2= ax n v n )1(2-= aax n nax a v v t n n n )1(221--=-='- 所以t 1′∶t 2′∶t 3′∶…∶t n ′＝1∶(2－1)∶(3－2)∶…∶(n －n －1)．注意以上比例式成立的前提是物体做初速度为零的匀加速直线运动，对于末速度为零的匀减速直线运动，可把它看成逆向的初速度为零的匀加速直线运动，应用比例关系，可使问题简化．对于一般的匀变速直线运动，连续相等的时间T 内的位移之差是个定值，即2aT x =∆。

粤教版物理必修一第二章探究匀变速直线运动规律2 章末总结

1 2 1 【答案】由题设可知，因 s＝ 2at ＝2×2.5×62m＝45 m＜ 85 m，故乙车运动前，甲车没有与乙车相遇，设甲车与乙车相遇时，乙车已经运动的时间为 t，则甲车运动的时间为(t＋6) 由两车相遇的时间可知 1 1 2 ×2.5×(6＋t) ＝85＋ ×5×t2⇒t1＝4 s，t2＝8 s 2 2 可见，甲车与乙车相遇两次． 1 第一次相遇时 s1＝ ×2.5×102m＝125 m； 2 1 第二次相遇时 s2＝2×2.5×142m＝245 m.
【答案】(1)由匀减速直线运动的公式 vt2＝v2＋2as 可知， 0 当 vt＝0，a＝a1＝－5 m/s2 时得到 v0＝30 m/s. (2)由匀减速直线运动的公式 vt2＝v2＋2as 可知， 0 当 vt＝0，v0＝30 m/s，a＝a2＝－3 m/s2 时得到 s＝150 m，所以司机要提早 x＝150 m－90 m＝60 m.
3．要清楚公式都是矢量式，求解问题时首先要规定一个正方向，并以此来确定其他各矢量的正负，一般选取 v0 的方向为正方向． 4．一个匀变速直线运动的过程，一般用五个物理量来描述，v0，vt，a，s 和 t，只要知道其中三个量，就可以求解其他两个未知量，即知三求二．
5．在分析不知道时间或不需知道时间的问题时，一般用速度位移关系的推论． 6．处理初速度为零的匀加速直线运动和末速度为零的匀减速直线运动时，通常用比例关系的方法来解比较方便．应用比例时，可任意从比例中取出两个或一部分进行应用．但比例顺序要对应，不能颠倒，比例数值也不能改变．
4．临界条件：当两个物体的速度相等时，可能出现恰好追上、恰好避免相撞、相距最远、相距最近等情况，即出现上述四种情况的临界条件为 v1＝v2. 5．解题思路 (1)根据两个物体的运动性质，列出两个物体的位移方程，并注意两物体的时间关系． (2)画出两物体运动过程的示意图，明确两物体的位移关系． (3)注意挖掘题中的隐含条件，如速度相等的临界条件．

习题课《五个比例式》

习题课《五个比例式》复习：v= △x==x= v t22ax= v s=2x=新课：初速度为零的匀加速直线运动的规律(设T为等分时间间隔)1. 1T末、2T末、3T末……nT末的速度之比v1∶v2∶v3∶…∶v n＝________2. 1T内、2T内、3T内……nT内的位移之比x1∶x2∶x3∶…∶x n＝________3. 第一个T内、第二个T内、第三个T内……第nT内的位移xⅠ∶xⅡ∶xⅢ∶…∶x N＝________4. 从静止开始通过x、2x、3x ……nx所用时间之比t1∶t2∶t3∶…∶t n＝________5. 从静止开始通过连续相等的位移所用时间之比为tⅠ∶tⅡ∶tⅢ∶…∶t N＝________例题1做初速度为零的匀加速直线运动的物体，将其运动时间顺次分成1:2:3的三段，则每段时间内的位移之比为例题2 物体从静止开始做匀加速直线运动,测得它在第n秒内的位移为x,则物体运动的加速度为例题3 一列火车由静止开始做匀加速直线运动，一个人站在第一节车厢前端的站台上观察，第一节车厢通过他历时2s，全部车厢通过他历时8s，忽略车厢之间的距离，车厢长度相等，求：（1）.这列火车共有多少节车厢？（2）.第9节车厢通过他所用时间为多少？逆向思维：把匀减速直线运动看成初速度为零的匀加速直线运动例题4 做匀变速直线运动的物体经过4s后停止，若在第1s内的位移是14m，则最后1s的位移是例题5 一滑块以某一速度从斜面底端滑到顶端，其速度恰好减为零。

若设斜面全长L，滑块通过最初3/4L所需时间为t，则滑块从斜面底端到顶端所用时间为例题6一颗子弹垂直穿过三块紧挨在一起的木块后，速度刚好为零，设子弹在各木板中运动的加速度大小恒定。

（1）若子弹穿过每块木板的时间相同，则三块木板的厚度之比为_______ ；（2）若三块木板的厚度相同，则子弹先后穿过三块木板的时间之比为_________。

初速度为0的匀加速直线运动的推论

解法一：用基本公式、平均速度．
质点在第7s内的平均速度为：Fra bibliotek6则第6s末的速度：v =4（m/s）求出加速度：a=（0-v ）/t= -4（m/s2）求初速度：0=v +at， v =-at=-(-4)×7=28（m/s）
6 0 0
千万不要忘了：
末速度为
零的匀减速直线
运动也可以认为是反向的初速度为零的匀加速直线运动
移为
11
D
4.如右图所示，在水平面上固定着三个完全相同的木块，一粒子弹以水平速度 v 射入．若子弹在木块中做匀减速直线运动，当穿透第三个木块时速度恰好为零，则子弹依次穿入每个木块时的速度之比和穿过每个木块所用时间之比分别为( D ) A．v1∶v2∶v3＝3∶2∶1 B．v1∶v2∶v3＝ 3∶ 2∶1 C．t1∶t2∶t3＝1∶ 2∶ 3 D．t1∶t2∶t3＝( 3－ 2)∶( 2－1)∶1
2、一小球以某一初速度沿光滑斜面匀减速上滑，到达顶端时速度为0，历时3s,位移9m, 求其第1秒内的位移。（答案：5m ) （用两种方法解）
解法一：基本公式求加速度a 解法二：能不能用推论呢？ v0 0 a 5m 1s
初速度为0的匀加速直线运动用推论，OK!
0 3m 2s 1m 3s
图 2－2 A．vb＝2 C．de＝3 m 2 m/s B．vc＝3 m/s D．从 d 到 e 所用时间为 4 s
ad BD [解析] 对 ad 段，经 c 时为中间时刻，则 vc＝ 2T ＝3 m/s，选项 B 正确；由 Δx＝aT2，则 a＝0.5 m/s2；经 d vd 时的速度 vd＝vc－aT＝2 m/s，d 到 e 的时间 t＝＝4 s， a vd＋0 de＝ 2 t＝4 m，选项 C 错误，选项 D 正确；经 a 时的速度 va＝a(2T＋t)＝4 m/s，经 b 时的速度 vb＝ 10 m/s，选项 A 错误．

初速度为零的匀加速直线运动推论

X1∶X2∶X3∶……Xn＝12∶22∶32∶……n2
创新微课
初速度为零的匀加速直线运动推论
关于初速度为零的匀加速直线运动的几个比例关系式：
创新微课
3、第一个T秒内，第二个T秒内，第三个T秒内，……
第n个T秒内位移之比为：
T
T
T
T
v
0
xXI 1
xII
xIII
X2
X3
第一个T秒内，第二个T秒内，第三个T秒内，……第n个T秒内位移之比为：
x
x
x
x
t
t
tⅢ
t
Ⅰ
Ⅱ
N
创新微课
初速度为零的匀加速直线运动推论
关于初速度为零的匀加速直线运动的应用：
创新微课
例题、一小球以某一速度沿光滑斜面匀减速上滑,达顶端时的速度为零,历时三秒,位移为9m,求其第1s内的位移.
5m
下节内容：匀变速直线运动位移与速度的关系，下节再见
a
a
创新微课
初速度为零的匀加速直线运动推论
关于初速度为零的匀加速直线运动的几个比例关系式：
2、1x末、2x末、3x末……速度之比为
x
x
x
x
v0
V1
V2
V3
由V at，得
创新微课
初速度为零的匀加速直线运动推论
关于初速度为零的匀加速直线运动的几个比例关系式：
3、第1x、第2x、第3x……所用的时间之比为
创新微课现在开始
夏基业
初速度为零的匀加速直线运动推论
初速度为零的匀加速直线运动推论
关于初速度为零的匀加速直线运动的几个比例关系式
创新微课
一、初速度为零的匀加速直线运动（设T为等分时间间隔）

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题二：初速度为零的匀加速直线运动的几个比例式
设物体做00=v ，加速度为a 的匀加速直线运动，从0=t 时刻开始计时，以T 为时间单位，则：
一．1T 末、2T 末、3T 末、…、nT 末瞬时速度之比为：:::321v v v …
::3:2:1=n v …n :。

由at v =可证。

二．1T 内、2T 内、3T 内、…、n T 内位移之比为：:::321x x x …:3:2:1:222=n x …2:n 。

由22
1at x =可证。

三．第1个T 内、第2个T 内、第3个T 内、…、第n 个T 内位移之比为：
证明：
因此：
例1．一质点从静止开始做匀加速直线运动，则在第1个2s 、第2个2s 和第5s 内的三段位移之比为（ C ）
A.2∶6∶5
B.2∶8∶7
C.4∶12∶9
D.2∶2∶1
解析：
方法一：
设质点的加速度为a ，则
第1个2s 内的位移a x 2
11=×a 222= 第2个2s 内的位移a x 212=×a 2
142-×a 622= 第5s 内的位移a x 213=×a 2152-×a 2
942= x Ⅰ:x Ⅱ:x Ⅲ: …:x n =1:3:5: …:（2n -1） x Ⅰ=2121aT x = x Ⅱ=222122
321)2(21aT aT T a x x =-=- x Ⅲ=2222325)2(21)3(21aT T a T a x x =-=- …… 22)12(aT n x n -= x Ⅰ:x Ⅱ:x Ⅲ: …:x n =1:3:5: …
:(2n -1).
则9:12:4::321=x x x ，C 正确。

方法二：
将2s 时间分成1s 、1s 的时间段，由
知 9:12:49:)75(:)31(::321=++=x x x
练习1.汽车刹车后做匀减速直线运动，经3s 后停止运动，那么，在这连续的三个1s 内汽车通过的位移之比为（ B ）
A.1：3：5
B.5：3：1
C.1：2：3
D.3：2：1
提示：逆向思维。

四．通过连续相等的位移末的瞬时速度之比为：
:::321v v v …:3:2:1:=n v …n :
由ax v 22=可证。

五．通过前x 、前x 2、前x 3、…、前nx 的位移所用时间之比为：
由可证得a
x t at x 2212==。

六．通过连续相等的位移所用时间之比为：
例2．一列车由等长的车厢组成（车厢间的间隙忽略不计）。

一人站在站台上与第1节车厢的最前端对齐，当列车由静止开始做匀加速直线运动，测量第1节车厢通过他的时间为2s ，则从第5节至第16节车厢通过他的时间多长？
解析：由得： :::651t t t …:)56(:)45(:1:16--=t …)1516(:-
则：++651(:t t t ...)16t =1:+-+-5645( (1516)
∴++65t t …==+1162t t 4s
t Ⅰ:t Ⅱ:t Ⅲ: …:t n =:3:2:1…n :
t Ⅰ:t Ⅱ:t Ⅲ: …:t n =:)23(:)12(:1--…)1(:--n n
t Ⅰ:t Ⅱ:t Ⅲ: …:t n =:)23(:)12(:1--…
)1(:--n n =)416(:1-
=1:2 x Ⅰ:x Ⅱ:x Ⅲ: …:x n =1:3:5: …:(2n -1)
练习2．如图所示，完全相同的三木块并排固定在水平面上，一颗子弹以某一速度水平射入，若子弹在木块中做匀减速直线运动，且穿过第3块木块后速度恰好为零，则子弹依次射入每块木板时的速度比和穿过每块木板所需时间比分别为（ BD ）
A.1:2:3::321=v v v
B.1:2:3::321=v v v
C.3:2:1::321=t t t
D.1:)12(:)23(::321--=t t t
解析：逆向思维：子弹向左做初速度为零的匀加速直线运动，则通过连续相等的位移末的瞬时速度之比为：3:2:1::123=v v v ，B 正确；通过连续相等的位移所用时间之比为：)23(:)12(:1::123--=t t t ，D 正确。

1 2 3 1v 2v 3v a 1t 2t 3t 0=v。