高频电子线路(第二版)课件 第四章讲解
《高频电子技术(第2版)》电子教案 课程思政PPT 4.1反馈振荡器的工作原理

EXIT
高频电子线路
4.1 反馈振荡器的工作原理
(3)爱祖国的灿烂文化
• 文化传统作为一个民族群体意识的载体,常常被称为 国家和民族的“胎记”,是一个民族得以延续的“精神 基因”,是培养民族心理、民族个性、民族精神的“摇 篮”,是民族凝聚力的重要基础。人们在现实生活中, 或许会背井离乡,或许会彼此隔绝,但对祖国灿烂文化 和历史传统的认同总会把人们的心连在一起。
4.1 反馈振荡器的工作原理
振荡条件讨论与小结
振荡条件:同时满足起振条件和平衡条件
引入正反馈是构成振荡器的关键。
同时T必须具有随振荡电压Ui 增大而下降的特性
平衡点
为获得这样的
环路增益特性,反 馈环路中要有非线 性环节。
为获得正弦波,振荡电 路中要有选频环节。振荡频 率通常就由选频环节确定。
O
UiA
EXIT
高频电子线路
4.1 反馈振荡器的工作原理
4.1.3 振荡的稳定条件
干扰破坏原平衡状态后, 振荡器自动回到原平衡状态所需条件
EXIT
高频电子线路
4.1 反馈振荡器的工作原理
4.1.3 振荡的稳定条件
一、 振幅稳定条件
T
T
0
U i U i U iA
B 1
A 当反馈网络为线性网络时,
O UiB
Uf
Fu
.
.
要满足 Uf Ui
Uo 起始信号来自电扰动
.
.
起振时要满足 Uf Ui
输出信号大小满足要求
放大器 Ui Ui Au
时,要能自动稳定输出电压,
.
.
Uo
实现 Uf Ui ,使电路进入
稳定状态,输出幅度和频率
高频电子线路 第四章 2

第4章
正弦波振荡器
第二节
LC振荡器 振荡器
一般情况: 一般情况:
g
ie
( g
ω
2 0
g o e + C 1 C 2'
' L
)
< < 1
1 LC
工程估算近似认为: 工程估算近似认为:
ω1 ≈ ω o =
满足以上条件: 满足以上条件:
ϕ f = 0, ϕ F = 0
根据ϕL = 0
ω1 =
C 1C 2 1 ,C = C1 + C 2 LC
1 + g′ ) + g ie k F L kF
由不同的电路求得的值也不相 、 由不同的电路求得的值也不相
k 、g L
F
高频电子线路
第4章
正弦波振荡器
第二节
LC振荡器 振荡器
3、振荡角频率 1/ LC 、 kF不宜太大也不宜太小,否则导致停振。 不宜太大也不宜太小,否则导致停振。 一般取k 一般取 F=0.1~0.5, 起振时 ω)=3 ~5 ~ , 起振时T( 电容三点式和电感三点式区别参考P125 电容三点式和电感三点式区别参考
结论: 结论: 1、判断三点式振荡器是否可能振荡的方法:在电路供电 、判断三点式振荡器是否可能振荡的方法: 正确前提下 判断电路是否满足三点式电路的构成法则 前提下, 三点式电路的构成法则。 正确前提下, 判断电路是否满足三点式电路的构成法则。 2、无论是什么形式的三点式振荡器——振幅的起振条件 、无论是什么形式的三点式振荡器 振幅的起振条件 均 应满足: 应满足: g m ≥ ( g oe 不同的仅仅是 同。
V X1 C2 X3 L X2 C1 L2 X1 X3
高频电子线路-第4章--习题答案
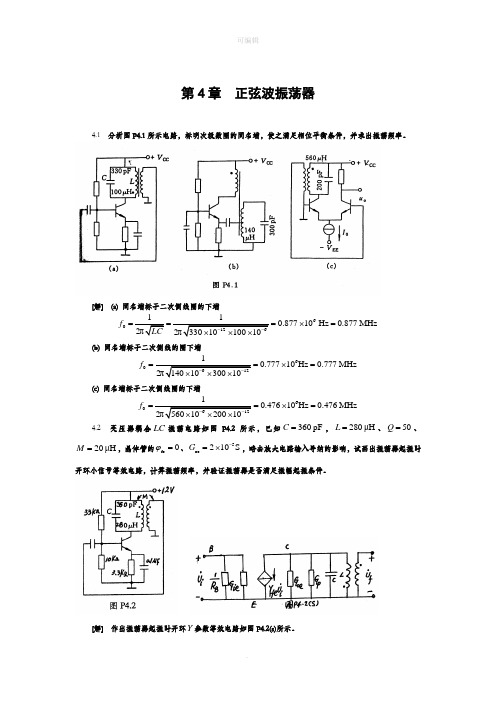
第4章 正弦波振荡器4.1 分析图P4.1所示电路,标明次级数圈的同名端,使之满足相位平衡条件,并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端601260.87710Hz 0.877MHz 2π2π3301010010f LC--===⨯=⨯⨯⨯(b) 同名端标于二次侧线的圈下端606120.77710Hz 0.777MHz 2π1401030010f --==⨯=⨯⨯⨯(c) 同名端标于二次侧线圈的下端606120.47610Hz 0.476MHz 2π5601020010f --==⨯=⨯⨯⨯4.2 变压器耦合LC 振荡电路如图P4.2所示,已知360pF C =,280μH L =、50Q =、20μH M =,晶体管的fe 0ϕ=、5oe 210S G -=⨯,略去放大电路输入导纳的影响,试画出振荡器起振时开环小信号等效电路,计算振荡频率,并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环Y 参数等效电路如图P4.2(s)所示。
略去晶体管的寄生电容,振荡频率等于0612Hz =0.5MHz 2π2π2801036010f LC--==⨯⨯⨯略去放大电路输入导纳的影响,谐振回路的等效电导为5661121042.7μS 502π0.51028010e oe oe o G G G G S S Q Lρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流EQ I 为12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以,三极管的正向传输导纳等于/0.6/260.023S fe m EQ T Y g I U mA mV ≈===因此,放大器的谐振电压增益为o muo eiU g A G U -==而反馈系数为f oU j M M F j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280meg M T A F G L -====⨯ 由于T >1,故该振荡电路满足振幅起振条件。
高频电子线路第4章1-7节201310

Cb c
b'
rb' c
c
rce
Cb' c Cb' e gmVb' e
Cce
c
13
4.2.3 混合π等效电路参数与形式等效电路y 参数的转换
Cb c
根据π等效电路, 写出节点电流方程。
b
rb b '
r b' e Cb e
b +
V1 I1
-
c +
I2 V2
e
I1
+
V1 yi
-
b'
rb' c
c
rce
Cb' c Cb' e gmVb' e
I1
I2
yr
I1 V2
输入短路反向传输导纳
V1 0
+
V1
yi
yr V2
+ yo V2
yf
I2 V1
V2
输出短路正向传输导纳
0
-
yf V1 图4.2.2 y 参数等效电路
-
c
+
yo
I2 V2
输入短路时输出导纳
V1 0
b +
V1 I1
I2 V2
-
-8
e
图4.2.3是晶体管 放大器的基本电路。
17
图4.3.1为单调谐回路
谐振放大器原理性电路与
等效电路,图中为了突出
输入
+
所要讨论的中心问题,故 信号 Vi1
-
略去实际电路中的附属电
路等。
晶体管
a
高频电子线路课件第四章ppt课件

运用较少
4.3.3 LC三端式振荡器相位平衡条件的判别准那么
C
1、XCE与XBE的电抗性质一样;
X1
2、XBC与XCE、XBE的电抗性质相反;
3、对于振荡频率fo,应满足:
E
X3
XCE+XBE+XBC=0
X2 B
集基一样余相反
C
C1
E
L
C2
B
考毕兹电路
C
L1
E
C
L2
B
哈脱莱电路
gn
1 rn
uD
适用中,隧道二极管具有电压控制型负阻器件特性; 单结晶体管、雪崩管具有电流控制型负阻器件特性。
iD
iD
Q
IQ
Im
uUmcost
0
UQ
uD0
t
0
设将负阻特性直线化,并在任务点
电压UQ上叠加一正弦电压u
Um
iurnUm crnotsImcots
t
u D U Q u U Q U m cot s
0.01uF
200pF 100pF C3 C4
C2 200pF
L 8uH
C55.1pF
C1 51pF
4.5 石英晶体振荡器
频率稳定度可到达10-6~10-11。 石英晶体振荡器的优点: 石英晶体的等效谐振回路有很高的规范性; 石英晶体的Q值可高达数百万量级; 在串并联谐振频率之间很窄的任务频带内,
4.3.1 电感反响式三端振荡器〔哈脱莱电路〕
一、电路方式
C
B E
C E
B
二、交流等效电路
三、起振条件 四、振荡频率
hfe L1M 1 hiehoe L2 M hfe
高频电路第四章课件

Department of P.&E.I.S
高频电子线路
振荡线路举例——互感耦合振荡器
在谐振频率 0 1 LC 的情况下,LC并联回路呈纯电 阻性,集电极输出电压与基极 a 180; 输入电压反相,即 根据图中变压器的同名端,次 f 180 , 级线圈引入的相位移 这样 a f 0 ,满足相位 平衡条件。
Department of P.&E.I.S
高频电子线路
振荡线路举例——互感耦合振荡器
电路的振荡频率为:
1 f0 2 LC 1 f 0≈ 2 LC
1 g r
1 g为回路总电导,r为变 r
压器初级线圈损耗电阻。
Department of P.&E.I.S
高频电子线路
振荡线路举例——互感耦合振荡器
环路增益 T ( s) 1 时,即 U (s) Ui (s) i
表明即使外加信号 Us (s) 0 ,也可以维持振荡输出 Uo (s)
Department of P.&E.I.S
高频电子线路
(二)
振荡器的平衡条件****
Department of P.&E.I.S
高频电子线路
振荡器的平衡条件
Department of P.&E.I.S
高频电子线路
振荡电路的组成
正弦波振荡电路一般由以下几个环节组成:
④稳幅环节:稳定输出信号的幅度,改善波形。注意这个 环节既可以直接利用放大器件的非线性自动实现稳幅,也可 以通过加入特定的稳幅电路来实现。
Department of P.&E.I.S
高频电子线路
高频电子线路
(一)
《高频电子线路》PPT课件

uo(t)
uΩ(t)
Δuc
uo(t)=uΩ(t)+UDC
包含了直流及低频调制分量。
峰值包络检波器的应用型输出电路
+ (a) ui
-
VD
Cd
+
+UDC -
+
C uo R
RL uΩ
-
-
(b)
+ ui
-
VD
Rφ
+
C uo R Cφ
-
t
UDC t
+ UDC -
图(a):电容Cd的隔直作用,直流分量UDC被隔离,输出信号为解调恢复后 的原调制信号uΩ,一般常作为接收机的检波电路。 图(b):电容Cφ的旁路作用,交流分量uΩ(t)被电容Cφ旁路,输出信号为直 流分量UDC,一般可作为自动增益控制信号(AGC信号)的检测电路。
rd C R
②对高频载波信号uc来说,电容C的容抗
1 R ,电容C相当于短
cC
路,起到对高频电流的旁路作用,即滤除高频信号。
理想情况下,RC低通滤波网络所呈现的阻抗为分析
+ uD -
当输入信号ui(t)为调幅波时,那么载波正半 +
周时二极管正向导通,输入高频电压通过二 ui
☺调幅解调的分类
振幅调制
AM调 制DSB调制
SSB调制
包络检波 解调
同步检波
峰值包络检波 平均包络检波 叠加型同步检波 乘积型同步检波
☺调幅解调的方法
1. 包络检波
调幅波
t 调幅波频谱
非线形电路
ωc-Ω ωc ωc+Ω ω
低通滤波器
包络检波输出
t 输出信号频谱
高频电子线路课件4-1剖析

振幅平衡的稳定条件表示放大器的电压增
益随振幅增大而减小,它能保证电路参数发生 变化引起的A、F变化时,电路能在新的条件下 建立新的平衡,即振幅产生变化来保证AF=1。
相位平衡的稳定条件表示振荡回路的相移
随频率增大而减小。它能保证振荡电路的参数 发生变化时,能自动通过频率的变化来调整
A F 2n ,保证振荡电路处于正反馈。
用瞬时极性法判断图4-6能否振荡(是否为正反馈)
3⊕
5○
2○
6⊕ 1⊕
4⊕
5○
6⊕ 1⊕
2⊕
3⊕
4○
答案:都是正反馈
总结:互感耦合反馈振荡器通过互感(变 压器)进行反馈,用同名端来保证正反馈。
第三节 反馈型LC振荡器
二 、电容反馈振荡电路
Rb1、Rb 2、Re直流偏压;Ce、Cb直流开路, 交流短路; Lc直流短路,交流开路。从b, c, e三极分析得图(b)
Q点是稳定平衡点
B点是不稳定平衡点
振幅稳定条件:A U c
U c U cQ
0
(2)相位稳定条件为 :Z 0 (4 ─ 16)
分析外因的影响:
当若外输因入使电U压bU的b和相位反超馈前电于压UUbb(相差为L )2则平衡
则相差 2 ,即T ,f ( )
即 L , L
外因的影响是
Z
0
显然,上述三个条件均与电路参数有关,
A由放大器的参数决定,除与工作点有关外, 还与晶体管的参数有关,而反馈系数F是与反馈 元件的参数值有关。
第三节 反馈型LC振荡器
一 、互感耦合振荡电路
5⊕ 1⊕
2⊕ 3⊕
4⊕
振荡条件:用瞬时极 性法判断是否为正反 馈。
振荡频率:0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、元器件作用分析
Ec R1 Cb R2 V Re Ce Lc
C1 L C2
V
C2 L (b)
C1
(a)
2、电路的振荡频率及起振条件
电路的高频小信号等效电路如图4-9(c)所示。其中做了如
下简化:
+ . Ub - g′ L gie . gmUb e (c)
图 4-9 (a) 实际电路; (b) 交流等效电路; (c) 高频等效电路
K ( s) U o ( s) U i ( s)
(4-1) (4-2)
电压反馈系数为F(s),则
由 得
U i( s) F ( s) U o ( s)
(4-3)
(4-4) (4-5) (4-6)
Ui (s) U s (s) Ui(s)
K ( s) K ( s) Ku ( s) 1 K ( s) F ( s) 1 T ( s)
图 4-6
(a) 电容反馈振荡器;
(b) 电感反馈振荡器
图4-6 (b)中X1和X2为感性, X3为容性, 满足三端式振荡 器的组成原则, 反馈网络是由电感元件完成的, 称为电感 反馈振荡器, 也称为哈特莱(Hartley)振荡器。
V X1 C2 X3 L (a) X2 C1 L2 X1 X3
V L1 X2 C (b)
U i( s) 其中T(s)称为环路增益: T ( s) K ( s) F ( s) U i ( s)
自激振荡的条件:就是环路增益为1, 即
T ( j ) K ( j ) F ( j ) 1
通常又称为振荡器的平衡条件。
由式(4-5)还可知
T ( j ) 1 T ( j ) 1 , U i( s ) U i ( s) , , U i( s ) U i ( s ) ,
比较
读教材P125
四、两种改进型电容反馈振荡器
前面分析了电容反馈振荡器和电感反馈振荡器的原理和 特点:
对于电容反馈振荡器:输出波形较好、输出频率较高, 但振荡频率调节不方便;
对于电感反馈振荡器:振荡频率调节比较方便,但输出 波形较差、输出频率不能太高。 无论是电容反馈振荡器还是电感反馈振荡器,晶体管的极 间电容均会对振荡频率有影响,而极间电容受环境温度、电 源电压等因素的影响较大,故他们的频率稳定度不高,需要 对其进行改进,因此得到两种改进型电容反馈振荡器——克 拉泼振荡器和西勒振荡器。
同电容反馈振荡器的分析一样, 振荡器的振荡频率可 以用回路的谐振频率近似表示, 即
1 0
1 LC
(4-30)
式中的L为回路的总电感, 由图4-9有
L L1 L2 2M
(4-31)
实际上,由相位平衡条件分析, 振荡器的振荡频率表达式为
1
1 2 LC gie ( goe g )( L L M ) L 1 2
dt
设振荡器原在ω 1 时处于相位平衡,即有:
(4-19b)
0 f L (1 ) F
相位稳定条件为:
L
1
0
(4-20)
L, - ( f+F ′) L
0
1 2
- ( f+F ′) -
图 4-4 互感耦合振荡器
五、振荡线路举例——互感耦合振荡器 图4-4是一LC振荡器的实际电路, 图中反馈网络由L和 L1 间的互感 M 担任 , 因而称为互感耦合式的反馈振荡器 , 或称为变压器耦合振荡器。 分析教材图4-4的正反馈过程。
式(4-9a)和(4-9b)分别称为振幅平衡条件和相位平衡条件。
现以单调谐谐振放大器为例来看K(jω)与F(jω)的意义。 若
U o U c ,U i 由式 U b (4-2)可得
K ( j )
Uo Ui
Uc Ub
Ic Uc Ub Ic
Y f ( j ) Z L
反馈型振荡器是由放大器和反馈网络组成的一个闭合环 路, 放大器通常是以某种选频网络(如振荡回路)作负载, 是 一调谐放大器, 反馈网络一般是由无源器件组成的线性网 络。
2、自激振荡的条件分析
U o (s) 根据图4.1.1,闭环电压放大倍数Ku(s): Ku U S ( s)
开环电压放大倍数为K(s):
. I C1 C2
b gie
go e
+ . Ub -
A、忽略了晶体管内部反馈的影响,即Yre=0
B、忽略了晶体管的输入输出电容的影响
C、忽略了晶体管集电极电流对输入信号的的相移,将Yfe 用跨导gm表示。
(1)振荡频率
由4-9©可得:
I U b jc2 gie I g mU b U j LI b g oe jc1 g 'L
(4-15b)
(1)平衡时电源供给的能量等于环路消耗的能量;
(2)通常环路只在某一特定才满足相位条件。
三、起振条件 为了使振荡过程中输出幅度不断增加, 应使反馈回来 的信号比输入到放大器的信号大, 即振荡开始时应为增幅 振荡, 因而由式(4-8)可知
T ( j ) 1
称为自激振荡的起振条件, 也可写为
(4-32)
2、起振条件
工程上在计算反馈系数时不考虑gie的影响, 反馈系数的 大小为 L2 M K F G( j ) (4-33) L1 M 由起振条件分析, 同样可得起振时的gm应满足
1 gm ( goe g gie K F L) KF
(4-34)
3 、电容反馈式振荡器与电感反馈式振荡器特点
联立求解I的表达式,令其虚部为零可得振荡频率:
) 1 gie ( goe g L 1 LC C1C2
其中:C为回路的总电容
C1C2 C C1 C2
(4-23)
(4-24)
1 0
(2)起振条件
1 LC
(4-25)
由图4-8(c)可知, 当不考虑gie的影响时, 反馈系数F(jω)的大 小为
A
1 F Ub
图 4-2 振幅条件的图解表示
起振过程:开始增幅振荡
非线性
稳幅振荡
四、稳定条件 1、振荡器稳定概念的提出: 2、振荡器的稳定条件 振荡器的稳定条件分为振幅稳定条件和相位稳定条件。 (1) 振幅稳定条件 要使振幅稳定,振荡器在其平衡点必须具有阻止振幅 变化的能力。具体来说,就是在平衡点附近,当不稳定因 素使振幅增大时,环路增益将减小,从而使振幅减小。 振幅稳定条件为:
第4章 正弦波振荡器
4.1 反馈振荡器的原理 4.2 LC 振 荡 器
4.3 振荡器的频率稳定度
4.4 LC振荡器的设计方法
4.5 石英晶体振荡器
4.6 振荡器中的几种现象
4.1 反馈振荡器的原理
一、反馈振荡器的原理分析 1、反馈振荡器的组成 反馈振荡器由放大器和反馈网络两大部分组成。
反馈型振荡器的原理框图如图 4-1 所示。由图可见 ,
T ( j ) Y f RL F 1
(4-16a)
n 0,1,2,
T f L F 2n
(4-16b)
式(4-16a)和(4-16b)分别称为起振的振幅条件和相位条件, 其中起振的相位条件即为正反馈条件。
Uo 放大特性 A
Uo K
反馈特性 0 (a) Ub 0 (b)
1、振荡频率
Ec R1 Cb + . Ub - R2 Re V + . Ucb - Ce L1 L2
V L2 L1
C
C
(a)
(b)
+ . Ub - (c) gie . gmUb go e
. Uc g′ L
+ c L1
C . I
- b L2 gie
+ . Ub′ -
M e
图 4-10
(a) 实际电路; (b) 交流等效电路; (c) 高频等效电路
(4-28)
则由振荡器的振幅起振条件YfRLF′>1, 可以得到
故有起振条件为:
gm kF 1 2 k F gie g oe g L 1 gie kF kF
通常起振时通常环路 增益取3~5
) gm ( goe g L
(4-29)
三、电感反馈振荡器
图4-9是一电感反馈振荡器的实际电路和交流等效 电路。
1 U C2 C1 k F F ( j ) b 1 Uc C2 C1
(4-26)
将gie折算到放大器输出端, 有
Ub 2 2 ( ) gie kF gie gie Uc
(4-27)
因此, 放大器总的负载电导gL为
2 g L kF gie goe gL
4.2 LC 振 荡 器
一、振荡器的组成原则
1、振荡基本电路——三端式的概念
基本电路就是通常所说的三端式 ( 又称三点式 ) 的振荡器 , 即LC回路的三个端点与晶体管的三个电极分别连接而成的电 . Ic 路, 如图4-5所示。
. Ub X2 X3 V - - . I . Uc X1
+
+
图 4-5三端式振荡器的组成
T U i
U i U iA
0
(4-17)
由于反馈网络为线性网络, 即反馈系数大小F不随输入信 号改变, 故振幅稳定条件又可写为
K U i
U i U iA
0
(4-18)
(2)、相位稳定条件 我们知道,一个正弦信号的相位 φ 和它的频率 ω 之间 的关系: d (4-19a) dt
(4-7)
形成增幅振荡
形成减幅振荡
(4-8)
二、平衡条件
根据前面分析,振荡器的平衡条件即为
