三角形的中心及其性质
三角形的重心、外心、垂心、内心和旁心(五心定理)

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称之为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
一、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG∶GH=1∶2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
三角形的中心与重心性质分析

三角形的中心与重心性质分析在几何学中,三角形是最基本的图形之一,三角形的中心与重心是研究三角形性质时非常重要的概念。
本文将对三角形的中心与重心进行深入分析,并探讨它们的性质与应用。
一、三角形的中心性质分析三角形的中心是指三角形内部某个特殊点,具有一系列独特的性质。
常见的三角形中心有重心G、外心O、内心I以及垂心H等。
1. 重心G:三角形的重心G是三条中线的交点,即三角形三个顶点与对边中点的连线交于一点。
重心G到三角形的顶点距离相等,且重心G将中线分成2:1的比例。
设三角形ABC的重心为G,则有AG:BG:CG=2:2:2。
2. 外心O:三角形的外心O是三角形外接圆的圆心,即三角形三个顶点的垂直平分线交于一点。
外心O到三角形的顶点距离相等,且外心O到各边的距离相等。
外心O是三角形内角平分线相互垂直的点。
3. 内心I:三角形的内心I是三角形内切圆的圆心,即三角形三个内角的角平分线交于一点。
内心I到三角形三边的距离相等,且内心I是三角形外接圆的切点。
4. 垂心H:三角形的垂心H是三角形三条高的交点,即三角形三个顶点作高的垂线交于一点。
垂心H是三角形两条边的中垂线的交点,且垂心H到三角形三个顶点的距离相等。
二、三角形的重心性质分析重心是三角形最重要的中心之一,具有许多重要性质和应用。
1. 坐标表示:设三角形ABC的顶点分别为A(x1, y1),B(x2, y2),C(x3, y3),则三角形的重心G坐标为:G((x1+x2+x3)/3, (y1+y2+y3)/3)。
2. 重心的位置关系:三角形的重心G位于三个顶点所在直线上的2:1的比例处。
即AG:BG:CG=2:2:2,且AG∥BG∥CG。
3. 重心与中心性质的关联:三角形的重心G是三个中心(重心、外心、内心)连线的中点,即重心与外心的连线、重心与内心的连线以及重心与垂心的连线经过同一个点。
三、三角形的性质与应用通过对三角形的中心与重心的性质分析,我们可以得到许多有用的结论,可以应用于解决实际问题。
三角形的重心、外心、垂心、内心和旁心(五心定理)

三角形五心定理(三角形的重心,外心,垂心,内心和旁心称之为三角形的五心)三角形五心定理是指三角形重心定理,外心定理,垂心定理,内心定理,旁心定理的总称。
之巴公井开创作一、二、三角形重心定理三角形的三条边的中线交于一点。
该点叫做三角形的重心。
三中线交于一点可用燕尾定理证明,十分简单。
(重心原是一个物理概念,对于等厚度的质量均匀的三角形薄片,其重心恰为此三角形三条中线的交点,重心因而得名)重心的性质:1、重心到顶点的距离与重心到对边中点的距离之比为2∶1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
即重心到三条边的距离与三条边的长成反比。
3、重心到三角形3个顶点距离的平方和最小。
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其重心坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3。
二、三角形外心定理三角形外接圆的圆心,叫做三角形的外心。
外心的性质:1、三角形的三条边的垂直平分线交于一点,该点即为该三角形外心。
2、若O是△ABC的外心,则∠BOC=2∠A(∠A为锐角或直角)或∠BOC=360°-2∠A(∠A为钝角)。
3、当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
4、计算外心的坐标应先计算下列临时变量:d1,d2,d3分别是三角形三个顶点连向另外两个顶点向量的点乘。
c1=d2d3,c2=d1d3,c3=d1d2;c=c1+c2+c3。
重心坐标:( (c2+c3)/2c,(c1+c3)/2c,(c1+c2)/2c )。
5、外心到三顶点的距离相等三、三角形垂心定理三角形的三条高(所在直线)交于一点,该点叫做三角形的垂心。
垂心的性质:1、三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点圆。
2、三角形外心O、重心G和垂心H三点共线,且OG∶GH=1∶2。
(此直线称为三角形的欧拉线(Euler line))3、垂心到三角形一顶点距离为此三角形外心到此顶点对边距离的2倍。
三角形的中线与中心线的性质

三角形的中线与中心线的性质在学习三角形的性质时,我们经常会涉及到中位线、中线和中心线的概念。
本文将探讨三角形的中线与中心线的性质,以加深对它们的理解。
中线是指连接三角形两个顶点与中点的线段,即三角形的一边的中点与对角线的交点。
相应地,中心线是指连接三角形两个顶点与三角形的垂心的线段,即三角形的一边的垂心与对角线的交点。
首先,我们来探讨中线的性质。
在任意三角形中,三条中线交于一点,该点被称为三角形的重心。
重心是三角形内接圆圆心与外接圆圆心连线的中点。
此外,重心到三角形各顶点的距离之比为2:1,可以用来计算三角形内部的重心位置。
另外,三角形的中线被重心平分。
接下来,我们研究中心线的性质。
与中线类似,中心线也有交于一点的性质。
在任意三角形中,三条中心线交于一点,该点被称为三角形的垂心。
垂心到三角形各顶点连线上的高之和为垂心到三边的距离之和。
此外,中心线与三角形的三个外接圆相切,且垂直于相应边。
中心线还与三角形的外心发生关系,外心到三角形各顶点的距离相等。
综上所述,三角形的中线与中心线具有以下性质:1. 三条中线交于一点,该点为三角形的重心,中心线也交于同一点,该点为三角形的垂心。
2. 三角形的中线被重心平分,即重心到顶点的距离等于重心到中点的距离。
3. 中心线与三角形的外接圆相切,与三角形的外心垂直相交。
4. 垂心到三角形各顶点连线上的高之和等于垂心到三边的距离之和。
5. 中心线与外心、内心之间存在一定的关系,例如垂心到三角形各顶点的距离相等。
通过研究三角形的中线与中心线的性质,我们不仅能够更深入地理解三角形的结构,还可以应用这些性质解决与三角形相关的问题。
同时,这些性质也是进一步学习三角形相关定理的基础。
总结起来,三角形的中线与中心线具有多个重要性质,包括重心和垂心的定义、中线平分重心到顶点的距离、中心线与外接圆、垂心到三角形各顶点连线的高之和等等。
这些性质对于我们深入理解和应用三角形相关知识都具有重要意义。
三角形重心、外心、垂心、内心的向量表示及其性质

向量的重心、垂心、内心、外心、旁心三角形重心、内心、垂心、外心的概念及简单的三角形形状判断方法。
重心:ABC ∆中、每条边上所对应的中线的交点; 垂心:ABC ∆中、每条边上所对应的垂线上的交点;内心:ABC ∆中、每个角的角平分线的交点(内切圆的圆心); 外心:ABC ∆中、每条边上所对应的中垂线的交点(外接圆的圆心)。
一、重心1、O 是ABC ∆的重心⇔0=++OC OB OA若O 是ABC ∆的重心,则ABC AOB AOC BOC ∆=∆=∆=∆31故=++,)(31PC PB PA PG ++=⇔G 为ABC ∆的重心.2、 P 是△ABC 所在平面内任一点.G 是△ABC 的重心⇔)(31++=.证明:+=+=+=⇒)()(3PC PB PA CG BG AG PG +++++= ∵G 是△ABC 的重心∴0=++GC GB GA ⇒0=++CG BG AG ,即PC PB PA PG ++=3由此可得)(31++=.(反之亦然(证略))3、已知O 是平面上一定点,A B C ,,是平面上不共线的三个点,动点P 满足()OP OA AB AC λ=++u u u r u u u r u u u r u u u r,(0)λ∈+∞,,则P 的轨迹一定通过ABC △的重心.例1 若O 为ABC ∆内一点,0OA OB OC ++=u u u r u u u r u u u r r,则O 是ABC ∆ 的( )A .内心B .外心C .垂心D .重心二、垂心1、O 是ABC ∆的垂心⇔•=•=•若O 是ABC ∆(非直角三角形)的垂心,则 故tan tan tan =++C B A2、H 是面内任一点,⋅=⋅=⋅⇔点H 是△ABC 的垂心. 由⊥⇔=⋅⇔=-⋅⇔⋅=⋅00)(, 同理AB HC ⊥,BC HA ⊥.故H 是ABC ∆的垂心. (反之亦然(证略))3、P 是ABC △所在平面上一点,若⋅=⋅=⋅,则P 是ABC △的垂心. 由PA PB PB PC ⋅=⋅u u u r u u u r u u u r u u u r ,得()0PB PA PC ⋅-=u u u r u u u r u u u r ,即0PB CA ⋅=u u u r u u u r ,所以PB CA u u u r u u u r⊥.同理可证PC AB u u u r u u u r ⊥,PA BC u u u r u u u r ⊥.∴P 是ABC △的垂心.如图1.4、已知O 是平面上一定点,A B C ,,是平面上不共线的三个点,动点P 满足cos cos AB AC OP OA AB B AC C λ⎛⎫ ⎪=++ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r u u u r,(0)λ∈+∞,,则动点P 的轨迹一定通过ABC △的垂心.例2 P 是△ABC 所在平面上一点,若⋅=⋅=⋅,则P 是△ABC 的() A .外心B .内心C .重心D .垂心三、内心1、O 是ABC ∆的内心的充要条件是图图=⎫⎛•=⎫⎛•=⎫⎛•OCOBOA引进单位向量,使条件变得更简洁。
初高中衔接 数学专题八 三角形“四心”定义与性质
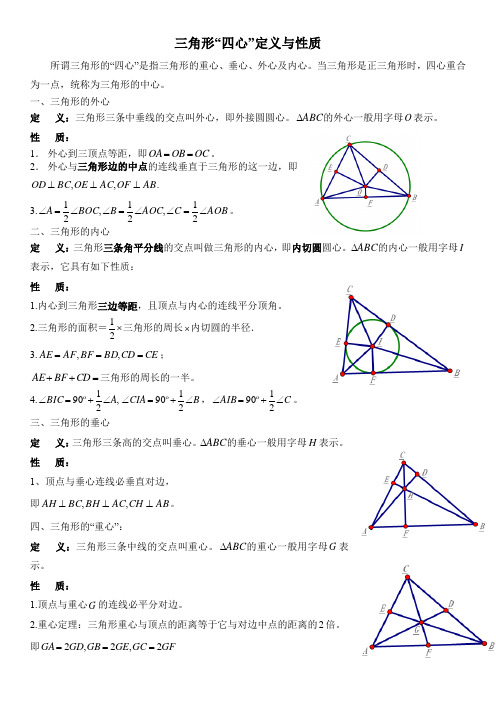
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的外心一般用字母O 表示。
性 质:1. 外心到三顶点等距,即OC OB OA ==。
2. 外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心 定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫垂心。
ABC ∆的垂心一般用字母H 表示。
性 质:1、顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===三角形的三条中线相交于一点,这个交点称为三角形的重心.三角形的重心在三角形的内部,恰好是每条中线的三等分点.例1 求证三角形的三条中线交于一点,且被该交点分成的两段长度之比为2:1.已知 D 、E 、F 分别为ABC V 三边BC 、CA 、AB 的中点,求证 AD 、BE 、CF 交于一点,且都被该点分成2:1.证明:三角形的三条角平分线相交于一点,是三角形的内心. 三角形的内心在三角形的内部,它到三角形的三边的距离相等.例 2 已知ABC ∆的三边长分别为,,BC a AC b AB c ===,I 为ABC ∆的内心,且I 在ABC ∆的边BC AC AB 、、上的射影分别为D E F 、、,求证:2b c a AE AF +-==. 证明例3若三角形的内心与重心为同一点,求证:这个三角形为正三角形.已知 O 为三角形ABC 的重心和内心.求证 三角形ABC 为等边三角形.证明正三角形三条边长相等,三个角相等,且四心(内心、重心、垂心、外心)合一,该点称为正三角形的中心.。
三角形重心、外心、垂心、内心的向量表示及其性质

向量的重心、垂心、内心、外心、旁心三角形重心、内心、垂心、外心的概念及简单的三角形形状判断方法。
重心:ABC 中、每条边上所对应的中线的交点;垂心:ABC 中、每条边上所对应的垂线上的交点;内心:ABC 中、每个角的角平分线的交点(内切圆的圆心);外心:ABC 中、每条边上所对应的中垂线的交点(外接圆的圆心)。
一、重心1、 O 是 ABC 的重心OA OB OC 0若 O 是 ABC 的重心,则BOC AOC AOB 1 ABC 故 OA OB OC 0 ,1 (PA 3PG PB PC) G 为 ABC 的重心 .3、 P 是△ ABC所在平面内任一点. G是△ ABC的重心 1 (PA) .2 PG PB PC3证明:PG PA AG PB BG PC CG 3PG ( AG BG CG) (PA PB PC) ∵ G是△ ABC的重心∴ GA GB GC 0 AG BG CG 0,即 3PG PA PB PC由此可得 PG 1 (PA PB PC ) . (反之亦然(证略))33、已知 O 是平面上一定点, A, B, C 是平面上不共线的三个点,动点P 满足OP OA ( AB AC) ,(0,) ,则 P 的轨迹一定通过△ ABC 的重心 .例 1 若 O 为ABC 内一点, OA OB OC 0 ,则 O 是ABC 的()A.内心 B .外心 C .垂心 D .重心第 1 页共 10 页二、垂心1、 O 是 ABC 的垂心OA OB OB OC OA OC若 O 是 ABC ( 非直角三角形 ) 的垂心,则故 tan AOA tan BOB tanCOC 02、H是面内任一点,HA HB HB HC HC HA 点 H 是△ ABC的垂心 .由 HA HB HB HC HB ( HC HA) 0 HB AC 0 HB AC ,同理 HC AB , HA BC . 故 H 是 ABC 的垂心 . (反之亦然(证略))3、 P 是△ ABC 所在平面上一点,若 PA PB PB PC PC PA ,则 P 是△ ABC 的垂心.由 PA PB PB PC ,得 PB (PA PC ) 0 ,即 PB CA 0 ,所以 PB⊥ CA .同理可证 PC ⊥ AB , PA ⊥ BC .∴ P 是△ ABC 的垂心.如图 1.A CCB PEMHPA FB图 1 O 图⑷4、已知 O 是平面上一定点,A, B, C 是平面上不共线的三个点,动点P 满足AB AC,(0,) ,则动点 P 的轨迹一定通过OP OAAC cos CAB cos B△ ABC 的垂心.例 2 P 是△ ABC所在平面上一点,若PA PB PB PC PC PA ,则 P 是△ ABC 的()A.外心B.内心C.重心D.垂心第 2 页共 10 页三、内心1、 O 是ABC 的内心的充要条件是OA AB ACOBBA BC CA CBOCAB AC BA BC CA CB Ae1e2B引进单位向量,使条件变得更简洁。
三角形外心内心重心垂心与向量性质

三 角 形 的“四 心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.3.向量性质:若点O 为ABC ∆所在的平面内一点,满足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(,则点O 为ABC ∆的外心。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.向量性质:设()+∞∈,0λ,则向量||||(AC AB AP =λ,则动点P 的轨迹过ABC ∆的内心。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.向量性质:结论1:若点O 为ABC ∆所在的平面内一点,满足OA OC OC OB OB OA ⋅=⋅=⋅,则点O 为ABC ∆的垂心。
结论2:若点O 为△ABC 所在的平面内一点,满足222222AB OC CA OB BC OA +=+=+, 则点O 为ABC ∆的垂心。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;(2))(31PC PB PA PG ++=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的中心及其性質學習階段 : 三學習範疇 : 度量、圖形與空間範疇 學習單位 : 以演繹法學習幾何 基本能力 : KS3-MS9-3識別三角形的中線、垂直平分線、高線及角平分線簡介:1. 教師派發「三角形的中心及其性質」工作紙。
2. 學生利用Java 檔案 “ABC2.html ”及“Centres.html ”去完成工作紙。
(此檔案需與其他所有檔案放於同一folder 內才可執行,電腦亦需安裝了Java 軟體。
)3. 學生利用檔案 “ABC2.html ”,在Java 的互動幾何的環境中,透過特別設計的工具簡便地分別作出三角形的中線、角平分線、高線及垂直平分線,從而認識這些線的共點性質。
4. 學生再利用檔案 “Centres.html ”,透過拖拉頂點到不同的位置,認識形心將以2:1這個比將各中線分成兩份。
5. 學生再使用「圓」工具()及特別設計的工具,在各個中心點嘗試構作外接圓及內切圓,從而認識外心和內心分別是外接圓及內切圓的中心。
學習單位:以演繹法學習幾何– 「三角形的中心及其性質」工作紙三角形的中心及其性質開啟檔案“ABC2.html ”,可看到以下畫面:畫面顯示的 ABC ,它的三個頂點A 、B 、C 可被隨意拖拉到不同的位置。
題一:三角形的三條中線 1. 點選「中線」工具(),再依次點選A 、B 、C 三點,構作中線AD (圖1)。
2.再依次點選B 、C 、A 及C 、A 、B ,構作中線BE 及CF 。
3. 拖拉三個頂點A 、B 、C ,觀察三條中線的變化,回答以下問題: (a) 三條中線是否相交於同一點? 是☐ 否☐ (b) 若三條中線相交於同一點,這交點是否一定會在三角形 之內? 是☐否☐(c) 若否,在甚麼情況下這交點會在三角形之外?圖11.。
2.,再依次點選A 、B 、C三點,構作角平分線AD (圖2)。
3. 再依次點選B 、C 、A 及C 、A 、B ,構作角平分線BE及CF 。
4. 拖拉三個頂點A 、B 、C ,觀察三條角平分線的變化,回答以下問題: (a) 三條角平分線是否相交於同一點? 是☐ 否☐ (b) 若三條角平分線相交於同一點,這交點是否一定會在 三角形之內? 是☐ 否☐(c) 若否,在甚麼情況下這交點會在三角形之外?題三:三角形的三條高線 1.。
2.點選「高線」工具,再依次點選A 、B 、C 三點,構作高線AD (圖3)。
3. 再依次點選B 、C 、A 及C 、A 、B ,構作角高線BE 及CF 。
4. 拖拉三個頂點A 、B 、C ,觀察三條高線的變化,回答以下問題: (a) 三條高線是否相交於同一點? 是☐ 否☐ (b) 若三條高線相交於同一點,這交點是否一定會在三角形 之內? 是☐ 否☐ (c) 若否,在甚麼情況下這交點會在三角形之外?圖2 圖31.。
2.),再點選線段BC ,構作它的垂直平分線(圖4)。
3. 再依次點選線段CA 及AB ,構作它們的垂直平分線。
4. 拖拉三個頂點A 、B 、C,觀察三條垂直平分的變化,回答以下問題: (a) 三條垂直平分線是否相交於同一點? 是☐ 否☐ (b) 若三條垂直平分線相交於同一點,這交點是否一定會在 三角形之內? 是☐ 否☐(c) 若否,在甚麼情況下這交點會在三角形之外?題五:三角形的中心及其性質從題一至題四,我們發現三角形的三條中線、三條角平分線、三條高線及三條垂直平分線都分別相於一點,這些交點都稱為三角形的中心。
開啟檔案“Centres.html ”,可看到以下畫面:畫面顯示四個全等的 ABC ,拖拉任何一點紅色點可一起改變四個三個形的形狀,拖拉綠點可改變三角形的位置。
圖41. 分別點選「形心」、「內心」、「垂心」及「外心」鈕,可看到三角形的四個中心如下:形心:三角形的三條中線的交點G;內心:三角形的三條角平分線的交點I;垂心:三角形的三條高線的交點H;外心:三角形的三條垂直平分線的交點O。
2. 圖中,三角形的形心、內心及垂心分別將各中線、角平分線及高線分成兩份。
點選「長度及比」鈕,顯示各線段的長度及它們之間的比。
拖拉紅色點改變三角形的形狀。
觀察各線段的長度及它們之間的比的變化。
那一個中心點會以一個固定的比將每條線分成兩份?在以下空位寫下你的發現,並將相關的圖畫出。
3. 再點選「長度及比」鈕,隱藏各線段的長度及它們之間的比。
,再分別點選三角形的形心G點及A點,畫一個以G為圓心、通過A的圓,如圖所示。
這個圓是否也通過B及C?是☐否☐一個通過三角形三個頂點的圓稱為三角形的外接圓。
用「圓」工具,分別以內心、垂心及外心為圓心,畫一個通過A的圓。
拖拉紅點改變三形的形狀,觀察圓形的變化。
以那一點為圓心,可以畫出❒ABC的外接圓?形心☐內心☐垂心☐外心☐4.。
分別點選「形心」、「內心」、「垂心」及「外心」鈕,顯示三角形的四個中心。
點選工具,再分別點選三角形的形心G點及線段AB,畫一個以G為圓心、與AB只相交於一點的圓,如圖所示。
這個圓是否也與BC及CA只相交於一點?是☐否☐一個與三角形三條邊只相交於一點的圓稱為三角形的內切圓。
用工具,分別以內心、垂心及外心為圓心,畫一個與AB只相交於一點的圓。
拖拉紅點改變三形的形狀,觀察圓形的變化。
以那一點為圓心,可以畫出❒ABC的內切圓?形心☐內心☐垂心☐外心☐完學習單位:以演繹法學習幾何– 「三角形的中心及其性質」工作紙三角形的中心及其性質(答案)開啟檔案“ABC2.html ”,可看到以下畫面:畫面顯示的 ABC ,它的三個頂點A 、B 、C 可被隨意拖拉到不同的位置。
題一:三角形的三條中線 1. 點選「中線」工具(),再依次點選A 、B 、C 三點,構作中線AD (圖1)。
2.再依次點選B 、C 、A 及C 、A 、B ,構作中線BE 及CF 。
3. 拖拉三個頂點A 、B 、C ,觀察三條中線的變化,回答以下問題: (a) 三條中線是否相交於同一點? 是☑ 否☐ (b) 若三條中線相交於同一點,這交點是否一定會在三角形 之內? 是☑否☐(c) 若否,在甚麼情況下這交點會在三角形之外?圖11.。
2.,再依次點選A 、B 、C三點,構作角平分線AD (圖2)。
3. 再依次點選B 、C 、A 及C 、A 、B ,構作角平分線BE及CF 。
4. 拖拉三個頂點A 、B 、C ,觀察三條角平分線的變化,回答以下問題: (a) 三條角平分線是否相交於同一點? 是☑ 否☐ (b) 若三條角平分線相交於同一點,這交點是否一定會在 三角形之內? 是☑ 否☐(c) 若否,在甚麼情況下這交點會在三角形之外?題三:三角形的三條高線 1.。
2.點選「高線」工具,再依次點選A 、B 、C 三點,構作高線AD (圖3)。
3. 再依次點選B 、C 、A 及C 、A 、B ,構作角高線BE 及CF 。
4. 拖拉三個頂點A 、B 、C ,觀察三條高線的變化,回答以下問題: (a) 三條高線是否相交於同一點? 是☑ 否☐ (b) 若三條高線相交於同一點,這交點是否一定會在三角形 之內? 是☐ 否☑ (c) 若否,在甚麼情況下這交點會在三角形之外?ABC 為鈍角三角形時。
圖2 圖31.。
2.),再點選線段BC ,構作它的垂直平分線(圖4)。
3. 再依次點選線段CA 及AB ,構作它們的垂直平分線。
4. 拖拉三個頂點A 、B 、C,觀察三條垂直平分的變化,回答以下問題: (a) 三條垂直平分線是否相交於同一點? 是☑ 否☐ (b) 若三條垂直平分線相交於同一點,這交點是否一定會在 三角形之內? 是☐ 否☑(c) 若否,在甚麼情況下這交點會在三角形之外?❒ABC 為鈍角三角形時。
題五:三角形的中心及其性質從題一至題四,我們發現三角形的三條中線、三條角平分線、三條高線及三條垂直平分線都分別相於一點,這些交點都稱為三角形的中心。
開啟檔案“Centres.html ”,可看到以下畫面:畫面顯示四個全等的❒ABC ,拖拉任何一點紅色點可一起改變四個三個形的形狀,拖拉綠點可改變三角形的位置。
圖41. 分別點選「形心」、「內心」、「垂心」及「外心」鈕,可看到三角形的四個中心如下:形心:三角形的三條中線的交點G;內心:三角形的三條角平分線的交點I;垂心:三角形的三條高線的交點H;外心:三角形的三條垂直平分線的交點O。
2. 圖中,三角形的形心、內心及垂心分別將各中線、角平分線及高線分成兩份。
點選「長度及比」鈕,顯示各線段的長度及它們之間的比。
拖拉紅色點改變三角形的形狀。
觀察各線段的長度及它們之間的比的變化。
那一個中心點會以一個固定的比將每條線分成兩份?在以下空位寫下你的發現,並將相關的圖畫出。
KS3-MS9-3-f2 /p.11 of 12 3. 再點選「長度及比」鈕,隱藏各線段的長度及它們之間的比。
,再分別點選三角形的形心G點及A點,畫一個以G為圓心、通過A的圓,如圖所示。
這個圓是否也通過B及C?是☐否☑一個通過三角形三個頂點的圓稱為三角形的外接圓。
用「圓」工具,分別以內心、垂心及外心為圓心,畫一個通過A的圓。
拖拉紅點改變三形的形狀,觀察圓形的變化。
以那一點為圓心,可以畫出❒ABC的外接圓?形心☐內心☐垂心☐外心☑5.。
分別點選「形心」、「內心」、「垂心」及「外心」鈕,顯示三角形的四個中心。
點選工具,再分別點選三角形的形心G點及線段AB,畫一個以G為圓心、與AB只相交於一點的圓,如圖所示。
這個圓是否也與BC及CA只相交於一點?是☐否☑一個與三角形三條邊只相交於一點的圓稱為三角形的內切圓。
用工具,分別以內心、垂心及外心為圓心,畫一個與AB只相交於一點的圓。
拖拉紅點改變三形的形狀,觀察圓形的變化。
以那一點為圓心,可以畫出❒ABC的內切圓?形心☐內心☑垂心☐外心☐完。
