大学物理习题4答案
大学物理刚体的定轴转动习题及答案
第4章 刚体的定轴转动 习题及答案1．刚体绕一定轴作匀变速转动,刚体上任一点是否有切向加速度是否有法向加速度切向和法向加速度的大小是否随时间变化答：当刚体作匀变速转动时,角加速度β不变;刚体上任一点都作匀变速圆周运动,因此该点速率在均匀变化,v l ω=,所以一定有切向加速度t a l β=,其大小不变;又因该点速度的方向变化,所以一定有法向加速度2n a l ω=,由于角速度变化,所以法向加速度的大小也在变化;2. 刚体绕定轴转动的转动定律和质点系的动量矩定理是什么关系答：刚体是一个特殊的质点系,它应遵守质点系的动量矩定理,当刚体绕定轴Z 转动时,动量矩定理的形式为zz dL M dt=,z M 表示刚体对Z 轴的合外力矩,z L 表示刚体对Z 轴的动量矩;()2z i iL m l I ωω==∑,其中()2i iI m l =∑,代表刚体对定轴的转动惯量,所以()z z dL d d M I I I dt dt dtωωβ====;既 z M I β=; 所以刚体定轴转动的转动定律是质点系的动量矩定理在刚体绕定轴转动时的具体表现形式,及质点系的动量矩定理用于刚体时在刚体转轴方向的分量表达式; 3．两个半径相同的轮子,质量相同,但一个轮子的质量聚集在边缘附近,另一个轮子的质量分布比较均匀,试问：1如果它们的角动量相同,哪个轮子转得快2如果它们的角速度相同,哪个轮子的角动量大答：1由于L I ω=,而转动惯量与质量分布有关,半径、质量均相同的轮子,质量聚集在边缘附近的轮子的转动惯量大,故角速度小,转得慢,质量分布比较均匀的轮子转得快；2如果它们的角速度相同,则质量聚集在边缘附近的轮子角动量大; 4．一圆形台面可绕中心轴无摩擦地转动,有一玩具车相对台面由静止启动,绕轴作圆周运动,问平台如何运动如小汽车突然刹车,此过程角动量是否守恒动量是否守恒能量是否守恒答：玩具车相对台面由静止启动,绕轴作圆周运动时,平台将沿相反方向转动；小汽车突然刹车过程满足角动量守恒,而能量和动量均不守恒;5．一转速为1200r min 的飞轮,因制动而均匀地减速,经10秒后停止转动,求：（1） 飞轮的角加速度和从开始制动到停止转动,飞轮所转过的圈数； （2） 开始制动后5秒时飞轮的角速度; 解：1由题意飞轮的初角速度为飞轮作均减速转动,其角加速度为故从开始制动到停止转动,飞轮转过的角位移为 因此,飞轮转过圈数为/2θπ∆=100圈;2开始制动后5秒时飞轮的角速度为6．如图所示, 一飞轮由一直径为2()d m ,厚度为()a m 的圆盘和两个直径为1()d m ,长为()L m 的共轴圆柱体组成,设飞轮的密度为3(/)kg m ρ,求飞轮对轴的转动惯量;解：如图所示,根据转动惯量的可加性,飞轮对轴的转动惯量可视为圆盘与两圆柱体对同轴的转动惯量之和;由此可得7. 如图所示,一半径为r,质量为m 1的匀质圆盘作为定滑轮,绕有轻绳,绳上挂一质量为m 2的重物,求重物下落的加速度;解：设绳中张力为T对于重物按牛顿第二定律有22m g T m a -= 1对于滑轮按转动定律有212Tr mr β=2 由角量线量关系有a r β= 3联立以上三式解得8. 如图所示,两个匀质圆盘同轴地焊在一起,它们的半径分别为r 1、r 2,质量为1m 和2m ,可绕过盘心且与盘面垂直的光滑水平轴转动,两轮上绕有轻绳,各挂有质量为3m 和4m 的重物,求轮的角加速度β;解：设连接3m 的绳子中的张力为T1,连接4m 的绳子中的张力为T2; 对重物3m 按牛顿第二定律有3133m g T m a -= 1 对重物4m 按牛顿第二定律有2444T m g m a -= 2对两个园盘,作为一个整体,按转动定律有112211221122T r T r m r m r β⎛⎫-=+ ⎪⎝⎭3aLd 1d 2由角量线量之间的关系有 31a r β=442a r β= 5联立以上五式解得9. 如图所示,一半径为R,质量为m 的匀质圆盘,以角速度ω绕其中心轴转动;现将它平放在一水平板上,盘与板表面的摩擦因数为μ;1求圆盘所受的摩擦力矩；2问经过多少时间后,圆盘转动才能停止 解：分析：圆盘各部分的摩擦力的力臂不同,为此,可将圆盘分割成许多同心圆环,对环的摩擦力矩积分即可得总力矩;另由于摩擦力矩是恒力矩,由角动量定理可求得圆盘停止前所经历的时间;1圆盘上半径为r 、宽度为dr 的同心圆环所受的摩擦力矩为负号表示摩擦力矩为阻力矩;对上式沿径向积分得圆盘所受的总摩擦力矩大小为2由于摩擦力矩是一恒力矩,圆盘的转动惯量212I mr =,由角动量定理可得圆盘停止的时间为10. 飞轮的质量m ＝60kg,半径R ＝0.25m,绕其水平中心轴O 转动,转速为900rev ·min -1．现利用一制动的闸杆,在闸杆的一端加一竖直方向的制动力F ,可使飞轮减速．已知闸杆的尺寸如题4-10图所示,闸瓦与飞轮之间的摩擦系数μ=,飞轮的转动惯量可按匀质圆盘计算．试求：1设F ＝100 N,问可使飞轮在多长时间内停止转动在这段时间里飞轮转了几转2如果在2s 内飞轮转速减少一半,需加多大的力F解: 1先作闸杆和飞轮的受力分析图如图b ．图中N 、N '是正压力,r F 、r F '是摩擦力,x F 和y F 是杆在A 点转轴处所受支承力,R 是轮的重力,P 是轮在O 轴处所受支承力．杆处于静止状态,所以对A 点的合力矩应为零,设闸瓦厚度不计,则有对飞轮,按转动定律有I R F r /-=β,式中负号表示β与角速度ω方向相反．∵ N F r μ=N N '=∴F l l l N F r 121+='=μμ 又∵ ,212mR I = ∴ F mRl l l I R F r 121)(2+-=-=μβ ① 以N 100=F 等代入上式,得由此可算出自施加制动闸开始到飞轮停止转动的时间为 这段时间内飞轮的角位移为可知在这段时间里,飞轮转了1.53转． 210s rad 602900-⋅⨯=πω,要求飞轮转速在2=t s 内减少一半,可知 用上面式1所示的关系,可求出所需的制动力为11. 如图所示,主动轮A 半径为r 1,转动惯量为1I ,绕定轴1O 转动；从动轮B 半径为r 2,转动惯量为2I ,绕定轴2O 转动；两轮之间无相对滑动;若知主动轮受到的驱动力矩为M ,求两个轮的角加速度1β和2β;解：设两轮之间摩擦力为f 对主动轮按转动定律有:111M fr I β-= 1对从动轮按转动定律有222fr I β= 2由于两个轮边沿速率相同,有1122r r ββ= 3联立以上三式解得12. 固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴O O '转动．设大小圆柱体的半径分别为R 和r ,质量分别为M 和m ．绕在两柱体上的细绳分别与物体1m 和2m 相连,1m 和2m 则挂在圆柱体的两侧,如题4-12a 图所示．设R ＝0.20m, r ＝0.10m,m ＝4 kg,M ＝10 kg,1m ＝2m ＝2 kg,且开始时1m ,2m 离地均为h ＝2m ．求：1柱体转动时的角加速度； 2两侧细绳的张力．解: 设1a ,2a 和β分别为1m ,2m 和柱体的加速度及角加速度方向题4-12b图．(1) 1m ,2m 和柱体的运动方程如下：2222a m g m T =- ① 1111a m T g m =- ②βI r T R T ='-'21 ③式中 ββR a r a T T T T ==='='122211,,,而 222121mr MR I += 由上式求得 2由①式 由②式13. 一质量为m 、半径为R 的自行车轮,假定质量均匀分布在轮缘上,可绕轴自由转动．另一质量为0m 的子弹以速度0v 射入轮缘如题2-31图所示方向． 1开始时轮是静止的,在质点打入后的角速度为何值2用m ,0m 和θ表示系统包括轮和质点最后动能和初始动能之比． 解: 1射入的过程对O 轴的角动量守恒 ∴ Rm m v m )(sin 000+=θω2020*********sin 21])(sin ][)[(210m m m v m R m m v m R m m E E k k +=++=θθ14. 如图所示,长为l 的轻杆,两端各固定质量分别为m 和2m 的小球,杆可绕水平光滑固定轴O 在竖直面内转动,转轴O 距两端分别为13l 和23l ．轻杆原来静止在竖直位置．今有一质量为m 的小球,以水平速度0υ与杆下端小球m 作对心碰撞,碰后以021υ 的速度返回,试求碰撞后轻杆所获得的角速度．解：碰撞过程满足角动量守恒：而 222212()2()333I m l m l ml =+=2m m O21 0vl l 31l所以 2023mv l ml ω=由此得到：032vlω=15. 如图所示,A 和B 两飞轮的轴杆在同一中心线上,设两轮的转动惯量分别为 J A ＝10 kg ·m2 和 J B ＝20 kg ·m2．开始时,A 轮转速为600 rev/min,B 轮静止．C 为摩擦啮合器,其转动惯量可忽略不计．A 、B 分别与C 的左、右两个组件相连,当C 的左右组件啮合时,B 轮得到加速而A 轮减速,直到两轮的转速相等为止．设轴光滑,求：1 两轮啮合后的转速n ；2 两轮各自所受的冲量矩．解：1 两轮啮合过程满足角动量守恒： 所以 A AA BI I I ωω=+ 因为 2n ωπ= 故 10600200/min 1020A A AB I n n r I I ⨯===++ 2 两轮各自所受的冲量矩： 末角速度：2200202/603n rad s ππωπ⨯=== A 轮各所受的冲量矩：202060040010(2) 4.1910()3603A A L I I N m s ππωωπ∆=-=⨯-⨯=-=-⨯⋅⋅B 轮各所受的冲量矩：16. 有一半径为R 的均匀球体,绕通过其一直径的光滑固定轴匀速转动,转动周期为0T ．如它的半径由R 自动收缩为R 21,求球体收缩后的转动周期．球体对于通过直径的轴的转动惯量为J ＝2mR2 / 5,式中m 和R 分别为球体的质量和半径．解：1 球体收缩过程满足角动量守恒：所以17. 一质量均匀分布的圆盘,质量为M,半径为R,放在一粗糙水平面上圆盘与水平面之间的摩擦系数为,圆盘可绕通过其中心O 的竖直固定光滑轴转动．开始时,圆盘静止,一质量为m 的子弹以水平速度v0垂直于圆盘半径打入圆盘边缘并嵌在盘边上,求1 子弹击中圆盘后,盘所获得的角速度．2 经过多少时间后,圆盘停止转动．解：1 子弹击中圆盘过程满足角动量守恒： 所以 002211()22mRv mv mR MR m M Rω==++ 2圆盘受到的摩擦力矩为 由转动定律得 M Iβ'=。
大学物理第四章习题解
第四章 刚体的定轴转动4–1 半径为20cm 的主动轮，通过皮带拖动半径为50cm 的被动轮转动，皮带与轮之间无相对滑动，主动轮从静止开始作匀角加速度转动，在4s 内被动轮的角速度达到π/s 8，则主动轮在这段时间内转过了 圈。
解：被动轮边缘上一点的线速度为πm/s 45.0π8222=⨯==r ωv在4s 内主动轮的角速度为πrad/s 202.0π412111====r r v v ω主动轮的角速度为2011πrad/s 540π2==∆-=tωωα在4s 内主动轮转过圈数为20π520ππ2(π212π212121=⨯==αωN （圈）4–2绕定轴转动的飞轮均匀地减速，t ＝0时角速度为0ω＝5rad/s ，t ＝20s 时角速度为08.0ωω=，则飞轮的角加速度α＝ ，t ＝0到t ＝100s 时间内飞轮所转过的角度θ＝ 。
解：由于飞轮作匀变速转动，故飞轮的角加速度为20s /rad 05.020558.0-=-⨯=-=tωωα t ＝0到t ＝100s 时间内飞轮所转过的角度为rad 250100)05.0(21100521220=⨯-⨯+⨯=+=t t αωθ4–3 转动惯量是物体 量度，决定刚体的转动惯量的因素有 。
解：转动惯性大小，刚体的形状、质量分布及转轴的位置。
4–4 如图4-1，在轻杆的b 处与3b 处各系质量为2m 和m 的质点，可绕O 轴转动，则质点系的转动惯量为 。
解：由分离质点的转动惯量的定义得221i i i r m J ∆=∑=22)3(2b m mb +=211mb =4–5 一飞轮以600r/min 的转速旋转，转动惯量为·m 2，现加一恒定的制动力矩使飞轮在1s 内停止转动，则该恒定制动力矩的大小M ＝_________。
解：飞轮的角加速度为20s /rad 20160/π26000-=⨯-=-=tωωα制动力矩的大小为m N π50π)20(5.2⋅-=-⨯==αJ M负号表示力矩为阻力矩。
大学物理第四章 刚体的转动部分的习题及答案
第四章 刚体的转动一、简答题：1、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案：刚体定轴转动时，若所受合外力矩为零或不受外力矩，则刚体的角动量保持不变。
2、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案：刚体绕定轴转动的转动定律：刚体绕定轴转动时，刚体的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比。
表达式为：αJ M =。
3、写出刚体转动惯量的公式，并说明它由哪些因素确定?答案：dm r J V⎰=2①刚体的质量及其分布；②转轴的位置；③刚体的形状。
二、选择题1、在定轴转动中，如果合外力矩的方向与角速度的方向一致，则以下说法正确的是 ( A )A.合力矩增大时，物体角速度一定增大；B.合力矩减小时，物体角速度一定减小；C.合力矩减小时，物体角加速度不一定变小；D.合力矩增大时，物体角加速度不一定增大2、关于刚体对轴的转动惯量，下列说法中正确的是 ( C ) A.只取决于刚体的质量，与质量的空间分布和轴的位置无关； B.取决于刚体的质量和质量的空间分布，与轴的位置无关； C.取决于刚体的质量，质量的空间分布和轴的位置；D.只取决于转轴的位置，与刚体的质量和质量的空间分布无关；3、有一半径为R 的水平圆转台，可绕通过其中心的竖直固定光滑轴转动， 转动惯量为J ，开始时转台以匀角速度0ω转动，此时有一质量为m 的人站住转台中心，随后人沿半径向外跑去，当人到达转台边缘时，转台的角速度为 ( A ) A.()2mR J J +ω B.()2Rm J J +ω C.20mR J ω D.0ω4、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示。
今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的? ( A )A.角速度从小到大，角加速度从大到小．B.角速度从小到大，角加速度从小到大．C.角速度从大到小，角加速度从大到小．D.角速度从大到小，角加速度从小到大．5、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度( C )A.增大B.不变C.减小 (D) 、不能确定6、在地球绕太阳中心作椭圆运动时，则地球对太阳中心的 ( B ) A.角动量守恒，动能守恒 B.角动量守恒，机械能守恒 C.角动量不守恒，机械能守恒 D.角动量守恒，动量守恒7、有两个半径相同,质量相等的细圆环A 和B ，A 环的质量分布均匀，B 环的质量分布不均匀，它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ，则 ( C )A.B A J J >；B.B A J J <；C.B A J J =；D.不能确定A J 、B J 哪个大。
大学物理学课后习题4第四章答案
k
m1g x1
1.0 103 9.8 4.9 102
0.2
N m1
而 t 0 时， x0 1.0 102 m,v0 5.0 102 m s-1 ( 设向上为正)
又
k m
0.2 8 103
5,即T
2
1.26s
A
x02
(
v0
)2
(1.0 102 )2 (5.0 102 )2 5
（7）两列波叠加产生干涉现象必须满足的条件
是
，
和
。
[答案：频率相同，振动方向相同，在相遇点的位相差恒定。]
4.3 质量为10 103 kg 的小球与轻弹簧组成的系统，按
x 0.1cos(8t 2 ) (SI) 的规律作谐振动，求： 3
(1)振动的周期、振幅和初位相及速度与加速度的最大值； (2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与 势能相等?
习题 4.2(2) 图 [答案：b、f； a、e]
（3）一质点沿 x 轴作简谐振动，振动范围的中心点为 x 轴的原点，已知周 期为 T，振幅为 A。
（ a ） 若 t=0 时 质 点 过 x=0 处 且 朝 x 轴 正 方 向 运 动 ， 则 振 动 方 程 为 x=___________________。
[答案： 2 s ] 3
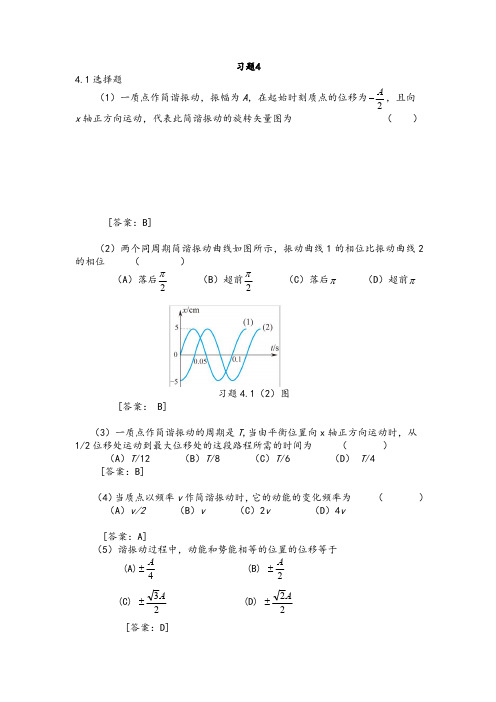
（2）一水平弹簧简谐振子的振动曲线如题 4.2(2)图所示。振子在位移为零， 速度为－A、加速度为零和弹性力为零的状态，对应于曲线上的____________ 点。振子处在位移的绝对值为 A、速度为零、加速度为－2A 和弹性力为－KA 的 状态，则对应曲线上的____________点。
103
(
)2
大学物理教程第4章习题答案
思考题4.1 阿伏伽德罗定律指出：在温度和压强相同的条件下，相同体积中含有的分子数是相等的，与气体的种类无关。
试用气体动理论予以说明。
答：据压强公式，当压强和温度相同时，n也相同，与气体种类无关；4.2 对一定量的气体来说，当温度不变时，气体的压强随体积的减小而增大。
当体积不变时，压强随温度的升高而增大。
从微观角度看，两种情况有何区别。
答：气体压强是器壁单位面积上受到大量气体分子频繁地碰撞而产生的平均作用力的结果。
当温度不变时，若体积减小，分子数密度增大，单位时间内碰撞器壁的分子数增加，从而压强增大；而当体积不变时，若温度升高，分子的平均平动动能增大，分子碰撞器壁的力度变大，从而压强增大；4.3 从气体动理论的观点说明：（1）当气体的温度升高时，只要适当地增大容器的容积，就可使气体的压强保持不变。
（2）一定量理想气体在平衡态（p1，V1，T1）时的热动平衡状况与它在另一平衡态（p2，V2，T2）时相比有那些不同?设气体总分子数为N，p2< p1，V2< V1。
（3）气体在平衡状态下，则，。
(式中、、，是气体分子速度v的三个分量)。
答：（1）由可知，温度升高时，n适当地减小，可使压强不变；（2）在平衡态（，,）时分子的平均平动动能较在平衡态（，，）时小，但分子数密度较大；（3）因分子向各方向运动的概率相同，并且频繁的碰撞，速度的平均值为零，速度平方的平均值大小反映平均平动动能的大小，所以各分量平方平均值相等；4.4 有人说“在相同温度下，不同气体分子的平均平动动能相等，氧分子的质量比氢分子的大，所以氢分子的速率一定比氧分子大”。
这样讲对吗？答：不对，只能说氢分子的速率平方平均值比氧分子的大。
4.5 为什么说温度具有统计意义？讲几个分子具有多大的温度，可以吗？答：温度的微观本质是气体分子平均平动动能大小的量度，而平均平动动能是一个统计平均值，只有大量分子才有统计规律，讲几个分子有多大温度，无意义。
《大学物理》习题答案4-匡乐满主编-北京邮电大学出版社省名师优质课赛课获奖课件市赛课一等奖课件
0.5
0.30s
7. 粒子在加速器中被加速到动能为静止能量旳4倍时，其质量 m
与静止质量 m0 旳关系为：
（A）m 4m0；(B) m 5m0；(C) m 6m0； (D) m 8m0
答案（B） mc2 Ek m0c2 4m0c2 m0c2 5m0c2
大学物理 盛忠志主讲
8. Ek 是粒子旳动能，p 是它旳动量，那么粒子旳静能 m0c 2等于
大学物理 盛忠志主讲
大学物理作业四参照答案
一、选择题
1. 一刚性直尺固定在S系中，它与 X 轴正向夹角 45，
在相对 S系以速度 u 沿 X 轴作匀速直线运动旳 S 系中，
测得该尺与 X 轴正向夹角为 （A） 45；(B) 45 ； (C) 45； (D)不懂得
答案（A）
大学物理 盛忠志主讲
2. 惯性系 S 、S沿X 轴做相对运动，在 S 系中测得两个同步发 生旳事件沿运动方向空间距离为1m，在 S系中测得这两个事件
旳空间间隔为2m。则在 S 系中测得这两个事件旳时间间隔为
（A）
3c
；
（B）1 3
c
；
（C） 3 c
； （D）3 c
x x
1
u c
2 2
答案（C）
u 3c 2
t t1 t2
1 (t u x) 3
1
u2 c2
c2
c
3. 两火箭A、B沿同一直线相向运动，测得两者相对地球旳速度
大小分别是 vA 0.9c ，vB 0.8c 。则两者互测旳相对运动速度为
(A)1.7c ； (B) 0.988c ； (C) 0.956c ； (D) 0.975c
答案（B）
v v u 0.9c (0.8c) 0.988c
大学物理课后习题答案(第四章) 北京邮电大学出版社
习题四4-1 符合什么规律的运动才是谐振动?分别分析下列运动是不是谐振动： (1)拍皮球时球的运动；(2)如题4-1图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很短)．题4-1图解：要使一个系统作谐振动，必须同时满足以下三个条件：一 ，描述系统的各种参量，如质量、转动惯量、摆长……等等在运动中保持为常量；二，系统是在 自己的稳定平衡位置附近作往复运动；三，在运动中系统只受到内部的线性回复力的作用． 或者说，若一个系统的运动微分方程能用0d d 222=+ξωξt描述时，其所作的运动就是谐振动．(1)拍皮球时球的运动不是谐振动．第一，球的运动轨道中并不存在一个稳定的平衡位置；第二，球在运动中所受的三个力：重力，地面给予的弹力，击球者给予的拍击力，都不是线 性回复力．(2)小球在题4-1图所示的情况中所作的小弧度的运动，是谐振动．显然，小球在运动过程中，各种参量均为常量；该系统(指小球凹槽、地球系统)的稳定平衡位置即凹槽最低点，即系统势能最小值位置点O ；而小球在运动中的回复力为θsin mg -，如题4-1图(b)所示．题 中所述，S ∆＜＜R ，故R S∆=θ→0，所以回复力为θmg -.式中负号，表示回复力的方向始终与角位移的方向相反．即小球在O 点附近的往复运动中所受回复力为线性的．若以小球为对象，则小球在以O '为圆心的竖直平面内作圆周运动，由牛顿第二定律，在凹槽切线方向上有θθmg t mR -=22d d令R g=2ω，则有0d d 222=+ωθt4-2 劲度系数为1k 和2k 的两根弹簧，与质量为m 的小球按题4-2图所示的两种方式连 接，试证明它们的振动均为谐振动，并分别求出它们的振动周期．题4-2图解：(1)图(a)中为串联弹簧，对于轻弹簧在任一时刻应有21F F F ==，设串联弹簧的等效倔强系数为串K 等效位移为x ，则有111x k F x k F -=-=串222x k F -=又有 21x x x +=2211k F k F k Fx +==串所以串联弹簧的等效倔强系数为2121k k k k k +=串即小球与串联弹簧构成了一个等效倔强系数为)/(2121k k k k k +=的弹簧振子系统，故小球作谐振动．其振动周期为2121)(222k k k k m k mT +===ππωπ串(2)图(b)中可等效为并联弹簧，同上理，应有21F F F ==，即21x x x ==，设并联弹簧的倔强系数为并k ，则有2211x k x k x k +=并故 21kk k +=并同上理，其振动周期为212k k m T +='π4-3 如题4-3图所示，物体的质量为m ，放在光滑斜面上，斜面与水平面的夹角为θ，弹簧的倔强系数为k ，滑轮的转动惯量为I ，半径为R ．先把物体托住，使弹簧维持原长，然 后由静止释放，试证明物体作简谐振动，并求振动周期．题4-3图解：分别以物体m 和滑轮为对象，其受力如题4-3图(b)所示，以重物在斜面上静平衡时位置为坐标原点，沿斜面向下为x 轴正向，则当重物偏离原点的坐标为x 时，有221d d sin t xm T m g =-θ①βI R T R T =-21②βR t x=22d d )(02x x k T +=③ 式中k mg x /sin 0θ=，为静平衡时弹簧之伸长量，联立以上三式，有kxRt xR I mR -=+22d d )(令I mR kR +=222ω 则有0d d 222=+x t x ω故知该系统是作简谐振动，其振动周期为)/2(22222K R I m kR I mR T +=+==ππωπ4-4 质量为kg 10103-⨯的小球与轻弹簧组成的系统，按)SI ()328cos(1.0ππ+=x 的规律作谐振动，求：(1)振动的周期、振幅和初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差；解：(1)设谐振动的标准方程为)cos(0φω+=t A x ，则知：3/2,s 412,8,m 1.00πφωππω===∴==T A又πω8.0==A v m 1s m -⋅51.2=1s m -⋅2.632==A a m ω2s m -⋅(2)N63.0==m m a FJ 1016.32122-⨯==m mv EJ1058.1212-⨯===E E E k p 当pk E E =时，有pE E 2=，即 )21(212122kA kx ⋅=∴ m 20222±=±=A x(3) ππωφ32)15(8)(12=-=-=∆t t4-5 一个沿x 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，其振动方程用余弦函数表示．如果0=t 时质点的状态分别是：(1)Ax -=0；(2)过平衡位置向正向运动；(3)过2Ax =处向负向运动； (4)过2A x -=处向正向运动． 试求出相应的初位相，并写出振动方程．解：因为 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式，使两式同时成立之值即为该条件下的初位相．故有)2cos(1πππφ+==t T A x )232cos(232πππφ+==t T A x )32cos(33πππφ+==t T A x )452cos(454πππφ+==t T A x 4-6 一质量为kg 10103-⨯的物体作谐振动，振幅为cm 24，周期为s 0.4，当0=t 时位移为cm 24+．求：(1)s 5.0=t 时，物体所在的位置及此时所受力的大小和方向； (2)由起始位置运动到cm 12=x 处所需的最短时间； (3)在cm 12=x 处物体的总能量． 解：由题已知s 0.4,m 10242=⨯=-T A ∴1s rad 5.02-⋅==ππωT又，0=t 时，0,00=∴+=φA x故振动方程为m )5.0cos(10242t x π-⨯= (1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点，即沿x 轴负向．(2)由题知，0=t 时，00=φ，t t =时3,0,20πφ=<+=t v A x 故且 ∴s322/3==∆=ππωφt (3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为J 101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E4-7 有一轻弹簧，下面悬挂质量为g 0.1的物体时，伸长为cm 9.4．用这个弹簧和一个质量为g 0.8的小球构成弹簧振子，将小球由平衡位置向下拉开cm 0.1后 ，给予向上的初速度10s cm 0.5-⋅=v ，求振动周期和振动表达式．解：由题知 12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k而0=t 时，-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又s 26.12,51082.03===⨯==-ωπωT m k 即m 102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωφ==⨯⨯⨯=-=--即x v∴ m)455cos(1022π+⨯=-t x4-8 图为两个谐振动的t x -曲线，试分别写出其谐振动方程．题4-8图解：由题4-8图(a)，∵0=t 时，s2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m)23cos(1.0ππ+=t x a由题4-8图(b)∵0=t 时，35,0,2000πφ=∴>=v A x 01=t 时，22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯=∴πω65=故 mt x b )3565cos(1.0ππ+=4-9 一轻弹簧的倔强系数为k ，其下端悬有一质量为M 的盘子．现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起，于是盘子开始振动． (1)此时的振动周期与空盘子作振动时的周期有何不同? (2)此时的振动振幅多大?(3)取平衡位置为原点，位移以向下为正，并以弹簧开始振动时作为计时起点，求初位相并写出物体与盘子的振动方程．解：(1)空盘的振动周期为k M π2，落下重物后振动周期为k mM +π2，即增大． (2)按(3)所设坐标原点及计时起点，0=t 时，则k mg x -=0．碰撞时，以M m ,为一系统动量守恒，即0)(2v M m gh m +=则有M m ghm v +=20 于是gM m khk mg M m gh m k mg v x A )(21))(2()()(22222++=++=+=ω（3）g m M kh x v )(2tan 000+=-=ωφ(第三象限)，所以振动方程为 ⎥⎦⎤⎢⎣⎡+++++=g m M kh t M m k g M m kh k m g x )(2arctan cos )(214-10 有一单摆，摆长m 0.1=l ，摆球质量kg 10103-⨯=m ，当摆球处在平衡位置时，若给小球一水平向右的冲量14s m kg 100.1--⋅⋅⨯=∆t F ，取打击时刻为计时起点)0(=t ，求振动的初位相和角振幅，并写出小球的振动方程．解：由动量定理，有0-=∆⋅mv t F∴1-34s m 01.0100.1100.1⋅=⨯⨯=∆⋅=--m t F v按题设计时起点，并设向右为x 轴正向，则知0=t 时，100s m 01.0,0-⋅==v x ＞0∴ 2/30πφ= 又1s rad 13.30.18.9-⋅===l g ω∴m 102.313.301.0)(302020-⨯===+=ωωv v x A故其角振幅rad 102.33-⨯==Θl A小球的振动方程为rad)2313.3cos(102.33πθ+⨯=-t4-11 有两个同方向、同频率的简谐振动，其合成振动的振幅为m 20.0，位相与第一振动的位相差为6π，已知第一振动的振幅为m 173.0，求第二个振动的振幅以及第一、第二两振动的位相差．题4-11图解：由题意可做出旋转矢量图如下． 由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A∴ m 1.02=A设角θ为O AA1，则 θcos 22122212A A A A A -+=即1.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ即2πθ=，这说明，1A 与2A 间夹角为2π，即二振动的位相差为2π.4-12 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅：(1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm)343cos(5cm )33cos(521ππt x t x解： (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A(2)∵ ,334πππφ=-=∆∴合振幅 0=A4-13 一质点同时参与两个在同一直线上的简谐振动，振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x试分别用旋转矢量法和振动合成法求合振动的振动幅和初相，并写出谐振方程。
大学物理课后习题答案第四章
第四章机械振动4．1一物体沿x 轴做简谐振动，振幅A = 0.12m ，周期T = 2s ．当t = 0时，物体的位移x = 0.06m ，且向x 轴正向运动．求：（1）此简谐振动的表达式；（2）t = T /4时物体的位置、速度和加速度；（3）物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间． [解答]（1）设物体的简谐振动方程为x = A cos(ωt + φ)，其中A = 0.12m ，角频率ω = 2π/T = π．当t = 0时，x = 0.06m ，所以cos φ = 0.5，因此φ = ±π/3． 物体的速度为v = d x /d t = -ωA sin(ωt + φ)．当t = 0时，v = -ωA sin φ，由于v > 0，所以sin φ< 0，因此：φ = -π/3．简谐振动的表达式为：x = 0.12cos(πt – π/3)．（2）当t = T /4时物体的位置为;x = 0.12cos(π/2 – π/3) = 0.12cosπ/6 = 0.104(m)． 速度为；v = -πA sin(π/2 – π/3) = -0.12πsinπ/6 = -0.188(m·s -1)．加速度为：a = d v /d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s -2)． （3）方法一：求时间差．当x = -0.06m 时，可得cos(πt 1 - π/3) = -0.5， 因此πt 1 - π/3 = ±2π/3．由于物体向x 轴负方向运动，即v < 0，所以sin(πt 1 - π/3) > 0，因此πt 1 - π/3 = 2π/3，得t 1 = 1s ．当物体从x = -0.06m 处第一次回到平衡位置时，x = 0，v > 0，因此cos(πt 2 - π/3) = 0， 可得 πt 2 - π/3 = -π/2或3π/2等．由于t 2> 0，所以πt 2 - π/3 = 3π/2， 可得t 2 = 11/6 = 1.83(s)．所需要的时间为：Δt = t 2 - t 1 = 0.83(s)．方法二：反向运动．物体从x = -0.06m ，向x 轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m ，即从起点向x 轴正方向运动第一次回到平衡位置所需的时间．在平衡位置时，x = 0，v < 0，因此cos(πt - π/3) = 0，可得 πt - π/3 = π/2，解得t = 5/6 = 0.83(s)．[注意]根据振动方程x = A cos(ωt + φ)，当t = 0时，可得φ = ±arccos(x 0/A )，（-π<φ<= π）， 初位相的取值由速度决定．由于v = d x /d t = -ωA sin(ωt + φ)，当t = 0时，v = -ωA sin φ，当v > 0时，sin φ< 0，因此 φ = -arccos(x 0/A )；当v < 0时，sin φ> 0，因此φ = arccos(x 0/A )π/3．可见：当速度大于零时，初位相取负值；当速度小于零时，初位相取正值．如果速度等于零，当初位置x 0 = A 时，φ = 0；当初位置x 0 = -A 时，φ = π．4．2已知一简谐振子的振动曲线如图所示，试由图求：（1）a ，b ，c ，d ，e 各点的位相，及到达这些状态的时刻t 各是多少？已知周期为T ； （2）振动表达式； （3）画出旋转矢量图． [解答]方法一：由位相求时间．（1）设曲线方程为x = A cos Φ，其中A 表示振幅，Φ = ωt + φ表示相位． 由于x a = A ，所以cos Φa = 1，因此Φa = 0．由于x b = A /2，所以cos Φb = 0.5，因此Φb = ±π/3；由于位相Φ随时间t 增加，b 点位相就应该大于a 点的位相，因此Φb = π/3．由于x c = 0，所以cos Φc = 0，又由于c 点位相大于b 位相，因此Φc = π/2．同理可得其他两点位相为：Φd = 2π/3，Φe = π．c 点和a 点的相位之差为π/2，时间之差为T /4，而b 点和a 点的相位之差为π/3，时间之差应该为T /6．因为b 点的位移值与O 时刻的位移值相同，所以到达a 点的时刻为t a = T /6． 到达b 点的时刻为t b = 2t a = T /3．图4.2到达c 点的时刻为t c = t a + T /4 = 5T /12． 到达d 点的时刻为t d = t c + T /12 = T /2． 到达e 点的时刻为t e = t a + T /2 = 2T /3．（2）设振动表达式为：x = A cos(ωt + φ)，当t = 0时，x = A /2时，所以cos φ = 0.5，因此φ =±π/3； 由于零时刻的位相小于a 点的位相，所以φ = -π/3， 因此振动表达式为． 另外，在O 时刻的曲线上作一切线，由于速度是位置对时间的变化率，所以切线代表速度的方向；由于其斜率大于零，所以速度大于零，因此初位相取负值，从而可得运动方程．（3）如图旋转矢量图所示．方法二：由时间求位相．将曲线反方向延长与t 轴 相交于f 点，由于x f = 0，根据运动方程，可得所以：．显然f 点的速度大于零，所以取负值，解得t f = -T /12．从f 点到达a 点经过的时间为T /4，所以到达a 点的时刻为：t a = T /4 + t f = T /6， 其位相为：． 由图可以确定其他点的时刻，同理可得各点的位相．4．3 有一弹簧，当其下端挂一质量为M 的物体时，伸长量为9.8×10-2m ．若使物体上下振动，且规定向下为正方向．（1）t = 0时，物体在平衡位置上方8.0×10-2m 处，由静止开始向下运动，求运动方程；（2）t = 0时，物体在平衡位置并以0.60m·s -1速度向上运动，求运动方程． [解答]当物体平衡时，有：Mg – kx 0 = 0， 所以弹簧的倔强系数为：k = Mg/x 0， 物体振动的圆频率为：s -1)． 设物体的运动方程为：x = A cos(ωt + φ)．（1）当t = 0时，x 0 = -8.0×10-2m ，v 0 = 0，因此振幅为：=8.0×10-2(m)；由于初位移为x 0 = -A ，所以cos φ = -1，初位相为：φ = π． 运动方程为：x = 8.0×10-2cos(10t + π)．（2）当t = 0时，x 0 = 0，v 0 = -0.60(m·s -1)，因此振幅为：v 0/ω|=6.0×10-2(m)；由于cos φ = 0，所以φ = π/2；运动方程为：x = 6.0×10-2cos(10t +π/2)．4．4 质量为10×10-3kg 的小球与轻弹簧组成的系统，按的规律作振动，式中t 以秒(s)计，x 以米(m)计．求： （1）振动的圆频率、周期、振幅、初位相； （2）振动的速度、加速度的最大值；（3）最大回复力、振动能量、平均动能和平均势能；cos(2)3t x A T ππ=-cos(2)03t T ππ-=232f t Tπππ-=±203a a t T πΦπ=-=ω==0||A x ==A =20.1cos(8)3x t ππ=+（4）画出这振动的旋转矢量图，并在图上指明t 为1，2，10s 等各时刻的矢量位置． [解答]（1）比较简谐振动的标准方程：x = A cos(ωt + φ)，可知圆频率为：ω =8π，周期T = 2π/ω = 1/4 = 0.25(s)，振幅A = 0.1(m)，初位相φ = 2π/3．（2）速度的最大值为：v m = ωA = 0.8π = 2.51(m·s -1)； 加速度的最大值为：a m = ω2A = 6.4π2 = 63.2(m·s -2)． （3）弹簧的倔强系数为：k = mω2，最大回复力为:f = kA = mω2A = 0.632(N)； 振动能量为:E = kA 2/2 = mω2A 2/2 = 3.16×10-2(J)， 平均动能和平均势能为:= kA 2/4 = mω2A 2/4 = 1.58×10-2(J)． （4）如图所示，当t 为1，2，10s 等时刻时，旋转矢量的位置是相同的．4．5 两个质点平行于同一直线并排作同频率、同振幅的简谐振动．在振动过程中，每当它们经过振幅一半的地方时相遇，而运动方向相反．求它们的位相差，并作旋转矢量图表示．[解答]设它们的振动方程为:x = A cos(ωt + φ)， 当x = A /2时，可得位相为:ωt + φ = ±π/3．由于它们在相遇时反相，可取Φ1 = (ωt + φ)1 = -π/3，Φ2 = (ωt + φ)2 = π/3，它们的相差为:ΔΦ = Φ2 – Φ1 = 2π/3，或者:ΔΦ` = 2π –ΔΦ = 4π/3．矢量图如图所示．4．6一氢原子在分子中的振动可视为简谐振动．已知氢原子质量m = 1.68×10-27kg ，振动频率v = 1.0×1014Hz ，振幅A = 1.0×10-11m ．试计算：（1）此氢原子的最大速度； （2）与此振动相联系的能量．[解答]（1）氢原子的圆频率为:ω = 2πv = 6.28×1014(rad·s -1)， 最大速度为:v m = ωA = 6.28×103(m·s -1)．（2）氢原子的能量为:= 3.32×10-20(J)．4．7 如图所示，在一平板下装有弹簧，平板上放一质量为1.0kg 的重物，若使平板在竖直方向上作上下简谐振动，周期为0.50s ，振幅为2.0×10-2m ，求：（1）平板到最低点时，重物对平板的作用力；（2）若频率不变，则平板以多大的振幅振动时，重物跳离平板？ （3）若振幅不变，则平板以多大的频率振动时，重物跳离平板？ [解答]（1）重物的圆频率为：ω = 2π/T = 4π，其最大加速度为：a m = ω2A ，合力为：F = ma m ，方向向上．重物受到板的向上支持力N 和向下的重力G ，所以F = N – G ． 重物对平板的作用力方向向下，大小等于板的支持力： N = G + F = m (g +a m ) = m (g +ω2A ) = 12.96(N)．（2）当物体的最大加速度向下时，板的支持为：N = m (g - ω2A )． 当重物跳离平板时，N = 0，频率不变时，振幅为：A = g/ω2 = 3.2×10-2(m)．（3）振幅不变时，频率为：3.52(Hz)．4．8 两轻弹簧与小球串连在一直线上，将两弹簧拉长后系在固定点A 和B 之间，整个系统放在光滑水平面上．设两弹簧的原长分别为l 1和l 2，倔强系统分别为k 1和k 2，A和B 间距为L ，小球的质量为m ．（1）试确定小球的平衡位置；k pE E =212m E mv=2ωνπ==（2）使小球沿弹簧长度方向作一微小位移后放手，小球将作振动，这一振动是否为简谐振动？振动周期为多少？[解答]（1）这里不计小球的大小，不妨设L > l 1 + l 2，当小球平衡时，两弹簧分别拉长x 1和x 2，因此得方程：L = l 1 + x 1 + l 2 + x 2；小球受左右两边的弹簧的弹力分别向左和向右，大小相等，即k 1x 1 = k 2x 2． 将x 2 = x 1k 1/k 2代入第一个公式解得：．小球离A 点的距离为：．（2）以平衡位置为原点，取向右的方向为x 轴正方向，当小球向右移动一个微小距离x 时，左边弹簧拉长为x 1 + x ，弹力大小为：f 1 = k 1(x 1 + x )， 方向向左；右边弹簧拉长为x 1 - x ，弹力大小为：f 2 = k 2(x 2 - x )， 方向向右．根据牛顿第二定律得：k 2(x 2 - x ) - k 1(x 1 + x ) = ma ，利用平衡条件得：，即小球做简谐振动．小球振动的圆频率为：．4．9如图所示，质量为10g 的子弹以速度v = 103m·s -1水平射入木块，并陷入木块中，使弹簧压缩而作简谐振动．设弹簧的倔强系数k = 8×103N·m -1，木块的质量为4.99kg ，不计桌面摩擦，试求：（1）振动的振幅；（2）振动方程．[解答]（1）子弹射入木块时，由于时间很短，木块还来不及运动，弹簧没有被压缩，它们的动量守恒，即：mv = (m + M)v 0．解得子弹射入后的速度为：v 0 = mv/(m + M) = 2(m·s -1)，这也是它们振动的初速度．子弹和木块压缩弹簧的过程机械能守恒，可得：(m + M ) v02/2 = kA 2/2， 所以振幅为：10-2(m)． （2）振动的圆频率为：= 40(rad·s -1)．取木块静止的位置为原点、向右的方向为位移x 的正方向，振动方程可设为：x = A cos(ωt + φ)．当t = 0时，x = 0，可得：φ = ±π/2；由于速度为正，所以取负的初位相，因此振动方程为：x = 5×10-2cos(40t - π/2)．4．10如图所示，在倔强系数为k 的弹簧下，挂一质量为M 的托盘．质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞，而使其作简谐振动，设两物体碰后瞬时为t = 0时刻，求振动方程．[解答]物体落下后、碰撞前的速度为：物体与托盘做完全非弹簧碰撞后，根据动量守恒定律可得它们的共同速度为，这也是它们振动的初速度．设振动方程为：x = A cos(ωt + φ)，211212()k x L l l k k =--+211111212()k L l x l L l l k k =+=+--+2122d ()0d xm kk x t++=ω=22T πω==A v =ω=v =0m v v m M ==+图4.9 图4.10其中圆频率为：物体没有落下之前，托盘平衡时弹簧伸长为x 1，则：x 1 = Mg/k ．物体与托盘磁盘之后，在新的平衡位置，弹簧伸长为x 2，则：x 2= (M + m )g/k ． 取新的平衡位置为原点，取向下的方向为正，则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k ．因此振幅为：初位相为：4．11 装置如图所示，轻弹簧一端固定，另一端与物体m 间用细绳相连，细绳跨于桌边定滑轮M 上，m 悬于细绳下端．已知弹簧的倔强系数为k = 50N·m -1，滑轮的转动惯量J = 0.02kg·m 2，半径R = 0.2m ，物体质量为m = 1.5kg ，取g = 10m·s -2．（1）试求这一系统静止时弹簧的伸长量和绳的张力；（2）将物体m 用手托起0.15m ，再突然放手，任物体m 下落而整个系统进入振动状态．设绳子长度一定，绳子与滑轮间不打滑，滑轮轴承无摩擦，试证物体m 是做简谐振动； （3）确定物体m 的振动周期；（4）取物体m 的平衡位置为原点，OX 轴竖直向下，设振物体m 相对于平衡位置的位移为x ，写出振动方程．[解答]（1）在平衡时，绳子的张力等于物体的重力T = G = mg = 15(N)．这也是对弹簧的拉力，所以弹簧的伸长为：x 0 = mg/k = 0.3(m)．（2）以物体平衡位置为原点，取向下的方向为正，当物体下落x 时，弹簧拉长为x 0 + x ，因此水平绳子的张力为：T 1 = k (x 0+ x )．设竖直绳子的张力为T 2，对定滑轮可列转动方程：T 2R – T 1R = Jβ， 其中β是角加速度，与线加速度的关系是：β = a/R ．对于物体也可列方程：mg - T 2 = ma ． 转动方程化为：T 2 – k (x 0 + x ) = aJ/R 2，与物体平动方程相加并利用平衡条件得：a (m + J/R 2) = –kx ，可得微分方程：，故物体做简谐振动． （3）简谐振动的圆频率为：s -1)． 周期为：T 2 = 2π/ω = 1.26(s)．（4）设物体振动方程为：x = A cos(ωt + φ)，其中振幅为：A = 0.15(m)． 当t = 0时，x = -0.15m ，v 0 = 0，可得：cos φ = -1，因此φ = π或-π， 所以振动方程为：x = 0.15cos(5t + π)，或x = 0.15cos(5t - π)．4．12一匀质细圆环质量为m ，半径为R ，绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动，求摆动的周期．[解答]通过质心垂直环面有一个轴，环绕此轴的转动惯量为：I c = mR 2．根据平行轴定理，环绕过O 点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2．当环偏离平衡位置时，重力的力矩为：M = mgR sin θ， 方向与角度θ增加的方向相反．ω=A ==00arctan v x ϕω-==222d 0d /x kx t m J R +=+ω=根据转动定理得：Iβ = -M ，即，由于环做小幅度摆动，所以sin θ≈θ，可得微分方程：． 摆动的圆频率为：周期为：4．13 重量为P 的物体用两根弹簧竖直悬挂，如图所示，各弹簧的倔强系数标明在图上．试求在图示两种情况下，系统沿竖直方向振动的固有频率．[解答]（1）前面已经证明：当两根弹簧串联时，总倔强系数为k = k1k 2/(k 1 + k 2)，因此固有频率为（2）前面还证明：当两根弹簧并联时，总倔强系数等于两个弹簧的倔强系数之和，因此固有频率为．4．14质量为0.25kg 的物体，在弹性力作用下作简谐振动，倔强系数k = 25N·m -1，如果开始振动时具有势能0.6J ，和动能0.2J ，求：（1）振幅；（2）位移多大时，动能恰等于势能？（3）经过平衡位置时的速度．[解答]物体的总能量为：E = E k + E p = 0.8(J)．（1）根据能量公式E = kA2/2，得振幅为：．（2）当动能等于势能时，即E k = E p ，由于E = E k + E p ，可得：E = 2E p ，即，解得：= ±0.179(m)． （3）再根据能量公式E = mv m2/2，得物体经过平衡位置的速度为： 2.53(m·s -1)．4．15 两个频率和振幅都相同的简谐振动的x-t 曲线如图所示，求： （1）两个简谐振动的位相差；（2）两个简谐振动的合成振动的振动方程． [解答]（1）两个简谐振动的振幅为：A = 5(cm)， 周期为：T = 4(s)，圆频率为：ω =2π/T = π/2，它们的振动方程分别为：x 1 = A cos ωt =5cosπt /2， x 2 = A sin ωt =5sinπt /2 =5cos(π/2 - πt /2)即x 2=5cos(πt /2 - π/2)．位相差为：Δφ = φ2 - φ1 = -π/2． （2）由于x = x 1 + x 2 = 5cosπt /2 +5sinπt /2 = 5(cosπt /2·cosπ/4 +5sinπt /2·sinπ/4)/sinπ/4 合振动方程为：(cm)．22d sin 0d I mgR tθθ+=22d 0d mgRt Iθθ+=ω=222T πω===2ωνπ===2ωνπ===A =2211222kA kx =⨯/2x =m v =cos()24x t ππ=- (b)图4.134．16 已知两个同方向简谐振动如下：，．（1）求它们的合成振动的振幅和初位相； （2）另有一同方向简谐振动x 3 = 0.07cos(10t +φ)，问φ为何值时，x 1 + x 3的振幅为最大？φ为何值时，x 2 + x 3的振幅为最小？（3）用旋转矢量图示法表示（1）和（2）两种情况下的结果．x 以米计，t 以秒计．[解答]（1）根据公式，合振动的振幅为：=8.92×10-2(m)． 初位相为：= 68.22°．（2）要使x 1 + x 3的振幅最大，则：cos(φ– φ1) = 1，因此φ– φ1 = 0，所以：φ = φ1 = 0.6π． 要使x 2 + x 3的振幅最小，则 cos(φ– φ2) = -1，因此φ– φ2 = π，所以φ = π + φ2 = 1.2π．（3）如图所示．4．17质量为0.4kg 的质点同时参与互相垂直的两个振动：， ．式中x 和y 以米(m)计，t 以秒(s)计．（1）求运动的轨道方程；（2）画出合成振动的轨迹；（3）求质点在任一位置所受的力．[解答]（1）根据公式：，其中位相差为：Δφ = φ2 – φ1 = -π/2，130.05cos(10)5x t π=+210.06cos(10)5x t π=+A =11221122sin sin arctancos cos A A A A ϕϕϕϕϕ+=+0.08cos()36x t ππ=+0.06cos()33y t ππ=-2222212122cos sin x y xyA A A A ϕϕ+-∆=∆所以质点运动的轨道方程为：． （2）合振动的轨迹是椭圆．（3）两个振动的圆频率是相同的ω = π/3，质点在x 方向所受的力为，即F x = 0.035cos(πt /3 + π/6)(N)．在y 方向所受的力为，即F y = 0.026cos(πt /3 - π/3)(N)．用矢量表示就是，其大小为，与x 轴的夹角为θ = arctan(F y /F x )．4．18 将频率为384Hz 的标准音叉振动和一待测频率的音叉振动合成，测得拍频为3.0Hz ，在待测音叉的一端加上一小块物体，则拍频将减小，求待测音叉的固有频率．[解答]标准音叉的频率为v 0 = 384(Hz)， 拍频为Δv = 3.0(Hz)， 待测音叉的固有频率可能是v 1 = v 0 - Δv = 381(Hz)， 也可能是v 2 = v 0 + Δv = 387(Hz)．在待测音叉上加一小块物体时，相当于弹簧振子增加了质量，由于ω2 = k/m ，可知其频率将减小．如果待测音叉的固有频率v 1，加一小块物体后，其频率v`1将更低，与标准音叉的拍频将增加；实际上拍频是减小的，所以待测音叉的固有频率v 2，即387Hz ．4．19示波器的电子束受到两个互相垂直的电场作用．电子在两个方向上的位移分别为x = A cos ωt 和y = A cos(ωt +φ)．求在φ = 0，φ = 30º，及φ = 90º这三种情况下，电子在荧光屏上的轨迹方程．[解答]根据公式，其中Δφ = φ2 – φ1 = -π/2，而φ1 = 0，φ2 = φ．（1）当Δφ = φ = 0时，可得，质点运动的轨道方程为y = x ，轨迹是一条直线．（2）当Δφ = φ = 30º时，可得质点的轨道方程， 即，轨迹是倾斜的椭圆．（3）当Δφ = φ = 90º时，可得， 即x 2 + y 2 = A 2，质点运动的轨迹为圆．4．20三个同方向、同频率的简谐振动为，，．222210.080.06x y +=22d d x x x F ma m t==20.08cos()6m t πωω=-+22d d y y y F ma m t==20.06cos()3m t ωω=--πi+j x y F F F =F =2222212122cos sin x y xyA A A A ϕϕ+-∆=∆2222220x y xyA A A+-=222214x y A+=222/4x y A +=22221x y A A +=10.08cos(314)6x t π=+20.08cos(314)2x t π=+350.08cos(314)6x t π=+求：（1）合振动的圆频率、振幅、初相及振动表达式； （2）合振动由初始位置运动到所需最短时间（A 为合振动振幅）． [解答]合振动的圆频率为：ω = 314 = 100π(rad·s -1)． 设A 0 = 0.08，根据公式得：A x = A 1cos φ1 + A 2cos φ2 + A 3cos φ3 = 0，A y = A 1sin φ1 + A 2sin φ2 + A 3sin φ3 = 2A 0 = 0.16(m)， 振幅为：，初位相为：φ = arctan(A y /A x ) = π/2．合振动的方程为：x = 0.16cos(100πt + π/2)．（2）当时，可得：，解得：100πt + π/2 = π/4或7π/4．由于t > 0，所以只能取第二个解，可得所需最短时间为t = 0.0125s ．x A =A =/2x =cos(100/2)2t ππ+。
大学物理课本答案习题 第四章习题解答
习题四4-1 一宇航员要到离地球为5光年的星球去旅行，如果宇航员希望把这路程缩短为3光年，则他所乘的火箭相对于地球的速度应是多少？解 5光年是在地球上测得的原长，由于此长度相对宇航员也是高速运动的，所以他测得收缩了的长度为3光年. 即3=火箭相对于地球的速度应为45u c =4-2 一飞船以0.99c 的速率平行于地面飞行，宇航员测得此飞船的长度为400 m.. （1）地面上的观察者测得飞船长度是多少？（2）为了测得飞船的长度，地面上需要有两位观察者携带着两只同步钟同时站在飞船首尾两端处.那么这两位观察者相距多远？ （3）宇航员测得两位观察者相距多远？解（1）56.4(m)l l ===（2）这两位观察者需同时测量飞船首、尾的坐标，相减得到飞船长度，所以两位观察者相距是56.4 m.（3）地面上的两位观察者相距56.4 m ，这一距离在地面参考系中是原长，宇航员看地面是运动的，他测得地面上两位观察者相距为7.96(m)l l ===所以宇航员测得两位观察者相距7.96 m.4-3 已知π介子在其静止系中的半衰期为81.810s -⨯。
今有一束π介子以0.8u c =的速度离开加速器，试问，从实验室参考系看来，当π介子衰变一半时飞越了多长的距离？解：在π介子的静止系中，半衰期80 1.810s t -∆=⨯是本征时间。
由时间膨胀效应，实验室参考系中的观察者测得的同一过程所经历的时间为8310s t -∆==⨯因而飞行距离为7.2m d u t =∆=4-4 在某惯性系K 中，两事件发生在同一地点而时间相隔为4s 。
已知在另一惯性系'K 中，该两事件的时间间隔为6s，试问它们的空间间隔是多少？解：在K系中，04st∆=为本征时间，在'K系中的时间间隔为6st∆=两者的关系为t∆==所以259β=故两惯性系的相对速度为8110m su cβ-==⋅由洛伦兹变换，'K系中两事件的空间间隔为)k kx x u t'∆=∆+∆两件事在K系中发生在同一地点，因此有0kx∆=，故810mkx'∆==4-5 惯性系'K相对另一惯性系K沿x轴作匀速运动，取两坐标原点重合的时刻作为计时起点。
大连理工大学大学物理作业4(静电场四)及答案详解
作业４ 静电场四它们离地球很远,内球壳用细导线穿过外球壳上得绝缘小孔与地连接,外球壳上带有正电荷,则内球壳上[ ]。
不带电荷 带正电 带负电荷外表面带负电荷,内表面带等量正电荷答案：【C 】解:如图,由高斯定理可知,内球壳内表面不带电。
否则内球壳内得静电场不为零。
如果内球壳外表面不带电(已经知道内球壳内表面不带电)，则两壳之间没有电场,外球壳内表面也不带电;由于外球壳带正电,外球壳外表面带正电;外球壳外存在静电场。
电场强度由内球壳向外得线积分到无限远,不会为零。
即内球壳电势不为零。
这与内球壳接地(电势为零）矛盾。
因此,内球壳外表面一定带电。
设内球壳外表面带电量为(这也就就是内球壳带电量),外球壳带电为，则由高斯定理可知,外球壳内表面带电为,外球壳外表面带电为。
这样,空间电场强度分布,(两球壳之间：) ,(外球壳外:)其她区域（,）,电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Qq R R q r d r rQq r d rr q r d r E r d r E l d E U R R R R R R R πεπεπεπε则,由于,,所以即内球壳外表面带负电,因此内球壳负电。
2.真空中有一组带电导体,其中某一导体表面某处电荷面密度为,该处表面附近得场强大小为,则。
那么,就是［ ］。
该处无穷小面元上电荷产生得场 导体上全部电荷在该处产生得场 所有得导体表面得电荷在该处产生得场 以上说法都不对 答案:【C 】解:处于静电平衡得导体，导体表面附近得电场强度为,指得就是:空间全部电荷分布，在该处产生得电场,而且垂直于该处导体表面。
注意:由高斯定理可以算得，无穷小面元上电荷在表面附近产生得电场为；无限大带电平面产生得电场强度也为,但不就是空间全部电荷分布在该处产生得电场。
3.一不带电得导体球壳半径为，在球心处放一点电荷。
大学物理第四课后习题及答案磁场
习题题10.1：如图所示，两根长直导线互相平行地放置，导线内电流大小相等，均为I = 10 A，方向相同，如图所示，求图中M、N两点的磁感强度B的大小和方向（图中r0 = 0.020 m）。
题10.2：已知地球北极地磁场磁感强度B的大小为6.0?10?5T。
如设想此地磁场是由地球赤道上一圆电流所激发的（如图所示），此电流有多大？流向如何？题10.3：如图所示，载流导线在平面内分布，电流为I，它在点O的磁感强度为多少？题10.4：如图所示，半径为R的木球上绕有密集的细导线，线圈平面彼此平行，且以单层线圈覆盖住半个球面，设线圈的总匝数为N，通过线圈的电流为I，求球心O处的磁感强度。
题10.5：实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场，其装置简图如图所示，一对完全相同、彼此平行的线圈，它们的半径均为R，通过的电流均为I，且两线圈中电流的流向相同，试证：当两线圈中心之间的距离d等于线圈的半径R时，在两线圈中心连线的中点附近区域，磁场可看成是均匀磁场。
（提示：如以两线圈中心为坐标原点O ，两线圈中心连线为x 轴，则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0；0d d 22=xB ）题10.6：如图所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量。
题10.7：如图所示，在磁感强度为B 的均匀磁场中，有一半径为R 的半球面，B 与半球面轴线的夹角为α，求通过该半球面的磁通量。
题10.8：已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热。
电流在导线横截面上均匀分布。
求：（1）导线内、外磁感强度的分布；（2）导线表面的磁感强度。
题10.9：有一同轴电缆，其尺寸如图所示，两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑。
试计算以下各处的磁感强度：（1）r <R 1；（2）R 1<r <R 2；（3）R 2<r <R 3；（4）r >R 3。
大学物理学课后习题4第四章答案
x 轴正方向运动，代表此简谐振动的旋转矢量图为
（）
[答案：B]
（2）两个同周期简谐振动曲线如图所示，振动曲线 1 的相位比振动曲线 2
的相位 （
）
（A）落后
2
（B）超前
2
（C）落后
（D）超前
[答案： B]
习题 4.1（2）图
（3）一质点作简谐振动的周期是 T,当由平衡位置向 x 轴正方向运动时，从
E
1 2
mvm2
3.16 102 J
E p E k 1 E 1.58102 J 2
当 Ek E p 时，有 E 2E p ，
即
1 kx 2 1 ( 1 kA2 )
2
22
∴
x 2 A 2m
2
20
(3)
(t2 t1 ) 8 (5 1) 32
4.4 一个沿 x 轴作简谐振动的弹簧振子，振幅为 A ，周期为T ，其振动 方程用余弦函数表示．如果 t 0 时质点的状态分别是：
的单位是 s，则 （A）波长为 5m
向传播 [答案：C]
（B）波速为 10ms-1
（C）周期为 1 s 3
（D）波沿 x 正方
（8）如图所示，两列波长为 的相干波在 p 点相遇。波在 S1 点的振动初相是 1 ，点 S1 到点 p 的距离是 r1。波在 S2 点的振动初相是2 ，点 S2 到点 p 的距离是
（A）它的动能转化为势能. （B）它的势能转化为动能. （C）它从相邻的一段质元获得能量其能量逐渐增大. （D）它把自己的能量传给相邻的一段质元，其能量逐渐减小.
[答案：D]
4.2 填空题 （1）一质点在 X 轴上作简谐振动，振幅 A＝4cm，周期 T＝2s，其平衡位置
大学物理习题及答案4
一 选择题 (共48分)1. (本题 3分)(1055) 一点电荷，放在球形高斯面的中心处．下列哪一种情况，通过高斯面的电场强度通量发生变化：(A) 将另一点电荷放在高斯面外． (B) 将另一点电荷放进高斯面内．(C) 将球心处的点电荷移开，但仍在高斯面内．(D) 将高斯面半径缩小． ［ ］2. (本题 3分)(5272) 在空间有一非均匀电场，其电场线分布如图所示．在电场中作一半径为R 的闭合球面S ，已知通过球面上某一面元∆S 的电场强度通量为∆Φe ，则通过该球面其余部分的电场强度通量为(A) - ∆Φe ． (B)e SR Φ∆∆π24． (C)e SSR Φ∆∆∆−π24． (D) 0． ［ ］3. (本题 3分)(1255) 图示为一具有球对称性分布的静电场的E ～r 关系曲线．请指出该静电场是由下列哪种带电体产生的．(A) 半径为R 的均匀带电球面．(B) 半径为R 的均匀带电球体． (C) 半径为R 的、电荷体密度为ρ＝A r (A 为常数)的非均匀带电球体．(D) 半径为R 的、电荷体密度为ρ＝A/r (A 为常数)的非均匀带电球体．[ ］E 4. (本题 3分)(1257) 图示为一具有球对称性分布的静电场的E ~r关系曲线．请指出该静电场是由下列哪种带电体产生的．(A) 半径为R 的均匀带电球面． (B) 半径为R 的均匀带电球体． (C) 半径为R 、电荷体密度ρ＝Ar (A 为常 数）的非均匀带电球体．(D) 半径为R 、电荷体密度ρ＝A/r (A 为常数)的非均匀带电球体．［ ］E关于高斯定理的理解有下面几种说法，其中正确的是：(A) 如果高斯面上E v处处为零，则该面内必无电荷．(B) 如果高斯面内无电荷，则高斯面上E v处处为零．(C) 如果高斯面上E v处处不为零，则高斯面内必有电荷．(D) 如果高斯面内有净电荷，则通过高斯面的电场强度通量必不为零．［ ］6. (本题 3分)(5084) A 和B 为两个均匀带电球体，A 带电荷＋q ，B 带电荷－q ，作一与A 同心的球面S 为高斯面，如图所示．则(A) 通过S 面的电场强度通量为零，S 面上各点的场强为零．(B) 通过S 面的电场强度通量为q / ε0，S 面上场强的大小为20π4rq E ε=． (C) 通过S 面的电场强度通量为(- q ) / ε0，S 面上场强的大小为20π4r qE ε=．(D) 通过S 面的电场强度通量为q / ε0，但S 面上各点的场强不能直接由高斯定理求出． ［ ］7. (本题 3分)(1415) 一“无限大”带负电荷的平面，若设平面所在处为电势零点，取x 轴垂直电平面，原点在带电平面处，则其周围空间各点电势U 随距离平面的位置坐标x 变化的关系曲线为： ［ ］(B)(D)8. (本题 3分)(1019) 在点电荷+q 的电场中，若取图中P 点处为电势零点 ， 则M 点的电势为(A) a q 04επ． (B) a q 08επ．(C)a q 04επ−． (D) aq08επ−． ［ ］电荷面密度为+σ和－σ的两块“无限大”均匀带电的平行平板，放在与平面相垂直的x 轴上的+a 和－a 位置上，如图所示．设坐标原点O 处电势为零，则在－a ＜x ＜+a 区域的电势分布曲线为[ ]10. (本题 3分)(1516) 如图所示，两个同心的均匀带电球面，内球面半径为R 1、带电荷Q 1，外球面半径为R 2、带电荷Q 2 .设无穷远处为电势零点，则在两个球面之间、距离球心为r 处的P 点的电势U 为：(A) r Q Q 0214επ+ (B)20210144R Q R Q εεπ+π(C)2020144R Q r Q εεπ+π(D) rQ R Q 0210144εεπ+π [ ]11. (本题 3分)(1623) 已知某电场的电场线分布情况如图所示．现观察到一负电荷从M 点移到N 点．有人根据这个图作出下列几点结论，其中哪点是正确的？ (A) 电场强度E M ＜E N ． (B) 电势U M ＜U N ．(C) 电势能W M ＜W N ． (D) 电场力的功A ＞0．［ ］12. (本题 3分)(1085) 图中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出： (A) E A ＞E B ＞E C ，U A ＞U B ＞U C ． (B) E A ＜E B ＜E C ，U A ＜U B ＜U C ． (C) E A ＞E B ＞E C ，U A ＜U B ＜U C ．(D) E A ＜E B ＜E C ，U A ＞U B ＞U C ． ［ ］13. (本题 3分)(1394) 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的： (A) 2倍． (B) 22倍． (C) 4倍． (D) 42倍． ［ ］一个带正电荷的质点，在电场力作用下从A 点经C 点运动到B 点，其运动轨迹如图所示．已知质点运动的速率是递增的，下面关于C 点场强方向的四个图示中正确的是： ［］(C)v (A)15. (本题 3分)(1299) 在一个带有负电荷的均匀带电球外，放置一电偶极子，其电矩p v的方向如图所示．当电偶极子被释放后，该电偶极子将(A) 沿逆时针方向旋转直到电矩p v沿径向指向球面而停止． (B) 沿逆时针方向旋转至p v沿径向指向球面，同时沿电场线方向向着球面移 动．(C) 沿逆时针方向旋转至p v沿径向指向球面，同时逆电场线方向远离球面移 动．(D) 沿顺时针方向旋转至p v沿径向朝外，同时沿电场线方向向着球面移动． ［］pv16. (本题 3分)(1300) 在一个带有正电荷的均匀带电球面外，放置一个电偶极子，其电矩p v的方向如图所示．当释放后，该电偶极子的运动主要是 (A) 沿逆时针方向旋转，直至电矩p v 沿径向指向球面而停止．(B) 沿顺时针方向旋转，直至电矩p v沿径向朝外而停止．(C) 沿顺时针方向旋转至电矩p v 沿径向朝外，同时沿电场线远离球面移动．(D) 沿顺时针方向旋转至电矩p v沿径向朝外，同时逆电场线方向向着球面移动．［ ］p v二 填空题 (共69分)17. (本题 5分)(1500) 如图所示，真空中两个正点电荷Q ，相距2R ．若以其中一点电荷所在处O 点为中心，以R 为半径作高斯球面S ，则通过该球面的电场强度通量＝______________；若以0r v表示高斯面外法线方向的单位矢量，则高斯面上a 、b 两点的电场强度分别为________________________．18. (本题 5分)(1042) A 、B 为真空中两个平行的“无限大”均匀带电平面，已知两平面间的电场强度大小为E 0，两平面外侧电场强度大小都为E 0/3，方向如图．则A 、B 两平面上的电荷面密度分别为σA ＝_______________, σB ＝____________________．A BE 0E 0/3E 0/319. (本题 4分)(1408) 一半径为R ，长为L 的均匀带电圆柱面，其单位长度带有电荷λ．在带电圆柱的中垂面上有一点P ，它到轴线距离为r (r >R )，则P 点的电场强度的大小：当r <<L 时，E ＝______________________；当r >>L 时，E ＝__________________．20. (本题 4分)(1058) 三个平行的“无限大”均匀带电平面，其电荷面密度都是＋σ，如图所示，则A 、B 、C 、D 三个区域的电场强度分别为：E A ＝_________________，E B ＝_____________，E C ＝_______________，E D =_________________ (设方向向右为正)．+σ+σ+σABCD21. (本题 5分)(5087) 两块“无限大”的均匀带电平行平板，其电荷面密度分别为σ( σ＞0)及－2 σ，如图所示．试写出各区域的电场强度E v ．Ⅰ区E v的大小__________________，方向____________． Ⅱ区E v的大小__________________，方向____________．Ⅲ区E v的大小__________________，方向_____________．σⅠⅡⅢ−2σ在点电荷＋q 和－q 的静电场中，作出如图所示的三个闭合面S 1、S 2、S 3，则通过这些闭合面的电场强度通量分别是：Φ1＝________，Φ2＝___________，Φ3＝__________．12323. (本题 3分)(1038) 在场强为E v的均匀电场中，有一半径为R 、长为l 的圆柱面，其轴线与E v 的方向垂直．在通过轴线并垂直E v的方向将此柱面切去一半，如图所示．则穿过剩下的半圆柱面的电场强度通量等于________________________ ．24. (本题 4分)(1499) 点电荷q 1、q 2、q 3和q 4在真空中的分布如图所示．图中S 为闭合曲面，则通过该闭合曲面的电场强度通量∫⋅SS E v v d ＝____________，式中的Ev是点电荷________在闭合曲面上任一点产生的场强的矢量和．q 1q 325. (本题 4分)(1194) 把一个均匀带有电荷+Q 的球形肥皂泡由半径r 1吹胀到r 2，则半径为R (r 1＜R ＜r 2)的球面上任一点的场强大小E 由______________变为______________；电势U 由 __________________________变为________________(选无穷远处为电势零点)．26. (本题 3分)(1592) 一半径为R 的均匀带电球面，其电荷面密度为σ．若规定无穷远处为电势零点，则该球面上的电势U ＝____________________．27. (本题 4分)(1176) 真空中，有一均匀带电细圆环，电荷线密度为λ，其圆心处的电场强度E 0＝__________________，电势U 0＝ __________________．(选无穷远处电势为零)28. (本题 4分)(1023) 一点电荷q ＝10-9 C ，A 、B 、C 三点分别距离该点电荷10 cm 、20 cm 、30 cm ．若选B 点的电势为零，则A 点的电势为______________，C 点的电势为________________． (真空介电常量ε0＝8.85×10-12 C 2·N -1·m -2)q真空中，有一均匀带电细圆环，电荷线密度为λ，其圆心处的电场强度E＝__________________，电势U＝ __________________．(选无穷远处电势为零) 30. (本题 5分)(1066)静电场的环路定理的数学表示式为：______________________．该式的物理意义是：_______________________________________________________________ ___________________________________________．该定理表明，静电场是______ ______________________________场．31. (本题 3分)(1041)在点电荷q的电场中，把一个－1.0×10-9 C的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m处，克服电场力作功1.8×10-5 J，则该点电荷q＝________________．(真空介电常量ε0＝8.85×10-12 C2·N-1·m-2 )32. (本题 3分)(1273)在点电荷q的静电场中，若选取与点电荷距离为r的一点为电势零点，则与点电荷距离为r处的电势U＝__________________．33. (本题 3分)(1177)图中所示以O为心的各圆弧为静电场的等势（位）线图，已知U1＜U2＜U3，在图上画出a、b两点的电场强度的方向，并比较它们的大小．E a________ E b(填＜、＝、＞)．O U U34. (本题 3分)(2791)带有N个电子的一个油滴，其质量为m，电子的电荷大小为e．在重力场中由静止开始下落(重力加速度为g)，下落中穿越一均匀电场区域，欲使油滴在该区域中匀速下落，则电场的方向为__________________，大小为_____________．三 计算题 (共62分)35. (本题 8分)(5090) 一段半径为a 的细圆弧，对圆心的张角为θ0，其上均匀分布有正电荷q ，如图所示．试以a ，q ，θ0表示出圆心O 处的电场强度．q36. (本题 8分)(1263) 如图所示，一长为10 cm 的均匀带正电细杆，其电荷为1.5×10-8C ，试求在杆的延长线上距杆的端点5 cm 处的P 点的电场强度．(041επ＝9×109 N ·m 2/C 2)37. (本题 5分)(1008) 如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．P38. (本题 5分)(1284) 真空中一立方体形的高斯面,边长a ＝0.1 m ，位于图中所示位置．已知空间的场强分布为：E x =bx , E y =0 , E z =0．常量b ＝1000 N/(C ·m)．试求通过该高斯面的电通量．39. (本题10分)(1653) 电荷以相同的面密度σ 分布在半径为r 1＝10 cm 和r 2＝20 cm 的两个同心球面上．设无限远处电势为零，球心处的电势为U 0＝300 V ． (1) 求电荷面密度σ．(2) 若要使球心处的电势也为零，外球面上应放掉多少电荷？ ［ε0＝8.85×10-12 C 2 /(N ·m 2)］40. (本题 5分)(1384) 若电荷以相同的面密度σ均匀分布在半径分别为r 1＝10 cm 和r 2＝20 cm 的两个同心球面上，设无穷远处电势为零，已知球心电势为300 V ，试求两球面的电荷面密度σ的值． (ε0＝8.85×10-12C 2 / N ·m 2 )41. (本题 5分)(1216) 如图所示两个平行共轴放置的均匀带电圆环，它们的半径均为R ，电荷线密度分别是＋λ和－λ，相距为l ．试求以两环的对称中心O 为坐标原点垂直于环面的x 轴上任一点的电势(以无穷远处为电势零点)．42. (本题 8分)(1024)有一电荷面密度为σ的“无限大”均匀带电平面．若以该平面处为电势零点，试求带电平面周围空间的电势分布．43. (本题 8分)(1598)电荷q均匀分布在长为2l的细杆上，求杆的中垂线上与杆中心距离为a的P点的电势(设无穷远处为电势零点)．一 选择题 (共48分)1. (本题 3分)(1055) (B)2. (本题 3分)(5272) (A)3. (本题 3分)(1255) (B)4. (本题 3分)(1257) (D)5. (本题 3分)(1434) (D)6. (本题 3分)(5084) (D)7. (本题 3分)(1415) (A)8. (本题 3分)(1019) (D)9. (本题 3分)(1020) (C)10. (本题 3分)(1516) (C)11. (本题 3分)(1623) (C)12. (本题 3分)(1085) (D)13. (本题 3分)(1394) (B)14. (本题 3分)(1442) (D)15. (本题 3分)(1299) (B)16. (本题 3分)(1300) (D)二 填空题 (共69分)17. (本题 5分)(1500) Q / ε0 2分a E v ＝0，()20018/5R r Q Eb επ=vv 3分19. (本题 4分)(1408) λ /(2πε0r ) 2分λ L /(4πε0r 2) 2分20. (本题 4分)(1058) －3σ / (2ε0) 1分 －σ / (2ε0) 1分 σ / (2ε0) 1分 3σ / (2ε0) 1分21. (本题 5分)(5087)02εσ向右 2分 023εσ 向右 2分 02εσ 向左 1分22. (本题 3分)(1600) q / ε0 1分0 1分 -q /ε0 1分23. (本题 3分)(1038) 2RlE 3分24. (本题 4分)(1499) ()042ε/q q +2分q 1、q 2、q 3、q 4 2分25. (本题 4分)(1194) Q / (4πε0R 2) 1分0 1分 Q / (4πε0R ) 1分 Q / (4πε0r 2)1分26. (本题 3分)(1592) R σ / ε0 3分27. (本题 4分)(1176) 0 2分 λ / (2ε0) 2分29. (本题 4分)(1176) 0 2分 λ / (2ε0) 2分30. (本题 5分)(1066) 0d =⋅∫Ll E vv 2分单位正电荷在静电场中沿任意闭合路径绕行一周，电场力作功等于零 2分有势（或保守力） 1分31. (本题 3分)(1041) -2×10-7 C 3分32. (本题 3分)(1273)⎟⎟⎠⎞⎜⎜⎝⎛−π00114rr qε 3分33. (本题 3分)(1177) 答案见图 2分＝ 1分OU U34. (本题 3分)(2791) 从上向下 1分 mg / ( Ne ) 2分三 计算题 (共62分)35. (本题 8分)(5090) 解：取坐标xOy 如图，由对称性可知：0d ==∫x x E E 2分 θελθεcos 4d cos 4d d 2020a la q E y π−=π−=θθελd cos 420a a ⋅π−=2分 θθελθθd cos 40021210∫−π−=aE y 2sin 22sin 2002000θθεθελa q a π−=π−=j a qE v v 2sin 20020θθεπ−= 4分解： 设P 点在杆的右边，选取杆的左端为坐标原点O ，x 轴沿杆的方向，如图，并设杆的长度为L ．P 点离杆的端点距离为d ．在x 处取一电荷元d q =(q /L )d x ，它在P 点产生场强()()20204d 4d d x d L L xq x d L q E −+π=−+π=εε 3分 P 点处的总场强为()()d L d qx d L x L q E L +π=−+π=∫00204d 4εε 3分 代入题目所给数据，得E ＝1.8×104 N/m 1分 E v 的方向沿x 轴正向． 1分 xO37. (本题 5分)(1008) 解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强： ()204d d x d L q E −+π=ε()204d x d L L x q −+π=ε 2分总场强为 ∫+π=Lx d L x L q E 020)(d 4－ε()d L d q+π=04ε3分方向沿x 轴，即杆的延长线方向．O38. (本题 5分)(1284) 解： 通过x ＝a 处平面1的电场强度通量Φ1 = -E 1S 1= -b a 3 1分通过x = 2a 处平面2的电场强度通量Φ2 = E 2 S 2 = 2b a 3 1分其它平面的电场强度通量都为零．因而通过该高斯面的总电场强度通量为Φ = Φ1+ Φ2 = 2b a 3-b a 3 = b a 3 =1 N ·m 2/C 3分解：(1) 球心处的电势为两个同心带电球面各自在球心处产生的电势的叠加，即⎟⎟⎠⎞⎜⎜⎝⎛+π=22110041r q r q U ε⎟⎟⎠⎞⎜⎜⎝⎛π−ππ=22212104441r r r r σσε ()210r r +=εσ3分 2100r r U +=εσ＝8.85×10-9C / m 2 2分(2) 设外球面上放电后电荷面密度为σ′，则应有()21001r r U σσε′+=′= 0即 σσ21r r −=′ 2分外球面上应变成带负电，共应放掉电荷()⎟⎟⎠⎞⎜⎜⎝⎛+π=′−π=′212222144r r r r q σσσ ()20021244r U r r r εσπ=+π=＝6.67×10-9C 3分40. (本题 5分)(1384) 解：球心处总电势应为两个球面电荷分别在球心处产生的电势叠加，即⎟⎟⎠⎞⎜⎜⎝⎛+π=2211041r q r q U ε⎟⎟⎠⎞⎜⎜⎝⎛π+ππ=22212104441r r r r σσε()210r r +=εσ3分故得 92101085.8−×=+=r r U εσ C/m 22分41. (本题 5分)(1216) 解：设轴线上任意点P 的坐标为x ，两带电圆环在P 点产生的电势分别为：()2202/2R l x RU +−=+ελ 2分 ()2202/2Rl x R U ++−=−ελ 2分 由电势叠加原理，P 点的电势为U =U ++U -()()⎥⎥⎦⎤⎢⎢⎣⎡++−+−=222202/12/12R l x R l x Rελ1分O x RP l /2-l /2+λ−λx解：选坐标原点在带电平面所在处，x 轴垂直于平面．由高斯定理可得场强分布为 E =±σ / (2ε0) 2分 (式中“＋”对x ＞0区域，“－”对x ＜0区域) . 平面外任意点x 处电势： 在x ≤0区域00002d 2d εσεσx x x E U x x =−==∫∫ 3分在x ≥0区域002d 2d εσεσx x x E U x x −===∫∫ 3分43. (本题 8分)(1598) 解：设坐标原点位于杆中心O 点，x 轴沿杆的方向，如图所示. 杆的电荷线密度λ=q / (2l )．在x 处取电荷元d q ．d q = l d x = q d x / (2l ) 它在P 点产生的电势2202208d 4d d x a l xq x a q U P +π=+π=εε 4分整个杆上电荷产生的电势∫−+π=l l P x a x l q U 220d 8ε()l lx a x lq −++π=220ln 8ε2220ln 8⎥⎦⎤⎢⎢⎣⎡++π=a l a l l qε⎥⎥⎦⎤⎢⎢⎣⎡++π=a l a l l q220ln 4ε 4分。
大学物理第四章习题解答
l
v v
O
以杆、摆锤和地球为整体，该系统在 摆动过程中机械能守恒，选择最低点 为重力势能零点。若刚好能完成一次
m/
A
m
/
v v 2
圆周运动，则系统在最高点的角速度 为0。
/ / 11 / 2 2 m gl 3m gl / 2 = + 2m / gl m l + m l ω0 + 23 2 2
解：有心力对地心的力矩为零， 有心力对地心的力矩为零， 卫星 m 对地心 o 角动量守恒
v 2 h2 r r 1
h1 m
mv1r1 = mv2 r2
卫星与地球系统机械能守恒： 1 2 GmM 1 2 GmM mv1 − = mv2 − 2 r1 2 r2
24
v1
r1 = R + h1 , r2 = R + h2
0
6
−t / τ
d ( − )]
t
τ
= ω 0 [t
−t / τ 6 + τe ]0
= 9[6 + 2(e −6 / 2 - e 0 )] = 36.9 rad
∆θ N= = 5.87 (圈) 2π
N ≠ ∆θ
6
4 − 9：一飞轮由一直径为30cm，厚度为2cm的圆盘和两个直径都为10cm ，长为8cm的共轴圆柱体组成，设飞轮的密度为7.8 ×103 kg / m 3，求飞轮 对轴的转动惯量。
有两个力作用在一个有固定转轴的刚体上： 4-1 有两个力作用在一个有固定转轴的刚体上： 力都平行于轴作用时 （1）这两个力都平行于轴作用时， ）这两个力都平行于轴作用时， 对轴的 一定是零 它们对轴 合力矩一定是 它们对轴的合力矩一定是零; 力都垂直于轴作用时 （2）这两个力都垂直于轴作用时， ）这两个力都垂直于轴作用时， 它们对轴的合力矩可能是 合力矩可能 它们对轴的合力矩可能是零; 合力为零时 （3）当这两个力的合力为零时， ）当这两个力的合力为零 它们对轴的合力矩也一定是零 合力矩也一定是 它们对轴的合力矩也一定是零； 4）当这两个力对轴的合力矩为 （4）当这两个力对轴的合力矩为 它们的合力也一定是零 合力也一定是 零时，它们的合力也一定是零。 对上述说法正确的是（ 对上述说法正确的是（ B ） (A) 只有 是正确的 只有(1)是正确的 (B) (1)(2)正确，(3)(4)错误 正确， 正确 错误 (C) (1)(2)(3)都正确，(4)错误 都正确， 错误 都正确
大学物理课后习题答案整理(杨晓峰版)-习题4-15答案
习题4-15解答：对转动系统而言，随着砂粒的下落，系统的转动惯量发生了改变。
但是，砂粒下落对转台并不产生力矩作用，因此，系统在转动过程中的角动量是守恒的。
假设转台的角速度由ω变为2ω
所用的时间为t ，这段时间内落
至台面的砂粒的质量可由其流量求出，从而可算出它所引起的附加转动惯量。
这样，时间t 可由角动量守恒定律求出。
解：设转台的角速度变为2ω
所用的时间为t ，则落至台面的砂粒质量为
t Qt m 3101−×==
根据系统的角动量守恒，有
()22ω
ωmr J J +=
联立以上两式，可得
()s 510
11.0105/325
2=×××==−−Q r J t。
大连理工大学大学物理作业4(静电场四)及答案详解
作业4 静电场四导线穿过外球壳上的绝缘小孔与地连接，外球壳上带有正电荷，则内球壳上[ ]。
.A 不带电荷.B 带正电 .C 带负电荷.D 外表面带负电荷，内表面带等量正电荷答案：【C 】解：如图，由高斯定理可知，内球壳内表面不带电。
否则内球壳内的静电场不为零。
如果内球壳外表面不带电（已经知道内球壳内表面不带电），则两壳之间没有电场，外球壳内表面也不带电；由于外球壳带正电，外球壳外表面带正电；外球壳外存在静电场。
电场强度由内球壳向外的线积分到无限远，不会为零。
即内球壳电势不为零。
这与内球壳接地（电势为零）矛盾。
因此，内球壳外表面一定带电。
设内球壳外表面带电量为q （这也就是内球壳带电量），外球壳带电为Q ，则由高斯定理可知，外球壳内表面带电为q -，外球壳外表面带电为Q q +。
这样，空间电场强度分布r r qr E ˆ4)(201πε=，（两球壳之间：32R r R <<）r r Qq r E ˆ4)(202πε+= ，（外球壳外：r R <4）其他区域（20R r <<，43R r R <<），电场强度为零。
内球壳电势为041)11(4ˆ4ˆ4)()(403202020214324322=++-=⋅++⋅=⋅+⋅=⋅=⎰⎰⎰⎰⎰∞∞∞R Q q R R q r d r rQq r d r r q r d r E r d r E l d E U R R R R R R R πεπεπεπε则04432=++-R QR q R q R q ，4324111R R R R Q q +--=由于432R R R <<，0>Q ，所以0<q即内球壳外表面带负电，因此内球壳负电。
2．真空中有一组带电导体，其中某一导体表面某处电荷面密度为σ，该处表面附近的场强大小为E ，则0E σ=。
那么，E 是[ ]。
.A 该处无穷小面元上电荷产生的场 .B 导体上全部电荷在该处产生的场 .C 所有的导体表面的电荷在该处产生的场 .D 以上说法都不对答案：【C 】解：处于静电平衡的导体，导体表面附近的电场强度为0E σ=，指的是：空间全部电荷分布，在该处产生的电场，而且垂直于该处导体表面。
大学物理课后题答案4
习 题 四4-1 质量为m =0.002kg 的弹丸，其出口速率为300s m ，设弹丸在枪筒中前进所受到的合力9800400x F -=。
开抢时，子弹在x =0处，试求枪筒的长度。
[解] 设枪筒长度为L ，由动能定理知2022121mv mv A -=其中⎰⎰-==L L dx xFdx A 00)98000400(940004002L L -=而00=v ， 所以有：22300002.05.094000400⨯⨯=-L L 化简可得： m45.00813604002==+-L L L即枪筒长度为0.45m 。
4-2 在光滑的水平桌面上平放有如图所示的固定的半圆形屏障。
质量为m 的滑块以初速度0v 沿切线方向进入屏障内，滑块与屏障间的摩擦系数为μ，试证明：当滑块从屏障的另一端滑出时，摩擦力所作的功为()121220-=-πμe mv W [证明] 物体受力：屏障对它的压力N ，方向指向圆心，摩擦力f 方向与运动方向相反，大小为 N f μ= (1)另外，在竖直方向上受重力和水平桌面的支撑力，二者互相平衡与运动无关。
由牛顿运动定律 切向 t ma f =- (2)法向Rv m N 2= (3)联立上述三式解得 Rv a 2t μ-=又 svv t s s v t v a d d d d d d d d t ===所以 Rv s v v 2d d μ-= 即 s Rv vd d μ-=两边积分，且利用初始条件s =0时，0v v =得0ln ln v s Rv +-=μ即 sRe v v μ-=0由动能定理 2022121mv mv W -=，当滑块从另一端滑出即R s π=时，摩擦力所做的功为 ()121212122020220-=-=--πμπμe mv mv e mv W R R4-3 质量为m 的质点开始处于静止状态，在外力F 的作用下沿直线运动。
已知TtF F π2sin0=，方向与直线平行。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题四4-1 符合什么规律的运动才是谐振动分别分析下列运动是不是谐振动：(1)拍皮球时球的运动；(2)如题4-1图所示，一小球在一个半径很大的光滑凹球面内滚动(设小球所经过的弧线很 短)．题4-1图解：要使一个系统作谐振动，必须同时满足以下三个条件：一 ，描述系统的各种参量，如质量、转动惯量、摆长……等等在运动中保持为常量；二，系统 是在 自己的稳定平衡位置附近作往复运动；三，在运动中系统只受到内部的线性回复力的作用． 或者说，若一个系统的运动微分方程能用0d d 222=+ξωξt描述时，其所作的运动就是谐振动．(1)拍皮球时球的运动不是谐振动．第一，球的运动轨道中并不存在一个稳定的平衡位置； 第二，球在运动中所受的三个力：重力，地面给予的弹力，击球者给予的拍击力，都不是线 性回复力．(2)小球在题4-1图所示的情况中所作的小弧度的运动，是谐振动．显然，小球在运动过程中 ，各种参量均为常量；该系统(指小球凹槽、地球系统)的稳定平衡位置即凹槽最低点，即系统势能最小值位置点O ；而小球在运动中的回复力为θsin mg -，如题4-1图(b)所示．题中所述，S ∆＜＜R ，故RS ∆=θ→0，所以回复力为θmg -.式中负号，表示回复力的方向始终与角位移的方向相反．即小球在O 点附近的往复运动中所受回复力为线性的．若以小球为对象，则小球在以O '为圆心的竖直平面内作圆周运动，由牛顿第二定律，在凹槽切线方向上有θθmg tmR -=22d d 令Rg =2ω，则有 0d d 222=+ωθt4-2 劲度系数为1k 和2k 的两根弹簧，与质量为m 的小球按题4-2图所示的两种方式连 接，试证明它们的振动均为谐振动，并分别求出它们的振动周期．题4-2图解：(1)图(a)中为串联弹簧，对于轻弹簧在任一时刻应有21F F F ==，设串联弹簧的等效倔强系数为串K 等效位移为x ，则有111x k F xk F -=-=串222x k F -=又有 21x x x +=2211k F k F k F x +==串 所以串联弹簧的等效倔强系数为 2121k k k k k +=串 即小球与串联弹簧构成了一个等效倔强系数为)/(2121k k k k k +=的弹簧振子系统，故小球作谐振动．其振动周期为2121)(222k k k k m k m T +===ππωπ串 (2)图(b)中可等效为并联弹簧，同上理，应有21F F F ==，即21x x x ==，设并联弹簧的倔强系数为并k ，则有2211x k x k x k +=并故 21k k k +=并同上理，其振动周期为212k k m T +='π 4-3 如题4-3图所示，物体的质量为m ，放在光滑斜面上，斜面与水平面的夹角为θ，弹簧的倔强系数为k ，滑轮的转动惯量为I ，半径为R ．先把物体托住，使弹簧维持原长，然 后由静止释放，试证明物体作简谐振动，并求振动周期．题4-3图解：分别以物体m 和滑轮为对象，其受力如题4-3图(b)所示，以重物在斜面上静平衡时位置为坐标原点，沿斜面向下为x 轴正向，则当重物偏离原点的坐标为x 时，有221d d sin tx m T mg =-θ ① βI R T R T =-21 ②βR tx =22d d )(02x x k T += ③ 式中k mg x /sin 0θ=，为静平衡时弹簧之伸长量，联立以上三式，有kxR tx R I mR -=+22d d )( 令 I mR kR +=222ω 则有0d d 222=+x tx ω 故知该系统是作简谐振动，其振动周期为)/2(22222K R I m kR I mR T +=+==ππωπ4-4 质量为kg 10103-⨯的小球与轻弹簧组成的系统，按)SI ()328cos(1.0ππ+=x的规律作谐振动，求：(1)振动的周期、振幅和初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等(3)s 52=t 与s 11=t 两个时刻的位相差； 解：(1)设谐振动的标准方程为)cos(0φω+=t A x ，则知：3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅ (2) N 63.0==m m ma FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p 当p k E E =时，有p E E 2=，即 )21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t4-5 一个沿x 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，其振动方程用余弦函数表示．如果0=t 时质点的状态分别是：(1)A x -=0；(2)过平衡位置向正向运动；(3)过2A x =处向负向运动； (4)过2Ax -=处向正向运动． 试求出相应的初位相，并写出振动方程．解：因为 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式，使两式同时成立之值即为该条件下的初位相．故有 )2cos(1πππφ+==t TA x )232cos(232πππφ+==t T A x )32cos(33πππφ+==t T A x )452cos(454πππφ+==t T A x 4-6 一质量为kg 10103-⨯的物体作谐振动，振幅为cm 24，周期为s 0.4，当0=t 时位移为cm 24+．求：(1)s 5.0=t 时，物体所在的位置及此时所受力的大小和方向；(2)由起始位置运动到cm 12=x 处所需的最短时间；(3)在cm 12=x 处物体的总能量．解：由题已知 s 0.4,m 10242=⨯=-T A∴ 1s rad 5.02-⋅==ππωT又，0=t 时，0,00=∴+=φA x故振动方程为 m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN 102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点，即沿x 轴负向．(2)由题知，0=t 时，00=φ，(3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E 4-7 有一轻弹簧，下面悬挂质量为g 0.1的物体时，伸长为cm 9.4．用这个弹簧和一个质量为g 0.8的小球构成弹簧振子，将小球由平衡位置向下拉开cm 0.1后 ，给予向上的初速度10s cm 0.5-⋅=v ，求振动周期和振动表达式． 解：由题知12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k 而0=t 时，-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT m k 即 m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A 45,15100.1100.5tan 022000πφωφ==⨯⨯⨯=-=--即x v ∴ m )455cos(1022π+⨯=-t x4-8 图为两个谐振动的t x -曲线，试分别写出其谐振动方程．题4-8图解：由题4-8图(a)，∵0=t 时，s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4-8图(b)∵0=t 时，35,0,2000πφ=∴>=v A x∴ πω65= 故 m t x b )3565cos(1.0ππ+= 4-9 一轻弹簧的倔强系数为k ，其下端悬有一质量为M 的盘子．现有一质量为m 的物体从离盘底h 高度处自由下落到盘中并和盘子粘在一起，于是盘子开始振动． (1)此时的振动周期与空盘子作振动时的周期有何不同(2)此时的振动振幅多大(3)取平衡位置为原点，位移以向下为正，并以弹簧开始振动时作为计时起点，求初位相并写出物体与盘子的振动方程．解：(1)空盘的振动周期为k M π2，落下重物后振动周期为km M +π2，即增大． (2)按(3)所设坐标原点及计时起点，0=t 时，则kmg x -=0．碰撞时，以M m ,为一系统动量守恒，即 0)(2v M m gh m +=则有 Mm gh m v +=20 于是gM m kh k mg M m gh m k mg v x A )(21))(2()()(2222020++=++=+=ω（3）gm M kh x v )(2tan 000+=-=ωφ (第三象限)，所以振动方程为 ⎥⎦⎤⎢⎣⎡+++++=g m M kh t M m k g M m kh k mg x )(2arctan cos )(21 4-10 有一单摆，摆长m 0.1=l ，摆球质量kg 10103-⨯=m ，当摆球处在平衡位置时，若给小球一水平向右的冲量14s m kg 100.1--⋅⋅⨯=∆t F ，取打击时刻为计时起点)0(=t ，求振动的初位相和角振幅，并写出小球的振动方程．解：由动量定理，有0-=∆⋅mv t F∴ 1-34s m 01.0100.1100.1⋅=⨯⨯=∆⋅=--m t F v按题设计时起点，并设向右为x 轴正向，则知0=t 时，100s m 01.0,0-⋅==v x ＞0∴ 2/30πφ=又 1s rad 13.30.18.9-⋅===l g ω ∴ m 102.313.301.0)(302020-⨯===+=ωωv v x A 故其角振幅 rad 102.33-⨯==ΘlA 小球的振动方程为 rad )2313.3cos(102.33πθ+⨯=-t4-11 有两个同方向、同频率的简谐振动，其合成振动的振幅为m 20.0，位相与第一振动的位相差为6π，已知第一振动的振幅为m 173.0，求第二个振动的振幅以及第一、第二两振动的位相差．题4-11图解：由题意可做出旋转矢量图如下．由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A∴ m 1.02=A设角θ为O AA 1，则θcos 22122212A A A A A -+=即 01.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ 即2πθ=，这说明，1A 与2A 间夹角为2π，即二振动的位相差为2π. 4-12 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅： (1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm )343cos(5cm )33cos(521ππt x t x 解： (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A(2)∵ ,334πππφ=-=∆ ∴合振幅 0=A 4-13 一质点同时参与两个在同一直线上的简谐振动，振动方程为⎪⎩⎪⎨⎧-=+=m )652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动的振动幅和初相，并写出谐振方程。