三维曲面重构方法分析
曲面重建技术
曲面重建技术
曲面重建技术是通过对点云数据进行处理和分析，从而重建出曲面模型的一种技术。
常见的曲面重建技术包括以下几种：
1. Delaunay三角网格：该方法将点云数据转换为三角网格，
通过最小化三角形的边长和最大化角度来生成平滑的曲面。
这种方法适用于点云密度较高且曲面比较平滑的场景。
2. 体素网格(Voxel Grid)：通过将点云数据划分为一系列小的
立方体单元，然后分析每个单元内的点云分布情况，从而确定曲面的形状。
该方法适用于处理点云分布不均匀且曲面存在较大变化的情况。
3. 法向量估计：利用点云数据中的法向量信息来推测曲面的形状。
通过计算每个点的邻域内点的平均法向量，可以得到点云数据的平滑曲面。
该方法对于点云数据中存在噪音和不完整的情况具有较好的鲁棒性。
4. 基于隐函数的方法：用函数来表示曲面，在点云数据的基础上拟合出一个适合曲面的隐函数，并使用隐函数的等值面来表示曲面模型。
这种方法可以较好地处理点云数据中存在噪音和不完整的情况，但对于大规模点云数据的处理较为复杂。
以上仅是一些常见的曲面重建技术，根据具体应用场景和需求，可以选择合适的方法进行曲面重建。
三维CAD模型重构方法、过程及实例
特征的定义及表达
几何特征是几何造型的关键，他们对控制几何形体的形状 有极为重要作用，同时几何特征之间还具有确定的几何约束 关系。
因此，在产品模型的重构过程中，一个重要的目标就是 还原这些特征以及他们之间的约束，得到一个优化的CAD模型， 使孤立的曲面片转化成一个整体的几何模型。
三维CAD模型重构方法、 过程和实例
输出匹配的 文件格式
自动将点云 数据转换为
多边形
Geomagic Studio
主要功能
快速减少 多边形数目
(Decimate)
曲面分析 (公差分析等)
把多边形 转换为曲面
三维CAD模型重构方法、 过程和实例
Geomagic Studio软件工作流程如下图所示：
这和多数工业产品的设计意图相符合。可有效解决产品 的装配对齐、造型的对称等问题，进而减小误差，提高产品 质量。
三维CAD模型重构方法、 过程和实例
约束的定义、分类及表达
逆向工程中的曲面重构不是对数据的简单拟合，而是 要满足几何约束下的重构。
三维CAD模型重构方法、 过程和实例
Imageware 软件
• 应用曲线拟合造型的典型商用软件 • 广泛应用于汽车、航天、消费家电、模具、计算机零部
件等设计与制造领域。 • 软件包括以下几个模块：基础模块、点处理模块、曲线、
曲面模块、多边形造型模块、检验模块和评估模块。
三维CAD模型重构方法、 过程和实例
曲
面
模
模
型
型
评
重
价
建
实 体 模 型
下 游 应 用
三维CAD模型重构方法、 过程和实例
➢ 应用这种三边域曲面重构方法的典型商用软件是 Geomagic Studio软件。该软件可轻易地从扫描所得的 点云数据创建出完美的多边形模型和网格，并可自动 转换为 NURBS 曲面。
三维重构
三维重构三维重构（一）(2007-08-29 11:00:26)标签：知识/探索（一）空间的三维重构问题按照不同的实际情况来看算法的种类非常多，但核心的思想还是利用三角形来覆盖待重构区域的表面。
传统的算法将“覆盖”的思想体现的并不是非常形象，通常只是将待重构区域利用各种方法撒一些点，然后利用三角形来连接这些节点。
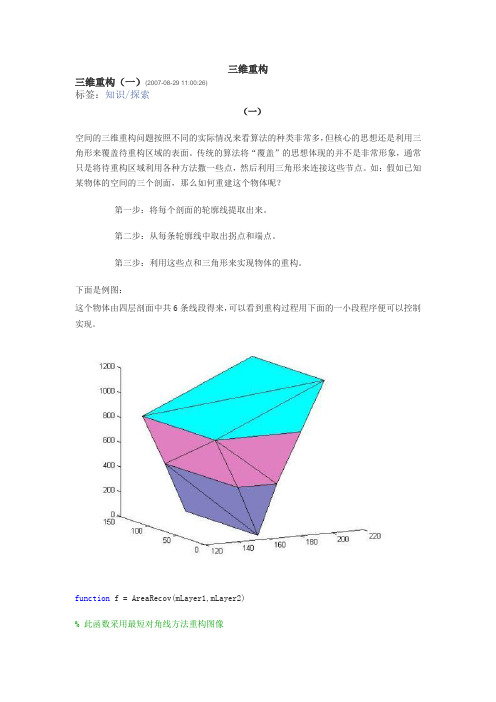
如：假如已知某物体的空间的三个剖面，那么如何重建这个物体呢？第一步：将每个剖面的轮廓线提取出来。
第二步：从每条轮廓线中取出拐点和端点。
第三步：利用这些点和三角形来实现物体的重构。
下面是例图：这个物体由四层剖面中共6条线段得来，可以看到重构过程用下面的一小段程序便可以控制实现。
function f = AreaRecov(mLayer1,mLayer2)% 此函数采用最短对角线方法重构图像% 输入:% mLayer1 第一层的点坐标集 n*3% mLayer2 第二层的点坐标集 m*3% 输出:% f 输出的三角形顶点集 max(n,m)*3*3 max(n,m)*三个顶点*三维坐标% 注: 原对角线的重构方法只适用于两层点数相同的情况,% 现在的算法对原算法进行了一些改动。
[Len1,vTemp2,vTemp3] = size(mLayer1) ;[Len2,vTemp2,vTemp3] = size(mLayer2) ;mMaxNum = max([Len1,Len2]) ;f = zeros(mMaxNum,3,3) ;if mMaxNum == Len1vLayer1 = mLayer1 ;vLayer2 = mLayer2 ;elsevLayer1 = mLayer2 ;vLayer2 = mLayer1 ;Len2 = Len1 ; % 用Len2存储小长度endfor counter = 1:mMaxNum-1f(counter,1,:) = vLayer1(counter,:) ;[f(counter,2,:),mIndexTemp] = NearPoint(vLayer1(counter,:),vLayer2) ;% 寻找三角形的第三个顶点if mIndexTemp<=Len2-1 %如果点少的一层还有剩余点vTemp2 = DistanJudg( vLayer1(counter,1:2),vLayer1(counter+1,1:2),...vLayer2(mIndexTemp,1:2),vLayer2(mIndexTemp+1,1:2) ) ;f(counter,3,:) = vLayer2(mIndexTemp+1,:) ;if vTemp2 == -1f(counter,3,:) = vLayer1(counter+1,:) ;endelse% 如果点少的一层没有剩余点，则直接取临点作为第三个顶点f(counter,3,:) = vLayer1(counter+1,:) ;endend对于这个简单的例子来说实现的很完美，但实际中的问题有如下几点：1，寻找物体表层的点时会有很复杂的判断问题，即选择哪几个点作为小三角形的定点来连接。
曲面重构技术文档
由点云重构CAD模型的基本步骤包括：点云分块、点云切片、曲面重构、CAD模型。
1.点云分块由于工程实际中原型往往不是由一张简单曲面构成，而是由大量初等解析曲面(如平面、圆柱面、圆锥面、球面、圆环面等)及部分自由曲面组成，故三维实体重构的首要任务是将测量数据按实物原型的几何特征进行分割成不同的数据块，使得位于同一数据块内的数据点可以一张特定的曲面来表示，然后针对不同数据块采用不同的曲面建构方案(如初等解析曲面、B-spline 曲面、Bezier曲面、NURBS 曲面等)进行曲面重建，最后将这些曲面块拼接成实体，它包括点集分割与曲面重建两部分。
为了实现点云的分块功能，同时也为了后续曲线拟合中重要点的选取工作，我们建立了图元的拾取模块。
它包括多边形拾取、矩形拾取、点选三个小的部分，运用此模块我们可以利用鼠标对空间点云进行任意的分割和提取。
多边形拾取与矩形拾取类似，都是在视图上确定一个选择区域，然后根据视图上的图形是否完全落在这个选择区域中来决定视图上的图形是否被选取。
由于我们针对的对象是三维空间中的图元，因此在视图窗口中所确定的区域实际上是一个矩形体或者多面体，所拾取的图元是位于这个体中的对象。
问题的关键在于如何确定图元是否位于矩形体或多面体中。
基于OpenGL的拾取机制很好的解决了这个问题。
物体的实际坐标经模型视图变换、投影变换、视口变换后显示为屏幕上的一点，OpenGL的gluUnProject（）可以做该过程的逆变换，即根据已知屏幕上点的二维坐标以及经过的变换矩阵可求出该点变换前在三维空间的坐标位置，但需要事先给定二维屏幕坐标的深度坐标。
考虑OpenGL的投影原理，将0.0和1.0作为前后裁剪面的深度坐标。
因此两次调用gluUnProject()可得到视图体前后裁剪面上的两个点，也就是屏幕上点的两个三维坐标。
对于矩形拾取而言，判断点是否位于矩形体中比较简单，可以选取每个空间点，判断点的坐标是否位于矩形盒三个方向的极限范围内，如果满足条件，则可认为该点符合条件，被拾取到了，并高亮显示。
三维曲面重建方法
三维曲面重建方法
嘿，朋友们！今天咱就来唠唠三维曲面重建方法。
你说这三维曲面重建啊，就像是给一个物体来了个全方位的“画像”，而且还是超级逼真的那种！想象一下，你能把一个奇形怪状的东西，通过一些神奇的手段，变成一个能在电脑里清晰呈现的曲面，多有意思呀！
这可不是一件容易的事儿哦！就好像搭积木，得一块一块精心拼凑起来。
首先得有数据呀，这些数据就像是积木的小块，得收集得足够多、足够准确，不然怎么能搭出漂亮的“建筑”呢？然后就是处理这些数据啦，这可需要点真功夫，把那些杂乱无章的数据整理得井井有条。
咱就说，这过程就跟雕刻大师工作似的。
一点点地打磨，一点点地塑造，直到那个完美的曲面展现在眼前。
要是数据处理不好，那可就像雕刻出了个歪瓜裂枣，多难看呀！
在这个过程中，算法就像是一把神奇的钥匙。
不同的算法就好比不同形状的钥匙，得找到那把最合适的，才能打开三维曲面重建的大门。
而且哦，还得不断地尝试、改进，就像我们不断调整自己做事的方法一样。
这可不是随便玩玩就能搞定的，得下功夫呀！但当你看到最终呈现出来的那个三维曲面，哇塞，那种成就感，简直无与伦比！就好像你创造了一个全新的世界一样。
三维曲面重建在好多领域都大显身手呢！医学上，能帮医生更清楚地看到人体内部的结构，这多重要啊！建筑设计里，能让设计师提前看到建筑物的样子，是不是很厉害？还有好多好多地方都离不开它呢！
所以呀，朋友们，可别小瞧了这三维曲面重建方法。
它就像是一个隐藏在科技世界里的魔法，能给我们带来意想不到的惊喜和改变。
让我们一起好好探索这个神奇的领域吧，说不定你就能成为那个掌握魔法的大师呢！。
一种基于单目多幅图像的三维曲面重构方法
ｉｕ ｉａｉ ｕ ａｅ ｅ ｈ ｃｎ ｅ ｂ ｉｅ ｂ ｓｌｎ ｓｓ ｍ ｆ ｑ ａｉ ｓ ａｄ ａｐｙ ｇ ｃｍ ｏｉ ｎｍｅｌ ］ ｌ ｍ ｎｔ ｎ ｒ ｃ ｈ ｉ ｔ ａ ｂ ｏ ｔｎ ｄ ｙ ｏｖ ｇ ｙｔ ｏ ｅｕｔ ｎ ｎ ｐ ｌｉ ｏ ｐ ｓｅ ｕ ｒａ ｌ ｏ Ｓｆ ｇ ａ ｉ ｅ ｏ ｎ ｔ ｅ
ｉｔｇａｉｎ ｔｅ ｔｅ ｉｔｄ ｕ ａ ｅ ａｌ ｅ ｕ ｔｅ ｉ ｒｔｄ ｎ ｄ ｎｅ ｒｔ ．ｈ ｎ ｈ ｆ ｅ ｓ ｒ ｃ ｃ ｌ ｆｒ ｒ ｔ ａｅ ａ ｍｏ ｉ ｅ ａ ｃ ｒｉｇ ｏ ａ ｉｔ ￣ ］ ｃ ｌｕｕ ａ ｄ ｉ ｉ ｏ ｔ ｆ ｂ ｈ ｅ ｄｆ ｄ ｃ ｏｄ ｎ ｔ ｖ ｒ ｉ ｌ ｉ ａ ｏａ ａｃ ｌｓ ｎ ｆ ｔ ｎｅ
有限差分方 法
文 章 编 号 １０ — ３ ｌ （０ ２ ０ ￣ ０ ５ ０ 文 献 标 识码 Ａ ０ ２ ８ ３ 一 ２０ ）９ ）５— ３ 中 国分 粪号 Ｔ ３ ｌ Ｐ ９
Ａ ｅ ｈ ｄ ｆ ｒ ３ Ｓ ｒ ａ ｅ Ｒｅ ｏ ｓｒ ｃ ｉｎ Ｂａ ｅ ｎ Ｍ ｔ ｏ ｏ Ｄ ｕ ｆ ｃ ｃ ｎ ｔ ｕ ｔｏ ｓ ｄ ｏ
精度地提取零件的二堆 信息成为 实现曲面重构的关键问题 。 三 三
维 数 据 的采 集 有 很 多方 法 ． 统 的接 触 式 方 法 虽 然 町以 选到 很 传 高 的删 量精 度 ， 是 由于 自动 化 程度 低 ． 格 吊 贵 ． Ｉ 速 度慢 但 价 羽 １量 等 特 点使 其 应 用 范 围 受到 限制
ｄ ｆ ｒ ｎ ｅ ｍｅｈ ｄ．０ ｔｅ ｂ ｓ ￣ ｏ Ｍｒ ｅ ｉｎ ｓ ｒ ｃ ｉ ｏ ｔ ｉ ｅ ． ｙ ｔ ｅ ｎ ｌ ｓ ｆ ｔ ｅ ｅ ａ ｌ ．ｈ ｌ ｏ ｉ ｍ ｓ ｖ ｒ ｅ ｉｅ ｅ ｃ ｔ ｏ ｓ ｈ ｅ ｔ ｉｃ Ｒ ｃ ｔ ｕ ａ ｅ ｓ ｂａ ｎ ｄ Ｂ ａ ａｙ ｉ ｏ ｈ ｘ ｍｐ ｅ ｔｅ ａｇ ｒｔ ｌ ｏ ｆ ｈ ｓ ｈ ｉ ｅ ｉ ｄ ｉ ｆ ｔ ｅ ａ ｃ ｒ ｔ ａ ｄ ａ ｐ ｉ ａ ｌ ‘ 】ｂ ｃ ｕ ａｅ ｎ ｐ ｌ ｂ ｅ ｃ Ｋｅ ｗｏ ｄ ｙ ｒ ｓ： Ｉ ｕ ｎ ｔ ｎ ｌ ｍｉ ａｉ Ｍｏ ｅ ， ｍｐ ｓｔ ｍｅ ｃ ｌ ｎｅ ｒ ｔ ｎ， ａ ａ ｏ ａ ｏ ｃ ｌ ｓ Ｆ ｎ ｔ ｉ ｅ ｃ ｔ ｏ ｌ ｏ ｄ ｌＣｏ ｏ ｉ Ｎｕ ｒ ａ ｅ ｉ Ｉ ｔｇ ａ ｉ Ｖ ｒ ｔ ｎ ｌ Ｃ ｌｕ ｕ ， ｉｉ Ｄ ｆ 代ｎ ｅ Ｍｅ ｄ ｏ ｉｉ ｅ ｆ ｈ
曲面重组技术
曲面重组技术
曲面重组技术是一种在数字建模中常见的技术，主要用于从离散的三维点云数据中重建连续的曲面。
该技术常用于如3D扫描、计算机视觉、机器人技术等领域，能够帮助从复杂的三维数据中提取有用信息。
一、曲面重组技术在哪些领域有应用？
曲面重组技术广泛应用于多个领域。
在计算机图形学中，它用于从三维扫描器获取的粗糙、离散的点云数据中重建精细、连续的三维模型。
在计算机视觉中，曲面重组技术可以帮助从二维图像中提取三维信息，以理解物体的形状和结构。
在机器人技术中，曲面重组可以帮助机器人理解其周围的环境，从而实现自主导航或者物体操控。
二、曲面重组技术的主要步骤是什么？
曲面重组技术的主要步骤包括数据预处理、曲面重建和曲面优化。
数据预处理包括去噪、滤波等，以提高点云数据的质量。
曲面重建是通过各种算法（如Delaunay三角化、Voronoi图、八叉树等）把处理后的点云数据转化为连续的曲面。
曲面优化则进一步提升了重建曲面的精度和质量，包括平滑处理、细分处理等。
三、曲面重组技术面临哪些挑战？
尽管曲面重组技术已经取得了显著的进步，但仍然面临一些挑战。
首先，对于复杂或者非常规形状的物体，使用当前的技术可能无法获取满意的重建效果。
其次，大规模的点云数据处理需要大量的计算资源，这在一定程度上限制了曲面重组技术的应用。
最后，点云数据的质量直接影响曲面重组的结果，因此需要高效的数据预处理技术来提高数据质量。
医学影像学中的三维重构技术使用方法
医学影像学中的三维重构技术使用方法医学影像学是现代医学领域中非常重要的一个分支，它通过使用各种影像设备，如CT扫描、MRI和超声波等，来获取人体内部的结构和功能信息。
在医学影像学中，三维重构技术是一种十分重要的图像处理方法，它可以将二维的医学影像转换为更直观和准确的三维图像，从而帮助医生进行更精确的诊断和治疗。
一、三维重构技术的基本原理三维重构技术的基本原理是根据二维影像中的像素值和位置信息，通过计算机算法将其转换为三维模型。
一般来说，三维重构技术包括以下几个基本步骤：1. 数据获取：医学影像的数据可以通过多种方式获取，如CT扫描、MRI或超声波等。
通过这些设备可以得到人体内部的不同层面、不同角度的二维图像。
2. 图像处理：在二维影像获取后，需要对其进行一定程度的图像增强和滤波处理。
这样可以减少噪声和干扰，提高图像质量。
3. 特征提取：特征提取是将医学影像中的感兴趣结构区域提取出来的过程。
这涉及到使用图像处理算法，如边缘检测、分割和分类等，以便将结构从背景中分离出来。
4. 三维重建：在特征提取完成后，可以使用三维重建算法将二维结构转换为三维模型。
这些算法可以根据不同的需求进行选择，如三维体素化、三角网格化或曲面拟合等。
5. 可视化和分析：最后，通过将三维模型进行可视化显示，医生可以更直观地观察人体内部的结构，进行进一步的分析和诊断。
二、三维重构技术的应用三维重构技术在医学影像学中有着广泛的应用，具体包括以下几个方面：1. 可视化解剖学：通过对人体内部结构进行三维重建，医生可以更直观地了解器官的位置、形状和关系。
这对于手术前的规划和术中导航非常有帮助。
2. 病变识别和分析：三维重构技术可以帮助医生更准确地识别和分析肿瘤、血管病变、骨折等疾病。
医生可以从不同角度和层面观察病变的形态和位置，以制定更合理的治疗方案。
3. 药物递送和内窥镜：三维重建技术可以用于模拟和优化药物在人体内的输送。
通过对人体各个区域的三维模型进行分析，可以找到最佳的递送路径和剂量。
基于点云数据的三维模型重构与分析算法研究
基于点云数据的三维模型重构与分析算法研究近年来，随着三维技术的发展和广泛应用，基于点云数据的三维模型重构与分析算法的研究逐渐成为计算机视觉领域的热点。
点云数据是一种由大量三维点组成的离散数据集合，可以通过激光扫描或摄影测量等手段获取。
本文将介绍基于点云数据的三维模型重构与分析算法的研究现状、方法和应用。
首先，我们来了解一下点云数据的特点。
点云数据是以点为基本元素的三维数据表达形式，每个点都有自己的位置和属性信息。
相较于传统的三维建模方法，点云数据具有较高的准确性和真实性，能够更好地反映真实世界中的物体形态和细节。
然而，点云数据的不规则性和噪声干扰给其处理和分析带来了挑战，因此需要研究有效的算法来重构和分析点云数据。
一种常见的点云重构算法是基于表面重建的方法。
该算法通过对点云数据进行表面重建，生成连续的三维模型。
其中，一种常用的表面重建方法是基于移动最小二乘（Moving Least Squares, MLS）的方法。
该方法通过拟合每个点的邻域曲面，将点云数据表达为连续的曲面模型。
此外，还有一些基于体素的方法，通过将点云数据转化为体素（Voxel）表示，然后进行光滑和分割操作，最终生成三维模型。
在点云数据分析方面，一种常见的问题是点云配准（Registration）问题。
点云配准是指将多个点云数据集合对齐到一个公共坐标系中，以实现点云数据的融合和比较。
配准算法通常包括特征提取、特征匹配和变换估计等步骤。
特征提取常用的方法有SIFT、SURF等，通过提取点云数据的局部特征，从而进行匹配和对齐。
此外，还有一些基于深度学习的方法，如PointNet和PointNet++，能够直接在点云数据上进行特征提取和配准。
除了点云配准，点云数据还可以用于三维物体识别和分类。
三维物体识别是指从点云数据中检测和识别出特定的三维物体，常用的方法有基于形状描述子和基于深度学习的方法。
基于形状描述子的方法从点云数据中提取出形状特征，然后使用机器学习算法进行分类和识别。
基于三维散乱点云的曲面重构技术研究
研究方法
3、曲面重构：在数据预处理之后，我们采用基于网格的方法进行曲面重构。 具体而言，我们首先构建点云的三角形网格模型，然后通过对网格模型进行平滑 处理来重建曲面。在平滑处理过程中，我们采用优化算法来调整网格节点的位置， 以获得更加光滑的曲面。
实验结果与分析
实验结果与分析
为了验证本次演示所提出技术的有效性，我们进行了一系列实验。首先，我 们采集了一组复杂的三维散乱点云数据，并对其进行了预处理和曲面重构。实验 结果表明，本次演示所提出的技术能够有效地重建出目标曲面，并具有较高的精 度和效率。与现有的方法相比，本次演示所提出的技术在处理噪声和缺失数据方 面表现出更好的鲁棒性，同时计算效率也得到了提高。
谢谢观看
结论与展望
然而，在处理大规模点云数据时，本技术仍存在一定的性能和稳定性问题。 此外，本技术在面对复杂和动态变化的三维几何形态时仍需进一步改进和完善。
结论与展望
展望未来，我们计划进一步优化算法性能和提高计算效率，以实现对更大规 模点云数据的处理。我们将探索更加稳健和自适应的数据处理方法，以更好地应 对各种复杂和动态的三维几何形态。另外，我们也将相关领域的前沿技术和发展 趋势，以便及时进行技术更新和创新。最终，我们期望将本技术应用于更多的实 际场景中，为推动复杂三维几何形态的测量、建模、分析等方面的发展做出贡献。
文献综述
文献综述
近年来，基于三维散乱点云的曲面重构技术已取得了长足的发展。按照重构 原理，这些方法可以分为基于拟合的方法、基于网格的方法、基于点云分割的方 法等。其中，基于拟合的方法通过拟合点云数据来重建曲面，如多项式拟合、样 条插值等；基于网格的方法则通过构建网格模型来重建曲面，
文献综述
如三角形网格、四边形网格等；基于点云分割的方法通过对点云数据进行分 割来重建曲面，如区域增长、聚类等。然而，这些方法都存在一定的局限性和不 足之处，如对噪声和缺失数据的鲁棒性不强、计算效率低下等。
基于三维重构的车身曲面设计方法研究
在 进 行 汽 车 车 身 曲 面 设 计 时 ，由 于 车身 曲 面
外 形 的 高 度 复 杂 性 ，设 计 人 员很 难 用 二 维 图 纸 来 清 晰 地 表 达 和 反 映 曲面 的 形 状 。 车 身外 形 曲面 为 Ｃ ＡＳ 曲面 ，光 顺 质 量 要 求 较 高 。在 保 证 车 身 Ｌ ＳＡ 外 观设 计 美 观 的 前 提 下 ，要达 到 车 身 表 面 曲 面 光
ｌ 甸 似 注
基于三维重构 的车身 曲面设计方法研 究
Ｂａｓ ｅｄ ｈｅ ｈｒ ｏｎ ｔ ｔ ｅｅ ｍ ｅｎｓｉ ｄｉ ｏｎａｌｒ ｅｃｏｎｓ ｒ ｔ ｕｃｔｏｎ ｔ ｉ ｅｃｈｎ ｏｇｙ ｏｆｔ ｏｌ ｈｅ ａｕｔ ｏｍ ｏｔｖ ｂｏｄｙ ｉ ｅ ｓ ｆ ｕｒ ａｃｅ ｄｅｓｉ ｅｔ ｇｎ ｍ ｈ０ｄ ｒ ｅｓｅａｒ ｃｈ
设 计造型 图图片资料 或工程图 ， 过Ｐ ｏ Ｅ 通 ｒ ／ 曲面造型技 术以及造型模 块中功能 ，将 二维迅速 转化 为高 品质 的三维数字 模型 ， 到复杂的 车身空间 自由曲面。 同时对重建过程中 的关键技 得 术进 行了分析 研究。 关键词 ： 车身 曲面 ；建 模 ；三维重构 ；Ｐ ｏ Ｅ ｒ／ 中图分类号 ：Ｔ ２７ Ｂ ３ 文献标 识码 ：Ａ 文章编号 ：１０－ １４２１）（ － ｌ９ ０ ９ ０３ （０ ２３下） Ｏ３— ３ ０
顺 、各 曲面 连 接 过 渡处 也 必 须 达 到 平 滑 、过 渡 光
二 维信 息的 三维形 体 ，实现 三维 形体 的重建 。
基 于 图像 技 术三 维 重建 理论 的车身 曲面重 构 ，
常 应 用 于 车 身 的 自主 开 发 设 计 和 改型 设 计 中 口。 】 车 身 曲面 重 构 是基 于工 业 设 计 师 设 计 效 果 图 或工
三维曲面拟合方法
三维曲面拟合方法摘要：1.三维曲面拟合方法概述2.常见的三维曲面拟合算法介绍3.各算法的优缺点比较4.实际应用中的三维曲面拟合方法选择5.总结与展望正文：【提纲】1.三维曲面拟合方法概述在科学研究和工程领域，对三维数据进行曲面拟合是一项常见的任务。
三维曲面拟合方法旨在通过数学公式或算法，找到一个能够描述数据集中各个点关系的曲面。
这一过程通常包括选择合适的拟合函数、计算拟合参数以及评估拟合效果等步骤。
2.常见的三维曲面拟合算法介绍常见的三维曲面拟合算法包括多项式拟合、非线性最小二乘法、径向基函数网络（RBFN）、支持向量机（SVM）等。
a) 多项式拟合：通过构造一个多项式函数来描述三维数据集。
优点是计算简单，易于实现。
缺点是对于复杂的数据分布，多项式拟合可能无法很好地捕捉到数据的整体特征。
b) 非线性最小二乘法：通过最小化误差平方和来寻找最佳拟合函数。
优点是适用于多种类型的数据，具有较强的适应性。
缺点是需要迭代计算，且容易受到异常值的影响。
c) 径向基函数网络（RBFN）：通过径向基函数的加权和来构建拟合曲面。
优点是拟合效果较好，参数较少。
缺点是网络的构造和优化较为复杂。
d) 支持向量机（SVM）：将数据映射到高维空间，在该空间中寻找一个最佳分隔超平面。
优点是具有良好的泛化能力，适用于分类和回归任务。
缺点是计算复杂度较高，需要大量的训练数据。
3.各算法的优缺点比较在实际应用中，根据数据特点和任务需求，选择合适的三维曲面拟合算法至关重要。
以下是对各算法优缺点的比较：a) 多项式拟合：适用于数据较为简单的情况，计算简单，易于实现。
但对于复杂数据分布，拟合效果可能不佳。
b) 非线性最小二乘法：具有较强的适应性，适用于多种类型的数据。
但需要迭代计算，易受异常值影响。
c) 径向基函数网络（RBFN）：拟合效果较好，参数较少。
但网络构造和优化较为复杂。
d) 支持向量机（SVM）：具有良好的泛化能力，适用于分类和回归任务。
逆向工程中三维曲面重构技术研究
２１ 曲 面 逼 近 的基 本 理 论 ．
逆 向工 程 （ ｖｒ ｎ ｉｅｒ ｇ ｒ ｅｓ ｅ ｇｎ ｅｉ ）又称 为 反求 工 ｅ ｅ ｎ 程， 是一 个 复杂 的 系统工 程 。逆 向工 程技 术 的概 念
给 出已知数 据点 的格 式如 下 ： Ｐ， ｉ０ ， ｉ ＝ …ｎ ｊ ０ …ｍ
收 稿 日期 ： Ｏ １ ０ － ３ ２ ｌ— ５ ０
基 金 资 助 ： ０ １年 江 西 省 教 学 改 革 立项 课 题 （ Ｘ Ｇ １ ２ － ） ２１ Ｊ Ｊ 一１ — ９ ６ 。 作 者简 介 ： 曾文 瑜 （ ９ ３ ） 女 ， 州 平 坝 人 ， 算机 辅 助 设 计 副教 授 ， 程 硕 士 。 研 究 方 向 ： 算 机 辅 助设 计教 学 与研 究。 １７ 一 ， 贵 计 工 计
造 型 的重 要性 绝 不亚 于 产 品功能 ， 因为造 型 是最 直
观具 体 的 。为获 得 良好 的商业 效 果 ， 品的 外观 正 产 变得 越来 越重 要 。 计者 们通 过对 曲 面构建 技术 的 设 提 高来 提高 产 品外形 质 量 。对逆 向工程 而言 ， 产 在
品设 计 和生 产 过 程 中如 何 实 现 和 产 品最 初 设 计 的 造 型一致 显得 尤 其重要 。
第 ２ 卷 第 ４期 ６ ２ １ 年 ７月 ０１
岳 阳 职 业 技 术 学 院 学 报
Ｊ ＯＵＲ Ｌ ＯＦ ＹＵ ＮＡ ＥＹＡ ＶＯ Ａ￣ＯＮ Ｅ ＮＧ Ｃ ＡＬ Ｔ ＣＨＮ Ｃ Ｌ ＯＵ正ＧＥ Ｉ Ａ Ｃ
三维重构算法简述
系统的控制函数（特征函数）：1、单点概率函数，即孔隙率，重构前后2个模型具有相同的孔隙率（空隙相元素个数相等）。
2、三点概率函数，对于三维模型需要分别计算沿着x轴方向、y轴、z轴方向的三点概率函数。
3、线性路径函数，与三点概率函数相似，也需要计算三维空间的三个正交方向的线性路径函数。
计算过程：1、计算参考模型的各个控制函数。
2、生成初始模型随机生成一个512*512*200的“0、1”矩阵，“0”表示岩石基质，“1”表示空隙。
3、计算当前模型（或称为系统）的控制函数。
4、计算系统的能量E1——是一个关于三点概率函数和线性路径函数及其导数的表达式。
5、更新系统，即随机从中选取一个0和1对换位置，形成一个新系统，计算新系统的能量E2。
6、判断是否满足系统更新条件，满足转到5，否则转到7。
系统更新条件：记系统在第K+1次搜索时的状态的接受概率为P，且其中，T为程序中的一个控制参数，称为“温度”，那么系统状态接受准则定义为：，表示随机生成[0,1）区间的任意数。
若当前系统的P满足接受准则，则接受当前系统，需在其基础上进行第k+2次搜索，即转到5，否则转到7。
7、判断是否满足降温条件，满足转到8，否则转到5。
降温条件：记，其中为某一温度下失败率，为该温度下更新失败的次数，为该温度下系统更新的总次数。
设定一个值，如果大于它，那么就认为该温度下，大部分性能优异的解都已经找到，继续搜素对结果没有影响，可以对系统进行降温处理，即转到8，否则转到5。
8、系统降温。
降温方案为：，为降温速率，0<<1,通常取>0.9。
9、判断是否满足终止条件，满足输出最优系统，否则转到5。
终止条件：记n E为系统某一个状态连续更新失败的次数，当n E>10000次时则认为系统更新下去基本上不会找到比当前性能更好的状态，此时的状态可以被认为是满足要求的全局最优解的近似解，终止系统更新，并输出最终系统状态，否则转到5。
基于逆向工程的玩偶三维曲面模型重构技术
基于逆向工程的玩偶三维曲面模型重构技术摘要：本文研究了应用ug软件对“点云”数据进行曲面重构的过程：扫描线的生成、扫描线的排序、曲面裁剪和曲面的拼接直至曲面的构成，提出了一种先平面裁剪后拼接融合的多个小平面拼接方法，可使多个曲面光滑地连接成为一体。
关键词：点云逆向工程三维曲面模型重构一、引言cad/cam技术的日益成熟，并与现代加工设备的有机结合，只要有了三维cad模型，就可实现对产品进的新设计和各种工程分析，结合产品开发的要求进而创造出新产品。
二、基于ug软件的玩偶曲面重构在玩偶的曲面逆向工程中，玩偶曲面重构是设计玩偶cad模型构建的关键。
这里重点以玩偶的点云数据为对象，对玩偶曲面的特征曲线进行重构，如图1所示。
在对玩偶曲面的构建之前，首先对玩偶曲面构建进行规划，通过分析玩偶曲面的结构特征，可以将玩偶点云数据曲面的构建分为5部分：耳朵、脸、眼睛、嘴巴、鼻子，对这五个部分分别进行曲面构建后再进行拼合，如图2所示。
在玩偶曲面的重构过程中，为了便于元素的选择，采取了将耳朵、脸、眼睛、嘴巴、鼻子分别建立在不同的层上，各自的特征线也归属于自己的层，这样便于玩偶各部分曲面重构方便操作。
（一）玩偶逆向建模曲线构建特征线是cad模型重构的重要信息，特征线构建质量直接影响逆向建模的质量。
本节以玩偶的点云数据为例，说明应用ug软件构建曲线的过程。
对于以自由曲面为主要构成要素的产品，型面分析师建模规划的主要内容，即如何将一个复杂曲面产品分解成单张自由曲面。
以玩偶点云数据为例，该cad模型可以分解为耳朵、脸、眼睛、嘴巴、鼻子，这些部分又可以再次细分为四边形构成的曲面。
将玩偶点云数据作截面点，形成一条水平截面线。
截面点云数据以x=0坐标平面呈对称。
故在轮廓线的构建过程中，只要构建一般的曲线轮廓，然后使用镜像操作就可生成全部的曲线轮廓。
对玩偶耳边边界曲面由截面点云数据插值生成，以此选择点云数据生成一条b样条曲线，由于耳朵边沿曲线变化平缓，在取点时尽量使插值点分布均匀，分析重构曲线的曲率分布情况。
三维曲面重构技术
轴 的平 移）完 成一 次测量 任 务 所得 到 的数据 称 为单 视 图数 据 ．相 应地 ， 换 被 测工 件 与测量 机 的 相对 位 置 变 关系 （ 工件 的旋转 ） 称之 为视 图的变换 ， 如 ， 而处理 多视 图数 据 涉及到 曲面 匹配 技术 ． 单 视 图数 据 中每条 扫 描 线数据 排 列杂 乱 ， 与线 线 之 间 的数 据点 没有 明显 的拓 扑 关 系 ， 同时也 受 到 传感 器 噪声 的 污染 ． 接 用 这些 数 据 进行 发 展 起 来 的 一 个 领 域 ， 在 它
扫描 ．激 光测 头 由光 源 、 信号接 收单 元 （ Ｃ Ｃ Ｄ摄像 机 ） 和信 号处理 单 元（ 图像 采集 卡 ） 成 ， 图 ２所示 ． 组 如
飞 机 、 车 、 舶 、 具 制 造 业 和其 他 涉 及 自由曲线 曲 汽 船 玩 面 的工业 领域 内得 到 了广泛 的应 用 ．复杂 曲线 曲面实
ｎｏ ｃ ｎｔ ｃ ｅ ｓ ｒ ｎｇ ｓ ｓ ｅｍ ｎ－ ｏ ａ ｔ ｍ ａ ｕ ｉ ｙ ｔ
１ ． ＭＭ 在 整个测 量过 程 中起 着 至关重 要 的作 用 ． ）Ｃ 通 过它 高精度 的运动完 成测 量 系统 的定位 和测头 的在线
１ 数 据 预 处 理
不 改变被 测 工 件和 三坐 标 测量 机平 台相 对 位 置 ， 仅 通 过 测 量 机 带 动 测 头 进 行 扫 描 运 动 （ 括 Ｘ， 和 ｚ 包 ｙ
天 津 大 学 学 报
２０ ０ ２年 第 ０ ｊ卷 第 ２期
曲面 型值 点 ．其 中为 了 滤 除传 感 器 噪声 ． 可对 扫 描 数 据进 行最 小 二乘 曲线拟 合 ． 大 限 度地 减 小数 据 抖 动 最 带来 的影 响 ： 此基 础上 定制 出合理 的采 样 策略 ， 在 从而
三维模型修复和重构的原理与方法
三维模型修复和重构的原理与方法你有没有想过，我们眼前的一些超酷的三维模型，背后可能经历了怎样一番“惊心动魄”的修复和重构过程？说起来，三维模型就像是我们做的“拼图”，它们有时候完美无瑕，有时候却破碎得像是从天而降的玻璃片。
那修复这些“破碎的梦”可不是一件简单的事儿。
这其中的原理和方法，不得不让人感叹：科技进步真是牛逼！从一个坏掉的物体，到完美的模型，甚至恢复到最初的状态，这背后可有很多门道。
而这整套修复和重构的流程，就像是把一个被摔得稀巴烂的瓷器，轻轻地粘回去，再用镶金技艺修复，让它又恢复了原来的光泽。
听着很有艺术感吧？对，这就是三维模型修复和重构的魅力所在。
修复三维模型的关键是弄清楚它“崩溃”的原因。
模型就像一个受伤的战士，掉了些块儿，裂开了些缝。
啥原因？可能是扫描的时候精度不够，或者是数据丢失，甚至是我们手动操作中犯了错。
就像在画画的时候，笔一滑，突然画面就毁了，但这不代表画作不能再修复，恰恰是从这些细节入手，才能让它重生。
修复的过程就像是给这个模型“补充营养”，你得一步步地给它“填补”空缺，让它变得完整。
这时候，首先要用一些软件对模型进行修补，就像把裂缝填上，再用更高的精度去补充遗漏的细节。
没错，想象一下，原本是一个断裂的“古董”，经过重新拼接、加固后，居然又焕发了生机，简直就是神奇。
接下来的重构就更像是一场艺术创作了。
因为即使修复了这些碎片，它们依然无法完美地回到原来的模样。
这时候，重构就变得尤为重要。
要怎么做？首先得恢复那些丢失的数据，甚至通过一些推测和人工补充，把模型的形状给重新构建出来。
哎，说起来有点儿像解密，一步一步推理，还得保证重构出的新部分看起来与原模型无异。
这个过程其实不简单，你想想，如果是一个古代的雕像，已经有些部分被风化损坏，那就要靠设计师的眼力和经验，逐渐补充这些“空白”，最终还得确保整件作品看起来不突兀，甚至在视觉上能和原始设计浑然一体。
重构和修复最令人佩服的就是，它不只是一项技术活，更是一项艺术活。
三维数字重构算法
三维数字重构算法三维数字重构算法是一种将二维图像或点云数据转化为三维模型的计算方法。
它在计算机视觉、计算机图形学和计算机辅助设计等领域有着广泛的应用。
本文将介绍三维数字重构算法的原理、方法和应用。
三维数字重构算法的原理是基于从二维图像或点云数据中提取出的特征信息，通过计算和推断来还原出三维模型的形状和结构。
这个过程可以分为三个主要步骤：特征提取、点云生成和三维模型重建。
在特征提取阶段，算法会对输入的二维图像或点云数据进行处理，提取出其中的特征点、边缘、纹理等信息。
这些特征信息可以用来描述物体的形状、轮廓和表面特征，为后续的点云生成和三维模型重建提供基础。
在点云生成阶段，算法会根据特征信息生成一组三维点云数据。
这些点云数据可以看作是物体表面上的一系列离散点，它们的位置和密度可以反映出物体的形状和结构。
点云生成可以通过多种方法实现，如三角剖分、体素化和深度图像重建等。
在三维模型重建阶段，算法会根据点云数据还原出物体的三维模型。
这个过程可以通过点云的拟合、曲面重建和纹理映射等技术来实现。
最终得到的三维模型可以用于可视化、仿真、分析和设计等应用。
三维数字重构算法在许多领域都有着广泛的应用。
在计算机视觉领域，它可以用于三维重建、目标检测和姿态估计等任务。
在计算机图形学领域，它可以用于虚拟现实、游戏开发和动画制作等应用。
在计算机辅助设计领域，它可以用于产品设计、建筑规划和医学影像处理等任务。
然而，三维数字重构算法也面临着一些挑战和限制。
首先，特征提取的准确性和鲁棒性对算法的性能有着重要影响。
如果特征提取不准确或受到噪声干扰，将会导致点云生成和三维模型重建的结果不准确。
其次，算法的计算复杂度较高，需要大量的计算资源和时间。
这对于实时应用和大规模数据处理来说是一个挑战。
总之，三维数字重构算法是一种将二维图像或点云数据转化为三维模型的计算方法。
它在计算机视觉、计算机图形学和计算机辅助设计等领域有着广泛的应用。
随着计算机技术的不断发展和算法的改进，三维数字重构算法将会在更多的领域发挥重要作用，为人们带来更多的便利和创新。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三维曲面重构方法分析
摘要：曲面重构是逆向工程中CAD建模中的重要组成部分，三维曲面的重构方法决定了获得的曲面精度与光滑性，直接决定了逆向工程的效果，文章针对逆向工程中的关键技术三维曲面的重构方法进行了分析与讨论。
关键词：曲面重构；逆向工程；三维曲面
逆向工程是在吸收现有技术优点的基础上进行更优化的再创造技术，是针对现有设计方案的再设计过程。
设计师使用逆向工程技术能够从实物上获取该物体的三维数据，并生成数据模型，这样可以将数据模型与实体进行比较，从而得到两者之间的异同点。
使得在设计新产品过程中起点更高，设计周期更短，获得成效更快。
1 曲面重构算法的分类
三维曲面的重构，首先要进行点云的采集，然后进行曲面重构，并且结合正逆向工程的软件，重新设计比较复杂的三维曲面，得到光滑的无误的实体模型，并应用3D点云对齐的方式对重构模型进行误差分析，以达到最佳的重构效果。
在进行逆向工程的过程中，最重要的一步是重新对实体进行三维曲面重构。
这是因为产品的再设计、模型分析、虚拟仿真、加工制造过程等应用都需要根据三维数据模型来进行。
三维数据模型越准确这些过程得到的结果也会越准确。
要获得精确的数据模型，一方面需要良好的硬件设备和操作软件，另一方面与操作人员的熟练程度有很大的关系。
这是一个复杂、繁琐、技术性强的过程，国内外的众多学者都针对如何快速、准确地实现模型重构进行了大量的实验与总结，得到了很多曲面重构的算法，现在常用的曲面重构算法根据曲面类型、数据来源、造型方式能分为：
①按点云类型可分为规则排序的点与不规则排序的点。
②按数据来源可分为三坐标测量、软件造型、光学测量等途径。
③按造型的方式可分为根据曲线生成曲面与根据曲面拟合实体模型。
④按曲面表现形式可分为曲面边界表示、曲面四边B-样条表示、三角面片和三角网格表示的模型重构。
通常，采用NURBS、有理B-样条、Bezier曲面来表示长方形区域面重构的自由曲面，而采用NURBS和三角域的拓扑结构来进行散乱点的自由曲面重构。
2 曲面重构的精度
在进行曲面重构前，必须先对数据模型的基本信息与要求进行了解。
基本信息包括了实体的几何特征、构造特点等；应用要求包括了数据分析、产品制造、
模具设计、快速成型制造等，根据数据模型的基本信息与要求来进行曲面重构。
在进行逆向工程中，如何构建出比较精确的数据模型是一个十分重要的内容。
如果在进行数据模型建立的过程中精度达不到要求，那么在后期就无法完全将实体模型还原出来。
使用多面体来拟合曲面，可以提高模型的建立和修改速度，并且在仿真、3D 演示与数控加工过程中也更加快速，所以使用多面体进行曲面重构具有很高的效率，然而要形成多面体数据模型，需要把所获得的点云连接成面片，需要大量的计算时间，而且获得的模型中也不可避免地存在重叠等错误；而且对于平面的数据区域，也没有必要构建复杂而紧密的网格数据。
这样，对点云数据的后处理过程就非常的重要。
3 三维曲面重构的方法与过程
在逆向工程中，如果要建立模型，通常先建立三维曲面数据，然后再根据曲面数据生成实体数据。
在进行三维曲面重构时，一般遵循先后构建点—曲线—曲面的原则。
在进行三维曲面构建时，需要根据曲面的类型选择合适的建立方式，以使得生成的曲面更加的光顺、精确。
曲面的建立方法多种多样，根据不同的曲面类型可以灵活选择，如可以根据点云数据直接获得曲面，可以通过蒙皮、扫掠等方法获得曲面，或者根据点阵和曲线进行三维曲面的建立等。
下面将对三种创建三维曲面的方法进行介绍。
3.1 根据曲线建立三维曲面模型
根据曲线建立三维曲面模型是先将数据点通过插值或逼近拟合成样条曲线或参数曲线，然后完成曲面面片的造型，再将曲面通过延伸、剪裁等曲面编辑手段，获得三维曲面模型。
其过程如图1（a）中所示。
这种方法适用于数据不大，并且数据点的排列也比较有规律的情况。
如果处理数据量不大，而且数据呈有序排列的情况。
如果曲线比较密集的话，建立的曲面就不易获得良好的光顺性，而曲线的选择过少的话，又无法获得很好的精度。
这是这种方法比较明显的缺点。
3.2 通过拟合生成三维曲面
通过拟合生成三维曲面是对测量数据点直接进行曲面片拟合形成曲面模型，其过程如图1（b）所示。
这种方法既能处理有序的点，也可以处理点云数据。
使用这种方法来进行三维曲面造型时，需要特别注意应精确的对数据进行分割。
假如采用一张曲面片去拟合由两个或两个以上类型的曲面，那么拟合后获得的曲面将是不光滑的。
在进行数据分割时，不同的分割方法获得的结果也有很大不同。
使用这种方法建立曲面时，应根据测量数据的类型、曲面的复杂程度等选择合适的曲面造型方法，在实际造型过程中，有可能会采用两种不同的方法来对一个实体模型进行造型。
3.3 根据曲面特征及约束建立三维曲面模型
在进行产品设计时，很多零件都可以根据一些特征点来进行设计与制造，在曲面造型时，也可以根据零件的几何特征来进行曲面的生成，特征之间还具有确定的几何约束关系。
这样，三维曲面模型的重构还应考虑产片的设计特征与特征间的约束关系，将他们还原生成所需要的数据模型。
这个过程与多数的工业产品没计意图相符合，能够有效地解决产品的装配对齐、造型的对称问题，进而减小误差，提高三维曲面的造型质量。
根据曲面特征来进行三维曲面的重构将正向设计中的特征技术引入到逆向工程中，根据测量得到的点云数据得到设计的特征，然后再根据这些特征以及特征间的约束关系重新建立三维曲面模型。
这种方法的关键是要在点云数据中获取设计意图以及明显的设计特征。
多数的机械零件产品都是按一定特征设计和制造的，利用特征技术构造的数据模型包含了原始的、表达产品设计思路的特征信息，同时机械零件产品特征之间具有确定的几何约束关系。
这样当进行实体模型重建过程中，必须能够将其中的特征以及它们之间的约束进行还原，如果忽略掉特征或几何约束的话，所得到的数据模型都是不准确的。
而在数据处理过程中，约束的确定是非常困难的，因为测量的数据点只有位置信息，并不包括特征关系与约束关系，需要对整个模型重新分析和判断，即使这样得到的约束关系仍然有很大的不确定性。
这个过程一般通过人工引导，半自动地实现。
根据模型特征及约束进行三维曲面建立并生成模型的方法不仅是数据建模的发展方向，也是产品设计的一种新方法。
现在根据产品的特征以及约束条件进行曲面建立，对于比较复杂的自由曲面、复合曲面仍然比较困难。
对于实际产品的设计与生产，很多产品并不是简单的用一个曲面构成的，很多都是由多个曲面拼接、过渡所得到的，这样的复杂曲面在进行特征的提取与约束条件的判定过程会变得困难，并且在进行数据分割的时候也有较大的难度。
这样想建立精确而光滑的曲面模型仍然是比较困难的。
4 结语
三维曲面重构技术是逆向工程的重要组成部分，获得的曲面模型质量与精度将直接影响到实体模型精度以及后续的模型分析、三维仿真、产品制造等过程。
本文对三维曲面的重构方法进行了分析与讨论，在实际操作中，还应根据实际的模型特征，合理选择合适的曲面重构方法，以获取高质量的数据模型。
参考文献：
[1] 仇灿华，成思源，张湘伟.基于反求工程技术的零件有限元分析[J].机械设计与制造，2009，（9）：35-36.
[2] 刘金颂，张庆阳.反求工程技术研究[J].机械工程与自动化，2009，（8）：196-200.
[3] 徐慧朴，马孜，吴德烽.逆向工程中三维离散点云的平滑整定新算法[J].工程设计学报，2008，15（2）：128-133.
[4] 李国富.基于反求工程的倒车灯开关设计[J].鄂州大学学报，2008，15（5）：25-28.。