MIT普通物理习题4
MIT普通物理习题5

麻省理工学院物理系
物理8.04 2003年春季
第五部分问题
阅读:French and Taylor ,第三章。
1. 高斯量子波函数 (25 分)。
一个质量为m 的离子处于下面的状态
Ψ(x , t ) = ,
[]it mx a Ae +−)/(2 在此A 和a 为正常数。
(a) 找出 A.。
(b) 为每个Ψ态满足的薛定谔方程找到势能函数 V (x )。
我们把这个电势叫什么? (c) 计算 x , x 2,p ,和 p 2的期望值。
找到 σx 和 σp ,这些结果是不是与海森堡不确定
关系相一致, σx σp ≥ 2/=? 对关于高斯波函数假设做出评论。
[提示: a dx e ax π=∫∞∞−2, 以及应用da
d 推导另一个有用的关系式] 2. 概率事件 (25 分)。
一个粒子处于被波函数 Ψ(x, t )所描述的状态. 假设 P ab (t ) 是在时间t 点(a < x < b )范围内找到粒子的概率。
可以看出
dt
dP ab = J (a, t ) - J (b, t ), 在此
[提示: 计算 2Ψ∂∂t
] J (x, t )的单位是什么?
J 被称为是概率, 因为它告诉你可能通过x 点的概率。
如果P ab (t )增加,很可能是从一点流进区域的内部而非从其它地方流出。
最新新概念物理教程-力学答案详解(四)

3vm新力学习题答案(四)4—1.如本题图,一质量为m 的质点自由降落,在某时刻具有速度v 。
此时它相对于A 、B 、C 三参考点的距离分别为d 1、d 2、d 3。
求(1)质点对三个点的角动量;(2)作用在质点上的重力对三个点的力矩。
0sin (sin ()2(00sin (sin (131213121=====⨯=⨯======⨯=mg d M mg d mg d M mgd M gm r F r M mv d J mv d mv d J mvd J vm r J A B A C B A 方向垂直纸面向里)方向垂直纸面向里)方向垂直纸面向里)方向垂直纸面向里))解:(θθϖϖϖϖϖϖϖϖ的力矩。
的角动量和作用在其上。
求它相对于坐标原点的力方向并受到一个沿处,速度为的粒子位于(一质量为—f x j v i v v y x m y x -+=,ˆˆ),.24ϖ()()()()()()i ymg kyf j xmg k mg if j y i xg m f r F r M k myv mxv jv i v m j y i x v m r J x y yx ˆˆˆˆˆˆˆˆˆˆˆˆ-+=--⨯+=+⨯=⨯=-=+⨯+=⨯=ϖϖϖϖϖϖϖϖϖ解:()()秒弧解:依题有:求其角速度。
为普朗克常量,等于已知电子的角动量为率运动。
的圆周上绕氢核作匀速,在半径为电子的质量为—/1013.1103.5101.914.321063.622),1063.6(2/103.5101.9.3417211313422341131⨯=⨯⨯⨯⨯⨯⨯=====⋅⨯⨯⨯------mR h h mR Rmv J s J h h m kg πωπωπ什么变化?为多少?圆锥的顶角有的速度时,摆锤,摆长拉倒时摆锤的线速度为设摆长为我们可将它逐渐拉短。
,子,系摆锤的线穿过它央支柱是一个中空的管如本题图,圆锥摆的中—2211.44v lv l解:分析:摆锤受到绳子张力和重力的作用,此二力对过O 沿管子方向均无力矩分量, 所以过O 沿管子方向(即竖直方向)上角动量守恒。
MIT量子力学作业4

MIT量⼦⼒学作业4Homework 43.23 Electrical, Optical and Magnetic Properties of Materials, Fall 2014Due on Monday, October 13 at noonin the problem set box outside 13-4138PROBLEM 1.Consider a particle in a 1D potential box of length L.1)Quickly derive the eigenstates of this problem and their respective energies.2)If a particle is in the ground state of such a well and the potential then instantly double its size(length: 2L). What are the eigenstates of the new potential? Project the initial wave function on these harmonics.3)Using the relevant harmonics (after justifying why they are relevant), describe the motion of theparticle. What is the period of this movement?4)After a certain amount of time, the particle is measured at the fourth energy state. Calculate theenergy change of the particle. Does it mean that conservation of energy is not respected in quantum mechanics?PROBLEM 2.Below are represented two eigenstates of the Hydrogen atom. For each of them, answer the following questions:1)What is the number of angular nodes? What is the number of radial nodes?2)What is the energy of the orbital? What is the principle quantum number n? What is thedegeneracy of this energy level?3)What is the l quantum number? What is the name of the orbital (eg: 1s, 2p, etc.)?Figure 1: orbital 1 and orbital 2PROBLEM 3.The Hückel model treats planar hydrocarbons by considering only the unsaturated C atoms (i.e. those C atoms for which not all of the outer shell electrons are already involved in σ-bonding with H or C atoms.) Hückel ‘s technique is based on the variational method using a basis of p z orbitals localized on these unsaturated C atoms, neglecting all overlap integrals and making the further simplifications:1) For each of the structures above, identify the unsaturated C atoms, which contain the pz orbitalconsidered in the Hückel model.2) For each of these structures, write out the Hückel determinantal equation (i.e. the matrix whosedeterminant gives the energy levels of the system).3) Solve for the energy levels, and sketch an energy level diagram including any degeneracies.PROBLEM 4. Variational principlesThe idea behind using the variational principal is to find a function as close as possible to the ground state of the system by starting with a family of functions expected to reasonably contain a good approximation the actual ground state.1) Consider the (1D) harmonic oscillator: H ?=p2?2m +12mω2x2. First, we will consider a rational function as a possible eigenstate.Ψa (x )=1x2+a (a is a parameter). Is Ψa normalized? Calculate E a =<Ψa |H|Ψa >. Minimize this energy with respect to the parameter a . What is the value of a that gives the energy minimum? What is the minimum energy? CalculateΔE E o =E a ?E 0E o, where E 0 is the true ground state energy.2) Now, let’s consider another test function Ψa (x )=e ?ax2. Following the same process as before, what is the closest state to the ground state? What is the value of ΔE E o ?PROBLEM 5.Consider a cubic crystal where atoms of mass M 1 lie on one set of planes and atoms of mass M 2 lie on planes interleaved between those of the first set. Let a represent the repeat distance of the lattice in the direction normal to these planes. Consider waves that propagate in a symmetry direction for whicha single plane contains only a single type of ion. (such directions are [111] in the NaCl structure and[100] in the CsCl structure.)1) Write the two equations of motion under the assumption that each plane interacts only with itsnearest neighbor planes and that the force constants, C , are identical between all pairs of nearest neighbor planes. (Use u s for the displacement of plane ‘s ’ of the M 1 atoms and v s for the M 2 atom plane displacements.)2) Look for solutions in the form of traveling waves, now with different amplitudes u , v onalternate planes.3) Substitute your solutions, obtain a 2x2 determinant, and thus the resultant equation for theangular frequency. (do not solve but go on to (d)).4) Consider the limiting cases 1<5) Sketch the particle displacements, label, and discuss. Be sure to include in your discussion thequestion of energy continuity.。
大学物理期末复习题精选(北京邮电大学第4版)

习题11.1选择题(1) 一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为(A)dtdr(B)dt r d(C)dt r d || (D) 22)()(dtdy dt dx +[答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为(A)tRt R ππ2,2 (B) t R π2,0(C) 0,0 (D) 0,2tRπ [答案:B]1.2填空题(1) 一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是 ;经过的路程是 。
[答案: 10m ; 5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m·s -1,则当t 为3s 时,质点的速度v= 。
[答案: 23m·s -1 ]1.3 一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状; (2) 物体的内部结构; (3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1.4 下面几个质点运动学方程,哪个是匀变速直线运动?(1)x=4t-3;(2)x=-4t 3+3t 2+6;(3)x=-2t 2+8t+4;(4)x=2/t 2-4/t 。
给出这个匀变速直线运动在t=3s 时的速度和加速度,并说明该时刻运动是加速的还是减速的。
(x 单位为m ,t 单位为s )解:匀变速直线运动即加速度为不等于零的常数时的运动。
加速度又是位移对时间的两阶导数。
2022届湖北省新高考信息卷(四)物理试题

2022届湖北省新高考信息卷(四)物理试题一、单选题 (共6题)第(1)题如图为美国物理学家密立根测量金属的遏止电压与入射光频率的实验图像,该实验证实了爱因斯坦光电效应方程的正确性,并且第一次利用光电效应实验测定了普朗克常量h 。
若该图线的斜率和纵截距的绝对值分别为k 和b ,电子电荷量的绝对值为e ,则普朗克常量h可表示为( )A .kB .ekC .bD .eb第(2)题如图,钢架雪车比赛中,雪车以速率v 通过截面为四分之一圆弧的弯道,弯道半径为R ,不计雪车受到冰面摩擦力。
在此情况中( )A .运动员和雪车所受合外力为零B .轨道对雪车的弹力为其转弯的向心力C .若仅增大v ,则雪车离轨道底部更高D .若仅增大R ,则雪车离轨道底部更高第(3)题如图所示是α粒子(氦原子核)被重金属原子核散射的运动轨迹,M 、N 、P 、Q 是轨迹上的四点,在散射过程中可以认为重金属原子核静止.图中所标出的α粒子在各点处的加速度方向正确的是( )A .M 点B .N 点C .P 点D .Q 点第(4)题金属钛由于其稳定的化学性质,良好的耐高温、耐低温、抗强酸、抗强碱,以及高强度、低密度,被美誉为“太空金属”。
用频率为2.5×1015Hz 的单色光照射金属钛表面,发生光电效应。
从钛表面放出光电子的最大初动能与入射光频率的关系图线如图所示。
普朗克常数h =6.63×10−34J·s,则下列说法正确的是( )A .钛的极限频率为2.5×1015HzB .钛的逸出功为6.63×10-19JC .随着入射光频率的升高,钛的逸出功增大D .光电子的最大初动能与入射光的频率成正比如图所示,有一块半径为R的半圆形玻璃砖,OO'是对称轴。
现有平行单色光垂直照射到AB面,玻璃砖对该单色光的折射率为。
已知,不考虑二次反射,则( )A.玻璃砖的弧面上有光射出的区域弧长为B.若在纸面内将玻璃砖绕圆心逆时针旋转,有光射出的区域弧长不变C.所有从射出的光线都将汇于一点D.入射光线距OO'越远,出射光线与OO'的交点离AB面越远第(6)题一列向右传播的简谐横波在时刻的波形图如图所示,A、B两质点间距为,B、C两质点的平衡位置间距为,时质点C恰好向下通过平衡位置,则该波的最小波速为( )A.B.C.D.二、多选题 (共4题)第(1)题如图所示,某同学在操场上练习投掷铅球,将铅球从某一水平面的A点以仰角斜向上抛出,铅球运动过程中经过同一水平面上、与A点相距的B点,且最高点距该水平面。
麻省理工学院(MIT)相关课程习题9
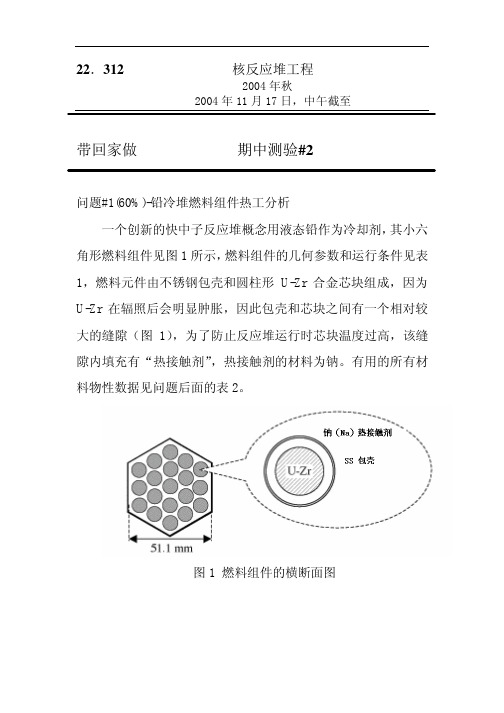
22.312核反应堆工程2004年秋2004年11月17日,中午截至带回家做期中测验#2问题#1(60%)-铅冷堆燃料组件热工分析一个创新的快中子反应堆概念用液态铅作为冷却剂,其小六角形燃料组件见图1所示,燃料组件的几何参数和运行条件见表1,燃料元件由不锈钢包壳和圆柱形U-Zr合金芯块组成,因为U-Zr在辐照后会明显肿胀,因此包壳和芯块之间有一个相对较大的缝隙(图1),为了防止反应堆运行时芯块温度过高,该缝隙内填充有“热接触剂”,热接触剂的材料为钠。
有用的所有材料物性数据见问题后面的表2。
图1 燃料组件的横断面图表1 运行条件和燃料组件几何参数参数值燃料组件热功率456kW入口/出口温度400 o C /500o C轴向功率分布因子 1.0燃料组件内宽度51.1mm(见图1)燃料棒数量19燃料棒中心距11.0mm燃料棒外直径9.0mm包壳厚度0.6mm燃料芯块直径 6.8mm活性区燃料长度 1.2m问题:a)(10%)从教科书中选择一个合适的传热关系式。
(假设垂直于流动方向的速度和温度分布均是充分发展的)b)(10%)计算燃料组件入口区长度,评价问题a中假设温度和速度均为充分发展的精度。
如果用充分发展的传热关系式计算,实际的传热系数是被高估还是低估了?解释之。
c)(10%)假设轴向发热均匀分布,画出冷却剂主流温度和包壳外表面温度随着轴向位置的变化曲线。
(假设冷却剂的物性参数可作为常数)d)(10%)计算包壳外表面最高温度和芯块中心最高温度。
(在计算缝隙的温降中只考虑其导热作用)e)(10%)假如运行人员提高10%的功率而并没有改变冷却剂的流量和入口温度,包壳外表面最高温度和芯块中心最高温度如何变化?f)(10%)金属绕丝型格架经常被用于液态金属冷却快堆,如果在图1中的燃料组件采用该方法,冷却剂的流速、主流温度、传热系数和压降会增大、减小、还是维持不变?为什么?(假设功率、质量流量、入口温度和燃料几何参数维持不变)表2 物性(所有物性均不随温度变化)材料ρ(kg/m3) k(W/m.K) µ(Pa.s) C p(J/kg.K) 液态铅10400 16 0.0019 155不锈钢8000 14 / 470液态钠780 60 0.00017 1300U-Zr合金16000 20 / 120六边形面积和周长分别为:问题#2(40%)—双层芯块的最大线功率密度为了提高舰用轻水堆的功率,一家电力公司采用双层芯块燃料元件,双层芯块包括两个区域,一个区域装载UO2,另一个区域装载PuO2(图2所示),芯块外表面温度固定在400o C。
大学物理(第四版)课后习题及答案 动量
题3.1:质量为m 的物体,由水平面上点O 以初速为0v 抛出,0v 与水平面成仰角α。
若不计空气阻力,求:(1)物体从发射点O 到最高点的过程中,重力的冲量;(2)物体从发射点到落回至同一水平面的过程中,重力的冲量。
题3.1分析:重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可。
由抛体运动规律可知,物体到达最高点的时间g v t αsin 01=∆,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍。
这样,按冲量的定义即可求出结果。
另一种解的方法是根据过程的始、末动量,由动量定理求出。
解1:物体从出发到达最高点所需的时间为g v t αsin 01=∆ 则物体落回地面的时间为gv t t αsin 22012=∆=∆ 于是,在相应的过程中重力的冲量分别为 j j F I αsin d 0111mv t mg t t -=∆-==⎰∆j j F I αsin 2d 0222mv t mg t t -=∆-==⎰∆解2:根据动量定理,物体由发射点O 运动到A 、B 的过程中,重力的冲量分别为j j j I αsin 00y Ay 1mv mv mv -=-= j j j I αsin 200y By 2mv mv mv -=-=题3.2:高空作业时系安全带是必要的,假如质量为51.0kg 的人不慎从高空掉下来,由于安全带的保护,使他最终被悬挂起来。
已知此时人离原处的距离为2米,安全带的缓冲作用时间为0.50秒。
求安全带对人的平均冲力。
题3.2解1:以人为研究对象,在自由落体运动过程中,人跌落至2 m 处时的速度为ghv 21= (1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有()12mv mv t -=∆+P F (2)由(1)式、(2)式可得安全带对人的平均冲力大小为 ()N 1014.123⨯=∆+=∆∆+=tgh m mg t mv mg F解2:从整个过程来讨论,根据动量定理有N 1014.1/23⨯=+∆=mg g h tmgF 题 3.3:如图所示,在水平地面上,有一横截面2m 20.0=S 的直角弯管,管中有流速为1s m 0.3-⋅=v 的水通过,求弯管所受力的大小和方向。
MIT普通物理习题2
麻省理工学院物理系物理8.04 2003年春季 第二部分习题阅读:French and Taylor ,第二章。
1. 光电效应中的时间延迟(20分)。
一束强度为每秒107eV 的紫外光突然间射在金属的表面,通过光电效应打出了电子。
紫外光束的横截面面积为1cm 2,对应的电子能量为10eV 的光电子,金属逸出功为5eV 。
紫外光照射后多长时间可以预期发生光电效应?(a ) 一般来说,我们可以估计在一个原子(半径约为1)表面聚集5eV 的能量所需要的时间。
假设光粒子束的能量均匀分布在它的横截面上,计算这个时间大约多长。
oA (b ) 实际上(就像1916年瑞利展示的那样),来自(a )部分的估计过于消极。
一个原子存在一个面积大约为的有效区域,此时光的波长2λλ对应它的共振频率(例如瑞利散射)。
在这个基础上计算一个经典延迟时间。
(c ) 在这个过程的量子描述下,当第一个光子一撞击到散射面上时,光电效应可能就会立刻发生。
但是为了得到一个可以与经典估计相比的时间,考虑10eV 能量的光子是一个接一个连续到达金属表面的,它们的平均时间间隔可视为接通光束到打出第一个光电子的平均时间延迟。
2.普朗克常量的确定(20分)。
干净的钠金属表面(在真空中)被单色光照亮。
在一系列的测量中,运用了各种各样的波长,延迟势被观测到了,这个延迟势是为了阻止最大能量的光电子所必需的,如下图所示:用这样的方法划分这些数据,是为了说明它们(近似)沿着一条在光电公式中所预言的直线,并且获得了一个普朗克常数h 的数值。
3.康普顿散射(25分)。
(a ) 可以看出一个自由电子不可能吸收一个碰撞到它上面的单光子所有的能量。
(b ) 对于一个光子被一个自由的,稳定的电子散射,由康普顿波长差公式可得:在这里θ为光子的散射角。
(c ) 康普顿波长差λ∆,与入射光子能量E 0=hv 0=hc/0λ无关。
但是,康普顿能量差为,却与入射光的能量有关。
请找出康普顿能量差的表达式。
麻省理工学院物理系
3
质量 M 2.0 10 30 kg 1000g 1m 3 1.4g / cm 体积 4 3 4 r (7.0 10 8 m) 1kg 100cm 3 3
1.38 同样的道理。
问题 1.10(位置,速度和加速度)
问题 1.12(脑筋急转弯——回到地球上的同一点)
解决脑筋急转弯没有什么特别好的方法, 但是一种非常有用的提示, 那就是考虑 “特殊情况” 。 在这些特殊情况中,我们可以寻找地球上的特殊点。我们最好从北极点、南极点和赤道上入 手。 北极点是一个满足条件的点——如果你从它出发向南走一定的距离 d,然后走一个圈,长度 由你定,再向北走相同的距离 d,你就回到了北极点上。很好。 另一些满足条件的点必须在围绕着南极点的特殊圆上且满足以下条件:其周长为 10/n,其 中 n=1,2,3,… 令圆 1 的周长为 10 公里。在向东走过 10 公里后,你回到了出发点。令圆 2 的周长为 5 公 里。在向东走 10 公里后,你依然回到了出发点。这样对于任意正整数 n 来说都是成立的。 每一个这样的圆在整个运动中都是第二个过程。起始位置可以设置在这些特殊圆北面 10 公 里的任意一点(这些起始位置也构成了一个圆) 。这样,第一个过程就是向南走 10 公里到 达特殊圆,第二个过程就是沿着特殊圆向东走 10 公里并回到这一过程的出发点,而后第三 个过程就是向北走 10 公里回到出发点(实际上就是第一个过程的返回) 。
a) b) 求导即可。 c) 再次求导得 d) 用 b)部分的方程 (见图表) (见图表) (见图表)
e) 使用c)部分的方程:a(0)=4m/s2 a (2)= 4m/s2 f) a (4)= 4m/s2 令 ,以求出t=3s。现在,把t带入方程x(t)中 以求得物体速度为零时的位置。简单的答案如下x(3)= –2m v(3)=0m/s
2022届湖北省新高考信息卷(四)物理试题
2022届湖北省新高考信息卷(四)物理试题一、单选题 (共6题)第(1)题如图所示,某激光器的一端固定于圆心O点,以角速度绕O点转动,转动过程中从激光器的另一端连续发出波长为的细激光束(不计光束截面积),在半径为R的虚线圆某处固定一弧形接收屏,接收屏沿虚线圆的长度为l。
激光器转动一周的过程中,接收屏接收到的光子数为n,已知普朗克常数为h,激光传播的速度为c,则激光器的发射功率为( )A.B.C.D.第(2)题位于坐标原点处的波源发出一列沿x轴正方向传播的简谐横波。
t= 0时波源开始振动,其位移y随时间t变化的关系式为,则t=T时的波形图为()A.B.C.D.第(3)题水平地面上有一个固定的粗糙斜面,斜面顶端固定一个光滑定滑轮,如图所示一轻质细绳跨过滑轮,其一端悬挂小球N,另一端与斜面上的物块M相连,系统处于静止状态。
现用图示的拉力F缓慢拉动N,且拉动过程中力F的方向与悬挂N的细绳保持某个钝角不变,使悬挂N的细绳由竖直达到水平位置。
此过程中物块M始终保持静止,则在此过程中( )A.拉力F先增大后减小B.细绳对M的拉力先增大后减小C.M对斜面的压力逐渐增大D.斜面对M的摩擦力一直增大第(4)题如图是某液面高度测量仪内部的原理图,该仪器通过电容器电容的变化来检测容器内液面高低,容器中的导电液体和导电芯柱分别是电容器的两个电极,芯柱外面套有绝缘管作为电介质,电容器的这两个电极分别用导线与一个线圈的两端相连,组成LC振荡电路。
容器内的导电液体与大地相连,若某时刻线圈内的磁场方向向右,且正在减弱,则该时刻( )A.磁场能正向电场能转化B.电容器两极板间电压正在减小C.导电芯的电势低于导电液的电势D.若容器内液面升高,则LC振荡电路的频率变大第(5)题牛顿认为物体落地是由于地球对物体的吸引,这种吸引力可能与天体间(如地球与月球)的引力具有相同的性质、且都满足。
已知地月之间的距离r大约是地球半径的60倍,地球表面的重力加速度为g,根据牛顿的猜想,月球绕地球公转的周期为()A.B.C.D.第(6)题如图所示,在竖直平面内,截面为三角形的小积木悬挂在离地足够高处,一玩具枪的枪口与小积木上点等高且相距为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
麻省理工学院物理系
物理8.04 2003年春季 第四部分作业
阅读:Liboff ,第三章。
Gasiorowicz ,第二章 包含了关于不确定关系的一些有用的部分。
1. 粒子衍射以及不确定关系(20分)。
一束具有确定动量p x ,且已经校准的粒子束,穿过一个宽度为d 的狭缝投射到屏幕上。
粒子束沿传播方向有一个轻微的散射,散射角d /λθ≈。
用德布罗意波长公式x p h /=λ描述为衍射。
可以看出,这种衍射的散射角也可以粗略的用(y ∆)(y p ∆)的不确定度来描述。
(y 方向与粒子束最初的方向x 垂直)
2.不确定原则和精确度实验(25分)。
一个孩子在高度为H 的梯子顶部,把一个质量为m 的弹性球投到地板上,并且想在地板上砸一个裂缝。
为了达到这个目的,孩子使用了最高精度的设备。
假设空气阻力和微风的作用可以完全忽略不计。
由经典公式得到的距离,可以看出弹球将不会砸出裂缝。
这里g 为重力加速度。
赋予H 和m 合理的值,计算这个距离的数值。
1/41/2(2H/g)/m)(=3.三角波包和不确定关系(35分)。
我们假设前面问题中涉及的三角形脉冲为一个波函数。
(a ) 运用标准化条件找出N 值。
(b ) 在x 点的期望值由下列公式给出:
dx x x x 2
)(∫∞∞−=〉〈ψ 动量p 的期望值由下列公式给出:
计算x 和p 的值。
(提示:利用宇称的性质)。
(c ) 由公式(△x )2=〈x 2〉-〈x 〉2可以计算出在x ∆位置的不确定度。
对于动量为的
位置有相似性的原理。
计算p ∆x ∆和p ∆的数值。
用p x ∆∆的乘积与海森堡不确定关系
所允许的最小值做比较。
提示:你将会发现下列公式非常有用:
4.巴塞伐尔定理(20分)。
证明下面的理论(已知的巴塞伐尔定理):如果)(~k ψ
为)(x ψ的傅立叶变换形式,那么它们就有相似的标准化过程。
就是
(注意:验证过程并不是很长。
)。
