-第十三章《轴对称》小结与复习

合集下载

轴对称知识点整理总结

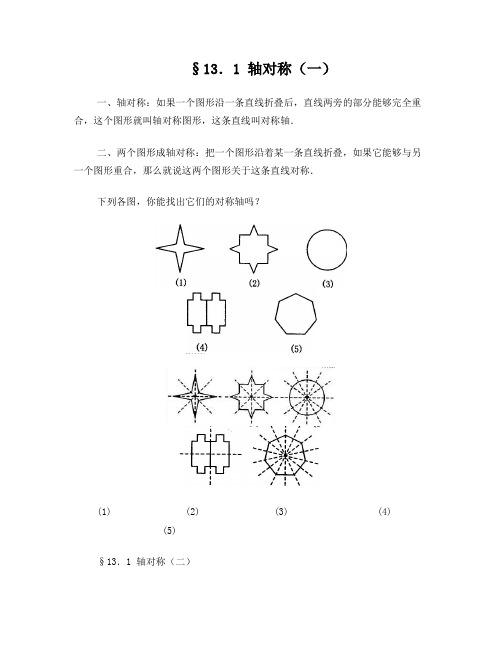
§13．1 轴对称（一）一、轴对称：如果一个图形沿一条直线折叠后，直线两旁的部分能够完全重合，这个图形就叫轴对称图形，这条直线叫对称轴．二、两个图形成轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称．下列各图，你能找出它们的对称轴吗？(1) (2) (3) (4)(5)§13．1 轴对称（二）一、线段垂直平分线的定义：经过线段中点并且垂直于这条线段的直线，叫做线段的垂直平分线．二、图形轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对称点所连线段的垂直平分线．类似地，轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线．三、线段垂直平分线的性质：线段垂直平分线的点到这条线段两个端点的距离相等；反过来，与这条线段两个端点距离相等的点都在它的垂直平分线上．[探究1]线段垂直平分线上的点与这条线段两个端点的距离相等．即AP1=BP1，AP2=BP2，…证明．证法一：利用判定两个三角形全等．如下图，在△APC和△BPC中，△APC≌△BPCPA=PB.证法二：利用轴对称性质．由于点C是线段AB的中点，将线段AB沿直线L对折，线段PA与PB是重合的，•因此它们也是相等的．[探究2]1.作线段AB，取其中点P，过P作L，在L上取点P1、P2，连结AP1、AP2、BP1、BP2．会有以下两种可能．2．讨论：要使L与AB垂直，AP1、AP2、BP1、BP2应满足什么条件？探究过程：1．如上图甲，若AP1≠BP1，那么沿L将图形折叠后，A与B不可能重合，也就是∠APP1≠∠BPP1，即L与AB不垂直．2．如上图乙，若AP1=BP1，那么沿L将图形折叠后，A与B恰好重合，就有∠APP1=∠BPP1，即L与AB重合．当AP2=BP2时，亦然．§12．2作轴对称图形一．如何由一个平面图形得到它的轴对称图形．【探究】四边形ABCD的四个顶点的坐标分别为A(－5,1)、B(－2,1)、C(－2,5)、D(－5,4)，分别作出与四边形ABCD关于x轴和y轴对称的图形．（归纳：与已知点关于y 轴或x轴对称的点的坐标的规律；）【引申】分别作出△PQR关于直线x=1(记为m)和直线y=－1(记为n)对称的图形，你能发现它们的对应点的坐标之间分别有什么关系吗？若△PQR中P(x,y)关于x=1(记为m)轴对称的点的坐标P(x,y) ，则，y= y．若△PQR中P(x,y)关于y=－1(记为n)轴对称的点的坐标P(x,y) ，则x= x，=n．13．3. 1等腰三角形等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．同学们在自己作出的等腰三角形中，注明它的腰、底边、顶角和底角．思考：1．等腰三角形是轴对称图形吗？请找出它的对称轴．2．等腰三角形的两底角有什么关系？3．顶角的平分线所在的直线是等腰三角形的对称轴吗？4．底边上的中线所在的直线是等腰三角形的对称轴吗？底边上的高所在的直线呢？结论：等腰三角形是轴对称图形．它的对称轴是顶角的平分线所在的直线．因为等腰三角形的两腰相等，所以把这两条腰重合对折三角形便知：等腰三角形是轴对称图形，它的对称轴是顶角的平分线所在的直线．沿等腰三角形的顶角的平分线对折，发现它两旁的部分互相重合，由此可知这个等腰三角形的两个底角相等，而且还可以知道顶角的平分线既是底边上的中线，也是底边上的高．由此可以得到等腰三角形的性质：1．等腰三角形的两个底角相等（简写成“等边对等角”）．2．等腰三角形的顶角平分线，底边上的中线、•底边上的高互相重合（通常称作“三线合一”）．例题与练习1．如图2其中△ABC是等腰三角形的是 [ ]2．①如图3，已知△ABC中，AB=AC．∠A=36°，则∠C______(根据什么？)．②如图4，已知△ABC中，∠A=36°，∠C=72°，△ABC是______三角形(根据什么？)．③若已知∠A＝36°，∠C＝72°，BD平分∠ABC交AC于D，判断图5中等腰三角形有______．④若已知 AD＝4cm，则BC______cm．3．以问题形式引出推论l______．4．以问题形式引出推论2______．13．3.2等边三角形等边三角形定义：在等腰三角形中，有一种特殊的情况，就是底边与腰相等，这时，三角形三边都相等。

第13章轴对称知识点

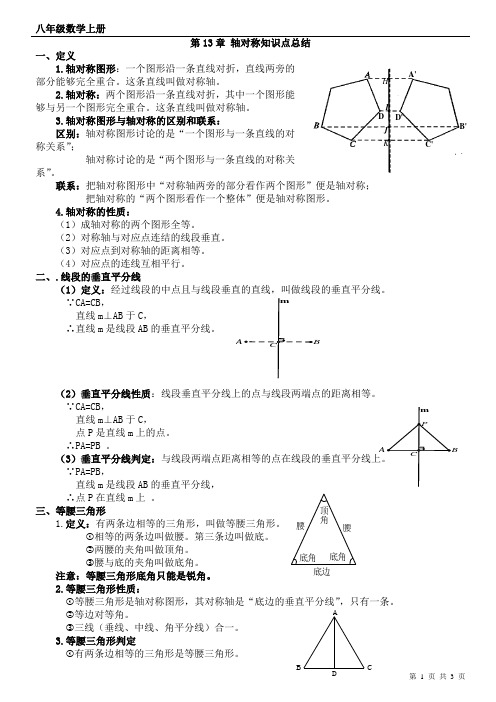
第13章轴对称知识点总结一、定义1.轴对称图形：一个图形沿一条直线对折，直线两旁的部分能够完全重合。

这条直线叫做对称轴。

2.轴对称：两个图形沿一条直线对折，其中一个图形能够与另一个图形完全重合。

这条直线叫做对称轴。

3.轴对称图形与轴对称的区别和联系：区别：轴对称图形讨论的是“一个图形与一条直线的对称关系”；轴对称讨论的是“两个图形与一条直线的对称关系”。

联系：把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称；把轴对称的“两个图形看作一个整体”便是轴对称图形。

4.轴对称的性质：（1）成轴对称的两个图形全等。

（2）对称轴与对应点连结的线段垂直。

（3）对应点到对称轴的距离相等。

（4）对应点的连线互相平行。

二、.线段的垂直平分线（1）定义：经过线段的中点且与线段垂直的直线，叫做线段的垂直平分线。

∵CA=CB ，直线m ⊥AB 于C ，∴直线m 是线段AB 的垂直平分线。

（2）垂直平分线性质：线段垂直平分线上的点与线段两端点的距离相等。

∵CA=CB ，直线m ⊥AB 于C ，点P 是直线m 上的点。

∴PA=PB 。

（3）垂直平分线判定：∵PA=PB ，直线m 是线段AB 的垂直平分线，∴点P 在直线m 上。

三、等腰三角形1.定义：有两条边相等的三角形，叫做等腰三角形。

①相等的两条边叫做腰。

第三条边叫做底。

②两腰的夹角叫做顶角。

③腰与底的夹角叫做底角。

注意：等腰三角形底角只能是锐角。

2.等腰三角形性质：①等腰三角形是轴对称图形，其对称轴是“底边的垂直平分线”，只有一条。

②等边对等角。

③三线（垂线、中线、角平分线）合一。

3.等腰三角形判定①有两条边相等的三角形是等腰三角形。

m CA B D'D C'B'A'K J I H 底边底角底角顶角腰腰CBA②有两个角相等的三角形是等腰三角形。

四、等边三角形1.等边三角形定义：三条边都相等的三角形，叫做等边三角形。

说明：等边三角形就是腰和底相等的等腰三角形，因此，等边三角形是特殊的等腰三角形。

轴对称章节复习要点总结

轴对称章节复习要点总结知识复习重联系本章知识内容是⼀个有机的整体，理顺知识的相互联系，有助于学⽣数学意识、数学精神的产⽣。

在复习时，按照知识的产⽣发展理出下⾯的顺序，实际⽣活中轴对称的感受，轴对称与轴对称图形的区别和联系，轴对称的三条性质，性质的三⽅⾯应⽤（作对称轴、作轴对称图形、⽤坐标表⽰轴对称），线段的垂直平分线（三句话），在平⾯上,若点在已知线段的垂直平分线上,则它到这条线段的两个端点的距离相等。

由此可见,通过改写定理中的三句话,可以把定理分成三部分:论域(平⾯上所有点组成的集合I);题设(点在线段的垂直平分线上);结论(点到线段两端点的距离相等)。

与此相对偶的⾓平分线（三句话），等腰三⾓形（定义、性质和判定），等边三⾓形（定义、性质和判定）。

注重轴对称在各知识点中的应⽤和指导作⽤，例如，已知：B、E、D、F、C再同⼀条直线上，且点D是BC的中点，AB=AC，AE=AF，图中全等三⾓形有哪⼏对。

有轴对称的意识，△ABF≌△ACE这⼀对全等就不容易遗忘。

⽅法应⽤重优选由于有线段中垂线的两条性质，⾓平分线的两条性质，等边对等⾓，等⾓对等边，三线合⼀等知识，在应⽤中可以优化全等三⾓形的证明思路，不断地进⾏⽐较学习，使学⽣对新知识的应⽤意识加强。

例如，点E是∠AOB的平分线，EC⊥OA，ED⊥OB，垂⾜分别是C、D。

求证：（1）∠ECD＝∠EDC；（2）OE是CD的垂直平分线。

多数学⽣⽤两次全等证明，徐叶琳同学在利⽤⾓平分线性质得到ED=EC后绕道全等得到∠ECD＝∠EDC，真是“过家门⽽不⼊”，同学对于性质“等边对等⾓”是很熟悉的，为什么没有及时想到呢，还是新知识的应⽤意识不强，⼀时没有想到。

本题证题思路是：⼀平分两垂直得相等ED=EC，等边对等⾓得∠ECD＝∠EDC，等⾓的余⾓相等得∠OCD＝∠ODC，等⾓对等边得OD=OC，由到线段两端点距离相等的点在线段的垂直平分线上，得到点O、E都在线段CD 的垂直平分线上，从⽽证得OE是CD的垂直平分线。

人教版八年级数学上册第13章轴对称小结与复习

则 1=2= 1 BAC. 2
∵ AB = AC，∴ AE⊥BC.
∴∠2 +∠C = 90°.
A
∵ BD⊥AC，∴∠DBC +∠C = 90°. ∴∠2 =∠DBC.
12 D
∴∠BAC = 2∠DBC.
B
E
C
方法总结
在涉及等腰三角形的有关计算和证明中，常见的辅助线的作法是作顶角的平分线(或底边上的高、中线)，然后利用等腰三角形“三线合一”的性质，实现线段或角之间的相互转化.
A D
6. 如图，已知等边△ABC 中，点 D、E B
分别在边 AB、BC 上，把△BDE 沿直线
DE 翻折，使点 B 落在 B1 处，DB1，EB1 D
分别交边 AC 于 M、H 点. 若∠ADM =
50°，则∠HEC 的度数为 70° .
B
AC M B1 H
EC
7. 如图，在△ABC 中，AD 是角平分线，AC = AB + BD.
一、轴对称的相关定义和性质 1.定义 (1) 如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做_轴__对__称__图__形___，这条直线就是它的__对__称__轴___.
(2) 将一个平面图形沿一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对
2. 如图，∠3 = 30°，为了使白球反弹后能将黑球直接
撞入袋中，那么击打白球时，必须保证∠1 的度数为
__6_0_°__.
考点二关于坐标轴对称的点的坐标
例2 按要求完成作图：
y
(1) 作△ABC 关于 y 轴对称的
△A1B1C1； (2) 在 x 轴上找出点 P，使 PA

人教版八年级上册数学第13章《轴对称》小结与复习.doc

轴对称小结与复习。

•知识梳理1.如果一个平面图形沿一条直线折卺，直线两旁的部分能够 ____________ ，这个图形就叫做轴对称图形，这条直线就足它的对称轴.2.把一•个阁形沿着某一条直线折佥，如果它能够与另一个阁形 __________ ,那么就说这两个阁形欠于这条直线（成轴）对称，这条直线叫做对称轴.温馨提示：把成轴对称的两个图形看成一个整体，它就是一个轴对称图形；把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条对称轴对称.3.经过线段__________ 丼且 _________ 这条线段的直线，叫做这条线段的®直平分线.4. _____________ 上的点与这条线段两个端点的距离相等.与一条线段两个端点距离相等的点，在这条线段的___________ .温馨提示：（1）如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的_________ ;⑵轴对称图形的对称轴，是任何一对对应点所连线段的_____________ .5. __________________________________________ 点P（x，y）关于x轴对称的点的华标为__________________________________________ ，点P（x: y）关于y轴对称的点的叱标为__________ .6.等腰三角形的性质：（1） __________________________________________等腰三角形的两个底角_（简写成：）.（2） ___________________________________________________________________________________ 等腰三角形的顶角平分线、底边上的屮线、底边上的高____________________________ （简写成：_________ ）.7.等腰三角形的判定：如果一个三角形有W个角相等，那么这两个角所对的边也__________ （简写成“等角对等边”）.8.等边三角形的性质：等边三角形的三个内角___________ ，并且每一个角都等于__________ •9.等边三角形的判定：（1） _____________________ 三个角的三角形是等边三角形.（2） __________________________________ 有一个角是60°的是等边三角形.10. _____________________________________________________________________ 在直角三角形屮，如果一个锐角等于30°,那么它所对的直角边等于斜边的 ______________ .•考点呈现考点1判别轴对称图形例1 （2013年咸宁）下列学习用具中，不是轴对称图形的是（）分析：根据轴对称图形的概念：把-个图形沿一条直线折叠，K 线两旁的部分能够互相重合的图形是轴对称图形，对各选项逐一判断即可.解:选项A 、B 、D 是轴对称图形，选项C 不是轴对称图形.故选C. 考点2线段的垂直平分线的性质例2 （2013年泰州）如图1,在AABC 中，AB+AC=6 cm, BC 的垂直平分线7与AC 相交于点D,则AABD 的周长为分析：根据线段乖直平分线的性质，可得DC=DB,进而可确定AABD 的周长. 解：因为7 :世:直平分BC ，所以DB=DC.所以AABD 的周长=AB+AD+BD=AB+AD+DC=AB+AC=6 cm.故填 6. 考点3画轴对称图形例3 （2013年哈尔滨）如图2所示，在每个小正方形的边长均为1个单位长度的方格纸屮，有线段AB 和直线MN,点A, B, M, N 均在小正方形的顶点上，在方格纸屮画四边形 ABCD （四边形的各顶点均在小正方形的顶点上），使四边形ABCD 是以直线MN 为对称轴的轴对称阁形，点A 的对称点为点D ，点B 的对称点为点C.分析：过点A M 直线MN 的■线，画足为0,在垂线上截収0D=0A ，D 就是A 关于直线. 的对称点；同现，岡出点B 关于直线MN 的对称点C;连接BC ，CD, DA ，即可得到四边形ABCD.cm.r•I 11暴• •f' ' I 1 1 費 1///• •參•• . ••17BA图2解：正确画阁如阁3所示.例4 (2013年重庆)作图题：(不要求写作法)如图4所示，AABC 在平刖直角坐标系中，点 A,B ，C 的坐标分别为 A (―2，1) , B (―4，5)，C (-5, 2).(1)作AABC 关于直线7: x=-l 对称的△A 1B 1C 1，其中,点A, B ，C 的对应点分别为 B,, C 1；⑵写山点A ：, B,, G 的坐标.分析：⑴根椐网格结构找出点A, B, C 关于直线7的对称点A ：, B:, G,然后顺次连接即可;⑵直接根据平面直角坐标系写出点A:, B B (；的坐标.解：如图5所示.(2)A, (0, 1)、B, (2, 5)、C, (3, 2).考点4关于x 轴或y 轴对称的点的坐标例5 (2013年遂宁)将点A (3, 2)沿x 轴向左平移4个单位长度得到点A',点A' 关于y 轴对称的点的坐标是()A. (-3, 2)B. (-1,2)C. (1, 2)D. (-1,-2)分析：先利川平移中点的变化规律求出点A'的嫩标，再根据关于y 轴对称的点的坐标特征即可求解.解：因为将点A (3, 2)沿x 轴叫左平移4个单位长度得到点A',所以点A'的坐标为(一1，2).所以点A'关于y 轴对称的点的坐标是(1, 2).故选C.考点5等腰三角形的性质B\ A/L/ \/ \CA** 1 C r1A ；5o ‘fJB阁6例6 （2013年台湾）如阁6，在长方形ABCD中，M为CD中点，分别以B, M为圆心, BC, MC长为半径画弧，两弧相交于点P.若ZPBO70",则ZMPC的度数为（）A. 20°B. 35°C. 40°D. 55°分析：根据等腰三角形两底角相等求出ZBCP，然后求出ZMCP,再根据“等边对等角” 求解即可.解：因为分别以B，M为圆心，BC, MC长为半径的两弧相交于点P,所以BP=BC, MP=MC.因为ZPBC=70°,所以ZBCP=A （180°— ZPBC）（180°—70°）=55° •2 2在长方形ABCD 中，ZBCD=90° ,所以Z.MCP=90° -ZBCP=90°一55° =35° .所以ZMPC=ZMCP=35°.故选 B.考点6等腰三角形的判定例7 （2013年河北）如图7所示，一艘海轮位于灯塔P的南偏东70°方向的M处，它以每小时40海里的速度向正北方向航行，2小吋后到达位于灯塔P的北偏东40°的N处，则N处与灯塔P 的距离为（）A. 40海.里B. 60海里C. 70海里D. 80海里分析：根裾题意，可得ZM=70°，ZN=40°，在AMXP屮求得ZNPM的度数，证明ANINP 足等腰三角形，即可求解.解：依题意，知MN=2X40=80（海里），ZM=70°，ZN=40°，所以ZNPM=180° -ZM-ZN: 180° -70° -40° =70° .所以ZNPM=ZM.所以XP=MN=80海里.故选D.考点7等边三角形的性质例8 （2013年黔西南州）如|冬|8,己知AABC是等边三角形，点AB, C, D, E 在M—直线上，J1.CG=CD, DF=DE,则ZE 的度数/分析：根裾等边三角形的性质，可知ZACB=60°，根据等腰三角图8形底角相等即可得illZE的度数.解：因为AABC是等边三角形，所以ZACB=60° , ZACD=120° .因为CG=CD,所以ZCDG=30u , ZFDE=150° .因为DF=DE ，所以ZE=15° .故填15° .考点8含30°角的直角三角形的性质例9 （2013年泰安）如图9，在RtAABC 中，ZACB=90°垂直平分线DE 交AC 于点E ，交BC 的延长线于点F ，若ZF=30° 则BE 的长是 ______________ .分析:根据题意推得ZDBE=30° ,则在RtADBE 中由“30° 半”即可求得线段BE 的长度.解：因为 FD 丄AB,所以ZACB=ZFDB=90° . 因为ZF=30° ,所以ZA=ZF=30° .又DE 垂直平分线AB,所以ZEBA=ZA=30° . 因为DE=1,所以HE=2DE=2.故填2.參误区点拨误区1轴对称含义理解不清致错例1如图1中的（1）、（2）两个阁形成轴对称，请画ili 它们的对称轴.错解：如图1所示的直线..剖析：沿直线MX 对折，在直线MN 两旁的图形的确可以互相重合，似这里要求的是画（1）、（2）的对称轴，而MN 并不是这两个阁形的对称轴.画成轴对称的两个阁形的对称轴时耍注意所指的是哪个两个阁形，特别注意当这两个图形木身也是轴对称阁形时，不要把各自图形的对称轴作为两个图形的对称轴.正解：如图1所示的直线PQ. 误区2对轴对称的性质理解不深致误例2如图2,已知A, C 两点关于BD 对称，下列结论：®0A=0C ；②0B=0D;③AD=CD;④AB=CB.其中正确的有 _______________ （填序兮即可）.错解：填①②③④.AB 的 DE=1,3角所对的直角边是斜边的一©(1) (2)图 1阁2剖析：错解“A ，C 两点关于I3D 对称”错误理解为“AC, BD 互相垂直平分”，实际上 OA=OC,AB=CB, AD=CD 成立，但 OB=OD 不一定成立.正解：填①③④.參跟踪训练1. （2013年铁岭）下列图形中，是轴对称图形的有（）2. （2013年山西）如图1所示，正方形地砖的图案是轴对称图形，该图形的对称轴有（）3. （2013年德州）如图2, AB//CD,点E 在BC 上，且CD=CE, ZD=74°，则ZB 的度数为（）A. 68°B. 32°C. 22°D. 16°4. （2013年广州）点P 在线段AB 的垂直平分线上，PA=7，则PB= _________________ .5. 如图3, AABC 与△/VBA 关于直线m 成轴对称，若ZA=35°, ZB=55°,则ZC ：的度数为 ____________ .6. （2013年盐城改编）如图4-①是3X3正方形网格，将M:中两个方格涂黑，井且使得涂黑后的整个图案足轴对称图形，约定绕正方形ABCD 的中心旋转能重合的图案都视为同一种阁案，例如阁4-②中的四幅阁就视为M —种阁案，试画岀W 种不|u 個案（不M 于阁4-②）.1条 B图12条C. 4条②7.若在等腰三角形中作出一些线段（如角平分线、屮线、高等），你能发现其中一些相等的线段吗？你能证明你的的结论吗？（1） ______________________________________________________________________ M答：等腰三角形两条腰上的中线相等吗？答：____________________________________ （填“相等”或“不相等”）；（2）证明⑴中你的结论.耍求：用图5中的符号表达己知、求证，并证明，证明对各步骤要注明依据.轴对称小结与复习知识梳理.•略.跟踪训练：1. D 2. C 3. B4. 75. 90°6.解：答案不唯一，给出两种如图所示.7.解：⑴相等（2）已知:在AABC中，AB=AC, BD, CE分别为中线，求证:BD=CE. 证明：••• BD, CE分别为中线（已知），... AD=-AC, AE=-AB （中线的定义）.2 2••• AB=AC （已知），...AD二AE.在AABD 和AACE 屮，AD=AE, ZA=ZA （公共角相等），AB=AC, ••• AABD^AACE （SAS）./. BD=CE （全等三角形的对应边相等）.。

八年级数学上册人教版《轴对称复习与小结》导学案

第十三章轴对称复习与小结教学稿〔定稿〕课型：新授课主备：张艳玲协备：王明杰【教学内容】：轴对称复习【教学目标】：1.进一步认识轴对称、轴对称图形, 掌握轴对称的根本性质, 对应点连线被对称轴垂直平分的性质；2.能按照要求作出简单图形经过一次或两次轴对称后的图形；3.熟练掌握线段的垂直平分线的概念、等腰三角形、等边三角形的有关概念, 并能用它们的性质及判定方法解决相关问题【教学重点】：线段的垂直平分线、等腰三角形、等边三角形的性质及判定【教学难点】：运用线段的垂直平分线、等腰三角形、等边三角形的性质及判定解决相关问题.【教法学法】：教法：归纳总结学法：思考合作交流展示【教学准备】：多媒体课件【教学过程】：一、自主明标〔一〕诊断练习1.以下图案是轴对称图形的有〔〕A．1个B．2个C．3个D．4个2.△ABC中, DE是AC的垂直平分线, 垂足为E,交AB于点D, AE=5cm, △CBD的周长为24cm, △ABC的周长是 .3.等腰三角形是轴对称图形, 其对称轴是_______________________________．°, 那么另外两个角的度数是A〔x, －4〕与点B〔3, y〕关于x轴对称, 那么x＋y的值为____________.6. 如图, △ABC中, ∠ACB=错误! 未找到引用源. , CD是△ABC的高, ∠A=错误! 未找到引用源. , AB=4, 求BD长．〔二〕明标预习板书目标：会用线段的垂直平分线、等腰三角形、等边三角形的性质及判定解决相关问题一．本章知识框架图1、轴对称、线段垂直平分线、角平分线、等腰三角形性质判定的应用2、等腰三角形边与角计算中的分类讨论思想与方程思想〔1〕、等腰三角形的一个内角是800, 那么它的另外两个内角是〔2〕、等腰三角形的周长为24, 一边长为6, 那么另外两边的长是〔3〕、等腰三角形一腰上的高与另一腰的夹角为30°, 那么它的底角为二、互动达标(轴对称、线段垂直平分线、角平分线、等腰三角形性质判定的应用〕探究一轴对称、线段垂直平分线、角平分线、等腰三角形性质判定的应用3．如下图, AD是△ABC的角平分线, EF是AD的垂直平分线, 交BC的延长线于点F, 连结AF．求证：∠BAF=∠ACF．探究一等边三角形的性质, 30°所对的直角边等于斜边的一半的应用例2：如图, 在等边ABC△中, 点D E，分别在边BC AB，上, 且BD AE, AD与CE交于点F．〔1〕求DFC∠的度数．〔2〕假设CH⊥AD于H, 求证：CF=2FH〔3〕假设FH=3,EF=1,求AD的长.例:3：如图1, △ACB和△DCE均为等边三角形, 点A, D, E在同一直线上,连接BE．〔1〕①∠AEB的度数为_____②线段AD, BE之间的数量关系为______．〔2〕如图2, △ACB和△DCE均为等腰直角三角形, ∠ACB=∠DCE=90°, 点A, D, E在同一直线上, CM为△DCE中DE边上的高, 连接BE, 请判断∠AEB的度数及线段CM, AE, BE之间的数量关系, 并说明理由．〔三〕归纳小结〔1〕本章的核心知识有哪些？这些知识间有哪些联系？〔2〕通过本节课的复习, 你学会了哪些数学方法？四、多元测标〔5分钟, 1、2号互换, 对抗批阅, 核算达标人数进行小组考核〕1.点P(3, -1)关于y轴的对称点Q的坐标为(a+b, 1-b), 那么a b的值为.2.如图, AB∥CD, 点E在BC上, 且CD=CE, ∠D=74°, 那么∠B的度数为()A.68°B.32°C.22°D.16°3.如图, 在△ABC中, ∠B=30°, BC的垂直平分线交AB于E, 垂足BAFED C为D .假设ED =4, 那么CE 的长为()4.如图, 在△ABC 中, ∠ABC 和∠ACB 的平分线交于点E , 过点E 作MN ∥BC 交AB 于M , 交AC 于N , 如果MB +CN =6, 那么线段MN 的长为.5. 如图, ∠DEF =36°, AB=BC=CD=DE=EF, 求∠A 五、拓展练习1.等腰三角形一腰上的高与另一腰的夹角为60°, 那么这个等腰三角形的顶角为2.A 〔2, -1〕为平面直角坐标系内一点, O 为原点, P 是x 轴上的一个动点, 如果以点P 、O 、A 为顶点的三角形是等腰三角形, 那么符合条件的动点P 共有个.3.如下图, ∠ABC =90°, AB =BC , AE 平分∠BAC 交BC 于E , CD ⊥AE 交AE 的延长线于D . 求证:CD =21AE .4.如图, 在Rt △ABC 中, AB=AC, ∠BAC=90°, D 为 BC 的中点.〔1〕写出点D 到ΔABC 三个顶点 A 、B 、C 的距离的关系〔不要求证明〕〔2〕如果点M 、N 分别在线段AB 、AC 上移动, 在移动中保持AN=BM, 请判断△DMN 的形状, 并证明你的结论6、如图, △ABC, △ADE 是等边三角形, B, C, D 在同一直线上．求证：(1)CE ＝AC ＋DC ；(2)∠ECD ＝60°第四单元第1课函数一、根底稳固1．一般地, 如果在一个变化过程中有两个变量x 和y , 并且对于变量x 的每一个值, 变量y 都有________的值与它对应, 那么我们称y 是x 的________, 其中________是自变量． 2．下面选项中给出了某个变化过程中的两个变量x 和 y , 其中y 不是．．x 的函数的是( )A ．y ：正方形的面积, x ：这个正方形的周长B ．y ：等边三角形的周长, x ：这个等边三角形的边长C ．y ：圆的面积, x ：这个圆的直径D ．y ：一个正数的平方根, x ：这个正数 3．以下关系式中, y 不是．．x 的函数的是( )A ．y ＝xB ．y ＝x 2＋1C ．y ＝|x |D ．|y |＝2x4．(泸州)以下曲线中不能．．表示y 是x 的函数的是( ) 5．表示函数的方法一般有________、__________和__________；函数的表示方法可以互相转化, 应用中要根据具体情况选择适当的方法．6．在下表中, 设x 表示乘公共汽车的站数, y 表示应付的票价．x /站 1 2 3 4 5 6 7 8 9 10 y /元1112233344根据此表, 以下说法正确的选项是( )A ．y 是x 的函数B ．y 不是x 的函数C ．x 是y 的函数D ．以上说法都不对7．假设每上6个台阶就升高1 m, 那么上升高度h (单位：m)与上的台阶数m (单位：个)之间的函数关系式是( ) A ．h ＝6m B ．h ＝6＋mC ．h ＝m －6D ．h ＝m68．(随州)“龟兔赛跑〞这那么寓言故事讲述的是比赛中兔子开始领先, 但它因为骄傲在途中睡觉, 而乌龟一直坚持爬行最终赢得比赛, 以下函数图象可以表达这一故事过程的是( ) 9．对于一个的函数, 自变量的取值范围是使这个函数________的一切值；对于一个实际问题, 自变量的取值必须使____________有意义．如果当x ＝a 时y ＝b , 那么b 叫做当自变量x 的值为a 时的__________． 10．(内江)函数y ＝x ＋1x －1, 那么自变量x 的取值范围是( ) A ．－1＜x ＜1 B ．x ≥－1且x ≠1C ．x ≥－1D ．x ≠111．函数y ＝2x －1x ＋2中, 当x ＝a 时的函数值为1, 那么a 的值是( )A ．－1B ．1FEDCBADE CBAN MDCAC ．－3D ．312．函数y ＝⎩⎪⎨⎪⎧x 2－3〔x ≤2〕x －1〔x ＞2〕当函数值y ＝6时, 自变量的值是( )A ．7B ．－3C ．－3或7D ．±3或7 二、拓展提升13．在国内投寄本埠平信应付邮资如下表：信件质量x /g 0＜x ≤2020＜x ≤4040＜x ≤60邮资y /元(1)y 是x 的函数吗？为什么？(2)分别求当x 取5, 10, 30, 50时的函数值．14．某生态公园方案在园内的坡地上造一片只有A, B 两种树的混合林, 需要购置这两种树苗2 000棵, 种植 A, B 两种树苗的相关信息如下表：品种价格(单位：元/棵)成活率劳务费(单位：元/棵)A 15 95% 3 B2099%4设购置A 种树苗x 棵, 造这片树林的总费用为y 元, 解答以下问题： (1)写出y 与x 之间的函数表达式；(2)假设这批树苗种植后成活1 960棵, 那么造这片树林的总费用为多少元？第26章反比例函数实际问题与反比例函数2一、根底稳固1.某工厂现有原材料100吨, 每天平均用去x 吨, 这批原材料能用y 天, 那么y 与x 之间的函数表达式为〔〕 A ．y ＝100x B ．y ＝C ．y ＝+100D ．y ＝100﹣x2.如图, 市煤气公司方案在地下修建一个容积为104m 3的圆柱形煤气储存室, 那么储存室的底面积S 〔单位：m 2〕与其深度d 〔单位：m 〕的函数图象大致是〔〕A ．B ．C ．D ．3.甲、乙两地相距s 〔单位：km 〕, 汽车从甲地匀速行驶到乙地, 那么汽车行驶的时间y 〔单位：h 〕关于行驶速度x 〔单位：km /h 〕的函数图象是〔〕A ．B ．C ．D ．4.教室里的饮水机接通电源就进入自动程序, 开机加热每分钟上升10℃, 加热到100℃, 停止加热, 水温开始下降, 此时水温〔℃〕与开机后用时〔min 〕成反比例关系, 直至水温降至30℃, 饮水机关机．饮水机关机后即刻自动开机, 重复上述自动程序．水温y 〔℃〕和时间x 〔min 〕的关系如图．某天张老师在水温为30℃时, 接通了电源, 为了在上午课间时〔8：45〕能喝到不超过50℃的水, 那么接通电源的时间可以是当天上午的〔〕 A ．7：50B ．7：45C ．7：30D ．7：205.在温度不变的条件下, 通过一次又一次地对汽缸顶部的活塞加压, 测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强, 如下表：那么可以反映y 与x 之间的关系的式子是〔〕体积x 〔mL 〕10080604020压强y〔kPa〕6075100150300A．y＝3 000x B．y＝6 000x C．y ＝D．y ＝6.随着私家车的增加, 交通也越来越拥挤, 通常情况下, 某段公路上车辆的行驶速度〔千米/时〕与路上每百米拥有车的数量x〔辆〕的关系如下图, 当x≥8时, y与x成反比例函数关系, 当车速度低于20千米/时, 交通就会拥堵, 为防止出现交通拥堵, 公路上每百米拥有车的数量x应该满足的范围是〔〕A．x＜32B．x≤32C．x＞32D．x≥327.如图, 在平面直角坐标系中, 函数y ＝〔k＞0, x＞0〕的图象与等边三角形OAB的边OA, AB分别交于点M, N, 且OM＝2MA, 假设AB＝3, 那么点N的横坐标为〔〕A ．B ．C．4D．68.如图, 反比例函数y1＝〔k1＞0〕和y2＝〔k2＜0〕中, 作直线x＝10, 分别交x轴, y1＝〔k1＞0〕和y2＝〔k2＜0〕于点P, 点A, 点B, 假设＝3, 那么＝〔〕A ．B．3C．﹣3D ．9.直线y＝x+3与x轴、y轴分别交于A, B点, 与y ＝〔x＜0〕的图象交于C、D两点, E是点C关于点A的中心对称点, EF⊥OA于F, 假设△AOD的面积与△AEF 的面积之和为时, 那么k＝〔〕A．3B．﹣2C．﹣3D ．﹣10.如图, 点A、B 在双曲线〔x＜0〕上, 连接OA、AB, 以OA、AB为边作▱OABC．假设点C恰落在双曲线〔x＞0〕上, 此时▱OABC的面积为〔〕A ．B ．C ．D．411.某物体对地面的压强P〔Pa〕与物体和地面的接触面积S〔m2m2时, 该物体对地面的压强是Pa．12.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示, 售价是销量的反比例函数〔统计数据见下表〕．该运动鞋的进价为180元/双, 要使该款运动鞋每天的销售利润到达2400元, 那么其售价应定为元．售价x〔元/双〕200240250400销售量y〔双〕3025241513.小刚同学家里要用1500W的空调, 家里保险丝通过的最大电流是10A, 额定电压为220V, 那么他家最多还可以有只50W的灯泡与空调同时使用．14.在一个可以改变体积的密闭容器内装有一定质量的某种气体, 当改变容器的体积时, 气体的密度也会随之改变, 密度ρ〔单位：kg/m3〕与体积v〔单位：m3〕满足函数关系式〔k为常数, k ≠0〕其图象如下图过点〔6, 1.5〕, 那么k的值为．15.小丁在课余时间找了几副度数不同的老花镜, 让镜片正对太阳光, 上下移动镜片, 直到地上的光斑最小, 此时他测量了镜片与光斑的距离, 得到如下数据：老花镜的度数x/度…100125200250…镜片与光斑的距离y/m…1…m, 那么这副老花镜为度．16.为预防传染病, 某校定期对教室进行“药熏消毒〞, 药物燃烧阶段, 室内每立方米空气中的含药量y〔mg〕与燃烧时间x〔分钟〕成正比例；燃烧后, y与x成反比例〔如下图〕．现测得药物10分钟燃烧完, 此时教室内每立方米空气含药量为6mgmg时, 对人体方能无毒害作用, 那么从消毒开始, 至少需要经过分钟后, 学生才能回到教室．二、拓展提升17.近似眼镜片的度数y〔度〕是镜片焦距x〔cm〕〔x＞0〕的反比例函数, 调查数据如表：眼镜片度数y〔度〕4006258001000 (1250)镜片焦距x〔cm〕251610 (8)〔1〕求y与x的函数表达式；〔2〕假设近视眼镜镜片的度数为500度, 求该镜片的焦距．18.y〔毫克/百毫升〕与时间x〔时〕成正比例；1.5小时后〔包括1.5小时〕y与x成反比例．根据图中提供的信息, 解答以下问题：〔1〕写出一般成人喝半斤低度白酒后, y与x之间的函数关系式及相应的自变量取值范围；〔2〕按国家规定, 车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶〞, 不能驾车上路．参照上述数学模型, 假设某驾驶员晚上21：00在家喝完半斤低度白酒, 第二天早上7：00能否驾车去上班？请说明理由．19.教室里的饮水机接通电源就进入自动程序, 开机加热时每分钟上升10℃, 加热到100℃停止加热,水温开始下降, 此时水温y〔℃〕与开机后用时x〔min〕成反比例关系, 直至水温降至30℃, 饮水机关机, 饮水机关机后即刻自动开机, 重复上述自动程序．假设在水温为30℃时接通电源, 水温y〔℃〕与时间x〔min〕的关系如下图：〔1〕分别写出水温上升和下降阶段y与x之间的函数关系式；〔2〕怡萱同学想喝高于50℃的水, 请问她最多需要等待多长时间？20.某地建设一项水利工程, 工程需要运送的土石方总量为360万米3．〔1〕写出运输公司完成任务所需的时间y〔单位：天〕与平均每天的工作量x〔单位：万米3〕之间的函数关系式；〔2〕当运输公司平均每天的工作量15万米3, 完成任务所需的时间是多少？〔3〕为了能在150天内完成任务, 平均每天的工作量至少是多少万米3？21.蓄电池的电压为定值．使用此蓄电池作为电源时, 电流Ⅰ〔单位：A〕与电阻R〔单位：Ω〕是反比例函数关系, 它的图象如下图．〔1〕求这个反比例函数的表达式；〔2〕如果以此蓄电池为电源的用电器的电流不能超过8A, 那么该用电器的可变电阻至少是多少？22.某公司用100万元研发一种市场急需电子产品, 已于当年投入生产并销售, 生产这种电子产品的本钱为4元/件, 在销售过程中发现：每年的年销售量y〔万件〕与销售价格x〔元/件〕的关系如下图, 其中AB为反比例函数图象的一局部, 设公司销售这种电子产品的年利润为s〔万元〕．〔1〕请求出y〔万件〕与x〔元/件〕的函数表达式；〔2〕求出第一年这种电子产品的年利润s〔万元〕与x〔元/件〕的函数表达式, 并求出第一年年利润的最大值．23.为预防传染病, 某校定期对教室进行“药熏消毒〞．药物燃烧阶段, 室内每立方米空气中的含药量y〔mg〕与药物在空气中的持续时间x〔m〕成正比例；燃烧后, y与x成反比例〔如下图〕．现测得药物10分钟燃完, 此时教室内每立方米空气含药量为8mg．根据以上信息解答以下问题：〔1〕分别求出药物燃烧时及燃烧后y关于x的函数表达式mg时, 对人体方能无毒害作用, 那么从消毒开始, 在哪个时段消毒人员不能停留在教室里？mg的持续时间超过20分钟, 才能有效杀灭某种传染病毒．试判断此次消毒是否有效, 并说明理由．第四单元第1课函数二、根底稳固1．一般地, 如果在一个变化过程中有两个变量x和y, 并且对于变量x的每一个值, 变量y都有________的值与它对应, 那么我们称y是x的________, 其中________是自变量．2．下面选项中给出了某个变化过程中的两个变量x和y, 其中y不是．．x的函数的是()A．y：正方形的面积, x：这个正方形的周长B．y：等边三角形的周长, x：这个等边三角形的边长C．y：圆的面积, x：这个圆的直径D．y：一个正数的平方根, x：这个正数3．以下关系式中, y不是．．x的函数的是()A．y＝x B．y＝x2＋1C．y＝|x|D．|y|＝2x4．(泸州)以下曲线中不能．．表示y是x的函数的是()5．表示函数的方法一般有________、__________和__________；函数的表示方法可以互相转化, 应用中要根据具体情况选择适当的方法．6．在下表中, 设x 表示乘公共汽车的站数, y 表示应付的票价．x /站 1 2 3 4 5 6 7 8 9 10 y /元1112233344根据此表, 以下说法正确的选项是( ) A ．y 是x 的函数 B ．y 不是x 的函数C ．x 是y 的函数D ．以上说法都不对7．假设每上6个台阶就升高1 m, 那么上升高度h (单位：m)与上的台阶数m (单位：个)之间的函数关系式是( ) A ．h ＝6m B ．h ＝6＋mC ．h ＝m －6D ．h ＝m68．(随州)“龟兔赛跑〞这那么寓言故事讲述的是比赛中兔子开始领先, 但它因为骄傲在途中睡觉, 而乌龟一直坚持爬行最终赢得比赛, 以下函数图象可以表达这一故事过程的是( ) 9．对于一个的函数, 自变量的取值范围是使这个函数________的一切值；对于一个实际问题, 自变量的取值必须使____________有意义．如果当x ＝a 时y ＝b , 那么b 叫做当自变量x 的值为a 时的__________． 10．(内江)函数y ＝x ＋1x －1, 那么自变量x 的取值范围是( ) A ．－1＜x ＜1 B ．x ≥－1且x ≠1C ．x ≥－1D ．x ≠111．函数y ＝2x －1x ＋2中, 当x ＝a 时的函数值为1, 那么a 的值是( )A ．－1B ．1C ．－3D ．312．函数y ＝⎩⎪⎨⎪⎧x 2－3〔x ≤2〕x －1〔x ＞2〕当函数值y ＝6时, 自变量的值是( )A ．7B ．－3C ．－3或7D ．±3或7 三、拓展提升13．在国内投寄本埠平信应付邮资如下表：信件质量x /g 0＜x ≤2020＜x ≤4040＜x ≤60邮资y /元(2)分别求当x 取5, 10, 30, 50时的函数值．14．某生态公园方案在园内的坡地上造一片只有A, B 两种树的混合林, 需要购置这两种树苗2 000棵, 种植 A, B 两种树苗的相关信息如下表：品种价格(单位：元/棵)成活率劳务费(单位：元/棵)A15 95% 3 B2099%4(1)写出y 与x 之间的函数表达式；(2)假设这批树苗种植后成活1 960棵, 那么造这片树林的总费用为多少元？。

《轴对称》知识点总结及章节检测解析

《轴对称》知识点总结及章节检测解析一、知识点总结：1.轴对称的定义：如果一个图形经过其中一条直线折叠后，能够与自身完全重合，则这条直线被称为这个图形的轴对称线，这个图形是轴对称的。

2.旋转对称：如果一个图形能够围绕其中一点旋转一定的角度后，能够与自身完全重合，则这个图形是旋转对称的。

3.轴对称图形的特点：轴对称图形的特点是，对称轴两侧的各点关于对称轴对应，即对称轴上的一点与对应点互为图形的对称点。

4.轴对称的判定方法：判断一个图形是否为轴对称图形，可以按照以下方式进行判定：(1)观察是否能找到一个或多个对称轴；(2)沿对称轴将图形折叠，看是否能够重合。

5.制作轴对称图形：制作一个轴对称图形可按照以下步骤进行：(1)在纸上画出一条轴对称线；(2)沿着对称线将图形的一边折叠；(3)检查折叠后的图形与未折叠的图形是否重合，如重合则完成。

二、章节检测解析：以小学三年级数学教材为例，进行《轴对称》的章节检测解析。

教材章节：第三章图形与设计1.知识点掌握情况：首先，学生需要了解轴对称的概念、特点和判定方法，并能够制作轴对称图形。

2.基础练习题：对于基础的练习题，要求学生绘制给定图形的对称线，并判断是否为轴对称图形。

3.综合应用题：在综合应用题中，要求学生设计自己的轴对称图形，并描述其特点。

4.拓展思考题：为了拓展学生的思维，可以提出一些拓展思考题，如“如何判断一个图形是否为旋转对称图形”、“如何找到一个图形的所有对称轴”等。

总结：通过针对《轴对称》这一章节的检测解析，学生可以对轴对称的知识点进行复习和巩固。

同时，综合应用题和拓展思考题能够提高学生的思维能力和创造力。

第十三章轴对称_小结与复习

跟踪训练
• 1.把一圆形纸片两次对折后，得到右图，
• 然后沿虚线剪开，得到两部分，其中一 • 部分展开后的平面图形是( B )
A
B
C
D
• 2.（福州·中考）下面四个中文艺术字中，不是轴对称图形的是（ C ）
3、（日照·中考）已知以下四个汽车标志图案：其中是轴对称图形的图案是(1),(3) （只需填入图案代号）.
P C
• 的垂直平分线上
B
• 结论：三角形三条边的垂直平分线相交于一
点，这个点到三角形三个顶点的距离相等.
• 2.如图所示，在△ABC中，∠CAB的平分线AD和BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC于N。 • 求证：ＢＭ＝ＣＮ。
思路分析
1。要证明ＢＭ＝ＣＮ需构造什么？ 2.D是BC的垂直平分线上的点应添加什么辅助线？ 3.点D是∠CAB的平分线上的点能得到什么结论？Ｍ请自己分析后写出证明过程ＢＤＡ
知识要点
• （一）轴对称 • 观察图形的变换过程，回想什么是轴对称图形？它有什么性质？
┐
这是对称轴呀!
要仔细观察哦！
•
定义：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴．这时，我们也说这个图形关于这条直线（成轴）对称．
1 -1 -2 -3 -4 1 2 3 4 5
x
B (3,2)
C (-2,3)
【跟踪训练】
1.点P(-5,
6)与点Q关于x轴对称，则点
Q的坐标为__________. (- 5 ,-6 ) 2.点M(a, -5)与点N(-2, b)关于x轴对称，则a=_____,b =_____. 5 -2

(完整)初二数学八上第十三章轴对称知识点总结复习和常考题型练习,推荐文档

第十三章轴对称、知识框架:二、知识概念：1.基本概念：⑴轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形•⑵两个图形成轴对称：把一个图形沿某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称 •铀对称图形AA\L区別只对f —冲-)ft-fKmr150对裤轴CF 一佥只冇一舉>(“轴对称旳睛(WK 予秤瓚的俭M 工菲.矗麹»JSt :t 鹽个、曲擢：心)只有1一頭〉对務柄联系却晁把射对材囲宼泊对禅轴曲卿撷甘"么卿牛曲癣轶夭于迭条 W 鑽處抽对耕-如杲把.阿十庇抽对秤的国招拼& — 妊呑虑一* 益林.外也亡赣足一亍轴对STSJ 搭-(4) 线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线• (5) 等腰三角形：有两条边相等的三角形叫做等腰三角形 •相等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角(6) 等边三角形：三条边都相等的三角形叫做等边三角形 2.基本性质：⑴对称的性质：① 不管是轴对称图形还是两个图形关于某条直线对称，对称轴都是任何一对对应点所连线段的垂直平分线.② 对称的图形都全等•③ 如果两个图形的对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

④ 两个图形关于某条直线成轴对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

⑵线段垂直平分线的性质：① 线段垂直平分线上的点与这条线段两个端点的距离相等 ② 与一条线段两个端点距离相等的点在这条线段的垂直平分线上 ⑶关于坐标轴对称的点的坐标性质①点(x, y )关于x 轴对称的点的坐标为(x, -y ).②点（x, y ）关于y轴对称的点的坐标为（-x, y ）.③点（x, y ）关于原点对称的点的坐标为（-x,- y ）⑷等腰三角形的性质：①等腰三角形两腰相等•②等腰三角形两底角相等（等边对等角）③等腰三角形的顶角角平分线、底边上的中线，底边上的高相互重合•④等腰三角形是轴对称图形，对称轴是三线合一（1条）.⑸等边三角形的性质：①等边三角形三边都相等•②等边三角形三个内角都相等，都等于60 °③等边三角形每条边上都存在三线合一④等边三角形是轴对称图形，对称轴是三线合一（3条）.（6）三角形三条边的垂直平分线相交于一点，这个点到三角形三个顶点的距离相等3.基本判定：⑴等腰三角形的判定：①有两条边相等的三角形是等腰三角形•②如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）•⑵等边三角形的判定：①三条边都相等的三角形是等边三角形•②三个角都相等的三角形是等边三角形•③有一个角是60°的等腰三角形是等边三角形.4.基本方法：⑴做已知直线的垂线：⑵做已知线段的垂直平分线：⑶作对称轴：连接两个对应点，作所连线段的垂直平分线⑷作已知图形关于某直线的对称图形：⑸在直线上做一点，使它到该直线同侧的两个已知点的距离之和最短•常考例题精选1. （2015 •三明中考）下列图形中，不是轴对称图形的是（）2. （2015 •日照中考）下面所给的交通标志图中是轴对称图形的是（）ABC3. （2015 •杭州中考）下列“表情图”中，属于轴对称图形的是（）4. （2015 •凉山州中考）如图，/ 3=30°,为了使白球反弹后能将黑球直接撞入袋中，那么击打白球时，必须保证/ 1的度数为（）A.30 °B.45 °C.60 °D.755. （2015 •德州中考）如图，动点P从（0，3）出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2013次碰到矩形的边时，点P的坐标为（）771 ~1 ~2 ~~ ~~6 ~7 d F A.（1，4） B.（5，0） C.（6，4）D.（8，3）6. （2015 •南充中考）如图，△ ABC中, AB=AC Z B=70，则/A的度数是（）A.70 ° B.55C.50 °D.407. （2015 •玉溪中考）若等腰三角形的两边长分别为4和8,贝尼的周长为（）A.12B.16C.20D.16 或208. （2014 •海门模拟）如图，在边长为1的正方形网格中，将△ ABC向右平移两个单位长度得到△ A B' C',则与点B'关于x轴对称的点的坐标是（）A.（0，-1） B.（1，1） C.（2，-1）D.（1，-1）9. （2015 •绵阳中考）如图，AC BD相交于O, AB// DC AB=BC / D=40，/ ACB= 35°，则/ AOD= ______ .10. （2015 •丽水中考）如图，在等腰厶ABC中，AB=AC Z BAC=50，/ BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合，则/ CEF的度数1. （2015遵义）观察下列图形，是轴对称图形的是（）2. 点P（5，—4）关于y轴的对称点是（）A. （5，4）B. （5，—4）C. （4，—5）D. （—5，—4）3. 如图，△ ABC与厶ADC关于AC所在的直线对称，/ BCD= 70° ，/ BA B C D=80°，则/ DAC的度数为（）D. 854. 如图，在Rt A ABC 中，/ C= 90° ，/ B = 15° ，DE 垂直平分AB 交BC于点E，BE = 4，则AC长为（），第4题图）A. 2B. 3C. 4 D .以上都不对6. 如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是8. 如图，D ABC 内一点，CD 平分Z ACB ，BE 丄CD ，垂足为D ，交AC 于点 E ，Z A ABE ，AC = 5，BC = 3，贝U BD 的长为（）9.如图，已知S A ABC = 12, AD 平分Z BAC ，且AD 丄BD 于点D ，则S ^ADC的值是（）5. 如图，AB = AC = AD ,若/ BAD = 80则/ BCD =(C. 140 D . 1607. （2015玉林）如图，在厶ABC正确的是（）EC C . 中，AB = AC ，DE // BC ，则下列结论中不 Z ADE = Z C D . DE = *BC，第5题图）(A . 10 B. 8 C . 610. 如图，C为线段AE上一动点（不与点A , E重合）,在AE同侧分别作正三角形ABC和正三角形CDE, AD 与BE交于点O, AD与BC交于点P，BE 与CD交于点Q,连接PQ.以下五个结论：①AD = BE;②PQ// AE ;③AP= BQ; ④DE= DP;⑤/ AOB = 60° .其中正确的结论的个数是（）A. 2个B. 3个C. 4个D. 5个12. 如图，D, E ABC两边AB , AC的中点,将厶ABC沿线段DE折叠，使点A落在点F处，若/ B = 55° ,则/BDF等于____________ .A「，第12题图）13. ____________________________________________________________ 如图，在3X 3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有________________________ 种.14. 如图，在厶ABC中，AB = AC , AB的垂直平分线交BC于点D ,垂足15. _______ 在厶ABC中，AC = BC,过点A作厶ABC的高AD ,若/ ACD = 30 贝B = __________ .16. ____ 如图，△ ABC中，D, E分别是AC , AB上的点，BD与CE交于点O. 给出下列三个条件：①/ EBO = /DCO;②/ BEO = /CDO:③BE = CD.上述三个条件中，哪两个条件可判定△ ABC是等腰三角形（用序号写出一种情形）：.，第16题图）17. _________________________ 如图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是2,则六边形的周长是 .' ，第17题图）18. __ 如图，已知/AOB = 30° ，OC平分/ AOB，在OA上有一点M，OM =10 cm,现要在OC, OA上分别找点Q，N，使QM + QN最小，则其最小值为.，第18题图）19. 如图，某校准备在校内一块四边形草坪内栽上一棵银杏树，要求银杏树的位置点P到边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出银杏树的位置点P.不写作法，保留作图痕迹）23.如图，△ ABC，△ ADE是等边三角形，B，求证：(1)CE=AC + DC; (2)Z ECD = 60° . C，D在同一直线上.20. 如图，在平面直角坐标系中，A( —2, 2), B( —3, —2).(1) 若点D与点A关于y轴对称，则点D的坐标为__________ ;(2) 将点B先向右平移5个单位再向上平移1个单位得到点C，则点C的坐标为________ ;(3) 求A，B，C，D组成的四边形ABCD的面积.■I r厂m ! I I_ ■i == = Ji1 l:-一十一4二* t： 1 ER I r21. 如图，在厶ABC 中，AB = AC, D 为BC 为上一点，/ B = 30° ，/ DAB45(1) 求/ DAC的度数；(2)求证：DC = AB.22. (2015潜江)我们把两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AB = CB，AD = CD，角或者对角线有关的一个结论，并证明你的结论.请你写出与筝形ABCD的24. 如图,在等腰Rt A ABC中,/ ACB = 90° , D为BC的中点,DE丄AB , 垂足为E,过点B作BF // AC交DE的延长线于点F,连接CF.(1) 求证：AD丄CF;(2) 连接AF ,试判断△ ACF的形状，并说明理由.25. 如图，已知AE丄FE,垂足为E,且E是DC的中点.(1) 如图①，如果FC丄DC, AD丄DC,垂足分别为C, D,且AD = DC,判断AE是/ FAD的角平分线吗？(不必说明理由)(2) 如图②，如果(1)中的条件“ AD = DC”去掉，其余条件不变，⑴中的结论仍成立吗？请说明理由；(3) 如图③，如果⑴的条件改为“ AD // FC” , (1)中的结论仍成立吗？请说明理由.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

当堂检测
教材91页第3、4、5、6题
要求：限时内独立完成，做在课本上.
【流程】独立完成—点将口答—全班评价（8′） —最先举手的3或4的同学优先展示
课堂小结
（1）想一想本节课复习了本章的核心知识有哪些？（2）通过本节课的复习，你认为线段的垂直平分线的性质和判定在解题中有哪些作用？如果已知线段的垂直平分线一般如何添加辅助线？
思路分析清晰、格式规范的成员
C Ｃ
Ｅ
N Ｎ
Ｄ
合作探究
已知：如图，△ABC 是等边三角形，BD 是 AC 边上的高，延长BC 到E，使CE =CD，过点D 作DF ⊥BE于F．求证：（1）BD =DE； A
（2）BF =EF （3）请猜想FC 与BF 之间的数量关系.
Hale Waihona Puke DBFC
E
【流程】独立思考—组内交流—上台展示（10′ ） —由最先完成的小组派代表上台板演展示
看图形回想本章的知识内容
线段的垂直平分线
B
A C
轴对称图形
等腰三角形
画轴对称图形
轴对称
等边三角形
知识概况
流程：独立思考-个人口答（2'）
本章的知识结构图:
线段的垂直平分线
生活中的轴对称
作轴对称图形的对称轴
轴对称画轴对称图形关于坐标轴对称的点的坐标的关系等腰三角形等边三角形
自主学习
1.（1）如图，作出△ABC关于
x轴的对称图形△A'B'C'，
写出A'、B'、C'的坐标；
C
A
（2）判断这两个三角形是
通过怎样的变换而得到的？（3）如果M（m+1，n-3）与 M'（2m+1，-8+n）是两个三角形中的对应点，求m、n的值.
B
合作学习二
【流程】独立思考—小组代表板演展示（8′ ） ——抽签确定小组展示
【流程】独立思考——自由举手发言
【流程】独立思考—个人口头展示（6′） ——按举手的先后顺序口头展示
1、小明照镜子的时候，发现T恤上的英文单词在镜子中呈现“
”的样子，请你判断这个英文单词是（
(A) (B) (C)
）
(D)
A
E B D C
2、如图，在△ABC中，DE是AC的垂直平分线,AE=3cm, △ABD的周长是13cm,则△ABC的周长为_____.
3.点M(a, -5)与点N(-2, b)关于x轴对称，则a=___,b =____.点 M关于y轴对称的点M'的坐标为______；点N关于原点对称的点N' 的坐标为______. 4.等腰三角形一腰上的高与另一腰的夹角为50°，则这个等腰三角形的顶角为____.
合作学习一
【流程】独立思考-小组交流-小组代表展示（5′ ） ——按小组举手的先后顺序展示
学习目标
1．复习本章的重点内容，整理本章知识，形成知识体
系．
2．巩固和运用轴对称的性质、线段的垂直平分线的性
质和判定、等腰三角形的性质和判定解决相关问题;
3. 经历解题方法的探索过程，进一步发展推理能力，能够用符号表示推理证明，体会证明的必要性．
默读学习目标，读完举手示意（1分钟）
知识概况
流程：独立思考-个人口答（2'）
思路分析
如图所示，在△ABC中，∠CAB的平分线AD和BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC于N. 求证：ＢＭ＝ＣＮ. Ａ
1.要证明ＢＭ＝ＣＮ需构造什么？ 2.D是BC的垂直平分线上的点应添加什么辅助线？Ｍ 3.点D是∠CAB的平分线上的点能得到什么结论？Ｂ请自己分析后写出证明过程