三次函数常见的性质及应用
11三次函数的性质及其简单应用

所以 1 2 c 3c 或 1 2 c 3c 解之得 0 c 7 4 3或c 7 4 3 7 4 3 ) 故所求c的范围是(0, ( 7 4 3, )
例5 设
a为实数,函数 f ( ) 的极值; 在什么范围内取值时,曲线 y f ( x)与 x 轴仅有一个交点 (2)当 2 解:(1) f ( x ) 3 x 2 x 1 1 5 f ( x ) f ( ) a , 极小值是 f (1) a 1 ∴ 的极大值是 3 27 (2)函数
南京一中
孔凡海
由二次函数类比三次函数的图象和性质
二次函数
y ax2 bx c
三次函数
y ax3 bx2 cx d
图象特征 单调性 对称性
a 0 开口向上 a 0 开口向下
单调区间2个 对称轴 x
b 2a
a 0 朝向右上 a 0 朝向右下
单调区间1个或3个
所以
y ax3 bx2 cx d (a ≠0),函数的对称中心是(
b b ,f ( ) )。 3a 3a
3 2 f ( x ) ax bx cx d (a ≠0是中心对 ) 性质3:函数 b b , f ( ) )。 称图形,其对称中心是( 3a 3a
尽管如此,我们还要进一步加强对三次函数 的单调性、极值、对称性、图象变化规律、切线 方程等性质的研究,这也有助于提高知识的系统 性以及对三次函数的理解水平,拓宽解题思路。
解:(I)(b 1) 4c 3 2 2 (II)因为 F ( x) f ( x) g( x) x 2bx (b c) x bc ,2 3 x 4bx b 2 c 0 所以F(x)的导方程为:
例说三次函数图象性质的应用

万方数据
例说三次函数图象性质的应用
作者: 作者单位: 刊名:
减区间为[o,一半],由已知函数f(x)在[o,2]上是减函 j
1L
数,.·.2≤一{兰,b≤一3,.·.f(1)=1+b一8—4b=一3b一7≥2.
j
方法点拨:(1)本题中的字母较多。要求我们能够 利用消元的思想,与及相关知识消去中介变元,保留适 当“主变元”它是解决问题的基本原素。(2)利用三次函 数图象的性质,得出函数的单调递减区间,再由已知单 调递减区间是此单调递减区间的子集的关系求出主变 元的范围。从而证得不等式成立。
1.当△≤0时,三次函数f(x)在R上是单调函数; (1)当△≤O且a>0时;函数f(x)在R上单调递增下图:
‘y
汐
f. a<O
\
0/
i
/
O \\i
2.当△>0时,三次函数f(x)在R上必有一个极大值 点和一个极小值点(即三次函数f(x)在R上有极值的充 要条件是:△:4b2—12ac>o)。当△>0时,设方程f’(x)
X-xl X2x2
(一)
X=x1 X=。2
(二)
3.三次函数f(x)=a)【3“x2+cx+d(a≠o)的图象是中心对
称图形,其对称中心坐标为(嘉,f(害)).
X=x1 X=x2
.·.“x)在区间(0,2)上是减函数,又因为f(o)=1>0, “2)=9—4a<0,故选B.
方法点拨:本题的切入点是利用三次函数的图象 性质先判断“X1-x,一ax:+1在区润(0,2)上的单调性,再判 断“0)、“1)的符号是否异号。
5-4三次函数的图象和性质

293-b ±b2- 3ac专题4 三次函数的图像和性质第一讲三次函数的基本性质设三次函数为f (x)=ax3 +bx2 +cx +d (a 、b 、c 、d ∈R 且a ≠ 0 ),其基本性质有:性质一:定义域为R.性质二:值域为R,函数在整个定义域上没有最大值、最小值.性质三:单调性和图象.a > 0 a < 0图像∆>0 ∆≤ 0 ∆> 0 ∆≤ 0当 a > 0 时,先看二次函数 f '(x) = 3ax+ 2bx +c , ∆= 4b- 12ac = 4(b- 3ac)①当∆= 4b2 - 12ac = 4(b2 - 3ac) > 0 ,即b2 - 3ac > 0 时,f '(x) 与x 轴有两个交点x ,x ,f (x) 形成三个单1 2点区间和两个极值点x1,x2,图像如图1,2.②当∆= 4b2 - 12ac = 4(b2 - 3ac) = 0 ,即b2 - 3ac = 0 时,f '(x) 与x 轴有两个等根x ,x ,f (x) 没有极值点1 2图像如图3,4.③当∆= 4b2 - 12ac = 4(b2 - 3ac) < 0 ,即b2 - 3ac < 0 时,f '(x) 与x 轴没有交点,f (x) 没有极值点,图像如图5,6.图1 图2 图3 图4 图5 图6当 a < 0 时,同理先看二次函数 f '(x) = 3ax2 + 2bx +c ,. ∆= 4b2 - 12ac = 4(b2 - 3ac)①当∆= 4b2-12ac = 4(b2- 3ac) > 0 ,即b2- 3ac > 0 时,f '(x) 与x 轴有两个交点x ,x ,f (x) 形成三个单1 2点区间和两个极值点x1,x2.②当∆= 4b2 - 12ac = 4(b2 - 3ac) = 0 ,即b2 - 3ac = 0 时,f '(x) 与x 轴有两个等根x ,x ,f (x) 没有极值点.1 2③当∆= 4b2 - 12ac = 4(b2 - 3ac) < 0 ,即b2 - 3ac < 0 时,f '(x) 与x 轴没有交点,f (x) 没有极值点.性质四:三次方程 f (x )= 0 的实根个数对于三次函数 f (x )=ax3 +bx2 +cx +d (a 、b 、c 、d ∈R 且a ≠ 0 ),其导数为 f '(x) = 3ax2+ 2bx +c当b2-3ac > 0 ,其导数f '(x) = 0有两个解x1 ,x2 ,原方程有两个极值x1、x2 =3a.294x 1x 2x 1 x 2x①当 f (x 1 ) ⋅ f (x 2 ) > 0 ,原方程有且只有一个实根,图像如图 13,14. ②当 f (x 1 ) ⋅ f (x 2 ) = 0 ,则方程有 2 个实根,图像如图 15,16. ③当 f (x 1 ) ⋅ f (x 2 ) < 0 ,则方程有三个实根,图像如图 17.图 13 图 15 图 16 图 17性质五:奇偶性对于三次函数 f (x ) = ax 3 + bx 2 + cx + d ( a 、b 、 c 、 d ∈ R 且 a ≠ 0 ). ① f (x ) 不可能为偶函数;②当且仅当b = d = 0 时是奇函数. 性质六:对称性(1)结论一:三次函数是中心对称曲线,且对称中心是(- b , f (- b)) ;3a 3a(2)结论二:其导函数为 f '(x ) = 3ax 2+ 2bx + c = 0 对称轴为 x = - b 3a,所以对称中心的横坐标也就是导函数的对称轴,可见, y = f (x ) 图象的对称中心在导函数 y = f '(x )的对称轴上,且又是两个极值点的中点, 同时也是二阶导为零的点;(3)结论三: y = f (x ) 是可导函数,若 y = f (x ) 的图象关于点(m , n ) 对称,则 y = f '(x ) 图象关于直线 x = m对称.(4)结论四:若 y = f (x ) 图象关于直线 x = m 对称,则 y = f '(x ) 图象关于点(m , 0) 对称.(5)结论五:奇函数的导数是偶函数,偶函数的导数是奇函数,周期函数的导数还是周期函数.(6)结论六:已知三次函数 f (x ) = ax 3 + bx 2 + cx + d 的对称中心横坐标为 x 0 ,若 f (x )存在两个极值点 x 1,x ,则有 f (x 1 ) - f (x 2 ) = - a (x - x )2 = 2f '(x ).2 x - x 2 1 23 0 1 2性质七:切割线性质(1)设 P 是 f (x )上任意一点(非对称中心),过点 P 作函数 f (x )图象的一条割线 AB 与一条切线 PT ( P 点不为切点), A , B , T 均在 f (x )的图象上,则T 点的横坐标平分 A 、B 点的横坐标,如图 18.图 18图 19 图20295推论 1:设 P 是 f (x )上任意一点(非对称中心),过点 P 作函数 f (x )图象的两条切线 PM 、PN 切点分别为 M 、P ,则 M 点的横坐标平分 P 、N 的横坐标,如图 19.推论 2 : 设 f (x ) 的极大值为 M , 当成 f (x ) = M 的两根为 x 1 , x 2 (x 1 < x 2 ) , 则区间 [x 1 , x 2 ] 被中心(- b , f (- b)) 和极小值点三等分,类似的,对极小值点 N 也有此结论,如图 20. 3a 3a第二讲 三次函数切线问题一般地,如图,过三次函数 f (x )图象的对称中心作切线 L,则坐标平面被切线 L 和函数 f (x )的图象分割为四个区域,有以下结论:(1)过区域Ⅰ、IV 内的点作 f ( x )的切线,有且仅有 3 条;(2)过区域 II 、Ⅲ内的点以及对称中心作 f (x )的切线,有且仅有 1 条;(3)过切线 L 或函数 f (x )图象(除去对称中心)上的点作 f (x )的切线,有且仅有 2 条. 【例 1】过点(1,-1)与曲线 f (x ) = x 3 - 2x 相切的直线方程是.【例 2】若2 f (x ) + f (-x ) = x 3 + x + 3对 x ∈ R 恒成立,则曲线 y = f (x )在点(2, f (2))处的切线方程为.【例 3】过点 A (2 ,1)作曲线 f (x ) = x 3 - 3x 的切线最多有( )A . 3条B . 2 条C .1条D . 0 条秒杀秘籍:第三讲 四段论法则─“房间里装大象”f (x ) = ax 3 + bx 2 + cx + d (a > 0)且导函数∆ > 0 f (x ) = ax 3 + bx 2 + cx + d (a < 0)且导函数∆ > 0极大值极大值极小值等值点中心 极小值 极小值 中心 极小值等值点1.对称中心: ⎛ - b ,f ⎛ - b ⎫⎫ ;3a 3a ⎪⎪⎝⎝ ⎭⎭2.极大值到对称中心距离为∆x ,极小值到对称中心距离为∆x ,极小值等值点到极大值距离为 ∆x ,极大值等值点到极小值距离为 ∆x ;3.对称中心为极值与极值等值点的三等分点(三次函数性质七).2960 0 【例 4】函数 f (x ) = x 3 - 3x + 1在闭区间[-3 , 0]上的最大值、最小值分别是( )A .1, -1B . 3, -17C .1, -17D . 9 , -19【例 5】已知函数 f (x ) = x 3 + ax + b 的定义域为[-1 , 2] ,记 f (x ) 的最大值为 M ,则 M 的最小值为()A . 4B . 3C . 2D . 【例 6】已知 f (x ) = x 3 - 3x + m ,在区间[0 , 2] 上任取三个数 a , b , c ,均存在以 f (a ), f (b ), f (c )为边长的三角形,则 m 的取值范围是( )A . m > 2B . m > 4C . m > 6D . m > 8【例 7】已知 f (x ) = ax 3 - 2ax 2 + b 在区间[-2 , 1] 上的最大值是5 ,最小值为-11,求 f (x ) 解析式.图 1 (a > 0) 图 2 (a < 0)【例 8】若函数 f (x ) = 1 x 3 + x 2 - 2 在区间(a , a + 5) 内存在最小值,则实数 a 的取值范围是()3 3 A . [-5 , 0)B . (-5 , 0)C . [-3 , 0)D . (-3 , 0)【例 9】若函数 ax 3 - x 2 + 4x + 3 ≥ 0 对任意的 x ∈[-2 , 1]恒成立,求 a 的取值范围( )A . [-2 , 2]B . [-2 , 4]C . [-2 , 6]D . [-2 , 8]【例 10】设函数 f (x ) = x 3 + ax + bx + c , a ,b ,c ∈ R ,总存在 x ∈[0 ,4],使得不 f (x ) ≥ m 等式成立, 则实数 m 的取值范围是.达 标 训 练一.选择题1.函数 f (x ) = 3x 3 - 9x 2 + 5 在区间[-2 , 2] 上的最大值是( )A . 5B . 2C . -7D .142.已知 f (x ) = 2x 3 - 6x 2 + a ( a 是常数)在[-2 ,2] 上有最大值3,那么在[-2 ,2] 上的最小值是( )A . -5B . -11C . -29D . -373.函数 f (x ) = 3x - 4x 3 (x ∈[0 ,1]) 的最大值是()A .1B . 12C . 0D . -13297, ] 0 0 4.若函数 f (x ) = x 3 - 3x 2 + a 在[-1 , 1]上有最大值3,则该函数在[-1 , 1]上的最小值是()2A . - 1 2B . 0C . 1 2D .15.若函数 f (x ) = 3x - x 3 在区间(a 2 - 12 , a )上有最小值,则实数 a 的取值范围是( )A . (-1 , 11)B . (-1 , 4)C . (-1 , 2]D . (-1 , 2) 6.若函数 f (x ) = x 3 - 3x 在(a , 8 - a 2 ) 上有最小值,则实数 a 的取值范围是( ) A . (- , 1)B . [- 7 , 1)C . [-2 , 1)D . (-2 , 1)7.函数 f (x ) = x 3 - 3ax - a 在(0 , 1) 内有最小值,则 a 的取值范围是( )A . 0 ≤ a < 1B . 0 < a < 1C . -1 < a < 1D . 0 < a < 12 8.当 x ∈[-2 , 1] 时,不等式 mx3 ≥ x 2 - 4x - 3 恒成立,则实数 m 的取值范围是( )A . ⎡-6 , ⎣ - 8 ⎤9 ⎦ B . [-6 , - 2]C . [-5 , - 3]D . [-4 , - 3]9.若关于 x 的不等式 x 3 - 3x 2 - 9x + 2 ≥ m 对任意 x ∈[-2 , 2]恒成立,则 m 的取值范围是()A . (-∞ , 7]B . (-∞ , - 20]C . (-∞ , 0]D . [-12 , 7]10.函数 f (x ) = 1x 3 - x 2 + a ,函数 g (x ) = x 2 - 3x ,它们的定义域均为[1 , + ∞),并且函数 f (x )的图象始3终在函数 g (x )的上方,那么 a 的取值范围是( ) A . (0 , + ∞)B . (-∞ , 0)C . (- 4, + ∞)3D . (-∞ 4311.设函数 f (x ) = x 3 - 1x 2 - 2x + 5 ,若对于任意 x ∈[1 , 2],f (x ) < m 恒成立,则实数 m 的取值范围为()2A . (7 , + ∞)B . (8 , + ∞)C . [7 , + ∞)D . [8 , + ∞) 12.已知函数 f (x ) = ax 3 - 3x 2 + 1 ,若 f (x )存在唯一的零点 x ,且 x > 0 ,则 a 的取值范围是()A . (2 , + ∞)B . (-∞ , - 2)C . (1 , + ∞)D . (-∞ , - 1)13.已知 a ≥ - 3,b ≥ 0 ,函数 f (x ) = x 3 + ax + b (-1≤ x ≤ 1),设 4有 M ≥ k ,则实数 k 的最大值为( )f (x ) 的最大值为 M ,对任意的 a 、b ∈ R 恒A . 4B . 2C . 1D . 12 4 14.曲线 y = x3 - x 的所有切线中,经过点(1 , 0) 的切线的条数是( )A . 0B .1C . 2D . 3 15.已知函数 f (x ) = 1x 3 - x 2 + ax + 3(a ∈ R ) 有两个极值点 x , x (x < x ) ,则()31 2 1 2A . f (x ) 3 , f (x ) < 10B . f (x ) 3 , f (x ) > 101 2 3 1 23 C . f (x ) 3 , f (x ) < 10 D . f (x ) 3 , f (x ) > 101 2 3 1 2316.已知函数 f (x ) = -x 3 + 6x 2 - 9x + 8 ,则过点(0 , 0) 可以作几条直线与曲线 y = f (x ) 相切()7298, ] x A . 3条 B .1条 C . 0 条 D . 2 条17.已知函数 f (x ) = x 3 + ax 2 + bx + c , x ∈[-3 ,3] 的图象过原点,且在点(1 , f (1)) 和点(-1 , f (-1)) 处的切线斜率为 -2 ,则 f (x ) = ( ) A .是奇函数B .是偶函数C .既是奇函数又是偶函数D .是非奇非偶函数18.已知函数 f (x ) = x 3 - ax 2- bx + c 有两个极值点 x ,x ,若 x < x = f (x ) ,则 f (x ) = x 的解的个数为()121221A . 0B .1C . 2D . 319.已知函数 f (x ) = x 3 - mx 2 + 2nx + 1, f '(x ) 是函数 f (x ) 的导数,且 f '(2 + x ) = f '(- 2- x ) ,若在[1,π] 上3f (x ) 1 恒成立,则实数 n 的取值范围为( )A . (-∞ 1 2B . (-∞ , - 1 ] 2C . [ 1 , + ∞) 2D . [π, + ∞)20.(2019•汕头月考)函数 f (x ) = 1x 3 - x 2 + ax 在[-1, 2] 上单调递增,则 a 的取值范围是( )3A . a > 0B . a 0C . a 1D . a > 121.(2019•浙江期中)已知函数 f (x ) = 1x 3 + ax 2 - 2x 在区间(1, +∞) 上有极小值无极大值,则实数 a 的取值3 范围( )A . a < 12B . a > 12C . a 12D . a 1222.(2019•长沙期中)已知函数 f (x ) = 4x 2 - 3x + 1,g (x ) = 3x 3 - x -1,则 f (x ) 与 g (x ) 的大小关系是()A . f (x ) = g (x )B . f (x ) > g (x )C . f (x ) < g (x )D .随 x 的变化而变化23.(2019•临川月考)正项等差数列{a }中的 a , a 是函数 f (x ) = 1x 3 - 4x 2 + 4x - 3 的极值点,则log 2 a 2019 = ( )n 114027 3 A . 2B . 3C . 4D . 5324.若函数 f (x ) = - a x 2 + x + 1 在区间(1 , 2) 上单调递减,则实数 a 的取值范围为( )5 [2 , ] 23 2 B . [ 5 , + ∞) 2 C . ( 5 2 , + ∞)D . (2 , + ∞) 25.(2019•醴陵期中)函数 f (x ) = x 3 - 3x 2 - 9x + 4 ,若函数 g (x ) = f (x ) - m 在 x ∈[-2 , 5] 上有 3 个零点, 则 m 的取值范围为()A . (-23 , 9)B . (-23 , 2]C . [2 , 9]D . [2 , 9)26.(2019•湛江一模)已知函数 f (x ) = x 3 - x 2+ ax - a 存在极值点 x ,且 f (x ) = f (x ) ,其中 x ≠ x ,x + 2x =1( )11A . 3B . 2C .1D . 027.(2019•邯郸一模)过点 M (-1, 0) 引曲线C : y = 2x 3 + ax + a 的两条切线,这两条切线与 y 轴分别交于 A ,B 两点,若| MA |=| MB | ,则 a = ()A . - 25 4B . - 274C . - 2512D . - 491228.(2019•黔东南州一模)已知函数 f (x ) = 2x 3 - (6a + 3)x 2 + 12ax + 16a 2 (a < 0) 只有一个零点 x 0 ,且 x 0 < 0 ,A .2990 0 6 则 a 的取值范围为()A . (-∞, - 1)2B . (- 1 , 0) 2C . (-∞, - 3)2 D . (-3 , 0) 229.(2019•莆田一模)若函数 f (x ) = ax 3 - x 2 + 2x 没有极小值点,则 a 的取值范围是( )31 [0 , ]2 B . [ 1 , +∞)2 C .{0} ⋃ [ 1 , 2 +∞) D . {0} ⋃ ( 1 , 2+ ∞) 30.(2018 秋•晋中期末)已知 f (x ) = 1 x 3 - 5 ax 2 + 6ax + b 的两个极值点分别为 x ,x (x ≠ x ) ,且 x = 3x ,3 2 则函数 f (x 1 ) - f (x 2 ) = ( )1 2 1 2 22 1 A . -1B . 16C .1D .与b 有关31.(2019•陕西一模)已知函数 f (x ) = x 3 + 3x ,则不等式 8 (1 + x )3 +1 + x > x 3+ 3x 的解集为( )A . (-∞ , - 2) ⋃ (-1 , 1) C . (-∞ , - 2] ⋃ (1 ,+∞)B . [-2 , - 1) ⋃ [1 , + ∞) D . (-2 , 1)32.(2018•宜春期末)等比数列{a }的各项均为正数, a , a 是函数 f (x ) = 1x 3 - 3x 2 + 8x + 1的极值点,n 5 63 则log 2 a 1 + log 2 a 2 + ⋯ + log 2 a 10 = ( ( )A . 3 + log 2 5B . 8C .10D .1533.(2018•湖北期末)已知函数 f (x ) = ax 3 + bx 2 + cx -17(a , b , c ∈ R ) 的导函数为 f '(x ) , f '(x ) 0的解集为{x | -2 x 3} ,若 f (x ) 的极小值等于 -98 ,则 a 的值是( )A . - 8122 B . 1 3C . 2D . 534.(2019•朝阳二模)已知 f (x ) = - 1x 3 + x 在区间(a ,10 - a 2 ) 上有最大值,则实数 a 的取值范围是()3A . a < -1B . -2 a < 3C . -2 a < 1D . -3 < a < 1 35.(2018•海淀期末)函数 f (x ) = x 3 + kx 2 - 7x 在区间[-1 , 1]上单调递减,则实数 k 的取值范围是( )A . (-∞ , - 2]B . [-2 , 2]C . [-2 , + ∞)D . [2 , + ∞)36.(2019•汉阳模拟)函数 f (x ) = ax 3 + 3x 2 -1存在唯一的零点 x ,且 x < 0 ,则实数 a 的范围为( )A . (-∞, -2)B . (-∞, 2)C . (2, +∞)D . (-2, +∞)37.(2019•瀍河月考)设函数 f (x ) = ax 3 - bx + 2 的极大值和极小值分别为 M , m ,则 M + m = ( ( )A . 0B .1C . 2D . 438.(2018•南阳期末)函数 f (x ) = x 3 - 3x 2 - 9x + 2 在[0 , 4]上的最大值和最小值分别是()A . 2 , -18B . -18 , -25C . 2 , -25D . 2 , -2039.(2018•合肥期末)已知函数 f (x ) = -x 5 - 3x 3 - 5x + 3,若 f (a ) + f (a - 2) > 6 ,则实数 a 的取值范围是()A . (-∞, 3) 二 填空题B . (3, +∞)C . (1, +∞)D . (-∞,1)1.(2019•东城一模)已知函数 f (x ) = 4x - x 3 ,若∀x ,x ∈[a ,b ] ,x ≠ x 都有 2 f (x + x ) > f (2x ) + f (2x )12121212A .3000 0 成立,则满足条件的一个区间是.2.(2019•陕西二模)设函数 f (x ) = 2x 3 + ax 2 + bx + 1的导函数为 f '(x ) ,若函数 y = f '(x ) 的图象的顶点横坐 标为 - 1 ,且 f '(1) = 0 .则 a + b 的值为.23.(2019•新疆二模)已知函数 f (x ) = x 3 - ax 2 在(-1 , 1) 上没有最小值,则 a 的取值范围是.4.(2019•十堰模拟)对于三次函数 f (x ) = ax 3 + bx 2 + cx + d (a ,b ,c ,d ∈ R ,a ≠ 0) ,有如下定义:设 f '(x )是函数 f (x ) 的导函数, f '(x ) 是函数 f '(x ) 的导函数,若方程 f '(x ) = 0 有实数解 m ,则称点(m , f (m )) 为函数 y = f (x ) 的“拐点”.若点(1, -3) 是函数 g (x ) = x 3 - ax 2 + bx - 5,(a , b ∈ R ) 的“拐点”也是函数 g (x ) 图象上的点,则当 x = 4 时,函数 h (x ) = log 4 (ax + b ) 的函数值为.5.(2018•揭阳期末)已知函数 f (x ) = x 3 + 2x ,若 f (a -1) + f (2a 2 ) 0 ,则实数 a 的取值范围是.6.(2018•长治期末)已知函数 f (x ) = 2x 3 - 3x ,若过点 P (1,t ) 存在 3 条直线与曲线 y = f (x ) 相切,则t 的取值范围是.7.(2019•自贡模拟)已知 f (x ) = ax 3 + 3x 2 -1存在唯一的零点 x ,且x < 0 ,则实数 a 的取值范围是 .8.(2019•天山月考)设 f (x ) = x 3 - 1x 2 - 2x + 5 ,当 x ∈[-1, 2]时, f (x ) < m 恒成立,则实数 m 的取值范2 围为. 9.已知函数 f (x ) = 1 x 3 - x 2 - 3x + 4,直线l : 9x + 2 y + c = 0 .若当 x ∈[-2 , 2]时,函数 y = f (x )的图象恒3 3 在直线l 的下方,则c 的取值范围是 .三 解答题1.已知函数 f (x ) = 1ax 3 + 2x 2 ,其中 a > 0 .若 f (x ) 在区间[-1,1] 上的最小值为 -2 ,求 a 的值.32.知函数 f (x ) = ax 3 - 6ax 2 + b (x ∈[-1 ,2]) 的最大值为3,最小值为-29 ,求 a 、b 的值.3.已知函数 f (x ) = x 3 - 1x 2 + bx + c ;2(1)若 f (x ) 在(-∞ , + ∞) 上是增函数,求 b 的取值范围;301( , 0)(2)若 f (x ) 在 x = 1时取得极值,且 x ∈[-1 , 2] 时, f (x ) < c 2恒成立,求c 的取值范围.4.(2019•海淀期中)已知函数 f (x ) = ax 3+ bx 2+ x + c ,其导函数 y = f '(x ) 的图象过点 1 3和(1, 0) . (1)函数 f (x ) 的单调递减区间为 ,极大值点为 ;(2)求实数 a , b 的值;(3)若 f (x ) 恰有两个零点,请直接写出c 的值.5.(2019•莱西月考)设函数 g (x ) = x 3 - 3x 2 + 2 .(1)若函数 g (x ) 在区间(0, m ) 上递减,求 m 的取值范围;(2)若函数 g (x ) 在区间(-∞ , n ]上的最大值为 2,求 n 的取值范围.6.(2019•海淀一模)已知函数 f (x ) = 1 x 3 - 5x 2 + a | x | -1.3 2 (1)当 a = 6 时,求函数 f (x ) 在(0, +∞) 上的单调区间; (2)求证:当 a < 0 时,函数 f (x ) 既有极大值又有极小值.7.(2019•怀柔一模)已知函数 f (x ) = 2x 3 + 3ax 2 + 1(a ∈ R ) . (1)当 a = 0 时,求 f (x ) 在点(1 , f (1) ) 处的切线方程;302P (1, ) (2)求 f (x ) 的单调区间;(3)求 f (x ) 在区间[0 , 2] 上的最小值8.(2019•天津一模)已知函数 f (x ) = 2x 3 - ax 2 + 1(a ∈ R ) . (1) a = 6 时,直线 y = -6x + m 与 f (x ) 相切,求 m 的值;(2)若函数 f (x ) 在(0, +∞) 内有且只有一个零点,求此时函数(x ) 的单调区间;(3)当 a > 0 时,若函数 f (x ) 在[-1 , 1]上的最大值和最小值的和为 1,求实数 a 的值.9.(2018•镇海期末)已知函数 f (x ) = 1 x 3 + 1.3 2(1)求曲线 y = f (x ) 在点 5 6处的切线与 x 轴和 y 轴围成的三角形面积;(2)若过点(2, a ) 可作三条不同直线与曲线 y = f (x ) 相切,求实数 a 的取值范围.10.(2018•太原期末)若 x = 2 是函数 f (x ) = ax 3 - 3x 2 的极值点.(1)求 a 的值;(2)若 x ∈[n ,m ] 时, -4 f (x ) 0 成立,求 m - n 的最大值.11.(2018•佛山期末)已知函数f (x) =x3 + 3ax2 + 3(a2 -l)x .(1)若 f (x) 在x = 1处取得极小值,求 a 的值;(2)设x ,x 是g(x) =f (x) - 6ax2 - 3a2 x + 5a(a > 0) 的两个极值点,若g(x ) +g(x ) 0 ,求a 的最小值.1 2 1 2303。
三次多项式函数的性质研究与应用举例

三次 多项式 函数 的性质 研 究 与应 用 举 例
北 京市 六一 中学
1 教学 中学 习思考
10 4 0 12
康志 山
y( ) X 有两个不同的零点为 、 且 。 0 , ) )< . Ax 1 1 新课标 学 习 . ( Ⅲ )只有两个 不 同的零 点 的充要 条件 是 : x有 。 )=0 . 高中数学理科选修(_2 ( 2 ) 文科选修( 1—1 ) f( ) 两个不 同 的零 点为 、 且 。 : ) 导数 及其 应用一 章 , 学课 程标 准 中指 出 : 用导数 数 会 证 明 (I)充分性 : 1若厂( . )没有 零点或 只有一 个零 点 , 求不超过 三次 多项 式 函数 的极 值 ( 大值 、 极 极小 值)单调 区间以及 闭区间上的最值 ( 、 最大值、 最小
瓢 毛 %9 为
综上 )只有 一个 零点 , 厂( 则 )无零点 或 只 个 的零 点 与 由( Ⅱ
中学数学杂志 2 1 00年第 7 期
2 思考 中性质探 究
)>0 则 ) ,
1当 . ) R上单调时 , 在 即任 ∈R有厂()
≥ 0或 厂( )≤ 0恒成 立 , 以厂( ) 零点 或有一 所 戈 无 个 零点.
2 当在 R上 ) . 不单调时 , 则存在 ∈R使得
厂( >0, ) 还存在 ∈ R使得 厂( )<0成 立 所 以厂( )必有 零点 , 因为 厂( )为二 次 函数 , 所 以厂( )必有 两 个 不 同的 零 点 , 为 。 , 以 设 、 所 , ) ( ) ( 和, 为 ) 的极值 , 因为 ) 只有一个 零 点 , 以, )的零 点 只能 在 ( 所 ( 一∞ , 。 (: )或 ,
三次函数图像与性质(解析版)

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像,单调性,极值,最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式(1)一般式:()³²f x ax bx cx d =+++(a ≠0)(2)交点式:()123()()()f x a x x x x x x =---(a ≠0)1.若三次函数()f x 满足()()()()00,11,03,19f f f f ''====,则()3f =()A .38B .171C .460D .965【解析】待定系数法,求函数解析式设()³²f x ax bx cx d =+++,则()232f x ax bx c '=++,由题意可得:()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+,解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩,则()3210123f x x x x =-+,所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容,其考点广泛且深入,主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。
以下是对三次函数常见考点的详细分析:1.三次函数的定义与形式∙定义:形如f (x )=ax 3+bx 2+cx +d (其中a ≠=0)的函数称为三次函数。
∙形式:注意系数a ,b ,c ,d 的作用,特别是a 的正负决定了函数的开口方向(a >0开口向上,a <0开口向下)。
三次函数性质总结.
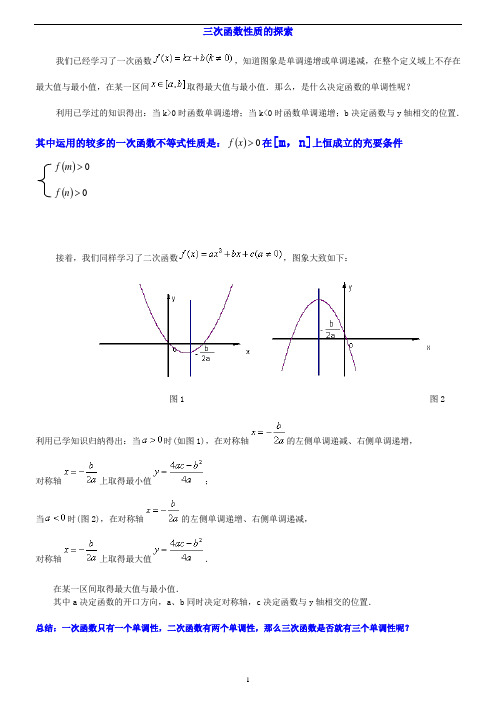
三次函数性质的探索我们已经学习了一次函数,知道图象是单调递增或单调递减,在整个定义域上不存在最大值与最小值,在某一区间取得最大值与最小值.那么,是什么决定函数的单调性呢?利用已学过的知识得出:当k>0时函数单调递增;当k<0时函数单调递增;b决定函数与y轴相交的位置.其中运用的较多的一次函数不等式性质是:()0>f在[m,n]上恒成立的充要条件x()0>fm()0>fn接着,我们同样学习了二次函数,图象大致如下:图1 图2利用已学知识归纳得出:当时(如图1),在对称轴的左侧单调递减、右侧单调递增,对称轴上取得最小值;当时(图2),在对称轴的左侧单调递增、右侧单调递减,对称轴上取得最大值.在某一区间取得最大值与最小值.其中a决定函数的开口方向,a、b同时决定对称轴,c决定函数与y轴相交的位置.总结:一次函数只有一个单调性,二次函数有两个单调性,那么三次函数是否就有三个单调性呢?三次函数专题一、定义:定义1、形如32(0)y ax bx cx d a =+++≠的函数,称为“三次函数”(从函数解析式的结构上命名)。
定义2、三次函数的导数232(0)y ax bx c a '=++≠,把2412b ac ∆=-叫做三次函数导函数的判别式。
由于三次函数的导函数是二次函数,而二次函数是高中数学中的重要内容,所以三次函数的问题,已经成为高考命题的一个新的热点和亮点。
特别是文科。
系列探究1:从最简单的三次函数3x y =开始反思1:三次函数31y x =+的相关性质呢? 反思2:三次函数31y x =-+的相关性质呢? 反思3:三次函数()311y x =-+的相关性质呢?(2012天津理)(4)函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B (A )0 (B )1 (C )2 (D )3系列探究2:探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质:先求导2()32(0)f x ax bx c a '=++>1.单调性:(1)若22120b ac =-≤△(),此时函数()f x 在R 上是增函数;(2)若22120b ac =->△(),令2()320f x ax bx c '=++=两根为12,x x 且12x x <,则()f x 在12(,),()x x -∞+∞上单调递增,在12(,)x x 上单调递减。
x三次方的导数定义式_解释说明

x三次方的导数定义式解释说明1. 引言1.1 概述在微积分中,导数是一个核心概念,用于描述函数在每个点处的变化率。
对于一次函数、二次函数以及常见的多项式函数,我们可以通过导数定义式来求出它们的导数,从而研究函数的性质和特点。
本文将重点讨论x三次方函数及其导数定义式,并展示推导过程和高阶导数计算方法。
1.2 文章结构本文将按照以下结构进行阐述:第二部分将介绍x的三次方函数的定义与性质,以及导数的概念和常见计算方法。
第三部分将详细解释x三次方函数导数定义式的推导过程,包括使用极限定义和幂函数求导法则。
第四部分将探讨x三次方函数高阶导数的计算方法,回顾一阶导数计算方法并推广至二阶和三阶导数,并介绍更高阶导数的递归计算方法。
最后,在结论部分对x三次方函数及其导数定义式进行总结与拓展思考,分析其理解与应用意义,并探讨其他类型函数类比思考与推广讨论。
同时给出一个综合案例分析:x四次方和更高次方函数的导数定义式解释说明。
1.3 目的通过本文的阐述,我们旨在帮助读者更深入地理解x三次方函数及其导数定义式。
同时,本文也将为读者提供进一步研究其他类型函数导数定义式和高阶导数计算方法的思路和启示。
希望读者能通过这篇长文,对微积分中函数的导数概念有更全面和深入的认识。
2. x的三次方函数2.1 定义与性质x的三次方函数是指形如f(x) = x^3的函数。
它是一个二次多项式函数,由x的立方项构成。
在数学中,我们通常将其称为立方函数或三次函数。
x的三次方函数具有以下性质:- 定义域为全体实数,即对于任意实数x都可以计算出对应的函数值;- 值域也是全体实数集合,因为无论x取任何实数值,其立方都是一个实数;- 函数图像关于原点对称,在第一象限、第三象限上呈现正增长趋势,在第二象限、第四象限上呈现负增长趋势;- 当x>0时,函数值随着自变量x的增大而增大;当x<0时,函数值随着自变量x的减小而减小。
2.2 导数的概念导数是描述函数斜率和变化率的概念。
三次函数有关极值的一个性质及应用

三次函数有关极值的一个性质及应用湖南省岳阳市华容县东山镇联校(414203)聂新军设三次函数/(尤)=似;3 + +c i + d(a #0),记/"(尤)=3似;2 + 2心;+ c的判别式为4= 4 (62 -3a c).我们有如下结论:命题1对于/(尤)=a x3+心;2 + cx + d(a ^0),若4= 4(62 -3a c)<0,则/(幻无极值♦证明••因4二4(62 - 3狀)彡0,当a> 0时,/(A〇>〇,当a<0 时,/(>) <0,均使/(A〇 为单调函数.故/(%)无极值.命题2对于/(%) = a?+ &r2cx + d(a0),若厶=4(62-3狀)>0,记/(%)二0的两根分别为A< %),则当^ > 〇时,/0)的极大值M为/(尤1),极小值肌为/(尤2),且肌;当^<0时,/(>)的极大值M为/(巧),极小值m为/(A),且M > m.证明:当a > 0时,由条件知当尤< ^,或%%时,/(X)>0,当A<x时,/(X)<0,于是可知/u)的极大值为/(^),极小值为y u2).注意到A,尤2(A-尤2< 0)是方程3ax2 + 26尤+ c= 0的两根,且 62 - 3ac > 0,a> 0•M - m = f(x1) -f(x2) -a(x\ - x32) + b{x\ -%2 ) + ~ X2) =~ X2) \-a(X l+ ^1^2+ X l)+b(x1+ x2)+ c] = (x1- x2) [a(x1+ x2)2- ax1x2 +b(x1+ ^;2)+ c]= (x}- x2)^a •(2b,3a/cTa +心•(-|^) +C] = («!X2)[~9~a{b2■3ac)]> 0.即M > m.同理,当a <0时,/(均的极大值M为/(尤2),极 小值m为/( a),且M > ??!♦综上可知,我们有如下推论:推论函数/($) = a%3 +心2+ cx + d(a7^0)有极值的充要条件是方程/u)=〇有两个不相等的实根.下面举例说明上述结论在解题中的应用.例1已知/(%)=似:3 + cx ,a b + c =〇,客O)=/0),若客(〇)客(1) > 〇,求证/〇)有两个极值.证明:由已知得g(%) =/(%)=3a%2+26A;+c,当 a=0时,6=-c,g(0)g(l) =c(3a+26+c)= -c2 $0与已知矛盾,故a #0.方程3a i2 + 26% + c =0 的判别式A = 4(62 - 3a c)•由a + 6 + c = 0,消去6,得4=4(62-3(!<:)=4(«2+,-狀)=2 ry 24[(C-f)+f]>〇,于是方程/(x)=〇有两个不等的实根',^2,由命题2知,/U)有两个极值f(Xl)/(%)'例 2 函数 /(尤)=%3 + 3 a%2 + 36x+c在尤=2处有极值,其图像在% = 1处的切线平行于直线心+ 2y+5=0,求极大值与极小值的差.解:,(%)= 3%2 + 6a i +36,/"(%) =0有根% = 2,所以4 +4« + 6二0①,由于图像在尤二1处的切 线平行于直线6a;+2;x+5二0,于是/(I)二-3,即3 +6a +36 = -3②,联立①,②解得a = - 1,6 = 0,从而/(%)=尤3-3尤2+c.2018年第8期令/(x)=0,得另一根为0,由命题2知,当% =〇时函数取极大值,当%= 2时取极小值.于是所求 之差为/(〇) _/(2) = c - (8 - 12 + c)= 4.例 3 已知,(尤)=3似3 + 9fcc2 + 9c i+ 15(a > 0)在% = -2和a; = 4处取得极值,而极大值与极小 值之差为27,求a,6,c的值.解:/"($) = 9ax2 + 186% +9c,令/"(i)= 0,得 似2 + + c=0,它应有根尤=-2及尤=4,由韦— = -2+4,— = (-2)- 4 = -8.a a故 6= _a,c= —8a.因a >0,由命题2知,/(均的极大值为/(-2),极小值为/(4),且/(-2)>/(4).由/(-2)-/(4) =27,得 324a= 27,解得 a= ‘ •••a=占,6=例 4 设函数/(%)=尤3 - 3%2 —= % + a.若/(a〇与g(>)的图像恰有三个交点,求实数a的取值范围.解:/(幻与g(幻的图像恰有三个交点,即方程 %3 - 3%2 - 8% = % + a恰有三个不等实根♦令_F(a;)= ^;3- 3x2- 8x - x - a = x3- 3x2-9x- a, ^ F(x)的图像与x轴有三个不同交点.= 3i2 - 6尤- 9,易知厂〇) =0有两个不等实根a=-1,%2 =3, 又尸(^)的/项的系数1> 0,由命题2知,均的极大值为- 1) = 5 -〜极小值为F(3) = -27 -a,且n-1) > ^(3),以均的图像与%轴有三个不同交点,从而F(i)的极大值大于零,极小值小于零.即|5 _ a > 1解得-27 < a < 5.故i-27 - a<0,例5 设函数/(x)= -~^2+c,其中a >〇,曲线y =/U)在点P(〇,/(〇))处的切线为%轴•若过点(〇,2)可作曲线^ =/U)的三条不同切 线,求实数a的取值范围.解:由/(x) = _f x2+&K +C,得/(0) = C,/(尤)=x2-似;+6,/(0) =6,又曲线 y=/(x)在点P(0,/(0))处的切线为%轴,故/(0)二0,/(0)=〇,•♦.6 = C = 0•于是/(>) = ^;3 -音:/,/(>)=尤2 - ax•点〇,/(〇)处的切线 y -/(〇=/(〇〇 - 〇,点(0,2)在切线上一2 -/(〇 二/(〇(-〇,化简整理得f r3- f r2 + 2 = 0.即£满足方程f r3- +2二0♦过点(0,2)可作曲线y二/(幻的三条 不同切线,等价于方程f f3 - f t2 + 2 = 0有三个相异实根■记g(f)= |^3+2,只需g(t)的图像与t轴有三个不同交点.从而贫(〇的极大值大于零,极小值小于零♦令g'(〇= 2i2 - ai = 0,得^ = 0^2=f因0 >0),由命题2知,g⑴的极大值为客(0)= 2,g(〇的极小值为客(^)= 2 - ^,由g(0)= 2 > 0,g(f)= 2 - ^ < 0,解得 a > 2灰.所以实数a的取值范围是(2灰,+ =〇).2018年新课标I卷理科数学第19题的研究与推广安徽省宣城中学(242000)项卫华众所周知,高考试题是命题专家集体智慧的结 晶,一道好的试题不仅具有典型性,代表性,还具有 进一步探索、研究的价值.本文对2018年高考数学 新课标I卷理科第19题进行了思考探究并做引申 推广.试题再现(2〇18年新课标理科第19题)设椭圆=1的右焦点为厂过F的直线Z与C交于S两点,点M的坐标为(2,0).(1)当Z与x轴垂直时,求直线的方程;(2) 设〇为坐标原点,证明:乙O M A =乙O M B.一见此题,笔者立即联想到下面两道高考试题: (2015年新课标理科第20题)在直角坐标系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三次函数常见的性质及应用
一、性质
1、三次函数的图像一定是一个闭合曲线,其中心点为原点(0,0);
2、三次函数的图像具有左右对称性;
3、三次函数图像的极值点(即最大值点和最小值点)一定位于曲线的拐点处;
4、三次函数的导数存在,其单调性与函数的单调性相反;
5、三次函数的二阶导数存在,其值大于等于0;
二、应用
1、三次函数可以用来描述经济学中的供求关系;
2、三次函数可以用来描述物理学中的力学变化;
3、三次函数可以用来描述数学中的曲线图形;
4、三次函数可以用来描述自然现象中的变化趋势;
5、三次函数可以用来描述计算机科学中的数据处理。
