高中数学：三次函数图像与性质

合集下载

初中高中数学七大函数的性质图像

初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数，在平面直角坐标系上的图象为直线。

定义域（下面没有说明的话，都是在无特殊要求情况下的定义域）：R值域：R奇偶性：无周期性：无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式]（k为直线斜率，b为直线纵截距，正比例函数b=0）③y-y1=k(x-x1)[点斜式]（k为直线斜率,(x1,y1)为该直线所过的一个点）④（y-y1）/(y2-y1)=(x-x1)/(x2-x1)[两点式]（（x1,y1）与（x2,y2）为直线上的两点）⑤x/a-y/b=0[截距式]（a、b分别为直线在x、y轴上的截距）解析式表达局限性：①所需条件较多（3个）；②、③不能表达没有斜率的直线（平行于x轴的直线）；④参数较多，计算过于烦琐；⑤不能表达平行于坐标轴的直线和过圆点的直线。

倾斜角：x轴到直线的角（直线与x轴正方向所成的角）称为直线的倾斜角。

设一直线的倾斜角为a，则该直线的斜率k=tg(a)。

2.二次函数：题目中常见的函数，在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。

定义域：R值域：（对应解析式，且只讨论a大于0的情况，a小于0的情况请读者自行推断）①[(4ac-b^2)/4a，正无穷）；②[t，正无穷）奇偶性：偶函数周期性：无解析式：①y=ax^2+bx+c[一般式]⑴a≠0⑵a＞0，则抛物线开口朝上；a＜0，则抛物线开口朝下；⑶极值点：（-b/2a，(4ac-b^2)/4a）；⑷Δ=b^2-4ac,Δ＞0，图象与x轴交于两点：（[-b+√Δ]/2a，0）和（[-b+√Δ]/2a，0）；Δ＝0，图象与x轴交于一点：（-b/2a，0）；Δ＜0，图象与x轴无交点；②y=a(x-h)^2+t[配方式]此时，对应极值点为（h，t），其中h=-b/2a，t=(4ac-b^2)/4a）；3.反比例函数在平面直角坐标系上的图象为双曲线。

三次函数的性质及简单应用

三次函数的性质及简单应用摘要：本文运用导数的知识来研究一般的三次函数的性质，为进一步探索高次函数的性质提供了方法依据，为解决高考中三次函数单调性、最值等问题找到了有效的方法。

关键词：三次函数；性质；最值；单调性；对称性作者简介：徐树富，任教于浙江省衢州高级中学。

二次函数的有关性质及其应用是函数内容中的一个重点，而随着导数知识的介入，三次函数在函数问题的研究中凸显出其重要性。

三次函数问题,可通过求导转化为二次函数或二次方程问题,然后结合导数的基本知识及二次函数的性质来解决，在高考和一些重大考试中频繁出现有关它的单独命题。

笔者就教学及解题中碰到的一些三次函数的性质进行一些初浅的探讨。

一、一般的三次函数的图象与性质：1．函数的定义域与值域均为R。

2．极值：3．单调性：（1）证明：三次函数关于点（m，n）对称的充要条件是，即（4）过对称中心的曲线的切线有且只有一条；（5）把函数的图象按向量平移后得到的图象关于原点中心对称。

6．图象有两种形状：图二图三二、与三次函数有关的问题2.三次函数解析式的形式三、应用举例三次函数的导函数是二次函数，因此，熟练把握二次函数的图像与性质便是研究三次函数图像与性质的起点。

函数是高中数学的核心内容，在新教材高三数学选修本中虽然利用了导数方法重新研究了函数的若干性质，但是在离开导数背景的函数问题的学习与研究中，大多数学生仍然未能自觉地想到用导数方法来解决高中数学教学中遇到的用初等方法较难解决的问题，为克服这一思维定势，在与二次函数比较的基础上，对三次函数的性质进行系统的梳理，旨在使学生真正学会用导数作为工具研究函数的性质、并能将该思想方法早日纳入到原有的知识结构之中，形成自觉的应用意识。

作者单位：浙江省衢州高级中学邮政编码：324006The Nature of Cubic Function and Its Simple ApplicationXU ShufuAbstract: This paper studies the nature of cubic function with derivative knowledge, which supplies ways to probe into the nature of higher-order function and finds effective methods of solving monotony and maxima and minima of cubic function.Key words: cubic function; nature; maxima and minima; monotony; symmetry。

三次函数图像与性质(解析版)

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像，单调性，极值，最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式（1）一般式：()³²f x ax bx cx d =+++（a ≠0）（2）交点式：()123()()()f x a x x x x x x =---（a ≠0）1．若三次函数()f x 满足()()()()00,11,03,19f f f f ''====，则()3f =（）A ．38B ．171C ．460D ．965【解析】待定系数法，求函数解析式设()³²f x ax bx cx d =+++，则()232f x ax bx c '=++，由题意可得：()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+，解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩，则()3210123f x x x x =-+，所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容，其考点广泛且深入，主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。

以下是对三次函数常见考点的详细分析：1.三次函数的定义与形式∙定义：形如f (x )=ax 3+bx 2+cx +d （其中a ≠=0）的函数称为三次函数。

∙形式：注意系数a ,b ,c ,d 的作用，特别是a 的正负决定了函数的开口方向（a >0开口向上，a <0开口向下）。

三次函数的一个性质

[]2012.589探索【成才纵横】对于二次函数的图像和性质，我们已做了深刻挖掘且对其结论也已铭记于心，而对于三次函数的图像和性质，我们却知之甚少。

由于三次函数是高中数学中研究导函数的载体，因而是我们高中数学教师必须研究的。

定理：任何一个三次函数的图像都是中心对称图形。

证明：设三次函数为f(x)=ax 3+bx 2+cx+d(a≠0)，∵f(-b 3a+x)+f(-b 3a -x)=[a(-b 3a +x)3+b(-b 3a +x)2+c(-b 3a +x)+d]+[a(-b3a -x)3+b(-b 3a -x)2+c(-b 3a -x)=a(-b 3a )[(-b 3a +x)2-(-b 3a +x)(-b 3a -x)+(-b 3a -x)2]+b (2b 29a 2+2x 2)+c (-2b 3a )+2d=2d-2bc 3a +4b 327a 2。

即对任意x 都有f(-b 3a +x)+f(-b 3a -x)=2d-2b 3a +4b 327a2，因而三次函数f(x)=ax 3+bx 2+cx+d(a≠0)关于点（-b 3a ，d-bc 3a +4b 327a 2）对称，因此任何一个三次函数的图像都是中心对称图形。

由上面的证明不难看出：对称中心的横坐标为函数f(x)二阶导的零点，即：函数f(x)的导数f'(x)=3ax 2+2bc+c 的导数6ax+2b 的零点，故x=-b 3a ；对称中心的纵标为函数值f(-b 3a )。

如三次函数f (x)=2x 3-3x 2+2x-1的对称中心的横坐标的求法：f'(x)=6x 2-6x+2，f'(x)=6x 2-6x+2的导数为f''(x)=12x-6，由f''(x)=0x =12对称中心的纵坐标为f (12)=2×18-3×14+2×12-1=-12，故对称中心为（12，-12）。

三次函数性质总结.

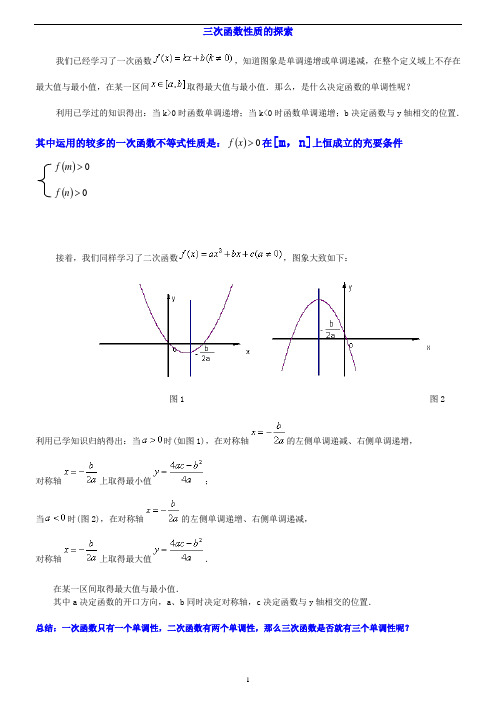
三次函数性质的探索我们已经学习了一次函数，知道图象是单调递增或单调递减，在整个定义域上不存在最大值与最小值，在某一区间取得最大值与最小值．那么，是什么决定函数的单调性呢？利用已学过的知识得出：当k>0时函数单调递增；当k<0时函数单调递增；b决定函数与y轴相交的位置．其中运用的较多的一次函数不等式性质是：()0>f在[m，n]上恒成立的充要条件x()0>fm()0>fn接着，我们同样学习了二次函数，图象大致如下：图1 图2利用已学知识归纳得出：当时(如图1)，在对称轴的左侧单调递减、右侧单调递增，对称轴上取得最小值；当时(图2)，在对称轴的左侧单调递增、右侧单调递减，对称轴上取得最大值．在某一区间取得最大值与最小值．其中a决定函数的开口方向，a、b同时决定对称轴，c决定函数与y轴相交的位置．总结：一次函数只有一个单调性，二次函数有两个单调性，那么三次函数是否就有三个单调性呢？三次函数专题一、定义：定义1、形如32(0)y ax bx cx d a =+++≠的函数，称为“三次函数”（从函数解析式的结构上命名）。

定义2、三次函数的导数232(0)y ax bx c a '=++≠，把2412b ac ∆=-叫做三次函数导函数的判别式。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题，已经成为高考命题的一个新的热点和亮点。

特别是文科。

系列探究1：从最简单的三次函数3x y =开始反思1：三次函数31y x =+的相关性质呢？反思2：三次函数31y x =-+的相关性质呢？反思3：三次函数()311y x =-+的相关性质呢？（2012天津理）（4）函数22)(3-+=x x f x在区间(0,1)内的零点个数是 B （A ）0 （B ）1 （C ）2 （D ）3系列探究2：探究一般三次函数)0()(23>+++=a d cx bx ax x f 的性质：先求导2()32(0)f x ax bx c a '=++>1．单调性：（1）若22120b ac =-≤△()，此时函数()f x 在R 上是增函数；（2）若22120b ac =->△()，令2()320f x ax bx c '=++=两根为12,x x 且12x x <，则()f x 在12(,),()x x -∞+∞上单调递增，在12(,)x x 上单调递减。

一元三次函数的图象和性质

２００７．１０教与学科学思想方法!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Ａ．抛物线Ｂ．椭圆Ｃ．双曲线Ｄ．线段失误分析：学生凭猜想选Ａ，但稍一细想，就觉不对．因为这不是同一平面内到定点和定直线的距离相等，必须转化到同一平面内来研究．解：过点Ｍ在底面上的射影Ｎ作ＮＱ⊥ＡＣ于Ｑ，连接ＭＱ，则ＭＱ⊥ＡＣ．如图５．在直角三角形ＭＮＱ中，∠ＭＱＮ为二面角Ｐ－ＡＣ－Ｂ的平面角，ＭＮ∶ＭＱ＝ｓｉｎ∠ＭＱＮ．因ＭＰ＝ＭＮ，所以ＭＰ∶ＭＱ＝ｓｉｎ∠ＭＱＮ（常数），即点Ｍ到定点Ｐ和定直线ＡＣ的距离之比等于定值，且定值在０和１之间．故点Ｍ的轨迹是椭圆的一段．空间轨迹问题分两大类，一类是利用基本轨迹，另一类是利用转化思想进行化归．基本轨迹有：（１）到定点的距离等于定长的点的轨迹是球面；（２）到定直线的距离等于定长的点的轨迹是圆柱面；（３）到一个定平面的距离等于定长的点的轨迹是到这个平面的距离等于该定长的两个平行平面；（４）到两定点的距离相等的点的轨迹是这两点连线段的垂直平分面；（５）到两相交平面距离相等的点的轨迹是两组二面角的平分面；（６）与两定点连线段的夹角等于定值的点的轨迹是两个球冠．所谓转化化归就是利用基本轨迹及交轨的方法（如例１和例２）或利用立体几何知识把空间问题平面化来解决（如例３）．图４图５在高中阶段，一元二次函数一直是函数部分教学的重点和难点，在教学中对这部分内容相当重视，因此，学生对一元二次函数的图象及性质比较熟悉．随着导数的引入，由于一元三次函数的导数是一元二次函数，因此，在综合性考试中，常见一元三次函数和一元二次函数综合考查的题目．学生应掌握一元三次函数的图象和性质．下面，讨论一下一元三次函数的图象和性质．性质１：对函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０），若ａ＞０，则当ｘ→＋∞时，ｆ（ｘ）→＋∞，当ｘ→－∞时，ｆ（ｘ）→－∞；若ａ＜０，则当ｘ→＋∞时，ｆ（ｘ）→－∞，当ｘ→－∞时，ｆ（ｘ）→＋∞．一元三次函数的图象和性质□河北邢台市第八中学袁胜新４５２００７．１０教与学证明：ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ＝ｘ（ａｘ２＋ｂｘ＋ｃ）＋ｄ．若ａ＞０，当ｘ→＋∞时，ａｘ２＋ｂｘ＋ｃ→＋∞，ｘ（ａｘ２＋ｂｘ＋ｃ）→＋∞，∴ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ→＋∞．当ｘ→－∞时，ａｘ２＋ｂｘ＋ｃ→＋∞，ｘ（ａｘ２＋ｂｘ＋ｃ）→－∞，∴ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ→－∞．同理可证当ａ＜０时的情况．由此可知，在画ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ的图象时，若ａ＞０，左侧应从下逐渐上升，右侧自右至左应从上逐渐下降．若ａ＜０，左侧应从上逐渐下降，右侧自右至左应从下逐渐上升．性质２：对函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０），其导函数为一元二次函数ｆ′（ｘ）＝３ａｘ２＋２ｂｘ＋ｃ，它的!＝（２ｂ）２－４×（３ａ）ｃ＝４（ｂ２－３ａｃ）．当!＝４（ｂ２－３ａｃ）≤０时，函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０）在Ｒ上为单调函数．若ａ＞０，导函数ｙ＝ｆ′（ｘ）≥０恒成立，函数ｆ（ｘ）为增函数；若ａ＜０，导函数ｙ＝ｆ′（ｘ）≤０恒成立，函数ｆ（ｘ）为减函数．当!＝４（ｂ２－３ａｃ）＞０时，导函数ｆ′（ｘ）＝３ａｘ２＋２ｂｘ＋ｃ＝０有两个相异实数根ｘ１，ｘ２且ｘ１＜ｘ２，因此，若ａ＞０，导函数ｆ′（ｘ）在（－∞，ｘ１）和（ｘ２，＋∞）上恒正，故函数ｆ（ｘ）在（－∞，ｘ１）和（ｘ２，＋∞）上为增函数；导函数ｆ′（ｘ）在（ｘ１，ｘ２）上恒负，所以函数ｆ（ｘ）在（ｘ１，ｘ２）上为减函数；同样可得，若ａ＜０，函数ｆ（ｘ）在（－∞，ｘ１）和（ｘ２，＋∞）上为减函数，在（ｘ１，ｘ２）上为增函数．性质３：对函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０），其导函数为一元二次函数ｆ′（ｘ）＝３ａｘ２＋２ｂｘ＋ｃ，它的!＝（２ｂ）２－４×（３ａ）ｃ＝４（ｂ２－３ａｃ）．由性质２可得当!＝４（ｂ２－３ａｃ）≤０时，函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０）不存在极值．当!＝４（ｂ２－３ａｃ）＞０时，函数ｙ＝ｆ（ｘ）在ｘ＝ｘ１和ｘ＝ｘ２处取极值，若ａ＞０，函数ｆ（ｘ）在ｘ１处取极大值ｆ（ｘ１），在ｘ２处取极小值ｆ（ｘ２）．若ａ＜０，函数ｆ（ｘ）在ｘ１处取极小值ｆ（ｘ１），在ｘ２处取极大值ｆ（ｘ２）．性质４：对函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０），其导函数为一元二次函数ｆ′（ｘ）＝３ａｘ２＋２ｂｘ＋ｃ，!＝（２ｂ）２－４×（３ａ）ｃ＝４（ｂ２－３ａｃ）．当!＝４（ｂ２－３ａｃ）≤０时，方程ａｘ３＋ｂｘ２＋ｃｘ＋ｄ＝０有且只有一个实数根．当!＝４（ｂ２－３ａｃ）＞０时，函数ｙ＝ｆ（ｘ）在ｘ＝ｘ１和ｘ＝ｘ２处分别取极值ｆ（ｘ１），ｆ（ｘ２），当函数ｆ（ｘ）的极大值小于０或极小值大于０时，方程ａｘ３＋ｂｘ２＋ｃｘ＋ｄ＝０有且只有一个实数根；当函数ｆ（ｘ）的极大值等于０或极小值等于０时，方程ａｘ３＋ｂｘ２＋ｃｘ＋ｄ＝０有且只有两个实数根；当函数ｆ（ｘ）的极大值大于０且极小值小于０时，方程ａｘ３＋ｂｘ２＋ｃｘ＋ｄ＝０有且只有三个实数根．性质５：函数ｆ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ（ａ≠０）关于（－ｂ３ａ，ｆ（－ｂ３ａ））呈中心对称图形．例题（２００５年全国统考卷ＩＩ（文））２２．设ａ为实数，函数ｆ（ｘ）＝ｘ３－ｘ２－ｘ＋ａ．（１）求ｆ（ｘ）的极值；科学思想方法４６２００７．１０教与学!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!随着信息社会的迅猛发展，多媒体教学正逐步融入我们的课堂，它以特有的功能，弥补了传统教学方式在直观性、主体性和动态感等方面的不足，使一些抽象难懂的内容，变得易于理解和掌握，能取得传统教学方法无法取得的效果．在教学中，教师应结合数学学科内容和学生年龄小的特点，合理地运用电教媒体，发挥电教媒体教学的功能优势，激发学习兴趣，从而达到优化数学课堂教学，提高效率的目的．下面就如何合理运用电教媒体谈一些体会．一、运用电教媒体，激发学习兴趣兴趣是学生学习的最佳动力，是发展智力的基础．在目标教学的前提测评环节中，我充分利用电教媒体的直观性与可操作性强等特点，结合教材内容，或以鲜艳的图片刺激学生的感官，或以有趣的情境激发学生的兴趣，或以直观演示展现新旧知识的矛盾点，激发学生的探究欲．例如，在讲“平行四边形面积的计算”时，我首先出示一张投影，通过数方格的方法求出投影上所画的平行四边形的面积，然后启发学生思考：如果一块地或一个操场是平行四边形，能用数方格的方法求出面积吗？不用数方格的方法，又怎样计算平行四边形的面积呢？通过设问，学生感到有趣，急于知晓计算平行四边形面积的方法．二、运用电教媒体，培养创新能力从发展的求异思维入手，培养和训练学生敏锐的洞察力和迅捷的判断力，鼓励学生大胆质疑，标新立异，沿着不同的方向去思考，以求获得尽可能多的解决问题的方法，从而培养学生的创新能力．运用电教媒体，可化静为动，化抽象为具体，展现给学生一个丰富多彩的世界．在这种极富创新的空间中，学生也会不知制作运用电教媒体提高数学教学效率□河南临颍县北街学校丁书贞（２）当ａ在什么范围内取值时，曲线ｙ＝ｆ（ｘ）与ｘ轴有且只有一个交点．解：（１）三次项系数＝１＞０，!＝（－１）２－３×１×（－１）＝４＞０，故函数ｙ＝ｆ（ｘ）存在极值．ｙ＝ｆ（ｘ）的导函数为ｆ′（ｘ）＝３ｘ２－２ｘ－１，令ｆ′（ｘ）＝３ｘ２－２ｘ－１＝０，解得ｘ１＝－１３和ｘ２＝１．所以函数ｙ＝ｆ（ｘ）在ｘ１＝－１３处取极大值ｆ（－１３）＝ａ－７２７，函数ｙ＝ｆ（ｘ）在ｘ２＝１处取极小值ｆ（１）＝ａ－１．（２）要使曲线ｙ＝ｆ（ｘ）与ｘ轴有且只有一个交点，即ｆ（ｘ）＝０有且只有一个实根，只需极大值ｆ（－１３）＝ａ－７２７＜０或极小值ｆ（１）＝ａ－１＞０，解得ａ＜７２７或ａ＞１．现代教育技术４７。

【高中数学考点精讲】考点三幂函数的图象和性质

考点三幂函数的图象和性质（一）幂函数的图象（1）依据图象高低判定幂指数大小21．（2022·全国·高一课时练习）图中，，分别为幂函数，，在第一象限内的图象，则，，依次可以是（）A．，3，B．，3，C．，，3 D．，，3【解析】由题图知：，，，所以，，依次可以是，，3．故选：D22．（2022·全国·高一课时练习）幂函数在第一象限的图像如图所示，则的大小关系是（）A．B．C．D．【解析】根据幂函数的性质，在第一象限内，的右侧部分的图像，图像由下至上，幂指数增大，所以由图像得：，故选：D23．（2022·全国·高一课时练习）如图所示是函数(且互质)的图象，则（）A．是奇数且B．是偶数，是奇数，且C．是偶数，是奇数，且D．是偶数，且【解析】函数的图象关于轴对称，故为奇数，为偶数，在第一象限内，函数是凸函数，故，故选：C.24．（2022·四川凉山·高一期末）如图，①②③④对应四个幂函数的图像，其中①对应的幂函数是（）A．B．C．D．【解析】根据函数图象可得：①对应的幂函数在上单调递增，且增长速度越来越慢，故，故D选项符合要求.故选：D（2）图象的识别25．（2022·全国·高一单元测试）下列四个图像中，函数的图像是（）A．B．C． D．【解析】因为，即，所以，解得，即函数的定义域为，故排除A、C、D，且函数在定义域上单调递增，故B正确；故选：B26．（2022·上海·高一单元测试）已知幂函数的图象经过点，则该幂函数的大致图象是（）A．B．C．D．【解析】设幂函数为，因为该幂函数得图象经过点，所以，即，解得，即函数为，则函数的定义域为，所以排除CD，因为，所以在上为减函数，所以排除B，故选：A27．（2022·全国·高一单元测试）如图为某体育赛事举重成绩与运动员体重之间关系的折线图，下列模型中，最能刻画举重成绩（单位：千克）和运动员体重（单位：千克）之间的关系的是（）A．B．C．D．（，且）【解析】因为折线图是单调递增且越来越缓，而幂函数在时也是单调递增且越来越缓，因此最能刻画举重成绩和运动员体重之间关系的是，故选：A．（二）幂函数的性质（1）由幂函数的单调性求参数28．（2022·广东广州·高一期末）函数是幂函数，且在上是减函数，则实数__________.【解析】由题设，，即，解得或，当时，，此时函数在上递增，不合题意；当时，，此时函数在上递减，符合题设.综上，.故答案为：229．（2022·河南开封·高一期末）已知函数幂函数，且在其定义域内为单调函数，则实数（）A．B．C．或D．【解析】因为函数为幂函数，则，即，解得或.若，函数解析式为，该函数在定义域上不单调，舍去；若，函数解析式为，该函数在定义域上为增函数，合乎题意.综上所述，.故选：A.30．（2022·云南德宏·高一期末）“当时，幂函数为减函数”是“或2”的（）条件A．既不充分也不必要 B．必要不充分C．充分不必要D．充要【解析】当时，幂函数为减函数，所以有，所以幂函数为减函数”是“或2”的充分不必要条件，故选：C31．（2022·江西省铜鼓中学高一期末）已知函数是减函数，则实数的取值范围是（）A．B．C．D．【解析】因为函数是减函数，所以，解得，所以实数的取值范围是，故选：A.（2）由幂函数的单调性解不等式32．（2022·上海中学高一期末）不等式的解为______．【解析】将不等式转化成（Ⅰ），解得；（Ⅱ），解得；（Ⅲ），此时无解；综上，不等式的解集为：故答案为：33．（2022·海南鑫源高级中学高一期末）已知幂函数的图象经过点.（1）求幂函数的解析式；（2）试求满足的实数a的取值范围.【解析】（1）幂函数的图象经过点，，解得，幂函数；（2）由（1）知在定义域上单调递增，则不等式可化为解得，实数a的取值范围是.34（2022·上海金山·高一期末）已知幂函数在其定义域上是严格增函数，且（）.(1)求m的值；(2)解不等式：.【解析】（1）幂函数在其定义域上是严格增函数，则，即又，则，此时满足在定义域上是严格增函数.所以（2）由（1）函数在其定义域上是严格增函数根据，则，则所以，解得所以不等式的解集为（3）由幂函数的单调性比较大小35．（2022·重庆九龙坡·高一期末）已知，则的大小关系为（）A．B．C．D．【解析】，因为函数是实数集上的增函数，所以由可得：，即，故选：C36．（2022·青海·大通回族土族自治县教学研究室高一期末）幂函数在区间上单调递增，且，则的值（）A．恒大于0 B．恒小于0C．等于0 D．无法判断【解析】由函数是幂函数，可得，解得或．当时，；当时，．因为函数在上是单调递增函数，故．又，所以，所以，则．故选：A．（4）幂函数奇偶性的应用37．（2022·全国·高一课时练习）求出下列函数的定义域，并判断函数的奇偶性：（1）；（2）；（3）；（4）.【解析】（1）的定义域为.，是偶函数；（2）的定义域为R.,.既不是奇函数，也不是偶函数；（3）的定义域为R.,是奇函数；（4）的定义域为，既不是奇函数，也不是偶函数.38．（2022·全国·高一专题练习）已知幂函数的图象关于y轴对称，则___________．【解析】由于是幂函数，所以，解得或.当时，，图象关于轴对称，符合题意.当时，，图象关于原点对称，不符合题意.所以的值为，∴. ，.故答案为：4.39．（2022·重庆九龙坡·高一期末）已知幂函数为奇函数，则___________.【解析】因为是幂函数，所以，或，当时，，因为，所以函数是偶函数，不符合题意；当时，，因为，所以函数是奇函数，符合题意，故答案为：40．（2022·山东济宁·高一期末）已知是奇函数，当时，，则______．【解析】因为是奇函数，当时，，所以，得，所以，，因为是奇函数所以，故答案为：（5）幂函数的单调性和奇偶性的综合应用41．（2022·河南开封·高一期末）下列函数中，既是奇函数，又是增函数的是（）①；②；③；④．A．①② B．①④ C．②③ D．③④【解析】对于①，，奇函数，在和上分别单增，不满足条件；对于②，，偶函数，不满足条件；对于③，，奇函数，在R上单增，符合题意；对于④，，奇函数，在R上单增，符合题意；故选：D42．（2022·云南玉溪·高一期末）幂函数的图象关于轴对称，且在上是增函数，则的值为（）A．B．C．D．和【解析】因为，，所以当时，，由幂函数性质得，在上是减函数；所以当时，，由幂函数性质得，在上是常函数；所以当时，，由幂函数性质得，图象关于y 轴对称,在上是增函数；所以当时，，由幂函数性质得，图象关于y 轴对称,在上是增函数；故选：D.43．（2022·重庆巫山·高一期末）若幂函数过点，则满足不等式的实数的取值范围是______【解析】由题意，不妨设，因为幂函数过点，则，解得，故为定义在上的奇函数，且为增函数，因为，则，故，解得，从而实数的取值范围是.故答案为：.44．（2022·湖北·高一期末）已知函数，若，则实数a的取值范围是（）A．B． C．D．【解析】设，，则，即为奇函数，容易判断在R上单调递增（增+增），又可化为，，所以a >1－2a，∴a >．故选：A.45．（2022·黑龙江·大庆实验中学高一期末）已知幂函数的图象关于轴对称，且在上单调递减，则满足的的取值范围为________. 【解析】幂函数在上单调递减，故，解得.，故，，.当时，不关于轴对称，舍去；当时，关于轴对称，满足；当时，不关于轴对称，舍去；故，，函数在和上单调递减，故或或，解得或.故答案为：（6）幂函数性质的综合应用46．（2022·全国·高一）已知幂函数（a是常数），则（）A．的定义域是R B．在单调递增C．过定点D．可能过定点【解析】已知幂函数（a是常数），当，，此时定义域为，A错误，当，，此时在单调递减，B错误，当时，，过定点，C正确，D错误.故选：C.47．【多选】（2022·广西玉林·高一期末）已知函数的图象经过点则（）A．的图象经过点B．的图象关于y轴对称C．在上单调递减D．在内的值域为【解析】将点的坐标代入，可得，则的图象不经过点，A错误；在上单调递减，C正确；根据反比例函数的图象与性质可得B 错误，D正确．故选：CD.48．【多选】（2022·广东揭阳·高一期末）已知幂函数的图象经过点(9,3)，则下列结论正确的有（）A．为偶函数B．为增函数C．若，则D．若，则【解析】将点代入函数得：，则，所以，∴的定义域为，所以不具有奇偶性，所以A不正确；函数在定义域上为增函数，所以B正确；当时，，即，所以C正确；若时，==.即成立，所以D正确.故选：BCD.。

三次函数的图像与性质

三次函数的图像与性质形如f（x）=ax3+bx2+cx+d（a≠0）的函数叫做三次函数。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题已经成为高考命题的一个新的热点和亮点，尤其是文科数学更是如此。

我们可以采用类比的方法，利用几何画板，较为深入地研究三次函数的图像与性质以及三次方程的解的个数的问题。

１三次函数的图像与性质设三次函数f（x）=ax3+bx2+cx+d（a≠0），其导函数f’（x）=3ax2+2bx+c，其判别式△=4b2-12ac=4（b2-3ac）。

当a>0时，若△>0，方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1f（x2）。

结论1：f（x1）·f（x2）>0时，函数f（x）的图像与x轴有且仅有一个公共点；f（x1）·f（x2）=0时，函数f（x）的图像与x轴有且仅有两个公共点；f （x1）·f（x2）０，f（x2）0为例）：当a>0时，f（x）的四种图象３推论设三次函数f（x）＝ax3+bx2+cx+d（a>0），其导函数f’（x）=3ax2+2bx+c 的判别式△=4b2-12ac=4（b2-3ac）>0。

方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1<x2，则函数f（x）在x=x1处取得极大值f（x1），函数f（x）在x=x2处取得极小值f（x2）。

类似可知a<0的情形（其余条件同前）：函数在x=x1处取得极小值f（x1），函数f（x）在x=x2处取得极大值f（x2）。

４例题例1.（湖南卷）用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？解：设长方体的宽为x（m），则长为2x（m），高为h==4.5-3x（m）（0<x<），故长方体的体积为V（x）=2x2（4.5-3x）＝９x2－６x３（m３）（0<x<），从而V’（x）=18x-18x2（4.5-3x）=18x（１－x）。

《高中数学课件：几种常见函数的图像和性质》

高中数学课件：几种常见函数的图像和性质
探索几种常见函数的图像和性质，包括一次函数、二次函数、反比例函数、幂函数、指数函数、对数函数、三角函数和常函数。
一次函数
一次函数是指具有形式y = kx + b的函数，图像为一条直线，斜率k决定了直线的倾斜程度，纵截距b决定了直线与y轴的交点。
二次函数
Step 3
根据底数a的不同，求解指数函数的通式。
推导对数函数的通式
1
Step 2
2
代入任意一点的坐标和底数a到对数函数
的通式y = log_a(x)中。
3
Step 1
通过两个点的坐标(x1, y1)和(x2, y2)计算底数a：a = 10^((y1 - y2) / (x1 - x2))。
Step 3
推导反比例函数的通式
1 Step 1
2 Step 2
通过两个点的坐标(x1, y1)和(x2, y2)计算比例系数k：k = y1 * x1 = y2 * x2。
代入一个点的坐标(x, y)和比例系数k到反比例函数的通式y = k/x中，得到反比例函数的通式。
推导幂函数的通式
Step 1
取幂函数的对数y = log_a(x)，其中a为底数。
二次函数是指具有形式y = ax^2 + bx + c的函数，图像为一条开口向上或向下的曲线，顶点坐标为(-b/2a, c-b^2/4a)。
反比例函数
反比例函数是指具有形式y = k/x的函数，图像为一条曲线，呈现出一个反比例的关系，x越大，y越小。
幂函数
幂函数是指具有形式y = kx^n的函数，图像的形态取决于指数n的值，n为正偶数时，图像在原点右侧上升，n为正奇数时，则图像在全范围上升。

(完整版)高中数学常用函数图像及性质

1.指数函数0(>=a a y x 且)1≠a图像：性质：恒过定点（0,1）；当0=x 时，1=y ；当1>a 时，y 单调递增，当)0,(-∞∈x 时，)1,0(∈y ；当),0(+∞∈x 时，),1(+∞∈y .当10<<a 时，y 单调递减，当)0,(-∞∈x 时，),1(+∞∈y ；当),0(+∞∈x 时，)0,1(∈y .2.对数函数0(log >=a x y a 且)1≠a对数运算法则：N M MN a a a log log log += N M NMa a alog log log -= M n M a n a log log =)(R n ∈ N N a a =log （对数恒等式）aNN b b a log log log =（换底公式）图像x)1>(=a y x性质：恒过定点（1,0）；当1=x 时，0=y ；当1>a 时，y 单调递增，当)1,0(∈x 时，)0,(-∞∈y ；当),1(+∞∈x 时，),0(+∞∈y .当10<<a 时，y 单调递减，当)1,0(∈x 时，),0(+∞∈y ；当),1(+∞∈x 时，)0,(-∞∈y .指数函数和对数函数的关系：互为反函数3.初等函数⑴：2x y ±= 图像2x y = ：开口向上，)0,(-∞∈x 时，),0(+∞∈y ，函数单调递减；),0(+∞∈x ，时，),0(+∞∈y ，函数单调递增，且是偶函数。

2x y -= ：开口向下，)0,(-∞∈x 时，)0,(-∞∈y ，函数单调递增；),0(+∞∈x ，时，)0,(-∞∈y ，函数单调递减。

)0(>a x )10(<<a x性质：图像都是关于y 轴对称 ⑵：3x y = 图像性质：R y R x ∈∈,，函数是增函数，也是奇函数 ⑶：1-=x y 图像x性质：R x ∈且0≠x ，R y ∈且0≠y ；函数在)0,(-∞∈x 内和),0(+∞∈x 内都是单调递减，且函数是奇函数。

湘教版高中数学选修1-1第3章 3.3.3 三次函数的性质：单调区间和极值

3．3.3三次函数的性质：单调区间和极值[读教材·填要点]设F(x)＝ax3＋bx2＋cx＋d(a≠0)，则F′(x)＝3ax2＋2bx＋c是二次函数，可能有以下三种情形：(1)函数F′(x)没有零点，F′(x)在(－∞，＋∞)上不变号．①若a>0，则F′(x)恒正，F(x)在(－∞，＋∞)上递增；②若a<0，则F′(x)恒负，F(x)在(－∞，＋∞)上递减．(2)函数F′(x)有一个零点x＝w.①若a>0，则F′(x)在(－∞，w)∪(w，＋∞)上恒正，F(x)在(－∞，＋∞)上递增；②若a<0，则F′(x)在(－∞，w)∪(w，＋∞)上恒负，F(x)在(－∞，＋∞)上递减．(3)函数F′(x)有两个零点x＝u和x＝v，设u<v.①若a>0，则F′(x)在(－∞，u)和(v，＋∞)上为正，在(u，v)上为负；F(x)在(－∞，u)上递增，在(u，v)上递减，在(v，＋∞)上递增.可见F(x)在x＝u处取极大值，在x＝v处取极小值．②若a<0，则F′(x)在(－∞，u)和(v，＋∞)上为负，在(u，v)上为正；F(x)在(－∞，u)上递减，在(u，v)上递增，在(v，＋∞)上递减.可见F(x)在x＝u处取极小值，在x＝v处取极大值．[小问题·大思维]1．在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，想一想，在[a，b]上一定存在最值和极值吗？在区间(a，b)上呢？提示：在区间[a，b]上一定有最值，但不一定有极值．如果函数f(x)在[a，b]上是单调的，此时f(x)在[a，b]上无极值；如果f(x)在[a，b]上不是单调函数，则f(x)在[a，b]上有极值；当f(x)在(a，b)上为单调函数时，它既没有最值也没有极值．2．若函数y＝f(x)的图象是一条连续不断的曲线，且在区间[a，b]上有且只有一个极小值点，那么该极小值是否是函数的最小值？提示：借助图象可知，该极小值就是函数的最小值．求下列函数的单调区间和极值．(1)y＝2x3＋6x2－18x＋3；(2)y＝－x3＋12x＋6.[自主解答](1)函数的定义域为R.y′＝6x2＋12x－18＝6(x＋3)(x－1)，令y′＝0，得x＝－3或x＝1.当x变化时，y′，y的变化情况如下表：当x＝－3时，函数有极大值，且y极大值＝57；当x＝1时，函数有极小值，且y极小值＝－7.(2)y′＝－3x2＋12＝－3(x＋2)(x－2)，令y′＝0，则x1＝－2，x2＝2.当x变化时，y′，y的变化情况如下表：∴函数f(x)的单调减区间为(－∞，－2)，(2，＋∞)；单调增区间为(－2,2)．当x＝－2时，y有极小值，且y极小值＝f(－2)＝－10；当x＝2时，y有极大值，且y极大值＝f(2)＝22.(1)求多项式函数的单调区间，关键是求出f′(x)后，解不等式f′(x)>0和f′(x)<0.(2)单调区间可以是开区间，如果区间端点在定义域内，也可写成闭区间．1．求函数y＝8x3－12x2＋6x＋1的极值．解：y′＝24x2－24x＋6＝6(4x2－4x＋1)，令y′＝6(4x2－4x＋1)＝0，解得x1＝x2＝1 2.当x变化时，y′，y的变化情况如表所示：所以此函数无极值．求下列各函数的最值．(1)f (x )＝－x 3＋x 2＋x ＋1，x ∈[－3,2]； (2)f (x )＝x 3－3x 2＋6x －2，x ∈[－1,1]． [自主解答] (1)f ′(x )＝－3x 2＋2x ＋1，令f ′(x )＝－(3x ＋1)(x －1)＝0，得 x ＝－13或x ＝1.当x 变化时f ′(x )及f (x )的变化情况如下表：∴当x ＝2时，f (x )取最小值－1；当x ＝－3时，f (x )取最大值34.(2)f ′(x )＝3x 2－6x ＋6＝3(x 2－2x ＋2)＝3(x －1)2＋3， ∵f ′(x )在[－1,1]内恒大于0， ∴f (x )在[－1,1]上为增函数．故x ＝－1时，f (x )最小值＝－12； x ＝1时，f (x )最大值＝2.即f (x )的最小值为－12，最大值为2.求函数f (x )在[a ，b ]上的最大值和最小值的步骤：(1)求函数的导数f ′(x )；(2)求方程f ′(x )＝0的全部实根x 0，且x 0∈[a ，b ]；(3)求最值，有两种方式：①是将f (x 0)的值与f (a )，f (b )比较，确定f (x )的最大值与最小值；②是判断各分区间上的单调性，然后求出最值．2．求函数f (x )＝4x 3＋3x 2－36x ＋5在区间[－2,2]上的最大值和最小值．解：f ′(x )＝12x 2＋6x －36＝6(2x 2＋x －6)，令f ′(x )＝0，解得x 1＝－2，x 2＝32.又f (－2)＝57，f ⎝⎛⎭⎫32＝－1154，f (2)＝－23， ∴函数f (x )的最大值为57，最小值为－1154.设f (x )＝－13x 3＋12x 2＋2ax .(1)若f (x )在⎝⎛⎭⎫23，＋∞上存在单调递增区间，求a 的取值范围； (2)当0＜a ＜2时，f (x )在[1,4]上的最小值为－163，求f (x )在该区间上的最大值．[自主解答] (1)由f ′(x )＝－x 2＋x ＋2a ＝－⎝⎛⎭⎫x －122＋14＋2a ，当x ∈⎣⎡⎭⎫23，＋∞时，f ′(x )的最大值为f ′⎝⎛⎭⎫23＝29＋2a ；令29＋2a ＞0，得a ＞－19. 所以，当a ∈⎝⎛⎭⎫－19，＋∞时，f (x )在⎝⎛⎭⎫23，＋∞上存在单调递增区间． (2)令f ′(x )＝0，得两根x 1＝1－1＋8a2， x 2＝1＋1＋8a2.所以f (x )在(－∞，x 1)，(x 2，＋∞)上单调递减，在(x 1，x 2)上单调递增．当0＜a ＜2时，有x 1＜1＜x 2＜4，所以f (x )在[1,4]上的最大值为f (x 2)，又f (4)－f (1)＝－272＋6a ＜0，即f (4)＜f (1)．所以f (x )在[1,4]上的最小值为f (4)＝8a －403＝－163. 得a ＝1，x 2＝2，从而f (x )在[1,4]上的最大值为f (2)＝103.(1)f (x )在区间I 上为增函数⇒f ′(x )≥0在区间I 上恒成立，f (x )在区间I 上为减函数⇒f ′(x )≤0在区间I 上恒成立．(2)由函数的最值来确定参数的问题是利用导数求函数最值的逆向运用，解题时一般采用待定系数法，列出含参数的方程或方程组，从而求出参数的值，这也是方程思想的应用．3．已知函数f (x )＝x 3＋ax 2＋bx ＋5，曲线y ＝f (x )在点P (1，f (1))处的切线方程为y ＝3x ＋1.(1)求a ，b 的值；(2)求y ＝f (x )在[－3,1]上的最大值．解：(1)依题意可知点P (1，f (1))为切点，代入切线方程y ＝3x ＋1可得，f (1)＝3×1＋1＝4，∴f (1)＝1＋a ＋b ＋5＝4，即a ＋b ＝－2，又由f (x )＝x 3＋ax 2＋bx ＋5得，又f ′(x )＝3x 2＋2ax ＋b ，而由切线y ＝3x ＋1的斜率可知f ′(1)＝3， ∴3＋2a ＋b ＝3，即2a ＋b ＝0，由⎩⎪⎨⎪⎧ a ＋b ＝－2，2a ＋b ＝0.解得⎩⎪⎨⎪⎧a ＝2，b ＝－4，∴a ＝2，b ＝－4.(2)由(1)知f (x )＝x 3＋2x 2－4x ＋5， f ′(x )＝3x 2＋4x －4＝(3x －2)(x ＋2)，令f ′(x )＝0，得x ＝23或x ＝－2.当x 变化时，f (x )，f ′(x )的变化情况如下表：∴f (x )的极大值为f (－2)＝13，极小值为f ⎝⎛⎭⎫23＝9527，又f (－3)＝8，f (1)＝4，∴f (x )在[－3,1]上的最大值为13.已知f (x )＝x 3＋ax 2＋bx ＋c 在x ＝1与x ＝－2时都取得极值． (1)求a ，b 的值；(2)若x ∈[－3,2]时都有f (x )>2c －12恒成立，求c 的取值范围．[巧思] 解决不等式恒成立问题，大多可用函数的观点来审视，用函数的有关性质来处理，而导数是研究函数性质的有力工具，因而常将不等式f (x )>g (x )(f (x )<g (x ))恒成立问题转化为F (x )＝f (x )－g (x )>0(F (x )＝f (x )－g (x )<0)恒成立问题，再用导数方法探讨F (x )的单调性及最值．[妙解] (1)f ′(x )＝3x 2＋2ax ＋b ，由题意，得⎩⎪⎨⎪⎧ f ′(1)＝0，f ′(－2)＝0，即⎩⎪⎨⎪⎧3＋2a ＋b ＝0，12－4a ＋b ＝0，解得⎩⎪⎨⎪⎧a ＝32，b ＝－6.(2)由(1)知f ′(x )＝3x 2＋3x －6. 令f ′(x )＝0得x ＝－2或x ＝1.当x 变化时，f ′(x )，f (x )的变化情况如表所示：∴f (x )在[－3,2]上的最小值为c －72.即2c －12<c －72，∴c <－3，∴c 的取值范围为(－∞，－3)．1．下面四幅图都是在同一坐标系中某三次函数及其导函数的图象，其中一定不．正确的序号是( )A ．①③B ．③④C ．②③④D ．②④解析：根据函数的单调性与其导函数函数值之间的关系，易得③④一定不正确．答案：B2．函数f (x )＝2x 3－9x 2＋12x ＋1的单调递减区间为( ) A ．(1,2) B ．(2，＋∞)C ．(－∞，1)D ．(－1，＋∞)，(2，＋∞)解析：f ′(x )＝6x 2－18x ＋12，令f ′(x )＜0，得1＜x ＜2. 答案：A3．函数f (x )＝x 3－3x (|x |<1)( ) A ．有最大值，但无最小值 B ．有最大值，也有最小值 C ．无最大值，但有最小值 D ．既无最大值，也无最小值解析：f ′(x )＝3x 2－3＝3(x ＋1)(x －1)，当x ∈(－1,1)时，f ′(x )<0，所以f (x )在(－1,1)上是单调递减函数，无最大值和最小值．答案：D4．若函数y ＝－x 3＋6x 2＋m 的极大值等于13，则实数m 等于________．解析：y ′＝－3x 2＋12x ，由y ′＝0，得x ＝0或x ＝4，容易得出当x ＝4时函数取得极大值，所以－43＋6×42＋m ＝13，解得m ＝－19.答案：－195．若f (x )＝ax 3＋bx 2＋cx ＋d (a >0)是R 上的增函数，则a ，b ，c 的关系式为________．解析：f ′(x )＝3ax 2＋2bx ＋c ≥0在R 上恒成立，则⎩⎪⎨⎪⎧a >0，Δ＝4b 2－12ac ≤0，从而解得a >0，且b 2≤3ac .答案：a>0且b2≤3ac6．已知函数f(x)＝2x3－6x2＋a在[－2,2]上有最小值－37，求a的值及f(x)在[－2,2]上的最大值．解：f′(x)＝6x2－12x＝6x(x－2)，由f′(x)＝0得x＝0，或x＝2.当x变化时，f′(x)，f(x)变化情况如下：∴当x＝－2时，f(x)min＝－40＋a＝－37，得a＝3.故x＝0时，f(x)最大值是3.一、选择题1．函数y＝f(x)在[a，b]上()A．极大值一定比极小值大B．极大值一定是最大值C．最大值一定是极大值D．最大值一定大于极小值解析：由最值与极值的概念可知，D选项正确．答案：D2．函数y＝x3－3x＋3在区间[－3,3]上的最小值为()A．1B．5C．12 D．－15解析：y′＝3x2－3，令y′＝0，得3x2－3＝0，∴x＝1或x＝－1.当－1<x<1时，y′<0；当x>1或x<－1时，y′>0，∴y极小值＝1，y极大值＝5.又当x＝－3时，y＝－15；当x＝3时，y＝21，∴y min＝－15.答案：D3．若x＝－2与x＝4是函数f(x)＝x3＋ax2＋bx的两个极值点，则有()A ．a ＝－2，b ＝4B ．a ＝－3，b ＝－24C ．a ＝1，b ＝3D ．a ＝2，b ＝－4解析：f ′(x )＝3x 2＋2ax ＋b ，依题意有－2和4是方程3x 2＋2ax ＋b ＝0的两个根，所以有－2a 3＝－2＋4，b3＝－2×4，解得a ＝－3，b ＝－24.答案：B4．函数f (x )＝x 3－3x 2－9x ＋k 在区间[－4,4]上的最大值为10，则其最小值为( ) A ．－10 B ．－71 C ．－15D ．－22解析：f ′(x )＝3x 2－6x －9＝3(x －3)(x ＋1)．由f ′(x )＝0得x ＝3或x ＝－1. 又f (－4)＝k －76，f (3)＝k －27， f (－1)＝k ＋5，f (4)＝k －20. 由f (x )max ＝k ＋5＝10，得k ＝5， ∴f (x )min ＝k －76＝－71. 答案：B 二、填空题5．函数f (x )＝x 3－15x 2－33x ＋6的单调递减区间为________．解析：f ′(x )＝3x 2－30x －33＝3(x －11)(x ＋1)，令f ′(x )<0，得－1<x <11. ∴f (x )的单调递减区间为(－1,11)．答案：(－1,11)6．若函数f (x )＝x 3＋x 2＋mx ＋1是R 上的单调函数，则实数m 的取值范围是________．解析：f ′(x )＝3x 2＋2x ＋m ，∵f (x )在R 上是单调函数， ∴Δ＝4－12m ≤0，即m ≥13.答案：⎣⎡⎭⎫13，＋∞7．若a >0，b >0，且函数f (x )＝4x 3－ax 2－2bx ＋2在x ＝1处有极值，则ab 的最大值等于________．解析：∵f ′(x )＝12x 2－2ax －2b ， ∴Δ＝4a 2＋96b >0，又x ＝1是极值点， ∴f ′(1)＝12－2a －2b ＝0，即a ＋b ＝6.ab ≤(a ＋b )24＝9，当且仅当a ＝b 时“＝”成立，∴ab 的最大值为9.答案：98．函数f (x )＝x 3－12x 2－2x ＋5，对任意x ∈[－1,2]都有f (x )>m ，则实数m 的取值范围是________．解析：由f ′(x )＝3x 2－x －2＝0，得x ＝－23或x ＝1，由题意知只要f (x )min >m 即可，易知f (x )min ＝f (1)＝72，所以m <72.答案：⎝⎛⎭⎫－∞，72 三、解答题9．求下列各函数的最值： (1)f (x )＝－x 3＋3x ，x ∈[－3，3]； (2)f (x )＝x 2－54x (x <0)．解：(1)f ′(x )＝3－3x 2＝3(1－x )(1＋x )．令f ′(x )＝0，得x ＝1或x ＝－1，当x 变化时，f ′(x )，f (x )变化情况如下表：又因为f (x )在区间端点处的函数值为f (－3)＝0， f (3)＝－18，所以f (x )max ＝2，f (x )min ＝－18. (2)f ′(x )＝2x ＋54x 2.令f ′(x )＝0，得x ＝－3. 当x 变化时，f ′(x )，f (x )的变化情况如下表：所以x 故f (x )的最小值为f (－3)＝27，无最大值．10．已知函数f (x )＝x 3＋ax 2＋bx ＋c 在x ＝－23与x ＝1处都取得极值．(1)求a ，b 的值及函数f (x )的单调区间．(2)若x ∈[－1,2]，不等式f (x )<c 2恒成立，求c 的取值范围．解：(1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b ，因为f ′(1)＝3＋2a ＋b ＝0，f ′⎝⎛⎭⎫－23＝43－43a ＋b ＝0，解得a ＝－12，b ＝－2，所以f ′(x )＝3x 2－x －2＝(3x ＋2)(x －1)，当x 变化时，f ′(x )，f (x )的变化情况如表：单调递增单调递减单调递增所以函数f (x )的递增区间为⎝⎭⎫－∞，－23和(1，＋∞)；递减区间为⎝⎛⎭⎫－23，1. (2)由(1)知，f (x )＝x 3－12x 2－2x ＋c ，x ∈[－1,2]，当x ＝－23时，f ⎝⎛⎭⎫－23＝2227＋c 为极大值，因为f (2)＝2＋c ，所以f (2)＝2＋c 为最大值．要使f (x )<c 2(x ∈[－1,2])恒成立，只需c 2>f (2)＝2＋c ，解得c <－1或c >2.故c 的取值范围为(－∞，－1)∪(2，＋∞)．。

高二年级数学《三次函数的图象与性质》教学设计

3、思想方法：数形结合分类讨论转化与化归函数与方程
五、布置作业
1、已知函数 f (x) x3 bx2 cx d （ b,c, d 为常数），当 k (,0) (5, ) 时， f (x) k 0 只有一个实数根；当 k (0,5) 时， f (x) k 0有 3 个相异实根，现给出下列 4 个命题：
a0
a0
0
图象 =0
0
三次函数的单调性、极值、最值
函
三次函数 f (x) ax3 bx2 cx d (a 0；a,b, c, d是常数)
数
b2 3ac 0
b2 3ac 0
f (x)
f (x)
图
象
x1
x2
极值
极大值f (x1)，极小值f (x2 )
单调
增区间：, x1 和 x2, +
人民教育出版社高中数学选修1-1第三章导数及其应用
三次函数的图象和性质
高二文数专题课
一、问题情景、引入课题
问题：请你画出下列函数的大致图像
1、f (x) x3 3x 2、f (x) 2x3 5 x2 x 1
2 3、f (x) 2x3 5 x2 x 3
2 4、f (x) x3 3x2 3x 1
二、自主探索，总结规律
1.类比二次函数，三次函数一般式是怎样？
形如：y ax3 bx2 cx d (a 0)
2.我们如何研究三次函数的图象和性质？
f (x) 3ax2 2bx c 4b2 12ac 4(b2 3ac)
二、自主探索，总结规律
函数
二次函数 y ax2 bx c(a 0；a,b,c是常数)
【变 1】已知函数 f x x3 3x ⑴求函数 f x 的单调区间及极值；⑵求 f x 在0,3 上的最值.

高考数学常考问题专题讲解三次函数专题—全解全析

三次函数专题—全解全析一、定义：定义1、形如的函数，称为“三次函数”（从函数解析式的结构上命名）定义2、三次函数的导数，把叫做三次函数导函数的判别式由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题，已经成为高考命题的一个新的热点和亮点。

二、三次函数图象与性质的探究：1、单调性一般地，当时，三次函数在上是单调函数；当时，三次函数在上有三个单调区间（根据两种不同情况进行分类讨论）2、对称中心三次函数是关于点对称，且对称中心为点，此点的横坐标是其导函数极值点的横坐标。

证明：设函数的对称中心为（m，n）。

按向量将函数的图象平移，则所得函数是奇函数，所以化简得：上式对恒成立，故，得，。

所以，函数的对称中心是（）。

可见，y＝f(x)图象的对称中心在导函数y＝的对称轴上，且又是两个极值点的中点，同时也是二阶导为零的点。

3、三次方程根的问题（1）当△=时，由于不等式恒成立，函数是单调递增的，所以原方程仅有一个实根。

（2）当△=时，由于方程有两个不同的实根，不妨设，可知，为函数的极大值点，为极小值点，且函数在和上单调递增，在上单调递减。

此时：①若，即函数极大值点和极小值点在轴同侧，图象均与轴只有一个交点，所以原方程有且只有一个实根。

2_x0001_若，即函数极大值点与极小值点在轴异侧，图象与轴必有三个交点，所以原方程有三个不等实根。

3若，即与中有且只有一个值为0，所以，原方程有三个实根，其中两个相等。

4、极值点问题若函数f(x)在点x0的附近恒有f(x)≥f(x)(或f(x)≤f(x))，则称函数f(x)在点x0处取得极大值（或极小值），称点x为极大值点（或极小值点）。

当时，三次函数在上的极值点要么有两个。

当时，三次函数在上不存在极值点。

5、最值问题函数若，且，则：；三、三次函数与导数专题：1.三次函数与导数例题例1.函数.（1）讨论函数的单调性；（2）若函数在区间（1，2）是增函数，求的取值范围.解：（Ⅰ），的判别式△=36（1-a）.（ⅰ）当a≥1时，△≤0，则恒成立，且当且仅当，故此时在R上是增函数.（ⅱ）当且，时，有两个根：，若，则,当或时，，故在上是增函数；当时，，故在上是减函数；若，则当或时，，故在和上是减函数；当时，，故在上是增函数；（Ⅱ）当且时,,所以当时，在区间（1，2）是增函数.当时，在区间（1,2）是增函数，当且仅当且，解得.综上，的取值范围是.例2.设函数，其中。

高中数学新湘教版精品学案《三次函数的性质：单调区间和极值》

三次函数的性质：单调区间和极值
【学习目标】
1．了解三次函数的图象和简单性质，三次函数与二次函数的联系。

2．会用导数研究三次函数的单调性，并且求解出三次函数的单调区间，认识它们之间的内在联系，进一步培养运算能力。

3．会用导数研究三次函数的极值，并且学会求解，认识事物之间的相互联系，培养辨证思维能力
【学习重难点】
重点：理解并掌握三次函数的单调区间和极值。

难点：理解并掌握求解三次函数的单调区间和极值的步骤，会运用到解决实际问题当中。

【学习过程】
一、新课学习。

知识点一：三次函数的单调区间和极值。

三次函数的导数是二次函数，二次函数的零点是容易求出的。

所以，用导数方法可以彻底了解三次函数的增减变化和极大极小，这个增减区间，就是三次函数的单调区间，列出表格，对函数的极大极小值点就可以一目了然。

根据前面的知识做一做：
练习：
1．指出函数3234y x x =+-的单调递增区间。

2．指出函数32454y x x x =+-的单调递减区间。

3．若函数()323321y x ax a x =++++有极大值和极小值，求a 的取值范围。

4．函数326y x x a =-+的极值是什么？
二、课程总结。

1．这节课我们主要学习了哪些知识？
2．它们在解题中具体怎么应用？
三、习题检测。

1．求下列函数在指定闭区间上的最大值和最小值。

（1）()[]32241,2,1f x x x x =+-+-；（2）()()[]2e 43,3,2x f x x x =-+-。

2．求解函数322611y x x =-+的单调减区间及极值。

二次函数与三次函数的性质比较

二次函数与三次函数的性质比较在高中数学中，二次函数和三次函数都是很重要的函数类型。

它们在数学及其它学科中有广泛的应用，因此，深入了解它们的性质及其比较是很重要的。

以下是二次函数与三次函数的性质比较。

1. 定义二次函数是指函数 $y = ax^2+bx+c$，其中 $a\ne 0$。

它是一个二次多项式函数，其图像为开口向上或向下的抛物线。

三次函数是指函数 $y = ax^3+bx^2+cx + d$，其中 $a\ne 0$。

它是一个三次多项式函数，其图像通常呈现 S 曲线形态。

2. 对称性质二次函数的图像是关于其顶点对称的，在抛物线的开口方向垂直于轴线的方向与轴断面重合的位置处，有一个顶点。

顶点的横坐标为 $x = -\frac{b}{2a}$，纵坐标为 $y = c-\frac{b^2}{4a}$。

此外，二次函数的图像在横轴上有一条对称轴，其方程为 $x = -\frac{b}{2a}$。

而三次函数的图像通常具有对称性，其对称轴通常是 $x$ 轴或 $y$ 轴，或经过其中某个极值点。

3. 单调性二次函数的单调性和其开口方向有关。

若开口向上，则函数在$(-\infty,-\frac{b}{2a})$ 上单调递增，在 $(-\frac{b}{2a},+\infty)$ 上单调递减；若开口向下，则函数在 $(-\infty,-\frac{b}{2a})$ 上单调递减，在 $(-\frac{b}{2a},+\infty)$ 上单调递增。

三次函数的单调性则要依据其导数的正负性来分析。

当导数 $f'(x)>0$ 时，函数单调递增；当导数 $f'(x)<0$ 时，函数单调递减。

4. 零点二次函数的零点可以通过求解 $ax^2+bx+c=0$ 得到。

其判别式为 $D=b^2-4ac$，若 $D>0$，则有两个不同实根；若 $D=0$，则有一个重根；若 $D<0$，则无实根。

三次函数求根公式高中.docx

三次函数求根公式高中标题：三次函数求根公式在高中数学中的实际应用引言：在高中数学中，我们学习了各种函数和方程，并且通过解方程的方法来解决实际问题。

其中，三次函数是一个非常重要的概念，它在数学和科学领域有着广泛的应用。

本文将阐述三次函数求根公式在高中数学中的实际应用。

一、三次函数与其求根公式的概念1.1 三次函数的定义三次函数是指次数为3的多项式函数，通常表示为f(x) = ax^3 + bx^2 + cx + d。

其中，a、b、c、d是实数，而x是自变量。

三次函数的图像通常是一个弯曲的曲线，具有很多特性和性质。

1.2 求根公式的定义求根公式是指用数学方法解三次函数方程的公式。

对于一般的三次函数方程f(x) = 0，可以通过求根公式来求解方程的根。

二、高中数学中的实际应用2.1 物理学中的牛顿运动定律牛顿运动定律是物理学中的基本定律之一，它描述了物体在外力作用下的运动规律。

在求解牛顿运动方程中，经常会出现三次函数方程，通过求根公式可以得到方程的实根，从而求解出物体的位置和速度等信息。

2.2 经济学中的需求与供给在经济学中，需求与供给是两个基本概念，它们关系到社会的经济发展和资源的分配。

通过建立数学模型，可以用三次函数来描述需求与供给的关系，通过求根公式可以确定平衡点，从而得到市场均衡时的价格和数量。

2.3 生态学中的物种数量动态生态学研究物种的数量动态与生态系统的平衡。

生态学家通过观测和实验，建立了各种模型来描述物种数量与环境因素的关系。

很多模型中都存在三次函数方程，通过求根公式可以确定物种数量的平衡点，从而分析生态系统的稳定性和变化趋势。

三、解决实际问题的思考对于高中生来说，学习三次函数求根公式不仅仅是为了应对考试，更重要的是培养批判性思维和解决实际问题的能力。

通过应用数学知识，我们可以在生活和学习中更好地理解和分析现象，解决实际问题。

结论：三次函数求根公式在高中数学中具有重要的实际应用，尤其在物理学、经济学和生态学等领域中。

全国高中数学青年教师展评课三次函数的图象和性质教学设计(青海西宁五中)

“三次函数的图象与性质”教学设计一、教学内容解析：三次函数是高中数学人教版选修2-2第一章第三节的内容。

三次函数是中学数学利用导数研究函数的一个重要载体，有着重要的地位，围绕三次函数命制的试题，近几年来在全国各地高考及模拟试题中频繁出现，已成为高考数学的一大亮点，特别是文科数学。

因此学习和掌握三次函数的基本性质很有必要。

但教材也没提及三次函数的这一概念，题型也局限在只是解决系数为常数的极值和单调区间问题，各种教辅资料中也往往只从求导、求极值、求单调区间等角度进行一些零碎的、浅表的探索，而很少对它作出比较系统地、实质性地阐述。

本节课是高三复习探究课，具体内容是：借助信息技术、通过几何画板的操作生成关于三次函数的动态效果，从而以三次函数的图像的形状特征为主线，探究三次函数的单调性和极值问题，加强学生对三次函数图像与性质的感性认识、引发学生的理性思考，形成经验。

同时在此过程中体会数形结合、分类讨论、化归与类比等思想方法。

基于对教材的认识和分析，本节课的教学重点和难点分别确定为：重点：（1）探究系数a,b,c,d的大小的变化与三次函数图像之间的变化规律；（2）根据图像探究三次函数的性质：单调性和极值。

难点：根据图像分析出三次函数的性质：单调性和极值。

二、教学目标设置：根据本节课的内容和地位，让学生通过这节课的教学达到下列三个目标：1、知识与能力：①加深对三次函数图像和性质的认识，学会利用三次函数解决问题；增强分析问题，解决问题的能力。

②培养自主学习的能力和利用计算机软件《几何画板》探求新知识的能力。

③掌握一定的多媒体环境下研究性学习的方法和手段，提高现代教育技术素养。

2、过程与方法：通过对函数)0(,)(23≠+++=a d cx bx ax x f 性质的研究，引导学生建立讨论函数性质的基本框架，知道函数性质的基本内容及其作用，掌握研究函数性质的基本过程和方法。

3、情感态度与价值观：通过直观的图形和抽象的函数性质的统一，培养学生的辨证唯物主义思想观；在研究的过程中，通过同学之间的讨论与协作，培养合作精神。