奥数-分数与繁分数化简
六年级奥数第四讲繁分数的计算
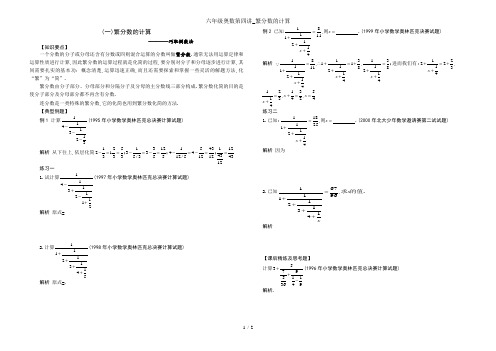
(一)繁分数的计算--------巧取倒数法【知识要点】一个分数的分子或分母还含有分数或四则混合运算的分数叫做繁分数.通常无法用运算定律和运算性质进行计算,因此繁分数的运算过程就是化简的过程,要分别对分子和分母逐步进行计算,其间需要扎实的基本功:概念清楚,运算迅速正确,而且还需要探索和掌握一些灵活的解题方法,化“繁”为“简”.繁分数由分子部分、分母部分和分隔分子及分母的主分数线三部分构成.繁分数化简的目的是使分子部分及分母部分都不再含有分数.连分数是一类特殊的繁分数,它的化简也用到繁分数化简的方法.【典型例题】例1计算11413123---(1995年小学数学奥林匹克总决赛计算试题)解析从下往上,依层化简125131221;33;3335/355-==-=-=154311244;.4312/512124312-=-==练习一1.试计算1141312112-+-+(1997年小学数学奥林匹克总决赛计算试题)解析原式=2.计算1111213145++++(1998年小学数学奥林匹克总决赛计算试题)解析原式=. 例2已知==+++xx则,1184112111.(1999年小学数学奥林匹克决赛试题)解析181313,11,;111118812211121444x xx=∴+=+=+++++++进而我们有:1222,134x+=++12135,,.134244x xx=+==+练习二1.已知:==+++xx则,25184112111.(2000年北大少年数学邀请赛第二试试题) 解析因为2.已知167,1961121314xx=++++求的值.解析【课后精练及思考题】计算53795113649++-(1996年小学数学奥林匹克总决赛计算试题)解析.(二)分数的简便计算1 3x4 +14x5+15x6+16x7+17x8+18x9=1 1x2 +12x3+13x4+……+12005X2006+12006=1 6 +112+120130+142+156172+190=1+2120+3130+4142+5156+6172+7190+81110+91132=3 2 +76+1312+2120+3130+4342+5756=1+11+2+11+2+3+11+2+3+4+11+2+3+4+5+ …+11+2+3+4+5 (50)=1 1x3 +13x5+15x7+……+197x99=2 3 +215+235+263+299+2143= 32x5 +35x8+38x11+311x14+314x17=4 1X5 +45X9+49X13+413X17+417X21=1 2 +14+18+116+132+164=56-712+920-1130+1342=1+12-56+712-920+1130-1342+1556-1772=12+(23+13)+(34+24+14)+…+(3940+3840+…+240+140)=7116×67+6115×56+5114×45+4113×34+3112×23=112×113×114×115×……×1199×11100=(1+12)×(1+14)×(1+16)×…×(1+120)×(1-13)×(1-15)×…×(1—119)×(1—121)=(1+12+13+14)×(12+13+14+15)-(1+12+13+14+15)×(12+13+14)=(9-1639×4)+(8-1639×5)+……+(4-1639×9)=155+255+355+…+955+1055+11155+121551355+……+19155+20155=251+451+651+……+5051-151-351-551-……-4951=。
六年级下册奥数专题练习-分数与繁分数化简-全国通用

分数与繁分数化简【分数化简】讲析:容易看出,分子中含有因数37,分母中含有因数71。
所以可得(长沙地区小学数学奥林匹克选拔赛试题)讲析:注意到,4×6=24,2+4=6,由此产生的一连串算式:16×4=64166×4=6641666×4=6664……(全国“育苗杯”小学数学竞赛试题)讲析:容易看出分子中含有因数3。
把48531分解为48531=3×16177,然后可试着用16177去除分母:【繁分数化简】(1990年马鞍山市小学数学竞赛试题)讲析:如果分别计算出分子与分母的值,则难度较大。
观察式子,可发现分子中含有326×274,分母中含有275×326。
于是可想办法化成相同的数:(全国第三届“华杯赛”复赛试题)讲析:可把小数化成分数,把带分数都化成假分数,并注意将分子分母同乘以一个数,以消除各自中的分母。
于是可得例3 化简(全国第三届“华杯赛”复赛试题)讲析:由于分子与分母部分都比较复杂,所以只能分别计算。
计算时,哪一步中能简算的,就采用简算的办法去计算。
所以,原繁分数等于1。
(北京市第一届“迎春杯”小学数学竞赛试题)讲析:连分数化简,通常要从最下层的分母开始,自下而上逐步化简。
依此法计算,题目的得数是2。
(计算过程略)55、对称变换【将军饮马】据说古代希腊有一位将军向当时的大学者海伦请教一个问题:从A地出发到河边饮马,再到B地(如图4.32所示),走什么样的路最近?如何确定饮马的地点?海伦的方法是这样的:如图4.33,设L为河,作AO⊥L交L于O点,延长AO至A',使A'O=AO。
连结A'B,交L于C,则C点就是所要求的饮马地点。
再连结AC,则路程(AC+CB)为最短的路程。
为什么呢?因为A'是A点关于L的对称点,AC与A'C是相等的。
而A'B 是一条线段,所以A'B是连结A'、B这两点间的所有线中,最短的一条,所以AC+CB=A'C+CB=A'B也是最短的一条路了。
创新思维·小学奥数·解题思路和知识点归纳(运算法则方法、技巧与规律)

第八讲:运算法则或方法(技巧与规律)一、繁分数化简方法繁分数化简的方法,一般有以下两种方法。
(1)利用分数基本性质,把繁分数的分子、分母同乘以所有分母的最小公倍数,从而化简繁分数。
(2)利用分数与除法的关系,将繁分数化简。
这是因为繁分数实际上是分数除法的另一种表示形式的缘故。
例如【求连分数的值的方法】由数列a 0,a 1,……及b 1,b 2,……所组成的表达式称为“连分数”。
它可简记为为连分数的值。
连分数有两种,一是有限连分数,二是无限连分数。
例如,求有限连分数的值,也称化简连分数,它的化简方法与繁分数的化简方法基本相同。
一般是从最下面的分母运算开始,逐步向上计算。
例如上面的这个有限连分数:求无限连分数的值,就是求它的有限层的值作为它的近似值。
当层次愈多时,就愈接近它的值。
注意:繁分数和连分数,都不是“分数”定义里所定义的一种分数。
分解为两个单位分数的和,可按以下步骤去完成:的任意两个约数a 1,a 2;(2)扩分:将单位分数的分子、分母同乘以两约数的和(a 1+a 2),(3)拆分:将扩分后所得的分数,按照同分母分数相加的法则反过来(4)约分:将拆开后的两个分数约分,便得到两个单位分数。
注意:(1)因大于1的自然数的约数有时不止2个,有多个,从中任取两个约数的取法也有多种,只要每次取出的两个约数之间不成比例,则将一个单位分数拆成两个单位分数的和的结果也各不相同。
例如,15的约数有1,3,5,15四个,从中任取两个的取法有(1,3)、(1,5)、(1,15)、(3,5)、(3,15)、(5,15)六种,而取(1,3)和(5,15)、(1,5)和(3,15)是成比例(2)若要将单位分数拆成两个相等的单位分数之和,那只要在扩分时,分子、分母同乘以分母的任何一个约数的2倍或乘以2即可。
拆成n 个单位分数的和的方法和步骤与拆成两个单位分数的方法和步骤相同,不同点只在扩分时,分子、分母同乘以分母A 的n 个约数的和(a 1+a 2+…+a n )。
小学奥数繁分数计算定义及解题技巧

小学奥数繁分数计算定义及解题技巧
1、繁分数的定义
如分数形式,分子或分母含有分数,或分子与分母都含有分数的数,叫繁分数。
2、繁分数计算的技巧
(1)先找出繁分数中主分数线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分的计算结果能约分的要约分,最后改成“分子部分/分母部分”的形式,再求出结果。
(2)繁分数化简的另一种方法是:根据分数的基本性质,将繁分数的分子部分和分母部分同时扩大相同的倍数(这个倍数必须是分子部分与分母部分所有分母的最小公倍数),从而却掉分子部分和分母部分的分母,然后通过计算划分为最简分数或整数。
六年级奥数 计算 突破繁分数(ABC级).学生版

六年级奥数计算突破繁分数(ABC级).学生版六年级奥数计算突破繁分数(abc级).学生版突破繁分数科学知识框架一、定义:在一个分数的分子和分母里,至少存有一个又所含分数,这样形式的分数,叫作繁分数。
繁分数中,把分子部分和分母部分分开的那条分数线,叫做繁分数的主分数线(也叫主分线)。
主分线比其他分数线要长一些,书写位置要取中。
在运算过程中,主分线要对准等号。
如果一个繁分数的分子部分和分母部分又是繁分数,我们就把最长的那条主分线,叫做中主分线,依次向上为上一主分线,上二主分线……;依次向下叫下一主分线,下二主分线……;两端的叫末主分线。
根据分数与乘法的关系,分数乘法的运算也可以译成繁分数的形式。
二、繁分数化简把繁分数化成最简分数或整数的过程,叫作繁分数的化简。
繁分数化简通常使用以下四种方法:(1)先找到中主分线,确认出来分母部分和分子部分,然后这两部分分别展开排序,每部分的排序结果,能约分的要约分,最后写成“分子部分÷分母部分”的形式,再求出最后结果。
此题也可以重写成分数乘法的运算式,再展开排序。
分级讲义体系六年级奥数.排序.突破繁分数(abc级).学生版page1of18(2)繁分数化简的另一种方法就是:根据分数的基本性质,经繁分数的分子部分、分母部分同时倍增大相同的倍数(这个倍数必须是分子部分与分母部分所有分母的最小公倍数),从而去掉分子部分和分母部分的分母,然后通过计算化为最简分数或整数。
(3)繁分数的化简通常由下至上,由左至右,逐次展开化简。
繁分数的分子部分和分母部分有时也出现是小数的情况,如果分子部分与分母部分都就是小数,可以依据分数的基本性质,把它们都化成整数,然后再展开排序。
如果是分数和小数混合出现的形式,可按照分数、小数四则混合运算的方法进行处理。
即:把小数化成分数,或把分数化成小数,再进行化简。
当分子部分和分母部分都统一成小数后,化简的方法就是:中间约分时,把小数看作整数,但必须特别注意小数点不要点错边线。
小学数学奥数解题技巧(8)运算法则或方法

小学数学奥数解题技巧
8、运算法则或方法
【四则运算法则】整数、小数、分数的加、减、乘、除四则运算法则,见小学数学课本,此处略。
【四则运算顺序】见小学数学课本,略。
【繁分数化简方法】繁分数化简的方法,一般有以下两种方法。
(1)利用分数基本性质,把繁分数的分子、分母同乘以所有分
母的最小公倍数,从而化简繁分数。
(2)利用分数与除法的关系,将繁分数化简。
这是因为繁分数
实际上是分数除法的另一种表示形式的缘故。
例如
【求连分数的值的方法】由数列a0,a1,……及b1,b2,……所组成的表达式
1。
六年级的奥数第四讲_繁分数计算.doc

5 7 9 11 13 6 - 12 + 20 - 30 + 42 =
1 5 7 9 11 13 15 17 1+2- 6 + 12- 20 + 30 - 42 + 56 - 72 =
1
21
321
39 38
21
2 +( 3 + 3 )+( 4 + 4 + 4 )+…+( 40 + 40 +…+ 40 + 40 ) =
5
解析 原式 =.
例 2 已知 1
1 1 1
2 1
x 4
8 ,则 x 11
解析
1
1
1 1
2x1
4
8, 1
11
2
1 2 13 5
x1
,x
,x .
3 42 4
Hale Waihona Puke 4练习二1. 已知 : 1
1 1 1
2 x1 4
18 , 则x 25
解析 因为
.
1
1
1
1 x
4
.
(1999 年小学数学奥林匹克决赛试题 )
3, 1
“繁”为“简” . 繁分数由分子部分、分母部分和分隔分子与分母的主分数线三部分构成
. 繁分数化简的目的是
使分子部分与分母部分都不再含有分数 .
连分数是一类特殊的繁分数 , 它的化简也用到繁分数化简的方法 .
【典型例题】
例 1 计算
1
(1995 年小学数学奥林匹克总决赛计算试题 )
4
1
3
1 1
2
3
解析 从下往上 , 依层化简 2
1
1
1+220 +330 +442 +556 +672 +790 +8110 + 9132 =
繁分数化简方法

繁分数化简方法
嘿,朋友们!今天咱来聊聊繁分数化简方法,这可真是个有趣又实用的玩意儿!
你看啊,繁分数就像是一团乱麻,但咱可不能被它吓住!就好比你要解开一个复杂的谜题,得有耐心和技巧。
比如说,遇到一个繁分数,咱先得找到它的关键所在。
就跟找宝藏一样,得先找到那关键的线索。
然后呢,根据分数的基本性质,分子分母同时乘或除以一个相同的数,把它一点点化简。
这就像给繁分数来个“瘦身计划”,让它变得苗条又清晰。
有时候啊,你得把那些复杂的式子一点点拆开来看,不能着急。
这就好像剥洋葱一样,一层一层地剥开,才能看到里面的核心。
哎呀,要是没耐心,那可就搞不定啦!
举个例子吧,就像这样一个繁分数,乍一看好像很吓人,但只要咱静下心来,一步一步来,肯定能把它化简得明明白白。
你想想,要是你掌握了这个技巧,以后再遇到繁分数,那还不是手到擒来?
繁分数化简可不仅仅是数学里的一个小技巧,它更像是一把钥匙,能打开很多难题的大门。
它能让我们更清楚地看到问题的本质,就像在迷雾中找到了方向。
所以啊,朋友们,别小瞧了繁分数化简方法,它真的很重要!好好去钻研它,去掌握它,让它成为你数学道路上的得力助手!咱可不能被小小的繁分数给难住,对吧?要勇敢地去挑战,去探索!相信自己,一定能行!。
