M二次谐波计算
谐波计算

§12 –3 3
有效值、 有效值、平均值和平均功率
前已指出,任一周期电流i 有效值I 前已指出,任一周期电流i的有效值I已经定义
1 T 2 I= i dt ∫0 T
•当然可以用非正弦周期函数直接进行上述定义的 当然可以用非正弦周期函数直接进行上述定义的 积分求有效值。 积分求有效值。这里主要是寻找有效值和各次谐 波有效值之间的关系。 波有效值之间的关系。
第十二章 非正弦周期电流电路和信号的 频谱
§12 –1 §12 –2 §12 –3 §12 –4 非正弦周期信号 周期函数分解为傅利叶级数 有效值、 有效值、平均值和平均功率 非正弦周期电流电路的计算
§12 –2 周期函数分解为傅利叶级数 2
周期电流、电压、 周期电流、电压、信号等都可以用一个周期 函数表示, 函数表示,即:
§12 –1 1
非正弦周期信号
图(a)脉冲波形
图(b)方波电压
图
12- 12-1
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图(c) 锯齿波 图 12- 12-1
图(d)磁化电流
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图(e)半波整流波形 图 12- 12-1 非正弦周期电流、 非正弦周期电流、电压波形
f (t ) = f (t + kT)
式中, 为周期函数 为周期函数f 的周期。 式中,T为周期函数f(t)的周期。 k=0,1,2,… =
§12 –2 周期函数分解为傅利叶级数 2
如果给定的周期函数满足狄里赫利条件, 如果给定的周期函数满足狄里赫利条件,它就能 展开成一个收敛的傅立叶级数, 展开成一个收敛的傅立叶级数,即
合并单元测试:插值法与同步法

合并单元测试时需要对其额定延迟时间、角差以及比差等参数进行验证,测试原理一般采用插值法和同步法。
合并单元将模拟量转化成9-2输出时,由于装置硬件固有的特性,在同一个时间坐标系中,其9-2输出的波形必然会滞后模拟量波形,因此在9-2报文中,一般将通道一的属性定义为通道额定延时,其反映了9-2波形滞后模拟量波形的时间,保护装置在解析9-2报文后,会根据通道一的额定延迟时间还原模拟量波形并进行相关计算。
如果通道一延迟时间设置错误,则差流、角度等均会出现错误的数值,影响保护装置的可靠性。
1、插值法由傅里叶变化可知:A=A0+A1+A2+A3+A4+……Ai,其中A1、A2、A3……Ai的表达式为正弦表达式。
在4K采样率的情况下,若将4000个点的数据进行离散傅氏变换,则可认为基波频率为1Hz,即A1为1Hz的正弦波形,A2为2Hz的正弦波形。
当需要50Hz的波形数据时,取A50的波形数据即可。
设置自身晶振控制采样,此时有可能出现模拟量的采样点无对应的9-2点,则需插值计算出9-2点的大小,如上图中X点需要插值计算得到。
假定9-2为Am,模拟量为An:▪相差计算:上位机取软件界面的设置频率,相应地计算出9-2及模拟量Ai表达式。
令:当前频率下9-2的相位为φm;模拟量相位为φn;9-2数字报文中通道一的延时为t;当前软件设置频率为f;计算公式为:Δφ=2πf*t-|φm-φn|(最后结果会涉及各计算量的单位换算)▪时差计算:上位机计算出角差之后,取软件界面的频率设置值参与时差计算,在已知频率的情况下,可通过相差计算出时差。
计算公式为:Δt=|Δφ|/2πf(最后结果会涉及各计算量的单位换算)▪比差计算:离散傅氏变换法得到当前频率下9-2和模拟量的幅值,在比差计算中,测试机设定模拟量的幅值为基准值,从而得到比差。
计算公式为:(Am-An)/An*100%▪谐波计算:测试仪输出包含多次谐波分量的模拟量,在基波频率为50Hz的情况下,根据傅氏变换可得A50为基波含量,A100为二次谐波含量,A150为三次谐波含量,以此类推,以模拟量各次谐波含量的幅值为基准值,得到谐波含量的比差。
二次谐波理论相关

Engineering the second harmonic generation pattern from coupled gold nanowiresA.Benedetti,M.Centini,*C.Sibilia,and M.BertolottiDipartimento di Energetica,Universitàdi Roma,La Sapienza,Via A.Scarpa16,00161Roma,Italy*Corresponding author:marco.centini@uniroma1.itReceived November2,2009;accepted December16,2009;posted January5,2010(Doc.ID119439);published February4,2010We numerically investigated second harmonic generation from systems composed of two coupled gold nano-wires.The developed method allows one to arbitrarily change the shape of the wire cross section in order to explore the generated and scatteredfield patterns.Our results suggest that the overall second harmonic gen-eration is related to the electromagnetic energy per unit length stored in the gap area between the wires.These geometrical considerations make further optimization possible.As an example we discuss the possibility to select dipolar emission and/or quadrupolar emission patterns.The selection mechanism responsible for this kind of emission can be traced back to the interaction between nonlinear sources with the surface plasmon resonance of the metallic wires.©2010Optical Society of AmericaOCIS codes:160.4330,190.3970,190.4350,290.5850.1.INTRODUCTIONThe second order nonlinear response fromflat metal screens has been widely investigated,both theoretically and experimentally,from the late1960s–1980s[1–11]. Some of this work was devoted to the study of the second harmonic generation(SHG)in reflection by thin metal layers and/or metallic gratings,with the subsequent re-porting of the enhancement of nonlinear conversion effi-ciencies due to the surface plasmon polariton(SPP)exci-tation at the metal/dielectric interface[12–15].Regarding the SHG in systems composed of many metallic particles and/or percolated systems,several models have been pro-posed that utilize the effective medium approximation and experimental techniques have been developed to characterize the nonlinear optical responses[16–20]. Also,a large number of works have been devoted to the study of materials and single molecule behavior to en-hance and characterize the nonlinear response[21–27].The last few years witnessed renewed interest in the study of nonlinear second order properties of metal/ dielectric composites thanks to the development of nano-technologies and nanoscience.The SHG has been de-tected in metal nanoparticles and the effects of scatterer size on the dipole or multipole contributions have been ex-perimentally investigated[28,29].A strong second har-monic(SH)signal has been found emanating from sharp metal tips[30],thus opening the way to interesting appli-cations for nearfield nonlinear microscopy and spectros-copy.The SHG enhancement from nanoantennas and nanodimers has been observed both in near and farfields [31–34].Other recent works[35,36]deal with the SHG in gold nanowires.In these studies the effect offield polar-ization direction with respect to the direction of the wires is emphasized.Moreover,the SHG from metamaterials composed of split-ring resonators was experimentally re-ported by Klein et al.[37,38].Another experimental pa-per,recently published,reports the SHG from a gold plate having a periodic pattern of rectangular apertures on top [39].In[39]the effect reported is connected to the shape of the apertures and to the propagation constants of the guided electromagnetic(e.m.)modes inside the apertures. This feature has been employed to enhance the nonlinear response of GaAs using it tofill patterned metallic screens with holes,taking advantage of the high trans-mission regime and strongfield localization inside the holes[40].All these aspects,combined with the state of art technology capabilities,make these materials very in-teresting for basic and applied research.From a theoretical point of view,the farfield pattern of the generated SH has been studied in detail for a single metallic cylinder or other two-dimensional(2D)single ob-jects as well as for nanospheres and deformed nano-spheres[41–45].Also,the scattered SH generated by a SPP at a surface nanodefect was theoretically investi-gated[46].Recent works report on numerical results ob-tained by the implementation of afinite difference time domain(FDTD)algorithm[47–50].Reference[48]deals with the SHG from resonant nanoslits on a silver sub-strate,by taking into account the nonlinearity arising in the free electron response from the magnetic Lorentz force.In[47]the quantum jellium model[10]for the non-linear response of a metal was implemented in a FDTD algorithm;numerical results are shown for periodically patterned metallic screens.Limitations of the validity of the approach used in[47]for nanostructured objects are related to the parameterization procedure used for the nonlinear coefficient of the metal,performed assuming an infiniteflat surface.In[49]a semiclassical approach, based on the free electron gas model for the nonlinear op-tical response of a metal,has been adopted to successfully analyze experimental results of[50].Also,in[51]the au-thors showed that for patterned metallic membranes hav-0740-3224/10/030408-9/$15.00©2010Optical Society of Americaing thicknesses of a few tens of nanometers the farfield SH is dominated by dipole contributions of the nonlinear response.In this work we study the enhancement of the SHG due to the interaction between two2D metallic wires with sec-tions of arbitrary shape,focusing on the possibility of tai-loring the emission pattern by properly designing the shape and the position of the wires.Numerical calcula-tions on two different kinds of double-wire systems,rect-angular section(RS)and trapezoidal section(TS)of the wires,are performed.The SHG as a function of the dis-tance(air gap)between the wires is investigated in both the near and farfield regimes.The enhancement of the SH signal is then explained in terms of the pump energy stored inside the gap.Our results reveal a high sensitivity of the emission pattern and the overall power with re-spect to displacements of just a few nanometers.In par-ticular we show that the SHfield with dipole and quad-rupole symmetries can be achieved by changing the geometrical parameters.Although we only consider sys-tems composed of two wires,our approach can be applied for an arbitrary number of objects with different shapes and sizes.Wefinally investigate localization effects of the SHfield at the surface,revealing the existence of hot spots that can be used for nanoillumination and single molecule spectroscopy[52].The paper is divided into four main sections:Following this introduction,in Section2,we describe the used the-oretical model and integration method.In Section3we show the results of our numerical analysis focusing our attention on the different behaviors of emittedfields as functions of the nano-object shape and position.Finally, in Section4the main conclusions and perspectives for fu-ture work are drawn.2.THEORETICAL MODELAt optical frequencies the linear response of a metal is strongly affected by the bound valence electrons.We chose to model the electric permittivity of gold from the far infrared to the ultraviolet range with a Drude–Lorentz model by consideringfive Lorentz-like[53–55] resonators,r͑͒=D͑͒+͚k=15G kP20,k2−2−i␥k,D͑͒=1−G0P2͑+i␥0͒=1−02͑+i␥0͒,͑1͒whereD is the electric permittivity obtained by consider-ing the Drude model only.p is the plasma frequency as-sociated with the total number of electrons per unit vol-ume.G k and0,k are,respectively,the oscillator strengths and resonant frequencies and␥k are damping constants related to each oscillator.0=ͱG0p is the plasma fre-quency associated with intraband transitions(relatedonly to the free electron density)with damping constant ␥0.Indeed we assume that,in the absence of external ex-citation,the free electron density n is constant and equal to its bulk value n0,being02=͑e2n0/m0͒,where e is the absolute value of the electron charge and m is the effec-tive electron mass.The values of the parameters of the Drude–Lorentz model are reported in[53].We model the optical response of the metal by assum-ing an effective current density,Jជ=JជD+ץPជb.e.ץt,͑2͒where JជD is the current density induced by the e.m.field on the free electrons and Pជb.e.is the polarization vector due to the presence of bound electrons.Each term on the right hand side of Eq.(2)contains both linear and nonlin-ear contributions.At this stage we focus our attention on the nonlinear contributions arising from conduction elec-trons only.We study the SHG process in the undepleted pump ap-proximation from a metallic2D structure that reacts in the presence of a transverse magnetic͑p-͒polarized e.m.field;the system is completely2D.The nonlinear second order response of the conduction electrons is then evalu-ated as in[49]and the dynamic equations for JជD and n areץJជDץt=JជDneٌជ·JជD+͑JជD·ٌជ͒JជDne−␥0JជD+e2mnEជ−e0mJជD∧Hជ,͑3aٌ͒ជ·JជD=eץnץt,͑3b͒where␥0is defined in Eqs.(1)and it represents losses due to Coulomb scattering of conduction electrons with the lattice ions.By adopting a perturbative approach as in[8]we move into the frequency domain and write the current density at the SH frequency as a function of the fundamental fre-quency(FF)field by collecting terms up to the second or-der.Thus,the expressions of thefields,the current,and free electron densities areJជ͑rជ,t͒=͚m=1,2Jជm͑rជ͒e−imt+c.c.,Eជ͑rជ,t͒=͚m=1,2Eជn͑rជ͒e−imt+c.c.,Hជ͑rជ,t͒=͚m=1,2Hជm͑rជ͒e−imt+c.c.,n͑rជ,t͒=n0+͚m=1,2n m͑rជ͒e−imt+c.c.,͑4͒where the subscript m=1,2refers to the FF͑͒and SH ͑2͒angular frequencies.Due to the weak nature of the nonlinear interaction,we consider that the dynamics for the FF is completely described by the linear response,Jជ1=−i͑r,1−1͒0Eជ1,͑5͒wherer,1is calculated by using Eqs.(1).For the SHfield we haveJ 2ជ=−i 20r ,2E 2ជ−i 20ͫabE 1ជٌជ·͓D ,1E 1ជ͔+b ͑a −1͒D ,12͑E 1ជ·ٌជ͒E 1ជ+bD ,14ٌជ͓E 1ជ·E 1ជ͔ͬ,͑6͒wherea =+i ␥0,b =22+i ␥0,=−e 2m 2,͑7͒and r ͑r ជ͒=r ͑r ជ͒−1,D ͑r ជ͒=D ͑r ជ͒−1are the expressionsfor the spatially dependent electric susceptibility accord-ing to the definitions given in Eqs.(1).We note that the coefficients a and b are exactly equal to unity in the case of no losses.The first term on the right hand side of Eq.(6)represents the linear contribution,which depends on both bound and free electrons;the remaining terms are the nonlinear sources.The evaluation of the nonlinear terms of Eq.(6)requires a detailed analysis to separate bulk and surface contributions.In the bulk,the first non-linear term of Eq.(6)vanishes and the other terms,evalu-ated only for the points inside the metallic objects,are re-sponsible for the bulk contribution to the nonlinear current density,J ជNL Bulk =−i 20D ,12b ͫ͑a −1͒͑E 1ជ·ٌជ͒E 1ជ+12ٌជ͓E 1ជ·E 1ជ͔ͬ.͑8͒In order to evaluate surface contributions we assume thatthe transition from metal to surrounding air is achieved by varying the value of the parameter P 2from the value it assumes in the metal to zero in the vacuum.Thus the other parameters,i.e.,damping coefficients and electron effective mass,are considered as constant coefficients.Following the procedure outlined in [56],modified and adapted to our case (losses and linear contribution of bound electrons),we evaluate the nonlinear surface cur-rents acting as sources for the SH field,X ˆ·J ជNL Surface =−i 20abE 1,X ͑−͒E 1,Y ͑−͒͑1−D ,1͒␦͑Y ͒,Y ˆ·J ជNL Surface =−i 20ab ͓E 1,Y͑−͔͒24͓͑1−D ,1͒͑r ,1+3͔͒␦͑Y ͒.͑9͒Calling r ជЈthe vectors defining the coordinates of theboundaries,X ˆ͑r Јជ͒and Yˆ͑r Јជ͒are the local unit vectors tan-gential and normal (outgoing)to the surface,respectively.In order to provide a comparison with previous results wechoose to evaluate the continuous function r ,1͑r Јជ͒E 1,Y ͑r Јជ͒below the surface as r ,1E 1,Y ͑−͒͑r Јជ͒.Equations (9)are equivalent to the results of [56]with the exceptions of themultiplicative coefficients a and b which account forlosses;the presence of D ,1represents the response of con-ducting electrons only and r ,1accounts for the total lin-ear response of both bound and free electrons.Even though we do not use it in the calculations pre-sented in this work,we add the expression for the surface nonlinear terms evaluated at the interface metal/dielectric,when a dielectric B is considered,X ˆ·J ជNL Surface =−i 20abE 1,X ͑−͒E 1,Y͑−͒B͓r ,1͑B −1͒+B ͑1−D ,1͔͒␦͑Y ͒,Y ˆ·J ជNL Surface =−i 20ab ͓E 1,Y ͑−͔͒24B2͓3r ,12͑B −1͒+B ͓r ,1͑B −D ,1͒+3B ͑1−D ,1͔͔͒␦͑Y ͒.͑10͒This feature will be used in the future to analyze realstructures composed of metal particles on top of a dielec-tric substrate,for example.Adding the expressions of Eqs.(8)and (9)we finally write the current density for the field at the SH frequency,J 2ជ=−i ͑r ,2−1͒20E 2ជ+J ជNL Bulk +J ជNLSurface .͑11͒The generated field pattern can be calculated by insertingEq.(11)into the equation for the generated SH electric field,ٌͩជ∧ٌជ∧−͑2͒2c2I ញͪE ជ2͑r ជ͒=i ͑2͒0J ជ2͑r ជ͒,͑12͒where Iញis the identity matrix.The formal solution is ob-tained by substituting Eq.(11)into Eq.(12),E ជ2͑r ជ͒=͵⌺ЈG ញ2͑r ជ,r Јជ͒ͩ2cͪ2͓r ,2͑r Јជ͒−1͔E 2ជ͑r Јជ͒d ⌺Ј+i 20͵⌺ЈG ញ2͑r ជ,r Јជ͒J ជNL Bulk ͑r Јជ͒d ⌺Ј+i 20͵⌺ЈG ញ2͑r ជ,r Јជ͒J ជNLSurface ͑r Јជ͒d ⌺Ј,͑13͒where the Green’s tensor G is defined asG ញ2͑r ជ,r Јជ͒=ͫI ញ+ٌជٌជk 0,22ͬg 2͑r ជ,rЈជ͒,͑14͒with g 2being the 2D Green’s scalar function [57]in thehomogeneous background medium,corresponding to the Bessel function of the first order for the SH frequency.⌺Јis the section area of the 2D metallic scatterers.Effects due to the substrate can be included by calculating the Green’s tensor for a stratified medium as outlined in [58].The numerical integration of Eq.(13)is performed us-ing a procedure detailed in [58,59]and adapted to the case of the SHG as shown in [55].Once the field inside the scatterers is calculated,it is straightforward to calculate the SH field at every other point in space.In particular,itis possible to depict the near field as well as the far field pattern.Then we numerically evaluate the nonlinear scattering cross section (NSCS)Q ͑͒as defined in [41],Q ͑2͒=P ͑2͒sc ͓P ͑͒inc ͔2=͵2q ͉͑2͒d ,͑15͒where q ͉͑2͒is the differential scattering cross section.Here we consider P ͑͒inc as the power flow per unit length (watt/meter)of the FF field across the segment as shown in Fig.1.P ͑2͒sc is the generated SH power flow per unit length calculated across a circumference of ra-dius R ӷ.As already mentioned,Eq.(3a)is formally identical to Eq.(7)of [49],as we began from the same model for the nonlinear response of the metal.However,there are some differences between the two models that can be summa-rized as follows:(i)we study the phenomena in the fre-quency domain,describing the SHG from a monochro-matic pump excitation.(ii)We analytically evaluate the surface contribution by considering a hard interface(abrupt change in the dielectric constant).Using this ap-proach improves the convergence of our numerical algo-rithm.Moreover,the integration method can handle both surface and bulk nonlinear sources thus making it pos-sible to directly compare our results with other models of metal response [4,8,10].(iii)We calculate both far and near field emissions by single or multiple 2D scatterers of arbitrary shapes.The periodicity of the system is not re-quired.Our approach is aimed to the studies of nonlinear microscopy and of nonlinear generation from single nano-sized objects.It may be used,for example,to design and optimize the nonlinear response from single molecules at-tached to metallic nanoantennas for detection and sens-ing applications.In our opinion,the method of [49]ap-pears to be more suitable and efficient for the study of the SHG in periodic metamaterials and sub-wavelength pat-terned screens in the time domain.(iv)We consider the linear response of bound electrons in order to obtain a more realistic value of the linear dielectric constant of the metal both at the FF and SH frequencies.Fig.1.Sketch of the scattering geometry for the FF field.Inset:(up)dimensions of the trapezoid section wires;(down)dimen-sions of the RS wires.102030401020304050012345Gap (nm)r e l a t i v e e n e r g y p e r u n i t l e n g t h i n s i d e t h e g a p r e g i o nN o n l i n e a r s c a t t e r i n g c r o s s s e c t i o n (c m 2/W )Fig.2.Relative energy per unit length inside the gap region incases of TS (solid line)and RS (dashed line)wires.NSCS for the TS (triangles)and RS (squares)wires.Fig.3.(Color online)Modulus of the normalized electric field (a),(c)y -and (b),(d)x -components normalized with respect to the incident field amplitude for gap values of (a),(b)18and (c),(d)38nm.3.NUMERICAL ANALYSISWe consider two different configurations composed of coupled gold wires with (a)RS 300nm ϫ145nm and (b)TS “bowtie antenna type”with B =420nm,d =145nm,and h =300nm (inset of Fig.1).We chose these geom-etries because they both exhibit a resonant behavior when a monochromatic p -polarized (electric field direction along the y axis)FF field with a wavelength of 800nm im-pinges along the horizontal ͑x ͒axis.We point out that the sizes of the objects that we consider have wires dimen-sions ͑h ,B ,d ͒that are not negligible with respect to the in-cident wavelength.As a result we are exploring a different regime with respect to [28,29,51].Our analysis is per-formed by comparing the generated SH fields from the two geometries,relating the enhancement of the emission to the energy confinement of the FF field in the gap re-gion.We will also show that SH patterns are extremely sensitive to the shape of the emitters and the distance be-tween wires.As a first step we study the localization prop-erties for the FF field.We considered a p -polarized plane wave,monochromatic FF electric field of amplitude equal to 100MV/m,traveling from left to right along the x axis.Calculations of the linear FF fields were performed under the Comsol Multiphysics simulation environment.We cal-culated the average energy per unit length in the gap re-gion of area=gd (see Fig.1)as a function of the gap.In order to quantify the localization effect we normalize it with respect to the energy per unit length stored intheFig.4.Differential scattering cross section for the TS wires when different values of the distance between wires ͑g ͒areconsidered.Fig.5.Differential scattering cross section for the RS wires when different values of the distance between wires ͑g ͒areconsidered.Fig. 6.(Color online)z -component of the SH magnetic field (ampere/meter)(snapshots in time)for the (a)TS and (b)RS wires.same area for the same incident field propagating in free space by applying the formulaW =͐gap ͓0͉Eជ1͑x ,y ͉͒2+0͉H ជ1͑x ,y ͉͒2͔d x d y 20͉H 1,0͉2gd,͑16͒where H 1,0is the amplitude of the incident plane wavemagnetic field,Hជ1͑inc ͒͑x ,y ͒=͑H 1,0e i ͑/c ͒x +c.c.͒z ˆ.͑17͒The results are shown in Fig.2.In both cases the maxi-mum energy confinement is observed for a value of thegap of 18nm.We note that the TS wires exhibit a higher value of the relative energy inside the gap region.As an example,in Figs.3(a)–3(d)we depict the behavior of themodulus of the FF electric field y -and x -components nor-malized with respect to the input electric field modulus for the TS and gap values of 18and 38nm.We note the strong confinement inside the gap region.We obtain simi-lar behavior if RS wires are considered.Then we use the linear solutions for the FF fields to calculate the nonlin-ear source terms as described in the previous section.Fi-nally we calculate the generated SH field by the numeri-cal integration of Eq.(13)and the NSCS as defined in Eq.(15)for different values of the air gap between wires.Re-sults are shown in Fig.2.We note that the NSCS follows the FF energy inside the gap behavior for both cases of TS and RS wires.This means that,as expected,most of the SHG is due to FF localization effects in the gap region.TS wires provide better performances with respect to the RS[x10-20cm 2/W][x10-20cm 2/W][x10-20cm 2/W]x (µm)x (µm)x (µm)y (µm )y (µm )y (µm )(a)(b)(c)Fig.7.(Color online)Differential scattering cross section (left column)and magnetic field (ampere/meter)(snapshots in time,right column)calculated for different configurations obtained by varying the value of B (see inset of Fig.1),from (a)45to (b)245and (c)345nm.wires according to the higher values of energy stored in-side the gap.Nevertheless,the contrast between resonant ͑g =18nm ͒and non-resonant emissions is higher for the RS wires.This suggests that further optimizations of the TS scheme are possible (for example,by changing the ra-tio between the major and the minor bases B /d ),in order to increase the SHG efficiency.A deeper look at the SH far field emission pattern re-veals interesting features:Figs.4and 5present the polar plots of the differential nonlinear cross section as a func-tion of the angle of emission.We note that emission pat-terns for the TS and RS wires are very different.Also,sig-nificant differences emerge by varying the size of the gap between wires.In particular,we note that for a gap of 18nm the TS wires exhibit the typical quadrupolar emission related to the quadrupole contribution of the nonlinear re-sponse of the metal.On the other hand,for RS wires the emission pattern is reminiscent of an electric dipole oscil-lating along the x axis.Further details can be obtained by analyzing the magnetic field:In Figs.6(a)and 6(b)we plot the generated SH magnetic field,z -component,for both TS and RS wires with an air gap of 18nm.We note that TS and RS wire emissions correspond to quadrupole and dipole emitters,respectively.Moreover,the RS show aresonant behavior due to the fact that the total length is close to 3/22,with 2being the SH wavelength.The modification of the characteristics of emitted radia-tion by multipolar sources close to nanostructured metal surfaces was investigated in [60]where interesting appli-cations to single molecule spectroscopy and imaging are envisioned.Here we stress the point that the source of the SH field inside the gap is coupled to the far field through the wires and,depending on their shapes,the surface plasmon resonances can affect the field emission.For this purpose we performed a set of calculations keeping the values of h =300nm,d =145nm,and g =18nm constants and by varying the value of B .This way we can explore the transition regime from the dipolar emission to the quadrupolar regime.Results are shown in Fig.7.Figures 7(a)–7(c)describe the differential scattering cross section (left side)and the real part of the magnetic field (right side)corresponding to values of B equal to 45,245,and 345nm,respectively.We note that,by increasing the value of B ,the symmetry of the emission pattern gradu-ally shifts from dipolar [Figs.7(a)and 6(b)]to quadrupole-like in intensity but still of dipolar symmetry if we con-sider the field wave fronts [Figs.7(b)and 7(c)]to be purely quadrupolar [Fig.6(a)].Looking at the differential NSCS,we note that the efficiency of the SH generation re-mains of the same order of magnitude.These results il-lustrate that the generation process is mainly driven by the field confinement in the space between the two wires.We note that starting from Fig.7(b),the emission at the four corners of the gap area has a quadrupolar pattern.Nevertheless,the resonant behavior of the coupled wires is responsible for the dipolar emission symmetry.This can be ascertained by analyzing the case of Fig.7(c):The gen-erated field is out of resonance so that the building up of the dipolar mode is inhibited.Finally,the emission pat-tern has the typical quadrupolar symmetry for higher val-ues of B as shown in Fig.6(b).We also plot the modulus of the Poynting vector in the space near the wires for gap values of 18and 38nm for TS [Figs.8(a)and 8(b)]and RS [Figs.9(a)and 9(b)]wires corresponding to the cases discussed in Figs.4and 5.The near field emission patterns show very interesting fea-tures.In particular,for the resonant case ͑gap=18nm ͒,a sub-wavelength hot spot forms.These features could be used for nanoillumination of single dots or for molecule detection and analysis.4.CONCLUSIONSWe numerically studied the second harmonic generation (SHG)from coupled gold nanowires and highlighted the relevance of the distance between wires and the sections of the SH intensity and emission patterns.Our results suggest that the overall SHG is related to the electromag-netic (e.m.)energy per unit length stored in the gap area between the wires,although finer optimizations of the shape and size of the wires need a more accurate investi-gation and goes beyond this work.We also emphasized the effect of the shape of the wire sections and the possi-bility to obtain dipolar and/or quadrupolar emission pat-terns.Different emission symmetry properties are not re-lated to the dipolar and quadrupolar nonlinearresponsesFig.8.(Color online)Modulus of the Poynting vector ͑W/m 2͒outside the TS wires:air gaps of (a)18and (b)38nm.of metals but are determined by the interaction of the nonlinear sources with the plasmon resonance of the me-tallic wires.The numerical method we developed provides an accurate,efficient,and reliable tool for tailoring the emission of the SHG from nanoparticles and nanowires and can be applied to the study of the nonlinear response of a single molecule trapped between the two metallic wires.By introducing a periodic Green’s function formal-ism it is possible to consider periodic arrangements of wires to study nonlinear properties of metamaterials and periodic metallo-dielectric structures.This feature,as well as the extension to a full three-dimensional code,will be the subject for future work.ACKNOWLEDGMENTSWe thank M.Scalora for discussions and comparisons of different numerical tools for the evaluation of the SHG.We also thank rciprete,A.Belardini,and M.Braccini for stimulating and fruitful discussions.REFERENCES1. E.Adler,“Nonlinear optical frequency polarization in a dielectric,”Phys.Rev.134,A728–A733(1964).2.S.Jha,“Theory of optical harmonic generation at a metal surface,”Phys.Rev.140,A2020–A2030(1965).3. F.Brown,R. E.Parks,and A.M.Sleeper,“Nonlinear optical reflection from a metallic boundary,”Phys.Rev.Lett.14,1029–1031(1965).4.N.Bloembergen,R.K.Chang,S.S.Jha,and C.H.Lee,“Optical second-harmonic generation in reflection from media with inversion symmetry,”Phys.Rev.174,813–822(1968).5.N.Bloembergen,R.K.Chang,and C.H.Lee,“Second-harmonic generation of light in reflection from media with inversion symmetry,”Phys.Rev.Lett.16,986–989(1966).6. C.K.Chen,A.R.B.de Castro,and Y.R.Shen,“Coherent second-harmonic generation by counterpropagating surface plasmons,”Opt.Lett.4,393–394(1979).7.G.I.Stegeman,J.J.Burke,and D.G.Hall,“Nonlinear optics of long range surface plasmons,”Appl.Phys.Lett.41,906–908(1982).8.J. E.Sipe and G.I.Stegeman,in Nonlinear Optical Response of Metal Surfaces ,Surface Polaritons,V .M.Agranovich and ls,eds.(North-Holland,1982),pp.661–701.9.M.Corvi and L.W.Schaich,“Hydrodynamic-model calculation of second-harmonic generation at a metal surface,”Phys.Rev.B 33,3688–3695(1986).10. A.Liebsch,Electronic Excitations at Metal Surfaces (Plenum,1997),Chap 5.11.T.F.Heinz,in Second-Order Nonlinear Optical Effects at Surfaces and Interfaces ,Review Chapter in Nonlinear Surface Electromagnetic Phenomena,H.Ponath and G.Stegeman,eds.(Elsevier,1991),p.353.12.J.C.Quail and H.J.Simon,“Second harmonic generation from silver and aluminium films in total internal reflection,”Phys.Rev.B.31,4900–4905(1985).13.H.J.Simon,C.Huang,J.C.Quail,and Z.Chen,“Second-harmonic generation with surface plasmons from a silvered quartz grating,”Phys.Rev.B 38,7408–7414(1988).14.G. A.Farias and A. A.Maradudin,“Second harmonic generation in reflection from a metallic grating,”Phys.Rev.B 30,3002–3015(1984).15.R.Reinisch and M.Nevière,“Electromagnetic theory of diffraction in nonlinear optics and surface-enhanced nonlinear optical effects,”Phys.Rev.B 28,1870–1885(1983).16.K.Li,M.I.Stockman,and D.J.Bergman,“Enhanced second harmonic generation in a self-similar chain of metal nanospheres,”Phys.Rev.B 72,153401(2005).17.S.Ducourtieux,S.Grésillon,A.C.Boccara,J.C.Rivoal,X.Quelin,C.Desmarest,P .Gadenne,V .P .Drachev,W.D.Bragg,V .P .Safonov,V . A.Podolskiy,Z. C.Ying,R.L.Armstrong,and V .M.Shalaev,“Percolation and fractal composites:optical studies,”J.Nonlinear Opt.Phys.Mater.9,105–116(2000).18.V .M.Shalaev,ed.,Optical Properties of Nanostructured Random Media (Springer,2002).19.B.K.Canfield,S.Kujala,K.Jefimovs,J.Turunen,and M.Kauranen,“Linear and nonlinear optical responses influenced by broken symmetry in an array of gold nanoparticles,”Opt.Express 12,5418–5423(2004).20.J.I.Dadap,H.B.de Aguiar,and S.Roke,“Nonlinear light scattering from clusters and single particles,”J.Chem.Phys.130,214710(2009).21.H.E.Katz,G.Scheller,T.M.Putvinski,M.L.Schilling,W.Fig.9.(Color online)Modulus of the Poynting vector ͑W/m 2͒outside the RS wires:air gaps of (a)18and (b)38nm.。
(推荐)二次谐波的产生及其解

§2.3 二次谐波的产生及其解二次谐波或倍频是一种很重要二阶非线性光学效应,在实践中有广泛的应用,如Nd:YAG 激光器的基频光(1.064μm)倍频成0.532m 绿光,或继续将0.532μm 激光倍频到0.266μm 紫外区域。
本节从二阶非线性耦合波方程出发,求解出产生的二次谐波光强小信号解,并解释相位匹配对二次谐波产生的影响。
2.3.1 二次谐波的产生设基频波的频率为1ω,复振幅为1E u r;二次谐波的频率为()2212ωωω=,复振幅2E u r 。
由基频波在介质中极化产生的二阶极化强度()2P u r ,辐射出的二次谐波场()3E z u r所满足的非线性极化耦合波方程()()()222202222ik z d E z i P z e dz k μω-= u ru r (2.3.1-1) ()()()()()1222110211;,ik z P z z E z e εχωωω=-:E u r u r u r t (2.3.1-2)注意简并度1D =,212ωω=()()()()()()()()()22202110211221112112;,2;,i kzi kzd E z i E z E ze dz k i E z E z e n cμωεχωωωωχωωω∆∆=-:=-:u ru r u r t u r u r t (2.3.1-3)波矢失配量,122k k k ∆=-(2.3.1-4)写成单位矢量(光波的偏振方向或电场的振动方向)和标量的乘积形式333E a E =u r r,基频光场可能有两种偏振方向,即'1111,a E a E r r ,两种偏振方向可以是相互平行也可以是相互垂直,并有331a a ⋅=r r()()()()'222121121112;,i kz dE z i a a a E z e dz n c ωχωωω∆⎡⎤=⋅-::⎢⎥⎣⎦r r r t (2.3.1-5)基频波与产生的二次谐波耦合产生的极化场强度()21P u r ,辐射出基频光场满足的非线性极化耦合波方程。
二次谐波转换中的衍射和离散效应

第12卷 第2期强激光与粒子束V o l.12,N o.2 2000年4月H IGH POW ER LA SER AND PA R T I CL E B EAM S A p r.,2000 文章编号: 1001—4322(2000)02—0201—03二次谐波转换中的衍射和离散效应Ξ何钰娟1,2, 魏晓峰2, 蔡邦维1, 马 驰2, 张 彬1, 袁 静2(1.四川大学光电系,成都610064;2.中物院核物理与化学研究所激光技术工程部,四川绵阳919-219信箱,621900) 摘 要: 以 类匹配KD P晶体中高斯光束的二倍频为例,对衍射和离散两种因素对二次谐波转换效率的影响进行了数值模拟计算。
结果表明,衍射的影响非常小。
当入射超高斯光束口径非常小时,离散效应的存在将大大降低倍频转换效率。
随着入射光束口径的增大,离散效应的影响相应地减小,甚至可以忽略。
关键词: 离散; 衍射; 高斯光束; 二次谐波转换 中图分类号: O43711 文献标识码: A 由于I CF靶对短波长激光的吸收比对长波长激光的吸收更有效[1],因此,用KD P晶体进行的高功率钕玻璃激光辐射的高效二、三次谐波转换成为I CF研究中的重要内容之一。
自从1961年F ranken等首次实现激光的二次谐波转换以来,人们对此已作了广泛的研究[1~3];但是迄今为止,国内的谐波转换理论大都只限于理想情况下的谐波转换过程,而忽略了实际谐波转换中存在的各种各样影响谐波转换的因素(如光束的衍射和离散效应、晶体体损耗和端面反射、群速度色散、B 积分效应,晶体表面粗糙度等等)。
针对以上的情况,本文采用 类匹配的KD P晶体,分别对衍射和离散两种因素对二次谐波转换效率的影响作了数值模拟计算。
1 物理模型 对于包括衍射、离散两种因素的谐波转换过程可以用如下的非线性耦合波方程来描述。
1.1 耦合波方程组[1] 对于 类匹配二倍频,耦合波方程组为52H 5x2+52H5y2+2in e(2Ξ)2Ξc5H5z+Θ2Ξ(Η)5H5y=-(2Ξ)22c2ςθF2exp(-i∃kz)(1) 52F5x2+52F5y2+2in o(Ξ)Ξc5F5z=-Ξ2c2ςθF3H exp(i∃kz)(2)其中,F、H分别是1Ξ光和2Ξ光的复振幅;Θ2Ξ(Η)=1n e(2Ξ,Η)5n e(2Ξ,Η),是离散因子;ςθ=-ςsinΗsin2<,ς是非线性极化系数;∃k=2Ξc[n e(2Ξ,Η)-n o(Ξ)],是位相失配量;Η是光传播方向z与光轴的夹角; <=45°,是方位角;n e(2Ξ,Η)是e光的折射率;n o(Ξ)是o光的折射率。
整流电路的谐波和功率因数

2 3
电流基波和各次谐波有效值分别为
6 Id I1 = π I = 6 I , n nπ d
n = 6k ±1 k =1 2,3,L , ,
电流中仅含6k±1(k为正整数)次谐波 各次谐波有效值与谐波次数成反比,且与基波有效值的比值
为谐波次数的倒数
λ1 = cos1 = cosα
I 所以,功率因数为 = 2 2 cosα ≈ 0.9cosα λ =νλ1 = 1 cos1 I π
二,R,L负载时交流侧谐波和功率因数分析 2. 三相桥式全控整流 电路
1)阻感负载,忽略换相 过程和电流脉动,直流 电感L为足够大 2)以 α =30°为例,交流 侧电压和电流波形如图 中的ua 和ia 波形所示. 此时,电流为正负半周 各120°的方波,其有效 值与直流电流的关系为
3)变压器二次侧电流谐波分析:
1 1 1 1 ω ia = Id[sin ωt sin 5ωt sin 7ωt + sin 11 t+ sin 13ωt L ] π 5 7 11 13 2 3 2 3 k 1 = Id sin ωt + Id ∑ (1) sin nωt= 2I1 sin ωt + ∑(1)k 2In sin nωt π π n=6k±1 n n=6k ±1
In HRI n = ×100% I1
电流谐波总畸变率THDi(Total Harmonic distortion)定义为
THDi =
Ih ×100% I1
二,谐波和无功功率分析基础
2. 功率因数
(1) 正弦电路中的情况
电路的有功功率 有功功率就是其平均功率: 有功功率 平均功率
1 2π P= ∫0 uid (ωt) =UI cos 2π 视在功率为电压,电流有效值的乘积,即S=UI 视在功率
倍频效应(二次谐波) (2)

倍频现象的理论解释线性光学效应的特点:出射光强与入射光强成正比;不同频率的光波之间没有相互作用,没有相互作用包括不能交换能量;效应来源于介质中与作用光场成正比的线性极化。
非线性光学效应的特点:出射光强不与入射光强成正比(例如成平方或者三次方的关系);不同频率光波之间存在相互作用,可以交换能量;效应来源于介质中与作用光场不成正比的非线性极化。
倍频效应是非线性的光学效应,当介质在光波电场的作用下时,会产生极化。
设P是光场E在介质中产生的极化强度。
对于线性光学过程:P=对于非线性光学过程:P可以展开为E的幂级数:...…其中:,分别为线性以及2,3,…,n阶非线性极化强度。
为n阶极化率。
正是这些非线性极化项的出现,导致了各种非线性光学效应的产生。
而倍频效应,就是由其中的二阶极化强度所导致产生的:设光场是频率为、波矢为的单色波,即:则中将出现项:该极化项的出现,可以看作介质中存在频率为的振荡电偶极矩,它的辐射便可能产生频率为2的倍频光。
介质产生非线性极化:从微观上看,非线性是由原子、分子非谐性所造成的。
物质受强光作用后,电子发生位移x,具有位能V(x),对于无对称中心晶体,与电子位移+x和-x相对应的位能并不相等,即:V(+X)≠V(-x),因而位能函数V(x)应该包含奇次项:相应的,电子与核之间的恢复力为:当D时,正位移引起的恢复力大于负位移引起的恢复力。
如果作用在电子上的电场力是正的,则会引起一个相对较小的位移;反之,则会引起一个相对较大的位移。
那么,电场正方向产生的极化强度就比电场反方向产生的极化强度小。
这就使得非线性极化的产生。
有了非线性极化,那么,一个给定的强光波电场对应的极化波就是一个正峰值b比负峰值b’小的非线性极化波:而根据傅里叶分析,任何一个非正弦的周期函数,都可以分解成角频率为、2、3、…的正弦波。
所以强光波电场在介质中引起的非线性极化波,可以分解成为角频率为的基频极化波,角频率为的二次谐频极化波,以及常值分量等成分。
Comsol经典实例012:高斯波速的二次谐波产生
Comsol经典实例012: 高斯波速的二次谐波产生激光系统是现代电子技术中的一个重要应用领域。
激光束的生成方法有很多种, 这些方法有个共同点: 波长由受激发射决定, 而受激发射取决于材料参数。
通常很难生成具有短波长的激光。
但是, 如果使用非线性材料, 就有可能产生频率为激光频率数倍的谐波。
通过使用二阶非线性材料可生成波长为基频光束波长一半的相干光。
本案例演示了如何设置非线性材料属性, 通过瞬态波仿真产生二次谐波。
模型中一束波长为1.06μm的激光聚焦于非线性晶体, 光束的腰部落于晶体内。
在激光的传播过程中, 大部分能量都集中在传播轴附近, 在求解麦克斯韦方程时可以近轴近似, 由此获得高斯波束。
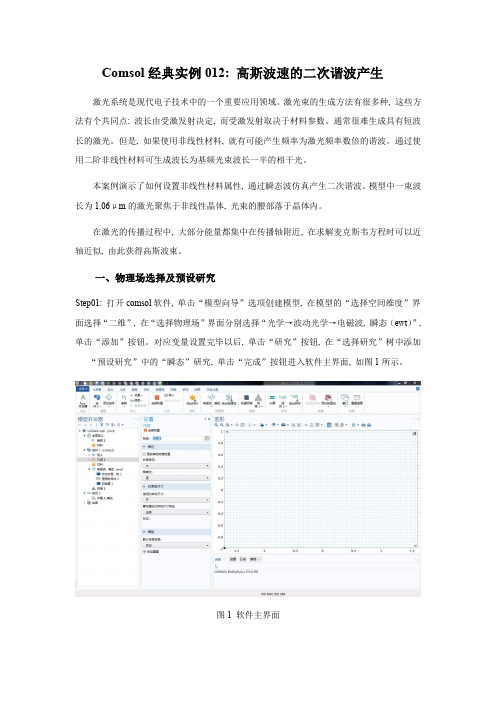
一、物理场选择及预设研究Step01: 打开comsol软件, 单击“模型向导”选项创建模型, 在模型的“选择空间维度”界面选择“二维”, 在“选择物理场”界面分别选择“光学→波动光学→电磁波, 瞬态(ewt)”, 单击“添加”按钮。
对应变量设置完毕以后, 单击“研究”按钮, 在“选择研究”树中添加“预设研究”中的“瞬态”研究, 单击“完成”按钮进入软件主界面, 如图1所示。
图1 软件主界面二、全局定义1.参数Step02: 参数设置。
在模型开发器窗口的全局定义节点下, 单击“参数”子节点, 在“参数”设置窗口中, 定位到“参数”栏, 输入如图2所示的参数。
图2 设置全局参数2.解析定义Step03: 在“主屏幕”工具栏中单击“函数”选项, 在下拉菜单中选择“全局→解析”选项。
单击“解析1”子节点, 在“解析”设置窗口中, 定位到“函数名称”栏, 在文本输入框中输入“w”;定位到“定义”栏, 在“表达式”文本输入框中输入“w0*sqrt(1+(x/x)^2)”;定位到“单位”栏, 在“变元”文本输入框中输入“m”, 在“函数”在文本输入框中输入“m”,如图3所示。
Step04:在“主屏幕”工具栏中单击“函数”选项, 在下拉菜单中选择“全局→解析”选项。
