昆明理工大学材料力学A80学时习题册
昆明理工大学工程力学习题册答案

第一章 静力学基础二、填空题–F sin α; F cos α; F cos α; F sin α ; 0 ;F ; F sin α; F cos α。
1200, 0 。
外 内 。
约束 ; 相反 ; 主动 主动 。
3 ,力偶矩代数值相等(力偶矩的大小相等,转向相同) 。
三、选择题(c) 。
3.2 A 。
D 。
D 。
3.5 A 。
B 。
3.7 C 。
四、计算题(emmKN F M ⋅-=18030)(mmKN F M ⋅=-=3.2815325)(20mmKN F M ⋅-=25210.)(01=)(F M x m N F M y ⋅-=501)(01=)(F M z mN F M x ⋅-=2252)(mN F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M z ⋅=2253)(五 、受力图(a(b(cB B(a(b(cP 2(dmN F M x ⋅=2253)(mN F M y ⋅-=2253)((1) 小球(2) 大球PPACB (a(1) AC 杆(2) CB 杆(1) AC 段梁 (2) CD 段梁(1) AB 杆(2) CD 杆P第二章 力系的简化一、是非判断题 ( × ) ( ∨ )( × )二、填空题 平衡 。
(1) CD 杆 (2) AB 杆(i(1) 滑轮D (2) AB 杆(jDDF PPAB KIBCF AY AX IY IX KY CID,DF ,BCF 'IX 'I Y DCE,EFFCF ABE.EF AY AX BY BX CA O,C F ,A Y ,AXY 0X ACP FBCPA Y AX B Y BX CY CX CX 'CY 'CX 'CY 'DY分布载荷图形的面积 , 合力矩定理 , 分布载荷图形的形心 。
平行力系合力的作用点 ; 物体合重力的作用点 ; 物体的几何中心 。
昆明理工大学工程力学习题册答案

昆明理工大学工程力学习题册答案一、选择题1. 在平面力系中,力对点的矩的常用单位是(A)A. N·mB. N/mC. N·sD. N·m^2答案:A2. 平面汇交力系的平衡方程是(C)A. Fx=0, Fy=0, M=0B. Fx=0, Fy=0C. Fx=0, Fy=0, M=0(其中M为力矩)D. Fx=0, Fy=0, M≠0答案:C3. 在空间力系中,力的投影与原力的关系是(B)A. 投影等于原力B. 投影小于等于原力C. 投影大于原力D. 投影与原力无关答案:B二、填空题1. 力对物体的作用效果包括______和______。
答案:使物体发生形变,使物体产生运动2. 平面力系中的合力可以用______和______来确定。
答案:力的大小,力的方向3. 在平面力系中,力矩的计算公式为______。
答案:M=F×d(其中F为力,d为力臂)三、计算题1. 已知:力F=10N,作用点距离A点4cm,求力F 对A点的力矩。
解:力矩的计算公式为M=F×d,其中d为力臂,即作用点到力作用点的距离。
本题中,d=4cm=0.04m。
所以,M=10N×0.04m=0.4N·m。
答案:0.4N·m2. 平面汇交力系中,已知F1=20N,F2=30N,F3=40N,求该力系的合力。
解:首先,将F1和F2合成,得到合力F12。
F12的大小为F12=√(F1^2+F2^2+2F1F2cosθ),其中θ为F1和F2之间的夹角。
假设F1和F2之间的夹角为60°,则F12=√(20^2+30^2+2×20×30×cos60°)=√(400+900+ 1200×0.5)=√(2000)=44.72N。
然后,将F12与F3合成,得到合力F123。
F123的大小为F123=√(F12^2+F3^2+2F12F3cosθ),其中θ为F12和F3之间的夹角。
昆明理工大学材料力知识学习题册14概念标准答案

^`第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( × ) 1.2 内力只作用在杆件截面的形心处。
( × ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( × ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ∨ ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ∨ ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ∨ ) 1.7 同一截面上正应力σ与切应力τ必相互垂直。
( ∨ ) 1.8 同一截面上各点的正应力σ必定大小相等,方向相同。
( × ) 1.9 同一截面上各点的切应力τ必相互平行。
( × ) 1.10 应变分为正应变ε和切应变γ。
( ∨ ) 1.11 应变为无量纲量。
( ∨ ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ∨ ) 1.13 若物体内各点的应变均为零,则物体无位移。
( × ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( ∨ ) 1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( ∨ )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( × )二、填空题1.1 材料力学主要研究 受力后发生的以及由此产生1.2 拉伸或压缩的受力特征是 ,变形特征是 。
B题1.15图题1.16图外力的合力作用线通过杆轴线 杆件^`1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
材料力学-习题集(含答案)

《材料力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《材料力学》(编号为06001)共有单选题,计算题,判断题,作图题等多种试题类型,其中,本习题集中有[判断题]等试题类型未进入。
一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示,在P力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上,各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中,图所示杆是轴向拉伸杆。
(A) (B)(C) (D)P5.图示拉杆承受轴向拉力P的作用,斜截面m-m的面积为A,则σ=P/A为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后,消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍,则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示,已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面,则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等,正负号相同(B)绝对值相等,正负号不同(C)绝对值不等,正负号相同(D)绝对值不等,正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内;(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上,各个截面上的。
昆明理工大学材料力学A80学时练习册1-13章答案

第一章 绪论一、是非判断题1.1 ( × );1.2 ( × );1.3 ( × );1.4 ( ∨ );1.5 ( ∨ );1.6 ( ∨ ) 1.7 ( ∨ );1.8 ( × );1.9 ( × );1.10 ( ∨ );1.11 ( ∨ )1.12 ( ∨ );1.13 ( × );1.14 ( ∨ );1.15 ( ∨ ) ;1.16 ( × )二、填空题1.1 杆件 变形 , 应力,应变 。
1.2 外力的合力作用线通过杆轴线 , 沿杆轴线伸长或缩短 。
1.3 受一对等值,反向,作沿剪切面发生相对错动 , 沿剪切面发生相对错动 。
1.4 外力偶作用面垂直杆轴线 。
任意二横截面发生绕杆轴线的相对转动 。
1.5 外力作用线垂直杆轴线,外力偶作用面通过杆轴线 , 梁轴线由直线变为曲线 。
1.6 包含两种或两种以上基本变形的组合 。
1.7 强度 , 刚度 , 稳定性 。
1.8 强度 , 刚度 , 稳定性 。
1.9 连续性 , 均匀性 , 各向同性 。
1.10 连续性假设 。
应力 、 应变 变形等 。
1.11 拉伸 , 压缩 , 弯曲 。
1.12 2α ; α-β ; 0 。
三、选择题1.1 1 。
1.2 C 。
1.3 C 。
四、计算题1.10=A X ∑=0X FF S =⇒∑=0Y 0=-F Y A F Y A =⇒∑=0A M 0=--FL M FL M -=⇒y x解:1. 求A 端的反力: 2. 求1-1截面的内力: ∑=0Y 0=F F S-∑=01C M 02=--/FL M 2/FL M -=⇒X A M1.2第二章 拉伸、压缩与剪切一、是非判断题2.1 ( × );2.2 ( ×);2.3 ( × );2.4. ( ×);2.5 ( × );2.6 ( × ) 2.7 ( × );2.9 ( × );2.10 ( × );2.11( × );2.12( ∨ )二、填空题2.1 2.22.3 最大工作应力σmax 不超过许用应力[σ] , 强度校核 ; 截面设计 ; 确定许可载荷 。
昆明理工大学工程力学练习册80
第一章 静力学基础一、是非判断题1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( ) 1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( ) 1.4 力的可传性只适用于刚体,不适用于变形体。
( ) 1.5 两点受力的构件都是二力杆。
( ) 1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( ) 1.7 力的平行四边形法则只适用于刚体。
( ) 1.8 凡矢量都可以应用平行四边形法则合成。
( ) 1.9 只要物体平衡,都能应用加减平衡力系公理。
( ) 1.10 凡是平衡力系,它的作用效果都等于零。
( ) 1.11 合力总是比分力大。
( ) 1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( ) 1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ) 1.14 当软绳受两个等值反向的压力时,可以平衡。
( ) 1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ) 1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( )1.17 凡是两端用铰链连接的直杆都是二力杆。
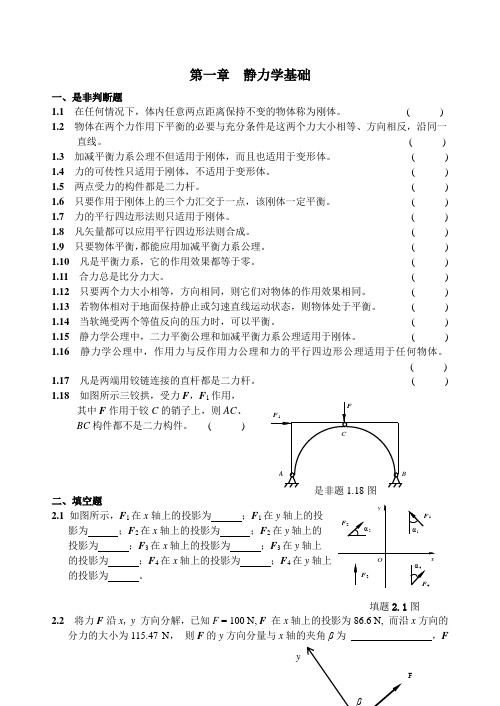
( ) 1.18 如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、 BC 构件都不是二力构件。
( )二、填空题 2.1 如图所示,F 1在x 轴上的投影为 ;F 1在y 轴上的投影为 ;F 2在x 轴上的投影为 ;F 2在y 轴上的投影为 ;F 3在x 轴上的投影为 ;F 3在y 轴上的投影为 ;F 4在x 轴上的投影为 ;F 4在y 轴上 的投影为 。
2.2 将力F 沿x , y 方向分解,已知F = 100 N, F 在x 轴上的投影为86.6 N, 而沿x 方向的分力的大小为115.47 N , 则F 的y 方向分量与x 轴的夹角β为 ,F填题2.1图βFy在y 轴上的投影为 。
《材料力学》习题册附答案

F12312练习 1 绪论及基本概念1-1 是非题(1) 材料力学是研究构件承载能力的一门学科。
( 是 )(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
(是)(3) 构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
( 是 ) (4) 应力是内力分布集度。
(是 )(5) 材料力学主要研究构件弹性范围内的小变形问题。
(是 ) (6) 若物体产生位移,则必定同时产生变形。
(非 ) (7) 各向同性假设认为,材料沿各个方向具有相同的变形。
(F ) (8) 均匀性假设认为,材料内部各点的力学性质是相同的。
(是)(9) 根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(非) (10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(非 )1-2 填空题(1) 根据材料的主要性质对材料作如下三个基本假设:连续性假设、均匀性假设 、各向同性假设 。
(2) 工程中的强度 ,是指构件抵抗破坏的能力; 刚度 ,是指构件抵抗变形的能力。
(3) 保证构件正常或安全工作的基本要求包括 强度 , 刚度 ,和 稳定性三个方面。
3(4) 图示构件中,杆 1 发生 拉伸 变形,杆 2 发生 压缩 变形,杆 3 发生 弯曲 变形。
(5) 认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为 连续性假设。
根据这一假设构件的应力,应变和位移就可以用坐标的 连续 函数来表示。
(6) 图示结构中,杆 1 发生 弯曲变形,构件 2发生 剪切 变形,杆件 3 发生 弯曲与轴向压缩组合。
变形。
(7) 解除外力后,能完全消失的变形称为 弹性变形,不能消失而残余的的那部分变形称为 塑性变形 。
(8) 根据 小变形 条件,可以认为构件的变形远 小于 其原始尺寸。
1-3选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
材料力学A80学时练习册

。
2.10 塑性材料与脆性材料的判别标准是
。
2.11 图示销钉连接中,2t2> t1,销钉的切应力 τ=
,销钉的最大挤压应力 σbs=
。
2.12 螺栓受拉力 F 作用,尺寸如图。若螺栓材料的拉伸许用应力为[σ],许用切应力为[τ],按
拉伸与剪切等强度设计,螺栓杆直径 d 与螺栓头高度 h 的比值应取 d/ h =
(
)
1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变
形、横截面或任意截面的普遍情况。
(
)
1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
(
)
1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
(
)
1.7 同一截面上正应力 σ 与切应力 τ 必相互垂直。
F
8
材料力学 练习册 80 学时
昆明理工大学
专业
学号
姓名
日期
评分
2.4 一阶梯形立柱受力如图示, F1=120kN, F2=60kN。柱的上、中、下三段的横截面面积
分别是 A1 = 2 ×104 mm2 , A2 = 2.4 ×104 mm2 , A3 = 4 ×104 mm2 ,试求:(1)各段横截
(C)铝杆的应力和变形均大于钢杆;
(D) 铝杆的应力和变形均小于钢杆。
正确答案是
2.4 在弹性范围内尺寸相同的低碳钢和铸铁拉伸试件,在同样载荷作用下,低碳钢试件的弹
性变形为δ1 ,铸铁的弹性变形为δ 2 ,则δ1 与 δ 2 的关系是;
(A)δ1 > δ 2 ; (B)δ1 < δ 2 ; (C)δ1 = δ 2 ; (D)不能确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴ [P ] = 57 .6 kN
]
2.9 * 图示组合柱由钢和铸铁制成,组合柱横截面是边长为 2b 的正方形,钢和铸铁各占横截 面的一半( b × 2b )。载荷 FP 通过刚性板沿铅垂方向加在组合柱上。已知钢和铸铁的弹 性模量分别为 Es=196GPa,Ei=98.OGPa。今欲使刚性板保持水平位置,试求加力点的位 置 x 应为多少。
l Δ =
AC
1
2.3 卧式拉床的油缸内径 D=186 mm,活塞杆直径 d1=65 mm,材料为 20 Cr 并经过热处理,[σ]
杆
=130 MPa。缸盖由六个 M20 的螺栓与缸体连接,M20 螺栓内径 d=17.3 mm,材料为 35 钢, 经
热处理后[σ]螺=110MPa。试按活塞杆和螺栓的强度确定最大油压 p。
解:欲使刚性板保持水平位置,FNs 和 FNi 应分
A
别作 用在各自截面的形心(如图)且△ls=△li
∑Y =
F Ns + F Ni − F P = 0
(a)
0 为 1 次超静定问题;
y
⇒ FNs FNi
由 Δsl = l Es Δ F Ns
F Ni = Ei
i
⇒
F Ns l F l = Ni E sA E iA
y
∴
FNs = ⋅⋅⋅ = ⇒ FNs = 0.1FNw 代入(a)式得: FNw 0.1 FNs = 0.071F FNw = 0.717F
σ w =
[σ FNs 0.071F ≤] 钢 σ = s = As As [σ
2.8 图示的杆件结构中 1、2 杆为木制,3、4 A1 = A2 = 4000 mm 2 ,3、4 杆的横截面面积
解:设木材承受的轴力为 FNw,每个等边角钢承受的轴力为 FNs
3
F
F
(a ) FNw + 4FNs − F = 0 F l 0 FNwl l= s 由 Δw ⇒ = Ns Ew Aw Es As Δl
∑Y =
为 1 次超静定问题
⇒
FNs Es As = FNw Ew Aw
查附录ⅡP393,每个等边角钢的横截面积 As =3.086cm2 。 FNw 4FNs
第一章
绪论
四、计算题 1.2 求图示结构中 1-1 和 2-2 截面的内力,并在分离体上画出内力的方向。
a a 2a
F
解:取 ABC 杆为研究对象:
A
2a 2
1 1
2
C
B
2 2
F
B
∑M
B
A
= 0
’
x1
1-1 截面:
FN2
a a 2a
F
y x
a 2a
∑ X= 0 ∑Y = 0 ∑M =
C1
⇒ FB = 2 2F ⇒ FN 1 = 2F ⇒ F s1 = −F ⇒ M1 = −aF
1
F2
1
F2
2
F2 3
2
F2 3
∴σ1 = A1 = −6MPa FN 1 A2 = σ 2 = FN = MPa −9MPa σ 10 −3 3 = N3 A F
杆内横截面上的最大正应力(压应力)为:
2
σc max = σ 2
= 10MPa
作用在中段(2-2)横截面上。
2
2.5 在图示简易吊车中,BC 为钢杆,AB 为木杆。木杆 AB 横截面积 A1=100 cm2,许用应力 [σ]1=7MPa;钢杆 BC 的横截面积 A2=6 cm2,许用拉应力[σ]2=160MPa。试求许可吊重 F。
2.6 图示拉杆沿斜面 m-n 由两部分胶合而成。设在胶合面上许用拉应力[σ]=100 MPa,许用 剪应力[τ]=50 MPa。并设胶合面的强度控制杆件的拉力。试问:为使杆件承受最大拉力
F,α角的值应为多少?若杆件横截面积为 4cm2,并规定α≤600,试确定许可载荷 F。
m F F
σ
α
2 = σ cos α
[τ]
= 1.5MPa ,试计算为使基础不被剪坏所需的厚度
F
四个可能的剪切面如图中红线所示 对下层基础如图:
F
y
⇒ q= F
a b t q a t t
b2
q
F
qa 2 + FS − F = 0 2 a2 Y ⇒ FS = F − qa = (1− 2 b )F 由(2.23)式:
∑
= 0
Fs
⇒ t≥
FBC
C
解:取整体为研究对象;
钢
∑Y =
30
o
⇒ FBC = 2 F
⇒ FAB = 3F 3FBC 2 =
FAB
A
木
B x F
0
y
∑X =
0
⇒ F≤ 40.4kN
σ = σ =
AB
FNAB ≤ A1 FNB AC 2
BC
[σ ≤ ]1[σ ]2
⇒ F ≤= 48kN
∴ [F ] = 40 .4 kN
解:Q FNBC = FNCD = F p 2 = 100 kN
FNAB = F p1 + F p 2 = 150 kN
由构件的胡克定律(2.13)式:
FNABlAB FNBClBC = 2.95 mm + ES A ES A FNCDlCD = ΔAD = AC + CD = AC + EC A l Δl Δl Δl 5.29mm
F F
FF F
d ≥ 0.0326 m = 32 .6 mm
2.11 木榫接头如图所示。a = b =12 cm,h =35 cm,c =4.5 cm。F = 40 kN。试求接头的剪切、 挤压应力。 F F
F F τ = s = = A hb
40 ×10 = 0.952 MPa 3 0.35 × 0.12 = 7.407MPa
D0
FS
m
m
解:假想沿 n-n 面切开,取右半部分为 研究对象并作左视图。由对称性可知, 每个螺栓所受的切力相等,设为 Fs。
o
∑
0
截面 n-n
M0=
FS×
= 0
D0 × − 4 m 2
= 1.25kN
n
⇒ F S =
m 200 = 2D0 2 × 0.08
F 4 Fs 4 × ∴τ = s = = 1250 A πd 2 π × 0.012
F
F
由(2.24)式: 40 Fbs F σ = = 3 bs = ×10 Abs cb 0.045 × 0.12
5
2.12
图示凸缘联轴节传递的力偶矩为 m =200N· m,凸缘之间由四只螺栓联接,螺栓内径 d
=10mm,对称地分布在 D0 = 80mm 的圆周上。如螺栓的剪切许用应力[τ]= 60 MPa,试校核螺 栓的剪切强度。 n m
FNw 0.717F ≤ = Aw Aw
木
⇒ F≤
A0.717 [σ ] ⇒ F ≤ 钢 s = 697.5kN 0.071 A
杆∴为 钢F 制
[σ 木 ] =1046kN
w
]
[
]
、2 杆的横截面面积 =,
A
3
已 知.5 k1N 2 = 800 mm ;1、2 杆的许用应力 =6A4 97
[σ]木=20MPa,3、4 杆的许用应力[σ]钢=120MPa,试求结构的许用载荷[P].
= 2
⇒ F Ns = 2 F Ni
FNi = FP 3
代入(a)式得:
FNs = 2FP 3
∑M
0
A
=
b
FNs + (b + 2
b
)FNi − xFP = 0 2
⇒
b2FP 3b F + ( ) P − xF P = 0 2 3 2 3 b b ⇒ x= 5b ⇒ + − x= 0 3 2 6
2.10 试校核图示连接销钉的剪切强度。已知 F =100kN,销钉直径 d =30 mm,材料的许用剪 应力[τ]= 60 MPa。若强度不够,应改用多大直径的销钉?
= 15 .92 MPa ≤ 60 MPa
[τ ]
=
2.13* 图示正方形截面的混凝土柱,其横截面边长为 200mm,浇注在混凝土基础上。基础 分两层,每层厚为 t,上层基础为边长 a=300mm 的正方形混凝土板。下层基础为边长 b=800mm 的正方形混凝土板。柱承受轴向压力 F=200kN,假定地基对混凝土板的反力 均匀分布,混凝土的许用剪应力 t 值。
∑
= 0
FS 1 (1 − 0 2 .2 2 a ) = ≤ τ A 0.2 t × F = [τ (1 − 0.2 4 2 a2 t 0.0926 m = 92 .6 ⇒ ≥ = ] )F mm 0.2 × 4 × 取 t = 96mm [τ ]
第章
四、计算题 3.2
扭转
图示一阶梯形传动轴,上面装有三个皮带轮。主动轮Ⅰ输出的功率为
2m
解:设各杆均受拉;先取销钉 B 为研究对象;
C
FN4
C θ B P
y
D
4
FN3 FN2
FN1
FN3
5m
3m
2 A 3 1B
∑Y = 0 X= ∑
P
⇒ FN 3 = 5P 3 ⇒ FN1 = − 4P = 4P 3 = −P N2
0 3 取销钉 C 为研究对象;
x
θ4m
∑X =
0 0
YNw = )max = FN1 = −4P 3 (F ∴ ∑
A 450 B
C
F
2-2 截面:
0
M1 FN1 FS1
