1、晶体特征和空间点阵
合集下载
晶体结构——精选推荐
第七章晶体结构第一节晶体的点阵结构一、晶体及其特性晶体是原子（离子、分子）或基团（分子片段）在空间按一定规律周期性重复地排列构成的固体物质。
晶体中原子或基团的排列具有三维空间的周期性，这是晶体结构的最基本的特征，它使晶体具有下列共同的性质：(1)自发的形成多面体外形晶体在生长过程中自发的形成晶面，晶面相交成为晶棱，晶棱会聚成顶点，从而出现具有几何多面体外形的特点。
晶体在理想环境中应长成凸多面体。
其晶面数（F）、晶棱数（E）、顶点数（V）相互之间的关系符合公式：F+V=E+2 八面体有8个面，12条棱，6个顶点，并且在晶体形成过程中，各晶面生长的速度是不同的，这对晶体的多面体外形有很大影响：生长速度快的晶面在晶体生长的时候，相对变小，甚至消失，生长速度小的晶面在晶体生长过程中相对增大。
这就是布拉维法则。
(2)均匀性：晶体中原子周期性的排布，由于周期极小，故一块晶体各部分的宏观性质完全相同。
如密度、化学组成等。
(3)各向异性：由于晶体内部三维的结构基元在不同方向上原子、分子的排列与取向不同，故晶体在不同方向的性质各不相同。
如石墨晶体在与它的层状结构中各层相平行方向上的电导率约为与各层相垂直方向上电导率的410倍。
(4)晶体有明显确定的熔点二、晶体的同素异构由于形成环境不同，同一种原子或基团形成的晶体，可能存在不同的晶体结构，这种现象称为晶体的同素异构。
如：金刚石、石墨和C60是碳的同素异形体。
三、晶体的点阵结构理论1、基本概念（1）点阵：伸展的聚乙烯分子具有一维周期性，重复单位为2个C原子，4个H 原子。
如果我们不管其重复单位的内容，将它抽象成几何学上的点，那么这些点在空间的排布就能表示晶体结构中原子的排布规律。
这些没有大小、没有质量、不可分辨的点在空间排布形成的图形称为点阵。
构成点阵的点称为点阵点。
点阵点所代表的重复单位的具体内容称为结构基元。
用点阵来研究晶体的几何结构的理论称为点阵理论。
（2）直线点阵：根据晶体结构的周期性，将沿着晶棱方向周期的重复排列的结构单元，抽象出一组分布在同一直线上等距离的点列，称直线点阵。
晶体的点阵结构和晶体的性质和分析原理
2、点阵 （3）空间点阵：阵点分布在三维空间的点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （1）点阵结构：
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （3）点阵中各要素与晶体中各要素的关系
一、晶体的点阵结构
3、晶胞 （1）晶胞：点阵结构中划分出的平行六面体叫晶胞，它代表晶体 结构的基本重复单位。
一、晶体的点阵结构
3、晶胞 （1）晶胞：点阵结构中划分出的平行六面体叫晶胞，它代表晶体 结构的基本重复单位。
（1） 点群通常采用熊夫利记号(Schöflies Symbol) （2） 点群的国际符号(International Symbol)表示
国际符号是用晶体在某特定方向上的对称元素来表示32 观对称性及32点群
3、晶体的宏观对称类型—32点群
二、晶体的宏观对称性及32点群
2、点阵
晶体宏观特征是由于晶体内原子分子等微粒在空间的周 期排列的结果，可抽象成为一个数学上的点阵。
一、晶体的点阵结构
2、晶体具有点阵结构 （1）点阵结构：
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
一、晶体的点阵结构
2、晶体具有点阵结构 （2）从晶体点阵结构中抽象出点阵
一、晶体的点阵结构
2、晶体具有点阵结构 （3）点阵中各要素与晶体中各要素的关系
一、晶体的点阵结构
3、晶胞 （1）晶胞：点阵结构中划分出的平行六面体叫晶胞，它代表晶体 结构的基本重复单位。
一、晶体的点阵结构
3、晶胞 （1）晶胞：点阵结构中划分出的平行六面体叫晶胞，它代表晶体 结构的基本重复单位。
（1） 点群通常采用熊夫利记号(Schöflies Symbol) （2） 点群的国际符号(International Symbol)表示
国际符号是用晶体在某特定方向上的对称元素来表示32 观对称性及32点群
3、晶体的宏观对称类型—32点群
二、晶体的宏观对称性及32点群
2、点阵
晶体宏观特征是由于晶体内原子分子等微粒在空间的周 期排列的结果，可抽象成为一个数学上的点阵。
材料化学 (第一章 晶体的特性与点阵结构)
m, n, p = 0, ±1, ±2, ...
3.点阵及其基本性质
（1）. 点阵: 连结任意两点所得向量进行平移后能够复原 的一组点称为点阵.
X X
不是点阵
不是点阵
点阵
（2）. 点阵的二个必要条件: (a)点数无限多 (b)各点所处环境完全相同
(3). 点阵与平移群的关系:
(a)连结任意两点阵点所得向量必属于平移群. (b)属于平移群的任一向量的一端落在任一点阵点时, 其另一端必落在此 点阵中另一点阵点上.
第一章 晶体的特性与点阵结构
第一部分 晶体学基础
一 晶体学发展的历史
二 晶体的特性
三 晶体结构 （一）晶体结构的周期性 （二）点阵结构与点阵 （三）晶体结构参数
第二部分 晶体中的对称
一 晶体的宏观对称性 二 晶体的微观对称性
第一部分 晶体学基础
一、晶体学发展的历史
西汉，《韩诗外传》“凡草木花多五出，雪花独六出”
六方素格子、正方素格子、矩形素格子、矩形带心格子和平行四边形格子。
空间点阵的七种类型、十四种型式
(1) 七种类型 — 7种对称类型对应7个晶系
•
•
一维平移群表示为：Tm ma
m = 0, ±1, ±2, ……
2.二维点阵结构与平面点阵 1)实例 (a) NaCl晶体中平行于某一晶面的一层离子 结构:
结构基元: 点阵:
(b)石墨晶体中一层C原子
结构： x
结构基元： 点阵：
2)平面格子 连结平面点阵中各点阵点所得平面网格.
2)平面格子 连结平面点阵中各点阵点所得平面网格.
4.晶胞参数与原子坐标参数
(1).晶胞(Unit cell)
空间格子将晶体结构截成的一个个大小、形状相等，包含等同 内容的基本单位。
晶体学第一章晶胞与点阵
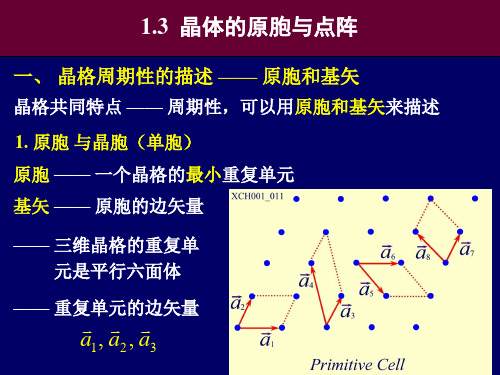
原胞体积
V
a1
(a2
a3)
a3
—— 原胞中只包含一个原子
2) 面心立方晶格
立方体的顶点到三个近邻的面心引三个基矢
基矢
a1
a 2
(
j
k)
a a2 2 (k i )
a3
a 2
(i
j)
原胞体积
V a1 (a2 a3)
1 a3 4
—— 原胞中只包含一个原子
3) 体心立方晶格
钛酸钡原胞可以取 作简单立方体 包含： 3个不等价的O原子 1个Ba原子 1个Ti原子 —— 共五个原子
六角密排晶格的原胞基矢选取
—— 一个原胞中包含A层 和B层原子各一个
—— 共两个原子
二、晶格周期性的描述 —— 布拉菲点阵，点阵平移矢量
1. 点阵（lattice），也叫空间点阵（space lattice）
以点（阵点或结点）代替晶体的基元（晶体的最小组成 单元，由原子、离子或分子构成），得到的描述晶体中质 点排列周期性的数学图形。
阵点（lattice point）—— 环境和性质完全相同； 基元（basis）—— 晶体的最小组成单元。
点阵 + 基元
晶体结构
简单晶格 —— 基元为单原子 复式晶格 —— 基元由多个原子、离子或分子组成
Rl ra l1a1 l2a2 l3a3, 1, 2, 3
原胞中各种等价原子之间的相对位移 例如： 金刚石晶格 —— 碳1位置 —— 碳2位置
对角线位移
B
可以用1，l2，l3的取值可以囊括所有的阵点
由
确定的晶体空间点阵 —— 布拉菲点阵
（布拉菲格子）
2）面网
晶面
， —— 基本平移矢量（基矢），l1， l2 取整数
材料科学基础 第1章 晶体学基础
人类使用的材料中大多为晶态(Crystalline)，包括单晶、 多晶、微晶和液晶等。那么什么是晶体？ 晶体有何特点？
金刚石
Nacl
水晶
CaF2
MoS2
闪锌矿
高分辨率电镜－High Resolution Electron Microscopy (HREM)
The surface of a gold specimen, was taken with a atomic force microscope (AFM). Individual atoms for this (111) crystallographic surface plane are resolved.
底心正方和简单 正方点阵的关系
例：结构对性能的影响－Sn 1850 in Russia. The winter that year was particularly cold, and record low temperatures persisted for extended periods of time. The uniforms of some Russian soldiers had tin buttons, many of which crumbled due to these extreme cold conditions, as did also many of the tin church organ pipes. This problem came to be known as the “tin disease.”
组平行的晶面应当包含点阵所有的阵点。 ● ２、晶向(lattice or crystal directions) 通过两阵点之间的直线。 ● ３、定量表示晶面和晶向的意义 各向异性，结构分析（需要表征晶体结构内部的不同
金刚石
Nacl
水晶
CaF2
MoS2
闪锌矿
高分辨率电镜－High Resolution Electron Microscopy (HREM)
The surface of a gold specimen, was taken with a atomic force microscope (AFM). Individual atoms for this (111) crystallographic surface plane are resolved.
底心正方和简单 正方点阵的关系
例：结构对性能的影响－Sn 1850 in Russia. The winter that year was particularly cold, and record low temperatures persisted for extended periods of time. The uniforms of some Russian soldiers had tin buttons, many of which crumbled due to these extreme cold conditions, as did also many of the tin church organ pipes. This problem came to be known as the “tin disease.”
组平行的晶面应当包含点阵所有的阵点。 ● ２、晶向(lattice or crystal directions) 通过两阵点之间的直线。 ● ３、定量表示晶面和晶向的意义 各向异性，结构分析（需要表征晶体结构内部的不同
2021-2022学年陕西师范大学奥赛辅导资料之晶体点阵理论基础
(注意: 坐标与原点选择有关)
32
结构基元:A-B (每个晶胞中有4个结构基元)
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
平面点阵指标（h*k*l* )
（h*k*l*)=(010)
33
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
Lab of Theoretical & Computational Chemistry
晶胞及晶胞的两个基本要素
晶胞的定义
晶体结构的基本重复单元称为晶胞. （能够反映晶体内部结构特征的最小单位）
整个晶体就是晶胞在三维空间周期性地重复排列堆砌而成. 晶 胞对应于正当格子只有7种形状. 一定是平行六面体.
正当单位的划分原则：
1. 对称性尽可能高 2. 含点阵点尽可能少
15
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
平面格子净含点阵点数：顶点为1/4；棱心为1/2；格内为1. 平面正当格子只有 4 种形状 5 种型式
b a
b ab ab源自 az就是分数坐标，它们永远不会大于1.
29
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
立方面心晶胞净含4个原子，所以写出4组坐标即可:
所有顶点原子： 0，0，0 (前)后面心原子： 0，1/2，1/2 左(右)面心原子： 1/2，0，1/2 (上)下面心原子： 1/2，1/2，0
32
结构基元:A-B (每个晶胞中有4个结构基元)
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
平面点阵指标（h*k*l* )
（h*k*l*)=(010)
33
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
Lab of Theoretical & Computational Chemistry
晶胞及晶胞的两个基本要素
晶胞的定义
晶体结构的基本重复单元称为晶胞. （能够反映晶体内部结构特征的最小单位）
整个晶体就是晶胞在三维空间周期性地重复排列堆砌而成. 晶 胞对应于正当格子只有7种形状. 一定是平行六面体.
正当单位的划分原则：
1. 对称性尽可能高 2. 含点阵点尽可能少
15
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
平面格子净含点阵点数：顶点为1/4；棱心为1/2；格内为1. 平面正当格子只有 4 种形状 5 种型式
b a
b ab ab源自 az就是分数坐标，它们永远不会大于1.
29
理论与计算化学实验室
Lab of Theoretical & Computational Chemistry
立方面心晶胞净含4个原子，所以写出4组坐标即可:
所有顶点原子： 0，0，0 (前)后面心原子： 0，1/2，1/2 左(右)面心原子： 1/2，0，1/2 (上)下面心原子： 1/2，1/2，0
材料科学基础,第2章,材料中的晶体结构
晶面间距与晶面指数的关系： 晶面间距是现代测试中一个重要的
参数。在简单点阵中，通过晶面指数 （hkl）可以方便地计算出相互平行的一 组晶面之间的距离d。
晶系 晶面间距
立方
1 h2 k 2 l2
d2
a2
正方
1
h2 k2
l2
d2
a2
c2
六方
( ) 1
4 h2 hk k 2
l2
d2
3
a2
c2
1.晶面、晶向及其表征
1）晶面 （1）定义：晶体点阵在任何方向上可分
解为相互平行的结点平面，称为晶面。 （2）特征： 晶面上的结点在空间构成一个二维点阵。 同一取向上的晶面，不仅相互平行、间
距相等，而且结点的分布也相同。 不同取向的结点平面其特征各异。
（3）晶面指数：
结晶学中经常用（hkl）来表示一组平 行晶面，称为晶面指数。
不同方向的直线组，其质点分布不尽相同。
（3）晶向指数： 用[uvw]来表示。 其 中 u 、 v 、 w 三 个 数 字 是 晶 向 矢 量
在参考坐标系X、Y、Z轴上的矢量 分量经等比例化简而得出。
晶向指数求法：
①确定坐标系； ②过坐标原点，作直线与待求晶向
平行； ③在该直线上任取一点，并确定该
{110}晶面族
Z
（011）
（110） （011） （101）
（101）
Y （110）
X
2）晶向：
（1）定义：
点阵可在任何方向上分解为相互平行的直线组， 结点等距离地分布在直线上。位于一条直线上 的结点构成一个晶向。
（2）特征：
同一直线组中的各直线，其结点分布完全相同， 故其中任何一直线，可作为直线组的代表。
潘金生材料科学基础(修订版)知识点笔记课后答案
第1章晶体学基础1.1复习笔记一、空间点阵1.晶体特征和空间点阵概述（1）晶体特征晶体的一个基本特征是具有周期性。
（2）空间点阵空间点阵是指用来描述晶体中原子或原子集团排列的周期性规律的在空间有规律分布的几何点的集合。
2.晶胞、晶系和点阵类型（1）晶胞①晶胞的定义空间点阵可以看成是由最小的单元——平行六面体沿三维方向重复堆积（或平移）而成。
这样的平行六面体称为晶胞。
②点阵常数a．描述晶胞的大小：三条棱的长度a，b和c；b．描述晶胞的形状：棱之间的夹角α，β和γ。
③选取晶胞的条件a.能反映点阵的周期性；b．能反映点阵的对称性；c．晶胞的体积最小。
（2）晶系按照晶胞的大小和形状的特点，或按照6个点阵常数之间的关系和特点，可以将各种晶体归为7种晶系。
表1-1 7种晶系（3）点阵类型①简单三斜点阵（如图1-1（1）所示）；②简单单斜点阵（如图1-1（2）所示）；③底心单斜点阵（如图1-1（3）所示）；④简单斜方点阵（如图1-1（4）所示）；⑤底心斜方点阵（如图1-1（5）所示）；⑥体心斜方点阵（如图1-1（6）所示）；⑦面心斜方点阵（如图1-1（7）所示）；⑧六方点阵（如图1-1（8）所示）；⑨菱方点阵（三角点阵）（如图1-1（9）所示）；⑩简单正方（或四方）点阵（如图1-1（10）所示）；⑪体心正方（或四方）点阵（如图1-1（11）所示）；⑫简单立方点阵（如图1-1（12）所示）；⑬体心立方点阵（如图1-1（13）所示）；⑭面心立方点阵（如图1-1（14）所示）。
图1-1 14种空间点阵（4）布拉维点阵与复式点阵①布拉维点阵：由等同点构成的点阵；②复式点阵：由几个布拉维点阵穿插而成的复杂点阵。
二、晶面指数和晶向指数1.晶面指数和晶向指数（1）晶面指数将截距的倒数化成三个互质的整数h，k，l，则（hkl）称为待标晶面的晶面指数。
（2）晶向指数将晶向上除原点以外的任一点的坐标x，y，z化成互质整数u，v，w，得到晶向指数[uvw]。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
的研究更加完美，而且逐渐走出大块晶体的范畴，开始了对微细材料
和无序固体的开发和利用，新发现、新进展接踵而来：
第 22 页
二、固体物理学发展历程
英国曼彻斯特大学科学家安德烈·海姆和康斯坦丁·诺沃
肖洛夫以石墨烯研究获得２０１０年度诺贝尔物理学奖
康斯坦丁·诺沃肖洛夫 1974年8月月出生
安德烈·海姆 1958年10月出生
因其电阻率极低，电子迁移的速度极快，因此被期待可用来发展更薄、导
例如液氦、液晶、熔盐、液态金属、电解液、玻璃、凝胶等。
第 14 页
二、固体物理学发展历程
凝聚态物理学研究对象日益扩展，更为复杂。一方面传统的固体物理 各个分支如金属物理、半导体物理、 磁学、低温物理和电介质物理等的研 究更深入，各分支之间的联系更趋密切； 另一方面许多新的分支不断涌现，如强关联电子体系物理学、无序体
第 23 页
二、固体物理学发展历程
人们常见的石墨是由一层层以蜂窝状有序排列的平面碳原子堆叠而形
成的，石墨的层间作用力较弱，很容易互相剥离，形成薄薄的石墨片。当把 石墨片剥成单层之后，这种只有一个碳原子厚度的单层就是石墨烯。
石墨烯是由碳六元环组成的两维(2D)周期蜂窝状点阵结构, 它可以翘曲成 零维(0D)的富勒烯(fullerene),卷成一维(1D)的碳纳米管(carbon nano-tube,
《固体物理学》教学课件
高
峰
合肥工业大学 电子科学与应用物理学院 2015年09月
第1页
绪论
一、固体物理学主要研究内容 二、固体物理学发展历程--为什么要学习固体物理学 三、固体物理学课程特点 四、固体物理学的研究方法 五、固体物理学参考教材
第2页
一、固体物理学主要研究内容
基本任务
研究固体物质的物理性质、微观结构、构成物质
第 13 页
二、固体物理学发展历程
凝聚态物理学是从微观角度出发，研究由大量粒子（原子、分子、 离子、电子）组成的凝聚态的结构、动力学过程及其与宏观物理性质之 间的联系的一门学科。 凝聚态物理是以固体物理为基础的外向延拓。
凝聚态物理的研究对象除晶体、非晶体与准晶体等固相物质外还包
括从稠密气体、液体以及介于液态和固态之间的各类居间凝聚相。
二、固体物理学发展历程
摩尔定律：是由英特尔（Intel）创始人之一戈登·摩尔（Gordon Moore）提 出来的。其内容为：集成电路上可容纳的晶体管数目，约每隔18个月便会增加一倍， 性能也将提升一倍，当价格不变时；或者说，每一美元所能买到的电脑性能，将每 隔18个月翻两倍以上。这一定律揭示了信息技术进步的速度。
子、分子种类有关，
固体的性质更主要的：是和这些原子采用什么方式结合在一起，他们的空 电子的运动 状态有关。
第6页
一、固体物理学主要研究内容 例如：
性质完全不同的无定形碳、石墨和金刚石都是由相同的碳原子组成的，
是碳原子空间排列和结合方式的差异带来了其物理性质的极端不同。 因此只有通过对固体微观结构和组成固体微观粒子之间的相互作用及 运动机制的研究才能理解固体的性质。 美国贝尔电话实验室两次Noble物理奖获得者 巴丁(J.Bardeen)说： 固体物理学依据物质的电子结构和原子结构 来了解固体的各种性质。
系物理学、准晶物理学、介观物理与团簇物理等。从而使凝聚态物理学成
为当前物理学中最重要的分支学科之一
第 15 页
二、固体物理学发展历程
例： J·巴丁、W·H·布拉顿和W·B·肖克利 1947年12月23日发现了半导 体晶体管的放大效应，由此带来的巨大影响是固体物理和高科技发展关 系的最典型的说明。
第 16 页
1853
由实验确定了金属导热性和导电性之间关系的经验定律
1905
荷兰物理学家、数学家洛伦兹 (Hendrik Antoon Lorentz， 1853—1928)
建立了自由电子的经典统计理论，能够解释上述经验定律， 但无法说明常温下金属电子气对比热容贡献甚小的原因；因 关于磁对辐射现象影响的研究，他与塞曼分享了1902年度的 诺贝尔物理学奖金。
的各种粒子的运动形态及其相互关系的科学。它是物 理学中内容极丰富、应用极广泛的分支学科
从微观上去解释固体材料的宏观性质，并阐明其规律性
第3页
一、固体物理学主要研究内容
基本问题主要有以下七个方面： 固体是由什么原子组成？
它们是怎样排列和结合的？
这种结构是如何形成的？
在特定的固体中，电子和原子取什么样的具体的运动形态？
CNT)或者堆垛成三维(3D)的石墨(graphite), 因此石墨烯是构成其他石墨材料
的基本单元。
第 24 页
二、固体物理学发展历程 石墨烯 石墨烯是已知的世上最薄、最坚硬的纳米材料，它几乎是完全透明的，只吸收 2.3%的光；导热系数高达5300 W/m·K，高于碳纳米管和金刚石，常温下其电 子迁移率超过15000 cm2/V·s，又比纳米碳管或硅晶体高，而电阻率只约10-8 Ω ·cm，比铜或银更低，为世上电阻率最小的材料。
德国科学家皮特-克鲁伯格Peter Grünberg
电阻变化的特殊效应
所谓巨磁阻效应 :是指磁性材料的电阻率在有外磁场作用时较之 无外磁场作用时存在巨大变化的现象
第 18 页
二、固体物理学发展历程
该层 磁化方向固定
巨磁阻是一种量子力学效应，它产生于层状的磁性薄膜结构。 这种结构是由铁磁材料和非铁磁材料薄层交替叠合而成。当铁磁层的 磁矩相互平行时，载流子与自旋有关的散射最小，材料有最小的电阻。当 铁磁层的磁矩为反平行时，与自旋有关的散射最强，材料的电阻最大。
凝聚态物理)是二十一世纪物理学中发展最快、影响最大、领域最广的一门
学科。 固体物理本身是微电子技术、光电子学技术、能源技术、材料科学等 技术学科的基础，也由于固体物理学科内在的因素，固体物理的研究论文 已占物理学中研究论文三分之一以上。
同时，固体物理学的成就和实验手段对化学物理、催化学科、信息科
学、生命科学、地学等的影响日益增长，正在形成新的交叉领域。
二、固体物理学发展历程
但是，即便是巨磁阻这项叱诧风云的技术，发展到现在也已经接近了 极限，硬盘容量的提升必须寻求新的技术。目前行业公认的下一代技术是 “垂直磁记录”技术，即“记录位”的S/N两极的连线垂直于盘片，而在此
之前的技术都属于“水平磁记录”技术。
第 21 页
二、固体物理学发展历程
上世纪六七十年代后，固体物理的发展更为迅速，不但晶体材料
它的宏观性质和内部的微观运动形态有什么联系？ 各种固体有哪些可能的应用？ 探索设计和制备新的固体，研究其特性，开发其应用。
第4页
一、固体物理学主要研究内容
固体物理学和普通物理不同
它的重点不在于描述固体的宏观物理性质
而是去阐明和理解固体的宏观性质
解释形成这些性质的原因，从而找出控制、利用、改善这些性质的方
第7页
一、固体物理学主要研究内容
第8页
二、固体物理学发展历程
年 份 学 发现者 内 容 科 1669 意大利科学家斯丹诺(Nicolaus 发现了晶面角守恒定律，指出在同一物质的晶体中，相应晶 面之间的夹角是恒定不变的。 Steno) 1784 物 法国科学家阿羽依(Rene Just 理 Hauy) 提出了著名的晶胞学说。根据这一学说，晶胞是构成晶体的 最小单位，晶体是由大量晶胞堆积而成的。
第 19 页
二、固体物理学发展历程
“看看你的计算机硬盘存储能力有多大，就知道他们的贡献有多大了。” 或许我们这才明白，司空见惯的笔记本电脑、MP3、U盘等消费品，居然都 闪烁着耀眼的科学光芒。诺贝尔奖并不总是代表着深奥的理论和艰涩的知 识，它往往就在我们身边，在我们不曾留意的日常生活中。
第 20 页
1931
19471948
巴丁、布喇顿以及肖克 莱
贝尔实验室的科学家巴丁、布喇顿以及肖克莱对晶体的能带 进行了系统的实验和理论的基础研究，同时掌握了高质量半 导体单晶生长和掺杂技术，于1947-1948年发明晶体管
第 12 页
二、固体物理学发展历程 今天可以毫不夸大地说： 已经成为当代科学重要支柱、高科技源泉的固体物理学 ( 严格地说是
第 11 页
固体物理学发展简史
年份 发现者 德国物理学家索末菲 （Arnold Sommerfeld，18681951） 内容 1928 用量子统计求得电子气的比热容和输运现象，解决了经典理 论的困难
1928
瑞士-美国物理学家布洛 分别从不同角度研究了周期场中电子运动的基本特点，为固 赫（Bloch）和法国物理 体电子的能带理论奠定了基础。1928年布洛赫提出了有名的 学家布里渊(Brillouin 布洛赫定理 威耳逊 提出金属和绝缘体相区别的能带模型，并预言介于两者之间 存在半导体，为尔后的半导体的发展提供理论基础
第 17 页
二、固体物理学发展历程
例：1988年发现巨磁电阻效应(GMR)--小硬盘大发现
硬盘技术之父2007年摘得诺贝尔物理学奖
得益于“巨磁电阻”效应这一重大
发现，我们开始能够在笔记本电脑、音 乐播放器、智能手机等安装越来越小的 硬盘中存储海量信息。
法国科学家艾尔伯-费尔Albert Fert
非常弱小的磁性变化就能导致巨大
1890
1914
发现 X射线通过晶体的衍射现象，证实了晶体内部原子周期 性排列的结构，证明了X射线的波动特性
第9页
固体物理学发展简史
年 份 学 发现者 内 容 科 英国物理学家亨利.布拉格Henry Bragg 晶体结构的X射线分析，建立了晶体结构分析的基础。布喇 物 1915 格父子分享了1915年诺贝尔物理学奖。父子两代同获一个诺 理 劳伦斯.布拉格Lawrence 贝尔奖，这在历史上恐怕是绝无仅有的。 Bragg. 德国物理学家维德曼 （GHWiedemann,1826—1899） 和夫兰兹（R.Franz）