国科大有限元作业3
2016年秋国科大有限元作业答案

∴ u(x) = ui +
1
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
图 2: 题图 2
2. 利用梁单元计算以下结构的应力。
解:将此梁划分为两个单元 AB 和 BC 。首先计算节点等效载荷阵列 { } [ ]T P = RyA + FyA RθA + MθA FyB MθB RyC RθC [ ]T = RyA − P /2 RθA − P l/8 −P /2 9P l/8 RyC RθC 计算各个单元刚度矩阵如下 12 6l −12 6l [ ](AB ) 2EI 6l 4l2 −6l 2l2 = 3 K l −12 −6l 12 −6l 2 2 6l 2l −6l 4l
6l 4l2 2EI −12 −6l = 3 l 6l 2l2 0 0
12
6l−126l Nhomakorabea2
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
[ ]AB [ ]AB [ ]AB { }AB ∴ σ =E ε =E B δ [
3
= Ey (6l − 12x)/l
3
有限元作业答案 smartsrh 2016 年秋季中国科学院大学张年梅教授
4. 证明三结点三角形单元的插值函数满足 Ni (xj , yj ) = δij 及 Ni + Nj + Nk = 1
证明: 假设三节点 i、j 、m 逆时针方向编号,不妨考虑横向位移,纵向位移与此同理 β1 β1 1 xi yi u ui xj ym − xm yj yi xm − xi ym xi yj − xj yi i uj = 1 xj yj β2 =⇒ β2 = 1 yj − ym ym − yi yi − yj uj 2∆ β3 β3 1 xm ym um um xm − xj xi − xm xj − xi β x y − x y y x − x y x y − x y u 1 j m m j i m i m i j j i [ ] ] i 1 [ ∴u= 1 x y = ym − yi yi − yj uj β2 2∆ 1 x y yj − ym β3 xm − xj xi − xm xj − xi um x y − x y y x − x y x y − x y j m m j i m i m i j j i [ ] ] 1 [ ∴ Ni Nj Nm = 1 x y yj − ym ym − yi yi − yj 2∆ xm − xj xi − xm xj − xi x y − x y 1 x y m j i i ] j m 1 1 [ det = ∴ Ni (xi , yi ) = 1 xi yi y − y 1 x y j m j j = 1 2∆ 2∆ xm − xj 1 xm ym xj ym − xm yj 1 yj − ym = 0 = Ni (xm , ym ) ∴ Ni (xj , yj ) = 2∆ xm − xj [ ] xj ym − xm yj 1 xi yi yi xm − xi ym xi yj − xj yi 1 x y yj − ym + ym − yi + yi − yj = 1 det 1 xj yj = 1 Ni +Nj +Nm = 2∆ 2∆ xm − xj 1 xm ym xi − xm xj − xi Ni + Nj + Nm = 1 ∴ Ni (xj , yj ) = δij
有限元习题及答案ppt课件

病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
中国科学院大学有限元试题及答案

(1)引入边界条件: v1 0,1 0, v2 0, M 3 m, M 2 0, Y3 0 由后三个方程可求得 2、v3、 3 ,然后把 2、v3、 3 代入前三个方程,求得 Y1、M 1、Y2 。
例1:已知:p,l,EA。求: u 2 , v 2
解:方法1:1)划分单元,给节点编号 2)单元分析 ①单元: 0, cos 1, sin 0
3
p
10
9
7
y
8 5
1
1
解:
6
9
8
x
6
3
7
5
2
2
4
3
题3 图
4
题3图. 三角形结构网 格
(2) d 4,
M B 2(d1 v4 0
4
4
7
15 10
11
3
1
2
6
13 15
题3图
5
9 12 14
答: (2) d=4 , B=2(d+1)=10 (3) u1 u15 v1 v15 0
p 作用。杆件沿 y 轴方向,长为 a 1 m ,截面积 A 0.01m 2 ,
E2 E0 。载荷及约束信息如图示,自重不计。试采用图示的
1个三角形常应变元和1个平面杆元求: (1)结构整体的等效结点力列阵; (2)采用划行划列法引入已知结 点位移,计算出结点1和2的 a 位移; (3)杆件中内力。 i j m 单元2: 1 3 2 单元1: 2 4
答: 在有限单元法中,采用低阶多项式拟合振型。结构的低阶振 型曲线与低阶多项式比较通配,结构的高阶振型曲线与低阶 多项式曲线有着显著的差异。因而,有限元法中求出的低阶 频率和振型是可信的,而所求出的高阶频率和振型误差较大 ,甚至无效。
ansys有限元分析国防科大教程

F N1 F N1 F N0
F
强相对极值
弱相对极值
18
四、泛函的变分
函数 y(x)与另一函数 y( x ) 之差
y y( x ) y ( x )
dy
y
y( x)
y
y( x )
称为函数的变分,δy 是x 的函数 o
3
一、几个典型的变分问题
例2 等周问题。 在平面上,给定长度为 l 的所 有光滑闭曲线中,求一条光滑 闭曲线,使得所围面积最大。 曲线方程
y
l o
t 0 t t1
x x(t ) y y( t )
x
x ( t 0 ) x ( t1 ) y ( t 0 ) y ( t1 )
x1
J J 2 J 3 ...
一次变分 二次变分
J ( Fy y Fy ' y ')dx
x0
x1
1 x1 2 2 J ( Fyy y 2Fyy ' y y ' Fy ' y ' y ' )dx 2! x0
2
20
L y( x ), z ( x )
o
B(x1,y1,z1)
x
dy dz 1 dx dx dx
2
2
问题定义
min L( y( x ), z( x )), ( x, y, z ) 0
9
回顾:
离散(剖分)结构 一、有限元方法的形成
x1 x0
f ( x ) ( x )dx
有限元课后习题答案

有限元课后习题答案1.1有限元法的基本思想和基本步骤是什么首先,将表示结构的连续离散为若干个子域,单元之间通过其边界上的节点连接成组合体。
其次,用每个单元内所假设的近似函数分片地表示求解域内待求的未知厂变量。
步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移。
1.2有限元法有哪些优点和缺点优点:有限元法可以模拟各种几何形状复杂的结构,得出其近似解;通过计算机程序,可以广泛地应用于各种场合;可以从其他CAD软件中导入建好的模型;数学处理比较方便,对复杂形状的结构也能适用;有限元法和优化设计方法相结合,以便发挥各自的优点。
缺点:有限元计算,尤其是复杂问题的分析计算,所耗费的计算时间、内存和磁盘空间等计算资源是相当惊人的。
对无限求解域问题没有较好的处理办法。
1.3有限元法在机械工程中有哪些具体的应用静力学分析模态分析动力学分析热应力分析其他分析2.1杆件结构划分单元的原则是什么?1)杆件的交点一定要取为节点2)阶梯形杆截面变化处一定要取为节点3)支撑点和自由端要取为节点4)集中载荷作用处要取为节点5)欲求位移的点要取为节点6)单元长度不要相差太多2.2简述单元刚度矩阵的性质。
单元刚度矩阵是描述单元节点力与节点位移之间关系的矩阵。
2.3有限元法基本方程中每一项的意义是什么?{Q}---整个结构的节点载荷列阵(包括外载荷、约束力);{}---整个结构的节点位移列阵;[K]---结构的整体刚度矩阵,又称总刚度矩阵。
2.4简述整体刚度矩阵的性质和特点。
对称性奇异性稀疏性主对角上的元素恒为正2.5位移边界条件和载荷边界条件的意义是什么由于刚度矩阵的线性相关性不能得到解,从而引入边界条件。
2.6写出平面刚架问题中单元刚度矩阵的坐标变换式2.7推导平面刚架局部坐标系下的单元刚度矩阵。
2.8简述整体坐标的概念。
单元刚度矩阵的坐标变换式把平面刚架的所有单元在局部坐标系X’O’Y’下的单元刚度矩阵变换到一个统一的坐标系xOy下,这个统一的坐标系xOy称为整体坐标系。
有限元方法例题解答
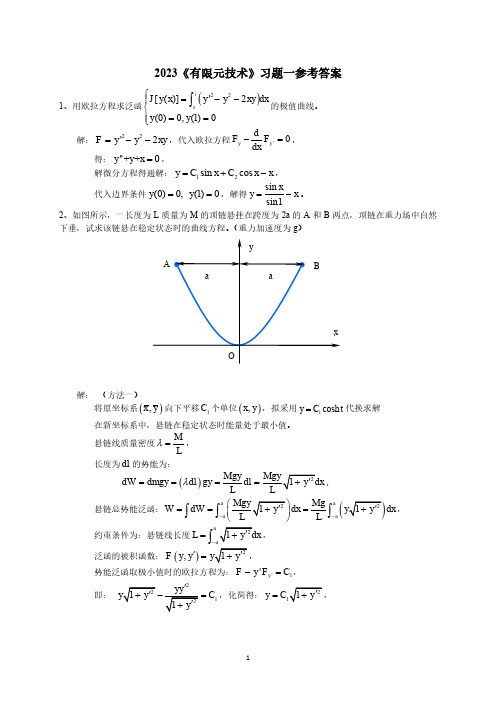
2023《有限元技术》习题一参考答案1、用欧拉方程求泛函()1022[()]'2(0)0,(1)0J y x y y xy dx y y ⎧=--⎪⎨⎪==⎩⎰的极值曲线。
解:22'2F y y xy =--,代入欧拉方程'0y y dF F dx-=, 得:''++0y y x =,解微分方程得通解:12sin cos y C x C x x =+-,代入边界条件(0)0,(1)0y y ==,解得sin sin1xy x =-。
2、如图所示,一长度为L 质量为M 的项链悬挂在跨度为2a 的A 和B 两点,项链在重力场中自然下垂,试求该链悬在稳定状态时的曲线方程。
(重力加速度为g )解: (方法一)将原坐标系(),x y 向下平移1C 个单位(),x y ,拟采用1cosh y C t =代换求解 在新坐标系中,悬链在稳定状态时能量处于最小值。
悬链线质量密度MLλ=, 长度为dl 的势能为:()Mgy dW dmgy dl gy dl L λ====,悬链总势能泛函:(a a a a Mg W dW dx dx L --===⎰⎰⎰,约束条件为:悬链线长度aL -=⎰,泛函的被积函数:(),F y y '=,势能泛函取极小值时的欧拉方程为:'1'y F y F C -=, 即:21C -=,化简得:y C =于是:dx =x =,令1cosh y C t =(在新坐标系下才能作此代换),得:1sinh sinh dy C tdt t =⎧=,代入x =,得112x C dt C t C ==+⎰所以,21x C t C -=,21cosh cosh x C t C ⎛⎫-= ⎪⎝⎭回代1cosh y C t =得:211cosh x C y C C ⎛⎫-= ⎪⎝⎭,曲线关于y 轴对称得20C =,1C由悬链线长度112sinhaaL C C -==⎰给出, 故新坐标系下所求曲线方程为11cosh x y C C ⎛⎫=⎪⎝⎭, 1C 由11sinh 2L aC C =确定。
中国科学院大学张年梅有限元基础复习题(参考)

b
xy
) y 0 dx0
将 xy 的表达式代入,并考虑到 C=0,则有
(3Ax
0
b
2
3 2 2 Bx )dx Ax 3 Bx 2 b 0 Ab Bb 0
而
(
0
b
xy
) y 0 0dx0 自然满足。又由于在这部分边界上没有垂直面力,这就要求 y 在这部分边界上合
d 4 f 1 ( x) 0 , dx 4
这两个方程要求
d 4 f 2 ( x) 0 dx 4
f 2 ( x)Dx3 Ex 2 Jx K
f1 ( x) Ax 3 Bx 2 Cx I ,
代入应力函数表达式,并略去对应力分量无影响的一次项和常数项后,便得
10
y( Ax 3 Bx 2 Cx) Dx3 Ex 2
从而应力分量为
x gxcot 2gycot 2 , y gy , xy gycot
设三角形悬臂梁的长为 l,高为 h,则 tan 。根据力的平衡,固定端对梁的约束反力沿 x 方向 的分量为 0,沿 y 方向的分量为 glh 。因此,所求 x 在这部分边界上合成的主矢应为零, xy 应当 合成为反力 glh 。
可见,所求应力分量满足梁固定端的边界条件。
6.如图所示的矩形截面的长坚柱,密度为 ,在一边侧面上受均布剪力,试求应力分量。 O b x 解:根据结构的特点和受力情况,可以假定纵向纤维互不挤压,即设 x 0 。 由此可知 q
g
x
2 0 y 2
将上式对 y 积分两次,可得如下应力函数表达式
2 2 2 0 x xl dy0 glcot 2gycot dyglhcot gh cot 0 h h
有限元作业试题及答案.doc

2
答:一般选用三角形或四边形单元,在满足一定精度情况,
有限元划分网格的基本原则是:
1、拓朴正确性原则。即单元间是靠单元顶点、或单元边、或单元面连接
2、几何保形原则。即网格划分后,单元的集合为原结构近似
3、特性一致原则。即材料相同,厚度相同
4、单元形状优良原则。单元边、角相差尽可能小
c j二elcm= —a
Ni = l/a2 • a x = x/a
同理可得:Nj二y/a
有限元方法及应用试题
1
答:单元离散(划分、剖分)一单元分析一整体分析
有限元分析的主要步骤主要有:
A结构的离散化
B单元分析。选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力
与位移的关系、根据虚功原理建立节点力与节点位移的关系(单元刚度方程)
C等效节点载荷计算
D整体分析,建立整体刚度方程
7、图示三角形ijni为等边三角形单元,边长为1,单位面积材料密度位P,集 中力F垂直作用于nij边的中点,集度为q的均布载荷垂直作用于im边。写出三 角形单元的节点载荷向量。
q:移到m, i点F:移到m, j点重力:移到m, I, j点
要证{8}=0
只需证,Nm = 0
Nm= 1/2A (am+bmx +cmy)
(d)平面三角形单元,29个节点,38个自由度
4、什么是等参数单元?。
如果坐标变换和位移插值采用相同的节点,并且单元的形状变换函数与位移插值的形函
数一样,则称这种变换为等参变换,这样的单元称为等参单元。
5பைடு நூலகம்
v(x, y)=
答:不能取这样的位移模式,因为在平面三节点三角形单元中,位移模式应该是呈线性的。
