小学人教版数学六年级下册课件:《圆柱的体积》教学课件
合集下载
六年级数学下册课件3.1.3圆柱的体积人教版共20张PPT
答:这个圆柱的体积是785立方厘米
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
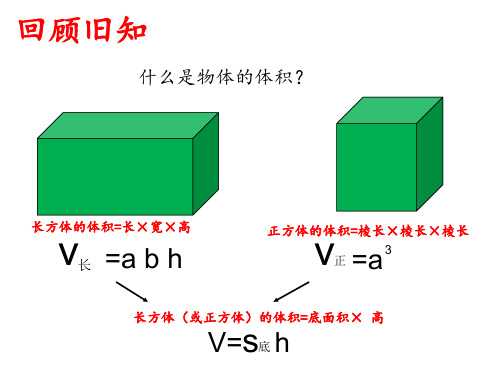
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
分享收获
这节课我收获 了……
这节课我知道 了……
0.9米=90厘米
V=Sh
=75×90 =6750(立方厘米) 答:它的体积是6750立方厘米。
解决问题
2、一根圆柱形的木料,横截面的半径是5厘米, 长是150厘米。这根木料的体积是多少立方厘米?
3.14×5²×150
=3.14×25×150
150cm
=78.5×150
=11775(cm³)
5cm
回顾旧知
什么是物体的体积?
长方体的体积=长×宽×高
v长 =a b h
正方体的体积=棱长×棱长×棱长
v正 =a3
长方体(或正方体)的体积=底面积× 高
V=s底 h
怎样求水泥 柱的体积呢?
下面长方体、正方体和圆柱的底面积都相等,高 也相等
想一想:谁和谁的体积相等?为什高么? 猜一猜:圆柱的体积和长方体、正方体的体积相等吗?
S=π r 2
r
πr
S=πr ×r =π r 2
自主探究
以小组为单位,结合手中的学具,探究圆柱的体 积
温馨提示: 1、圆柱体可以转化成已经学过的那种立体图形? 2、观察转化后的立体图形与原来的圆柱体有什么 关系?
如果把底面平均分的份数越多,结果会怎样呢?
把圆柱的底面平均分的份数越多,切拼 成的立体图形越接近长方体。
答:这根木料的体积是11775 cm³
解决问题
3、李家庄挖了一口圆柱形水井,地面 以下的井深10m,底面直径为1m。挖出 的土有多少立方米?
3.14 ×(1 ÷2)² ×10 =3.14 ×0.5² ×10 =3.14 ×0.25 ×10 =0.785 ×10 =7.85(m³)
人教版数学六年级下册 圆柱的体积课件(44张PPT)

=3.14×16×25
=1256(cm^3)
=1256(ml)
答:瓶子的容积是1256ml。
解:减少的表面积是两个底面面积 底面面积:25.12÷2=12.56(cm3)
底面半径为:
12.56÷3.14÷2=2(cm)
原圆柱的体积:
3.14×22×(20÷2)=125.6(cm3)
答:原来每个圆柱的体积为125.6cm3 。
答:这个圆柱的表面积是301.44cm2;体积是401.92cm3.
例7. 一个圆柱体底面周长和高相等。如果高缩短 2厘米,表面积就减少6.28平方厘米, 这个圆柱 体的体积是多少?
减少的6.28平方厘米 表面积是哪一块呢?
24cm
6.28平方厘米
C=6.28÷ 2=3.14(厘米) r=3.14÷ 3.14÷ 2=0.5(厘米) V=0.52× 3.14× 3.14=2.4649(立方厘米) 答:这个圆柱体的体积是2.4649立方厘米。
502.4 ml>498ml
答:能装下这袋奶。
例2. 若圆柱体的侧面展开后是一个边长为12.56分米正方形,求
这个圆柱的体积。
边长
r=12.56÷ 3.14÷ 2=2(分米12.)56厘米 S底=22× 3.14=12.56(平方分米) V=12.56× 12.56=157.7536(立方分米)
12.56分米
12.56 分米
答:这个圆柱的体积是157.7536立方分米。 “侧面展开 图是正方形”说明 什么呢?
例3.一个圆柱形粮囤,从里面量底面半径是2.5米,高是2米。如 果每立方米稻谷约重545千克,这个粮囤装的稻谷大约有多少千 克?
粮屯体积: 3.14×2.52×2 =3.14×6.25×2 =39.25(m2)
人教版六年级下册数学上课课件. 圆柱的体积优秀课件

能力提升
圆柱的体积=底面积×高 两个圆柱的高相同,底面积不同,哪个圆柱的 体积大? 高相同时,底面积越大的体积越大。
高相同时,体积之比等于( 底面积之比)
人教版六年级下册数学上课课件. 圆柱的体积优秀课件
甲
乙
人教版六年级下册数学上课课件. 圆柱的体积优秀课件
判断
圆柱的体积=底面积×高
(1)一个圆柱的高扩大为原来的2倍,底面积不
由v r 2h得
1升 1000 毫升
3.14 32 11
932 .58 1000
3.14 9 11 310.8( 6 cm3) 310.86(ml)
答:这些果汁够明明 和客人每人一杯。
新知应用
一根圆柱形木料底面半径是0.2m,长5m.如果 做一张课桌用去木料0.02m3。这根木料最多 能做多少张课桌?
人教版 六年级数学下册 第3单元 圆柱与圆锥
3.1.3 圆柱的体积(第2课时)
学习目标
1.学生能熟练运用圆柱的体积计算公式 解决实际问题; 2.通过经历发现和提出问题、分析和解 决问题的完整过程,掌握问题解决的策 略; 3.在解决问题的过程中体现数学中转化 的思想,培养学生的应用意识。
温故知新
如何求圆柱的体积?
解:由v r 2h得
0.628 0.02 31.4 3.14 0.22 5
3.14 0.04 5 0.628(m3 )
因为31.4不是整数 所以只能做31张课桌
根据实际情况用“去尾法”取近似值人教版六年级下册学上课课件. 圆柱的体积优秀课件
能力提升
圆柱的体积=底面积×高 将一个圆柱截成上下不相等的两段,两个圆 柱的(底面积)相同,( 高 )不同,哪个 圆柱的体积大?
8cm
圆柱的体积=底面积×高 两个圆柱的高相同,底面积不同,哪个圆柱的 体积大? 高相同时,底面积越大的体积越大。
高相同时,体积之比等于( 底面积之比)
人教版六年级下册数学上课课件. 圆柱的体积优秀课件
甲
乙
人教版六年级下册数学上课课件. 圆柱的体积优秀课件
判断
圆柱的体积=底面积×高
(1)一个圆柱的高扩大为原来的2倍,底面积不
由v r 2h得
1升 1000 毫升
3.14 32 11
932 .58 1000
3.14 9 11 310.8( 6 cm3) 310.86(ml)
答:这些果汁够明明 和客人每人一杯。
新知应用
一根圆柱形木料底面半径是0.2m,长5m.如果 做一张课桌用去木料0.02m3。这根木料最多 能做多少张课桌?
人教版 六年级数学下册 第3单元 圆柱与圆锥
3.1.3 圆柱的体积(第2课时)
学习目标
1.学生能熟练运用圆柱的体积计算公式 解决实际问题; 2.通过经历发现和提出问题、分析和解 决问题的完整过程,掌握问题解决的策 略; 3.在解决问题的过程中体现数学中转化 的思想,培养学生的应用意识。
温故知新
如何求圆柱的体积?
解:由v r 2h得
0.628 0.02 31.4 3.14 0.22 5
3.14 0.04 5 0.628(m3 )
因为31.4不是整数 所以只能做31张课桌
根据实际情况用“去尾法”取近似值人教版六年级下册学上课课件. 圆柱的体积优秀课件
能力提升
圆柱的体积=底面积×高 将一个圆柱截成上下不相等的两段,两个圆 柱的(底面积)相同,( 高 )不同,哪个 圆柱的体积大?
8cm
六年级下册数学课件3.1圆柱的体积人教新课标(共7张PPT)

是1:4,那么甲、乙体积的比是( D ),甲、 乙侧面积的比是( A )。
A、1:4 B、4:1 C、1:8 D、1:16 E、无法确定
当堂检测(2)
二、填空题:
1、把一个圆柱的底面分成(许多相等的扇形),然后切开,可 拼成一个近视的(长方体 );所得图形的底(面积 )等于圆 柱的(底面积 ),(高 )等于圆柱的(高 );变化
前后(体积 )不变,表面积与侧面积都(增加2rh )。
2、圆柱的底面积不变,高缩小7倍,那么体积就( 缩小7倍 )
3、一个圆柱的高不变,底面半径扩大3倍,那么圆柱的
体积就(扩大9倍
)。
4、一个圆柱的高扩大4倍、底面半径缩小3倍,那么体积
就( 缩小4/9
)。
5、一个圆柱的体积不变,高扩大5倍,那么圆柱的底面
V=Sh S=V÷h h=V÷S
V=∏r2h
②圆柱体积公式推导的主要过程是怎样底变面;的积体不积?变不;变高;不表 ③变化前后数量关系是怎样的? 面积与侧面积增加
h=V÷(∏r2)④用字母表示圆柱的体积公式及变形公式。
⑤决定圆柱体积大小有哪几个因素(或条件)。
2、组内交流、形成共识。决个定:圆 ①柱底体面积积大(小或的半因径素)有、两 3、全班展示、构建模型。 ②高 流程:自主学习----组内交流----全班展示(3+3+4)
《圆柱的体积》
1、说说什么叫做物体的体积? 体积:物体所占空间的大小叫做物体的体积。
2、长方体、正方体的体积公式分别是怎样的? V长=abh=s底面积×h=s横截面积×a;V正=a× a × a= a3 3、说说长方体、正方体的体积分别是由哪些因素决定的 4、圆柱的侧面积公式是采用什么方法推导出来的?其主
A、1:4 B、4:1 C、1:8 D、1:16 E、无法确定
当堂检测(2)
二、填空题:
1、把一个圆柱的底面分成(许多相等的扇形),然后切开,可 拼成一个近视的(长方体 );所得图形的底(面积 )等于圆 柱的(底面积 ),(高 )等于圆柱的(高 );变化
前后(体积 )不变,表面积与侧面积都(增加2rh )。
2、圆柱的底面积不变,高缩小7倍,那么体积就( 缩小7倍 )
3、一个圆柱的高不变,底面半径扩大3倍,那么圆柱的
体积就(扩大9倍
)。
4、一个圆柱的高扩大4倍、底面半径缩小3倍,那么体积
就( 缩小4/9
)。
5、一个圆柱的体积不变,高扩大5倍,那么圆柱的底面
V=Sh S=V÷h h=V÷S
V=∏r2h
②圆柱体积公式推导的主要过程是怎样底变面;的积体不积?变不;变高;不表 ③变化前后数量关系是怎样的? 面积与侧面积增加
h=V÷(∏r2)④用字母表示圆柱的体积公式及变形公式。
⑤决定圆柱体积大小有哪几个因素(或条件)。
2、组内交流、形成共识。决个定:圆 ①柱底体面积积大(小或的半因径素)有、两 3、全班展示、构建模型。 ②高 流程:自主学习----组内交流----全班展示(3+3+4)
《圆柱的体积》
1、说说什么叫做物体的体积? 体积:物体所占空间的大小叫做物体的体积。
2、长方体、正方体的体积公式分别是怎样的? V长=abh=s底面积×h=s横截面积×a;V正=a× a × a= a3 3、说说长方体、正方体的体积分别是由哪些因素决定的 4、圆柱的侧面积公式是采用什么方法推导出来的?其主
六年级下册数学课件-圆柱的体积 人教版(共44张PPT).pptx

=3.14×4² =3.14×16 =50.24(cm²)
杯子的容积: 50.24×10
=502.4(cm³) =502.4(mL) 答:因为502.4大于498,所以杯子能装下这袋牛奶。
做一做
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量 底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水, 带这杯水够喝吗?
V= πr²h
,
做一做
1.一根圆柱形木料,底面积为75cm²,长90cm。它的体积是 多少? 75×90=6750(cm³) 答:它的体积是6750cm³。
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直 径为1m。挖出的土有多少立方米? 3.14×(1÷2)²×10=7.85(m³) 答:挖出的土有7.85立方米。
第3单元 圆柱与圆锥
课题3 圆柱的体积
一、情境导入
放入石头后发生了什么?
水位变高了
你能用一句话说说什 么是圆柱的体积吗?
圆柱所占空间的大小就是圆柱的体积
二、探索新知
哪个圆柱的体积大?
我的体积大。
要比较两个圆柱的体 积,你有什么好办法?
可以将圆柱放进水中,比较哪个水面升得高。
把大小圆柱分别放入下面2个完全一样的水池中:
圆柱的底面分成的扇形越多,拼成的立体图形就越接近 于长方体。
把拼成的长方体与原来的圆柱比较, 你能发现什么?
长方体的底面积等于圆柱的 底面积 ห้องสมุดไป่ตู้ 高等于圆柱的 高 。 长方体的体积=底面积×高 圆柱的体积=底面积×高 V=Sh
=
如果知道圆柱的底面半径r和高h, 你能写出圆柱的体积公式吗?
圆柱的体积计算公式是:
3.14×(8÷2)²×15=753.6(cm³)=0.7536(L) 0.7536L<1L 答:带这杯水不够喝。
杯子的容积: 50.24×10
=502.4(cm³) =502.4(mL) 答:因为502.4大于498,所以杯子能装下这袋牛奶。
做一做
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量 底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水, 带这杯水够喝吗?
V= πr²h
,
做一做
1.一根圆柱形木料,底面积为75cm²,长90cm。它的体积是 多少? 75×90=6750(cm³) 答:它的体积是6750cm³。
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直 径为1m。挖出的土有多少立方米? 3.14×(1÷2)²×10=7.85(m³) 答:挖出的土有7.85立方米。
第3单元 圆柱与圆锥
课题3 圆柱的体积
一、情境导入
放入石头后发生了什么?
水位变高了
你能用一句话说说什 么是圆柱的体积吗?
圆柱所占空间的大小就是圆柱的体积
二、探索新知
哪个圆柱的体积大?
我的体积大。
要比较两个圆柱的体 积,你有什么好办法?
可以将圆柱放进水中,比较哪个水面升得高。
把大小圆柱分别放入下面2个完全一样的水池中:
圆柱的底面分成的扇形越多,拼成的立体图形就越接近 于长方体。
把拼成的长方体与原来的圆柱比较, 你能发现什么?
长方体的底面积等于圆柱的 底面积 ห้องสมุดไป่ตู้ 高等于圆柱的 高 。 长方体的体积=底面积×高 圆柱的体积=底面积×高 V=Sh
=
如果知道圆柱的底面半径r和高h, 你能写出圆柱的体积公式吗?
圆柱的体积计算公式是:
3.14×(8÷2)²×15=753.6(cm³)=0.7536(L) 0.7536L<1L 答:带这杯水不够喝。
人教版六年级数学下册《圆柱的体积》课件课件

人教版六年级数学下册 《圆柱的体积》课件PPቤተ መጻሕፍቲ ባይዱ 课件
# 人教版六年级数学下册《圆柱的体积》课件PPT大纲
引入
今天我们要学习《圆柱的体积》这个重要数学概念,通过本节课的学习,我们将了解圆柱的结构特点以 及计算方法。
知识点讲解
圆柱是一个常见的几何体,它具有底面、高度和侧面。我们将学习如何计算 圆柱的底面积、高度以及体积。
例题讲解
让我们通过数道练习题来巩固所学知识。这些例题将帮助我们更好地理解和应用圆柱的体积公式。
课堂练习
是时候进行一些实际的课堂练习了。我将提供一些问题供你们自主思考和解 答,然后我们一起进行讨论和分析。
总结
经过本节课的学习,我们已经掌握了计算圆柱体积的方法。别忘了继续巩固 和深化所学知识,以便在数学学习中取得更好的成绩。
课后作业
为了巩固所学知识,我将布置一些相应的课后作业。请合理安排时间完成作 业,并牢记作业的重要性。
课堂回顾
在开始新的课程内容之前,让我们先回顾一下上一课堂所学的内容,解决可能存在的问题,确保大家都 掌握了基础知识。
结束语
非常感谢大家的积极参与和表现,你们做得很好!下一课堂,我们将继续学习其他有趣的数学知识。
# 人教版六年级数学下册《圆柱的体积》课件PPT大纲
引入
今天我们要学习《圆柱的体积》这个重要数学概念,通过本节课的学习,我们将了解圆柱的结构特点以 及计算方法。
知识点讲解
圆柱是一个常见的几何体,它具有底面、高度和侧面。我们将学习如何计算 圆柱的底面积、高度以及体积。
例题讲解
让我们通过数道练习题来巩固所学知识。这些例题将帮助我们更好地理解和应用圆柱的体积公式。
课堂练习
是时候进行一些实际的课堂练习了。我将提供一些问题供你们自主思考和解 答,然后我们一起进行讨论和分析。
总结
经过本节课的学习,我们已经掌握了计算圆柱体积的方法。别忘了继续巩固 和深化所学知识,以便在数学学习中取得更好的成绩。
课后作业
为了巩固所学知识,我将布置一些相应的课后作业。请合理安排时间完成作 业,并牢记作业的重要性。
课堂回顾
在开始新的课程内容之前,让我们先回顾一下上一课堂所学的内容,解决可能存在的问题,确保大家都 掌握了基础知识。
结束语
非常感谢大家的积极参与和表现,你们做得很好!下一课堂,我们将继续学习其他有趣的数学知识。
《圆柱的体积》PPT课件
面测量得到的。)
8cm
杯子的容积。
杯子的容积: 50.24 ×10 =502.4(cm3)
10cm
杯子的底面积: 3.14 ×(8÷2)2
=3.14 ×16 =50.24(cm2)
=502.4(mL) 牛奶的体积: 240×2=480(mL) 502.4>480 答:杯子能装下2袋这样的牛奶。
课堂练习
小明和妈妈出去游玩,带了一个圆柱形保温壶,从里 面量底面直径是8cm,高是15cm。如果两人游玩期间 要喝1L水,带这壶水够喝吗?
保温壶的底面积:
3.14×(8÷2)2 =3.14×16 =50.24(cm2)
保温壶的容积:
50.24×15=753.6(cm3) =0.7536(L)
1L>0.7536L
答:带这壶水不够喝。
课堂练习
一根圆柱形木料底面直径是0.4m,长5m。如果做一张 课桌用去木料0.02m3,这根木料最多能做多少张课桌?
木料的体积:
3.14×(0.4÷2)2×5 =3.14×0.2 =0.628(m3)
“退一”法。
0.628÷0.02=31.4(张)
答:这根木料最多能做31张课桌。
已知底面直径和高求圆柱体积。 V=π(d2 )2h =3.14×(1÷2)2×10 =7.85(立方米) 答:挖出的土有7.85立方米。
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子 里面测量得到的。)
思考:
8cm
1.已知什么?
10cm
2.要求什么?
3.要注意什么?
探究新知
下图的杯子能不能装下2袋这样的牛奶?(数据是从杯子里
)
于土的高度有关。
两个花坛的体积
圆柱的体积 人教版六年级数学下册 教学PPT课件
迁移应用 拓展探究
一个圆柱形容器的底面周长是62.8厘米,把一块 铁块放入这个容器后,水面上升了2厘米,这块铁块
的体积是多少?
知道S和h: 知道r和h: 知道d和h: 知道C和h:
V=Sh
V=πr2×h
V (d)2 h
2
π V= (C÷π÷2)2×h
(2)圆柱体的高越长,它的体积越大。( )
×
(3)圆柱体的体积与长方体的体积相等。( )
×
(4)圆柱体的底面直径和高可以相等。( )
√
练习巩固 应用拓展
把一根长6分米的圆柱形钢材截成三段后,如图,表 面积比原来增加8平方分米,这根钢材原来的体积是
多少?
(8÷4)×6=12( 立方分米)
答Байду номын сангаас这根钢材原来的体积是12 立方分米。
圆柱的体积
什么叫物体的体积?你能计算下面哪些图形的体积?
√
√
2.5cm 4cm
5cm
V长=abh
4cm
V正=a3
V=Sh
能将圆柱转化成一种学过的图形, 计算出它的体积吗?
请大家想一想:在学习圆的面积时, 我们是怎样把圆转化成已学的图形,来
推导圆面积的计算公式的.
把圆等分切割,拼成一个近似的长方形,找出圆与所拼成的长方形之间的 关系,进而推导出圆面积的计算公式.
答:能装下这袋奶。
生活一中饮料的生产数商学生产一种饮料,采用圆柱形易
拉罐包装,从易拉罐的外面量,底面半径是3厘米, 高是12厘米,易拉罐侧面印有“净含量340毫升”字
样。请大家讨论:生产商是否欺骗了消费者?
判断正误,对的画“√”,错误的画“×” 。
(1)圆柱体的底面积越大,它的体积越大。( )
(赛课课件)六年级下册数学《圆柱的体积》 (共26张PPT)
•
17、一个人即使已登上顶峰,也仍要 自强不 息。2021/4/292021/4/292021/4/292021/4/29
谢谢大家
返回
•
9、 人的价值,在招收诱惑的一瞬间被决定 。2021/4/292021/4/29T hursday, April 29, 2021
•
10、低头要有勇气,抬头要有低气。2021/4/292021/4/292021/4/294/29/2021 8:52:03 PM
长方体(正方体)的体积=底面积×高
V=Sh
返回
怎样求它 们的体积呢?
返回
返回
返回
返回
返回
圆柱体积
长方体体积
返回
圆柱体积 底面积
长方体体积 底面积
返回
圆柱体积 底面积 高
长方体体积 底面积 高
返回
圆柱体积 = 底面积 × 高
长方体体积 = 底面积 × 高
返回
圆柱体积=底面积× 高
V=Sh
返回
二、填表。
底面积s (平方米)
高h (米)
圆柱体积 v (立方米)
15
3
45
40
4
160
返回
三、判断对错。
1、圆柱体体积与长方体体积相等。( × )
2、长方体、正方体、圆柱体的体积都可以用
底面积乘高的方法来计算。
( √)
3、圆的面积公式是S=π r 2 ( √ )
返回
四、求下面圆柱的体积。(只列式不计算。)
圆柱体积
圆面积
长方体
例题
练习
总结
延伸
返回
将圆分成16等份
返回
将圆分成16等份
六年级下册数学《圆柱的体积》人教新课标ppt(荐)(22张)标准课件
S=πr2
圆
长方形
运用了( 转化 )的思维方式
已知底面直径和高,怎样求圆柱的体积? V = π(c÷ π÷2)2h 圆柱的体积= 底面积 × 高 圆柱的体积= 底面积 × 高
分成的扇形越多,拼成的立体图形 已知底面周长和高,怎样求圆柱的体积?
答:它的体积是6750cm3。 V = π(c÷ π÷2)2h 14×32×4=113. 分成的扇形越多,拼成的立体图形就越接近于长方体。
一个圆柱的底面周长是18.84dm, 高4dm,这个圆柱的体积是多少?
18.84÷3.14÷2=3(dm) 3.14×32×4=113.04(dm3) 答:这个圆柱的体积是113.04dm3。
课堂小结
通过本节课的学习,你有什么收获?有
长方体的体积等于圆柱的体积。
什么感想? V = π(d÷2)2h
思 考:
已知底面半径和高,怎样求圆柱的体积? 已知底面直径和高,怎样求圆柱的体积? 已知底面周长和高,怎样求圆柱的体积?
如果知道圆柱的底面半径r和高h
圆柱体积计算公式是: V = πr²h
已知底面积和高:V = Sh 已知底面半径和高: V = πr2h 已知底面直径和高: V = π(d÷2)2h 已知底面周长和高: V = π(c÷ π÷2)2h
已知底面直径和高,怎样求圆柱的体积? V = π(d÷2)2h 18. V = π(c÷ π÷2)2h 分成的扇形越多,拼成的立体图形就越接近于长方体。
长方体的体积=底面积×高 圆柱所占空间的大小叫圆柱的体积。
我们先来看圆的面积计算公式的推导过程。 长方体的体积等于圆柱的体积。 你知道下面图形的体积计算公式吗? 通过本节课的学习,你有什么收获 你知道下面图形的体积计算公式吗? 圆柱的体积=底面积×高
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新知探究
图1:
h=h
甲
讨论:
乙
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
新知探究
图1:
h=h
甲 乙
高相等时,底面积越大的体积越大。
新知探究
将一个圆柱截成不相等的 图2: 两段,哪个圆柱体积大?
底面积相等时,高越长的体积越大。
新知探究
圆柱体积的大小与哪些条件有关?
eWTkEDhWLSFGRASAD1233@$#%%@!DVGTeWTkEDhWLSFGRASAD1233@$#%%@!DVGT
V; 先求r,再求S, 然后求V
课堂训练
求下面圆柱的体积。
小结与作业
本节课你有哪些收获?
作业:
课本第25页“做一做”第1题、第2题。
拓展延伸
(1)你会计算它们的体积吗?
(2)试写出它们的体积公式。
15平方米 8 米 16平方米 9 米
r
πr
S= π
2 r
5 探索圆柱的体积
5 探索圆柱的体积
5 探索圆柱的体积
长方体的体积
圆柱体的体积
=
=
底面积
底面积
× 高
× 高
新知探究
把圆柱的底面平均分的份数越多,切拼成的 立体图形越接近长方体。
新知探究
圆柱的体积=底面积×高 V圆柱=S底面积×h=πr2h
新知探究
圆柱体积的大小与哪些条件有关?
圆柱的体积
复习旧知
(1) 圆柱的侧面积=( 底面周长×高
)
(2) 圆柱的表面积=( 侧面积+底面积×2 )
(3) 长方体的体积=( 底面积×高 长×宽×高 )
=(
)
(4) 正方体的体积=( 棱长×棱长×棱长 ) (5) 圆柱的体积=?
复习旧知
圆的面积公式推导过程:
复习旧知
圆的面积公式推导过程:
