硕士-最优化理论与方法试题-2013
(精选)最优化方法复习题

《最优化方法》复习题第一章 概述(包括凸规划)一、 判断与填空题1)].([arg )(arg m in m ax x f x f n n R x R x -=∈∈ √ 2{}{}.:)(min :)(max n n R D x x f R D x x f ⊆∈-=⊆∈ ⨯3 设.:R R D f n →⊆ 若n R x ∈*,对于一切n R x ∈恒有)()(x f x f ≤*,则称*x 为最优化问题)(min x f D x ∈的全局最优解. ⨯4 设.:R R D f n →⊆ 若D x ∈*,存在*x 的某邻域)(*x N ε,使得对一切)(*∈x N x ε恒有)()(x f x f <*,则称*x 为最优化问题)(min x f Dx ∈的严格局部最优解. ⨯5 给定一个最优化问题,那么它的最优值是一个定值. √6 非空集合n R D ⊆为凸集当且仅当D 中任意两点连线段上任一点属于D . √7 非空集合nR D ⊆为凸集当且仅当D 中任意有限个点的凸组合仍属于D . √8 任意两个凸集的并集为凸集. ⨯9 函数R R D f n →⊆:为凸集D 上的凸函数当且仅当f -为D 上的凹函数. √ 10 设R R D f n →⊆:为凸集D 上的可微凸函数,D x ∈*. 则对D x ∈∀,有).()()()(***-∇≤-x x x f x f x f T ⨯11 若)(x c 是凹函数,则}0)( {≥∈=x c R x D n 是凸集。
√12 设{}kx 为由求解)(min x f D x ∈的算法A 产生的迭代序列,假设算法A 为下降算法,则对{} ,2,1,0∈∀k ,恒有 )()(1k k x f x f ≤+ .13 算法迭代时的终止准则(写出三种):_____________________________________。
14 凸规划的全体极小点组成的集合是凸集。
硕士研究生最优化复习题

硕士研究生最优化复习题硕士研究生最优化复习题1.线性规划问题CX z =min ,0,≥=X b AX 其可行域为R ,最优目标函数值为z ,若分别发生下列情形之一时,其新的可行域为R *,新的最优目标函数值为z *,试分别写出下列三个问题中R 与R *及z 与z *之间的关系:(1)增添一个新的约束条件。
(2)减少一个原有的约束条件。
(3)目标函数变为λCXz =min ,同时约束条件方程变为1,0,>≥=λλX b AX 。
2.线性规划问题CX z =min ,0,≥=X b AX ,设X (0)为问题的最优解,若目标函数中用C *代替C 后,问题的最优解变为X *,求证:(C *-C )(X *-X (0))≤03.若线性规划问题min z =CX ,AX =b, X ≥0具有最优解,试应用对偶理论证明下述线性规划问题min z =CX ,AX =d, X ≥0不可能具有无界解,d 可以是取任意值的向量。
4.试将图所示的求v 1到v 7点的最短路问题归结为求整数规划问题(建立整数规划模型),具体说明模型中变量、目标函数和约束条件的含义。
v 2 1 v 539 2 2v 1 5 v 4 4 v 7 8 38 4v 3 v 65.已知线性规划问题min Z=2x 1-x 2 +2x 3≥≤≤-+=++无约束 3 213 213 21x ,0x 0,x 6x x x - 4x x x -k 其最优解为x 1 = -5, x 2 =0, x 3 =-1(1)求k 的值。
(2)写出并求其对偶问题的最优解。
6.某公司要建立一线性规划模型,此模型受约束条件1或约束条件2约束。
如果满足约束条件1,必须同时满足另外p 1个约束条件中的k 1个(k 1 < p 1)约束;如果满足约束条件2,必须同时满足另外p 2个约束条件中的k 2个(k 2 < p 2)约束;要求建立整数规划的约束条件,满足上述要求。
最优化方法习题1

《最优化方法》期末考试练习题声明:仅供复习时参考。
实际考试题型类似,题量小于本练习。
一. 选择题:略第一题主要考察基本概念、定理,算法的基本思想和matlab 命令。
二.简答题1. 写出线性规划问题;0, ,94 3 ,5 32 4 s.t. ,823 max 21321321321≥≥-+-≥+-+-x x x x x x x x x x x 的对偶规划。
2.如果求解某整数规划问题的松弛问题得到如下的最优单纯形表:求以1x ,2x 为源行生成的割平面方程。
3.在区间[0,3]上用黄金分割法求函数12)(3+-=t t t ϕ的极小点,只要求求出 初始的迭代点和保留区间及此时的近似最优解。
4. 用tx ex y 21-=拟合下列数据1.0,24.0,11,07.2,1=======-=y t y t y t y t写出非线性最小二乘问题三.计算题1.分别用最速下降方法和修正的牛顿法求解无约束问题 22214)(min x x x f +=。
取初始点()()Tx2,21=,.1.0=ε2.讨论约束极值问题⎪⎪⎩⎪⎪⎨⎧≥≥≤-≤++--+=0004..866)(min212121212221x x x x x x t s x x x x x f 的Kuhn-Tucker 点。
3.用外点法(外部惩罚函数法)求解2s.t.)3()1()(min 212221≤-+-+-=x x x x x f4.用内点法求解非线性规划03)( 03)( s.t. 296)(min 22112121≥-=≥-=++-=x x g x x g x x x x f5.用乘子法求解1s.t.6121)(min 212221=++=x x x x x f 6.用表格单纯形法求解线性规划⎪⎪⎩⎪⎪⎨⎧≥≥-≥-≤++++=0,,34623max 3213231321321x x x x x x x x x x x x x Z并根据最优单纯形表格写出该线性规划的最优基和最优基的逆。
最优化方法习题答案
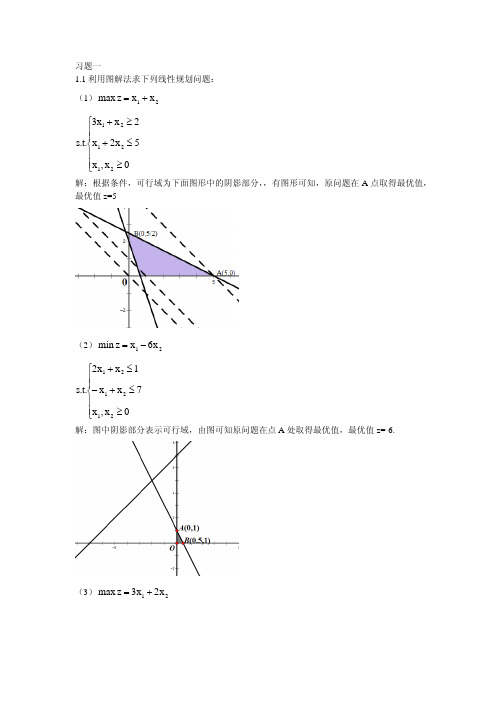
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化方法试卷

华东理工大学研究生《最优化方法》考试卷专业 ________ 班级 ________ 学号 ________ 姓名 ________ 成绩 ________2014年12月11日 一、简答题(40分,每小题4分)1.请写出最优化问题的一般模型形式。
2.试叙述局部最优解和全局最优解的定义。
3.请给出优化算法收敛速度的定义。
4.请给出优化算法的终止准则。
5.给出下降方向的定义和判别方法? 6.简述下降迭代法的基本步骤。
7.何谓共轭方向?你知道由线性无关向量组构造共轭向量组的方法吗? 8.最速下降法是最好的优化算法吗?为什么? 9.何谓可行方向及如何判别?10.优化问题的最优解与可行下降方向有什么关系?二、(10分)试用最速下降法(梯度法)求解如下问题,初始点⎪⎪⎭⎫⎝⎛=110x ,只迭代一次,并判断迭代结果是否为最优解。
21222122)(min 2x x x x x f Rx -+=∈三、(10分)试叙述Powell 基本算法步骤或单纯形替换法的步骤,并简述其特点。
四、(10分)试用惩罚函数求解如下的优化问题8 ..)3()(min 2≥--=x t s x x f五、(10分)考虑下述线性规划问题1223 1832 ..233)(max 321321321321≥=++=+++-=x x x x x x x x x t s x x x x f ,,1.求出该问题的所有基本解,并指出哪些是基本可行解; 2.该问题是否有最优解?若有,请求出其最优解。
六、(10分)考虑问题010)3( 010)3( ..)(max 211323212≥≤---≤+-+=x x x x x x t s x x f ,1.写出上述问题的Kuhn —Tucker 条件。
2.这个问题的最优解满足Kuhn —Tucker 条件吗?为什么?七、(10分)已知某化工反应y 与因数x 和时间t 之间的依赖关系为xa t a ta x a y 43211+++=其中4321,,,a a a a 是待定参数,为确定这三个参数,实验测得有关y x t ,,的五组数据如下:1.试用最小二乘法建立确定参数4321,,,a a a a 的数学模型;2.对于列出的非线性最小二乘问题,你知道有哪些优化算法可求解该问题,并请给出求解该问题的修正Gauss-Newton 算法的迭代公式。
北京化工大学-《最优化方法》研究生试卷

北京化⼯⼤学-《最优化⽅法》研究⽣试卷⼀、(15分)求下⾯LP 问题的所有基本解,指出哪些是基本可⾏解,并求最优解。
≥=+++=+++-+-=0,,,3227432.6325min 4321432143214321x x x x x x x x x x x x t s x x x x z⼆、(16分)已知线性规划问题≤≤-=--≤+--≥-+----=⽆约束321321321321321,0,052010651535.765min x x x x x x x x x x x x t s x x x z(1)化为标准型。
(2)列出⽤两阶段法求解时第⼀阶段的初始单纯形表。
三、(12分)设有LP 问题≥≤-+-≤++-+=.0,,122.max 32132132121x x x x x x x x x t s x x z (1)写出其对偶问题;(2)⽤对偶理论证明原问题⽆最优解。
四、(13分)已知某线性规划问题的⽬标函数是求最⼤值,各变量均⾮负,在⽤标准的单纯形法求解过程中,得到下表:(1)在所有空格中填上适当的数。
(2)分别确定a 1,a 2的取值范围,使以下情况成⽴:①此解为最优解。
②此解为最优解,且有⽆穷多最优解。
③此解不是最优解,且能由该解得到下⼀个解。
五、(12分)设212212)1()(100)(x x x x f -+-=,(1)求)(),(2x f x f ??;(2)证明T x )1,1(*=为 f (x )的⼀个极⼩点;(3)求f (x )在点T x )1,1()0(-=的最速下降⽅向和⽜顿⽅向。
六、(16分)⼀股民拟将90000元的资⾦⽤于购买A 、B 两种股票,有关数据如下,问股民如何购买股票,才能使(按优先级从⾼到低)(1)年风险系数不⾼于700;(2)年收益不低于10000元?七、(16分)分配甲、⼄、丙、丁去完成A 、B 、C 、D 、E 五项任务。
若任务E 必须完成,其它4项中可任选3项完成,每⼈完成各项任务的时间如下表:确定最优分配⽅案,使完成任务的总时间最少。
最优化考试题2.doc

最优化方法定义可行方案:如果一个方案能达到预定目的,则该方案就叫可行方案。
最优方案:可行方案中最好的方案叫最有方案,它能达到最优化效果。
最优化M题:如何从可行方案中找出最优方案就叫最优化M题。
最优化方法:求解最优化闷题的数学方法叫最优化方法。
最优化方法解决实际问题的一般步骤:1提出最优化问题,叙述目标是什么?约束条件是什么?求什么变量?即确定变量,列出目标函数及约束表达式,建立最优化问题的数学模型。
2分析模型,选择合适的求解方法。
3编制计算机程序,上机求最优解。
对算法的收敛性,通用性,简便性,效率及误差等作出评价。
系统:由相互联系的若干部分构成的具有一定功能的整体。
系统的基本特征:1系统巾若干部分组成,每一部分具有其特定的功能。
2系统屮的各个要素之间相互制约,联系和作用。
3系统是具有一定功能的整体,系统的总功能不等于各个部分功能的简单迭加,系统的功能大于各部分的功能之和。
4系统存在于一定的环境之中,系统与环境之间存在相互作川,系统与环境的划分是相对的,对于一个系统是环境,而对于另一个系统而言可能是其中的一部分。
系统分析法:1确定所研宄系统的范M及其所处的环境。
2确定系统的组成部分,结构,功能,目的,各部分的功能和闪部规律。
3明确系统各个部分之间的联系,及整个系统与环境之间的联系。
4在上述分析的基础上,确记问题的决策变量及评价方案优劣的指标。
决策变量:决定方案优劣的变量。
数学模型:用字母,数字,各种符号,图像,逻辑框图描述实际系统的特征和内在联系的模型。
数学模型的组成:1常数,指在所研究的问题中保持相对固定或变化不大的呈。
2参数由具体系统的内外部条件确定的量。
3变量,指在模型中待确定的量。
4函数关系描述模型中常数,参数,变量之间相互关系的方程式或不等式。
独立变量:彼此独立的变量。
相关变量:其值可由独立变量确定的量。
工程优化问题:最优准则包括系统性能准则和经济准则。
系统性能准则是指使系统的某些性能指标达到最大或最小。
最优化考试卷子

考试时间120分钟最优化试卷1.考试形式:闭卷;2.本试卷共十大题,满分100分班级学号姓名任课教师一.(20分)解释下列概念: (1)凸集,凸规划;(2)线性规划的基和基本解;(3)无约束优化算法的下降搜索方向,举出两种搜索方向;(4)约束最优化问题的可行解集合或容许解集合;(5)共轭方向;二.(10分)解答下列问题(1)判断函数22131212f(x)=10x 52x x x x x ---+为凸函数或凹函数或严格凸函数或严格凹函数;(2)求函数12212f(x)=34x x x x +的梯度和hessian 矩阵。
三.(15分)写出下列线性规划的对偶形式,并用单纯形法求解原规划的最优值和最优解 max 123z=33x x x ++ 123232x x x ++≤s.t 123235x x x ++≤ 123226x x x ++≤123,,0x x x ≥四.(10分)写出一维搜索0.618法的基本思想和算法步骤或框图。
五.(15分)分别利用内点法和外点法求解下列问题 min 3121(1)3x x ++s.t 1(1)0x -≥20x ≥六(15分).设A 为n 阶对称正定矩阵 (1) 写出A 的共轭向量组的定义;(2) 并证明该向量组必为线性无关向量组;(3)设n 维向量组12,,,n a a a 线性无关,如果存在n 维向量x ,满足'0i x a =,(i=1,2,…n),证明:n 维向量x=0.七.(15分)简述DFP 算法的优缺点:并证明迭代的尺度矩阵满足拟牛顿方程11其中x x x ,,x (x )(x )()()k k k k k k K k k k k K k K k k K kg g g C g H g H g g H g ++∇=-∇=-''''=∇∇∇∇-∇∇∇∇。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E2012-2013学年硕士《最优化理论与方法》课程试题
姓名 学号 成绩
第一部分 理论基础(每题10分,共50分)
要求:(1)请自备计算器以及excel 、lingo 、matlab 等计算软件进行计算;
(2)请自行准备A4纸张答题纸,可用蓝色或黑色钢笔(或签字笔)书写解题过程、小论文,写明题目番号,但不能使用铅笔(画图除外)、红笔、圆珠笔答题;答案也可用A4纸张打印提交。
提交时包含本试卷原题病写明姓名、学号。
(3)开卷考试。
但请考生独立完成,严禁互相抄袭答案。
一旦发现题目解答过程雷同,这些学生将统统记零分。
一、问:点 x * =(2,1)是否为以下非线性规划问题的K —T 点,为什么?
⎪⎪⎪⎩
⎪⎪⎪⎨⎧≥=+≤+-+-0,,425})2()3min{(212122212221x x x x x x x x 二、试用共轭梯度法求二次函数2212()4f x x x =+的极小值点。
三、试用步长加速法(模矢法)求下述函数2212
112min ()242f x x x x x x =+-- 的极小点。
初始点X (0)=(3,1)T ,步长△1=(0.5,0)T ,△2=(0,0.5)T ,并绘图表示整个迭代过程。
四、试用Zoutendijk 可行方向法求解下列线性约束的非线性目标函数的最优解: 其中ε1=ε2=0.1,初始点X (0)=(0,0)T ,迭代到得出X (2)和f(X (2))即可。
(计算过程中尽量保持分数计算,如果以小数计算尽量保持五位以上,最终结算结果保留四位小数。
222
121212121212min ()222462..55
,0 f x x x x x x x x R x x s t x x x x =+---∈+≤⎧⎪+≤⎨⎪≥⎩
五、用外点法(罚函数法)求解以下非线性规划的最优解。
并给出罚因子M 为1、
10、100、1000、10000时x 1和x 2的值。
22122min ()(2)..10
f x x x s t x =-+-≥
第二部分 小论文:案例编写及计算分析(共50分)
要求:
1.写一篇小论文,案例背景内容自拟(如果是写算法数学原理改进的论文,则可无案例背景,但须有一个算例),字数600字以上。
2.研究方法(以下三种方法任选一种):(1)多级模糊综合评价并用层次分析法确定权重,建立多级评价指标体系,指标含定性指标和定量指标,前者用专家投票法确定隶属度,后者用三角模糊数确定隶属度,通过计算得出评价结果并对结果进行定性分析;(2)模糊聚类分析(聚类过程中使用传递闭包法、直接聚类法或最大树法,如能使用F 统计量确定最佳阈值λ更好;画出动态聚类图;给出分类结论);(3)模糊TOPSIS 决策分析(建议:指标值采用三角模糊数,指标权重亦可采用模糊数;指标权重确定可用主客观权重综合——熵权法和层次分析法的结合;设定三个以上的备选方案,对各方案按贴进度进行综合评定排序)
3.可参考、借鉴中国期刊网或国外引文库中的论文写作思路,但严禁抄袭,也不能套用这些论文中的数据。
任课教师会在网上广泛搜索,一旦发现该校论文抄袭其他论文或搬用他人数据(可搬用数据统计年鉴中的数据),第二部分成绩记零分。
4.严格按照正规发表论文的格式来写(引言、数据用图表表示出来、计算原理步骤、公式及计算过程、定性分析结论),无须中英文摘要和关键词,但须有参考文献。
