有半径分别为R1和R2的同轴导体圆筒长为LLR1R2
《大学物理》第10章 电磁感应清华

(C)安培/米2; (D)安培·米2 。 18
21 在感应电场中电磁感应定律可写成
L
Ek
dl
d dt
,
式中 Ek为感应电场的电场强度。此式表明: [ D]
(A)闭合曲线 l 上
E
处处相等
k
;
(B)感应电场是保守力场 ;
(C)感应电场的电力线不是闭合曲线 ;
(D)在感应电场中不能像对静电场那样引入电势的概
)
2
;
[
B
]
(C)
1 2
(
2a 0 I
)2;
(D)
1
20
( 0 I
2a
)2。
解:距导线垂直距离为a的空间某点处的磁感强度为:
B
0 I 2a
则该点处的磁能密度为 :
wm
1
20
B2
1
20
(
0 I 2a
)
2
20((AP)15库0)仑电/米位2移;矢量(的B)时库间仑变/化秒率;ddDt 的单位是: [ C]
da
NL
0 I 2
(
1 d
d
1
a
)
1
103
0.2
2
4
107
2
5.0
(
1 0.1
0.1
1
0.1)
2 103 (V)
4
10.4 上题中若线圈不动,而长导线中通有交电流
i = 5sin100πt A,线圈内的感生电动势将为多大?
解:通 过N线圈的N磁链B为 ds s
2 自感互感磁场能量
µI
1 µI 2 = ( ) 2µ 2 π r
2
第十三章电磁感应 第十三章电磁感应 电磁场 2
=
µI
8π r
2
2
8π r
2 2
dV
单位长度壳层体积
d V = 2π r d r ⋅ 1 2 R2 µI µ I 2 R2 ln Wm = ∫ dr = R1 4 π r 4π R1
µ
r dr
R2
µ R2 1 2 ln Wm = LI L = 2 π R1 2
dΦ dI2 12 ε12 = − = −M dt dt
dΦ21 dI1 ε21 = − = −M dt dt
假设一个线圈电流I分布 假设一个线圈电流 互感的计算 •假设一个线圈电流 分布
•计算该线圈产生的磁场在另一线圈产生的磁通量Φ 计算该线圈产生的磁场在另一线圈产生的磁通量Φ 计算该线圈产生的磁场在另一线圈产生的磁通量
I a b l
v
13 - 3 自感和互感
第十三章 电磁感应 电磁场
一长直螺线管,单位长度上的匝数为n,另一半经为r 例3、一长直螺线管,单位长度上的匝数为 ,另一半经为 的圆环放在螺线管内,圆环平面与管轴垂直。 的圆环放在螺线管内,圆环平面与管轴垂直。求螺线管与 圆环的互感系数。 圆环的互感系数。
I
I r
P
R2
l
S
dr
Φ = ∫ dΦ =
∫ R1
R2
µI
2π r
ld r
Φ = ∫ dΦ = ∫
即
R2 R1
µI
2π r
ld r
R1 Q
R
R2 Φ= ln 2π R1
Φ µl R2 L= = ln I 2π R1
大学物理第11章习题解答

习题111. 选择题(1) 一圆形线圈在均匀磁场中作下列运动时, 哪些情况会产生感应电流( ) A. 沿垂直磁场方向平移B. 以直径为轴转动, 轴跟磁场垂直C. 沿平行磁场方向平移D. 以直径为轴转动, 轴跟磁场平行(2) 尺寸相同的铁环与铜环所包围的面积中, 通以相同变化率的磁通量, 环中( ) A. 感应电动势相同, 感应电流不同. B. 感应电动势相同, 感应电流相同. C. 感应电动势不同, 感应电流相同. D. 感应电动势不同.(3) 对于涡旋电场, 下列说法不正确的是( ) A. 涡旋电场对电荷有作用力. B. 涡旋电场由变化的磁场产生. C. 涡旋电场由电荷激发.D. 涡旋电场的电场线是闭合的.(4) 用线圈的自感系数L 来表示载流线圈磁场能量的公式212m W LI =( ) A. 只适用于单匝圆线圈.B. 只适用于一个匝数很多, 且密绕的螺线环.C. 适用于自感系数L 一定的任意线圈.D. 只适用于无限长密绕螺线管.(5) 有两个长直密绕螺线管, 长度及线圈匝数均相同, 半径分别为1r 和2r . 管内充满均匀介质, 其磁导率分别为1μ和2μ. 设1212r r =, 1221μμ=, 当将两只螺线管串联在电路中通电稳定后, 其自感系数之比12L L 与磁能之比12m m W W 分别为( ) A. 1211L L =, 1211m m W W =. B. 1212L L =, 1211m m W W =. C. 1212L L =, 1212m m W W =. D. 1221L L =, 1221m m W W =.答案:B A C D C2. 填空题(1) 电阻2R =Ω的闭合导体回路置于变化磁场中, 通过回路包围面的磁通量与时间的关系为23(582)10()m t t Wb -Φ=+-⨯, 则在2t s =至3t s =的时间内, 流过回路导体横截面的感应电荷等于______________C .(2) 长为l 的金属直导线在垂直于均匀磁场的平面内以角速度ω转动. 如果转轴在导线上的位置是在_______, 整个导线上的电动势为最大, 其值为_________; 如果转轴位置是在___________, 整个导线上的电动势为最小, 其值为____________.(3) 半径为a 的无限长密绕螺线管, 单位长度上的匝数为n , 通以交变电流sin m i I t ω=, 则围在管外的同轴圆形回路(半径为r )上的感生电动势为______________.(4) 一自感系数为0.25H 的线圈, 当线圈中的电流在0.01s 内由2A 均匀地减小到零. 线圈中的自感电动势的大小为______________.(5) 产生动生电动势的非静电力是______________, 产生感生电动势的非静电力是______________, 激发感生电场的场源是______________. 答案:(1) 21065.1-⨯ (2) 端点,2B lω;中点,0。
大学物理复习答案

3.半径为 R 1 和 R 2 的两个同轴金属圆筒,其间充满着相对介电常数为 r 的均匀介质。
设两圆筒上单位长度带电量分别为 和,则介质中的电位移矢量的大小D,电场强度的大小 E。
答案: D,Er r2 r 20 解:如图, 取柱面高斯面。
根据对称性, 柱面(高斯面)的上下底上,电位移矢量D 与高斯面法线 方向垂直;柱面(高斯面)的侧面上,电位移矢量 D 处处大小相等,并与高斯面法线方向平行。
由高斯定理,得到D dSQ 0, 2 rlDl , DrS2 电场强度为E D2 0 r r0 r4.一带电量 q 、半径为 R 的金属球壳,壳内充满介电常数为 的各向同性均匀电介质,壳外是真空,则此球壳的电势 U。
答案:q4R解:由高斯定理,可以求得球壳外电场强度Eq40 r2取无限远处电势为零,则UE cos dsqR4R5.两个点电荷在真空中相距为r 1 时的相互作用力等于在某一“无限大”均匀电介质中相距为 r 2 时的相互作用力,则该电介质的相对介电常数 r。
答案:r 12rr 22Q 1Q 2 解:在真空中,两个点电荷之间的作用力(库仑力)为F40 r 12点电荷 Q 1 在“无限大”电介质中产生的电场强度为E 1/Q 140 rr 2 点电荷 Q 2 受到的库仑力为 F /Q 2 E 1 /Q 1Q 224 0 r r 2依题F /FQ 1 Q 2 Q 1Q 2 rr 1240r 124 0 r r 22r 226.有一同轴电缆, 内、外导体用介电系数分别为 1 和2 的两层电介质隔开。
垂直于轴线的某一截面如图 5-2 所示。
求电缆单 位长度的电容。
解: 取高斯面为柱面。
柱面的半径为 r 、长度为 l ,对称轴为同轴电缆的对称轴, 柱面在同轴电缆的两极之间。
由对称性, 高斯面上的上下底面电位移矢量 与高斯面法线方向垂直;侧面上, 电位移矢量处处大小相等, 并且与高 斯面平行。
由高斯定理 , 有,r ,13DdS2 rlDq 0 lD ?r2 rRRS则同轴电缆的两极之间的电场强度为D?,;D?,E 1rR 1r R 2E 22rR 2r R 312 1 r22r同轴电缆的两极之间的电势差为R 2R 2R 3R 2R 3UE dlE 1 drE 1 dr?dr21 rr drR 22 rRRRR112121R 2 1R 3)2(lnlnR 21R 12单位长度的高斯面包围的自由电荷量为 q 0则单位长度的同轴电缆的电容为:Cq 02 0 1 2UUR 2 R 32ln1 lnR 1R 27.在一平行板电容器的两极板上, 带有等值异号电荷, 两极间的距离为 5.0mm ,充以 r的介质,介质中的电场强度为 1.0 106 V m 1 。
大学物理-第12章小结与习题分解

B 1 2 w H 2 2
2
真空中距该导线垂直距离为a的某点的磁感应强度大小为:
0 I B 2a
H
I 2a
4.一个中空的螺绕环上每厘米绕有20匝导线,当通以
电流I=3A时,环中的磁场能量密度
wm=
22.6 J/m3.
1 1 2 wm 0 H 0 n 2 I 2 2 2
A不动; B转动; C向左移动; D向右移动。
[ D ]
1.一自感线圈中,电流强度在0.002s内均匀地由 10A增加到12A,此过程中线圈内自感电动势为 400V,则线圈的自感系数为L= 0.400H .
dI L dt I 12 10 L 400 L t 0.002
( A ) L 1 = L2 = 0
(B)L1 =L2≠0
(C)L1=0 L2≠0 (D)L1≠0 L2=0
L = 2L-2M
a
a'
b
b'
图( 1 )
a
b
a'
b'
图(2)
M12 M21 M k LL
[ D ]
由于11 = LI,12 = -MI,22 = LI, 21 = -MI,21为线圈aa′在线圈bb′中 a 产生的磁链数,因为它与bb′由于自感 产生的磁链数相反,所以取负值,注 意两线圈的自感和相互的互感系数应 a 相等,则
B
]
2. 圆铜盘水平放置在均匀磁场中,B 的方向垂 直盘面向上,当铜盘绕通过中心垂直于盘面的 轴沿图示方向转动时 (A) 铜盘上有感应电流产生,沿 着铜盘转动的方向流动。
(B) 铜盘上产生涡流。
B
O
(C) 铜盘上有感应电流产生,铜盘边缘处 电势最高。
院大学物理作业题答案及详解1-22

大连理工大学软件学院大学物理作业及答案作业11.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:j y a qyE 23220)(2+=πε,2/a y ±=[解]21E E += )(422021y a qE E +==πε关于y 轴对称:θcos 2,01E E E y x ==y a qyE y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
大学物理第十二章 习题答案
第十二章 电磁感应及电磁场基本方程12–1 如图12-1所示,矩形线圈abcd 左半边放在匀强磁场中,右半边在磁场外,当线圈以ab 边为轴向纸外转过60º过程中,线圈中 产生感应电流(填会与不会),原因是 。
解:线圈以ab 边为轴向纸外转过60º过程中,尽管穿过磁感应线的线圈面积发生了变化,但线圈在垂直于磁场方向的投影的面积并未发生变化,因而穿过整个线圈的磁通量并没有发生变化,所以线圈中不会产生感应电流。
因而应填“不会”;“通过线圈的磁通量没有发生变化”。
12–2 产生动生电动势的非静电力是 力,产生感生电动势的非静电力是 力。
解:洛仑兹力;涡旋电场力(变化磁场激发的电场的电场力)。
12–3 用绝缘导线绕一圆环,环内有一用同样材料导线折成的内接正方形线框,如图12-2所示,把它们放在磁感应强度为B 的匀强磁场中,磁场方向与线框平面垂直,当匀强磁场均匀减弱时,圆环中与正方形线框中感应电流大小之比为___________。
解:设圆环的半径为a,圆环中的感应电动势1E 大小为2111d d d πd d d ΦB BS a t t t===E 同理,正方形线框中的感应电动势2E 大小为2212d d d 2d d d ΦB BS a t t t===E而同材料的圆环与正方形导线的电阻之比为12R R ==。
所以圆环与正方形线框中的感应电流之比为122I I a ==12–4 如图12-3所示,半径为R 的3/4圆周的弧形刚性导线在垂直于均匀磁感强度B 的平面内以速度v 平动,则导线上的动生电动势E = ,方向为 。
图12–5图12–4abdc图12–1Ba图12–2图12–3解:方法一:用动生电动势公式()d l =⨯⋅⎰B l v E 求解。
选积分路径l 的绕行方向为顺时针方向,建立如图12-4所示的坐标系,在导体上任意处取导体元d l ,d l 上的动生电动势为d ()d cos d B R θθ=⨯⋅B l =v v E所以导线上的动生电动势为3π3πd cos d 0BRBR θθ-===>⎰⎰v E E由于ε>0,所以动生电动势的方向为顺时方向,即bca 方向。
通过圆筒壁的热传导新
设保温层内半径为r处,温度为t,代入上式得:
2 0.40180 t 320 r ln 0.213
将上式整理得:
t 127 .3ln r 16.97
计算结果表明,圆筒壁内温度分布不是直线而是曲线。
一、单层圆筒壁的定态热传导 化工生产中常遇到圆筒壁(如圆筒形容器、 设备和管道)的热传导。单层圆筒壁的热传导如 图-1所示。
r1 λ
t1
r2
t2
设圆筒壁的内、外半径分别为r1和r2,长度为L, 内、外壁表面温度分别保持恒定温度t1和t2,且 t1>t2。若L很长,则沿轴向散热可忽略不计,温 度仅沿半径方向变化,此种热传导是一维定态热 传导。它与平壁热传导的不同处在于,圆筒壁的 热传面积不是常量,随半径而变。若在圆筒半径 为r处沿半径方向取微分厚度dr的薄壁圆筒,则 传热面积可视为常量,且等于2πrL;同时通过该 薄层的温度变化为dt,通过该薄圆筒壁的热传导 速率可以写为:
二、多层圆筒壁的定态热传导
多层圆筒壁(一三层为热系数分别为λ1、λ2和λ3,厚 度分别为b1=r2-r1、b2=r3-r2和b3=r4-r3。根据串联传热的原则, 可写出三层圆筒壁的热传导速率方程式为:
t1 t 2 t3 t1 t 4 Q ln(r2 / r1 ) ln(r3 / r2 ) ln(r4 / r3 ) R1 R2 R3 2L1 2L2 2L3
(式-7)
或
t1 t4 Q b3 b1 b2 1S m1 2 S m 2 3 S m3
(式-8)
对n层圆筒壁:
t 1 tn 1 Q ri 1 n ln ri 2Li i 1
(式-9)
或
t 1 tn 1 Q n bi iSmi i 1
12章 习题答案
[例题分析]例题12-1 有一半径为r 的均匀刚性导体圆环,其总电阻为R ,处于磁感应强度为B 的匀强磁场中以匀角速度ω (方向如图12-6所示)绕通过中心并处于圆面内的轴线旋转,该轴线垂直于B 。
试求当圆环平面转至与B 平行的瞬间: (1) ε ab 和εac (其中a 点是圆环与转轴的交点,ac是四分之一圆周,b 是ac 的中点); (2) 比较此时a 和c 两点的电势、a 和b 两点的电势。
解(1) 在环的a 、b 之间任意一点P 附近取元段d l ,d l 的方向沿环的切向,v ⨯ B 的方向与转轴平行并指向下方,如图12-6中虚线箭头所示。
故有⎰⎰⎰==⋅⨯=b a b a b a ab l B l B θαεsin d cos d d )(v v l B v ,因为θωsin r =v , d d l r =θ,代入上式,得εωθθωab r B B r ==-⎰2242814sin ()/ d 0ππ.用同样的方法可以得到εωθθωac r B B r ==⎰2224sin d 0/2ππ.积分所得皆为正值,这表示积分方向就是动生电动势的方向。
所以,如果把导体环的ab 段和ac 段看作电源内部,那么a 端是电源的负极,b 端和c 端是电源的正极。
从这里我们得到一个重要的启示:如果得到的电动势为负号,表示电动势的极性与积分方向相反,如果得到的电动势为正号,表示电动势的极性与积分方向相同。
我们曾经对电源电动势的极性作出过这样的规定:沿电源内部、从负极到正极的方向是电源的正方向。
(2) 根据动生电动势的方向,可以判断导体环中电流是沿顺时针方向的,电流的大小为 I R B r Rac ==42εωπ. 所以U I R B r B r ca ac =-=-=εωω444022ππ,这表示a 、c 两点等电势。
U I RB r ba ab=-=-εω842, 这表示a 点的电势高于b 点的电势。
15.4自感和互感
2 自感电动势
d m dI dL L ( L I ) dt dt dt dL 0 时, 当 dt dI L L dt dI 自感 L L dt
I
B
例1: 如图的长直密绕螺线管,已知 l,S,N,, 求其自感系数 L 解: 充满介质且磁场分布 S 的对称性 B H nI n N l l
N1 B1 0 I 1 0 n1 I 1 l
则穿过半径为 r2 的线圈 的磁通匝数为
15.4 自感和互感
N 2Φ21 N 2 B1 (πr12 ) n2lB1 (πr12 )
代入 B1 计算得
N 2Φ21
0 n1n2l ( πr ) I1
2 1
M 21
Il
R1
R1 Q
R
I
I r
P
R2
dr
l
S
单位长度的自感为:
L R2 In l 2π R1
二 互感现象
15.4 自感和互感
K
R
I1
I2
一个载流回路中电流变化,引起邻近另一回路中 产生感生电动势的现象 — 互感现象。
15.4 自感和互感
1 互感系数(M) 若两回路几何形状、尺寸及相对位置不变, 周围无铁磁性物质.实验指出:
15-4 自感和互感
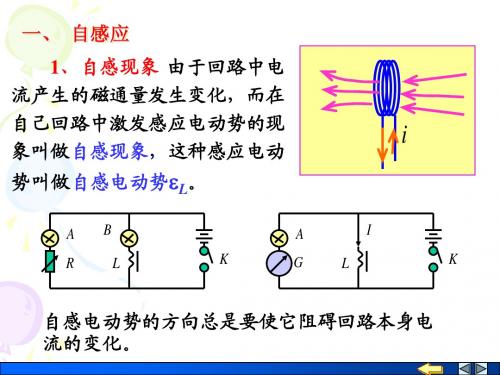
一 自感现象 由于回路自身电流、回路的形状、或回路周围 的磁介质发生变化时,穿过该回路自身的磁通量 随之改变,在回路中产生感应电动势的现象.
15.4 自感和互感
1 自感
m LI
自感
注意
I
B
L m I
无铁磁质时,自感仅与线圈形状、 磁介质有关.
15.4 自感和互感
