第二章参考答案
第2章作业-2 参考答案

二、综合题
1. 若X=-0.1110,Y=-0.1101,采用原码一位乘法运算求 X·Y=? 给出计算过程。
2.若X=-0.1101,Y=-0.1011 试利用补码Booth算法(比较 法)求X·Y=? 给出计算过程。
3. 将十进制数+76.75存入某微机中,试写出其IEEE754标准规 格化单精度浮点数形式。
第2章作业-2 参考答案
一、单项选择题: 1、两个浮点数相加,一个数的阶码值为7 ,另一个数的阶码值为9 ,则需要将阶码
值较小的浮点数的小数点( )。 A .左移1 位 B .右移1 位 C .左移2 位 D .右移2 位29 .
答案: C
2、如果某单精度浮点数、某原码、某补码、某移码的32位机器数均为 OxF0000000 。这些数从大到小的顺序是()。 A .浮原补移 B .浮移补原 C .移原补浮 D . 移补原浮 答案: D
说明
初始值,最后一位补0 Y4Y5=10 +[-X]补
右移一位 Y3Y4=01
+[X]补
右移一位 Y2Y3=10
+[-X]补
右移一位 Y1Y2=01
+[X]补
右移一位 Y0Y1=10 不移位
+[-X]补
3. 解:76.75 = 1001100.11 = 1.00110011 ×26 指数E = 7 + 127 = 133 = 1000 0101B 127是单精度浮点数应加的指数偏移量。
4. 某微机内存有一个单精度规格化浮点数(IEEE754标准)为 C2308000H,试写出其真值。
计算机组成原理
1. 解: X=-0.1110,Y=-0.1101 ,X*=0.1110,Y*=0.1101。 其中寄存器 B=X* ,计数器Cd=4。计算过程:
参考答案(第2章)

9 × 0.0049
= 9.3 × 10−3 m ⋅ s −1
3、 1、 根据均质形核的公式,得到:
r* =
2σ SLTm 2σ SLTm 2σ SLTmVm 2σ T V × N = = = SL m Fe * A * * Δ H ΔH v ΔT ΔH m × Δ T m × ΔT * ΔH m × ΔT Vm
= 1μ m 的液泡,需要的附加压力为
2σ 2 × 860 × 10−3 p= = = 1.72MPa r 10−6
对于半径 r
= 0.1μ m 的液泡,需要的附加压力为
2σ 2 × 860 × 10−3 p= = = 17.2MPa r 10−7
2、 根据 Stokes 公式,得到:
2r 2 (γ l − γ MnO ) 2r 2 ( ρl − ρ MnO ) g v= = 9η 9η = 2 × ( 0.1 × 10−3 ) × (7500 − 5400) × 9.8
其中 ΔH m 是摩尔原子的结晶潜热,Tm 是凝固点温度, R 是普适气体常数,η 是表面 配位数,ν 是晶体内部配位数,对于不同类型的晶体以及表面的晶面取向不同, 最大为 0.5。 当 α 1). Al
η ν
不同,
≤ 2 ,得到粗糙界面,当 α > 2 ,得到光滑界面。
Al 是 fcc 结构,
η Tm = 933K , ΔH b = 290.93 × 103 J/mol , = 0.5 , 从气态凝结时, ν
2
3
ρ MnO = 5400kg / m3 。若 MnO 为球形,半径为 0.1mm ,求它在钢液中的上浮速度?
3、 金属元素 Fe 的结晶潜热 ΔH m = 15.17 kJ / mol ,熔点 Tm = 1811K ,固/液界面张力
第二章作业 参考答案
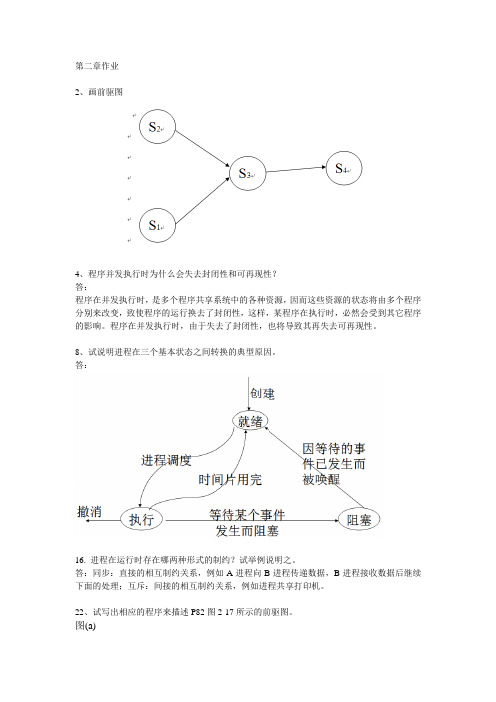
第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。
第2章作业参考答案

2. 一批晶体管中有个 9 个合格品和 3 个不合格品,从中任取一个安装在电子设备上。若取 出不合格品不再放回,求取得合格品前已取出的不合格品个数的分布律和分布函数。 解:
X0 1 2
3
p 3/4 9/44 9/220 1/220
⎧ 0,
x<0
F (x) = ⎪⎪⎪⎨321/ 4/ ,22,
0≤ x <1 1≤ x < 2
求: (1) 系数 A,B; (2) X 落在区间(-1,1)的概率; (3) X 的概率密度。 解:
x∈R
7. 从一批子弹中任意抽出 5 发试射,若没有一发子弹落在靶心 2 厘米以外,则接受该批子 弹。设弹着点与靶心的距离 X(厘米)的概率密度为
f
(
x)
=
⎪⎧ ⎨
Axe−
x2
,
⎪⎩ 0,
0< x<3 其他
X
~
B
⎛ ⎜⎝
4,
1 5
⎞ ⎟⎠
, 故分布律为
P( X = k) = C4k (0.2)k (0.8)4−k , k = 0,1, 2, 3, 4
( ) (2)P X = k
=
C5k
*
C 4− 20
k
C245
k = 0,1,2,3,4
5. 临床观察表明,某药物产生副作用的概率为 0.002。现在 900 个患者服用该药物,求至 少有3例患者出现副作用的概率.
试求:(1)系数 批子弹被接受的概率。 解:
⎧ 0,
x<0
∫ ∫ (2) F(x) =
x −∞
f
(t)dt
=
⎪⎪ ⎨ ⎪
x2 0 1 − e−9
马克思主义基本原理概论第二章习题及参考答案

其次章习题与参考答案一、单项选择题1.马克思主义认为,从人的活动机制看,实践是()A.主体与客体通过中介相互作用的过程B.道德行为和政治活动C.科学试验D.生活、行为、现实、实事等感性活动2.实践的主体是( )A.肯定精神B.具有思维实力、从事社会实践和相识活动的人C.人D.人的意识3.实践的客体是( )A.肯定精神的对象化B.客观物质世界C.人的意识的创建物D.进入主体的相识和实践范围的客观事物4.实践的中介是( )A.各种形式的工具、手段与其运用的程序和方法B.对一事物存在和发展有联系的各种要素的总和C.构成事物一切要素的总和D.受命于主观,见之于客观的活动5.马克思主义认为,主客体之间的价值关系是指( )A.主体对客体的物质欲望和要求B.主体对客体的能动反映C.主体对客体的改造和变革的结果D.客体对于主体的有用性和效益性6.“社会上一旦有技术上的须要,则这种须要会比十所高校更能把科学推向前进。
”这说明( A.实践是相识的来源B.技术推动了科学的发展C.实践是相识发展的动力D.科学进步是实践的目的7.恩格斯说:“人的智力是依据人如何学会改造自然界而发展的。
”这说明( )A.自然界是相识发展的动力B.实践是相识发展的动力C.人的相识具有主观能动性D.人具有相识自然的实力8.科学家尼葛庞蒂说:“预料将来的最好方法就是把它创建出来。
”从相识和实践的关系看,句话对我们的启示是( )A.相识总是滞后于实践B.实践和相识互为先导C.实践高于(理论的)相识,因为它不仅具有普遍性的品行,而且具有干脆现实性的品行D.实践与相识是合一的9.“纸上得来终觉浅,绝知此事要躬行”,陆游这一名句强调的是( )A.实践是相识的来源B.实践是推动相识发展的动力C.实践是相识的目的D.间接阅历毫无用处10.感性相识和理性相识的区分是( )A.感性相识是牢靠的,理性相识是不行靠的B.感性相识来源于实践,理性相识来源于书本C.感性相识是对现象的相识,理性相识是对本质的相识D.感性相识来源于干脆阅历,理性相识来源于间接阅历11.我们通过眼、耳、鼻、舌、身各种感官感觉到一个梨子的各种属性,在意识中把它们联系起形成了关于这个梨子的感性形象,这种反映形式是( )A.感觉B.知觉C.表象D.分析12.对于哲学史上长期争辩不休的唯理论和阅历论两大派别的正确评价是( )A.唯理论是正确的,阅历论是错误的B.阅历论是正确的,唯理论是错误地C.唯理论和阅历论各有片面的真理性D.唯理论和阅历论都是完全错误的13.“真理和谬误的对立,只是在特别有限的范围内才有意义”是( ) A.形而上学的观点B.唯物辩证法的观点C.诡辩论的观点D.相对主义的观点14.真理与谬误之间的相互关系是( )A.在任何状况下都是肯定对立的B.没有相互转化的可能性C.在肯定条件下可以相互转化D.两者之间没有原则区分15.“真理是人造的供人运用的工具”的看法是( )A.主观唯心主义B.客观唯心主义C.辩证唯物主义D.机械唯物主义16.“真理是思想形式,是人类阅历的组织形式”这是( )A.主观唯心主义真理论B.辩证唯物主义真理论C.客观真理论D.形而上学真理论17.“此亦一是非,彼亦一是非”的命题,其含义是( )A.强调真理的客观性B.否仔细理的客观性C.强调真理具有客观标准D.否仔细理具有客观标准18.“对客观事物的反映即是真理”,这是( )A.混淆了真理性相识与一般相识的错误观点B.辩证唯物主义的真理观C.一切唯物主义的真理观D.混淆了真理的客观性与规律客观性19.“听其言必责其用,观其行必求其功。
第二章 习题参考答案(修正)

第二章 需求、供给与均衡价格(题目及习题解答)一、判断题1.需求曲线描述了:其它条件不变,市场需求量与价格之间的关系。
解答:√。
知识点:课本第14页倒数第3行。
2.以纵轴代表价格,横轴代表数量,如果两条需求曲线通过同一点,则在那一点处,较陡的那条的弹性更大。
解答:×。
知识点:(考察弹性的几何意义)课本21页公式2.6和22页6-15行。
应该是“较陡的那条的弹性更小”。
理由:图中,直线AC 、BD 分别为需求曲线1和需求曲线2,AC 比BD 陡峭。
AC 之上的E 点弹性等于|AE|/|CE|,而BD 之上的E 点弹性等于|BE|/|DE|。
不难判定,|BE|>|AE|,而|DE|<|CE|,所以|AE|/|CE|<|BE|/|DE|,即“在那一点处,较陡的那条的弹性更小”。
3.如果需求是一条倾斜的直线,则价格水平越高,需求的价格弹性(绝对值)越大。
解答:√。
知识点:两种解法。
第一种是利用弹性的几何意义,课本22页6-7行。
如左下图所示:D 点价格大于B 点,D 点弹性=|AD|/|CD|>B 点弹性=|AB| /|BC|;第二种利用21页公式2.6。
因为B 点和D 点都在同一条直线上,所以dQ/dP 都相同,而P2<P 1,Q 2>Q1。
2121E E B D P P dQ dQ dP Q dP Q =⋅<=⋅ 4.如供给是一条直线,则供给的价格弹性为常数。
解答:×。
26页2.10b 。
“供给的价格弹性不确定”。
设供给函数为P=a+b ·Q s ,则dQ s /dP=-1/b 2,5.需求曲线越陡峭,则供给的变化对价格的影响越大。
P=a 1+b 1·Q s ,需求曲线P=a 2-b 2·Q d 。
令Q *=Q s =Q d ,得P *=(a 1b 2+b 1a 2)/(b 1+b 2)。
需求曲线a 1变化而b 1不变(平行移动)。
第二章 参考答案

第二章参考答案【思考题】一、资金时间价值同一般的利息率是什么关系?答:一般的利息率充分考虑了风险因素和通货膨胀因素,而表示资金时间价值的利息率则是指在无通货膨胀、无风险情况下的社会平均资金利润率。
二、对资金时间价值产生的原因通常有哪些解释?其真正的来源是什么?答:对资金时间价值产生的原因通常的解释有:其一,货币时间价值是人们认知心理的反映,认为现在单位资金价值要高于未来单位资金的价值;其二,资金时间价值是资源稀缺性的体现。
其三,资金时间价值是对机会成本的补偿。
因资金持有者的“放弃”而得到好处的人就应该做出相应的补偿,资金的时间价值就可以看出是对放弃流动偏好或者当前消费所产生的机会成本的补偿。
资金时间价值真正的来源是工人劳动者创造的剩余价值,资本使用者支付给资本所有者以利息,实质上是工人创造的剩余价值的再分配。
三、对单一项目进行取舍与否的决策,计算其风险价值的基本步骤有哪些?答:基本步骤如下:1.计算预期收益;2.计算收益标准差;3.计算收益标准差率;4.计算应得风险收益率;5.计算预测投资收益率和预测风险收益率;6.比较预测风险收益率和应得风险收益率,进行方案取舍。
四、后付年金和先付年金终值和现值之间有怎样的关联?答:n期后付年金和n期先付年金,两者付款期数相同,但先付年金终值比后付年金终值多一个计息期;n期后付年金和n期先付年金,两者付款期数相同,但先付年金现值比后付年金现值少一个贴现期。
【练习题】一、名词解释:资金时间价值资金风险价值年金风险性投资决策答:资金时间价值——资金的时间价值是指资金在周转过程中随着时间的推移而形成的增值。
资金风险价值——资金风险价值是指由于冒险投资而获得的超过资金时间价值的额外收益。
年金——年金是指在一定期限内等额定期的系列收付款项。
风险性投资决策——是指各个因素的未来情况不能完全确定,但未来情况发生的可能性即概率为已知的投资决策。
二、选择题(1-5为单项选择,6-9为多项选择)1.年金的收付款方式有多种,其中每期期末收付款的年金是( A )A.普通年金B.预付年金C.延期年金D.永续年金2.下面有关资金时间价值的表述,正确的是( A )A.资金时间价值的实质是资金周转使用后的增值额B.资金时间价值是推迟消费所获得的报酬C.资金时间价值只能用绝对数来表示D.资金时间价值的量无法进行计量3.下列可用于衡量投资风险程度的指标是( C )A.概率B.预期收益C.标准离差率D.风险价值系数4.用于比较预期收益不同的投资项目风险程度的指标是( A )A.标准离差率B.标准离差C.预期收益的概率D.预期收益5.在下列各项年金中,无法计算出确切终值的是( D )A.后付年金B.先付年金C.递延年金D.永续年金6.年金是指一定期间内每期相等金额的收付款项,通常采取年金形式的有( A C)A.保险金B.普通股股息C.租金 D.税金E.利润7.关于投资风险价值,下列表述正确的有( A C D E )A.投资风险价值有风险收益额和风险收益率两种表示方法B.风险收益额是投资者进行投资所获得的投资收益总额C.风险收益率是风险收益额与投资额的比率D.在实际工作中,投资风险价值通常以风险收益率进行计量E.一般来说,风险越大,获得的风险价值应该越高8.风险价值系数的确定方法包括( B C D )A.根据市场平均利润率确定B.由企业领导或有关专家确定C.根据以往同类项目的有关数据确定D.由国家有关部门组织专家确定E.根据投资人要求的最低报酬率确定9.下列关于年金的表述正确的有(C D E )A.年金是指一定时期发生的系列收付款项B.年金是指一定时期等额的系列收付款项C.普通年金是指一定时期每期期末等额的系列收付款项D.先付年金是指一定时期每期期初等额的系列收付款项E.递延年金是指最初若干期没有收付款项,随后若干期等额的系列收付款项【技能训练】一、向银行存入本金1000元,年利率为6%,则5年后的终值为多少?(分别用单利和复利计算)答:用单利计算有:F=P ×(1+i×n)=1000×(1+6%×5)=1300(元)用复利计算有:F=P ×(1+i) n =P ×(F/P ,6%,5)=1000×1.338=1338 (元)二、某人在5年后需要使用一笔20 000元资金,银行利率为8%,则现在应该一次存入本金多少钱?(分别用单利和复利计算)答:用单利计算有:11P F i n =⨯+⨯=20000×118%5+⨯=14286(元) 用复利计算有:1(1)nP F i =⨯+= F ×(P / F ,8%,5) =20000×0.681=13620 (元) 三、存入银行10 000元,年利率为10%,按季复利计息,存款期限2年,试计算: 1.两年后的本利和; 2.计算其实际利率。
第2章思考题参考答案_58809914

第二章 思考题参考答案1. 工质膨胀时是否必须对工质加热?工质边膨胀边放热可能否?工质边被压缩边吸入热量可以否?工质吸热后内能一定增加?对工质加热,其温度反而降低,有否可能?答:由闭口系统热力学第一定律关系式:Q U W =∆+规定吸热0Q >,对外做功0W >。
(1) 不一定;工质膨胀对外做功,0W >,由于可以使0U ∆<,因此可能出现0Q <,即对外放热;(2) 能,如(1)中所示;(3) 能;工质被压缩,对内做功,0W <,由于可以使0U ∆>,因此可能出现0Q >,即吸入热量;(4) 不一定;工质吸热,0Q >,由于可以使0W >,即工质对外做功,因此可能出现0U ∆<,即工质内能减小;(5) 可能;对工质加热,0Q >,由于可以使0W >,即工质对外做功,因此可能出现0U ∆<,对于理想气体,其内能仅为温度的单值函数,因此对于理想气体来说温度可能降低。
2. 一绝热刚体容器,用隔板分成两个部分,左边贮有高压气体,右边为真空。
抽去隔板时,气体立即充满整个容器。
问工质内能、温度将如何变化?如该刚体容器为绝对导热的,则工质内能、温度又如何变化?答:对于绝热刚体容器,以高压气体为对象。
由闭口系统热力学第一定律:Q =∆U +W (式1)。
其中容器绝热,则Q=0;且右边为真空,高压气体没有对外做功对象,即自由膨胀,有0W =。
所以:∆U =0,即工质的内能不发生变化。
如果工质为理想气体,那么其温度也不变;如果工质为实际气体,则温度未必不变。
如果该刚体容器为绝对导热,那么初始状态下容器内工质与外界环境等温,而自由膨胀过程终了时容器内工质仍旧与外界环境等温。
当外界环境温度不发生变化时,容器内工质温度在整个自由膨胀过程中温度不变。
自由膨胀0W =,所以Q =∆U 。
如果工质为理想气体,其温度不变则内能也不变,∆U =0,所以Q =0; 如果工质为实际气体,Q =∆U ,无法进一步推断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 参考答案2写出下列十进制数的原码、反码、补码和移码表示(用8位二进制数)。
如果是小数,则用定点小数表示;若为整数,则用定点整数表示。
其中MSB 是最高位(符号位),LSB 是最低位。
(1)-1 (2) -38/64解:(1)-1=(-0000001)2原码: 10000001反码: 11111110 吧 补码: 11111111移码: 01111111(2)-38/64=-0.59375=(-0.1001100)2或-38/64=-(32+4+2)*2-6=-(100110)*2-6=(-0.1001100)2原码: 1.1001100 反码: 1.0110011 补码: 1.0110100 移码: 0.0110100注:-1如果看成小数,那么只有补码和移码能表示得到,定点小数-1的补码为:1.0000000此例类似于8位定点整数的最小值-128补码为100000003 有一字长为32位的浮点数,符号位1位;阶码8位,用移码表示;尾数23位,用补码表示;基数为2.请写出:(1)最大数的二进制表示,(2)最小数的二进制表示,(3)规格化数所能表示的数的范围。
解:(题目没有指定格式的情况下,用一般表示法做)(1)最大数的二进制表示:0 11111111 11111111111111111111111(2)最小数的二进制表示:1 11111111 00000000000000000000000(1) )(231221*27--- (2) )(1*2127--(3)规格化最大正数:0 11111111 11111111111111111111111)(231221*27---规格化最小正数:0 00000000 10000000000000000000000122*27-- 规格化最大负数:1 00000000 01111111111111111111111 )(231222*27---+-规格化最小负数:1 11111111 00000000000000000000000)(1*2127-- 规格化数的表示的数的范围为: )]21*2,2*2[]22*2,1*2[231212*********---------+--()()(Y 4. 将下列十进制数表示成IEEE754标准的32位浮点规格化数。
-27/64解:X =(-27/64)10=(-11011.×2 _6)2 =(-0.011011)2 =-(1.1011×2 -2) S=1 E=-2+127=125=01111101 M=1011IEEE754标准的32位浮点规格化数为:1 01111101 101100000000000000000005. 已知X 和Y, 用变形补码计算X+Y, 同时指出运算结果是否溢出。
(1) x=11011 y=00011解: [X]补=0011011, [Y]补=0000011[X+Y]补=[X]补+ [Y]补[X]补 0011011+ [Y]补 0000011------------------------[X+Y]补 0011110符号位为00,结果无溢出X+Y =111106. 已知X 和Y, 用变形补码计算X-Y, 同时指出运算结果是否溢出。
(1) x=11011 y=-11111解:[X]补=0011011, [Y]补=1100001,[-Y]补=0011111[X+Y]补=[X]补+ [-Y]补[X]补0011011+ [-Y]补0011111------------------------[X-Y]补0111010符号位为01,结果溢出X-Y=110107. 用原码阵列乘法器计算X×Y。
(1)X=11011 Y= -11111解:[x]补=0 11011 [y]补=100001符号位单独运算:0⊕1=1尾数部分算前求补器输出为|x|=11011, |y|=111111 1 0 1 1×) 1 1 1 1 1----------------------------------1 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 11 1 0 1 1-----------------------------------------1 1 0 1 0 0 0 1 0 1乘积符号位1,算后求补器输出为0010111011,最后补码乘积值为:(算后求补器输出不带符号位,详见课本36页图2.7;该图中符号位输入到算后求补器是为了作为控制信号,详见课本35页图2.6中的控制性号线E)【x×y】补= 100101110118.用原码阵列除法器计算X÷Y。
(1)X=11000 Y= -11111解:X和Y先都乘以一个比例因子2-101X=0.11000 ,Y= -0.11111[∣x∣]补=0.11000,[∣y∣]补=0.11111,[-∣y∣]补=1.00001符号位单独运算:0⊕1=11)余数左移的解法(恢复余数法):被除数 X 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q0=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.11000左移 01.10000+[-|y|]补11.00001----------------------余数为正 00.10001 →q1=1余数为正,商上1左移 01.00010+[-|y|]补 11.00001----------------------余数为正 00.00011 →q2=1 余数为正,商上1左移 00.00110+[-|y|]补 11.00001----------------------余数为负 11.00111 →q3=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.00110左移 00.01100+[-|y|]补11.00001----------------------余数为负 11.01101 →q4=0余数为负,商上0+[|y|]补 00.11111 恢复余数----------------------00.01100左移 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q5=0余数为负,商上0+[|y|]补 00.11111----------------------余数 00.11000故[x÷y]原=1.11000 即x÷y= -0.11000,余数=0.11000*2-101*2101=0.110002)余数左移的解法(加减交替法):被除数 X 00.11000+[-|y|]补11.00001----------------------余数为负 11.11001 →q0=0余数为负,商上0左移 11.10010+[|y|]补 00.11111----------------------余数为正 00.10001 →q1=1余数为正,商上1左移 11.00010+[-|y|]补 11.00001----------------------余数为正 00.00011 →q2=1 余数为正,商上1左移 00.00110+[-|y|]补 11.00001----------------------余数为负 11.00111 →q3=0余数为负,商上0左移 10.01110+[|y|]补 00.11111----------------------余数为负 11.01101 →q4=0余数为负,商上0左移 10.11010+[|y|]补 00.11111----------------------余数为负 11.11001 →q5=0余数为负,商上0+[|y|]补 00.11111----------------------余数 00.11000故[x÷y]原=1.11000 即x÷y= -0.11000,余数=0.11000*2-101*2101 =0.11000 3)除数右移的解法(加减交替法):被除数 X 0.1100000000+[-∣y∣]补 1.00001-------------------------余数为负 1.1100100000 →q0=0余数为负,商上0+[|y|]补 0.011111-------------------------余数为正 0.010******* →q1=1余数为正,商上1+[-|y|]补 1.1100001------------------------余数为正 0.0000011000 →q2=1余数为正,商上1+[-|y|]补 1.11100001------------------------余数为负 1.1110011100 →q3=0余数为负,商上0+[|y|]补 0.000011111------------------------余数为负 1.1111011010 →q4=0余数为负,商上0+[|y|]补 0.0000011111------------------------余数为负 1.1111111001 →q5=0余数为负,商上0+[|y|]补 0.0000011111-------------------------余数 0.0000011000故[x÷y]原=1.11000 即x÷y= -0.11000,余数= 0.0000011*2101=0.110009 设阶码5位(包含2位符号位), 尾数9位(包含2位符号位), 都为补码表示,采用0舍1入,计算X+Y,X-Y:X=2-101×(-0.1001011) Y=2-011×0.0101011解:[x]=11011,11.0110101浮=11101,00.0101011[y]浮[-y]=11101,11.1010101浮① 0操作数检查两数都非0②对阶[ΔE]补=[Ex]补+[-Ey]补=11011+00011=11110可见ΔE =-2将M x 右移2位,[x]浮=11101,11.11 01101(01)③尾数相加相加 相减11.1101101(01) 11.1101101(01) + 00.0101011 + 11.1010101 ------------------------ ------------------------ 00.0011000(01) 11.1000010(01)④结果规格化[x+y]浮=11101,00.0011000(01) 左规 [x+y]浮=11011,00.1100001[x-y]浮=11101, 11.1000010(01) 左规 [x-y]浮=11100, 11.0000100(1) ⑤舍入处理 (用0舍1入)得[x+y]浮不需舍入处理[x-y]浮=11100, 11.0000101⑥判溢出X+Y 和X-Y 的阶符都是11,都没溢出最终的结果为:x+y=2-101×(0.1100001)x-y=2-100×(-0.1111011)。
