职高二年级数学段考试题
职高二年级第一次月考数学试题

职高二年级第一次月考数学试题时量:90分钟满分:100分一、选择题(每小题4分,共40分)1、空间中的两条直线a⊥b,则它们的位置关系是()A、相交B、异面C、相交或异面D、共面2、一条直线和两条异面直线中的一条平行,它和另一条的位置关系是()A、平行B、相交C、异面D、相交或异面3、直线l与平面α内的两条直线a、b都垂直,则()A、l⊥αB、l∥αC、l⊆αD、关系不能确定4、在一个平面内与这个平面的一条斜线垂直的直线()A、有无数条B、不存在C、有两条D、只有一条5、若α∥β,a⊆α,b⊆β,则a与b的位置关系是()A、平行B、异面C、相交D、平行或异面6、直线l和平面α都垂直于平面β,那么l与α的位置关系是()A、l∥αB、l∥α或l⊆αC、l⊥αD、l⊄α7、a、b是两条异面直线,且分别在平面α、β内,若α β=l,则直线l必定()A、分别于a、b相交B、至少与a、b之一相交C、与a、b都不相交D、至多与a、b之一相交8、下列四个命题中正确的命题是()A、三点确定一个平面B、两两相交于三点的三条直线共面C、若直线a平行于平面β内的一条直线b,则a∥βD、和两条异面直线都垂直相交的直线有无数条9、正方体ABCD-A1B1C1D1中,∠A1BC1的度数是( )A、30°B、45°C、60°D、90°10、空间四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是()A、棱形B、矩形C、梯形D、正方形二、填空题(每小题4分,共24分)11、在正方体ABCD-A1B1C1D1中,(1)BC与AD1所成的角的度数是_____________(2)AD1与底面ABCD所成的角的度数是_________12、正方体ABCD-A1B1C1D1中,二面角A-BC-D1的度数是______13、一条线段长为20cm,它的两端到平面的距离分别是15cm和25cm,则这条线段所在的直线和平面所成的角的大小是__________ 14、如果空间的两个角α和β的两组对应边分别平行,则α=β或α+β=____________15、在长方体ABCD-A1B1C1D1中,同时与棱AA1、棱BC都垂直的棱有__________条16、已知二面角α-AB-β的平面角为30°,点P在半平面α内,点P 到半平面β的距离为1,则点P到棱AB的距离是___________三、解答题(每小题12分,共36分)17、如图,已知长方体的棱AB=1,BC=2,AA1=3,(1)求A 1B 与C 1D 1所成的角的度数 (2)求BC 1与平面CD 1所成的角的正切值(3)求平面A 1BCD 1与平面ABCD 所成的角的度数18、如图,MA 垂直矩形ABCD 所在的平面,MA=2,AB=3,BC=4 (1)求点M 到点C 的距离 (2)求点C 到平面MADD 1ACBDAB C19、如图,在正方体ABCD-A1B1C1D1中,(1)判断A D1与BC1是否平行,请说明理由(2)判断AC与BD1是否垂直,请说明理由职高二年级第一次月考数学答题卡时量:90分钟满分:100分一、选择题(每小题4分,共40分)1、________2、________3、_________4、________5、________6、________7、________8、_________9、________10、_______二、填空题(每小题4分,共24分)11、(1)________(2)________12、_________13、__________14、________________15、______________16、______________三、解答题(每小题12分,共36分)17、 18、 19、CBA C 1。
高二职高数学练习题

高二职高数学练习题一、选择题1. 以下哪个不是函数?A. y = 2x + 3B. x^2 + y^2 = 9C. y = sin(x)D. x = 22. 若函数y = 2x^3 - 5x^2 + 3x - 7,求其一阶导数。
A. y' = 6x^2 - 10x + 3B. y' = 6x^2 - 5x + 3C. y' = 2x^2 - 5x + 3D. y' = 2x^3 - 5x^2 + 3x - 73. 已知函数f(x) = x^2 + 3x - 2,g(x) = 2x + 1,求f(g(x))的表达式。
A. 2x^2 + 6x - 3B. x^2 + 2x - 1C. 4x^2 + 4x - 6D. 2x^2 + 7x - 34. 若函数y = log(x) + ln(x),求其定义域。
A. x > 0B. x ≠ 0C. x > 1D. x ≠ 15. 已知直角三角形中,两条直角边分别为3和4,求其斜边长度。
A. 7B. 10C. 14D. 25二、填空题1. 设函数y = mx + b,已知其过点(2, 5),则b的值为____。
2. 已知函数f(x) = 2x^3 - 5x^2 + 3x - 7,求f(2)的值为____。
3. 若函数y = 2x^2 + bx + c在x = 1处有最小值,求b和c的值分别为____。
4. 若a + b = 6,2a + 3b = 15,则a的值为____。
5. 在等差数列2, 5, 8, 11, ...中,公差d的值为____。
三、解答题1. 解方程组:2x + 3y = 73x - 2y = 102. 求函数f(x) = x^3 + 2x^2 - 3x在区间[-2, 1]上的最大值和最小值。
3. 已知函数y = ax^2 + bx + c的图像经过点(1, -2),且在x = 2处的切线斜率为4,求a、b、c的值。
中职二年级数学试题

中职二年级数学试题一、选择题(每题2分,共20分)1、下列哪个选项是正确的?A. x+y=y+xB. x²>2xC. x+2>y+3D. x<y2、下列哪个函数在其定义域内是单调递增的?A. y=x²B. y=xC. y=2xD. y=x+23、下列哪个选项是方程x²-2x-3=0的解?A. x=3B. x=-1C. x=0D. x=24、下列哪个图形是平行四边形?A.矩形B.菱形C.梯形D.以上都是5、下列哪个数集是无穷集?A. {1,2,3}B. {1,1/2,1/3}C. {1,2,3,...}D. {1/2,1/3,1/4,...}二、填空题(每题3分,共30分)1、请填写正确的答案:3x+2y=____。
2、如果3x-2y=0,则x/y=____。
3、在数集{1,2,3,...}中,最小的数是____,最大的数是____。
4、下列哪个图形是三角形?请在是的选项中打√。
A B C D E F G √__________(请填写正确的答案)5、下列哪个数集是有限集?请在是的选项中打√。
A.{1,2,3}B.{1,1/2,1/3}C.{1,2,3,...}D.{1/2,1/3,1/4,...} √__________(请填写正确的答案)三、解答题(每题10分,共50分)6、解答题:请在解答题空白处填写完整的答案。
例如:解:由已知条件得方程x²+y²=5。
四、附加题(每题10分,共20分)小学二年级数学试题试题一、填空题(每题2分,共20分)1、一个四位数,它的千位上是8,十位上是4,其它数位上是0,这个数写作()。
2、用5、0、7、2组成一个四位数,其中最大的是(),最小的是()。
3、在有余数的除法中,被除数=商×除数+()。
4、一年有()个月,其中大月有()个月,小月有()个月。
5、8时敲8下,共用了10秒,那么10时敲10下,共用()秒。
中职数学2年级试卷【含答案】

中职数学2年级试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = x² 4x + 3,则f(2)的值为:A. 0B. 1C. -1D. 22. 下列函数中,奇函数是:A. f(x) = x³B. f(x) = x²C. f(x) = |x|D. f(x) = x² + 13. 若直线y = 2x + 3与x轴的交点为A,与y轴的交点为B,则三角形OAB的面积是:A. 3B. 4.5C. 6D. 94. 若一组数据2, 3, 5, 7, 11, x的平均数为6,则x的值为:A. 4B. 6C. 8D. 105. 在直角坐标系中,点(3, -4)关于原点的对称点是:A. (3, 4)B. (-3, 4)C. (-3, -4)D. (3, -4)二、判断题(每题1分,共5分)1. 若a > b,则a² > b²。
()2. 任何实数的平方都是非负数。
()3. 一元二次方程ax² + bx + c = 0(a ≠ 0)的判别式Δ = b² 4ac。
()4. 函数f(x) = 2x + 3的图像是一条直线。
()5. 对角线互相垂直的四边形一定是菱形。
()三、填空题(每题1分,共5分)1. 若sinθ = 1/2,且θ为第二象限角,则cosθ = _______。
2. 方程x² 5x + 6 = 0的解为x₁ = _______,x₂ = _______。
3. 若一组数据1, 3, 5, 7, 9的平均数为a,则数据2a 1, 2a + 1, 2a + 3, 2a + 5, 2a + 7的平均数为_______。
4. 在ΔABC中,若∠A = 30°,∠B = 60°,则∠C = _______°。
5. 若函数f(x) = 3x² 12x + 9,则f'(x) = _______。
高二职高期末数学试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共50分)1. 下列各数中,属于无理数的是()A. √4B. √9C. √16D. √252. 若函数f(x) = 2x + 1,则f(3)的值为()A. 7B. 8C. 9D. 103. 下列图形中,属于等边三角形的是()A. 图形1B. 图形2C. 图形3D. 图形44. 已知等差数列{an}的前三项分别为1,3,5,则该数列的公差为()A. 1B. 2C. 3D. 45. 若直线y = kx + b与圆x² + y² = 1相切,则k和b的关系为()A. k² + b² = 1B. k² - b² = 1C. k² + b² = 0D. k² - b² = 06. 下列各函数中,为奇函数的是()A. y = x²B. y = x³C. y = x⁴D. y = x⁵7. 若复数z满足|z - 2i| = 3,则复数z在复平面上的轨迹是()A. 一条射线B. 一个圆C. 一条直线D. 一条抛物线8. 下列各数中,属于正数的是()A. -3B. 0C. 1D. -19. 若a,b,c是等差数列,且a + b + c = 12,a² + b² + c² = 42,则ab + bc + ca的值为()A. 18B. 24C. 30D. 3610. 若sinα = 1/2,cosα = √3/2,则tanα的值为()A. 1B. √3C. -1D. -√3二、填空题(每题5分,共50分)1. 函数f(x) = x² - 4x + 3的图像与x轴的交点坐标为__________。
2. 若等比数列{an}的首项为a₁,公比为q,则a₃ = _________。
3. 圆的标准方程为(x - 2)² + (y + 3)² = 16,圆心坐标为__________。
职业中专二年级期末考试数学试题

一、选择题:(每小题3分,共计30分)1、已知数列{}n a 的通项公式这25n a n =-,那么n a =( ) A 、2n-5 B 、4n-5 C 、2n-10 D 、4n-102、753222----⋅⋅⋅等差数列、、、、的第n+1项为( )A 、1(7)2n -;B 、()142n -C 、42n -D 、72n-3、{}236,n n a s a ==在等差数列中,已知则( ) A 、18 B 、12 C 、9 D 、64、{}2582=6,n a a a ==在等比数列中,已知a ,则( ) A 、10 B 、12 C 、18 D 、 245、平面向量定义的要素是( )A 、大小和起点;B 、方向和起点;C 、大小和方向D 、大小、方向和起点 6、AB AC BC --=( )A 、BC ;B 、CB ;C 、0;D 、0 7、下列说法不正确的是( )A 、零向量和任何向量平行B 、平面上任意三点A 、B 、C ,一定有AB BC AC +=C 、AB=CDR AB CD m ∈若(m ),则 D 、若11a x e =,22b x e =时a b = 8、()()1212A ,B ,AB a a b b 设点及点,则的坐标是( )A 、1122(a -b ,a -b ) ;B 、1212(a -a ,b -b ) ;C 、1122(b a ,b -a )- ;D 、2121(a -a ,b -b )9、若4222a b a b a b =-==,,则,是( ) A 、00; B 、090; C、0180; D 、0270 10、下列各向量中互相垂直的是( )A 、a =(4,2),b =(-3,5)B 、a =(-3,4) ,b =(4,3)C 、a =(5,2),b =(-2,-5)D 、a =(2,-3),b =(3,-2) 二、填空题:(每小题2分,共计20分) 1、AC BC -=________________2、OP =设O 点为坐标原点,P(1,1),Q(4,5),则_______PQ =_______PQ =_______3、已知a =(1,3),b=(2,-4),c =(-2,5),则a +2b -3c =_________________________________4、设a =(-2,-3),b =(6,-5),则a b =_____________5、设a =(3,-1),b =(1,-2),则(2a +b )(a -b)=___________________6、数列1n ⎧⎫⎨⎬⎩⎭中,第7项为_______7、通项公式为32n a n =-的通项公式是公差为________的等差数列8、通项公式为42n a n n =+的数列的前项和的公式为______________________________9、在等比数列{}1413,2n a a q a ==-=中,已知,则____________10、在等比数列{}35711,4n a a a a ===中,已知,则_______________答题卡一、选择题(每小题3分,共计30分) 二、填空题:(每空2分,共计20分)1、_____2、______、______、______3、_______4、_________5、_________6、______7、______8、______________9、_________10、___________ 三、解答题:(每小题10分,共计50分) 1、 (1)、在等差数列{}4416,48,n a a s a ==中,求(2)、在等比数列{}36813,,9n a a a a =-=-中,求2、在等比数列{}35104,16,n a a a ==中,求s3、已知a=3,b=4,a与b的夹角为0120,求(1)、a b;(2)、(3a-2b)(a+2b)4、已知a=(1,3),b=(m,n),且a+2b=(5,-5),求实数m、n的值5、设向量a= (-1,3),b=(m,2),当m为何值时(1)、a与b垂直(2)、a与b平行。
中职数学2年级试卷

中职数学2年级试卷专业课原理概述部分一、选择题(每题1分,共5分)1. 若函数f(x) = 2x + 3,则f(4)的值为()A. 5B. 11C. 6D. 122. 已知等差数列的前三项分别为1, 3, 5,则第四项为()A. 4B. 6C. 7D. 83. 下列哪个图形不是正多边形()A. 正方形B. 正五边形C. 正六边形D. 等边三角形4. 若a, b为实数,且a > b,则下列哪个选项一定成立()A. a^2 > b^2B. a + b > 0C. a b > 0D. a/b > 15. 若一个三角形的两边长分别为3和4,则第三边的长度可能是()A. 1B. 5C. 6D. 7二、判断题(每题1分,共5分)1. 若两个角互为补角,则这两个角的和为90度。
()2. 任何两个奇数之和都是偶数。
()3. 一元二次方程ax^2 + bx + c = 0(a ≠ 0)的判别式Δ = b^2 4ac,若Δ > 0,则该方程有两个实数根。
()4. 两个等腰三角形的面积相等,则它们的周长也相等。
()5. 若函数f(x) = x^3,则f(-x) = -f(x)。
()三、填空题(每题1分,共5分)1. 若函数f(x) = x^2 2x + 1,则f(1) = _____。
2. 一个等差数列的前三项分别为2, 5, 8,则公差为_____。
3. 若一个三角形的三个内角分别为45度,45度和90度,则这个三角形是_____三角形。
4. 若a, b为实数,且a ≠ b,则下列哪个选项一定成立:_____。
5. 若一个圆的半径为r,则这个圆的周长为_____。
四、简答题(每题2分,共10分)1. 简述等差数列和等比数列的定义。
2. 什么是勾股定理?请给出一个具体的例子。
3. 请简述一元二次方程的求根公式。
4. 什么是函数的单调性?请给出一个具体的例子。
5. 什么是三角形的内角和定理?请给出一个具体的例子。
职高二年级数学段考试题
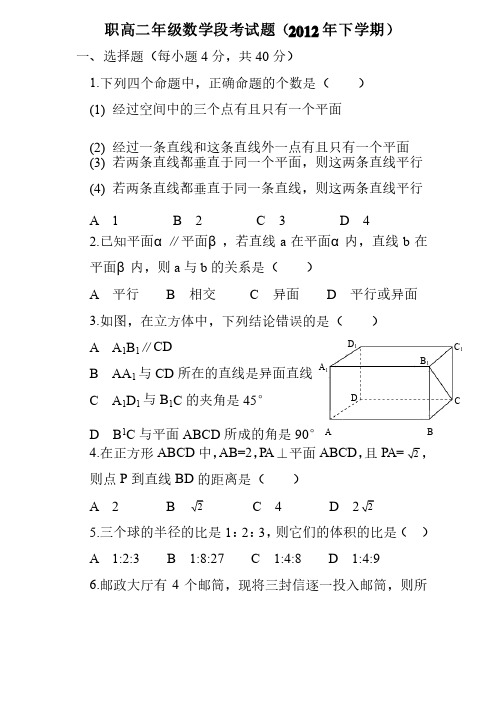
职高二年级数学段考试题(2012年下学期)一、选择题(每小题4分,共40分)分)1.下列四个命题中,正确命题的个数是(下列四个命题中,正确命题的个数是() (1) 经过空间中的三个点有且只有一个平面经过空间中的三个点有且只有一个平面(2) 经过一条直线和这条直线外一点有且只有一个平面经过一条直线和这条直线外一点有且只有一个平面(3) 若两条直线都垂直于同一个平面,则这两条直线平行若两条直线都垂直于同一个平面,则这两条直线平行(4) 若两条直线都垂直于同一条直线,则这两条直线平行若两条直线都垂直于同一条直线,则这两条直线平行 A 1 B 2 C 3D 42.已知平面α∥平面β,若直线a 在平面α内,直线b 在平面β内,则a 与b 的关系是(的关系是() A 平行平行 B 相交相交 C 异面异面 D 平行或异面平行或异面 3.如图,在立方体中,下列结论错误的是(如图,在立方体中,下列结论错误的是()A A 1B 1∥CD B AA 1与CD 所在的直线是异面直线所在的直线是异面直线C A 1D 1与B 1C 的夹角是45° D B 1C 与平面ABCD 所成的角是90°4.在正方形ABCD 中,AB=2,P A ⊥平面ABCD ,且P A=2, 则点P 到直线BD 的距离是(的距离是() A 2 B 2 C 4 D 22 5.三个球的半径的比是1:2:3,则它们的体积的比是( ) A 1:2:3 B 1:8:27 C 1:4:8D 1:4:9 6.邮政大厅有4个邮筒,现将三封信逐一投入邮筒,则所D 1 C 1 B 1 A 1 D CB A有投法种数为(有投法种数为() A 4 B 12 C 24D 64 7.一个口袋中装有2只不同的白球和1只黑球,每次取出1只球,取出后不放回。
现连续取2只球,则第一次取到黑球的概率是(黑球的概率是() A 12 B 23 C 13 D 348.湘北职专有2200名学生,其中高一年级950名学生,高二年级750名学生,高三年级500名学生,为了调查学生视力情况,要从中抽取一个容量为100名学生的样本,那么完成上述调查应采用的抽样方法是(么完成上述调查应采用的抽样方法是() A 随机抽样法随机抽样法 B 分层抽样法分层抽样法C 系统抽样法系统抽样法D 无法确定无法确定9.某种实验进行了10次,得到的实验数据是:20,18 22,19,21,20,19,19,20,21,则样本均值是(,则样本均值是( ) A 19.6 B 19.7 C 19.9D 19.8 10.已知某种商品的销售额y 万元与广告费x 万元之间的回归方程为y Ù=4.2857x+341.43,这说明(,这说明() A 广告费每增加1万元,商品销售额平均增加4.2857万元万元 B 广告费每增加1万元,商品销售额平均增加341.43万元万元 C 广告费为1万元时,商品销售额估计为4.2857万元万元 D 广告费为1万元时,商品销售额估计为341.43万元万元二、填空题(每小题5分,共20分)分)11.如图所示的正方体ABCD -A 1B 1C 1D 1中,中,∠A 1BC 1的度数为_________12.已知一个正三棱锥的底面边长为4,斜高为5,则这个正三棱锥的侧面积为,则这个正三棱锥的侧面积为____________ 13.200名高一年级学生,250名高二年级学生,300名高三年级学生,如果任意找其中1个谈话,则这个学生是高三年级的概率是__________14.从某工厂生产的某一批零件中,随机抽取10件,测得件,测得 长度为(单位:cm):79、81、80、78、79、81、79、82、79、78,则样本容量是___________三、解答题(每小题10分,共40分)分)15.如图,已知P A 垂直于三角形ABC 所在的平面,所在的平面, ∠ACB=90°AC=5,P A=53,(1) BC 与平面ACP 垂直吗?垂直吗?(2) 求二面角P -BC -A 的大小的大小D 1 C 1 B 1 A 1 D C B A C B A P16.如图,正四棱柱ABCD -A 1B 1C 1D 1的底面边长为32cm高为7cm , (1) 求正四棱柱的体积求正四棱柱的体积(2) 求顶点A 到底面对角线B 1D 1的距离AE17.某面试考场设有100张考签,编号为1,2,…,100,应试时,考生任意抽取一张考签答题,求:应试时,考生任意抽取一张考签答题,求:(1) 抽到10号考签的概率号考签的概率(2) 抽到前10号考签的概率号考签的概率18.科研人员在研究地里的麦苗长势时,随机抽取20株,测得各株高为(单位:mm):6167 58 67 65 64 5962 58 66 64 59 60 63 58 60 62 60 63 63,求样本均值、样本标准差.(精确到小数点后两位)(参考公式2222121[()()()]1n S x x x x x x n =-+-++--…) E D 1 C 1 B 1 A 1 D C B A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
职高二年级数学段考试题(2012年下学期)
一、选择题(每小题4分,共40分)
1.下列四个命题中,正确命题的个数是( )
(1) 经过空间中的三个点有且只有一个平面
(2) 经过一条直线和这条直线外一点有且只有一个平面
(3) 若两条直线都垂直于同一个平面,则这两条直线平行
(4) 若两条直线都垂直于同一条直线,则这两条直线平行
A 1
B 2
C 3
D 4
2.已知平面α∥平面β,若直线a 在平面α内,直线b 在平面β内,则a 与b 的关系是( )
A 平行
B 相交
C 异面
D 平行或异面
3.如图,在立方体中,下列结论错误的是( )
A A 1
B 1∥CD
B AA 1与CD
C A 1
D 1与B 1C 的夹角是45°
D B 1C 与平面ABCD 所成的角是904.在正方形ABCD 中,AB=2,PA ⊥平面ABCD ,且 则点P 到直线BD 的距离是( )
A 2
B
C 4
D 5.三个球的半径的比是1:2:3,则它们的体积的比是( )
A 1:2:3
B 1:8:27
C 1:4:8
D 1:4:9
6.邮政大厅有4个邮筒,现将三封信逐一投入邮筒,则所
有投法种数为()
A 4
B 12
C 24
D 64
7.一个口袋中装有2只不同的白球和1只黑球,每次取出1只球,取出后不放回。
现连续取2只球,则第一次取到黑球的概率是()
A 1
2B 2
3
C 1
3
D 3
4
8.湘北职专有2200名学生,其中高一年级950名学生,高二年级750名学生,高三年级500名学生,为了调查学生视力情况,要从中抽取一个容量为100名学生的样本,那么完成上述调查应采用的抽样方法是()
A 随机抽样法
B 分层抽样法
C 系统抽样法
D 无法确定
9.某种实验进行了10次,得到的实验数据是:20,18 22,19,21,20,19,19,20,21,则样本均值是()
A 19.6
B 19.7
C 19.9
D 19.8
10.已知某种商品的销售额y万元与广告费x万元之间的回归方程为y =4.2857x+341.43,这说明()
A 广告费每增加1万元,商品销售额平均增加4.2857万元B广告费每增加1万元,商品销售额平均增加341.43万元C广告费为1万元时,商品销售额估计为4.2857万元
D 广告费为1万元时,商品销售额估计为341.43万元
二、填空题(每小题5分,共20分)
11.如图所示的正方体ABCD -A 1B 1
∠A 1BC 1的度数为_________
12.
已知一个正三棱锥的底面边长为斜高为5____________ 13.200名高一年级学生,250名高二年级学生,300名高三年级学生,如果任意找其中1个谈话,则这个学生是高三年级的概率是__________
14.从某工厂生产的某一批零件中,随机抽取10件,测得 长度为(单位:cm):79、81、80、78、79、81、79、82、79、78,则样本容量是___________
三、解答题(每小题10分,共40分)
15.如图,已知PA 垂直于三角形ABC 所在的平面, ∠ACB=90°AC=5,
(1) BC 与平面ACP 垂直吗?
(2) 求二面角P -BC -A
16.如图,正四棱柱ABCD -A 1B 1C 1D 1的底面边长为
高为, (1) 求正四棱柱的体积
(2) 求顶点A 到底面对角线B 1D 1的距离AE
17.某面试考场设有100张考签,编号为1,2,…,100,应试时,考生任意抽取一张考签答题,求:
(1) 抽到10号考签的概率
(2) 抽到前10号考签的概率
18.科研人员在研究地里的麦苗长势时,随机抽取20株,测得各株高为(单位:mm):61 67 58 67 65 64 59 62 58 66 64 59 60 63 58 60 62 60 63 63,求样本均值、样本标准差.(精确到小数点后两位) (参考公式2222121[()()()]1n S x x x x x x n =-+-++--…)。
