主成分分析和聚类分析报告
高维数据分析方法
高维数据分析方法数据的快速增长和信息技术的快速发展带来了大规模、复杂和高维度的数据集，这对传统数据分析方法提出了新的挑战。
高维数据分析方法应运而生，为我们从庞大的数据中抽取有效信息提供了强有力的工具和技术。
本文将探讨几种常见的高维数据分析方法，包括主成分分析（PCA）、聚类分析、流形学习和深度学习。
一、主成分分析（PCA）主成分分析是一种常用的降维方法，通过将原始数据投影到新的低维空间上，保留最重要的特征，同时尽可能地减少信息损失。
它可用于数据可视化、特征提取等领域。
主成分分析基于数据的协方差矩阵，通过计算特征值和特征向量进行降维。
二、聚类分析聚类分析是将数据根据相似性进行分组的一种常见方法。
在高维数据中，聚类可以帮助我们发现潜在的模式和关系。
传统的聚类算法如K均值和层次聚类通常效果不佳，因为高维数据中存在维度灾难的问题。
为解决这一问题，一些新的聚类方法基于子空间聚类，将数据投影到不同的子空间中进行聚类。
三、流形学习流形学习是一种非传统的降维方法，通过在原始高维空间中构建数据的低维嵌入，将复杂的高维结构转化为简单的低维流形结构。
流形学习可以在保持数据相对距离的同时，显著降低维度，提高数据分析的效率。
常见的流形学习方法有等距映射（Isomap）、拉普拉斯特征映射（LE）和局部线性嵌入（LLE）等。
四、深度学习深度学习是一种通过多层神经网络进行特征学习和模式识别的方法。
在高维数据分析中，深度学习可以帮助我们自动学习数据的表征，发现复杂的模式和关系。
深度学习的关键是构建适当的神经网络模型，通过反向传播算法进行模型训练。
综上所述，高维数据分析方法在处理复杂的高维数据中起到了重要的作用。
无论是通过主成分分析进行降维，还是利用聚类分析、流形学习或深度学习方法进行数据挖掘，我们都可以从庞大的数据中提取有价值的信息。
随着数据规模和复杂度不断增加，我们需要不断改进和创新数据分析方法，以更好地应对高维数据分析的挑战。
聚类分析与主成分分析
二、聚类分析的典型(diǎnxíng)应 用
• 作为统计(tǒngjì)学的一个分支，聚类分析已有 多年的研究历史，这些研究主要集中在基于距 离的聚类分析方面。
• 许多统计(tǒngjì)软件包，诸如：SAS、SPSS 和S-PLUS等都包含它许多聚类分析工具。
第八页，共90页。
• 图论法。从几何观点来考虑。将n个样品看成m维空间的n个 点，点与点间用直线连接，从而构成m维空间的点的连接图， 再应用图论的观点将样本点在m维空间作最小支撑(zhī chēng)数，最终达到分类目的。
第十二页，共90页。
六、tree过程(guòchéng)
• 画出用于描述整个聚类过程的树状图
• 两种：
• 如何解释主成分所包含的经济意义。
第四十六页，共90页。
数学模型和几何(jǐ hé)解释
• 为了方便，我们在二维空间中讨论主成分的几何意义。 设有n个样品，每个样品有两个观测变量xl和x2，在 由变量xl和x2 所确定的二维平面中，n个样本点所散 布的情况如椭圆状。由图可以看出(kàn chū)这n个样 本点无论是沿着xl 轴方向或x2轴方向都具有较大的离 散性，其离散的程度可以分别用观测变量xl 的方差和 x2 的方差定量地表示。显然，如果只考虑xl和x2 中 的任何一个，那么包含在原始数据中的经济信息将会 有较大的损失。
第十一页，共90页。
五、聚类分析方法(fāngfǎ)
• 系统聚类法。先将n个元素看成n类，然后将性质最接近（或 相似程度最大）的两类合并为一个新类，得到n-1类。再从 中找出最接近的两类加以合并，变成n-2类。如此下去，最 后所有的元素全聚在一类之中。
• 调优法。先将样品做一个初始的分类，然后按照某种最优的 原则逐步调整，一直调整到分类比较合理为止。
主成分分析和聚类分析报告
北京建筑工程学院理学院信息与计算科学专业 实验报告课程名称〈数据分析》实验名称〈主成分分析和聚类分析》 实验地点：基础楼C-423日期2016.5.5 姓名张丽芝班级 信131 学号 201307010108指导教师 王恒友成绩实验目的】(1) 熟悉利用主成分分析进行数据分析，能够使用SPSS 软件完成数据的主成分分析； (2) 熟悉利用聚类分析进行数据分析，能够运用主成分分析的结果，做进一步分析，如聚类分析、回归分析等，能够使用SPSS 软件完成该任务。
实验要求】根据各个题目的具体要求，分别运用SPSS 软件完成实验任务。
实验内容】1、表4.9 (数据见exercise4_5.txt )给出了 1991年我国30个省市、城镇居民的月平均消 费数据，所考察的八个指标如下：(单位均为元/人)(2)从R 出发做主成分分析，求出各主成分的贡献率及前两个主成分的累积贡献率；2、( 1)对题1中的数据，按照原有的八个指标，对30个省份进行聚类，给出分为3 类的聚类结果X1:人均粮食支出； X3:人均烟酒茶支出； X5:人均衣着商品支出； X7:人均燃料支出；(1)求样本相关系数矩阵RX2：人均副食支出； X4:人均其他副食支出； X6:人均日用品支出； X8:人均非商品支出。
（2）利用题1得到的前2个主成分指标，分别按最短距离法（最近邻居距离）、最长距离法（最远邻居距离）、类平均距离法（组间平均距离）、重心距离法；其中距离均采用欧式平方距离，对样本进行谱系聚类分析，并画出谱系聚类图；给出分为3类的聚类结果。
并与（1）的结果进行比较实验步骤】（此部分主要包括实验过程、方法、结果、对结果的分析、结论等）2）表:方差贡献率和累计贡献率由上图可知，只有前两个成分的特征值大于1,所以只选择前两个主成分。
第一个主成分的 方差贡献率是38.704%，第二个主成分的方差贡献率是29.590%，前两个主成分的方差占所 有主成分方差的64.294% o 前两个主成分的累计贡献率为68.294%，选择前两个主成分即可 代表绝大多数原来的变量。
主成分分析、聚类分析比较
主成分分析、聚类欧阳家百（2021.03.07）分析的比较与应用主成分分析、聚类分析的比较与应用摘要：主成分分析、聚类分析是两种比较有价值的多元统计方法,但同时也是在使用过程中容易误用或混淆的几种方法。
本文从基本思想、数据的标准化、应用上的优缺点等方面,详细地探讨了两者的异同,并且举例说明了两者在实际问题中的应用。
关键词：spss、主成分分析、聚类分析一、基本概念主成分分析就是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。
综合指标即为主成分。
所得出的少数几个主成分，要尽可能多地保留原始变量的信息，且彼此不相关。
因子分析是研究如何以最少的信息丢失，将众多原始变量浓缩成少数几个因子变量，以及如何使因子变量具有较强的可解释性的一种多元统计分析方法。
聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构，并且对每一个数据集进行描述的过程。
其主要依据是聚到同一个数据集中的样本应该彼此相似，而属于不同组的样本应该足够不相似。
二、基本思想的异同（一）共同点主成分分析法和因子分析法都是用少数的几个变量(因子) 来综合反映原始变量(因子) 的主要信息，变量虽然较原始变量少，但所包含的信息量却占原始信息的85 %以上，所以即使用少数的几个新变量，可信度也很高，也可以有效地解释问题。
并且新的变量彼此间互不相关，消除了多重共线性。
这两种分析法得出的新变量，并不是原始变量筛选后剩余的变量。
在主成分分析中，最终确定的新变量是原始变量的线性组合，如原始变量为x1 ，x2 ，. . . ，x3 ，经过坐标变换，将原有的p个相关变量xi 作线性变换，每个主成分都是由原有p 个变量线性组合得到。
在诸多主成分Zi中，Z1 在方差中占的比重最大，说明它综合原有变量的能力最强，越往后主成分在方差中的比重也小，综合原信息的能力越弱。
因子分析是要利用少数几个公共因子去解释较多个要观测变量中存在的复杂关系，它不是对原始变量的重新组合，而是对原始变量进行分解，分解为公共因子与特殊因子两部分。
主成分分析,聚类分析比较
主成分分析、聚类分析的比较与应用主成分分析、聚类分析的比较与应用摘要：主成分分析、聚类分析是两种比较有价值的多元统计方法,但同时也是在使用过程中容易误用或混淆的几种方法。
本文从基本思想、数据的标准化、应用上的优缺点等方面,详细地探讨了两者的异同,并且举例说明了两者在实际问题中的应用。
关键词：spss、主成分分析、聚类分析一、基本概念主成分分析就是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。
综合指标即为主成分。
所得出的少数几个主成分，要尽可能多地保留原始变量的信息，且彼此不相关。
因子分析是研究如何以最少的信息丢失，将众多原始变量浓缩成少数几个因子变量，以及如何使因子变量具有较强的可解释性的一种多元统计分析方法。
聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构，并且对每一个数据集进行描述的过程。
其主要依据是聚到同一个数据集中的样本应该彼此相似，而属于不同组的样本应该足够不相似。
二、基本思想的异同（一）共同点主成分分析法和因子分析法都是用少数的几个变量(因子) 来综合反映原始变量(因子) 的主要信息，变量虽然较原始变量少，但所包含的信息量却占原始信息的85 %以上，所以即使用少数的几个新变量，可信度也很高，也可以有效地解释问题。
并且新的变量彼此间互不相关，消除了多重共线性。
这两种分析法得出的新变量，并不是原始变量筛选后剩余的变量。
在主成分分析中，最终确定的新变量是原始变量的线性组合，如原始变量为x1 ，x2 ，. . . ，x3 ，经过坐标变换，将原有的p个相关变量xi 作线性变换，每个主成分都是由原有p 个变量线性组合得到。
在诸多主成分Zi中，Z1 在方差中占的比重最大，说明它综合原有变量的能力最强，越往后主成分在方差中的比重也小，综合原信息的能力越弱。
因子分析是要利用少数几个公共因子去解释较多个要观测变量中存在的复杂关系，它不是对原始变量的重新组合，而是对原始变量进行分解，分解为公共因子与特殊因子两部分。
主成分和聚类分析
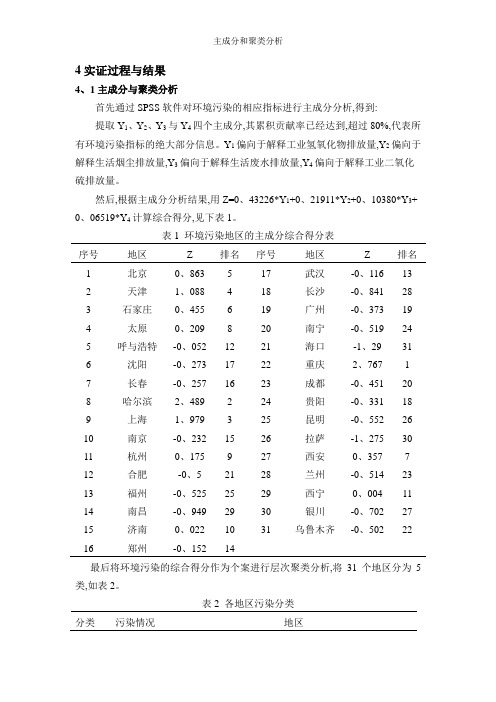
4实证过程与结果4、1主成分与聚类分析首先通过SPSS软件对环境污染的相应指标进行主成分分析,得到:提取Y1、Y2、Y3与Y4四个主成分,其累积贡献率已经达到,超过80%,代表所有环境污染指标的绝大部分信息。
Y1偏向于解释工业氢氧化物排放量,Y2偏向于解释生活烟尘排放量,Y3偏向于解释生活废水排放量,Y4偏向于解释工业二氧化硫排放量。
然后,根据主成分分析结果,用Z=0、43226*Y1+0、21911*Y2+0、10380*Y3+ 0、06519*Y4计算综合得分,见下表1。
表1 环境污染地区的主成分综合得分表序号地区Z 排名序号地区Z 排名1 北京0、863 5 17 武汉-0、116 132 天津1、088 4 18 长沙-0、841 283 石家庄0、455 6 19 广州-0、373 194 太原0、209 8 20 南宁-0、519 245 呼与浩特-0、052 12 21 海口-1、29 316 沈阳-0、273 17 22 重庆2、767 17 长春-0、257 16 23 成都-0、451 208 哈尔滨2、489 2 24 贵阳-0、331 189 上海1、979 3 25 昆明-0、552 2610 南京-0、232 15 26 拉萨-1、275 3011 杭州0、175 9 27 西安0、357 712 合肥-0、5 21 28 兰州-0、514 2313 福州-0、525 25 29 西宁0、004 1114 南昌-0、949 29 30 银川-0、702 2715 济南0、022 10 31 乌鲁木齐-0、502 2216 郑州-0、152 14最后将环境污染的综合得分作为个案进行层次聚类分析,将31个地区分为5类,如表2。
表2 各地区污染分类分类污染情况地区1 轻度污染海口、拉萨2 比较轻度污染合肥、乌鲁木齐、福州、南宁、兰州、,昆明、成都、银川、南昌、长沙、沈阳、长春、南京、广州、贵阳、郑州、武汉、济南、西宁、呼与浩特3 污染情况一般太原、杭州、石家庄、西安4 污染比较严重北京、天津5 污染十分严重上海、哈尔滨、重庆4、2主成分分析与聚类分析在SPSS中的操作过程打开S PSS,“文件-打开-数据”,选中excel,如下图结果。
主成分分析和聚类分析的比较
主成分分析和聚类分析的比较一、定义：1.主成分分析：PCA是一种数学方法，通过线性变换将原始数据投影到新的坐标系上，使得投影的数据在新的坐标系下具有最大的方差，从而达到降维和提取数据特征的目的。
2.聚类分析：聚类分析是一种无监督学习方法，通过对样本集合中的数据进行分类，使得同一类别的数据尽量相似，不同类别的数据尽量不相似。
二、目的：1.主成分分析：PCA的主要目的是降低数据的维度，同时保留尽可能多的数据信息。
通过确定主成分，可以选择保留最重要的几个主成分，达到降维的目的，同时避免信息损失。
2.聚类分析：聚类分析的主要目的是发现数据的内在结构和相似性，将数据分成若干个互不交叠的群组，使得同一群组的数据相似度较高，不同群组的数据相似度较低。
三、步骤：1.主成分分析：-对数据进行标准化处理。
-计算数据样本的协方差矩阵。
-对协方差矩阵进行特征值分解，得到特征值和特征向量。
-选择主成分并确定保留的主成分数目。
-根据主成分和原始数据计算得到新的数据集，即降维后的数据集。
2.聚类分析：- 选择合适的聚类算法（如K-means、层次聚类等）。
-初始化聚类中心。
-计算每个样本与聚类中心的距离。
-将样本分配到最近的聚类中心。
-更新聚类中心，重复上述步骤直到满足终止条件。
四、应用领域：1.主成分分析：-数据降维与特征提取：对于高维数据，可以通过PCA将数据降低到较低的维度，并保留主要特征信息。
-数据可视化：通过PCA将高维数据投影到二维或三维空间中，方便数据的可视化展示。
-噪声滤除：PCA可以去除数据中的噪声信息，保留主要特征。
2.聚类分析：-客户细分：在市场营销中，可以通过聚类分析将客户分为不同的群组，根据每个群组的特征制定相应的营销策略。
-图像分割：在图像处理中，可以利用聚类分析对图像进行分割，将图像中的不同物体分别提取出来。
-社交网络分析：通过对社交网络用户之间的关系进行聚类分析，可以发现群组内的用户行为模式和用户兴趣。
主成分分析聚类分析比较
主成分分析聚类分析比较
聚类分析（Cluster Analysis）是一种将数据划分为不同组（即簇）
的方法。
它通过根据数据之间的相似性度量来识别相似的数据点，并将它
们分配到同一个簇中。
聚类分析可以帮助我们在没有预先定义类别的情况下，发现数据中的特定模式和群集。
它在无监督学习中常用于探索性数据
分析和市场细分等领域。
然而，主成分分析和聚类分析也有一些明显的区别。
首先，在目标上，主成分分析旨在将原始数据映射到一个低维空间，以便更好地理解数据的
结构。
而聚类分析旨在将数据分成不同的组或簇，以便更好地识别数据中
的模式。
其次，在技术上，主成分分析使用线性变换和协方差矩阵来找到
数据中的主成分，而聚类分析使用不同的相似性度量方法（如欧氏距离、
余弦相似度等）来识别簇。
由于主成分分析和聚类分析的应用领域和基本原理不同，因此在具体
问题中选择使用哪种方法取决于数据的性质和分析的目的。
例如，如果我
们想要降低数据的维度以便更好的可视化，或者减少计算复杂性以便更容
易进行后续分析，那么主成分分析是一个不错的选择。
另一方面，如果我
们对数据中的模式和群集感兴趣，并希望找出数据中的隐藏结构，那么聚
类分析是更合适的选择。
综上所述，虽然主成分分析和聚类分析在目标和技术上存在一些差异，但它们都是有助于揭示数据的潜在结构和模式的无监督学习方法。
在数据
分析中，我们可以根据具体的需求选择适当的方法，以便更好地理解和利
用数据。
主成分分析聚类分析
主成分分析聚类分析主成分分析：利用降维（线性变换）的思想,在损失很少信息的前提下把多个指标转化为几个综合指标（主成分）,用综合指标来解释多变量的方差-协方差结构，即每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能（主成分必须保留原始变量90％以上的信息），从而达到简化系统结构，抓住问题实质的目的综合指标即为主成分.优点：首先它利用降维技术用少数几个综合变量来代替原始多个变量，这些综合变量集中了原始变量的大部分信息.其次它通过计算综合主成分函数得分,对客观经济现象进行科学评价。
再次它在应用上侧重于信息贡献影响力综合评价。
缺点:当主成分的因子负荷的符号有正有负时，综合评价函数意义就不明确.命名清晰性低.聚类分析：将个体（样品）或者对象（变量）按相似程度（距离远近）划分类别，使得同一类中的元素之间的相似性比其他类的元素的相似性更强.目的在于使类间元素的同质性最大化和类与类间元素的异质性最大化.。
其主要依据是聚到同一个数据集中的样本应该彼此相似，而属于不同组的样本应该足够不相似。
常用聚类方法：系统聚类法，K—均值法，模糊聚类法，有序样品的聚类，分解法，加入法.注意事项：1。
系统聚类法可对变量或者记录进行分类，K—均值法只能对记录进行分类;2.K—均值法要求分析人员事先知道样品分为多少类;3。
对变量的多元正态性,方差齐性等要求较高。
应用领域：细分市场，消费行为划分，设计抽样方案等。
因子分析:利用降维的思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子。
（因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系），就是研究如何以最少的信息丢失，将众多原始变量浓缩成少数几个因子变量,以及如何使因子变量具有较强的可解释性的一种多元统计分析方法.求解因子载荷的方法：主成分法，主轴因子法,极大似然法，最小二乘法，a因子提取法.注意事项：5。
主成分分析与因子分析聚类分析
主成分分析与因子分析聚类分析主成分分析通过寻找原始数据中的主要变化方向来降低维度。
它通过线性变换将原始数据变换为一组不相关的主成分，其中每个主成分都是原始数据中的线性组合。
这些主成分按照方差大小排序，从而找到原始数据中的主要变化模式。
主成分分析可以帮助我们理解数据中的主要模式，并在保留较少的维度的同时保留尽可能多的信息。
因子分析是一种统计方法，用于揭示观测数据背后的潜在因子。
因子分析假设一组观测数据是由一组潜在因子和测量误差共同决定的。
通过因子分析，我们可以确定潜在因子对观测数据的影响程度，并推断这些因子的含义。
因子分析可以帮助我们揭示观测数据背后的隐藏结构，并从中提取有意义的信息。
1.数据预处理：在进行聚类分析之前，我们经常需要对输入数据进行预处理，例如归一化或标准化。
主成分分析可以帮助我们对原始数据进行降维，从而减少数据维度，简化预处理过程。
2.特征提取：主成分分析和因子分析都可以用于提取数据中的主要特征。
主成分分析通过保留方差较大的主成分，提取数据中的主要模式。
因子分析则可以帮助我们发现观测数据背后的潜在因子，并从中提取有意义的特征。
3.可视化：主成分分析和因子分析可以将高维数据转换为低维数据，并将其可视化。
可视化降维后的数据可以帮助我们理解数据的结构和模式，并辅助聚类分析的结果解释。
4.噪声过滤：主成分分析和因子分析可以通过滤除方差较小的主成分或因子来减少数据中的噪声。
这可以帮助我们提高聚类分析的准确性和稳定性。
总之，主成分分析和因子分析是常用的降维方法，可用于聚类分析的数据预处理、特征提取、可视化和噪声过滤等方面。
它们可以帮助我们理解数据的结构和模式，并提高聚类分析的效果。
主成分分析聚类分析比较
主成分分析聚类分析比较主成分分析是一种数据降维技术，它能够将高维数据降低到低维，同时保留主要的信息。
它的原理是通过线性变换，将原始的维度高的数据线性变换到维度较低的新坐标系下，并且在新坐标系下保持数据的原有结构特征和方差。
1.数据标准化：为了消除量纲影响，需要对数据进行标准化处理。
2.计算协方差矩阵：将标准化后的数据计算协方差矩阵。
3.计算特征值和特征向量：通过解特征值问题，计算得到特征值和对应的特征向量。
4.选择主成分：将特征值从大到小排序，选择前k个特征值所对应的特征向量作为主成分。
5.构建新坐标系：将原始数据乘以特征向量，得到新的降维后的数据。
1.数据压缩：主成分分析可以将高维数据压缩到低维空间中，同时保留主要信息。
2.数据可视化：降维后的数据可以更方便地进行可视化展示和分析。
3.特征提取：主成分分析可以从原始数据中提取出最具有代表性的主成分。
4.数据预处理：主成分分析可以用于数据预处理，减少噪声和不必要的冗余信息。
二、聚类分析（Cluster Analysis）聚类分析是一种将相似对象组成簇的方法，以确定数据中的内在结构，它的目标是将相似的对象放在一个簇中，不相似的对象放在不同的簇中。
聚类分析的步骤如下：1.确定距离度量：选择适当的距离度量方法来度量不同对象之间的相似性。
2.计算距离矩阵：通过计算对象之间的距离，得到距离矩阵。
3. 构建聚类模型：根据距离矩阵，使用聚类算法（如K-means、层次聚类等）构建聚类模型。
4.确定聚类数目：根据业务需求和算法要求，确定合适的聚类数目。
5.分配对象到簇：将对象分配给合适的簇，并且根据一定的标准评估聚类模型的性能。
聚类分析的应用：1.模式识别：聚类分析可以用于模式识别，从数据中发现数据的内在结构和规律。
2.市场细分：聚类分析可以通过分析客户的购买行为和偏好，对市场进行细分，从而进行有针对性的营销策略。
3.图像分割：聚类分析可以用于图像分割和目标提取，将图像分成若干个簇，提取出目标区域。
主成分分析、聚类分析比较
主成分分析、聚类分析的比较与应用主成分分析、聚类分析的比较与应用摘要：主成分分析、聚类分析是两种比较有价值的多元统计方法,但同时也是在使用过程中容易误用或混淆的几种方法。
本文从基本思想、数据的标准化、应用上的优缺点等方面,详细地探讨了两者的异同,并且举例说明了两者在实际问题中的应用。
关键词：spss、主成分分析、聚类分析一、基本概念主成分分析就是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。
综合指标即为主成分。
所得出的少数几个主成分，要尽可能多地保留原始变量的信息，且彼此不相关。
因子分析是研究如何以最少的信息丢失，将众多原始变量浓缩成少数几个因子变量，以及如何使因子变量具有较强的可解释性的一种多元统计分析方法。
聚类分析是依据实验数据本身所具有的定性或定量的特征来对大量的数据进行分组归类以了解数据集的内在结构，并且对每一个数据集进行描述的过程。
其主要依据是聚到同一个数据集中的样本应该彼此相似，而属于不同组的样本应该足够不相似。
二、基本思想的异同（一）共同点主成分分析法和因子分析法都是用少数的几个变量(因子) 来综合反映原始变量(因子) 的主要信息，变量虽然较原始变量少，但所包含的信息量却占原始信息的85 %以上，所以即使用少数的几个新变量，可信度也很高，也可以有效地解释问题。
并且新的变量彼此间互不相关，消除了多重共线性。
这两种分析法得出的新变量，并不是原始变量筛选后剩余的变量。
在主成分分析中，最终确定的新变量是原始变量的线性组合，如原始变量为x1 ，x2 ，. . . ，x3 ，经过坐标变换，将原有的p个相关变量xi 作线性变换，每个主成分都是由原有p 个变量线性组合得到。
在诸多主成分Zi中，Z1 在方差中占的比重最大，说明它综合原有变量的能力最强，越往后主成分在方差中的比重也小，综合原信息的能力越弱。
因子分析是要利用少数几个公共因子去解释较多个要观测变量中存在的复杂关系，它不是对原始变量的重新组合，而是对原始变量进行分解，分解为公共因子与特殊因子两部分。
主成分分析、因子分析、聚类分析的比较与应用
主成分分析、因子分析、聚类分析的比较与应用一、本文概述在数据分析与统计学的广阔领域中，主成分分析（PCA）、因子分析（FA）和聚类分析（CA）是三种重要的数据分析工具。
它们各自具有独特的功能和应用领域，对数据的理解和解释提供了不同的视角。
本文将对这三种分析方法进行详细的比较，并探讨它们在各种实际场景中的应用。
我们将对每种分析方法进行简要的介绍，包括其基本原理、数学模型以及主要的应用场景。
然后，我们将详细比较这三种分析方法在数据降维、变量解释以及数据分类等方面的优势和劣势。
主成分分析（PCA）是一种常见的数据降维技术，通过找出数据中的主要变量（即主成分），可以在保留数据大部分信息的同时降低数据的维度。
因子分析（FA）则是一种通过寻找潜在因子来解释数据变量之间关系的方法，它在心理学、社会学等领域有着广泛的应用。
聚类分析（CA）则是一种无监督学习方法，通过将数据点划分为不同的类别，揭示数据的内在结构和分布。
接下来，我们将通过几个具体的案例，展示这三种分析方法在实际问题中的应用。
这些案例将涵盖不同的领域，如社会科学、生物医学、商业分析等，以展示这些方法的多样性和实用性。
我们将对全文进行总结，并提出未来研究方向。
通过本文的比较和应用研究，我们希望能为读者提供一个全面、深入的理解这三种重要数据分析方法的视角，同时也为实际问题的解决提供一些有益的启示。
二、主成分分析（PCA）主成分分析（Principal Component Analysis，简称PCA）是一种常用的数据分析方法，它旨在通过正交变换将原始数据转换为一组线性不相关的变量，即主成分。
这些主成分按照方差大小进行排序，第一个主成分具有最大的方差，后续主成分方差依次递减。
通过这种方式，PCA可以在保持数据主要特征的同时降低数据的维度，简化数据结构，便于进一步的分析和可视化。
PCA的核心思想是数据降维，它通过计算协方差矩阵的特征值和特征向量来实现。
特征值代表了各个主成分的方差大小，而特征向量则构成了转换矩阵，用于将原始数据转换为主成分。
基于主成分分析和聚类分析的我国各省市经济效益研究
基于主成分分析和聚类分析的我国各省市经济效益研究近年来，我国各省市经济效益差异逐渐凸显。
为了深入了解和研究各省市的经济效益，可以采用主成分分析和聚类分析的方法来进行研究。
主成分分析可以用来降维和提取数据特征，聚类分析可以用来发现数据之间的相似性和差异性。
首先，我们需要收集一些数据，例如各省市的GDP、人均收入、产业结构、消费水平、教育水平等指标，这些指标可以用来反映各省市的经济效益情况。
然后，我们可以利用主成分分析来降维和提取数据特征。
主成分分析是一种常用的降维方法，通过线性变换将原始数据映射到一个低维空间中，同时尽量保留原始数据的信息。
在这个过程中，我们可以得到一些主成分，主成分代表了原始数据中的一部分变异性。
通过主成分分析，我们可以将原始数据从多个指标中压缩为少数几个主成分。
通过主成分分析后，我们得到了一些主成分，每个主成分代表了原始数据中的一部分变异性。
接下来，我们可以利用聚类分析来发现数据之间的相似性和差异性。
聚类分析的目的是将数据集中的样本划分为不同的组别，每个组别内的样本应该尽可能相似，而不同组别之间的样本应该尽可能不相似。
在这个过程中，我们可以使用一些相似度或距离度量方法，例如欧氏距离或相关系数等。
通过聚类分析，我们可以将各省市划分为不同的类别，每个类别代表了一组经济效益相似的省市。
这样可以帮助我们更好地理解和分析各省市之间的经济效益差异，并挖掘出其中的规律和问题。
例如，我们可以找出经济效益较高的省市的共同特征，进而分析这些特征对经济效益的影响因素。
最后，我们可以通过可视化的方式展示各省市的经济效益研究结果。
例如，可以使用散点图来展示各省市在主成分空间中的分布情况，以及不同类别的省市的分布情况。
这样可以更直观地展示各省市之间的经济效益差异和相似性。
总之，基于主成分分析和聚类分析的研究可以帮助我们深入了解和分析我国各省市的经济效益。
通过这种研究方法，可以有效地发现各省市的经济效益差异以及其中的规律和问题，为相关决策提供科学的依据和参考。
主成分分析和聚类分析
主成分分析和聚类分析1.主成分分析（PCA）主成分分析是一种无监督学习方法，用于刻画数据集中的主要模式。
其基本思想是将高维数据转化为低维空间中的一组新变量，这些新变量被称为主成分。
主成分是原始数据按照方差大小依次降序排列的线性组合，其中第一主成分方差最大，第二主成分方差次之，以此类推。
通过对数据集的主成分进行分析，我们可以发现数据中的主要结构和关联，实现数据降维和可视化。
-标准化数据：对原始数据进行标准化处理，使得每个特征的平均值为0，方差为1-计算协方差矩阵：计算标准化后的数据的协方差矩阵。
-计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征向量和特征值。
-选择主成分：根据特征值的大小，选择前几个特征向量作为主成分。
-数据投影：将原始数据投影到主成分上，得到降维后的数据。
-数据可视化：通过主成分分析，可以将高维数据降维到二维或三维空间中，便于进行可视化展示。
-数据预处理：主成分分析可以用于去除数据中的冗余信息和噪声，提取数据中的主要结构。
-特征提取：主成分分析可以用于提取具有代表性的特征，用于后续的数据建模和分析。
-降低数据维度，去除冗余信息。
-可以发现数据的主要结构和关联。
-不受异常值的影响。
-主成分是基于方差最大化的，可能忽略其他重要信息。
-主成分的解释性较差。
2.聚类分析聚类分析是一种无监督学习方法，用于将数据集中的样本按照相似性进行分类。
聚类分析的目标是将数据集中的样本划分为不同的组别，每个组别内部的样本相似度高，不同组别之间的样本相似度低。
聚类分析的步骤如下：- 选择合适的聚类算法：根据数据的性质和目标，选择合适的聚类算法，如K-means聚类、层次聚类等。
-确定聚类数量：对于一些聚类算法，需要事先确定聚类的数量。
-计算相似度/距离：根据选择的聚类算法，计算样本之间的相似度或距离。
-执行聚类算法：将样本按照相似性进行聚类。
-评估聚类结果：对聚类结果进行评估，可以使用内部评估指标或外部评估指标。
主成分分析及聚类分析
主成分分析及聚类分析主成分分析（PCA）是一种无监督学习的技术，用于将数据从高维空间投影到低维空间，同时尽可能地保留原始数据的信息。
主成分分析通过线性变换将原始数据转化为具有最大方差的新特征，这些新特征被称为主成分。
第一主成分具有最大的方差，第二主成分则与前一主成分正交，并具有第二大的方差，依此类推。
主成分的数量等于原始数据维度。
主成分分析有很多应用。
首先，它可以用于数据降维。
通过选择较少的主成分，可以将高维数据转化为低维数据，从而降低计算复杂度和存储需求，同时保留数据的主要特征。
其次，主成分分析也可以用于提取数据中的主要特征。
通过选择具有较高方差的主成分，可以过滤掉噪声和次要特征，从而更好地理解数据。
此外，主成分分析还可以可视化数据，找出数据中的模式和相关结构。
聚类分析是一种将数据对象分组为无标记子集的技术。
相似的数据对象被分到同一组中，不相似的数据对象被分到不同的组中。
聚类分析可以帮助我们理解数据集中的结构和组织，发现隐藏的模式和规律。
聚类分析可以根据不同的算法进行，常用的包括k-means聚类、层次聚类和DBSCAN聚类等。
k-means聚类是一种迭代优化算法，根据样本之间的距离将数据划分为k个互不重叠的簇。
层次聚类将数据对象组织成一颗树状结构，根据样本之间的相似性递归地进行划分。
DBSCAN聚类是一种基于密度的聚类算法，将具有足够多相邻样本的区域定义为一个簇。
聚类分析可以在很多领域中应用。
在市场营销中，聚类分析可以根据顾客的购买行为和偏好将顾客分成不同的群体，从而定制个性化的营销策略。
在图像处理中，聚类分析可以将像素点按照颜色和纹理特征聚类，从而实现图像分割和目标检测。
在生物信息学中，聚类分析可以根据基因的表达数据将基因分成不同的表达模式，从而发现潜在的功能和相互作用。
总结起来，主成分分析和聚类分析是常用的统计技术，它们在数据分析和模式识别中有广泛的应用。
主成分分析可以用于数据降维、特征提取和可视化，聚类分析可以用于数据分组、模式发现和需求识别。
种质资源的主成分分析与聚类
种质资源的主成分分析与聚类本文主要针对种质资源的主成分分析和聚类进行研究，旨在提供关于分析和聚类种质资源的丰富内容，并阐明应用主成分分析和聚类来研究种质资源的优势。
种质资源的概念种质资源指的是一类具有特定和重要用途的有机物，例如种子、植物和微生物等，它们的概念源于自然界的多样性。
由于它们的重要性，大数据分析技术如主成分分析和聚类被用来分析种质资源的多样性和相关性。
主成分分析主成分分析（PCA）是一种常见的统计分析技术，旨在去除数据集中的冗余信息，以便减少特征维度，并有效地提取主要的结构或功能特征。
PCA的应用于种质资源的多样性分析，可以通过分析种质资源的数量和质量差异以及其他相关性质，提取种质资源的主要特征，便于种质资源研究人员对种质资源进行有效分类。
聚类聚类算法是一种有效的种质资源分析技术，它可以根据种质资源的特征，将种质资源分成几个不同的簇。
它可以将种子、植物、微生物等有机物分成几个不同的类别，使得种质资源的研究变得更加容易。
优势结合主成分分析和聚类技术，对于种质资源的研究具有重要意义，这一组合可以有效地提取种质资源的主要特征，消除冗余信息，并有效地将种质资源分组，有助于提高种质资源的研究价值和利用效率。
实例为了说明主成分分析和聚类技术在研究种质资源中的应用，以中国我爱你植物杂交研究所为例，提供一个实际使用案例，首先利用主成分分析技术，从原始数据中获取有关种质资源的主要特征，包括形态和生理特征等，然后利用聚类算法将种质资源分成几个不同的类别，从而方便并加快种质资源的研究。
结论从上面的案例可以看出，使用主成分分析和聚类技术可以有效地提取种质资源的主要特征，快速分组和分类，是研究种质资源和加快种质资源研究的有效工具。
此外，主成分分析和聚类算法的结合可以更有效地研究种质资源的多样性和相关性，从而更好地发掘和挖掘种质资源的价值。
主成分分析及聚类分析
泛珠三角区域物流发展水平综合评价研究资料来源：吴晓燕•泛珠三角区域物流发展水平综合评价研究泛珠三角区域是我国最主要的经济发达地区之一，也是现代物流最为强劲的“增长极”，具有优越的地理、交通与经济区位优势。
但是区域内有发达省份5也有不发达省份5有沿海的省份5也有内陆省份5有东部省份，也有西部省份，彼此之间存在不同的优势和劣势。
因此对泛珠三角区域物流发展水平进行评估与分析，有利于明确广东、福建、江西、广西、海南、湖南、四川、云南、贵州九省（区）的区域物流发展现状及差异，找出区域间的优势互补项目，为区域内物流资源有效利用和合理共享、促进区域物流一体化发展提供方向和依据。
评价区域物流综合发展水平是一项很复杂的工作。
选择并构建区域物流发展水平综合评价指标体系是评价的尖键。
因此选择指标构建评价指标体系，必须以综合评价目的为依据，对所要考察的事物进行认真分析,寻找出影响评价对象的因素，从中选出若干主要因素，构建成综合评价指标体系。
在多指标综合评价中，如果指标选择不当，再好的综合评价方法也会出现差错，甚至完全失败。
区域物流发展水平评价指标体系实际上就是利用具体的指标将区域物流所包括的功能、区域物流的内涵、特征具体化、层次化的统计描述和综合评价。
为了合理评估区域物流发展综合水平，我们主要选取6个一级评价指标，20个次级评价指标对其进行评估，具体结构如下表:表1区域物流发展水平评价指标体系1、社会经济发展类经济发展是区域物流发展的基础保障，一个地区雄厚的经济基础有利于该物流的加速发展。
一般来说，区域物流发展水平与区域的经济发展水平成正比。
因此，我们考虑GDP和人均GDP两个次级指标，他们综合反映了物流发展的社会经济基础。
2、生产、消费流通类从物流需求源考虑，农业、制造业等产业中的物流需求主要是生产资料的位移、储存和流通加工等，这类产业的物流需求与各行业的产量产值存在正比尖系，物流需求是商品需求的派生物，与消费品销售，生产资料市场直接相尖，商品市场的规模直接决定物流需求的大小，因此物流需求也与社会消费品零售总额与进出口总额密切相尖。
机器学习：聚类分析和主成分分析的比较
机器学习：聚类分析和主成分分析的比较聚类分析与主成分分析是机器学习中常用的两种数据分析方法。
聚类分析和主成分分析使用不同的技术来分析数据，且各有优缺点。
本文将介绍聚类分析和主成分分析的使用场景、工作原理、优缺点以及应用案例，以帮助读者更好地理解它们的差异和适用范围。
一、聚类分析聚类分析是一种无监督学习的方法，它试图将相似的数据点分组在一起。
其目标是将数据点分成多个聚类，并使得同一聚类中的数据点尽量相似，而不同聚类之间的数据点差异尽量大。
聚类分析的应用场景广泛，如市场营销、社会网络分析、医学诊断等。
聚类分析的工作原理是利用无监督算法在数据贴近度上进行计算（如欧式距离、余弦相似度等），从而找出相近的样本点。
然后，通过合适的算法将其归纳到同一类别中。
聚类分析有多种方法，如层次聚类、k-means聚类等。
聚类分析的优点是处理数据的速度快，而且适用于大规模数据集。
同时，聚类分析不需要先验知识并且是一种无监督学习的方法，这意味着它不需要人工标注数据。
此外，聚类分析的结果可以轻松地可视化，可以帮助人们更好地理解和解释数据。
聚类分析的缺点是容易受到噪声数据的影响，因为它是一种度量相似度的无监督学习方法。
在处理复杂数据时，聚类结果可能过于粗略或明显？不足，这需要在进一步的分析过程中进行更多的数据解释。
二、主成分分析主成分分析是一种降维技术，它通过识别和提取数据中的主要特征来降低计算复杂度。
它试图找到最有效的线性组合，通过使用这些线性组合，可以描述数据集中的大部分方差。
主成分分析的应用场景广泛，如金融数据分析、人脸识别、图像处理等。
主成分分析的工作原理是确定数据集中的主要成分，并将数据投影到新的坐标系中，从而通过保留关键信息来降低数据的维数。
通过保留足够数量的主成分，可以准确表示数据集的大部分方差。
因此，主成分分析可以快速提取有用的数据特征，加速模型的训练和预测。
主成分分析的优点是它能够提高模型的速度和性能。
多个特征可以被映射到更少的特征上，从而减少了计算复杂度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北京建筑工程学院
理学院信息与计算科学专业实验报告
课程名称《数据分析》实验名称《主成分分析和聚类分析》实验地点：基础楼C-423日期__2016.5.5_____ 姓名张丽芝班级信131 学号201307010108___指导教师王恒友成绩
【实验目的】
（1）熟悉利用主成分分析进行数据分析，能够使用SPSS软件完成数据的主成分分析；
（2）熟悉利用聚类分析进行数据分析，能够运用主成分分析的结果，做进一步分析，如聚类分析、回归分析等，能够使用SPSS软件完成该任务。
【实验要求】
根据各个题目的具体要求，分别运用SPSS软件完成实验任务。
【实验内容】
1、表4.9（数据见exercise4_5.txt）给出了1991年我国30个省市、城镇居民的月平均消
费数据，所考察的八个指标如下：（单位均为元/人）
X1: 人均粮食支出；X2：人均副食支出；
X3: 人均烟酒茶支出；X4: 人均其他副食支出；
X5:人均衣着商品支出；X6: 人均日用品支出；
X7: 人均燃料支出；X8: 人均非商品支出。
（1）求样本相关系数矩阵R。
（2）从R出发做主成分分析，求出各主成分的贡献率及前两个主成分的累积贡献率；
2、（1）对题1中的数据，按照原有的八个指标，对30个省份进行聚类，给出分为3
类的聚类结果。
（2）利用题1得到的前2个主成分指标，分别按最短距离法（最近邻居距离）、最长距离法（最远邻居距离）、类平均距离法（组间平均距离）、重心距离法；其中距离均采用欧式平方距离，对样本进行谱系聚类分析，并画出谱系聚类图；给出分为3类的聚类结果。
并与（1）的结果进行比较
【实验步骤】（此部分主要包括实验过程、方法、结果、对结果的分析、结论等）
1
1）
2）
表:方差贡献率和累计贡献率
由上图可知， 只有前两个成分的特征值大于1，所以只选择前两个主成分。
第一个主成分的方差贡献率是38.704%，第二个主成分的方差贡献率是29.590%，前两个主成分的方差占所有主成分方差的64.294%。
前两个主成分的累计贡献率为68.294%，选择前两个主成分即可代表绝大多数原来的变量。
2
每个聚类中的案例数 聚类
1 10.000
2 18.000 3
2.000 有效 30.000 缺失
.000
由上图可知，聚类2包含样本数最多，聚类3包含样本数最少。
通过K中心聚类分析，可以对我国各地区生活中的人均支出类别情况有一个基本的了解。
我们可以将不同地区的人均消费情况分为3类；其中第二类包含的省市最多，有18个，其他两类包含城市较少。
通过分析结果也可知每个地区所属类别。
（2）
按最短距离法（最近邻居距离）对样本进行谱系聚类分析
由聚类表可知聚类的具体过程。
以第一步为例，样品1和2合并为一类，距离系数为3.299，在“首次出现阶段集群”里显示为0，因此合并两项都是第一次出现，合并结果取15，即归为第15类。
群集成员
案例 3 群集
1:山西 1
2:内蒙古 1
3:吉林 1
4:黑龙江 1
5:河南 1
6:甘肃 1
7:青海 1
8:河北 1
9:陕西 1
10:宁夏 1
11:新疆 1
12:湖北 1
13:云南 1
14:湖南 1
15:安徽 1
16:贵州 1
17:辽宁 1
18:四川 1
19:山东 1
20:江西 1
21:福建 1
22:广西 1
23:海南 1
24:天津 1
25:江苏 1
26:浙江 1
27:北京 1
28:西藏 1
29:上海 2
30:广东 3
集群成员表如图，当划分为3个类别时，各个地区所属类别。
与上一问所得结论有较大出入。
最长距离法（最远邻居距离）
群集成员
案例 3 群集1:山西 1 2:内蒙古 1 3:吉林 1 4:黑龙江 1 5:河南 1 6:甘肃 1 7:青海 1 8:河北 1 9:陕西 1 10:宁夏 1 11:新疆 1 12:湖北 2 13:云南 2 14:湖南 2 15:安徽 2 16:贵州 2 17:辽宁 2 18:四川 2 19:山东 2 20:江西 1 21:福建 3 22:广西 3 23:海南 3 24:天津 2 25:江苏 2 26:浙江 2 27:北京 2 28:西藏 2 29:上海 3 30:广东 3
类平均距离法（组间平均距离）
群集成员
案例 3 群集1:山西 1 2:内蒙古 1 3:吉林 1 4:黑龙江 1
5:河南 1 6:甘肃 1 7:青海 1 8:河北 1 9:陕西 1 10:宁夏 1 11:新疆 1 12:湖北 1 13:云南 1 14:湖南 1 15:安徽 1 16:贵州 1 17:辽宁 1 18:四川 1 19:山东 1 20:江西 1 21:福建 1 22:广西 1 23:海南 1 24:天津 1 25:江苏 1 26:浙江 1 27:北京 1 28:西藏 2 29:上海 3 30:广东 3
重心距离法
群集成员
案例 3 群集1:山西 1 2:内蒙古 1
3:吉林 1 4:黑龙江 1 5:河南 1 6:甘肃 1 7:青海 1 8:河北 1 9:陕西 1 10:宁夏 1 11:新疆 1 12:湖北 1 13:云南 1 14:湖南 1 15:安徽 1 16:贵州 1 17:辽宁 1 18:四川 1 19:山东 1 20:江西 1 21:福建 1 22:广西 1 23:海南 1 24:天津 1 25:江苏 1 26:浙江 1 27:北京 1 28:西藏 1 29:上海 2 30:广东 3。