初中几何变式
正弦定理公式变式

正弦定理公式变式全文共四篇示例,供读者参考第一篇示例:正弦定理,又称正弦公式,是三角形中的重要定理之一,它描述了三角形中三个边和三个角之间的关系。
正弦定理公式有多种变式,适用于不同情况的三角形。
本文将介绍正弦定理公式及其变式的详细内容,并展示如何应用这些公式解决三角形的问题。
让我们回顾一下正弦定理的基本形式。
对于任意三角形ABC,其三条边长度分别为a,b,c,对应的角度分别为A,B,C,正弦定理可以表示为:\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\]这个公式说明了三角形中每条边与其对应角的正弦值之间的比例关系。
通过这个公式,我们可以计算出三角形中任意一个角的正弦值,或者通过已知的正弦值来求解三角形中的边长。
而在实际问题中,我们经常会遇到一些特殊情况,需要使用不同形式的正弦定理来求解。
以下是一些正弦定理的变式:1. 以角度为基准的正弦定理当我们已知一个角的正弦值以及其他两个角时,可以利用以这个角为基准的正弦定理来求解三角形的边长。
已知三角形中角A的正弦值为sinA,角B和角C的度数已知,则可以利用以下公式计算边长:通过这个公式,我们可以在已知一个角的情况下,求解出其他两个角所对应的边长。
2. 两倍角正弦定理在某些情况下,我们需要计算三角形中角度的两倍角的正弦值,这时可以使用两倍角正弦定理来求解。
该公式表示为:\[2\sin A\cos A = \sin 2A\]通过这个公式,可以将角A的正弦值和余弦值联系起来,进一步求解角A的两倍角的正弦值。
3. 倒数定理有时候我们需要找到一个角的余弦值,但只知道其正弦值,这时可以使用倒数定理来求解。
倒数定理表示为:\[\cos A = \frac{1}{{\sec A}} = \frac{1}{{\frac{1}{{\cos A}}}} =\frac{1}{{\frac{1}{{\sin A\div\sqrt{\sin^{2}A+\cos^{2}A}}}}} =\frac{\sqrt{\sin^{2}A+\cos^{2}A}}{\sin A}\]总结而言,正弦定理及其变式是解决三角形问题的基础工具之一。
巧用“复制、粘贴法”解决几何变式题

巧用“复制、粘贴法”解决几何变式题摘要:几何变式题一直是学生比较害怕的题型,文章通过三个例题的分析,让学生感受“复制、粘贴法”在几何变式题中的应用,从而得到推理能力的提升.培养和发展学生的数学推理能力不仅是数学学科价值的体现,同时也是“核心素养”的基础性条件.关键词:几何变式题、解法研究、核心素养初中阶段尤其是基础不好的学生对于几何压轴题往往都有畏难情绪,一看到冗长的题目,连题目都还没看清,就开始打退堂鼓,更不用说好好思考并解决了.现在我来介绍一类几何压轴题,并没有那么难“对付”,相信你能从中得到一点启发.接下来我从几个题目入手讲解如何用“复制、粘贴法”解决几何变式题.1.点的移动带来的变式例1.(2019•抚顺)如图,点E,F分别在正方形ABCD的边CD,BC上,且DE=CF,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90°得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.(1)如图1,若点E是CD的中点,点P在线段BF上,线段BP,QC,EC的数量关系为_________.(2)如图2,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)正方形ABCD的边长为6,AB=3DE,QC=1,请直接写出线段BP的长.此题是2019年抚顺的中考题,是四边形综合题目,考查了正方形的性质、旋转变换的性质、全等三角形的判定与性质、直角三角形的性质以及分类讨论等知识;此题综合性强,证明三角形全等是解题的关键.第1、2小题的区别在于点E是否为CD的中点,学生可以通过测量图1与图2中的BP、QC、EC的长度,初步猜想这三条线段都存在BP+QC=EC。
由于正方形的四边相等,只要满足PQ=DE即可证明猜想,线段EG又是由线段EP绕点E顺时针旋转90°得到的,可得EP=EG,只要证明△PEQ≌△EGD即可完成,证明过程如下:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,由旋转的性质得:∠PEG=90°,EG=EP,∴∠PEQ+∠GEH=90°,∵QH⊥GD,∴∠H=90°,∠G+∠GEH=90°,∴∠PEQ=∠G,又∵∠EPQ+∠PEC=90°,∠PEC+∠GED=90°,∴∠EPQ=∠GED,在△PEQ和△EGD中,,∴△PEQ≌△EGD(ASA),∴PQ=ED,∴BP+QC=BC﹣PQ=CD﹣ED=EC,即BP+QC=EC;第1、2小题的解题过程是一模一样的,完全可以用“复制、粘贴”的方式来完成证明。
初中几何等腰三角形三线合一经典题型及变式题汇总

初中几何等腰三角形三线合一经典题型及变式题汇总三线合一,是等腰三角形里最重要的性质定理之一。
所谓三线,就是等腰三角形中,顶角的角平分线,底边的中线,底边的高线。
必然三线合一。
今天主要举例说明一下等腰三角形三线合一,求解的问题。
并出几个变形题目,供大家练习,在从其他方面来解答等腰等腰三角形问题。
题:如图1,等腰△ABC中,AB=AC,P是BC上的点。
求证:PA^2=AB^2-PBPC。
证明:作高AD。
则由勾股定理,得AB^2-PA^2=BD^2+AD^2-( PD^2+AD^2)= BD^2-PD^2=(BD-PD)(BD+PD)=PB(BD+PD),因为AB=AC,AD⊥BC,所以BD=DC,所以BD+PD=DC+PD=PC,所以AB^2-PA^2=PBPC,所以PA^2=AB^2-PBPC。
变式一:如图2,D是等腰△ABC底边BC延长线上的点,AB=AC=CD=2BC,则AD:BC=______。
(答案:√10)变式二:已知等腰△ABC中,AB=AC,P是底边BC延长线上的点。
求证:PA^2=AB^2+PBPC。
(提示:作△ABC的高AD)变式三:已知等腰Rt△ABC中,AB=AC=2√2,∠BAC=90°,P 是BC上的点,Q是BC延长线上的点,且∠PAQ=90°,如果PQ=5,则PB=______.(答案:1)初中英语下册期末复习第11单元重点知识汇总Unit11 How was your school trip?【重点单词】milk v.挤奶cow n.奶牛milk a cow 给奶牛挤奶horse n.马ride a horse 骑马feed v.喂养;饲养feed chickens 喂鸡farmer n.农民;农场主quite adv.相当;安全quite a lot(of…) 许多anything pron.(常用于否定句或疑问句)任何东西;任何事物grow v.种植;生长;发育farm n.农场;务农;种田pick v.采;摘excellent adj.极好的;优秀的countryside n.乡村;农村in the countryside 在乡下;在农村yesterday n.昨天flower n.花worry v.担心;担忧luckily adv.幸运地;好运地sun n.太阳museum n.博物馆fire n.火灾fire station 消防站painting n.油画;绘画exciting adj.使人兴奋的;令人激动的lovely adj.可爱的expensive adj.昂贵的cheap adj.廉价的;便宜的slow adj.缓慢的;迟缓的fast adv&adj快地(的)robot n.机器人guide n.导游;向导gift n.礼物;赠品all in all 总的说来everything pron.一切;所有事物interested adj.感兴趣的be interested in 对……感兴趣dark adj.黑暗的;昏暗的hear(heard)v.听到;听见【重点短语】1. school trip 学校旅行2. go for a walk 去散步3. milk a cow 挤牛奶4. ride a horse 骑马5. feed chickens 喂鸡6. talk with a farmer 与农民交谈7. take some photos 照相8. ask some questions 问一些问题9. grow apples 种苹果10. show sb. around splace. 带某人逛某地11. learn a lot 学到许多12. pick some strawberries 摘草莓13. last week 上周14.In the countryside 在乡村15. visit my grandparents 拜访我的祖父母16. go fishing 去钓鱼17. sound good 听起来很好18. climb the mountains 去爬山19. play some games 玩一些游戏20. visit a museum 参观博物馆21. visit a fire station 参观消防站22.draw pictures 画画23. go on a school trip 去旅行24 visit the science museum 参观科技博物馆25. how to make a model robot 如何制作机器人模型26. gift shop 礼品店27. buy sth for sb. 为某人买某物28. all in all 总得来说29. be interested in... 对…感兴趣30. be expensive 昂贵的31. not...at all 一点儿也不【重点句型】1.—Did you see any cows?你见到奶牛了吗一Yes, I did. I saw quite a lot.我见到了而且见到了很多很多2.—Did Carol take any photos?罗尔拍照片了吗?—Yes, she did.是的,她拍了。
最新初中数学一题多变、一题多解
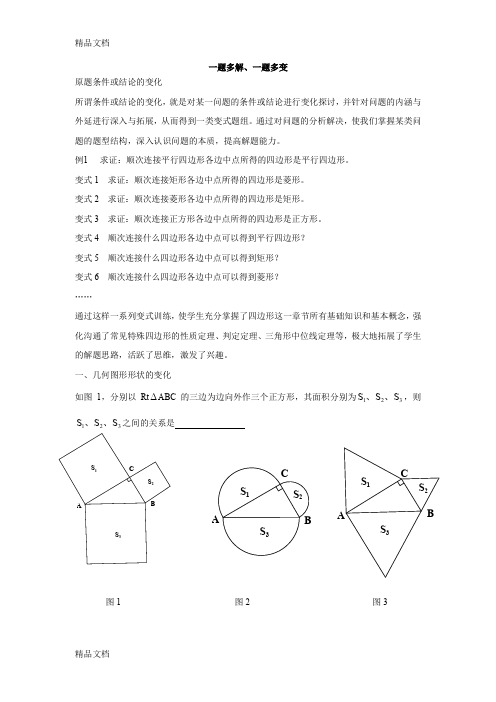
CBAS 2S 3S 1CBAS 3S 2S 1S 3S 2S 1CBA一题多解、一题多变原题条件或结论的变化所谓条件或结论的变化,就是对某一问题的条件或结论进行变化探讨,并针对问题的内涵与外延进行深入与拓展,从而得到一类变式题组。
通过对问题的分析解决,使我们掌握某类问题的题型结构,深入认识问题的本质,提高解题能力。
例1 求证:顺次连接平行四边形各边中点所得的四边形是平行四边形。
变式1 求证:顺次连接矩形各边中点所得的四边形是菱形。
变式2 求证:顺次连接菱形各边中点所得的四边形是矩形。
变式3 求证:顺次连接正方形各边中点所得的四边形是正方形。
变式4 顺次连接什么四边形各边中点可以得到平行四边形? 变式5 顺次连接什么四边形各边中点可以得到矩形? 变式6 顺次连接什么四边形各边中点可以得到菱形? ……通过这样一系列变式训练,使学生充分掌握了四边形这一章节所有基础知识和基本概念,强化沟通了常见特殊四边形的性质定理、判定定理、三角形中位线定理等,极大地拓展了学生的解题思路,活跃了思维,激发了兴趣。
一、几何图形形状的变化如图1,分别以Rt ABC 的三边为边向外作三个正方形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是图1 图2 图3E S 3S 2S 1DCBAS 3S 2S 1ABCDABCD S 3S 2S 1变式1:如图2,如果以Rt ∆ABC 的三边为直径向外作三个半圆,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式2:如图3,如果以Rt ∆ABC 的三边为边向外作三个正三角形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式3:如果以Rt ∆ABC 的三边为边向外作三个一般三角形,其面积分别为321S S S 、、,为使321S S S 、、之间仍具有上述这种关系,所作三角形应满足什么条件?证明你的结论。
浅谈初中数学教材几何习题的变式教学

浅谈初中数学教材几何习题的变式教学摘要:初中数学具有较强的抽象性和逻辑性,必须让学生深入理解知识的本质,才能够提高学生学习效果,实现知识的迁移运用。
习题变式教学有助于学生深入理解知识本质,落实一题多解、多题一法。
为强化初中几何教学效果,本文通过文献法和经验法对几何习题变式教学进行了研究,从变式教学的意义和策略两方面展开详细研究,以供参考。
关键词:初中数学;几何习题;变式研究引言:随着教育教学改革的深入,提升学生的核心素养变得愈发重要。
在这样的教育背景下,教师应该注重教学模式的优化,提高学生学习自主性,让学生在学习知识、训练技能的过程中,核心素养能够得到提升。
几何习题变式教学在核心素养培养上具有积极作用,赋予了学生更多的思考空间,在一定程度上加强了学生对几何基础知识的理解,能够促使学生深度学习,进行几何习题的探索。
基于此,教师应当注重初中数学教材几何习题的变式教学,以提高学生学习效果。
一、初中数学教材几何习题变式教学的意义在初中数学几何教学中,教师进行习题变式教学对学生核心素养的提升具有积极意义。
在传统的几何教学中,关于结合概念等知识学生习惯死记硬背,这样的学习模式下,学生的思维十分固定,只能解决标准化习题。
当题目出现一定的变形时,很多学生就会不知所措,主要原因在于不能理解知识的本质。
教师通过几何习题变式教学,可以让学生通过不同的习题深入感知几何概念,提高学生举一反三的能力。
除此之外,几何习题变式教学强调以学生为中心,引导学生主动进行知识的探索和分析,有助于学生学习兴趣的提升,强化学习效果。
二、初中数学教材几何习题变式教学的策略(一)注重习题典型资源的收集与分析从近几年中考数学几何习题上分析,很多题目源于教材中的习题,对教材中的习题进行了变式,难度并不大。
但是从学生们做题的实际情况上看,教材中涉及的几何题目,大部分学生都能够进行正确解答,但是对于中考的变式题目,很多学生在做题中出现了问题。
基于此,教师在进行教材中几何习题教学的过程中,不应该局限在教材题目中,应该适当进行习题变式,让学生以递进的形式进行习题练习,以此来促使学生深入理解知识的本质,对几何变形题有深刻的认识。
用好几何画板,提高初中数学课堂教学中变式训练有效性

用好几何画板,提高初中数学课堂教学中变式训练的有效性摘要:新课程改革要求数学教学中开展变式教学,增强学生解决问题的能力。
因此,初中数学教学中要设置变式教学情境;培养学生变式意识;提高学生应对变式问题的解决能力。
几何画板是一种工具软件,它能够在数学课堂中发挥重要的作用,它可以有效地改善教学环境,激活数学教材内容,可以把静止的图形变得运动起来,可以准确测算并处理数据。
它可以很好地适应新课改的初中数学教学要求,满足改善新课标的教学手段,实现初中数学变式教学。
关键词:几何画板;初中数学;课堂教学;变式训练初中数学教学提倡变式教学,所谓变式教学就是对同一问题,从不同的角度和思维去思考,在保持事物核心本质不变的前提下,使事物外在属性发生变化。
简单地说,就是换位思考,初中数学教学可以通过变式教学实现创新,帮助学生更加深刻地理解知识结构。
那么,如何才能使变式教学运用得当呢?要解决这个问题就要用到几何画板,发挥几何画板的作用来实现变式教学的可行性。
一、变式教学的有效性原则1.变式教学的变式设计要有差异性设计数学的问题变式,要注重一个“变”字,但是问题的设置又不能过于简单,不能让学生进行简单重复,要在教学中体现“一题多解、一题多变、一题多思、多题一法”的理念。
这方面的例子很多,尤其是几何证明题。
例1.已知,如图1,点o是等边△abc内一点,oa=4,ob=5,oc=3,求∠aoc的度数。
练习:把此题适当变式:变式1:如上图,在△abc中,ab=ac,∠bac=90°,oa=4,ob=6,oc=2,求∠aoc的度数。
变式2:如下图,点o是等边△abc内一点,∠aob=110°,∠boc=135°。
试问:(1)以oa、ob、oc为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由。
(2)如果∠aob的大小保持不变,那么当∠boc等于多少度时,以oa、ob、oc为边的三角形是一个直角三角形?2.变式教学的针对性目的变式教学的目标很明确就是通过教学中利用知识的灵活性,提高学生应对复杂问题的能力,那么如何才能实现这种变式教学的目的呢?首先要培养学生的灵活性,在课堂中设置一题多变的变式题目,变换题目的条件或者结论,而题目的本质不发生变化,以不同形式、不同角度来揭示题目本质。
余弦定理的变式及其应用举例

余弦定理的变式及其应用举例余弦定理是广为使用的几何学中定理,有着广泛的应用。
一般而言,它定义了在带有三条边的三角形中,两条边的乘积除以它们临边的余弦之乘积等于第三条边的平方(a²=b²+c²-2bc*cosA)。
以下是它最常见的一些变式,以及它们的应用举例。
一、泊松余弦定理泊松余弦定理是余弦定理变式,它定义了在带有四条边的四边形中,相邻连线段的乘积除以它们临边的余弦乘积,加上沿着外围的两条相邻的边的乘积的总和,等于最外面的角的平方(B²=a²+c²+2ac*cosA+2bc*cosB)。
应用举例:用泊松余弦定理解决日常现象。
如,排球比赛的时候,有一张台面的面积是8平方米,它的三个顶点的边长分别是2m,2.5m,2.5m,求台面的最外角的度数。
解:8=2 * 2.5 *cosB+2² *cosA,即cosA=(8-2²*cosB)/2*2.5;A=arccos((8-2²*cosB)/2*2.5);B=arccos((8-2*2.5*cosA)/2²);因此,最外角的度数为B=59.33度。
二、Jacobi-Bolyai-Gauss定理Jacobi-Bolyai-Gauss余弦定理是一个多边形余弦定理,它定义了在由M 条边构成的多边形中,相邻两条边的夹角余弦乘积的总和,等于第M 条边与第一条边的余弦乘积的积(cosA1*cosA2+cosA2*cosA3+…+cosAn*cosA1=cosA1*cosAn)。
应用举例:通过Jacobi-Bolyai-Gauss定理,可以解决多边形某一角度的大小问题。
例如,已知正八边形的八个角的余弦分别是x,x,-x,-x,x,x,-x,-x(x > 0),试求第3角的余弦值。
解:设第三角的余弦值为y,则有:x*x+x*(-x) + (-x)*y + y*x = x*x;y*y=2x*x-2x*x=2x*x;因此,第3角的余弦值为y=±√2x*x。
常见的几何习题变式方法同步练习-2024-2025学年人教版数学八年级上册+

常见的几何习题变式方法题设和结论互换的问题1、已知:∠CAE 是△ABC 的外角,∠1=∠2,AD ∥BC 。
求证:AB=AC.变式:(1)、已知:∠CAE 是△ABC 的外角,∠1=∠2,AB=AC. 求证:AD ∥BC 。
(2)、已知:∠CAE 是△ABC 的外角,AD ∥BC ,AB=AC.求证:∠1=∠2。
EA D CB 12E A D C B 1 2E A D C B 1 22、如图,∠B =∠C=90°,E 是BC 的中点,DE 平分∠ADC 。
求证:AE 是∠DAB 的平分线。
变式:在梯形ABCD 中,AM 平分∠BAD ,BM 平分∠ABC ,交点M 在CD 上。
求证:M 为CD 的中点,且AB=AD+BC 。
3、如图,△ABC 中,AB=AC ,∠BAC=90°,CD 平分∠ACB ,BE ⊥CD ,垂足E 在CD 的延长线上。
试探究线段BE 和CD 的数量关系,并证明你的结论。
变式:如图,△ABC 中,AB=AC ,∠BAC=90°, 2BE=CD , BE ⊥CD ,垂足E 在CD 的延长线上。
求证:CD 平分∠ACB 。
D CE B A A D M CB ADE BADE B综上所述:如图,△ABC 中,AB=AC ,∠BAC=90°,①CD 平分∠ACB ,②2BE=CD ,③BE ⊥CD.从三个条件中选取2个作为题设,1个作为结论,写出正确的命题,并加以证明。
4、如图,△ABC 中,AB=AC ,∠BAC=90°,点D 在线段BC 上,∠EDB=21∠C ,BE ⊥DE ,垂足E,DE 与AB 相交于点F 。
试探究线段BE 和FD 的数量关系,并证明你的结论。
变式:如图,△ABC 中,AB=AC ,∠BAC=90°,点D 在线段BC 上,2BE=FD , BE ⊥DE ,垂足E,DE 与AB 相交于点F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何变式题
1、已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
2、如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,
如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
3、Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段AC于点M,K.(1)观察:①如图2、图3,当∠CDF=0°或60°时,AM+CK与MK(填“>”,“<”或“=”);
②如图4,当∠CDF=30°时,AM+CK与MK(只填“>”或“<”);(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK>MK,证明你所得到的结论;(3)如果MK2+CK2=AM2,请直接写出∠CDF的度数
4.、已知:如图,点O为等腰直角三角形ABC的重心,∠CAB=90°,直线m过点O,过A、B、C三点分别作直线m的垂线,垂足分别为点D、E、F.
(1)当直线m与BC平行时(如图1),请你猜想线段BE、CF和AD 三者之间的数量关系并证明;
(2)当直线m绕点O旋转到与BC不平行时,分别探究在图2情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段AD、
BE、CF三者之间又有怎样的数量关系?请写出你的结论,不需证明.(3)如图3,上述结论是否还成立?若成立,请给予证明;若不成立,线段AD、BE、CF三者之间又有怎样的数量关系?请写出你的结论,不需证明,
5、已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与
B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,
①求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,结论
∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
(3)如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.
6、如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB 的延长线于点G.
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,。
