高考数学专题突破：外接球问题【精编】
立体几何高考专题--外接球的几种常见求法
立体几何高考专题--外接球的几种常见求法高三微专题：外接球在立体几何中，外接球问题是一个重点和难点。
其实质是确定球心O的位置和使用勾股定理求解外接球半径（其中底面外接圆半径r可根据正弦定理求得）。
一、由球的定义确定球心在空间中，如果一个定点与一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体的外接球的球心。
简单多面体外接球问题是立体几何中的重点和难点。
二、球体公式球的表面积公式为S=4R²，球体积公式为V=4/3R³。
三、球体几个结论：1）长方体、正方体外接球直径等于体对角线长。
2）侧棱相等，顶点在底面投影为底面外接圆圆心。
3）直径所对的球周角为90°（大圆的圆周角）。
4）正三棱锥对棱互相垂直。
四、外接球几个常见模型1.长方体（正方体）模型例1：长方体的长、宽、高分别为3、2、1，其顶点都在球O的球面上，则球O的表面积为14。
练1：体积为8的正方体的顶点都在同一球面上，则该球的表面积为12。
2.正棱锥（圆锥）模型对于侧棱相等，底面为正多边形的正棱锥，其外接球的球心位置位于顶点与底面外心连线线段（或延长线）上。
半径公式为R²=(h-R)²+r²（其中R为外接球半径，r为底面外接圆半径，h为棱锥的高，r可根据正弦定理a=2rsinA求得）。
例2：已知各顶点都在同一个球面上的正四棱锥高为h，体积为V，则这个球的表面积为____。
正四棱锥的高为h，体积为V，易知底面面积为，底面边长为。
正四棱锥的外接球的球心在它的高上，记为，得，在中。
由勾股定理，所以球的表面积为。
练2：正三棱锥S-ABC中，底面ABC是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于。
解析：ABC外接圆的半径为，三棱锥S-ABC的直径为2R=，外接球半径R=，外接球体积V=4/3R³=。
对于侧棱与底面垂直的直棱柱和圆柱，其外接球的球心位置在上下底面外心连线中点处。
高中数学空间几何体的外接球专题(附经典例题与解析)
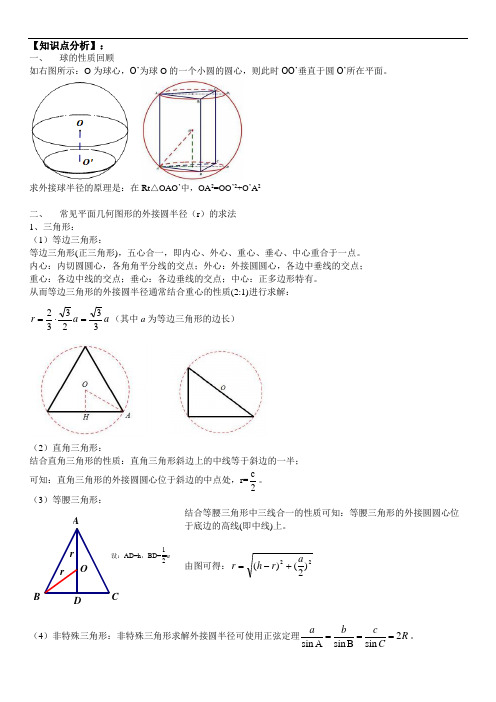
【知识点分析】： 一、 球的性质回顾如右图所示：O 为球心，O’为球O 的一个小圆的圆心，则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是：在Rt △OAO ’中，OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径（r ）的求法1、三角形：（1）等边三角形：等边三角形(正三角形)，五心合一，即内心、外心、重心、垂心、中心重合于一点。
内心：内切圆圆心，各角角平分线的交点；外心：外接圆圆心，各边中垂线的交点；重心：各边中线的交点；垂心：各边垂线的交点；中心：正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解：a a r 332332=⋅=（其中a 为等边三角形的边长）（2）直角三角形：结合直角三角形的性质：直角三角形斜边上的中线等于斜边的一半；可知：直角三角形的外接圆圆心位于斜边的中点处，r=2c 。
（3）等腰三角形： 结合等腰三角形中三线合一的性质可知：等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得：22)2()(a r h r +-=（4）非特殊三角形：非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ，BD=12a B CO2、四边形常见具有外接圆的四边形有：正方形、矩形、等腰梯形，其中正方形与长方形半径求解方法转化为直角三角形，等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点；外接球球心则是球心到几何体各个顶点距离相同的点。
结论：几何体的外接球球心与底面外心的连线垂直于底面，(也即球心落在过底面外心的垂线上，)简单称之为：球心落在底面外心的正上方。
【相似题练习】2．半径为2的球的内接三棱锥P﹣ABC，PA＝PB＝PC＝2，AB＝AC＝BC，则三棱锥的高为（）A．3B．C．2D．3【知识点分析】：类型一：直（正）棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直，从而球心O 必位于上下两底面外心连线的中点处，即121'AA OO =，从而R 可求.【相似题练习】1．三棱柱ABC ﹣A 1B 1C 1中，底面ABC 是边长为2的正三角形，侧棱AA 1垂直于底面ABC ，且AA 1＝4，则此三棱柱外接球的表面积为（ ）A ．B ．C ．D ．【知识点分析】：类型二：侧棱垂直底面的三棱锥，法一：补形法：该几何体可由正三棱柱沿平面PBC 切割得来，故可转化为原三棱柱的外接球；法二：先确定底面三角形ABC 的外心O’，从而球心位于O’的正上方，即OO’ ⊥平面ABC ，同时：OP=OA ，故，过O 作OM ⊥PA 于M ，此时M 必为PA 中点，从而四边形OMAO’为矩形，所以PA AM OO 21'==，在直角三角形OO’A 中有：222'OO r R +=.【相似题练习】2．已知在三棱锥P ﹣ABC 中，△ABC 是边长为2的正三角形，若PA ⊥底面ABC 且PA ＝2，则该三棱锥的外接球的表面积为（ ）A ．32πB ．28πC ．24πD ．20π3．在三棱锥P ﹣ABC 中，PA ⊥平面ABC ，PA ＝2，AB ＝4，AC ＝3，∠BAC ＝，则三棱锥P ﹣ABC 的外接球的半径R ＝（ ）A ．B ．C ．D ．【知识点分析】：类型三：正三棱锥：由底面正三角形边长可得r ，在直角三角形OO’A 中，222'OO r R +=，故只需确定OO’的长度即可，结合图形，OO’=PO’-OP=H-R ，代入222)(R H r R -+=即可求解.【相似题练习】3．正三棱锥P ﹣ABC 侧棱长为，侧棱与底面ABC 所成的角为60°，则该正三棱锥外接球半径为 .2．某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ ）【知识点分析】：类型四：侧面垂直于底面的三棱锥：设△ABC和△PAB的外心分别为O’,O’’，则PM⊥AB，球心设为O，则OO’ ⊥平面ABC，OO’’⊥平面PAB，从而四边形OO’MO’’是矩形，可得：OO’=O’’M，在Rt△OO’C中用勾股定理求解.【讲透例题】1．在四面体A﹣BCD中，AB＝5，BC＝CD＝3，DB＝2，AC＝4，∠ACD＝60°，则该四面体的外接球的表面积为．解析：如图：取AB的中点O，在△ACD中，由余弦定理得：AD2＝AC2+CD2﹣2×AC×CD cos60°＝13，在△ABD中，∵AB2＝BD2+AD2，∴∠ADB＝90°，∴OA＝OB＝OD，在△ABC中，∵AB2＝BC2+AC2，∴∠ACB＝90°，∴OA＝OB＝OC，∴OA＝OB＝OC＝OD，∴O为四面体ABCD的外接球的球心，其半径R＝AB＝，∴S球＝4πR2＝4π（）2＝25π．故答案为：25π．【相似题练习】4.在三棱锥P-ABC中，面PAB⊥面ABC，三角形ABC和三角形PAB均为等边三角形，且AB=3，求该几何体外接球半径.2．在边长为2的菱形ABCD中，，将菱形ABCD沿对角线AC折起，使得平面ABC⊥平面ACD，则所得三棱锥A﹣BCD的外接球表面积为（）A．B．C．D．1．已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC＝3，PB＝2，PC＝，则三棱锥P﹣ABC外接球的表面积为．5、如图，在四棱锥P﹣ABCD中，底面ABCD为长方形，PA⊥底面ABCD，AD＝AP＝2，AB＝2，E为棱PD中点．（1）求证：PD⊥平面ABE；（2）求四棱锥P﹣ABCD外接球的体积．1．如图，在正四棱锥P﹣AMDE，底面AMDE的边长为2，侧棱PA＝，B，C分别为AM，MD的中点．F为棱PE的中点，平面ABF与棱PD，PC，PM分别交于点G，H，K．（1）求证：AB∥FG；（2）求正四棱锥P﹣AMDE的外接球的表面积．1．如图，四凌锥P﹣ABCD而底面ABCD是矩形，侧面PAD是等腰直角三角形∠APD＝90°，且平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）在AD＝2，AB＝4，求三棱锥P﹣ABD的体积；（Ⅲ）在条件（Ⅱ）下，求四棱锥P﹣ABCD外接球的表面积．7、如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，已知其俯视图是正三角形，则该四棱锥的外接球的表面积是（）A．B．C．19πD．22π课后作业：1．如图，一个正三棱柱的主视图是长为，宽为2的矩形，俯视图是边长为的正三角形，则它的外接球的表面积等于（）A．16πB．12πC．8πD．4π2．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的表面积为（）A．πB．3πC．πD．π3．某四棱锥的三视图如图所示，则该棱锥的外接球的表面积为（）A．3πB．C．6πD．12π4．四棱锥P﹣ABCD中，ABCD为矩形，AD＝2，AB＝2，PA＝PD，∠APD＝，且平面PAD⊥平面ABCD．（1）证明：PA⊥PC；（2）求四棱锥P﹣ABCD的外接球的体积．参考答案与解析12．（5分）已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为（）A．64πB．48πC．36πD．32π【解答】解：由题意可知图形如图：⊙O1的面积为4π，可得O1A＝2，则AO1＝AB sin60°，，∴AB＝BC＝AC＝OO1＝2，外接球的半径为：R＝＝4，球O的表面积：4×π×42＝64π．故选：A．1．1．一个几何的三视图如图所示，它们都是腰长为1的等腰直角三角形，则该几何体的外接球的体积等于（）A．B．C．πD．2π解析：由三视图可知：该几何体是一个如图所示的三棱锥，其中底面是一个两直角边都为1的直角三角形，PC⊥底面ABC，且PC＝1．将此三棱锥恢复为棱长为1的正方体，可知该正方体的外接球的直径即为正方体的对角线，∴V外接球＝＝．故选：B．1．半径为2的球的内接三棱锥P﹣ABC，PA＝PB＝PC＝2，AB＝AC＝BC，则三棱锥的高为（）A．3B．C．2D．3【解答】解：三棱锥P﹣ABC中，PA＝PB＝PC＝2，AB＝AC＝BC，如图，过点p作PM⊥平面ABC的垂足为M，则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上，∵球O的半径为2，∴OB＝OP＝2，∴由余弦定理得cos∠BPM＝＝∴∠BPM＝30°，∴在Rt△PMB中，∠PBM＝60°，∴PM＝PB sin∠PBM＝3．故选：D．1．三棱柱ABC﹣A1B1C1中，底面ABC是边长为2的正三角形，侧棱AA1垂直于底面ABC，且AA1＝4，则此三棱柱外接球的表面积为（）A．B．C．D．【解答】解：∵正三棱柱ABC﹣A1B1C1的中，底面边长为2，高为4，由题意可得：三棱柱上下底面中心连线的中点，到三棱柱顶点的距离相等，说明中心就是外接球的球心，∴正三棱柱ABC﹣A1B1C1的外接球的球心为O，外接球的半径为r，表面积为：4πr2．球心到底面的距离为2，底面中心到底面三角形的顶点的距离为：＝，所以球的半径为r＝＝．外接球的表面积为：4πr2＝π故选：D．2．已知在三棱锥P﹣ABC中，△ABC是边长为2的正三角形，若PA⊥底面ABC且PA＝2，则该三棱锥的外接球的表面积为（）A．32πB．28πC．24πD．20π【解答】解：由正弦定理可知，正△ABC的外接圆的直径为，∵PA⊥平面ABC，所以，该三棱锥的外接球的直径为，则．因此，该三棱锥的外接球的表面积为4πR2＝20π．故选：D．3．在三棱锥P﹣ABC中，PA⊥平面ABC，PA＝2，AB＝4，AC＝3，∠BAC＝，则三棱锥P﹣ABC的外接球的半径R＝（）A．B．C．D．【解答】解：∵AC＝3，AB＝4，∠BAC＝，∴由余弦定理可得BC＝，∴△ABC外接圆的半径r＝，设球心到平面ABC的距离为d，则d＝PA＝1．由勾股定理可得R ＝，故选：D ．3．正三棱锥P ﹣ABC 侧棱长为，侧棱与底面ABC 所成的角为60°，则该正三棱锥外接球半径为 1 ． 【解答】解：过点P 作PH ⊥平面ABC 于H ，则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角，得∠PAH ＝60°， ∴Rt △PAH 中，AH ＝PA cos60°＝，PH ＝PA sin60°＝设三棱锥外接球的球心为O ，∵PA ＝PB ＝PC ，∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得，外接球心O 必定在PH 上，连接OA 、OB 、OC ∵△POA 中，OP ＝OA ， ∴∠OAP ＝∠OPA ＝30°，可得PA ＝OA ＝，∴三棱锥外接球的半径R ＝OA ＝1故答案为：1．2．某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ ）A ．16πB ．12πC ．9πD ．8π【解答】解：根据几何体的三视图转换为直观图为：该几何体为底面为等腰直角三角形，高为2的三棱锥体． 如图所示：所以该三棱锥体的外接球的球心为O ，外接球的半径为OA ＝r ，则：，解得．故S ＝．故选：C ．4.在三棱锥P-ABC 中，面PAB ⊥面ABC ，三角形ABC 和三角形PAB 均为等边三角形，且AB=3，求该几何体外接球半径.由题可得：333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2．在边长为2的菱形ABCD中，，将菱形ABCD沿对角线AC折起，使得平面ABC⊥平面ACD，则所得三棱锥A﹣BCD的外接球表面积为（）A．B．C．D．【解答】解：∵在边长为2的菱形ABCD中，；如图，由已知可得，△ABC与△ACD均为等边三角形，取AC中点G，连接BG，DG，则BG⊥AC，∴DG＝⇒cos∠GDA＝⇒∠GDA＝⇒∠ADC＝；∵二面角B﹣AC﹣D为直二面角，则BG⊥平面ACD，分别取△BCD与△ABD的外心E，F，过E，F分别作两面的垂线，相交于O，则O为三棱锥A﹣BCD的外接球的球心，由△BCA与△ACD均为等边三角形且边长为2，可得OE＝OF＝DG＝．∴DE＝DG﹣GE＝．∴OD＝＝＝．∴三棱锥A﹣BCD的外接球的表面积为4π×R2＝4π×（）2＝．故选：C．1．已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC＝3，PB＝2，PC＝，则三棱锥P﹣ABC外接球的表面积为10π．【解答】解：因为O为△ABC外接圆的圆心，且平面PBC⊥平面ABC，过O作面ABC的垂线l，则垂线l一定在面PBC内，根据球的性质，球心一定在垂线l，∵球心O1一定在面PBC内，即球心O1也是△PBC外接圆的圆心，在△PBC中，由余弦定理得cos B＝，⇒sin B＝，由正弦定理得：，解得R＝，∴三棱锥P﹣ABC外接球的表面积为s＝4πR2＝10π，故答案为：10π．1．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AD＝AP＝2，AB＝2，E为棱PD 中点．（1）求证：PD⊥平面ABE；（2）求四棱锥P﹣ABCD外接球的体积．【解答】证明：（1）∵PA⊥底面ABCD，AB⊂底面ABCD，∴PA⊥AB，又∵底面ABCD为矩形，∴AB⊥AD，PA∩AD，又PA⊂平面PAD，AD⊂平面PAD，∴AB⊥平面PAD，又PD⊂平面PAD，∴AB⊥PD，AD＝AP，E为PD中点，∴AE⊥PD，AE∩AB＝A，AE⊂平面ABE，AB⊂平面ABE，∴PD⊥平面ABE．解：（II）四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O，由已知BD＝＝＝4，设C为BD中点，∴AM＝2，OM＝AP＝1，∴OA＝＝＝3，∴四棱锥P﹣ABCD外接球的体积是＝36π．1．如图，在正四棱锥P﹣AMDE，底面AMDE的边长为2，侧棱PA＝，B，C分别为AM，MD的中点．F为棱PE的中点，平面ABF与棱PD，PC，PM分别交于点G，H，K．（1）求证：AB∥FG；（2）求正四棱锥P﹣AMDE的外接球的表面积．【解答】（1）证明：在正方形AMDE中，因为B是AM的中点，所以AB∥DE．又因为AB⊄平面PDE，DE⊂平面PDE,所以AB∥平面PDE．因为AB⊂平面ABF，且平面ABF∩平面PDE＝FG，所以AB∥FG．（2）解：连接AD，EM，相交于O′，易得AO′＝，PO′＝．由正四棱锥P﹣AMDE的对称性，得正四棱锥P﹣AMDE得外接球球心在线段PO′上，不妨设为O点．设OA＝OP＝R，则OO′＝﹣R，∵AO2＝AO′2+OO′2，∴R2＝2+（﹣R）2，∴R＝∴S＝4πR2＝，∴正四棱锥P﹣AMDE的外接球的表面积为．1．如图，四凌锥P﹣ABCD而底面ABCD是矩形，侧面PAD是等腰直角三角形∠APD＝90°，且平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）在AD＝2，AB＝4，求三棱锥P﹣ABD的体积；（Ⅲ）在条件（Ⅱ）下，求四棱锥P﹣ABCD外接球的表面积．【解答】解：（I）∵四边形ABCD是矩形，∴AD⊥CD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，CD⊂平面ABCD，∴CD⊥平面PAD，∵CD⊂平面PCD，∴平面PAD⊥平面PCD．（II）过P作PE⊥AD，垂足为E，∵△PAD是等腰直角三角形，∠APD＝90°，∴PE＝＝1．∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，PE⊂平面PAD，PE⊥AD，∴PE⊥平面ABCD，∴V棱锥P﹣ABD＝S△ABD•PE＝••2•4•1＝．（III）取BD中点M，过M作MN⊥平面ABCD，则球心O在直线MN上，连接AM，则AM＝＝．∵PE⊥平面ABCD，∴MN∥PE．∵四棱锥P﹣ABCD内接于球，，∴OA＝＝．∴S⊙O＝4πOA2＝20π．∴E为外心，∴OM＝1．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，已知其俯视图是正三角形，则该四棱锥的外接球的表面积是（）A．B．C．19πD．22π【解答】解：几何体的直观图如图：是长方体的一部分，上底面PCD的外接圆的半径：O1D＝＝，几何体的外接球的半径为：OD＝＝，该四棱锥的外接球的表面积是：4＝π．故选：A．课后作业答案：1．如图，一个正三棱柱的主视图是长为，宽为2的矩形，俯视图是边长为的正三角形，则它的外接球的表面积等于（）A．16πB．12πC．8πD．4π【解答】解：设正三棱柱的外接球的半径为R，则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为＝1，∵正三棱柱的高为2∴正三棱柱的外接球的半径为＝∴正三棱柱的外接球的表面积等于4π×＝8π故选：C．2．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的表面积为（）A．πB．3πC．πD．π【解答】解：由三视图可知：该四面体是正方体的一个内接正四面体．∴此四面体的外接球的直径为正方体的对角线长＝．∴此四面体的外接球的表面积为表面积＝＝3π．故选：B．3．某四棱锥的三视图如图所示，则该棱锥的外接球的表面积为（）A．3πB．C．6πD．12π【解答】解：由题意可知，几何体的直观图如图：是四棱锥D1﹣ABCD，是棱长为1的正方体的一部分，外接球奇数正方体的外接球，取得直径是体对角线，r＝，外接球的表面积为：4＝3π．故选：A．4．四棱锥P﹣ABCD中，ABCD为矩形，AD＝2，AB＝2，PA＝PD，∠APD＝，且平面PAD⊥平面ABCD．（1）证明：PA⊥PC；（2）求四棱锥P﹣ABCD的外接球的体积．【解答】证明：（1）设AD的中点为E，则∵PA＝PD，∴PE⊥AD，∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PE⊥平面ABCD，∵PA在平面ABCD内的射影为AE，AE⊥CD，∴PA⊥CD，∵PA⊥PD，CD∩PD＝D，∴PA⊥平面PCD∴PA⊥PC；解：（2）连接AC交BD于F，球心O在底面的射影必为点F，取截面PEF，PE＝，EF＝1．假设OF＝x，则由OA2＝x2+4＝1+得x＝0，∴球的半径为2，∴四棱锥P﹣ABCD的外接球的体积为＝．。
【高考数学精品】外接球内切球的9大题型
【高考数学专题】外接球内切球的9大类题型梳理与球有关的组合体问题，一种是内切，一种是外接，解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图．例如：球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径． 1. 球的表面积为S=4πR 2 2. 球的体积为V ＝43πR 3多面体、旋转体与球接、切问题的求解策略(1)过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题． (2)利用平面几何知识寻找几何体元素间的关系，或只画内切、外接的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解． (3)若球面上4点P ，A ，B ，C 构成的3条线段P A ，PB ，PC 两两互相垂直，且P A ＝a ，PB ＝b ，PC ＝c ，一般把有关元素“补形”成为一个球内接长方体，用4R 2＝a 2＋b 2＋c 2求解．一．球的性质应用例题1 已知三棱锥S ABC -的顶点都在球O 的球面上，ABC 是边长为6的正三角形，SC 为球O 的直径，且8SC =，则此三棱锥的体积为( )A ．B ．C ．D ．【解析】因为△ABC 是边长为6的正三角形,所以△ABC 外接圆的半径r =SC 为球O 的直径，且8SC =，球O 半径R =4，所以点O 到平面ABC 的距离2d ===，SC 为球O 的直径,点S 到平面ABC 的距离为2d =4，此棱锥的体积为11126643322ABCV S d =⨯=⨯⨯⨯⨯=，选C .巩固1 已知三棱锥O ABC -中，A ，B ，C 三点在以O 为球心的球面上，若2AB BC ==，120ABC ∠=︒，且三棱锥O ABC -的体积为3，则球O 表面积为（） A ．323πB ．16πC ．52πD ．64π【解析】由题意2AB BC ==，ABC 1120=||||sin 32ABC S AB BC ABC ∆∠=︒∠=， 1333O ABC ABC V S h h -∆==∴=.又ABC ∆的外接圆的半径222sin 2sin 30oAB r C ===因此球O 的半径222313R =+=球的表面积：2452S R ππ==，选C巩固2 已知三棱锥P-ABC 中，PA=4，3BC=6，PA ⊥面ABC ，则此三棱锥的外接球的表面积为（ ） A ．16πB ．32πC ．64πD ．128π【解析】∵底面ABC 中，2AB AC ==，6BC =，∴1cos 2BAC ∠=- ∴3sin BAC ∠=，∴ABC 的外接圆半径1 2323r == PA ⊥面ABC ，∴三棱锥外接球的半径(22222232162PA R r ⎛⎫=+=+= ⎪⎝⎭，所以三棱锥P ABC -外接球的表面积2464S R ππ==，选C ．二．最值问题例题2 已知三棱锥P ABC -的顶点都在半径为53的球面上，1AB =，3BC =，2AC =，则三棱锥P ABC -体积的最大值为（ ）A ．32B ．1C ．3D ．5318【解析】如图，设球心为O ，由1AB =，3BC =，2AC =可得ABC ∆为直角三角形，斜边AC 的中点O '为球小圆的圆心，接OO '，OA ，则OO '⊥平面ABC ，由53OA =，1O A '=可得43OO '=，故三棱锥P ABC -最大体积为113453()3333ABC S O P ∆⨯⨯'=⨯⨯+=，选A ． 巩固1 在三棱锥P ABC -中，PA ⊥底面ABC ，,6,8AB AC AB AC ⊥==，D 是线段AC 上一点，且3AD DC =.三棱锥P ABC -的各个顶点都在球O 表面上，过点D 作球O 的截面，若所得截面圆的面积的最大值与最小值之差为16π，则球O 的表面积为（ ） A ．72πB ．86πC ．112πD ．128π【解析】将三棱锥P ABC -补成直三棱柱，且三棱锥和该直三棱柱的外接球都是球O ， 记三角形ABC 的中心为1O ，设球的半径为R ，2PA x =， 则球心O 到平面ABC 的距离为x ，即1OO x =，连接1O A ，则15O A =，∴2225R x =+.在ABC 中，取AC 的中点为E ，连接11,O D O E ，则1132O E AB ==，124DE AC ==， 所以113O D =.在1Rt OO D 中，213OD x =+， 由题意得到当截面与直线OD 垂直时，截面面积最小，设此时截面圆的半径为r ，高中数学资料共享群（群号：734924357）则()22222251312r R OD x x =-=+-+=，所以最小截面圆的面积为12π，当截面过球心时，截面面积最大为2R π， 所以21216R π-π=π，228R =， 球的表面积为2112R 4π=π. 选C.巩固2 已知ABC ∆的三个顶点落在半径为R 的球O 的表面上，三角形有一个角为3π且其对边长为3，球心O 到ABC ∆所在的平面的距离恰好等于半径R 的一半，点P 为球面上任意一点，则P ABC -三棱锥的体积的最大值为（ ） A ．83B ．733C ．93D ．73【解析】设ABC ∆外接圆的圆心为1O ，则1OO ⊥平面ABC ，所以12R OO =设ABC ∆外接圆的半径为r ，3AB c ==，3C π∠=由正弦定理可得：32sin3rπ=，解得：3r =由球的截面圆性质可得：2222132R R OO r ⎛⎫=+=+ ⎪⎝⎭，解得：2R = 所以点P 到平面ABC 的距离的最大值为：13R OO +=.在ABC ∆中，由余弦定理可得：2222232cos 2a b ab C a b ab ab ab ab =+-=+-≥-=当且仅当3a b ==时，等号成立，所以()max 9ab =.高中数学资料共享群（群号：734924357）所以193sin 23ABCS ab π∆，当且仅当3a b ==时，等号成立. 当三棱锥P ABC -的底面面积最大，高最大时，其体积最大. 所以三棱锥P ABC -的体积的最大值为193933344P ABC V -=⨯⨯=选C三．球直径灵活应用例题3 已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（ ） A ．26B ．36C ．23D ．22【解析】作出图形，设球心为O ，过ABC 三点的小圆的圆心为O 1，则OO 1⊥平面ABC ， 延长CO 1交球于点D ，则SD ⊥平面ABC ∵CO 1=2333=，∴11613OO =-=，∴高SD=2OO 1=26，∵△ABC 是边长为1的正三角形，∴S △ABC =3，∴132623S ABC V -=⨯⨯=三棱锥． 四．球与其它几何体的综合例题4 如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为（ ）A ．3500cm 3πB ．3866cm 3πC ．31372cm 3πD ．32048cm 3π【解析】设球的半径为R cm ，根据已知条件知正方体的上底面与球相交所得截面圆的半径为4cm ，球心到截面圆的距离为()2R -cm 所以由()22242R R +-=，得5R = 所以球的体积为()333445005cm 333V R πππ==⨯= 选A巩固1 四面体ABCD 中，已知1DA DB DC ===，且DA DB DC 、、两两相互垂直，在该四面体表面上与点A 23的点形成一条曲线，则这条曲线的长度是( ) A 3 B 3 C 53D 3π【解析】在四面体表面上与点A 距离为33的点形成一条曲线 曲线分别与,,,AB BD AC CD 交于,,,E H F G3,cos 223AD Rt ADH DAH AH ∆∠===13,62DAH DH AH π∴∠===，4612HAE πππ∠=-=，同理12GAF π∠=， 23312318FG HE ππ∴==⨯=，232333,339236EF GH ππππ=⨯==⨯=， EF FG GH HE ∴+++32333218962ππππ=⨯++=. 选B.五．球定义的灵活应用例题5 如图，在底面为矩形的四棱锥E ABCD -中，DE ⊥平面ABCD ，F ，G 分别为棱DE ，AB 上一点，已知3CD DE ==，4BC =，1DF =，且FG ∥平面BCE ，四面体ADFG 的每个顶点都在球O 的表面上，则球O 的表面积为（ ）A ．12πB ．16πC ．18πD ．20π【解析】在棱CD 上取一点H,使得HD=1////CD DE FH CE FH =∴，，则平面BCE又//FG 平面BCE ，FG FH F ⋂=，∴平面//FGH 平面BCE ， 又平面FGH ⋂平面ABCD=GH ，平面BCE ⋂平面ABCD=BC,//BC GH ∴，AG ∴= HD=1,故四面体ADFG 可以补成一个长方体，且长，宽，高分别为4，1，1所以球O 的表面积为2222114418.ππ++=选C巩固1 如图所示，在三棱锥P ABC -中，AB BC ⊥，3AB =，2BC =，点P 在平面ABC 内的投影D 恰好落在AB 上，且1AD =，2PD =，则三棱锥P ABC -外接球的表面积为（ ）A ．9πB ．10πC ．12πD ．14π【解析】由已知可知PD ⊥平面ABC ，∴平面PAB ⊥平面ABC ， 又因为AB BC ⊥，BC ∴⊥平面PAB ，∴可构造直三棱柱PAB MNC -， 直三棱柱PAB MNC -的外接球就是三棱锥P ABC -的外接球， 且球心O 为直三棱柱上下底面三角形外接圆圆心连线的中点.在PAB △5102sin4π=，∴外接球半径为2101412⎛⎫+= ⎪⎝⎭，∴三棱锥P ABC -外接球的表面积为2144142ππ⎛⎫= ⎪⎝⎭，选D .六．多面体放球中的解题策略例题6 已知二面角P ﹣AB ﹣C 的大小为120°，且∠P AB ＝∠ABC ＝90°，AB ＝AP ，AB +BC ＝6．若点P ，A ，B ，C 都在同一个球面上，则该球的表面积的最小值为（ ）A ．45πB ．2887πC ．1447πD ．727π【解析】设AB ＝x ，（0＜x ＜6），则6BC x =-，由题意知三棱锥外接球的球心是过△P AB 和△ABC 的外心E ，H ， 且分别垂直这两个三角形所在平面的垂线的交点O ， OB 为三棱锥外接球半径，取AB 的中点为G ，如图， 由条件知,3,222x x xEG GH GB ==-= 在△EGH 中，由余弦定理得222223323cos 92222342x x x x x EH x π⎛⎫⎛⎫⎛⎫=+--⨯⨯-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴△EGH 的外接圆直径2392423sin3EH x OG x π==-+2222224371272934221277x x OB OG GB x x ⎛⎫⎛⎫⎛⎫=+=-++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭当127x =时，OB 2的最小值为727， ∴该球的表面积的最小值为228847OB ππ⨯=. 选B ．巩固1 等腰三角形ABC 的腰5AB AC ==，6BC =，将它沿高AD 翻折，使二面角B ADC --成60︒，此时四面体ABCD 外接球的体积为（ ）A ．7πB ．28πC 1919D 287【解析】由题意，设BCD ∆所在的小圆为1O ，半径为r ， 又因为二面角B AD C --为060， 即060BDC ∠=，所以BCD ∆为边长为3的等边三角形， 又正弦定理可得，03223sin 60r == 即23BE =设球的半径为R ，且4=AD ，在直角ADE ∆中，()22222244(23)28R AD DE R =+⇒=+=， 所以7R =，所以球的体积为3344287(7)33V R ππ==⨯=， 选D ．巩固2 在三棱锥S ABC -中，AB BC ⊥，2AB BC ==，22SA SC ==S AC B --的余弦值是3若S A B C ，，，都在同一球面上，则该球的表面积是（ ） A ．6πB ．8πC ．12πD ．18π【解析】取AC 的中点D ，连接SD BD ，.因为SA SC AB BC ==，，所以SD AC BD AC ⊥⊥，， 可得SDB ∠即为二面角S AC B --的平面角，故3cos SDB ∠=. 在直角SDC △中，226SD SC CD -=2BD =，由余弦定理得22232cos 26226()SB BD SD BD SD BDS =+-⋅⋅∠=+- 解得123SB ==在SCB 中，22228412)SC CB SB +=+==， 所以SCB 为直角三角形，同理可得SAB 为直角三角形，取SB 中点E ， 则3SE EB ==，在Rt SCB △与Rt SAB 中，32SBEA ==，32EC SB == 所以点E 3243)12S ππ=⨯⨯=. 选C巩固3 已知三棱锥S ABC -中，23AB AC BC ===，SB SC ⊥，平面SBC ⊥平面ABC ，则三棱锥的外接球的表面积为（ ）A ．8πB ．12πC ．16πD ．18π【解析】如图，取BC 的中点D ，连接AD ，SD ，则AD BC ⊥， 又平面SBC ⊥平面ABC ，平面SBC平面ABC AD =，AD ⊂平面ABC ，所以AD ⊥面SBC ，又SD ⊂平面SBC ， 所以AD SD ⊥，在AD 上取一点O ，使得OA OS =，则O 为球心， 设球的半径为R ， 因为SB SC ⊥，所以SBC ∆为直角三角形， 又D 为BC 的中点， 所以132SD BC ==，又3233AD =⨯=， 又在Rt SOD ∆中，222SO DO DS =+，即()()2223+3R R =-，解得2R =.所以外接球表面积为2416S R ππ==. 选C.巩固4 表面积为的球面上有四点，且是边长为的等边三角形，若平面平面，则三棱锥体积的最大值是【解析】∵，故当到面的距离最大时，三棱锥的体积最大，由图可知即当，为中点时，三棱锥的体积最大，作，面，连接，由，得，由于，得，故，，故，，，，故答案为七．球的截面问题例题7如图，正四面体A﹣BCD的棱长为a，点E、F分别是棱BD、BC的中点，则平面AEF截该正四面体的内切球所得截面的面积为_____.【解析】根据题意知,平面AEF截该正四面体的内切球所得截面一定是圆，设圆心为P，内切球的球心为O，作AN⊥平面BCD,则N为底面三角形的中心在等边三角形BCD中,233323 BN a a =⨯=在Rt ABN ∆中,由勾股定理知,2222363aAN AB BN a a ⎛⎫=-=-= ⎪ ⎪⎝⎭由图可知,AO 为四面体外接球的半径,设AO BO R ==在Rt BON ∆中,由勾股定理可得,2223633R a a R ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,解得6R a = 所以正四面体A ﹣BCD 的内切球半径为r =666ON AN OA a a a =-=-=, 因为OP ⊥AM ，AN MN ⊥,所以~AOP AMN ∆∆，又因为113366212MN BH a a ==⨯= 由AM 2＝NM 2+AN 2可得AM 114a =，∴OP AO MN AM =，即64311a a a =,解得OP 1811a = ∴平面AEF 截该正四面体的内切球所得截面圆半径r 12233r OP =-=平面AEF 截该正四面体的内切球所得截面的面积为22()3333a ππ⨯= 巩固1 已知三棱锥S ABC -的所有顶点在球O 的球面上，SA ⊥平面ABC ，ABC ∆是等腰直角三角形，2SA AB AC ===，D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是______.【解析】点D 是Rt ABC ∆的外心，过点D 作DO ⊥平面ABC 使112DO SA == O 是外接球球心，半径设为R ，OA OS R ==在直角梯形SADO 中，2SA =，1OD =，2AD =3R =过点D 作球O 的截面当OD ⊥截面时，截面面积最小，此时截面圆的半径为222R OD -= ∴截面面积的最小值是2π八．内切球问题例题8 图（1）为棱长为1的正方体，若正方体内有两个球相外切且又分别与正方体的三个面相切，则两球半径之和为________.【解析】如图（2）作出正方体的体对角面，易知球心1O 和2O 在AC 上 过点1O ，2O 分别作AD ，BC 的垂线，垂足分别为E ，F 设球1O 的半径为r ，球2O 的半径为R 由1AB =，3AC =13AO r =，23O C R =∴3()3r R r R +++=33331R r -+==+九．翻折问题与球例题9 在平行四边形ABCD 中，22AB =，3BC =，且2cos 3A =，以BD 为折痕，将BDC 折起，使点C 到达点E 处，且满足AE AD =，则三棱锥E ABD -的外接球的表面积为__________.【解析】解：在ABD △中，22AB =3BC =，且2cos A = 由余弦定理，得2222cos BD AB AD AB AD A =+-⋅ 即：(2222223222393BD =+-⨯⨯=，解得：3BD = 在四面体ABED 中，3AE BD ==，3AD BE ==，22AB ED ==三组对棱长相等，可将四面体ABED 放在长方体中设长方体的相邻三棱长分别为x ，y ，z ，设外接球半径为R 则229x y +=，229y z +=，228z x += 则22213x y z ++=，即213R =13R =所以，四面体E ABD -外接球的表面积为：2134413π4R ππ=⨯=巩固1 在矩形ABCD 中，4BC ＝，M 为BC 的中点，将ABM 和DCM △分别沿AM ，DM 翻折，使点B 与C 重合于点P .若150APD ∠︒＝，则三棱锥M PAD ﹣的外接球的表面积为_____.【解析】由题意可知，MP PA MP PD PD PA P ⊥⊥⋂，，＝， 所以可得PM ⊥面PAD ， 设ADP △外接圆的半径为r ， 由正弦定理可得AD 2sin APDr =∠，即42sin150r =︒，4r =， 设三棱锥M PAD ﹣外接球的半径R ，因为外接球的球心为过底面圆心垂直于底面的直线与中截面的交点，则222PM 116172R r ⎛⎫=+=+= ⎪⎝⎭，所以外接球的表面积为2468S R ππ＝＝.巩固2 在平面五边形ABCDE 中,60A ︒∠=,63AB AE ==,BC CD ⊥,DE CD ⊥,且6BC DE ==.将五边形ABCDE 沿对角线BE 折起,使平面ABE 与平面BCDE 所成的二面角为120︒,则沿对角线BE 折起后所得几何体的外接球的表面积是________.【解析】由题意知,ABE △是正三角形,BCDE 是矩形 设ABE △的中心为1O ,矩形BCDE 的中心为2O过1O 作垂直于平面ABE 的直线1l ,过2O 作垂直于平面BCDE 的直线2l 由球的性质可知,直线1l 与2l 的交点O 为几何体ABCDE 的外接球的球心 取BE 的中点F ,连接12,O F O F易得1133O F ==,21632O F =⨯=,12120O FO ︒∠=连接OF ,显然1OFO 与2OFO 全等,从而160O FO ︒∠=,1OO =,连接OA ,则OA 为所求几何体外接球的半径,又1263O A ==, 则22211273663OA OO O A =+=+=,故所得几何体外接球的表面积为24π252πS OA =⋅=.。
2024年高考数学二轮专题06 一网打尽外接球与内切球问题(精讲精练)(解析版)
专题06 一网打尽外接球与内切球问题【命题规律】纵观近几年高考对于组合体的考查，与球相关的外接与内切问题是高考命题的热点之一．高考命题小题综合化倾向尤为明显，要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答．从近几年全国高考命题来看，这部分内容以选择题、填空题为主，大题很少见，此部分是重点也是一个难点，属于中等难度．【核心考点目录】核心考点一：正方体、长方体外接球核心考点二：正四面体外接球核心考点三：对棱相等的三棱锥外接球核心考点四：直棱柱外接球核心考点五：直棱锥外接球核心考点六：正棱锥与侧棱相等模型核心考点七：侧棱为外接球直径模型核心考点八：共斜边拼接模型核心考点九：垂面模型核心考点十：二面角模型核心考点十一：坐标法核心考点十二：圆锥圆柱圆台模型核心考点十三：锥体内切球核心考点十四：棱切球【真题回归】1．（2022·全国·高考真题（文））已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（ ）A ．13B ．12C D 【答案】C【解析】[方法一]：【最优解】基本不等式设该四棱锥底面为四边形ABCD ，四边形ABCD 所在小圆半径为r ，设四边形ABCD 对角线夹角为α，则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅=（当且仅当四边形ABCD 为正方形时等号成立）即当四棱锥的顶点O到底面ABCD所在小圆距离一定时，底面ABCD面积最大值为22r 又设四棱锥的高为h，则22r h1+=，2123O ABCDV r h-=⋅⋅=≤=当且仅当222r h=即h.故选：C[方法二]：统一变量＋基本不等式由题意可知，当四棱锥为正四棱锥时，其体积最大，设底面边长为a，底面所在圆的半径为r，则r=，所以该四棱锥的高h，13V a===(当且仅当22142a a=-，即243a=时，等号成立)所以该四棱锥的体积最大时，其高h===故选：C．[方法三]：利用导数求最值由题意可知，当四棱锥为正四棱锥时，其体积最大，设底面边长为a，底面所在圆的半径为r，则r=，所以该四棱锥的高h，13V a=，令2(02)a t t=<<，V=()322t tft=-，则()2322tf t t-'=，43t<<，()0f t'>，单调递增，423t<<，()0f t'<，单调递减，所以当43t=时，V最大，此时h=故选：C.【整体点评】方法一：思维严谨，利用基本不等式求最值，模型熟悉，是该题的最优解；方法二：消元，实现变量统一，再利用基本不等式求最值；方法三：消元，实现变量统一，利用导数求最值，是最值问题的常用解法，操作简便，是通性通法．2．（2021·全国·高考真题（理））已知A，B，C是半径为1的球O的球面上的三个点，且,1AC BC AC BC⊥==，则三棱锥O ABC-的体积为（）A B C D 【答案】A【解析】,1AC BC AC BC ⊥== ，ABC ∴ 为等腰直角三角形，AB ∴=，则ABC 1，设O 到平面ABC 的距离为d ，则d ==所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯=故选：A.3．（2022·全国·高考真题）已知正三棱台的高为1，上、下底面边长分别为面上，则该球的表面积为（ ）A ．100πB ．128πC ．144πD ．192π【答案】A【解析】设正三棱台上下底面所在圆面的半径12,r r ，所以1222r r ==123,4r r ==，设球心到上下底面的距离分别为12,d d ，球的半径为R ，所以1d =2d =，故121d d -=或121d d +=1=，解得225R =符合题意，所以球的表面积为24π100πS R ==．故选：A ．4．（2022·全国·高考真题）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3l ≤≤，则该正四棱锥体积的取值范围是（ ）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]【答案】C【解析】∵球的体积为36π，所以球的半径3R =,[方法一]：导数法设正四棱锥的底面边长为2a ，高为h ，则2222l a h =+，22232(3)a h =+-,所以26h l =，2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭，所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭，当3l ≤≤0V '>，当l <≤时，0V '<，所以当l =时，正四棱锥的体积V 取最大值，最大值为643，又3l =时，274V =，l =814V =,所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦，.故选：C.[方法二]：基本不等式法由方法一故所以()()()3221224211646122(333333h h h V a h h h h h h h ⎡⎤-++==-=-⨯⨯=⎢⎥⎣⎦…当且仅当4h =取到)，当32h =时，得a 22min 11327;3324V a h ==⨯=当l =39322h =+=，a ⇒，正四棱锥体积221119816433243V a h ==⨯=<，故该正四棱锥体积的取值范围是2764[,].435．（2020·全国·高考真题（理））已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为（ ）A ．64πB ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r ππ=∴=， ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==，根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==.故选：A6．（2020·全国·高考真题（理））已知△ABC O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为（ ）AB ．32C ．1D 【答案】C 【解析】设球O 的半径为R ，则2416R ππ=，解得：2R =.设ABC 外接圆半径为r ，边长为a ，ABC212a ∴，解得：3a =，2233r ∴===∴球心O 到平面ABC 的距离1d ===.故选：C.【方法技巧与总结】1、补成长方体（1）若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．（2）若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．（3）正四面体-P ABC 可以补形为正方体且正方体的棱长=a ，如图3所示．（4）若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示图1 图2 图3 图4【核心考点】核心考点一：正方体、长方体外接球【规律方法】1、正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．2、长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．【典型例题】例1．（2023·全国·高三专题练习）已知正方体外接球的体积是323π，那么正方体的体对角线等于（ ）A B ．4C D 【答案】B【解析】正方体外接球的直径即为正方体的体对角线，设外接球的半径为R ，则343233V R ππ==，解得2R =，所以正方体的体对角线等于24R =；故选：B例2．（2022·陕西西安·模拟预测（文））长方体的过一个顶点的三条棱长分别是2，4，4，则该长方体外接球的表面积为（ ）A ．9πB ．18πC ．36πD ．48π【答案】C【解析】长方体外接球直径263R R ===⇒=，所以该长方体外接球的表面积2244336S R πππ==⋅=故选：C.例3．（2022·贵州黔南·高三开学考试（理））自2015年以来，贵阳市着力建设“千园之城”，构建贴近生活、服务群众的生态公园体系，着力将“城市中的公园”升级为“公园中的城市”．截至目前，贵阳市公园数量累计达到1025个．下图为贵阳市某公园供游人休息的石凳，它可以看做是一个正方体截去八个一样的四面体得到的，如果被截正方体的的棱长为，则石凳所对应几何体的外接球的表面积为________2cm ．【答案】1600π【解析】设正方体的中心为O ，E 为棱的中点，连接1111,,,A D B C A C B D ，则O 为矩形11A DCB 的对角线的交点，则1112022OE B C ==⨯=，同理，O 到其余各棱的中点的距离也为20，故石凳所对应几何体的外接球的半径为20，其表面积为224π201m 600πc ⋅=，故答案为：1600π核心考点二：正四面体外接球【规律方法】如图，设正四面体ABCD 的的棱长为a ，显然正四面体和正方体有相同的外接球．正方体外接球半径为==R ，即正四面体外接球半径为=R ．【典型例题】例4．（2022·黑龙江·哈九中模拟预测（理））已知正四面体P ABC -外接球O 表面积为54π，则该正四面体棱长为______；若M 为平面ABC 内一动点，且PM = ，则AM 最小值为______．【答案】 6 -【解析】设该正四面体棱长为a ，过点P 作PD ⊥面ABC ，则点D 为ABC 的重心，则AD =，PD =，又正四面体P ABC -外接球O 表面积为54π，则2454R ππ= ，则R =，即PO AO = 又222AO AD OD =+，则222)=+，解得：6a =；又M 为平面ABC 内一动点，且PM =，则DM ===，即点M 的轨迹为以D 为圆心，又AD =则由点与圆的位置关系可得AM最小值为：-故答案为：6；例5．（2022·江苏南京·高三开学考试）已知一个正四面体的棱长为2，则其外接球与以其一个顶点为球心，1为半径的球面所形成的交线的长度为___________.【解析】设外接球半径为r ，外接球球心到底面的距离为h ，则2243h r r h +==+，所以r =两球相交形成形成的图形为圆，如图，在PDO △中，cos DPO ∠==sin DPO ∠=在1PDO △中，1sin DO PD DOP =∠=所以交线长度为2π=例6．（2022·福建·福州三中模拟预测）表面积为）A．B．12πC．8πD．【答案】B【解析】设正四面体的棱长为a24⨯=a=该正四面体的外接球与棱长为2的正方体的外接球的半径相等，2412Sππ=⨯=.故选：B.核心考点三：对棱相等的三棱锥外接球【规律方法】四面体ABCD中，==AB CD m，==AC BD n，==AD BC t，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题．如图，设长方体的长、宽、高分别为,,a b c，则222222222⎧+=⎪+=⎨⎪+=⎩b c ma c na b t，三式相加可得222++=a b c222,2++m n t 而显然四面体和长方体有相同的外接球，设外接球半径为R，则22224+=+a b c R，所以=R．【典型例题】例7．（2022·全国·高三专题练习）在四面体ABCD中，2==AC BD，AD BC==AB CD==其外接球的表面积为___________.【答案】8π【解析】如图所示，将该四面体补成长方体，设该长方体的长､宽､高分别为a，b，c，则2,===解得2222224,5,7,a b b c c a ⎧+=⎪+=⎨⎪+=⎩所以2228a b c ++==，，其外接球的表面积为248ππ⨯=.故答案为：8π．例8．（2022·全国·高三专题练习）已知四面体ABCD中，AB CD ==BC AD ==AC BD =，若该四面体的各个顶点都在同一球面上，则此球的表面积为（ ）A ．42πB ．43πC ．14πD ．16π【答案】C设长方体的长、宽、高分为,,,x y z 所以2222225,10,13,x y x z z y ⎧+=⎪+=⎨⎪+=⎩∴∴，∴此球的表面积为144144ππ⋅=．故选：C ．例9．（2020·全国·模拟预测（文））在三棱锥A BCD -中，若2AB CD ==，3AD BC ==，4AC BD ==，其外接球的表面积为（ ）A ．27πB ．29πC ．294πD ．292π【答案】D【解析】三棱锥A BCD -中，∵2AB CD ==，3AD BC ==，4AC BD ==，显然这六条棱长恰为长方体的六个面的面对角线的长，设此长方体的长、宽、高依次为a 、b 、c ，其对角线的长恰为外接球的直径，如图所示．则有2222224916a b b c a c ⎧+=⎪+=⎨⎪+=⎩，则222292a b c ++=，易知长方体的体对角线长为2R =22942S R ππ==球面积．故选:D核心考点四：直棱柱外接球【规律方法】如图1，图2，图3，直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）图1图2图3第一步：确定球心O 1是∆ABC 的外心，则1⊥OO 平面ABC ；第二步：算出小圆1O 的半径1=AO r ，111122==OO AA h （1=AA h 也是圆柱的高）；第三步：勾股定理：22211=+OA O A O O ⇒222(2=+hR r ⇒=R R【典型例题】例10．（2022·河南新乡·一模（理））已知正三棱柱的侧棱长为l ，底面边长为a ，若该正三棱柱的外接球体积为32π3，当la +最大时，该正三棱柱的体积为（ ）A B C D 【答案】B【解析】因为正三棱柱外接球的体积为3432ππ33R =，所以2R =，设球心为O ，底面外接圆圆心为O '，由正三棱锥可得12OO l '=，底面外接圆半径r =，图3-1图3-2图3-3所以由勾股定理得22443l a +=，设l a m +=，当直线l a m +=与曲线22443l a +=相切时，m 最大，联立方程组22443l a m l a +=⎧⎪⎨+=⎪⎩得22763480a ma m -+-=，由Δ0=，得m =或-（舍去），此时a =l所以正三棱柱的体积2V l ==故选：B例11．（2022·湖南岳阳·高三阶段练习）已知直三棱柱111ABC A B C -中，12,AB AA BC ===，当该三棱柱体积最大时，其外接球的体积为（ ）AB ．323πCD【答案】C【解析】因为三棱柱111ABC A B C -为直三棱柱，所以，1AA ⊥平面ABC所以，要使三棱柱的体积最大，则ABC 面积最大，因为1sin 2ABC S BC AC ACB =⋅⋅∠△，令AC x=因为BC =，所以2sin ABC S x ACB ⋅∠ ，在ABC中，222cos 2AC BC AB ACB AC BC +-∠==⋅所以，224224416(1)43216sin 11212x x x ACB x x --+-∠=-=，所以，()22422424123384()sin 34434ABCx x x Sx ACB --+-+-=⋅∠=⋅=≤ ，所以，当24x =，即2AC =时，2()ABC S 取得最大值3，所以，当2AC =时，ABC SABC为等腰三角形，2,AB AC BC ===所以，()22244121cos ,0,22222AB AC BC BAC BAC AB AC π+-+-∠===-∠∈⋅⨯⨯，所以23BAC π∠=，所以，由正弦定理得ABC 外接圆的半径r42r==，即2r =，所以，直三棱柱111ABC A B C -外接球的半径222152AA R r ⎛⎫=+= ⎪⎝⎭，即R =所以，直三棱柱111ABC A B C -外接球的体积为343R π=.故选：C例12．（2021·四川泸州·二模（文））直六棱柱的底面是正六边形，其体积是，则该六棱柱的外接球的表面积的最小值是（ ）A ．4πB ．8πC ．12πD ．24π【答案】C【解析】设正六边形的边长为a，则底面面积为226S ==，设(0)AC x x =>，则正六棱柱的体积为2V Sh x =⨯=解得24xa =，即24a x=，又由该六棱柱的外接球的直径为2BC r ==所以该六棱柱的外接球的表面积为：2222164(4)(),(0)S r x a x x xπππ'==+=+>，令()216(0)f x x x x =+>，则()2162f x x x'=-，令()0f x '=，解得2x =，当02x <<时，()0f x '<，()f x 单调递减；当2x >时，()0f x '<，()f x 单调递增，所以当2x =时，()f x 取得最小值12，所以该六棱柱的外接球的表面积的最小值为12π.故选：C.核心考点五：直棱锥外接球【规律方法】如图，⊥PA 平面ABC ，求外接球半径．解题步骤：第一步：将∆ABC A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为∆ABC 的外心，所以1⊥OO 平面ABC ，算出小圆1O 的半径1=O D r (三角形的外接圆直径算法：利用正弦定理，得2sin sin sin ===a b c r A B C )，112=OO PA ；第三步：利用勾股定理求三棱锥的外接球半径：①222(2)(2)=+R PA r⇔2=R ②2221=+R r OO⇔=R ．【典型例题】例13．（2022·内蒙古鄂尔多斯·高三期中（文））三棱锥-P ABC 中，PA ⊥平面ABC ，ABC 为直角三角形，AB BC ⊥，1AB BC ==，2PA =，则三棱锥-P ABC 的外接球的表面积为（ ）A ．2πB ．3πC ．4πD ．6π【答案】D【解析】由于三棱锥-P ABC 中，PA ⊥平面ABC ，AB BC ⊥，1AB BC ==，2PA =故将该三棱锥置于一个长方体中，如下图所示：则体对角线PC 即为外接球的直径，所以2=故三棱锥-P ABC 的外接球表面积为246S R ππ==．故选：D例14．（2022·福建·宁德市民族中学高三期中）已知三棱锥P -ABC 中，PA ⊥底面ABC ，PA ＝AB ＝AC ＝2，∠BAC ＝120°，则三棱锥P -ABC 的外接球的表面积为（ ）A ．12πB ．16πC ．20πD ．24π【答案】C【解析】将三棱锥还原成直三棱柱，则三棱柱的外接球即为球O ，,D D '为上下底面的外心，O 为DD '的中点，AD 为底面外接圆的半径，由余弦定理得BC ==由正弦定理得24AD ==，由1,2OD AD ==，得AO =所以球O 的表面积为2420S r ππ==．故选：C例15．（2021·四川成都·高三开学考试（文））已知在三棱锥-P ABC 中，侧棱PA ⊥平面ABC ，3PA =，1AB =，BC =，2AC =，则三棱锥-P ABC 外接球的表面积为（ ）A ．13πB ．12πC ．9πD ．8π【答案】A【解析】因为PA ⊥平面ABC ，,AC BC ⊂平面ABC ，故,PA AC PA BC ⊥⊥，而1AB =，BC =，2AC =，则222AB BC AC +=，所以AB BC ⊥,又PA AB A = ，,PA AB ⊂平面PAB ,故BC ⊥平面PAB ,PB ⊂平面PAB ,所以BC PB ⊥,所以,PAC PBC △△都是以PC 为斜边的直角三角形，故取PC 中点O ，连接OA,OB ,则OA OB OP OC ===,即O 为三棱锥-P ABC外接球的球心，3,2,PA AC PC ==∴= ,故三棱锥-P ABC故三棱锥-P ABC外接球的表面积为24π13π⨯=，故选：A核心考点六：正棱锥与侧棱相等模型【规律方法】1、正棱锥外接球半径：=R ．2、侧棱相等模型：如图，P 的射影是∆ABC 的外心⇔三棱锥-P ABC 的三条侧棱相等⇔三棱锥-P ABC 的底面∆ABC 在圆锥的底上，顶点P点也是圆锥的顶点．解题步骤：第一步：确定球心O 的位置，取∆ABC 的外心1O ，则1,,P O O 三点共线；第二步：先算出小圆1O 的半径1=AO r ，再算出棱锥的高1=PO h （也是圆锥的高）；第三步：勾股定理：22211=+OA O A O O ⇒222()=-+R h R r ，解出222+=r h R h．【典型例题】例16．（2022·江西·金溪一中高三阶段练习（文））在正三棱锥S －ABC 中，23ASB BSC π∠+∠=，△ABC 的边长为2，则该正三棱锥外接球的表面积为______．【答案】6π【解析】2π3ASB BSC ∠+∠=，正三棱锥中ASB BSC ∠=∠，所以π3ASB BSC ∠=∠=，侧面是正三角形，则正三棱锥S ABC -为正四面体．将正四面体补成正方体（正四面体的四个顶点S ，A ，B ，C 均为正方体的顶点），，则其外接球的半径R =，所以该正三棱锥外接球的表面积为24π6πS R ==．故答案为：6π．例17．（2022·全国·高三专题练习）已知正三棱锥S ABC -，其外接球球O 的半径为R ，则该正三棱锥S ABC -的体积的最大值为__________．3【解析】如图，设正三棱锥S ABC -的高=SH h ，则由射影定理可得2=⋅HA SH HM ，2(2)∴=-HA h R h ，图5-12(2)∴==-△ABC S AB R h，21(2)3-∴=⋅=-△S ABC ABC V S h Rh (2)22=⋅⋅-≤h h Rh 33(2)223⎡⎤++-⎢⎥=⎢⎥⎢⎥⎣⎦h h R h ，当(2)2=-h R h ，即43h R =时，()3max-=S ABC V .例18．（2022·全国·高三专题练习）已知正三棱锥S ABC -的棱长为6．则该正三棱锥外接球的表面积为_______．【答案】2432π【解析】如图，∵正三棱锥S ABC -中，顶点S 在底面的射影为D ，该正三棱锥外接球的球心设为O ，因为底面边长为6，所以23AD ==∴高SD ===．由球心O 到四个顶点的距离相等，在直角三角形AOD 中，AO R =，DO SD OS R =-=，由222AO AD OD =+，得2212)R R =+，R =，∴外接球的表面积为：224342R ππ⋅⋅=．故答案为：2432π．例19．（2022·全国·高三专题练习）三棱锥-P ABC 且,1,PA PB PC AB AC BC =====则三棱锥外接球的表面积为____________．【答案】254π【解析】三棱锥-P ABC 中，取BC 中点D ，连PD ，连AD 并延长至O 1，使DO 1=AD ，连接BO 1，CO 1，PO 1，如图：于是得四边形1ABO C 为平行四边形，而1AB AC ==，1ABO C 是菱形，在ABC 中，BC =2221cos 22AB AC BC BAC AB AC +-∠==-⋅，即120BAC ∠= ，则160ABO ∠= ，1ABO △是正三角形，1111O A O B O C ===，于是得O 1是ABC 外接圆圆心，因PA PB PC ==，D 为BC 中点，则PD ⊥BC ，又AO 1⊥BC ，1PD AO D ⋂=，1,PD AO ⊂平面1PAO ，从而有BC ⊥平面1PAO ，1PO BC ⊥，同理1PO AC ⊥，而AC BC C = ，从而得1PO ⊥平面ABC ，由球的截面小圆性质知，三棱锥-P ABC 外接球球心O 在直线1PO 上，又1sin1202ABC S AB AC =⋅= 113P ABC ABC V PO S -=⋅= 12PO =，设球O 的半径为R ，则OB OP R ==，1|2|OO R =-，1Rt OO B △中，22211O B O O OB +=，即221(2)R R +-=，解得54R =，则球O 的表面积为22544S R ππ==，所以三棱锥外接球的表面积为254π.故答案为：254π例20．（2022·全国·高三专题练习）在三棱锥-P ABC 中，1====PA PC AB AC ，=PB BC ，则三棱锥-P ABC 的外接球的表面积为___________.【答案】73π【解析】在ABC 中，1AB AC ==，BC =所以222AB AC BC +=，所以AB AC ⊥，在PAB 中，1AB PA ==，PB =所以222AB PA PB +=，所以AB PA ⊥.又PA AC A = ，PA ，AC ⊂平面PAC ，所以AB ⊥平面PAC ，在PAC △中，1PA PC AC ===，所以PAC △的外接圆半径为112sin 3π⋅=不妨设PAC △的外接圆圆心为Q ，三棱锥-P ABC 的外接球球心为O连接,,OA OB OQ ，由于OA OB =，故O 在线段AB 的垂直平分线上，即1122OQ AB ==故三棱锥-P ABC 的外接球半径R OA ===外接球的表面积为2743R ππ=.故答案为：73π核心考点七：侧棱为外接球直径模型【规律方法】找球心，然后作底面的垂线，构造直角三角形．【典型例题】例21．（2022·河南河南·一模（文））三棱锥D ABC -的外接球的表面积为8,BD π是该球的直径，,22AC BC AB BC ⊥==，则三棱锥 D ABC -的体积为_____.【解析】如图，设球的半径为r ，由已知得248r ππ=，解得r =BD =，又由AC BC ⊥，所以，取AB 中点H ，H 为ABC 所在外接圆的圆心，故OH ⊥平面ABC ，又因为12OH AD ，所以，AD ⊥平面ABC ，得到AD AB ⊥，在ABD △中，2AD ==由22AB BC ==，AC BC ⊥，得到AC ==所以，12ABC S AC BC =⋅=△，所以，13D ABC ABC V AD S -=⋅=△例22．（2022·河南·一模（理））三棱锥D ABC -的外接球的表面积为20π，AD 是该球的直径，ABC 是边长为D ABC -的体积为______．【答案】【解析】设三棱锥D ABC -的外接球的球心为O ,半径为R ，则24π20πR =，解得R =设ABC 的外接圆圆心为1O ，半径为r ，则122sin BC r BAC ==∠，连接11,O A O O ，∵22211O A O O OA +=，即1=，则点D 到平面ABC 的距离为2，∴三棱锥D ABC -的体积11232V =⨯⨯=故答案为：例23．（2021·全国·高三专题练习（文））已知三棱锥P ﹣ABC 中，AB BC ==AC =2，PA 为其外接球___________．【答案】16π【解析】由题意可得ABC 为等腰直角三角形，AB BC ⊥，同时PA 为其外接球的一条直径，则,PBA PCA ∠∠都是直角，设球心为O ，取AC 的中点为M ，则OM ⊥平面ABC ，因为//OM PC ，则PC ⊥平面ABC ，则1132V =⨯⨯2PC =PC =，由勾股定理得4PA =，则外接球的半径为2，表面积为16.π故答案为：16π核心考点八：共斜边拼接模型【规律方法】如图，在四面体ABCD 中，⊥AB AD ，⊥CB CD ，此四面体可以看成是由两个共斜边的直角三角形拼接而形成的，BD 为公共的斜边，故以“共斜边拼接模型”命名之．设点O 为公共斜边BD 的中点，根据直角三角形斜边中线等于斜边的一半的结论可知，===OA OC OB OD ，即点O 到A ，B ，C ，D 四点的距离相等，故点O 就是四面体ABCD 外接球的球心，公共的斜边BD 就是外接球的一条直径．【典型例题】例24．在矩形ABCD 中，==4,3AB BC ，沿AC 将矩形ABCD 折成一个直二面角--B AC D ，则四面体ABCD 的外接球的体积为（）A ．π12512B ．π1259C ．π1256D ．π1253【答案】C【解析】设矩形对角线的交点为O ，则由矩形对角线互相平分，可知===OA OB OC OD ．∴点O 到四面体的四个顶点、、、A B C D 的距离相等，即点O 为四面体的外接球的球心，如图2所示．∴外接球的半径==52R OA ．故ππ==球3412536V R ．选C ．例25．三棱锥-P ABC 中，平面⊥PAC 平面ABC ， =2AC ，⊥PA PC ，⊥AB BC ，则三棱锥-P ABC 的外接球的半径为图 2A【答案】1【解析】AC 是公共的斜边，AC 的中点是球心O ，球半径为=1R ．例26．在平行四边形ABCD 中，满足2AB AD AB = ，2224AB BD =- ，若将其沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为( )A ．16πB ．8πC ．4πD ．2π【答案】C【解析】平行四边形ABCD 中，2AB AD AB = ，∴0AB BD = ，AB BD ∴⊥，沿BD 折成直二面角A BD C --，平面ABD ⊥平面BDC三棱锥A BCD -的外接球的直径为AC ，22222224AC AB BD CD AB BD ∴=++=+=∴外接球的半径为1，故表面积是4π．故选：C ．核心考点九：垂面模型【规律方法】如图1所示为四面体-P ABC ，已知平面⊥PAB 平面ABC ，其外接球问题的步骤如下：（1）找出△PAB 和△ABC 的外接圆圆心，分别记为1O 和2O ．（2）分别过1O 和2O 作平面PAB 和平面ABC 的垂线，其交点为球心，记为O ．（3）过1O 作AB 的垂线，垂足记为D ，连接2O D ，则2⊥O D AB ．（4）在四棱锥12-A DO OO 中，AD 垂直于平面12DO OO ，如图2所示，底面四边形12DO OO 的四个顶点共圆且OD 为该圆的直径．图1图2【典型例题】例27．（2022·全国·高三专题练习）三棱锥-P ABC 中，平面PAC ⊥平面ABC ， 2AC =，PA PC ⊥，AB BC ⊥，则三棱锥-P ABC 的外接球的半径为______【答案】1【解析】因为PA PC ⊥，AB BC ⊥，故AC 是公共的斜边，AC 的中点是球心O ，球半径为12AC R ==．故答案为：1例28．（2022·安徽马鞍山·一模（文））三棱锥-P ABC 中，PAC △与ABC 均为边长为平面PAC ⊥平面ABC ，则该三棱锥的外接球的表面积为________．【答案】20π【解析】等边三角形PAC 、等边三角形ABC 的高为πsin 33⨯==，等边三角形PAC 、等边三角形ABC 的外接圆半径为2323⨯=，设12,O O 分别是等边三角形PAC 、等边三角形ABC 的中心，设O 是三棱锥-P ABC 的外接球的球心，R 是外接球的半径，则2222215R OA ==+=，所以外接球的表面积为24π20πR =.故答案为：20π例29．（2022·全国·高三专题练习）三棱锥-P ABC 中，PAC △是边长为2AB BC ==，平面PAC ⊥平面ABC ，则该三棱锥的外接球的体积为______【解析】等边三角形PAC 的高为πsin 33⨯==，等边三角形PAC 的外接圆半径为222sin 6π=三角形ABC 2=，设12,O O 分别是等边三角形PAC 、等边三角形ABC 的中心，设O 是三棱锥-P ABC 的外接球的球心，R 是外接球的半径，则2222215R OA R ==+=⇒=，所以外接球的体积为34π3R =例30．（2021·全国·高三专题练习）已知在三棱锥-P ABC 中， 90,4,30BAC AB AC APC ︒︒∠===∠=，平面PAC ⊥平面ABC ，则三棱锥-P ABC 外接球的表面积为__________．【答案】80π【解析】如图12,O O 分别为,ABC PAC 的外心.由90BAC ∠=︒，即1O 为BC 中点，取AC 的中点,H 则1O H AC ⊥，又面PAC ⊥面ABC ，面PAC 面ABC AC =，1O H ⊂面ABC ，即1O H ⊥面,PAC 设球心为O ，则2OO ⊥平面,PAC ∴12//O H OO ，又2O H AC ⊥，2O H ⊂面PAC ，面PAC 面ABC AC =，面PAC ⊥面ABC ，∴2O H ⊥平面ABC ，又1OO ⊥平面ABC .∴12//OO O H ，即四边形12OO HO 为矩形. 由正弦定理知：228sin AC O P APC==∠，即24O P =，∴若外接球半径为R ，则2222216420R O P OO =+=+=，∴2480S R ππ==.故答案为：80π.核心考点十：二面角模型【规律方法】如图1所示为四面体-P ABC ，已知二面角--P AB C 大小为α，其外接球问题的步骤如下：（1）找出△PAB 和△ABC 的外接圆圆心，分别记为1O 和2O ．（2）分别过1O 和2O 作平面PAB 和平面ABC 的垂线，其交点为球心，记为O ．（3）过1O 作AB 的垂线，垂足记为D ，连接2O D ，则2⊥O D AB ．（4）在四棱锥12-A DO OO 中，AD 垂直于平面12DO OO ，如图2所示，底面四边形12DO OO 的四个顶点共圆且OD 为该圆的直径．【典型例题】例31．（2022·贵州·模拟预测（理））如图，在三棱锥A BCD -中，ABC 是边长为AD CD ==D AC B --的余弦值为23，则三棱锥A BCD -外接球的表面积为______.【答案】84π5【解析】如图1，取AC 中点E ，连接BE ，DE ，ABC 与ACD 为等边三角形，则,BE AC DE AC ⊥⊥,,,BE DE E BE DE =⊂ 平面BDE ,故AC ⊥平面BDE ,故二面角D AC B --的平面角为DEB ∠，又AC ⊂平面ABC ,所以平面BDE ⊥平面ABC ，平面BDE ⋂平面ABC BE =，过D 作DH BE ⊥于H ，DH ⊂平面BDE ,所以DH ⊥平面ABC ，由题意得2cos 3DEB ∠=，3DE BE ===，∴2323EH =⨯=，则DH ==，设ABC 外接圆圆心为2O ，则2O 在BE 上，半径为2BO ，过2O 作平面ABC 的垂线l ，则三棱锥A BCD -外接球的球心一定在直线l 上.∵21122sin 2AC BO B =⨯==，∴221,1EO O H =∴=，过D 作BE 的平行线交l 于点F ，则21FD O H ==，∵D ，B 在球面上，外接球球心可能在三棱锥内也可能在三棱锥外，取截面如图2,3，设外接球球心O ，半径R ，令2OO x =，则2FO FO x =±，2FO DH ==∴22222222FO FD R OO BO R⎧+=⎪⎨+=⎪⎩,当2FO FO x =+时，化简得64,x +==当2FO FO x =-时，化简得64,x -==得2215R =，∴284π4π5S R ==,故答案为：84π5.例32．（2022·江西赣州·高三阶段练习（文））已知菱形ABCD 的边长为2，且60DAB ∠=︒，沿BD 把ABD △折起，得到三棱锥A BCD '-，且二面角A BD C '--的平面角为120︒，则三棱锥A BCD '-的外接球的表面积为___________.【答案】283π【解析】取BD 的中点H ，连接A H '，CH ，因为ABCD 为菱形，所以A H BD '⊥，CH BD ⊥，故A HC '∠为二面角A BD C '--的平面角，则120A HC '∠=︒，由题意可知A BD '△，BCD △为正三角形，则外接球球心位于过A BD '△，BCD △的中心且和它们所在面垂直的直线上，故分别取A BD '△，BCD △的重心为1G ，2G ，过点1G ，2G 分别作两个平面的垂线，交于点O ，点O 即为三棱锥的外接球的球心，由题意可知A BD BCD '≅△△，球心到面A BD '和面BCD 的距离相等，即12OG OG =，连接OD ，OH ，则1260OHG OHG ∠=∠=︒，菱形ABCD 的边长为2，∴1123HG ==，1cos 60HG OH ===︒，∴2222713OD OH HD =+=+=，即三棱锥A BCD '-的外接球的半径273=，所以其外接球的表面积为27284433R πππ=⨯=.故答案为：283π例33．（2022·江苏·南京市金陵中学河西分校高三阶段练习）在三棱锥A BCD -中，△BCD 是边长为3的正三角形，且AD =，AB =A BD C --的大小为3π，则此三棱锥外接球的体积为________．【解析】根据题意，222AD BD AB +=，所以AD BD ⊥，取BD 中点为E ，AB 中点M ，则//ME AD ，12ME AD ==ME DB ⊥，BCD 是正三角形，CE DB ⊥，MEC ∠是二面角A ﹣BD ﹣C 的平面角，60MEC ∠=︒，90ADB ∠=︒，M 是ADB 的外心，设N 是DBC 的外心，设过M 与平面ABD 垂直的直线与过N 垂直于平面BCD 的直线交于点O ，则O 是三棱锥A DBC -外接球球心，3CN BN ===，EN =，又EM ，由于平面MNO 与MEO 同时垂直于BD ，所以M E N O 、、、共面，在四边形MENO 中，由60MEC ∠=︒，EN =ME 090OME ONE ∠=∠= ，可得：12ON =，外接球半径为r OB ====体积为343V π=⨯=．例34．（2022·广东汕头·高三阶段练习）在边长为2的菱形ABCD 中，BD =将菱形ABCD 沿对角线AC 对折，使二面角B AC D --的余弦值为13，则所得三棱锥A BCD -的外接球的表面积为___________.【答案】6π【解析】依题意在边长为2的菱形ABCD 中，BD =60ABC ADC ︒∠=∠=，如下图所示，易知ABC 和ACD 都是等边三角形，取AC 的中点N ，则DN AC ⊥，BN AC ⊥．DN BN N = ，,DN BN ⊂平面BND ，所以AC ⊥平面BND ，所以BND ∠是二面角B AC D --的平面角，过点B 作BO DN ⊥交DN 于点O ，由AC ⊥平面BND ，BO ⊂平面BND ，所以AC BO ⊥，DN AC N = ，,DN AC ⊂平面ACD ，所以BO ⊥平面ACD ．因为在 BDN 中，BN DN ==所以22212cos 332343BD BN DN BN DN BND =+-⋅⋅∠=+-⨯⨯=，则2BD =．故三棱锥A BCD -为正四面体，由BO ⊥平面ACD ，所以O 为底面ACD 的重心，所以23OD DN ==13ON DN ==则BO ==设外接球的半径为R ，则()222R OD BO R =+-，解得R =．因此，三棱锥A BCD -的外接球的表面积为22446R πππ=⨯=．故答案为：6π．核心考点十一：坐标法【规律方法】对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为(,,)O x y z ，利用球心到各顶点的距离相等建立方程组，解出球心坐标，从而得到球的半径长．坐标的引入，使外接球问题的求解从繁琐的定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度．【典型例题】例35．（2022·黑龙江·大庆实验中学模拟预测）直角ABC 中2,1AB BC ==，D 是斜边AC 上的一动点，沿BD 将ABD △翻折到A BD 'V ，使二面角A BD C '--为直二面角，当线段A C '的长度最小时，四面体A BCD'的外接球的表面积为（ ）A ．134πB ．215πC ．133πD ．143π【答案】D【解析】解：根据题意，图1的直角三角形沿BD 将ABD △翻折到A BD 'V 使二面角A BD C '--为直二面角，所以，过点'A 作A H BD '⊥交BD 延长线于H ，过点C 作CM BD ⊥交BD 于M ，再作//,//NH CM CN MH ，使得CN 与HN 交于点N ，所以，由二面角A BD C '--为直二面角可得'CM A H ⊥，设ABD θ∠=，即B A D θ'∠=，则2CBD πθ∠=-，因为2,1AB BC ==，所以'2,1A B BC ==，所以，在'Rt A BH 中，'2sin 2cos A H BH θ,θ==，在Rt BCM △中，cos sin sin cos 22BM CM ππθθ,θθ⎛⎫⎛⎫=-==-= ⎪ ⎪⎝⎭⎝⎭，所以2cos sin MH BH BM θθ=-=-，所以A C '==≥当且仅当22=πθ，即4πθ=时等号成立，此时，'A H BH ==BM CM ==MH =，在图1中，由于4πθ=，即BD 为角B 的角平分线，所以2AD AB DC BC ==，即AD =，所以'A D =，所以，DH =，由题知，',,HA HB HN 两两垂直，故以H 为坐标原点，以',,HB HN HA的方向为正方向建立空间直角坐标系，则()',,,A BC D ⎫⎫⎪⎪⎪⎪⎭⎭，所以，设四面体A BCD '的外接球的球心为(),,O x y z ，则',,AOOB OB OC OC OD ===，。
（完整版）高考数学中的内切球和外接球问题.
（完整版）高考数学中的内切球和外接球问题.高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上，那么称这个多面体是球的内接多面体，这个球称为多面体的外接球.有关多面体外接球的问题，是立体几何的一个重点，也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，并且还要特别注意多面体的有关几何元素与球的半径之间的关系，而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为______________ .例2一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体积为______________.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3，则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为（）.A. 16πB. 20πC. 24πD. 32π3.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为8 9，底面周长为3，则这个球的体积为 .解设正六棱柱的底面边长为x ，高为h ，则有==h x x 24368936==213x h ∴正六棱柱的底面圆的半径21=r ，球心到底面的距离23=d .∴外接球的半径22d r R +=. 体积：334R V π=. 小结本题是运用公式222d r R +=求球的半径的，该公式是求球的半径的常用公式.二、构造法(补形法) 1、构造正方体例5 若三棱锥的三条侧棱两两垂直，且侧棱长均为3，则其外接球的表面积是_______________.例3 若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 .故其外接球的表面积ππ942==r S .小结：一般地，若一个三棱锥的三条侧棱两两垂直，且其长度分别为c b a ,,，则就可以将这个三棱锥补成一个长方体，于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ，则有2222c b a R ++=. 出现“墙角”结构利用补形知识，联系长方体。
高中数学解题秘籍系列一篇文章攻克外接球
【高中数学解题秘籍系列】————一篇文章攻克外接球⚫外接球指一个空间几何图形的外接球，对于旋转体和多面体，外接球有不同的定义，广义理解为球将几何体包围，且几何体的顶点和弧面在此球上.正多面体各顶点同在一球面上，这个球叫做正多面体的外接球.⚫内切球球心到某几何体各面的距离相等且等于半径的球是几何体的内切球.如果一个球与简单多面体的各面或其延展部分都相切，且此球在多面体的内部，则称这个球为此多面体的内切球.一、外接球七大模型二、内切球万能公式(棱锥)①圆柱②直棱柱③侧棱垂直底面➢适用几何体：圆柱、直棱柱、一条侧棱垂直底面的棱锥.②和 ③ 可以通过补形转化为 ①，所以我们只需证明 ① 即可证明：设P 、O '分别为上下底面圆的圆心，O 为线段PO '的中点，( 2017•新课标 Ⅲ ) 已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( ) A ．πB ．3π4 C ．π2D ．π4由秒杀公式1得22222212=1442h R r r ⎛⎫+=+== ⎪⎝⎭，解得234r =， 因此圆柱的体积233πππ144V r h =⋅=⋅⋅=，故选B.( 2017•新课标 Ⅱ ) 长方体的长、宽、高分别为3，2，1，其顶点都在球O 的球面上，则 球O 的表面积为 ．由秒杀公式1得2222217=442h R r +=+=⎝⎭， 因此球O 的表面积为274π4π14π2S R ==⋅⋅=. 本题还可用秒杀公式4可得22222223217442a b c R ++++===，因此球O 的表面积为274π4π14π2S R ==⋅⋅=. 由此可知在选用公式的时候是比较灵活的，原因在于模型之间可以相互转化.典例例题1-1例题1-2( 2012•辽宁 ) 已知点P ，A ，B ，C ，D 是球O 表面上的点，PA ⊥平面ABCD ，四边形ABCD 是边长为PA =，则OAB △的面积为 ．由秒杀公式1得(22222=12424h R r +=⋅+=⎝，解得R =OAB △为等边三角形，所以(2OAB S ==△( 2011•四川 ) 如图，半径为R 的球O 中有一内接圆柱．当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是 ．由秒杀公式1得222=4h R r +，于是2224=2π=4π4π2π22h r h S r h r R+⋅⋅⋅=侧， 当且仅当2h r ==时不等式取“=”，于是 222=4π2π=2πSS R R R −−侧球.( 2010•辽宁 ) 已知S ，A ，B ，C 是球O 表面上的点，SA ⊥平面ABC ，AB BC ⊥，1SA AB ==，BC ，则球O 的表面积等于( )A ．4πB ．3πC ．2πD ．π由秒杀公式1得222221=144h R r +=+=⎝⎭， 解得1R =，则球O 的表面积为24π4πS R ==.故选A .( 2008•浙江 ) 如图，已知球O 的面上四点A ，B ，C ，D ，DA ⊥平面ABC ，AB BC ⊥，DA AB BC ==O 的体积等于 ．由秒杀公式1得222229=444h R r +=+=⎝⎭， 解得32R =，则球O 的体积为 334439πππ3322V R ⎛⎫==⋅⋅= ⎪⎝⎭.①圆锥 ②正棱锥➢适用几何体：圆锥、顶点在底面的射影是底面外心的棱锥(正棱锥).② 可以通过补形转化为 ①，所以我们只需证明 ① 即可心O 为PO '上一点，于是在Rt OO A '△中有解得( 2018•新课标 Ⅲ ) 设A ，B ，C ，D 是同一个半径为4的球的球面上四点，ABC △为等边三角形且面积为D ABC −体积的最大值为( ) A．B．C．D．依题意得，当三棱锥D ABC −为正三棱锥且hR 时，三棱锥D ABC −的体积最大，那么由秒杀公式2得22=42r h R h+=，①又因为ABC △为正三角形且面积为))1πsin23S =⋅⋅⋅=，解得r =①式解得2h =或6h =，又因为4hR =，所以6h =，于是()max 1=3D ABC V −⋅ 故选B .例题2-1典例( 2014•大纲版 ) 正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( ) A ．81π4B ．16πC ．9πD ．27π4由秒杀公式2得2222+49==2244r h R h+=⋅， 因此22981π=4π=4π=44S R ⎛⎫⋅ ⎪⎝⎭， 故选A .( 2020•银川模拟 ) 已知圆锥的母线与底面所成的角等于60︒，且该圆锥内接于球O ，则球O 与圆锥的表面积之比等于( ) A ．4:3B ．3:4C ．16:9D ．9:16由秒杀公式2得22=2r h R h+，依题意得h =，因此R =， 于是2222224164ππ4π1633=ππππ23π9r r S R S r rl r r r r ⋅===++⋅球锥. 故选C .例题2-2例题2-3( 2018秋•太原期末 ) 在三棱锥P ABC −中，顶点P 在底面ABC 的投影G 是ABC △的外心，2PB BC ==，平面PBC 与底面ABC 所成的二面角的大小为60︒，则三棱锥P ABC −的外接球的表面积为 .如图所示，作BC 的中点M ，在Rt PMB △[1]中有PM ==依题意知60PMG ∠=︒[2]，在Rt PGM △中有3sin 60cos602h PG PM GM PM ==︒==︒=， 于是在Rt BGM △中有r BG =， 由秒杀公式2可得224=23r h R h +=，因此264π4π9S R ==.[1] 因为顶点P 在底面ABC 的投影G 是ABC △的外心，所以PA PB PC ==. [2] 因为BC PM ⊥且BC GM ⊥，所以PMG ∠为二面角P BC A −−的平面角.( 2020•娄底模拟 ) 如图所示是某几何体的三视图，则该几何体的外接球的表面积为( )A ．25π8B ．25π4C ．25π2 D ．9π8由秒杀公式2得2222+=2r hR h+= 因此2225π=4π=4π=2S R ⋅⎝⎭， 故选C .( 2019秋•东莞市期末 ) 已知球O 是正四面体A BCD −的外接球，2BC =，点E 在线段BD 上，且3BD BE =，过点E 作球O 的截面，则所得截面圆面积的最小值是( )A ．8π9B ．11π18C ．5π12 D ．4π9依题意易知3r =，3h =，由秒杀公式2得2222+=2r h R h +=， 如图所示，在OBD △中，由余弦定理可得222cos 23OB BD ODOBD OB BD+−∠==⋅⋅， 那么在OBE △中，由余弦定理可得222112cos 18OE OB BE OB BE OBD =+−∠=， 当截面圆垂直OE 时面积最小，故截面圆的最小半径为3r '==， 因此截面圆面积的最小值为()288πππ99S r '==⋅=.故选A .( 学生答疑 ) 在《九章算术》卷商功中称正四棱锥为“方锥”. 现有一“方锥”的体积为若该“方锥”的五个顶点都在球O 的球面上，则球O 表面积的最小值为 A ．18πB ．27πC ．36πD ．75π由秒杀公式2得22=2r h R h+， 依题意得211=233V S h r h ⋅⋅=⋅⋅=底，即2r =2223263=32244h rh h h h R h h h ++==+⋅=4h”，即“h =”时不等式取“=”，因此 2min min 27=4π4π27π4S R =⋅=，故选B.➢适用几何体：三组线线垂直型三棱锥.证明：在三棱锥P ABC=，−中，AB AC APAB a，AC b、、两两垂直，= =，将三棱锥补成长方体，则长方体的体对角线PQ即为外接球的AP c直径，于是所以()22222R a b c=++，即( 2019•新课标 Ⅰ ) 已知三棱锥P ABC −的四个顶点在球O 的球面上，PA PB PC ==，ABC △是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为( ) A．B．C．D依题意得三棱锥P ABC −为正三棱锥，CE EF ⊥，因为//EF PB ，所以PB CE ⊥，由正三棱锥性质可得PB CA ⊥[1]，又因为CE ⊂面PAC ，CA ⊂面PAC ，=CE CA C ，因此PB ⊥面PAC ，因此PA PB PC ，，两两垂直[2]，由秒杀公式3得2222222++3===442a b cR ++， 于是3344=π=π332V R ⎛⎫⋅⋅⋅⋅ ⎪ ⎪⎝⎭， 故选D .[1] 设G 为AC 的中点，P 点在底面ABC 的投影为1O ，因为三棱锥P ABC −为正三棱锥， 所以1O 为ABC △的外心，故1B O G ，，三点共线，因为1AC PO AC BG ⊥⊥，，且 11PO BG O =，所以AC ⊥平面PGB ，又因为PB ⊂平面PGB ，故PB CA ⊥.[2] PAB PAC PBC ≅≅△△△.例题3-1典例( 2012•辽宁 ) 已知正三棱锥P ABC −，点P ，A ，B ，CPA ，PB ，PC 两两垂直，则球心到截面ABC 的距离为 ．由秒杀公式3可得2222222344PA PB PC a b c R ++++===，由正三棱锥性质可得PA PB PC ==，解得2PA PB PC ===，则球心到截面ABC 的距离为OH ===.( 2008•福建 ) 是 ．由秒杀公式3可得2222944a b c R ++===，故294π4π9π4S R ==⋅=. 例题3-3( 2020•山东学业考试 ) 在三棱锥P ABC −中，PA ，PB ，PC 两两垂直，且1PA =，2PB PC ==，则该三棱锥的外接球体的体积为( )A ．9π2B ．27π2C ．9πD ．36π由秒杀公式3可得22222221229444a b c R ++++===，于是334439πππ3322V R ⎛⎫==⋅=⎪⎝⎭. 故选A .( 2019春•湖南期末 ) 已知点P 在直径为2的球面上，过点P 作球的两两相互垂直的三条弦PA ，PB ，PC ，若PA PB =，则PA PB PC ++的最大值为( )A．B ．4C．2+D ．3由秒杀公式3可得22222222221444PA PB PC PB PC a b c R +++++====，即2224PB PC +=，因此()222PAPB PC PB PC⎡++=+=⎢⎣1PC =时，即3PB PC ==时不等式取“=”，故选A .例题3-5➢适用几何体：对棱长相等的三棱锥.证明：在三棱锥P ABC −中，PA BC x ==，PB AC y ==，PC AB z ==，将三棱锥P ABC −补成如图所示长方体，设DA a =，DB b =，DC c =，于是长方体的体对角线PD 即为三棱锥P ABC −外接球，因为222222222a b z a c y b c x ⎧+=⎪+=⎨⎪+=⎩，，， 所以()2222222x y z a b c ++=++，又因为那么即( 2020•红河州模拟 ) 在三棱锥A BCD −中，5AB CD AC BD ====，AD BC ==( )AB．C ．132D ．13由秒杀公式4得()((22222225+169==884x y z R +++=， 解得13=2R ，故选C .( 2016•蚌埠三模 ) 在四面体ABCD 中，2AB CD ==，AC BD AD BC ==== 面体的外接球的表面积为 ．由秒杀公式4得()22222222+==188x y zR +++=，因此四面体外接球的表面积为24π4πS R ==.典例例题4-1例题4-2( 2019秋•路南区校级期中 ) 四面体ABCD 的四个顶点在同一球面上中，4AB BC CD DA ====，AC BD ==E 为AC 的中点，过E 作其外接球的截面，则截面面积的最大值与最小值的比为( ) A ．5:4B2CD ．5:2由秒杀公式4得()()(22222224+4==588x y z R +++=，在等腰OAE △中，OE ==当截面圆所在平面垂直OE 时面积最小，截面圆所在平面过球心O 时面积最大，因此22min maxπ2ππ5πS SR =⋅==⋅=，，于是max min 52S S =， 故选D .例题4-3➢适用几何体：两全等等腰三角形折叠式棱锥.证明：在三棱锥P ABC −中，PAB CAB ≅△△，CA CB =，1O ，2O 分别是ABC △和PBC △的外心，M 为线段AB 的中点，1OO ⊥平面ABC ，2OO ⊥中有那么，在Rt MBO △中有( 2019•齐齐哈尔一模 ) 在边长为2的菱形ABCD中，BD =，将菱形ABCD 沿对角线AC 对折，使二面角B AC D −−的余弦值为13，则所得三棱锥A BCD −的外接球的表面积为.由秒杀公式5得因此三棱锥A BCD −的外接球表面积为234π4π6π2S R ==⋅=.典例例题5-1(2017•广西一模)在菱形ABCD中，60A=︒，AB=ABD∆的∆沿BD折起到PBD位置，若二面角P BD C−的外接球球心为O，BD的中−−的大小为120︒，三棱锥P BCD点为E，则(OE=)A．1B．2C D．由秒杀公式5得那么OE===，2故选B.( 原创 ) 已知空间四边形ABCD 中，2AB BD AD BC AC =====，若二面角C AB D −−的取值范围为π2π33⎡⎤⎢⎥⎣⎦，，则该几何体的外接球表面积的取值范围为 ．由秒杀公式5得又因为π2π33α⎡⎤∈⎢⎥⎣⎦，，所以ππ263α⎡⎤∈⎢⎥⎣⎦，，那么tan 2α∈⎣，因此213793R ⎡⎤∈⎢⎥⎣⎦，，又因为2=4πS R ，故外接球表面积的取值范围为52π28π93⎡⎤⎢⎥⎣⎦，.➢适用几何体：面面垂直型棱锥.证明：在三棱锥P ABC −中，平面ABP ⊥平面ABC ，1O ，2O 分别是ABP △和ABC △的外心，且1OO ⊥平面ABP ，2OO ⊥平面ABC ，1r ，2r 分别是ABP △和ABC △外接圆的半径，l 为线段AB 的长度，在2O BM △中有即同理所以( 原创 ) 在三棱锥S ABC −中，ABC △是边长为3的等边三角形，SA =，SB =面角S AB C −−的大小为90︒，则此三棱锥的外接球的半径为 ．由秒杀公式5得典例例题6-1( 2019•中卫一模 ) 一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几 何体的外接球的表面积为( ) A ．16π3B ．8π3C． D．由秒杀公式5得因此外接球的表面积为正视图侧视图俯视图( 2019•开福区校级模拟 ) 已知等腰ABC △的面积为4，AD 是底边BC 上的高，沿AD 将ABC △折成一个直二面角，则三棱锥A BCD −的外接球的表面积的最小值为 ．设AD x BD y ==，，因为等腰ABC △的面积为4，则=4xy ，又因为12r r ==， 那么由秒杀公式5得2211242x ⋅2212x y =时，即x y ==时，不等式取“=”，故三棱锥A BCD −的外接球的表面积的最小值为2min min =4πS R .如图，三棱锥P ABC −的底面是边长为2的等边三角形，若PA PB =二面角P BA C −− 的大小为90︒，则三棱锥P ABC −的外接球的表面积等于 ．由秒杀公式5得因此外接球的表面积为➢适用几何体：普通三棱锥.证明：在三棱锥P ABC −中，1O ，2O 分别是ABP △和ABC △的外心，二面角12P AB C O MO α−−=∠=，M 为AB 的中点，1O M m =，2O M n =，且1OO ⊥平面ABP ，2OO ⊥平面ABC ， l 为线段AB 的长度，在四边形12OO MO 中，因为所以12OO MO 四点共圆，设四边形12OO MO 的外接圆的半径为r ，则因此( 2019秋•迎泽区校级月考 ) 在三棱锥S ABC −中，ABC △是边长为3的等边三角形，SA，SB =二面角S AB C −−的大小为120︒，则此三棱锥的外接球的半径为 ． 由秒杀公式7得典例例题7-1( 2019春•孝感期末 ) 将边长为2的正三角形ABC 沿中线AD 折成60︒的二面角B AD C −−，则三棱锥A BDC −的外接球的表面积为 ．由秒杀公式7得因此外接球的表面积为( 2015秋•绍兴校级期中) 如图，三棱锥P ABC −的底面是边长为2的等边三角形，若PA PB ==P BA C −−的大小为60︒，则三棱锥P ABC −的外接球的表面积等于 ．由秒杀公式7得因此外接球的表面积为( 2017•葫芦岛模拟 ) 已知空间四边形ABCD 中，2AB BD AD ===，1BC =，CD =，若二面角A BD C −−的取值范围为π2π43⎡⎤⎢⎥⎣⎦，，则该几何体的外接球表面积的取值范围为 ．由秒杀公式7得因为π2π43α⎡⎤∈⎢⎥⎣⎦，，所以21sin 12α⎡⎤∈⎢⎥⎣⎦，，因此24533R ⎡⎤∈⎢⎥⎣⎦，，因此外接球的表面积的取值范围为➢适用几何体：所有棱锥.证明：设PAB PAC PBC ABC △、△、△、△的面积分别为1234S S S S 、、、，则那么即( 2020•来宾模拟 )已知正三棱锥的底面边长为，侧棱长为，则该正三棱锥内切球的表面积为 ．由秒杀公式8得所以外接球的表面积为典例例题8-1( 2020•浙江模拟 ) 几何体三视图如图所示，则该几何体的内切球表面积是 ．由秒杀公式8得所以外接球的表面积为( 2020•娄底模拟 ) 如图所示是某几何体的三视图，则该几何体的内切球与外接球的半径之比为( )A ．12B ．23C ．25 D ．13由秒杀公式2得2222=2r hR h++==外， 由秒杀公式8得故该几何体的内切球与外接球的半径之比为故选C .。
高考数学《复习纲要》之外接球问题(2)
第28个问题：空间球问题之外接球问题一、重点知识点归纳外接球：几何体的各个顶点都在同一个球上，则该球叫做几何体的外接球。
注意：球心与小圆心的连线垂直于小圆圆面，A为小圆上的一点。
这样就会出现一个直角三角形：批注：外接球可以不画球，但不能不见解题心脏；1.秒杀R 的方法（2）若几何体是三棱锥（四面体）满足：对棱相等的三棱锥2.秒杀r的方法：小圆一般是几何体下底面的外接圆，r 是下底面的外接圆的半径。
注意：某几何体的每个面都可以作底面；解题心脏必须掌握：R 为外接球半径.r为小圆的半径.d 为球心O 到小圆的距离.222rd R +=（1）若这个面为直角三角形（2）若这个面为一般的三角形，则利用正弦定理。
（3）若这个面为矩形或者正方形（4）若这个面为正六边形3.秒杀d 的给法：题目中若出现“直棱柱”，则()111.2CC BB AA h hd =====侧棱长二、题型归纳题型1：秒杀方法+解题心脏例1.已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC =O 表面积等于（）A.4πB.3πC.2πD.π变式1.若三棱锥三个面两两垂直且面积分别为262322，，，则该三棱锥的外接球的体积为_____.外接圆的半径是斜边的一半。
外接圆半径是对角线的一半.正六边形的外接圆的半径等于正六边形的边长a变式2.在四面体ABCD 中,3,24======BC AD BD AC CD AB 则该四面体的外接球的体积________.变式3.设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（）A.2a π B.273a πC.2113a π D.25aπ变式4.直三棱柱111C B A ABC -的六个顶点都在球O 的球面上，若,90,20=∠==ABC BC AB ，221=AA 则球O 的表面积为_________.题型2：顶点、球心、小圆圆心三点共线（针对椎体）解法归纳：(1).何时利用三点共线？①正棱锥（如正三棱锥,正四棱锥）②侧棱长相等的棱锥.③底面确定体积最大时（顶点无限制）(2)解题模型注意：一般建立两个方程⎩⎨⎧→=+→+=三点共线解题心脏h d R d r R 222解方程即可求出d （永远先解d ，若直接取正值；矛盾→<)(0d 11=⇒-=d d 则即若）例2.正四棱锥ABCD P -的5个顶点都在同一个球面上，若正四棱锥的底面边长为4，侧棱长为62，则此球的表面积为______.变式5.已知正三棱锥ABC P -的四个顶点均在球O 上，且,52===PC PB PA 32===AC BC AB 则球O 的表面积为（）A.π25 B.π6125 C.π25 D.π20变式6.在半径为2的球面上有不同的四个点A,B,C,D ，若2===AD AC AB ,则平面BCD 被球所截的图形的面积为__________.变式7.已知点A,B,C,D 均在球O 上，3==BC AB ，3=AC ，若三棱锥ABC D -体积的最大值为433，则球O 的表面积为（）π36.A B.π16 C.π12 D.316π类型3已知椎体的高或求高且球心不在高线上解法归纳：球心向高作“垂线”得到一个直角三角形+矩形关键问题：求l（1）若P 在下底面的投影落在下底面的顶点上，则r l =立马可以推出2hd =（2）若P 在下底面的投影不落在下底面的顶点上则；r l ≠（利用化立体为平面，只研究下底面即可来求l ）；例3.已知三棱锥ABC P -中，ABC ∆是边长为6的等边三角，ABC PA 平面⊥，且三棱锥外接球的表面积为π64，则.______=PA变式8.已知四棱锥ABCDP -的底面是正方形，223,2,==⊥∆PAB S AC ABCD PA 平面，则该四棱锥的外接球的表面积是_____.变式9.已知正方体1111D C B A ABCD -的棱长为1，点P 是线段11C A 上的动点，则三棱锥ABCD P -外接球半径R 的取值范围是________.类型4：已知某条棱是直径（SC 为直径）解法归纳：作一个球（只有这类题目）根据图象可得两个结论：①)(2到底面的距离为：S h h d =②得到两个垂直⎪⎩⎪⎨⎧=∠=∠09090SBC SAC （直径所对圆周角为90°）例4.已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（）()A 6()B ()C ()D2变式10.已知球的直径SC =4，A ，B 是该球球面上的两点，AB =3，30=∠=∠BSC ASC ，则棱锥S —ABC 的体积为（）33.A B ．32C ．1.3D 变式11.已知三棱锥ABC S -的所有顶点都在球O 的球面上，SC 是球O 的直径，若平面SCA⊥平面SCB，SA=AC,SB=BC,三棱锥ABC S -的体积为9，则球O 的表面积为________.三、课下巩固（高考+模拟题）1.已知四面体ABC P -中，1,3,==⊥BC AC BC AC ，△PAB 是正三角形，且ABC PAB 平面平面⊥，则四面体ABC P -的外接球的半径为_______.2.在四面体ABC S -中，平面SAC ⊥平面ABC ，AB ⊥BC,AB=BC=2,0120=∠ASC ，则该四面体的外接球的表面积为______.。
数学-一个公式搞定外接球问题10种题型(解析版)
外接球问题10种题型总结【题型目录】题型一：长方体正方体外接球（体对角线即为外接球的直径，()22222c b a R ++=）题型二：能在正方体（长方体）内还原的立方体，即长方体切割体的外接球（体对角线即为外接球的直径，()22222c b a R ++=）题型三：圆柱的外接球（2222r h R +⎪⎭⎫ ⎝⎛=，其中r 为底面圆的半径，h 为圆柱的高）题型四：直棱柱的外接球（2222r h R +⎪⎭⎫ ⎝⎛=，其中r 为底面外接圆的半径，h 为棱柱的高）题型五：侧棱垂直于底面的棱锥的外接球（2222r P A R +⎪⎭⎫ ⎝⎛=，其中r 为底面外接圆的半径，P A 为棱锥垂直于底面的棱）题型六：圆锥的外接球题型七：棱台圆台的外接球题型八：正棱锥的外接球题型九：侧面垂直于底面外接球（找球心，球心在每个面中垂线的交点处）题型十：多面体外接球（找球心，球心在每个面中垂线的交点处）【典型例题】题型一：长方体正方体外接球（体对角线即为外接球的直径，()22222c b a R ++=）【例1】若一个正方体的顶点都在球面上，它的棱长为1，则这个球的表面积是（）A ．π2B ．3π4C ．3πD ．12π【例2】已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为（）A．9π2B．C．9πD．27π【题型专练】1．长方体的过一个顶点的三条棱长分别是2，4，4，则该长方体外接球的表面积为（）A．9πB．18πC．36πD．48π2．已知球内接正方体的表面积为S，那么球体积等于_____________．题型二：能在正方体（长方体）内还原的立方体，即长方体切割体的外接球（体对角线即为外接球的直径，()22222c b a R ++=）设长方体相邻的三条边棱长分别为a ，b ，c．图1墙角体图1鳖臑图3挖墙角体图4对角线相等的四面体图1侧面（侧棱）两两垂直，图2所有面均为直角三角形，（线面垂直+线线垂直）；图3俯视图是一矩形，AC 为虚线，主视图和左视图为直角三角形，图4若是长方体则为对棱相等的四面体，若是正方体则是正四面体（所有棱长均相等）图4中（长方体），2222222222222222222a b BC AD BC AB CD b c AC a b c R AC BD c a AB ααβγβγ⎧+===⎫⎪++⎪=⇒+==⇒++=⇒=⎬⎨⎪⎪=+==⎭⎩abc abc abc V BCD A 31461=⨯-=-．【例1】_______________．可得该正方体的外接球就是三棱锥设球半径为R ，可得正方体的对角线长等于球直径【例2】已知三棱锥-P ABC 的四个顶点在球O 的球面上，PA PB PC ==，ABC 是边长为2的正三角形，E F ，分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为（）A B ．6πC ．24πD ．又1cos 2AD EAC PA x ∠==，∴2PA PB PC ∴===，又===2AB BC AC ，PA ∴，即三棱锥-P ABC 是以PA ，所以球O 的直径则球O 的体积333V R =π=π⨯【例3】表面积为）A ．B ．12πC ．8πD ．【例4】设,,,A B C D 是半径为2的球面上的四个不同点，且满足0AB AC ⋅=，0=⋅AD AC ，0AD AB ⋅=，用1S 、2S 、3S 分别表示ABC 、ACD 、ABD △的面积，则123S S S ++的最大值是______.【例5】我国古典数学著作《九章算术》中记载，四个面都为直角三角形的四面体称之为鳖臑现有一个“鳖臑”，PA ⊥底面ABC ，AC BC ⊥，且3PA =，2BC =，AC =则该四面体的外接球的表面积为__________．则长方体的外接球的半径为22229344R PA AC BC =++=++=故2R =所以三棱锥-P ABC 外接球的表面积为故答案为：16π【例6】如图，蹴鞠，又名“蹋鞠”、“蹴球”、“蹴圆”、“筑球”、“踢圆”等，“跳”有用脚蹴、蹋、踢的含义，“鞠”最早系皮革外包、内实米糠的球.因而“蹴鞠”就是指古人以脚蹴、蹋、踢皮球的活动，类似今日的足球.2006年5月20日，蹴鞠己作为非物质文化遗产经国务院批准列入第一批国家级非物质文化遗产名录.若将“鞠”的表面视为光滑的球面，已知某“鞠”表面上的四个点A ，B ，C ，D 满足AB CD ==，BD AC ==，5cm AD BC ==，则该“鞠”的表面积为____________.令此长方体的长、宽、高分别为,,a b c ，则有222222251320a b b c ca ⎧+=⎪+=⎨⎪+=⎩，即有22229a b c ++=，令该长方体的外接球的半径为R ，因此2222(2)29R a b c =++=，该“鞠”的表面积为2429S R ππ==.故答案为：29π【题型专练】1．四面体ABCD 的每个顶点都在球O 的球面上，,,AB AC AD 两两垂直，且AB =2AC =，3AD =，则球O 的表面积为________.2．据《九章算术》中记载，“阳马”是以矩形为底面，一棱与底面垂直的四棱锥.现有一个“阳马”，PA ⊥底面ABCD ，底面ABCD 是矩形，且543PA AB BC ===，，，则这个“阳马”的外接球表面积为（）A ．5πB ．200πC ．50πD ．100π【答案】C【分析】把四棱锥P ABCD -补成一个长方体，如图，长方体的对角线就是其外接球也是四棱锥P ABCD -的外接球直径，由长方体性质求得球半径后可得表面积．【详解】把四棱锥P ABCD -补成一个长方体，如图，长方体的对角线就是其外接球也是四棱锥P ABCD -的外接球直径，设球半径为R ，则2222(2)50R PA AB BC =++=，球表面积为24π50πS R ==．故选：C ．3．正四面体S ABC -内接于一个半径为R 的球，则该正四面体的棱长与这个球的半径的比值为（）A ．4B ．3C 3D 【答案】C【分析】设正四面体的棱长为2a ，由正四面体几何性质得出a 与外接球半径R 的关系式，即可求比值M 4．在四面体ABCD 中，已知点E ，F 分别为棱AB ，CD 中点，且EF AB ⊥，EF CD ⊥，若2AB CD ==，2EF =，则该四面体外接球半径为__________．【答案】2【分析】根据四面体的对棱性质，结合长方体面对角线的性质，即可将四面体的外接球问题转化为长方体外接球问题，即可得半径.【详解】解：根据长方体的面对角线特点，则可构造长方体使得四面体ABCD 设长方体的长、宽、高分别为则2224b c AB +==，a EF ==的外接球半径为5．在半径为R 的球面上有A ，B ，C ，D 四点，且直线,,AB AC AD 两两垂直，若,ABC ACD ADB △△，△的面积之和为6，则此球体积的最小值为______________．6．已知三棱锥A BCD -中，⊥AB 面902BCD BCD AB BC CD ∠==== ，，，则三棱锥的外接球的体积为___________.【详解】,该三棱锥在长方体中，且三棱锥的四个顶点为长方体的四个顶点，7.四面体A ﹣BCD 中，AB ＝CD ＝5，AC BD ==AD BC ==A ﹣BCD 外接球的表面积为_____．题型三：圆柱的外接球（2222r h R +⎪⎭⎫ ⎝⎛=，其中r 为底面圆的半径，h 为圆柱的高）【例1】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π4【题型专练】1.阿基米德是伟大的古希腊数学家，他和高斯､牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），在该图形中，球的体积是圆柱体积的23，并且球的表面积也是圆柱表面积的23，则该圆柱的体积与它的外接球的体积之比为___________.故答案为：328.题型四：直棱柱的外接球（2222r h R +⎪⎭⎫ ⎝⎛=，其中r 为底面外接圆的半径，h 为棱柱的高）【例1】设直三棱柱111ABC A B C -的所有顶点都在一个表面积是40π的球面上，且1,120AB AC AA BAC ∠=== ，则该直三棱柱的体积是（）A．B．3C ．D ．3【例2】在直三棱柱111ABC A B C -中，2AB =，AC =BC =14AA =，则该直三棱柱的外接球的表面积为_________.___________．圆柱12O O 的底面圆直径为2r 柱12O O 外接球的球心，设球可作出正六棱柱ABCDEF A -可将正六棱柱1ABCDEF A B -连接11O A 、11O B ，则111A O B ∠=则圆1O 的半径为111r O A A B ==正六棱柱1111ABCDEF A B C D E -设正六棱柱111ABCDEF A B C D -π【题型专练】1．如图，在直三棱柱111ABC A B C -中，12,90AB BC AA ABC ===∠=︒，则此直三棱柱的外接球的体积是___________.2．若三棱柱111ABCA B C ﹣的底面是以AB 为斜边的直角三角形，1AA ⊥平面ABC，AB =14AA =，则三棱锥1A ABC -的外接球的表面积为_____．3．已知直三棱柱111ABC A B C -中，12,6BB BC BAC π∠===，则该三棱柱外接球的体积为__________.4．已知在直三棱柱111ABC A B C -中，11AB AA ==，2BC =，AB BC ⊥，则点1A 到平面11AB C 的距离为______；若三棱锥111A A B C -的顶点都在同一个球面上，则该球体积为______．【详解】由题意，点1A 到平面11AB C 的距离可以看作三棱锥由于直三棱柱111ABC A B C -，故AA 11111111332A B C AA S =�创创22111162AA A C ,AB ,B +==1111122332AB C d S d =⨯=⨯⨯⨯ 题型五：侧棱垂直于底面的棱锥的外接球（2222r P A R +⎪⎭⎫ ⎝⎛=，其中r 为底面外接圆的半径，P A 为棱锥垂直于底面的棱）【例1】已知A ，B ，C ，D 在球O 的表面上，ABC AD ⊥平面ABC ，AD ＝2，则球O 的表面积为（）A ．πB ．2πC ．4πD ．8π【答案】D【分析】由正弦定理可得ABC 外接圆的半径，作图利用勾股定理可得四面体D ABC -的外接球的半径，即可求出球O 的表面积.【详解】ABC为等边三角形且其面积为1 2ABC的边长为3，设ABC外接圆的半径为由正弦定理可得322sin60r==，1r=平面ABC，AD＝2，1//O O AD，且取11= 2O O AD，【例2】已知在三棱锥P－ABC中，PA＝4，BC=PB＝PC＝3，PA⊥平面PBC，则三棱锥P－ABC 的外接球的表面积是（）A．40πB．43πC．45πD．48π故选：B.【例3】三棱锥-P ABC 中，PA ⊥平面ABC ，ABC 为直角三角形，AB BC ⊥，1AB BC ==，2PA =，则三棱锥-P ABC 的外接球的表面积为（）A ．2πB ．3πC ．4πD ．6π则体对角线PC 所以2R PC ==故三棱锥-P ABC 故选：D 【题型专练】1．如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，AB DC ，AD AB ⊥，2DC =，1AD AB ==，直线PA 与平面ABCD 成45︒角.设四面体PBCD 外接球的圆心为O ，则球的体积为__________.66【分析】先证明出△PCD 和△PBC 均为直角三角形，得到O 点位置，可求得外接球的半径，可求其体积．∵直线PA 与平面ABCD 则∠PAD ＝45°，∴PD ＝又22PC CD PD =+=∴四面体PBCD 外接球的半径为2．在三棱锥A BCD -中，BD ⊥平面ADC ，2BD =，AB =AC BC ==，则三棱锥A BCD -的外接球的体积为__________．AD 因为BD ⊥平面ADC ，AD ⊂所以BD AD ⊥，BD CD ⊥.因为2BD =，22AB =，所以因为2BD =，22BC =，所以在ADC △中，2AD =，CD =3．已知A ，B ，C ，D 是同一球面上的四个点，其中ABC 是正三角形，AD ⊥平面ABC ，2AD =，3AB =，则该球的表面积为______.故答案为：16π4．我国古典数学著作《九章算术》中记载，四个面都为直角三角形的四面体称之为鳖臑.现有一个“鳖臑”，PA ⊥底面ABC ，AC BC ⊥，且3PA =，2BC =，AC =__________．则长方体的外接球的半径为22229344R PA AC BC =++=++=故2R =所以三棱锥-P ABC 外接球的表面积为故答案为：16π题型六：圆锥的外接球【例1】一个圆锥母线长为6，侧面积，则这个圆锥的外接球体积为______________．【答案】43π【分析】由圆锥的侧面积得出圆锥的底面半径，设出球的半径，根据题意得出关系式求出球的半径，进而由题意可得，22()h R r -+所以，34R 433V ππ==．故答案为：43π．【例2】已知圆锥的底面半径为R ，高为3R ，它的内接圆柱的底面半径为4R ，该圆柱的全面积为（）A ．22R πB ．294RπC ．283RπD ．252Rπ易知△~CAB CPO ，故可得故圆锥的内接圆柱的全面积为：故选：B .【题型专练】1.两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为323π，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为（）A．3πB．4πC．9πD．12π设球的半径为R，则3432 33 Rππ=所以，1BD=，3AD=，CD AB⊥，则CAD ACD∠+∠又因为ADC BDC∠=∠，所以，所以，AD CDCD BD=，CD AD∴=因此，这两个圆锥的体积之和为题型七：棱台圆台的外接球【例1】已知正三棱台的高为1，上、下底面边长分别为面积为（）A．100πB．128πC．144πD．192π【例2】已知一圆台高为7，下底面半径长4，此圆台外接球的表面积为100π，则此圆台的体积为（）A ．84πB ．86πC ．2593πD ．2623π【答案】C【分析】根据旋转体的特点得到圆台的外接球的球心为圆台轴截面外接圆的圆心，然后结合题意得到7AB =，5OC =，4AC =，利用勾股定理得到3BD =，最后利用圆台的体积公式求体积即可.【详解】如图为圆台及其外接球的轴截面，O 为外接球球心，A ，B 为等腰梯形的下底和上底的中点，所以7AB =，【题型专练】1．我国古代数学名著《九章算术》中将底面为矩形的棱台称为“刍童”．已知侧棱都相等的四棱锥P ABCD -底面为矩形，且3AB =，BC =2，用一个与底面平行的平面截该四棱锥，截得一个高为1的刍童，该刍童的顶点都在同一球面上，则该球体的表面积为（）．A ．16πB ．18πC ．20πD ．25π【答案】C【分析】利用勾股定理列方程，求得球的半径，进而求得球的表面积.【详解】如图1，设棱台为1111ABCD A B C D -，如图2，该棱台外接球的球心为O ，半径为R ，上底面中心为1O ，下底面中心为2O ，则由题意121O O =，22AO =，111A O =，1OA OA R ==，当O 在12O O 下方时，设2OO h =，则在2AOO 中，有：224R h =+（1），在11A OO 中，有：()2211R h =++（2），联立（1）、（2）得1h =，25R =，所以刍童外接球的表面积为20π．同理，当O 在12O O 中间时，设1OO h =，则有221R h =+，()2214R h =-+，解得2h =，不满足题意，舍去．综上所述：当刍童外接球的表面积为20π．故选：C2．在正四棱台1111ABCD A B C D -中，1124A B AB ==，12AA =，则该棱台外接球的半径为（）A ．B ．3C D ．设0,2OG m ⎡⎤=∈⎣⎦，则()222228m R m ⎧+=⎪⎨-+⎪⎩设2OGm =>，则()222228m R m R ⎧+=⎪⎨-+=⎪⎩所以10=R ,故选：C.[解法2]同解法1，求得12CG GG ==则1CNC 为等腰直角三角形，四边形CGG 3．正四棱台高为2，上下底边长分别为，所有顶点在同一球面上，则球的表面积是_____．【答案】80π【分析】画出图形，设出未知数，利用半径相等列出方程，求出半径，从而得到球的表面积【详解】如图所示，AB AD BC ==O 为外接球球心，设外接球半径为故答案为：80π题型八：正棱锥的外接球【例1】已知底面为正三角形、侧棱都相等的三棱锥的体积为2，其各顶点都在同一球面上．则该球的表面积为__________________．【答案】9π【分析】如图设底面边长为a ，根据锥体体积公式求a ，设1O 为正三角形ABC 的中心，则1SO ⊥平面ABC ，正三棱锥S ABC -的外接球的球心O 在1SO 上，在1Rt O AO V 中利用勾股定理即可求出R 的值，从而得到球O 的表面积．【详解】由条件可得该三棱锥为正三棱锥，作出其图象，如图所示：设AB a =，则AC a =，CAB ∠=【例2】已知正四棱锥P ABCD -的底面是边长为2的正方形，其内切球的体积为6，则该正四棱锥的高为___________，外接球的表面积为___________.因为球O 与四棱锥相内切，所以由等体积法得：在PAD 中，22PA h =+，122PAD S =⨯⨯ 简得：2121h h +=-，解得，43h =，设正四棱锥外接球的半径为R ，外接球的球心为所以正四棱锥外接球的表面积为24π4πS R ==4289π【例3】点都在同一球面上，则该球的表面积的最小值为_____________．设BC a =，AH h =，OA R =根据题意可得133BCD S h ⨯=【题型专练】1.正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A ．814πB ．16πC ．9πD ．274π2.正四面体S ABC -内接于一个半径为R 的球，则该正四面体的棱长与这个球的半径的比值为（）A4B 3C 3D 【答案】C【分析】设正四面体的棱长为2a ，由正四面体几何性质得出a 与外接球半径R 的关系式，即可求比值【详解】设正四面体的棱长为2a ，正四面体的外接球心为O ，ABC 的内心为M ，则SM ⊥平面ABC ，由AM ⊂平面ABC ，则SM AM ⊥，3．已知正四棱锥的侧棱长l为3，其各顶点都在同一球面上，若该球的体积为36π，则该正四棱锥的体积是（）A．274B．814C．18D．27【答案】A【分析】根据正四棱锥的几何特征可知外接球的球心在其高上，利用勾股定理即可求解长度，进而由体积公式即可求解.【详解】如图，设正四棱锥的底面边长4.（2022·全国·高考真题）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3l ≤≤）A ．8118,4⎡⎤⎢⎥B ．2781,44⎡⎤⎢⎥C ．2764,43⎡⎤⎢⎥D ．[18,27][方法一]：导数法设正四棱锥的底面边长为2a ，高为则2222l a h =+，2232(3a =+所以26h l =，2222a l h =-所以正四棱锥的体积13V Sh =题型九：侧面垂直于底面外接球（找球心，球心在每个面中垂线的交点处）【例1】已知空间四边形ABCD的各边长及对角线BD的长度均为6，平面ABD⊥平面CBD，则空间四边形ABCD外接球的表面积为______.由平面ABD⊥平面CBD故AE⊥平面CBD，AE的投影为△【例2】）矩形ABCD 中，4AB =，3BC =，沿AC 将ABCD 矩形折起，使面BAC ⊥面DAC ，则四面体A BCD-的外接球的体积为（）A ．1256πB ．1259πC ．12512πD ．1253π矩形ABCD 中，因为43AB BC ==，，所以5DB AC ==，设DB 交AC 于O ，则O 是Rt ABC 和Rt V 所以O 到点,,,A B C D 的距离均为52，所以5【例3】已知在三棱锥中，S ABC -中，BA BC ⊥，2BA BC ==，SA SC ==B AC S --的大小为5π6，则三棱锥S ABC -的外接球的表面积为（）A ．56π3B ．58π3C ．105π4D ．124π9【题型专练】1.在三棱锥A BCD -中，平面⊥ABC 平面BCD ，ABC 与BCD △都是边长为6的正三角形，则该三棱锥的外接球的体积为________.【详解】的中点为,,M E F 分别是正三角形ABC 是该三棱锥外接球的球心，连接,AM DM 分别在,AM DM 上，OF ⊥平面BCD ABC ⊥平面BCD ，AM BC ⊥，平面⊥平面BCD ，所以//AM OF ，同理可得2．如图，在三棱锥-P ABC 中，PA ⊥平面ABC ，AB BC ⊥，2PA AB BC ===，AM PC ⊥，M 为垂足，则下列命题正确的是（）A ．三棱锥M ABC -的外接球的表面积为8π.B ．三棱锥M ABC -的外接球的体积为C ．三棱锥P MAB -的外接球的体积为D ．三棱锥P MAB -的外接球的表面积为16π【答案】AC【分析】根据给定条件，取AC 中点1O ，证明点1O 到点,,,M A B C 的距离相等，计算判断A ，B ；取PB ，PC 的中点D ，E ，证明DE ⊥平面PAB ，再确定三棱锥P MAB -的外接球球心位置，并计算半径作答.【详解】在三棱锥-P ABC 中，取AC 中点1O ，连接11,BO MO ，如图，于是得DE ⊥平面PAB ，而因此该球的球心O 在直线令OD d =，即有R OM =在Rt PAC △中，12PE PC =在OEM △中，cos OEM ∠题型十：多面体外接球（找球心，球心在每个面中垂线的交点处）【例1】半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美.二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体.它由八个正三角形和六个正方形围成（如图所示），若它的棱长为2，则下列说法错误的是（）A ．该二十四等边体的外接球的表面积为16πB ．该半正多面体的顶点数V 、面数F 、棱数E ，满足关系式2V F E +-=C ．直线AH 与PN 的夹角为60°D ．QH ⊥平面ABE 记正方体体心为O ，取下底面ABCD 易知112OO BO ==，则外接球半径所以外接球的表面积2=416S R π=由欧拉公式可知：顶点数+面数又因为PN ∥AD ，易知直线AH 直线AH 与PN 的夹角为60 ，故故选：D【例2】如图，已知正方体的棱长为1，1O ，2O 分别为正方体中上、下底面的中心，3O ，4O ，5O ，6O 分别为四个侧面的中心，由这六个中心构成一个八面体的顶点，则（）A ．直线13O O 与直线24O O 所成角为60︒B ．二面角1345O O O O --CD ．这个八面体外接球的体积为π6【答案】ACD 【分析】A.根据几何关系，将异面直线所成角，转化为相交直线所成角；B.构造二面角的平面角，再根据余弦定理求解，转化为正切值；C.根据几何体的特征，计算一个等边三角形的面积，再求八面体的表面积；D.由几何体确定外接球的球心和半径，再求外接球的体积.【详解】A.连结1235O O O O ，，交于点O ，由正方体的性质可知，点O 平分1235O O O O ，，所以四边形1325O O O O 是平行四边形，所以1325//O O O O ，所以直线13O O 与直线24O O 所成角为425O O O ∠,因为八面体的由8个全等的等边三角形构成，所以42560O O O ∠= ，故A 正确；B.取34O O 的中点M ，56O O 的中点由图可知，八面体的表面是所以134O M O O ⊥，MN O ⊥所以1O MN ∠是二面角1O O -2【例3】截角四面体是一种半正八面体，可由四面体经过适当的截角，即截去四面体的四个顶点处的小棱锥所得的多面体.如图，将棱长为3的正四面体沿棱的三等分点作平行于底面的截面得到所有棱长均为1的截角四面体，则（）A ．DE ⊥平面ABCB ．直线DE 与GH 所成的角为60°C ．该截角四面体的表面积为D ．该截角四面体的外接球半径为4选项B ，由题意//,//DE AJ GI 与GH 所成角为60 ，正确；选项C ，由题意，截角四面体由所以其表面积为23414S =⨯⨯选项D ，如下图所示，取上下底面的中心分别为故选：BCD【题型专练】1．如图，在几何体ABCDEF 中，底面ABCD 是正方形，EF 平面,4ABCD EF =，其余棱长都为2，则这个几何体的外接球的体积为（）A ．3B ．16π3C ．D ．32π3【答案】D【分析】由题意可知直线EF 在底面ABCD 上的射影即为,AD BC 的中点,N G 的连线所在直线,连接,AC BD 交于点M ，取EF 的中点O ，计算求得2OA OB OC OD OE OF ======，说明几何体的外接球的球心为O ，确定半径，根据球的体积公式即可求得答案.【详解】由题意在几何体ABCDEF 中，底面ABCD 是正方形，EF 平面,4ABCD EF =，其余棱长都为2，可知直线EF 在底面ABCD 上的射影即为,AD BC 的中点,N G 的连线所在直线,2NG =,连接,AC BD 交于点M ，则为,AC BD 的中点，取EF 的中点O ，四边形,ABFE CDEF 为全等的等腰梯形，则,OA OC OB OD ==，故,OM AC OM BD ⊥⊥,,,AC BD M AC BD =⊂ 平面ABCD ,由题意得，11()(42)21,2HF EF NG=-=-= 22312,HG FG HF OM HG∴=-=-=∴=222OA OM AM∴=+=，同理OB OC==2,OE OF OA OB OC OD OE==∴====2．勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触，因此它能像球一样来回滚动（如图甲），利用这一原理，科技人员发明了转子发动机．勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体如图乙所示，若正四面体ABCD的棱长为2，则下列说法正确的是（）A．勒洛四面体ABCD被平面ABC截得的截面面积是(8πB．勒洛四面体ABCD内切球的半径是4C．勒洛四面体的截面面积的最大值为2π-D．勒洛四面体能够容纳的最大球的半径为22-对于B ，由对称性知,勒洛四面体正BCD △外接圆半径1O B ABCD 的外接球半径为R 在1Rt BOO 中,2263R ⎛= ⎝此时我们再次完整地抽取部分勒洛四面体如图所示：对于C，显然勒洛四面体截面面积的最大值为经过正四面体某三个顶点的截面，由对()max 223Sπ=-截，故C正确；对于D，勒洛四面体能够容纳的最大球与勒洛四面体的面体ABCD能够容纳的最大球的半径为。
高中数学空间几何体的外接球专题(附经典例题与解析)
高中数学空间几何体的外接球专题(附经典例题与解析)球的性质回顾：球心O和小圆O'的连线OO'垂直于圆O'所在平面。
外接球半径的求法是利用直角三角形的勾股定理，在Rt△OAO'中，OA^2=OO'^2+O'A^2.常见平面几何图形的外接圆半径（r）的求法：1.三角形：1) 等边三角形：内心、外心、重心、垂心、中心重合于一点。
外接圆半径通常结合重心的性质(2:1)进行求解：r=a*(2/3)^(1/2) （其中a为等边三角形的边长）。
2) 直角三角形：外接圆圆心位于斜边的中点处，r=斜边/2.3) 等腰三角形：外接圆圆心位于底边的高线(即中线)上。
r=a/(2sin(A/2)) （其中A为顶角）。
4) 非特殊三角形：可使用正弦定理求解，XXX)。
2.四边形：常见具有外接圆的四边形有正方形、矩形、等腰梯形。
其中正方形与长方形半径求解方法转化为直角三角形。
几何体的外接球球心与底面外心的连线垂直于底面，即球心落在过底面外心的垂线上。
练：2.半径为2的球的内接三棱锥P-ABC，PA=PB=PC=2，AB=AC=BC，则三棱锥的高为3.1.三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，侧棱AA1垂直于底面ABC，且AA1=4，则此三棱柱外接球的表面积为8π。
本文介绍了三棱锥的外接球的求解方法，其中包括侧棱垂直底面的三棱锥、正三棱锥和侧面垂直于底面的三棱锥三种类型。
对于侧棱垂直底面的三棱锥，可以采用补形法或通过确定底面三角形的外心来求解外接球的半径。
补形法是指将该几何体转化为原三棱柱的外接球，从而求出外接球的半径。
而通过确定底面三角形的外心，则可以通过勾股定理求解外接球的半径。
对于正三棱锥，可以通过底面正三角形的边长来求解内切球的半径，然后再利用勾股定理求解外接球的半径。
对于侧面垂直于底面的三棱锥，则需要确定△ABC和△PAB的外心分别为O’和O’’，并通过勾股定理求解OO’的长度，从而求解外接球的半径。
外接球问题全搞定(学生版)
外接球、内切球专题外接球几何体的外接球一、定义1. 球的定义: 空间中到定点的距离等于定长的点的集合 (轨迹) 叫球面, 简称球.2. 外接球的定义: 若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3. 内切球的定义: 若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关性质1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面 (类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交, 交点是球心 (类比:在同圆 中,两相交弦的中垂线交点是圆心 ).2.结论:由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心是其对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心外心的连线的中点.结论4:正棱雉的外接球的球心在其高上, 具体位置可通过计算找到.结论5:若棱雉的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.正方体正方体的外接球、内切球和棱切球1.正方体的外接球的球心是其对角线的中点,若正方体的棱长为a ，则正方体外接球的半径为R =22a 2+a 2 2=32a .2.正方体的内切球的球心是其对角线的中点,若正方体的棱长为a ，则正方体内切球的半径为R =a 2.3.正方体的棱切球的球心是其对角线的中点,若正方体的棱长为a ，则正方体棱切球的半径为R =a 2 2+a 2 2=2a 2.正方体的每个面与其棱切球的交线轨迹为圆.正三棱锥正三棱锥的外接球结论：正三棱锥的外接球的球心在顶点与底面外接圆的圆心连线上,切球心到顶点与到底面的距离之比为3:1,即OP :OO 1=3:1.则若正三棱锥的边长为a ,则正三棱锥外接球的半径R =64a ,正三棱锥的高h =63a .【证明】：如图所示：将正三棱锥P -ABC 放进正方形中，由正三棱锥的边长为a 可得正方体的棱长为22a 故正三棱锥外接球的半径即为正方体外接球的半径∴R =32⋅22a =64a ,即OP =OC =64a 设底面ABC 外接圆的半径为r ，正三棱锥P -ABC 的高为h则a sin 60∘=2r ,即r =33a ,h =O 1P =PC 2-r 2=a 2-33a 2=63a ∴OO 1=OC 2-O 1C 2=R 2-r 2=612a 故OP OO 1=64a 612a =3正十四面体正十四面体的外接球定义：从正方体中切掉八个小的正三棱锥所得到的几何体称为正十四面体，如图所示，它有六个面为正方形，八个面为正三角形.正十四面体是阿基米德立体中的一种.结论①：正十四面体的外接球的球心就是正方体棱切球的球心.若正十四面体的边长为a ,则正方体的边长为2a ,正十四面体的高R =22⋅2a =a .结论②：若正十四面体的边长为a ,则正十四面体的体积V =532a 3.【证明】：由正十四面体的边长为a 可知：正方体的边长为2a 故切掉的一个小三棱锥的体积为V 0=13×12×22a 3=224a 3∴正十四面体的体积V =2a 3-8V 0=532a 3结论③：正十四面体的体积与正方体的体积之比为5∶6.【证明】：∵正十四面体的体积V =532a 3,正方体的体积为V 1=2a 3=22a 3∴正十四面体的体积与正方体的体积之比为V V 1=532a 322a 3=56.长方体长方体的外接球结论：长方体的外接球的球心是其对角线的交点,若长方体的长为a,宽为b，高为c，则长方体外接球的半径R=a2+b2+c22.【证明】：如图所示：AC=AB2+BC2=a2+b2∴2R=AC1=AC2+CC12=a2+b2+c2,即R=a2+b2+c22四种典型模型：外接球对棱相等模型结论：对棱相等模型是三棱锥的三组对棱长分别相等模型，用构造长方体的方法解决.若三棱锥的三组对棱长分别为x、y、z.,则几何体外接球的半径为R= x2+y2+z28.【证明】：如图，设长方体的长、宽、高分别为a,b,c，AC=BD=x,AB=CD=y, AD=BC=z.则b2+c2=z2 a2+c2=y2 a2+b2=x2三式相加可得a2+b2+c2=x2+y2+z22,而显然四面体和长方体有相同的外接球，设外接球半径为R，则a2+b2+c2=4R2，∴R=a2+b2+c22=x2+y2+z28.外接球墙角模型定义：墙角模型是指几何体中有三条棱两两互相垂直的模型，采用构造法长方体或正方体解决问题.1.如果两两互相垂直的三条棱相等，则构造正方体模型.若棱长为a ，则几何体的外接球半径为R =32a .2.如果两两互相垂直的三条棱不全相等，则构造长方体模型.若两两互相垂直的三条棱的棱长分别为a 、b 、c ,则几何体的外接球半径为：R =a 2+b 2+c 22柱体与锥体外接球①柱体的外接球：柱体的外接球的球心是上下底面圆心连线的中点,若柱体的底面半径为r,高为h，则柱体外接球的半径R=r2+h2 2.②锥体的外接球：锥体的外接球的球心在顶点与底面圆心的连线上,若锥体的底面半径为r,高为h，则锥体外接球的半径R=r2+h2 2.【证明】：如图所示：OA=OP=R,O1A=r,O1P=h则OO1=O1P-OP=h-R在△AOO1中：OA2=OO12+O1A2,即R2=h-R2+r2∴R=h2+r22h汉堡模型是直棱柱的外接球、圆柱的外接球模型，用找球心法解决找球心法:多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点．一般情况下只作出一个面的垂线，然后设出球心用算术方法或代数方法即可解决问题．有时也作出两条垂线，交点即为球心．则多面体外接球的半径为：R =r 2+h 24其中，h 为直棱柱的高，r 为底面外接圆的半径.以直棱柱为例，模型如下图：如图1，图2，图3，直三棱柱内接于球(同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形)第一步：确定球心O 的位置，O 1是ΔABC 的外心，则OO 1⊥平面ABC ；第二步：算出小圆O 1的半径AO 1=r ，OO 1=12AA 1=12h (AA 1=h 也是圆柱的高)；第三步：勾股定理：OA 2=O 1A 2+O 1O 2⇒R 2=h 2 2+r 2⇒R =r 2+h 2 2，解出R .注意：底面外接圆的半径r 的求法1.正弦定理：a sinA =2R (通用)；2.直角三角形：半径等于斜边的一半；3.等边三角形：半径等于三分之二高；4.长（正）方形：半径等于对角线的一半.结论：垂面模型是有一条侧棱垂直底面的棱锥模型，可补为直棱柱内接于球，由对称性可知球心O 的位置是△CBD 的外心O 1与△AB 2D 2的外心O 2连线的中点，算出小圆O 1的半径AO 1=r ，OO 1=h 2,则棱锥的外接球半径为：R =r 2+h 24．解题步骤：第一步：将ΔABC 画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：O 1为ΔABC 的外心，所以OO 1⊥平面ABC ，算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法：利用正弦定理，得a sin A =b sin B =c sin C =2r )，OO 1=12PA =12h ；第三步：利用勾股定理求三棱锥的外接球半径：①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2；②R 2=r 2+OO 12⇔R =r 2+OO 12=r 2+h 24外接球斗笠模型斗笠模型：棱锥、圆锥的顶点在底面的射影是底面外心的．多面体外接球公式为：R =h 2+r 22h其中h 为几何体的高，r 为几何体的底面半径或底面外接圆的半径.【证明】：∵P 的射影是△ABC 的外心∴三棱锥P -ABC 的三条棱相等 取△ABC 的外心O 1,球心O 的位置，则P ,O ,O 1三点共线； 由勾股定理可得：OA 2=O 1A 2+O 1O 2,即R 2=h -R 2+r 2解得：R =h 2+r 22h台体外接球台体的外接球结论：台体的外接球的球心在上下底面外接圆圆心的连线上,若台体下底面的外接圆半径为r 1,上底面的外接圆半径为r 2,高为h ，则台体外接球的半径为：R =r 12-r 22+h 22h2+r 22【证明】：如图所示：设球心到下底面的距离为h 1，到上底面的距离为h 2,则R 2=h 22+r 22⋯①R 2=h 12+r 12⋯②②-①得：h 22+r 22-h 12-r 12=0,即h 22+r 22-h -h 2 2-r 12=0整理得：r 22-h 2-r 12+2h ⋅h 2=0∴h 2=r 12-r 22+h 22h故R 2=h 22+r 22=r 12-r 22+h 22h2+r 22,即R =r 12-r 22+h 22h2+r 22切瓜模型是有一侧面垂直底面的棱锥型，常见的是两个互相垂直的面,即α⏊β.类型Ⅰ：△ABC与△BCD都是直角三角形,则三棱锥A-BCD的外接球球心在斜边BC的中点O.类型Ⅱ：△ABC是等边三角形，△BCD是直角三角形，则三棱锥A-BCD的外接球球心为△ABC外接圆的圆心O.类型Ⅲ：△ABC与△BCD都是等边三角形，解决方法是分别过△ABC与△BCD 的外心作该三角形所在平面的垂线，交点O即为球心．类型Ⅳ：侧面△ABC是一般三角形，设为α平面，底面是一般三角形或四边形，设为β平面，如图，解决方法是过α，β的外心O2,O1作所在平面的垂线，垂线必交于一点O，O即为外接球的球心.则几何体的外接球半径为R=r21+r22-l24其中r1、r2为平面α，β的外接圆的半径，l为两个面的交线BC的长.【证明】：过O1，O2作AB的垂线，则OO1⎳O2E,OO2⎳O1E∵α⏊β∴四边形OO2EO1为矩形∴R2=OB2=OO22+O2B2=O1E2+O2B2=O1B2-BE2+O2B2=r21+r22-l24即R=r21+r22-l2 4折叠模型：两个全等三角形或等腰三角形拼在一起，或菱形折叠.结论：如图所示：△ABD 和△CBD 是两个全等的三角形（或者等腰三角形），把△ABD 沿BD 折叠起来，使点A 折叠到点A ,E 为BD 的中点，设折叠的二面角 ∠A EC =α,CE =A E =h ，△ABD 和△BCD 的外接圆的半径为r ,H 1和H 2分别为△BCD ,△A BD 外心，过H 1作平面BCD 的垂线，过H 2作平面A BD 的垂线，这两条垂线相交于球心O ,则R =r 2+(h -r )2tan 2α2【证明】：在△BCD 中：CH 1=r ,CE =h ,EH 1=CE -CH 1=h -r ,在△COH 1中：OH 1=EH 1⋅tan α2=(h -r )tanα2由勾股定理可得：R 2=OC 2=OH 21+CH 21=(h -r )2tan 2α2+r 2.∴R =r 2+(h -r )2tan 2α2结论：鳄鱼模型即普通三棱锥模型（两个面不垂直），用找球心法可以解决.如果m 为平面ACD 外接圆圆心O 2到交线CD 的距离，n 为平面BCD 外接圆圆心O 1到交线CD 的距离，θ为二面角A -CD -B 的平面角，l 为交线CD 的长,R 为外接球半径,则R =m 2+n 2-2mn cos θsin 2θ+l 24【证明】：如图所示：∵OO 1⏊O 1E ,OO 2⏊O 2E∴O ,O 1,E ,O 2四点共圆在△O 1O 2E 中，由余弦定理可得：O 1O 22=m 2+n 2-2m ⋅n ⋅cosθ在△OO 1O 2中，由正弦定理可得：O 1O2sinθ=2r 0=OE（r 0为△OO 1O 2外接圆半径）∴R 2=OC 2=OE 2+CE 2=O 1O 2sinθ 2+l 2 2=m 2+n 2-2mn ⋅cos θsin 2θ+l 24内切球内切球结论以三棱锥P-ABC为例，如下图所示：求其内切球的半径r．方法：等体积法，三棱锥P-ABC体积等于内切球球心与四个面构成的四个三棱锥的体积之和；第一步：先求出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r，球心为O，建立等式：V P-ABC=V O-ABC+V O-PAB+V O-PAC+V O-PBC⇒V P-ABC=13S△ABC·r+13S△PAB·r+13S△PAC·r+13S△PBC·r=13(S△ABC+S△PAB+S△PAC+S△PBC)·r；第三步：解出内切球半径r=3V P-ABCS O-ABC+S O-PAB+S O-PAC+S O-PBC=3VS表．内切球半径公式：r=3VS表，其中S表为几何体的表面积，V表示几何体的体积.题型一：墙角模型1.长方体ABCD-A1B1C1D1的8个顶点在同一球面上，且AB=2,AD=3,AA1=1，则球面面积为()A.83πB.43πC.4πD.8π2.已知正三棱锥S-ABC的三条侧棱两两垂直，且侧棱长为2，则此三棱锥的外接球的表面积为()A.πB.3πC.6πD.9π3.已知三棱锥A-BCD的四个顶点A，B，C，D都在球O的表面上，AC⊥平面BCD，BC⊥CD，且AC=3，BC=2，CD=5，则球O的表面积为( )A.12πB.7πC.9πD.8π4.若三棱锥S−ABC的三条侧棱两两垂直，且SA=2，SB=SC=4，则该三棱锥的外接球半径为( ).A.3B.6C.36D.95.已知S，A，B，C，是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=1，BC=2，则球O的表面积等于( ).A.4πB.3πC.2πD.π6.点A，B，C，D均在同一球面上，且AB，AC，AD两两垂直，且AB=1，AC=2，AD=3，则该球的表面积为().A.7πB.14πC.72πD.714π37.三棱锥P-ABC中，△ABC为等边三角形，PA=PB=PC=3，PA⊥PB，三棱锥P-ABC的外接球的体积为()A.272πB.2732π C.273πD.27π8.已知球O的球面上有四点A，B，C，D，DA⊥平面ABC，AB⊥BC，DA=AB=BC=2，则球O的体积等于.9.已知三棱锥A-BCD的所有顶点都在球O的球面上，且AB⊥平面BCD，AB=23，AC= AD=4，CD=22，则球O的表面积为.10.已知正方体的所有顶点在一个球面上，若这个球的表面积为12π，则这个正方体的体积为.11.已知长方体ABCD-A1B1C1D1的体积为325，AA1=25，则当长方体ABCD-A1B1C1D1的表面积最小时，该长方体外接球的体积为.变式演练1.在正三棱锥S-ABC中，点M是SC的中点，且AM⊥SB，底面边长AB=22，则正三棱锥S-ABC的外接球的表面积为( )A.6πB.12πC.32πD.36π2.(多选题)一棱长等于1且体积为1的长方体的顶点都在同一球的球面上，则该球的体积可能是()A.22πB.32πC.πD.52π3.在古代将四个面都为直角三角形的四面体称之为鳖臑，已知四面体A-BCD为鳖臑，AB⊥平面BCD，且AB=BC=36CD，若此四面体的体积为833，则其外接球的表面积为.4.长方体ABCD-A1B1C1D1的长、宽、高分别为2，2，1，其顶点都在球O的球面上，则球O的表面积为.5.已知正四棱柱(底面为正方形且侧棱与底面垂直的棱柱)的底面边长为3，侧棱长为4，则其外接球的表面积为.6.在四面体S-ABC中，SA⊥平面ABC，三内角B，A，C成等差数列，SA=AC=2，AB=1，则该四面体的外接球的表面积为.7.如图，在△ABC中，AB=AC=3，cos∠BAC=-13，D是棱BC的中点，以AD为折痕把△ACD折叠，使点C到达点C 的位置，则当三棱锥C -ABD体积最大时，其外接球的表面积为.8.在三棱锥P-ABC中，点A在平面PBC中的投影是△PBC的垂心，若△ABC是等腰直角三角形且AB=AC=1，PC=3，则三棱锥P-ABC的外接球表面积为9.已知三棱锥S-ABC的三条侧棱SA,SB,SC两两互相垂直且AC=13,AB=5，此三棱锥的外接球的表面积为14π，则BC=．10.三棱锥P-ABC中，PA⊥平面ABC，直线PB与平面ABC所成角的大小为30°，AB=23，∠ACB=60°，则三棱锥P-ABC的外接球的表面积为．题型二：对棱相等模型1.在正四面体A-BCD中，E是棱AD的中点，P是棱AC上一动点，BP+PE的最小值为7，则该正四面体的外接球的体积是( )A.6πB.6πC.3632π D.3 2π2.四面体P-ABC的一组对棱分别相等，且长度依次为25，13，5，则该四面体的外接球的表面积为( )A.294πB.28πC.29296π D.29π3.在三棱锥P-ABC中，PA=BC=4，PB=AC=5，PC=AB=11，则三棱锥P-ABC的外接球的表面积为( )A.26πB.12πC.8πD.24π4.在三棱锥P-ABC中，PA=BC=3，PB=AC=2，PC=AB=5，则三棱锥P-ABC外接球的体积为( )A.2πB.3πC.6πD.6π5.正四面体的各条棱长都为2，则该正面体外接球的体积为________．6.在三棱锥A-BCD中，AB=CD=2，AD=BC=3，AC=BD=4，则三棱锥A−BCD外接球的表面积为________．7.在三棱锥A-BCD中，AB=CD=6，AC=BD=AD=BC=5，则该三棱锥的外接球的体积为．8.已知三棱锥A-BCD，三组对棱两两相等，且AB=CD=1，AD=BC=3，若三棱锥A-BCD的外接球表面积为9π2，则AC=．9.在四面体ABCD中，AD=AC=BC=BD，AB=CD=42，球O是四面体ABCD的外接球，过点A作球O的截面，若最大的截面面积为9π，则四面体ABCD的体积是．变式演练1.表面积为83的正四面体的外接球的表面积为( )A.43πB.12πC.8πD.46π2.正四面体ABCD中，E是棱AD的中点，P是棱AC上一动点，BP+PE的最小值为14，则该正四面体的外接球表面积是( )A.12πB.32πC.8πD.24π3.蹴鞠(如图所示)，又名蹴球，蹴圆，筑球，踢圆等，蹴有用脚蹴、踢、蹋的含义，鞠最早系外包皮革、内实米糠的球．因而蹴鞠就是指古人以脚蹴，蹋、踢皮球的活动，类似今日的足球．2006年5月20日，蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录，已知某鞠的表面上有四个点A，B，C，D，满足AB=CD=5，BD=AC=6，AD=BC=7，则该鞠的表面积为( )A.55πB.60πC.63πD.68π4.已知正四面体ABCD的外接球的体积为86π，则这个四面体的表面积为________．5.已知四面体ABCD满足AB=CD=6，AC=AD=BC=BD=2，则四面体ABCD的外接球的表面积是________．6.三棱锥中S-ABC，SA=BC=13，SB=AC=5，SC=AB=10．则三棱锥的外接球的表面积为______.7.已知一个四面体ABCD的每个顶点都在表面积为9π的球O的表面上，且AB=CD=a，AC= AD=BC=BD=5，则a=________.8.在三棱锥P-ABC中，若PA=PB=BC=AC=5，PC=AB=42，则其的外接球的表面积为 ．9.已知在四面体ABCD中，AB=CD=22,AD=AC=BC=BD=5，则四面体ABCD的外接球表面积为 ．10.若四面体ABCD中，AB=CD=BC=AD=5，AC=BD=2，则四面体的外接球的表面积为．11.在三棱锥P-ABC中，PA=BC=5，PB=AC=17，PC=AB=10，则该三棱锥外接球的表面积为；外接球体积为．12.在四面体ABCD中，AC=BD=2，AD=BC=5，AB=CD=7，则其外接球的表面积为.题型三：斗笠模型1.已知在高为2的正四棱锥P-ABCD中，AB=2，则正四棱锥P-ABCD外接球的体积为()A.4πB.9π2C.27π4D.8π32.正三棱锥P-ABC底面边长为2，M为AB的中点，且PM⊥PC，则三棱锥P-ABC外接球的体积为()A.32π3B.6πC.6πD.82π33.在三棱锥P-ABC中，PA=PB=PC=5，AB=AC=BC=3，则三棱锥P-ABC外接球的表面积是()A.9πB.152πC.4πD.254π4.已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB= BC=AC=OO1，则球O的表面积为( )A.64πB.48πC.36π D.32π5.在三棱锥P -ABC 中，PA =PB =PC =2，AB =AC =1，BC =3，则该三棱锥外接球的体积为( )A.4π3 B.823π C.43π D.323π6.正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4B.16πC.9πD.27π47.正三棱锥P -ABC 底面边长为2，M 为AB 的中点，且PM ⊥PC ，则三棱锥P -ABC 外接球的体积为()A.32π3B.6πC.6πD.82π38.已知一个圆锥的底面面积为3π，侧面展开图是半圆，则其外接球的表面积等于.9.一个圆锥恰有三条母线两两夹角为60°，若该圆锥的侧面积为33π，则该圆锥外接球的表面积为________．10.如图所示，在正四棱锥P -ABCD 中，底面ABCD 是边长为4的正方形，E ，F 分别是AB ，CD 的中点，cos ∠PEF =22，若A ，B ，C ，D ，P 在同一球面上，则此球的体积为．11.在三棱锥P -ABC 中，PA =PB =PC =26,AC =AB =4，且AC ⊥AB ，则该三棱锥外接球的表面积为．变式演练1.某圆锥的侧面展开后，是一个圆心角为23π的扇形，则该圆锥的体积与它的外接球的体积之比为()A.243256B.128243C.128729D.2567292.已知圆锥的顶点和底面圆周都在球O 的球面上，圆锥的母线长为3，侧面展开图的面积为3π，则球O 的表面积等于()A.81π8B.81π2C.121π8D.121π23.已知一个圆锥的底面圆面积为3π，侧面展开图是半圆，则其外接球的表面积等于()A.12πB.16πC.36πD.48π4.已知圆锥的顶点和底面圆周都在球O 面上，圆锥的侧面展开图的圆心角为2π3，面积为3π，则球O 的表面积等于()A.81π8B.81π2C.121π8D.121π25.已知一个圆锥的底面半径为2，高为3，其体积大小等于某球的表面积大小，则此球的体积是()A.43πB.833π C.4πD.4π36.两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为32π3，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为()A.3πB.4πC.9πD.12π7.在三棱锥P -ABC 中，PA =PB =PC =3，侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为( )A.πB.π3C.4π D.4π38.在三棱锥P -ABC 中，PA =PB =PC =6，AC =AB =2，且AC ⊥AB ，则该三棱锥外接球的表面积为( )A.4π B.8π C.16π D.9π9.已知体积为3的正三棱锥P -ABC 的外接球的球心为O ，若满足OA +OB +OC =0 ，则此三棱锥外接球的半径是( )A.2 B.2 C.32 D.3410.已知正四棱锥P -ABCD 的各顶点都在同一球面上，底面正方形的边长为2，若该正四棱锥的体积为2，则此球的体积为( )A.124π3 B.625π81 C.500π81D.256π911.已知在高为2的正四棱锥P -ABCD 中，AB =2，则正四棱锥P -ABCD 外接球的体积为()A.4πB.9π2C.27π4D.8π312.设圆锥的顶点为A ，BC 为圆锥底面圆O 的直径，点P 为圆O 上的一点(异于B 、C )，若BC =43，三棱锥A -PBC 的外接球表面积为64π，则圆锥的体积为.13.已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°，若ΔSAB的面积为8，则该圆锥外接球的表面积是．14.在六棱锥P-ABCDEF中，底面是边长为2的正六边形，PA=2且与底面垂直，则该六棱锥外接球的体积等于．题型四：汉堡模型1.已知正三棱柱的高与底面边长均为2，则该正三棱柱内半径最大的球与其外接球的表面积之比为()A.17B.77C.37D.2172.已知三棱锥P-ABC的四个顶点都在球O的表面上，PA⊥平面ABC，AB⊥BC且PA=8，AC=6，则球O的表面积为()A.10πB.25πC.50πD.100π3.三棱锥P-ABC中，PA⊥平面ABC，∠ABC=30°，ΔAPC的面积为3，则三棱锥P-ABC的外接球体积的最小值为()A.323π3 B.43π3 C.86π D.326π4.已知四棱锥P-ABCD的顶点都在球O的球面上，PA⊥底面ABCD，AB=AD=1，BC= CD=2，若球O的表面积为9π，则四棱锥P-ABCD的体积为()A.4B.43C.25D.2535.已知三棱锥A-BCD的所有顶点都在球O的球面上，且AB⊥平面BCD，AB=2，CD=2，AC=AD=5，则球O的表面积为()A.6πB.2πC.3πD.6π6.已知边长为3的正△ABC的顶点和点D都在球O的球面上.若AD=6，且AD⊥平面ABC，则球O的表面积为()A.323πB.48πC.24πD.12π7.已知各顶点都在同一球面上的正四棱柱的底面边长为a，高为h，球的体积为86π，则这个正四棱柱的侧面积的最大值为()A.482B.242C.962D.1228.(多选题)在四面体ABCD中，AB⊥AC，AC⊥CD，直线AB，CD所成的角为60°，AB=CD =43，AC=4，则四面体ABCD的外接球表面积为()A.16053π B.52π C.80π D.208π9.已知四棱锥P-ABCD的五个顶点都在球O的球面上，PA⊥平面ABCD，底面ABCD是高为12的等腰梯形，AD⎳BC，AD=PA=1，BC=2，则球О的表面积为()A.10πB.4πC.5πD.6π10.已知正三棱柱ABC-A1B1C1中，底面积为334，一个侧面的周长为63，则正三棱柱ABC-A1B1C1外接球的表面积为( )A.4πB.8πC.16πD.32π11.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的表面上，若AB=AC=1，AA1=23，∠BAC=2π3，则球O的体积为( )A.32π3B.3πC.4π3D.8π12.在四棱锥P-ABCD中，已知PA⊥底面ABCD,AB⊥BC,AD⊥CD，且∠BAD=120°,PA=设直三棱柱ABC-A1B1C1的所有顶点都在一个球面上，且球的体积是4010π3，AB=AC=AA1，∠BAC=120°，则此直三棱柱的高是______．变式演练1.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上．若AB=3，AC=4，AB⊥AC，AA1=12，则球O的半径为( )．A.3172 B.210 C.132D.3102.设三棱柱的侧棱垂直于底面，所有棱长都为a，顶点都在一个球面上，则该球的表面积为( )．A.πa2B.73πa2C.113πa2D.37πa23.直三棱柱ABC-A1B1C1的各顶点都在同一球面上，若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于( )．A.10πB.20πC.30πD.40π4.已知圆柱的高为2，底面半径为3，若该圆柱的两个底面的圆周都在同一个球面上，则这个球的表面积等于( )A.4πB.16π3C.32π3D.16π5.若一个圆柱的表面积为12π，则该圆柱的外接球的表面积的最小值为( )A.(125-12)πB.123πC.(123+3)πD.16π6.一直三棱柱的每条棱长都是2，且每个顶点都在球O的表面上，则球O的表面积为( )A.28π3B.22π3 C.43π3 D.7π7.已知三棱锥P-ABC的四个顶点都在球O的表面上，PA⊥平面ABC，AB⊥BC且PA=8，AC=6，则球O的表面积为()A.10πB.25πC.50πD.100π8.已知四棱锥P-ABCD的顶点都在球O的球面上，PA⊥底面ABCD，AB=AD=1，BC=CD =2，若球O的表面积为9π，则四棱锥P-ABCD的体积为()A.4B.43C.25D.2539.有一个圆锥与一个圆柱的底面半径相等，此圆锥的母线与底面所成角为60°,若此圆柱的外接球的表面积是圆锥的侧面积的4倍，则此圆柱的高是其底面半径的( )A.2倍B.2倍C.22倍D.3倍10.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=1，∠BAC=60°，AA1=2，则该三棱柱的外接球的体积为( )A.40π3B.4030π27 C.32030π27 D.20π11.三棱锥P-ABC中，PA⊥平面ABC，∠ABC=30°，ΔAPC的面积为3，则三棱锥P-ABC的外接球体积的最小值为()A.323π3 B.43π3 C.86π D.326π12.在直三棱柱ABC-A1B1C1中，若AB⊥BC,AB=6,BC=8,AA1=6，则该直三棱柱外接球的表面积为( )A.72πB.114πC.136πD.144π13.设直三棱柱ABC-A1B1C1的所有顶点都在一个球面上，AB=AC=AA1，∠BAC=120°，且底面△ABC的面积为23，则此直三棱柱外接球的表面积是( )A.16πB.4010π3 C.40π D.64π14.已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的表面积为( )A.36πB.144πC.169πD.256π题型五：垂面模型1.已知在三棱锥S-ABC中，SA⊥平面ABC，且∠ACB=30°，AC=2AB=23，SA=1．则该三棱锥的外接球的体积为( )A.13813πB.13πC.136πD.13136π2.三棱锥P-ABC中，平面PAC⊥平面ABC，AB⊥AC，PA=PC=AC=2，AB=4，则三棱锥P-ABC的外接球的表面积为( )A.23πB.234πC.64πD.643π3.在三棱锥S-ABC中，侧棱SA⊥底面ABC，AB=5，BC=8，∠ABC=60°，SA=25，则该三棱锥的外接球的表面积为( )A.643πB.2563πC.4363πD.2048327π4.在三棱锥P-ABC中，已知PA⊥底面ABC，∠BAC=120˚，PA=AB=AC=2，若该三棱锥的顶点都在同一个球面上，则该球的表面积为( )A.103πB.18πC.20πD.93π5.已知三棱锥P-ABC中，PA⊥平面ABC，BC⊥平面PAB，若AB=BC=1，PA=2，则此三棱锥的外接球的表面积为( )A.24πB.8πC.6πD.8π36.《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马．若四棱锥P-ABCD为阳马，底面ABCD为矩形，PA⊥平面ABCD，AB=2，AD=4，二面角P-BC-A为60°，则四棱锥P-ABCD的外接球的表面积为( )A.16πB.20πC.643πD.32π7.三棱锥S-ABC中，SA⊥底面ABC，若SA=AB=BC=AC=3，则该三棱锥外接球的表面积为( )A.18πB.21π2C.21πD.42π8.四面体ABCD的四个顶点都在球O的表面上，AB⊥平面BCD，△BCD是边长为3的等边三角形，若AB=2，则球O的表面积为( )A.4πB.12πC.16πD.32π9.在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=120°，AC=2，AB=1，设D为BC中点，且直线PD与平面ABC所成角的余弦值为55，则该三棱锥外接球的表面积为________．10.中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知PA⊥平面ABCE，四边形ABCD为正方形，AD=5，ED=3，若鳖臑P-ADE的外接球的体积为92π，则阳马P-ABCD的外接球的表面积为________．11.我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”，现有一“阳马”如图所示，PA⊥平面ABCD，PA=4，AB=3，AD=1，则该“阳马”外接球的表面积为．12.如图，在三棱锥P-ABC中，PA⊥平面ABC，∠ABC=120°，PA=4．若三棱锥P-ABC外接球的半径为22，则直线PC与平面ABC所成角的正切值为．13.如图，在三棱锥P-ABC中，PA⊥平面ABC，PA=4，cos∠ACB=13，若三棱锥P-ABC外接球的表面积为52π，则三棱锥P-ABC体积的最大值为．变式演练1.已知三棱锥S-ABC的所有顶点都在球O的球面上，SA⊥平面ABC，SA=23，AB=1，AC =2，∠BAC=60°，则球O的表面积为( )A.4πB.12πC.16πD.64π2.在三棱锥P-ABC中，已知PA⊥底面ABC，∠BAC=60°，PA=2，AB=AC=3，若该三棱锥的顶点都在同一个球面上，则该球的表面积为( )A.4π3B.82π3 C.8πD.12π3.如图，在△ABC中，AB=BC=6，∠ABC=90°，点D为AC的中点，将△ABD沿BD折起到△PBD的位置，使PC=PD，连接PC，得到三棱锥P-BCD，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是( )A.7πB.5πC.3πD.π4.已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为23的正方形．若PA=26，则△OAB的面积为( )．A.3B.22C.33D.635.在三棱锥S-ABC中，SA⊥平面ABC，SA=4，底面ΔABC是边长为3的正三角形，则三棱锥S-ABC的外接球的表面积为( )A.19πB.28πC.43πD.76π6.三棱锥P-ABC中，PA⊥平面ABC且PA=2，ΔABC是边长为3的等边三角形，则该三棱锥外接球的表面积为( )A.4π3B.4πC.8πD.20π7.三棱锥P-ABC中，AB=BC=15，AC=6，PC⊥平面ABC，PC=2，则该三棱锥的外接球表面积为( )A.253πB.252πC.833πD.832π8.在三棱锥S-ABC中，侧棱SC⊥平面ABC，SA⊥BC，SC=1，AC=2，BC=3，则此三棱锥的外接球的表面积为( )A.14πB.12πC.10πD.8π9.在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=60°,AB=AC=23,PA=2，则三棱锥P-ABC的外接球的表面积为( )A.20πB.24πC.28πD.32π10.三棱锥P-ABC中，PA⊥平面ABC，BC⊥CA，AC=1，BC=2，PA=2，则该三棱锥外接球的表面积为( )A.9πB.36πC.92πD.94π11.三棱锥P-ABC中，AB=BC=15，AC=6，PC⊥平面ABC，PC=2，则该三棱锥的外接球表面积为________．12.已知三棱锥S-ABC中，SA⊥平面ABC，SA=AB=4，BC=6，AC=213，则三棱锥S-ABC外接球的表面积为．13.已知四面体P-ABC中，PA=PB=4，PC=2，AC=25，PB⊥平面PAC，则四面体P-ABC外接球的表面积为．14.在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=120°，AC=2，AB=1，设D为BC中点，且直线PD与平面ABC所成角的余弦值为55，则该三棱锥外接球的表面积为．15.在四棱锥P-ABCD中，PA⊥平面ABCD，AP=2，点M是矩形ABCD内(含边界)的动点，且AB=1，AD=3，直线PM与平面ABCD所成的角为π4．记点M的轨迹长度为α，则tanα= ；当三棱锥P-ABM的体积最小时，三棱锥P-ABM的外接球的表面积为．题型六：切瓜模型1.在矩形ABCD中，AB=4,BC=3，沿AC将矩形ABCD折成一个直二面角B-AC-D，则四面体ABCD的外接球的体积为()A.12512πB.1259πC.1256πD.1253π2.已知三棱锥A-BCD中，△ABD与△BCD是边长为2的等边三角形且二面角A-BD-C为直二面角，则三棱锥A-BCD的外接球的表面积为( )A.10π3B.5πC.6πD.20π33.已知三棱锥A-BCD中，CD=22，BC=AC=BD=AD=2，则此几何体外接球的表面积为。
高考数学专题突破：外接球题型总结
高考数学专题突破：外接球模型模板一：222)2(r h R += 即422r h R +=一、题型描述几何体的外接球问题：题目中涉及几何体外接球体，或者球内接几何体，再或者说成球面上有几个点围成几何体，这类题型称之为几何体的外接球问题。
二、模法讲解以下这幅图，大家应该都能看明白吧！一个底面半径为，高为的圆柱，求它的外接球半径。
那么问题来了？422r h R +=这个式子怎么来的。
那么这个式子有何妙用？1、如果我们对圆柱上下底面对应位置处，取相同数量的点，比如都取三个点，如图所示：我们可以得到（直）三棱柱，它的外接球其实就是这个圆柱的外接球，所以说直棱柱的外接球求半径符合这个模型。
在这里棱柱的高就是公式中h的，而棱柱底面外接圆的半径则是公式中的r（至于怎么求外接圆半径可以用正弦定理。
2、我们再继续进行，如果我把刚刚那个三棱柱上面的两点去掉，我将得到三棱锥，如图：这个三棱锥的特点是AA1⊥底面ABC，即有一根侧棱⊥底面的锥体，依然符合这个模型。
那条竖直棱AA1就是公式中的h，而底面ABC的外接圆半径是公式中的r。
3、题目还喜欢这么干：面PAD垂直面ABCD。
它非常符合圆柱外接球模型！我们知道，这里的r为PAD的外接圆半径，h为AB或者CD为的长。
接着看，当我对第二幅图中的三棱柱 ABC-A1B1C1只去掉C1这个点，会得到什么呢？没错！这就是刚刚那个四棱锥放倒了！它的特点是：底面A1B1AB⊥CAB侧面，出题的时候则不会这么仁慈，就会像上一幅图那样，有一个侧面⊥矩形底面的四棱锥！圆柱外接球模型——适用于：①圆柱-------r,h自带②直棱柱-------r:底面外接圆半径；h:直棱柱的高③一根侧棱⊥底面的锥体-------r:底面外接圆半径；h:垂直于底面的那条侧棱④一个侧面⊥矩形底面的四棱锥-------r:垂直底面的侧面的外接圆半径；h:垂直于那个侧面的底边长那么接下来第二步就是找到，求出，而又怎么求呢？用正弦定理。
高考数学中的内切球和外接球问题---专题复习
高考数学中的内切球和外接球问题---专题复习高考数学：内切球和外接球问题多面体的顶点都在同一球面上时，称该多面体为球的内接多面体，该球为多面体的外接球。
多面体外接球问题是立体几何的重点，也是高考的热点，考查学生的空间想象能力和化归能力。
解决该问题需要运用多面体和球的知识，并特别注意多面体的几何元素与球的半径之间的关系。
多面体外接球半径的求法在解题中往往起到至关重要的作用。
一、直接法（公式法）1、求正方体的外接球的有关问题例1：若正方体的棱长为3且顶点都在同一球面上，求该球的表面积。
解析：要求球的表面积，只需知道球的半径。
由于正方体内接于球，所以它的体对角线正好为球的直径，因此求球的半径可转化为先求正方体的体对角线长，再计算半径。
故表面积为27π。
例2：一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体积为多少？解析：要求球的体积，还需先求出球的半径。
由正方体表面积可求出棱长，从而求出正方体的体对角线长为3√3.因此，该球的半径为3，故该球的体积为36π。
2、求长方体的外接球的有关问题例1：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1、2、3，则该球的表面积为多少？解析：关键是求出球的半径，因为长方体内接于球，所以它的体对角线正好为球的直径。
长方体体对角线长为√14，故球的表面积为14π。
例2：已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则该球的表面积为多少？解析：正四棱柱也是长方体。
由长方体的体积16及高4可以求出长方体的底面边长为2，因此，长方体的长、宽、高分别为2、2、4.故该球的表面积为24π。
3、求多面体的外接球的有关问题例：一个底面为正六边形的六棱柱，侧棱垂直于底面，已知该六棱柱的顶点都在同一球面上，且该六棱柱的体积为8，底面周长为3，则该球的体积为多少？解析：设正六棱柱的底面边长为x，高为h。
由底面周长可得x=3/6=1/2，由体积可得h=4/3.因此，正六棱柱的底面圆的半径为√3/2，外接球的半径为√13/2.故该球的体积为(52/3)π。
高考数学专题突破：外接球和内切球问题【解析版】
高考数学专题突破：外接球模型模板一：222)2(r h R += 即422r h R +=一、题型描述几何体的外接球问题：题目中涉及几何体外接球体，或者球内接几何体，再或者说成球面上有几个点围成几何体，这类题型称之为几何体的外接球问题。
二、模法讲解以下这幅图，大家应该都能看明白吧！一个底面半径为，高为的圆柱，求它的外接球半径。
那么问题来了？422r h R +=这个式子怎么来的。
那么这个式子有何妙用？1、如果我们对圆柱上下底面对应位置处，取相同数量的点，比如都取三个点，如图所示：我们可以得到（直）三棱柱，它的外接球其实就是这个圆柱的外接球，所以说直棱柱的外接球求半径符合这个模型。
在这里棱柱的高就是公式中h 的，而棱柱底面外接圆的半径则是公式中的r （至于怎么求外接圆半径可以用正弦定理。
2、我们再继续进行，如果我把刚刚那个三棱柱上面的两点去掉，我将得到三棱锥，如图：这个三棱锥的特点是AA1⊥底面ABC，即有一根侧棱⊥底面的锥体，依然符合这个模型。
那条竖直棱AA1就是公式中的h，而底面ABC的外接圆半径是公式中的r。
3、题目还喜欢这么干：面PAD垂直面ABCD。
它非常符合圆柱外接球模型！我们知道，这里的r为PAD的外接圆半径，h为AB或者CD为的长。
接着看，当我对第二幅图中的三棱柱 ABC-A1B1C1只去掉C1这个点，会得到什么呢？没错！这就是刚刚那个四棱锥放倒了！它的特点是：底面A1B1AB⊥CAB侧面，出题的时候则不会这么仁慈，就会像上一幅图那样，有一个侧面⊥矩形底面的四棱锥！圆柱外接球模型——适用于：①圆柱-------r,h自带②直棱柱-------r:底面外接圆半径；h:直棱柱的高③一根侧棱⊥底面的锥体-------r:底面外接圆半径；h:垂直于底面的那条侧棱④一个侧面⊥矩形底面的四棱锥-------r:垂直底面的侧面的外接圆半径；h:垂直于那个侧面的底边长那么接下来第二步就是找到，求出，而又怎么求呢？用正弦定理。
【高考数学】外接球问题
专题1外接球问题一、单选题1．在三棱锥S ABC -中，2,1SA SB AC BC SC =====，二面角S AB C --的大小为60︒，则三棱锥S ABC -的外接球的表面积为（ ）A ．43π B ．4π C ．12π D ．523π2．在四面体S —ABC 中，AB BC AB BC SA SC 2⊥====，，二面角S —AC —B的余弦值是 （ ）A ．BC ．24πD ．6π3．有一个长方形木块，三个侧面积分别为8，12，24，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为（ ）A ．2B ．C ．4D ．4．三棱锥P ABC -的四个顶点都在球O 上，PA ⊥平面ABC ，2PA =，4AB =，2AC =，BC = ）A ．16πB ．20πC ．24πD ．28π5．已知三棱锥S ABC -，SC 的中点O 为三棱锥S ABC -外接球球心，且SC ⊥平面OAB ，OA AB =，则球O 的体积为（ ）A ．36πB ．43π C ．323π D ．92π6．已知球的直径SC ＝2，A ，B 是该球球面上的两点，AB ＝1，∠ASC ＝∠BSC ＝45°，则棱锥S ABC -的体积为( )AB C D ．67．在四棱锥P ABCD -中，PA ⊥平面ABC ，ABC ∆中，3BA BC AC ===，2PA =，则三棱锥P ABC -的外接球的表面积为( )A ．B ．22πC ．12πD ．20π8．正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且12EF =，则 AC BE ⊥①；//EF ②平面ABCD ；③三棱锥B AEF -的体积是定值；AEF ④的面积和BEF 的面积相等．以上命题中正确的是( ) A ．①②B ．①②④C ．①②③D ．①③④9．在三棱锥P ABC -中，已知PA ⊥底面ABC ，60BAC ∠=，2PA =，AB AC ==若该三棱锥的顶点都在同一个球面上，则该球的表面积为（ ）A ．43πB ．3C ．8πD ．12π10．已知正方体的棱长为1，平面α过正方体的一个顶点，且与正方体每条棱所在直线所成的角相等，则该正方体在平面α内的正投影面积是（ ）A B CD 11．如图，11,AA BB 均垂直于平面ABC 和平面111111,90A B C BAC A B C ∠=∠=，111AC AB A A BC ====111ABC A B C -的外接球的表面积为( )A ．2πB ．4πC ．6πD ．8π12．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为（ ）A B C D 13．在三棱锥P ABC -中，AB BC ⊥，P 在底面ABC 上的投影为AC 的中点D ，1DP DC ==.有下列结论：①三棱锥P ABC -的三条侧棱长均相等；②PAB ∠的取值范围是,42ππ⎛⎫⎪⎝⎭；③若三棱锥的四个顶点都在球O 的表面上，则球O 的体积为23π；④若AB BC =，E 是线段PC 上一动点，则DE BE +的最小值为2. 其中所有正确结论的编号是（ ） A ．①②B ．②③C ．①②④D ．①③④14．已知四棱锥S ABCD -的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥体积取得最大值时，其表面积等于2+O 的体积等于（ ） A ．43πB ．83π C ．163πD ．223π15．如图，正三棱锥S ABC -中，30BSA ︒∠=，2SB =，一质点自点B 出发，沿着三棱锥的侧面绕行一周回到点B 的最短路线的长为( )A ．2B ．4C ．D ．16．已知三棱锥P −ABC 的四个顶点均在半径为1的球面上，且满足PA ⃗⃗⃗⃗⃗ ⋅PB ⃗⃗⃗⃗⃗ =0，PB ⃗⃗⃗⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =0，PC⃗⃗⃗⃗⃗ ⋅PA ⃗⃗⃗⃗⃗ =0，则三棱锥P −ABC 的侧面积的最大值为（ ）A ．12B ．1C ．2D ．417．设球O 与圆锥1SO 的体积分别为1V ，2V ，若球O 的表面积与圆锥1SO 的侧面积相等，且圆锥1SO 的轴截面为正三角形，则12V V 的值是（ ） ABCD18．网络用语“车珠子”，通常是指将一块原料木头通过加工打磨，变成球状珠子的过程，某同学有一圆锥状的木块，想把它“车成珠子”，经测量，该圆锥状木块的底面直径为12cm ，体积为396cm π，假设条件理想，他能成功，则该珠子的体积最大值是（ ）. A ．336cm π B ．312cm πC ．39cm πD ．372cm π第II 卷（非选择题)请点击修改第II 卷的文字说明二、填空题19．已知正四面体ABCD 的棱长为2，E 为棱AB 的中点，过E 作其外接球的截面，则截面面积的最小值为__________．20．已知四棱锥P ﹣ABCD 的顶点都在球O 的球面上，底面ABCD 是边长为2的正方形，且P A ⊥面ABCD ，若四棱锥的体积为163，则该球的体积为_____． 21．如图，四棱锥P ABCD -中，PA ABCD ⊥平面，四边形ABCD 为正方形，2PA AB ==，四棱锥P ABCD -的五个顶点都在一个球面上，则这个球的表面积是 ．22．如图，正方体1111ABCD A B C D -的棱长为2，点P 在正方形ABCD 的边界及其内部运动，平面区域W由所有满足1A P ≥P 组成，则W 的面积是__________．23．已知菱形ABCD 的边长为4，且∠BAD ＝60°，将△ABD 沿BD 折起，使A 、C 两点之间的距离为4，则所得三棱锥的外接球的表面积为_____．24．设地球的半径为R ，地球上A ，B 两地都在北纬45︒的纬度线上，且其经度差为90︒，则A ，B 两地的球面距离是________.25．圆锥SD （其中S 为顶点，D 为底面圆心）的侧面积与底面积的比是2:1，则圆锥SD 与它的外接球（即顶点在球面上且底面圆周也在球面上）的体积比为__________．26．已知四面体ABCD 内接于球O ，且2AB BC AC ===，若四面体ABCD 的体积，球心O 恰好在棱DA 上，则球O 的表面积是_____． 27．如图，正方体1111ABCD A B C D -的棱长为1，,E F 分别为11,AA CC 的中点，过直线EF 的平面分别与棱11,BB DD 交于点,M N .设,[0,1]=∈BM x x ，给出以下四个结论：①平面MENF ⊥平面11BDD B ； ②当且仅当12x =时，四边形MENF 的面积最小； ③四边形MENF 的周长(),[0,1]=∈L f x x 是单调函数； ④四棱锥1-C MENF 的体积是定值.其中正确结论的序号为______（请写出所有正确结论的序号）．28．如图，已知正方体1111A B C D ABCD -的棱长为a ，点P 为线段1BC 上一点，Q 是平面ABCD 上一点，则1D P PQ +的最小值是______．29．已知等腰△ABC 的面积为4，AD 是底边BC 上的高，沿AD 将△ABC 折成一个直二面角，则三棱锥A 一BCD 的外接球的表面积的最小值为______。
2022年高考数学基础题型重难题型突破类型五 空间几何外接球(解析版)
2022年高考数学基础题型重难题型突破类型五空间几何外接球1.已知在三梭锥A BCD -中，2AB CD ==，3AD AC BC BD ====，则该三棱锥内切球的体积为（）A．64B．6C．3D．1922.在四棱锥P ABCD -中，已知PA ⊥底面,,ABCD AB BC AD CD ⊥⊥，且120,2BAD PA AB AD ∠=︒===，则该四棱锥外接球的体积为（）A．B．203πC．3πD．3.已知三棱锥P ABC ﹣的四个顶点都在球O 的表面上，PA ⊥平面ABC ，AB BC ⊥且8PA =，6AC =，则球O 的表面积为（）A．10πB．25πC．50πD．100π4.半球内有一个内接正方体，则这个半球的体积与正方体的体积之比为()A.5π∶6B.6π∶2C．π∶2D．5π∶125.已知四棱锥P ABCD -的顶点都在球O 的球面上，PA ⊥底面ABCD ，1AB AD ==，2BC CD ==，若球O 的表面积为9π，则四棱锥P ABCD -的体积为（）A．4B．43C．D．2536.已知在三棱锥S－ABC 中，AB⊥BC，AB＝BC＝2，SA＝SC＝22，二面角B－AC－S 的大小为2π3，则三棱锥S－ABC 的外接球的表面积为()A.124π9B.105π4C.105π9D.104π97.在三棱锥P ABC -中，PA PB PC ===AB AC BC ===，则三棱锥P ABC -外接球的表面积是（）A．9πB．15π2C．4πD．25π48.正四棱锥的顶点都在同一球面上．若该棱锥的高为4，底面边长为2，则该球的表面积为()A.81π4B．16πC．9πD.27π49.在四面体ABCD 中，AB AC ⊥，AC CD ⊥，直线AB ，CD 所成的角为60°，AB CD ==，4AC =，则四面体ABCD 的外接球表面积为（）A．π3B．52πC．80πD．208π10.在三棱锥P ABC -中，PAC △是等边三角形，平面PAC ⊥平面,ABC AB AC ==，60CAB ∠= ，则三棱锥P ABC -的外接球体积为（）A．43πB．3C．323πD．311.在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是。
【帮帮群】高考数学专题08 破译空间中有关外接球的问题
一、选择题1．如图中的三个直角三角形是一个体积为320cm 的几何体的三视图，则该几何体外接球的面积（单位：2cm ）等于()．A ．55πB ．75πC ．77πD ．65π【答案】C 【解析】2．已知三棱锥P ABC -的三条侧棱两两互相垂直，且5,7,2AB BC AC ===，则此三棱锥的外接球的体积为（）A ．83πB ．823πC ．163πD ．323π【答案】B【解析】由题意可知：可将三棱锥放入长方体中考虑，则长方体的外接球即三棱锥的外接球，故球的半径为长方体体对角线的一半，设PA x =，则2222275471PB PC BC x x x +==⇒-+-=⇒=，故2221231,2,322PA PB PC R ++===⇒==，得球的体积为：348233R ππ=3．三棱锥A BCD -内接于半径为2的球O ，BC 过球心O ，当三棱锥A BCD -体积取得最大值时，三棱锥A BCD -的表面积为A ．63+B ．823+C ．43+D ．83+【答案】D4．已知△ABC 的顶点都在半径为R 的球O 的球面上，球心O 到平面ABC 的距离为32R ，3AB BC AC ===，则球O 的体积是（）A ．163πB ．16πC ．323πD ．32π【答案】C【解析】ABC ∆是等边三角形，所以球心O 在底面的射影是ABC ∆的中心'O ，点'OO A 是直角三角形，满足222312R R ⎛⎫=+ ⎪ ⎪⎝⎭，解得：24R =，2R =，所以343233V R ππ==，故选C ．【点睛】本题考查了球与几何体的组合体问题，考查了空间想象能力以及计算能力，球心与截面圆的圆心连线垂直于截面，所以很多求球心问题，可先找底面多边形的外接圆的圆心，过圆心垂直于多边形的直线必过球心，然后再利用球心到所有顶点的距离相等的性质和构造直角三角形求球的半径．5．已知三棱锥—P ABC 的四个顶点均在同一个球面上，底面ABC ∆满足6BA BC ==，π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（）A ．8πB ．16πC ．16π3D ．32π3【答案】D【解析】6．正四面体ABCD的棱长为4，E为棱AB的中点，过E作此正四面体的外接球的截面，则截面面积的最小值是（）A．4πB．8πC．12πD．16π【答案】A【解析】将四面体ABCD放置在正方体中，如图所示，可得正方体的外接球就是四面体ABCD的外接球，因为正四面体ABCD的棱长为4，所以正方体的棱长为，可得外接球的半径满足2R==，即R=，又E为BC的中点，过E作其外接球的截面，当截面到球心O的距离最大时，此时截面圆的面积最小，此时球心O到截面的距离等于正方体r==，得到截面圆的面积的最小值为棱长的一半，可得截面圆的半径为224==，故选AS rππ二、单选题7．若一个正三棱柱存在外接球与内切球，则它的外接球与内切球表面积之比为A .3：1B .4：1C .5：1D .6：1【答案】选C8．在正四棱锥S -ABCD 中，侧面与底面所成的角为3π，则它的外接球半径R 与内切球半径r 之比为（）A .5B .32C .10D .52【答案】D【解析】由于侧面与底面所成角为，可知底面对边中心线与两个对面斜高构成正三角形，设底面边长为a ，则斜高也为a ，进而可得侧棱长为：，高为四棱锥的内切球半径就是上述正三角形的内切圆半径为，其外接球球心必在顶点与底面中心连线上，如图：半径为R ，球心为O ，顶点为P ，底面中心为O 1，底面一个顶点为B ，则OB =OP ，于是就有：（﹣R ）2+（）2=R 2解得R =．所以两者的比为：．故选D三、填空题9．已知,,,A B C D 是球面上不共面的四点，AB AC BD CD BC =====，平面ABC ⊥平面BCD ，则此球的体积为_________．【答案】823π10．直角ABC 的三个顶点都在球O 的球面上，2AB AC ==，若球O 的表面积为12π，则球心O 到平面ABC 的距离等于__________．[【答案】1【解析】直角ABC 的斜边CB 为ABC 所在截面小圆的直径，则该截面小圆的半径为2r =，由球的表面积为12π可得球的半径3R =，球心O 到平面ABC 的距离221d R r =-=．11．在三棱锥中，侧棱两两垂直，的面积分别为，则三棱锥的外接球的体积为_______.【答案】考点：球与几何体【方法点睛】球与几何体的问题，属于中档题型，当条件为三棱锥有同一顶点的三条棱两两垂直时，可联想到长方体，这样的三棱锥就是长方体的一部分，如图所示，此时三棱锥的外接球就是长方体的外接球，而长方体的外接球的直径就是长方体的对角线，.12．在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑中平面，，则该鳖臑的外接球与内切球的表面积之和为__________.【答案】【解析】设的中点为，如图，由，且为直角三角形，得.由两两垂直，可知为和的斜边，故点到点的距离相等，故点为鳖臑的外接球的球心，设高鳖臑的外接球的半径与内切球的半径分别为,则由.得，解得.由等体积法，知.即，解得.故该鳖臑的外接球与内切球的表面积之和为.13．已知边长为3的菱形ABCD 中，∠BAD ＝60°，沿对角线BD 折成二面角A BD C 的大小为120°的四面体，则四面体的外接球的表面积为________．【答案】28π【解析】14．在四棱锥P ABCD -中，PC ⊥底面ABCD ，底面为正方形，//QA PC ，PBC AQB∠=∠=60 ，记四棱锥P ABCD-的外接球与三棱锥B ACQ-的外接球的表面积分别为12,S S，则21SS=___．【答案】157点睛：球的半径的计算，关键在球心位置的确定，三棱锥B AQC-中,QAC QBC∆∆均为直角三角形，因此外接球的球心就是QC的中点，因为它到四个顶点的距离是相等的．同理四棱锥P ABCD-外接球的球心就是AP的中点．15．已知直三棱柱中，，侧面的面积为，则直三棱柱外接球表面积的最小值为．【答案】考点：1、几何体的外接球；2、基本不等式；3、球的体积和表面积.【方法点睛】设，则有，利用直三棱柱中，，从而直三棱柱外接球的半径为，所以其比表面积的最小值为.根据直三棱柱中，，侧面的面积为，设，，利用均值不等式，确定直三棱柱外接球的半径的最小值是关键．16．如图所示，三棱锥P ABC -中，ABC 是边长为3的等边三角形，D 是线段AB 的中点，DE PB E ⋂=，且DE AB ⊥，若120EDC ∠=︒，32PA =，2PB =，则三棱锥P ABC -的外接球的表面积为__________．【答案】13π【解析】三棱锥P ABC -中，ABC 是边长为3的等边三角形，设ABC ∆的外心为1O ，外接圆的半径1032sin60O A ==，在PAB ∆中，333,,323PA PB AB ===，满足222PA PB AB +=，PAB ∆为直角三角形，PAB ∆的外接圆的圆心为D ，由于,CD AB ED AB ⊥⊥，0120EDC ∠=为二面角P AB C --的平面角，分别过两个三角形的外心1,O D 作两个半平面的垂线交于点O ，则O 为三棱锥P ABC -的外接球的球心，在1Rt OO D ∆中，01130,2ODO DO ∠==，则01cos30,12O D OD OD OD===，连接OA ，设OA R =，则22222313124R AD OD ⎛⎫=+=+= ⎪⎝⎭，21344=134S R πππ==⨯球.【点睛】求多面体的外接球的面积和体积问题常用方法有（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心，本题就是第三种方法.。
高三数学专题外接球
高三数学专题外接球1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ．B ．C ．D ．2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ． 3．依据垂直关系找球心例3：已知三棱锥的四个顶点均在同一个球面上，底面满足，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ．B ．C ．D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ） A ．B ．C ．D ．2．设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为（ ） A ．12πB ．28πC ．44πD ．60π20π24π32π图2图3P ABC -ABC △BA BC ==π2ABC ∠=16π16π332π324π48π3．把边长为3的正方形沿对角线对折，使得平面平面，则三棱锥的外接 球的表面积为（ ） A ．B ．C ．D ．4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．C ．D ．5．三棱锥的所有顶点都在球的表面上，平面，，，则球的表面积为（ ）A ．B ．C ．D ．6．如图是边长为1的正方体，是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．B ．C ．D ．7．已知球的半径为，，，三点在球的球面上，球心到平面的距离为，，ABCD ABC ⊥ADC D ABC -32π27π22πa 23πa 24πa A BCD -AB ⊥BCD 2BC BD ==2AB CD ==32π60π64π1111ABCD A B C D -S ABCD-9π1625π1649π1681π16ABC 12R 2AB AC ==，则球的表面积为（ ） A ．B ．C ．D ．8．已知正四棱锥(底面四边形是正方形，顶点在底面的射影是底面的中心)，若该正四棱锥的体积为，则此球的体积为（）A ．B ．C ．D ．9．如图，在中，，点为的中点，将沿折起到的位置，使，连接，得到三棱锥．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．10．四面体中，，，，则此四面体外接球的表面积为（ ） A ．BC ． D11．将边长为2的正沿着高折起，使，若折起后四点都在球的表面上，则球的表面积为（ ）A ．B ．C ．D ．12．在三棱锥中，，，则该三棱锥的外接球的表面积为（ ）120BAC ∠=︒16π916π364π964π3P ABCD -ABCD 50336πABC △AB BC ==90ABC ∠=︒ABD △PBD △PC PD =P BCD -A BCD -60ABC ABD CBD ∠=∠=∠=︒3AB =2CB DB ==19π2ABC △120BDC ∠=︒A B C D 、、、7π213π213π3A BCD -6AB CD ==5AC BD AD BC ====ABC ．D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．14．已知棱长都相等正四棱锥的侧面积为，则该正四棱锥内切球的表面积为________．15．已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，，则此球的表面积等于______．16．在三棱锥中，，，，，则三棱锥外接球的体积的最小值为_____． 1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ． B ．20πC ．24πD ．32π【答案】C【解析】162==h a V ，2=a ，24164442222=++=++=h a a R ，24πS =，故选C ． 2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ． 【答案】43π243π111ABC A B C -2AB =1AC =60BAC ∠=︒A BCD -AB AC =DB DC =4AB DB +=AB BD ⊥A BCD-图2图3【解析】933342=++=R ，24π9πS R ==． 3．依据垂直关系找球心例3：已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足BA BC ==π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ． B ．16πC ．16π3D ．32π3【答案】D【解析】因为ABC △是等腰直角三角形，所以外接球的半径是12r =的半径是，球心到该底面的距离，如图，则1632ABC S =⨯=△，BD =116336ABC V S h h ==⨯=△，最大体积对应的高为3SD h ==，故223R d =+，即()2233R R =-+，解之得2R =，所以外接球的体积是3432ππ33R =，故答案为D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ） A ．B ．C ．24πD ．48π【答案】B【解析】设长方体的外接球半径为，由题意可知：()222222R =++，则：23R =，该长方体的外接球的表面积为24π4π312πS R ==⨯=．本题选择B 选项．2．设三棱柱的侧棱垂直于底面，所有棱的长都为面积为（ ） A ．12π B ．28π C ．44π D ．60π【答案】B【解析】设底面三角形的外接圆半径为，由正弦定理可得：2r =2r =， 设外接球半径为，结合三棱柱的特征可知外接球半径22227R =+=，外接球的表面积24π28πS R ==．本题选择B 选项．3．把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（ ） A ．32π B ．27πC ．D ．【答案】C【解析】把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ， 则三棱锥D ABC -的外接球直径为AC =24π18πR =，故选C ． 4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．22πaC ．23πaD ．24πa【答案】C【解析】由题可知，该几何体是由同底面不同棱的两个三棱锥构成，的正四面体，如图所示：该几何体的外接球与棱长为a 的正方体的外接球相同，因此外接球的直径即为正方体的体对角线，所以2R R =⇒，所以该几何体外接球面积2224π4π3πS R a ⎫==⨯=⎪⎪⎝⎭，故选C ．5．三棱锥A BCD -的所有顶点都在球的表面上，AB ⊥平面BCD ，2BC BD ==，2AB CD ==，则球的表面积为（ ）A ．B ．32πC ．60πD ．64π【答案】D【解析】因为2BC BD ==，CD =(222221cos 2222CBD +-∠==-⨯⨯，2π3CBD ∴∠=， 因此三角形BCD 外接圆半径为122sin CDCBD=∠，设外接球半径为，则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭，2=4π64πS R ∴=，故选D ．6．如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．9π16B ．25π16C ．49π16D ．81π16【答案】D【解析】如图所示，连结11A C ，11B D ，交点为，连结SM ，易知球心在直线SM 上，设球的半径R OS x ==，在1Rt OMB △中，由勾股定理有：22211OM B M B O +=，即：()2222x x -+=⎝⎭，解得：98x =，则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭．本题选择D 选项．7．已知球的半径为，，，三点在球的球面上，球心到平面ABC 的距离为12R ，2AB AC ==，120BAC ∠=︒，则球的表面积为（ ）A ．16π9B ．16π3C ．64π9D ．64π3【答案】D【解析】由余弦定理得：BC =设三角ABC 2r =，则2r =，又22144R R =+，解得：2163R =，则球的表面积2644ππ3S R ==．本题选择D 选项． 8．已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点P 在底面的射影是底面的中心)503，则此球的体积为（ ）A ．B ．C ．36πD ．【答案】C 【解析】如图，设正方形ABCD 的中点为，正四棱锥P ABCD -的外接球心为， EA ∴=正四棱锥的体积为503，215033P ABCD V PE -∴=⨯⨯=， 则5PE =，5OE R ∴=-，在AOE △中由勾股定理可得：()2255R R -+=，解得3R =，34π36π3V R ∴==球，故选C ．9．如图，在ABC △中，AB BC ==90ABC ∠=︒，点为的中点，将ABD △沿折起到PBD △的位置，使PC PD =，连接，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．【答案】A【解析】由题意得该三棱锥的面PCD 是边长为的正三角形，且BD ⊥平面PCD ， 设三棱锥P BDC -外接球的球心为，PCD △外接圆的圆心为，则1OO ⊥面PCD ，∴四边形1OO DB 为直角梯形，由BD11O D =，及OB OD =，得OB =R =∴该球的表面积274π4π7π4S R ==⨯=．故选A ． 10．四面体A BCD -中，60ABC ABD CBD ∠=∠=∠=︒，3AB =，2CB DB ==，则此四面体外接球的表面积为（ ）A ．19π2BC ．D 【答案】A【解析】由题意，BCD △中，2CB DB ==，60CBD ∠=︒，可知BCD △是等边三角形，BF =∴BCD △的外接圆半径r BE ==，FE ∵60ABC ABD ∠=∠=︒，可得AD AC ==可得AF =∴AF FB ⊥，∴AF BCD ⊥，∴四面体A BCD -高为AF =设外接球，为球心，OE m =，可得：222r m R +=……①， )222πEF R +=……②由①②解得：R =2194ππ2S R ==．故选A ． 11．将边长为2的正ABC △沿着高折起，使120BDC ∠=︒，若折起后A B C D 、、、四点都在球的表面上，则球的表面积为（ ）A ．7π2B ．C ．13π2D ．13π3【答案】B【解析】BCD △中，1BD =，1CD =，120BDC ∠=︒， 底面三角形的底面外接圆圆心为，半径为，由余弦定理得到BC =21r r =⇒=， 见图示：是球的弦，DA =的位置，∴OM ，在直角三角形OMD 中，应用勾股定理得到，即为球的半径．∴球的半径OD =．该球的表面积为24π7πOD ⨯=；故选B ． 12．在三棱锥A BCD -中，6AB CD ==，5AC BD AD BC ====，则该三棱锥的外接球的表面积为（ ）A B C ．43π2 D ．43π【答案】D【解析】分别取，的中点，，连接相应的线段，，， 由条件，4AB CD ==，5BC AC AD BD ====，可知，ABC △与ADB △，都是等腰三角形，AB ⊥平面ECD ，∴AB EF ⊥，同理CD EF ⊥，∴是与的公垂线， 球心在上，推导出AGB CGD △≌△，可以证明为中点，4DE ==，3DF =，EF =∴GF =，球半径DG ==24π43πS DG =⨯=． 故选D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为1612sin602r =⨯==︒ 则外接球的半径R ， 则外接球的表面积为24π4π2184πS R ==⨯=．14．已知棱长都相等正四棱锥的侧面积为则该正四棱锥内切球的表面积为________．【答案】(32π-【解析】设正四棱锥的棱长为，则24⎫=⎪⎪⎝⎭4a =．于是该正四棱锥内切球的大圆是如图PMN △的内切圆，其中4MN =，PM PN ==PE =．设内切圆的半径为，由PFO PEN ≅△△，得FO PO EN PN =，即2r =，解得r == ∴内切球的表面积为(224π4π32πS r ===-． 15．已知三棱柱111ABC A B C -的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，则此球的表面积等于______．【答案】【解析】∵三棱柱111ABC A B C -的侧棱垂直于底面，棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，1121sin 602AA ∴⨯⨯⨯︒⨯=12AA ∴=， 2222cos60412BC AB AC AB AC =+-⋅︒=+-，BC ∴=， 设ABC △外接圆的半径为，则2sin 60BC R ︒＝，1R ∴=， =24π8π⨯=．故答案为．16．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为_____．【答案】3【解析】如图所示，三棱锥A BCD-的外接圆即为长方体的外接圆，外接圆的直径为长方体的体对角线，⊥，所以AD=设AB AC x==-，AB BDDB DC x==，那么4积的最小值即为最小，AD2x=时，的最小值为。
高考数学立体几何专题：外接球
b2
1 a2 3
PO1
b2
1 a2 3
OO1
PO1
PO
b2 1 a2 R ； 3
在 RtOO1A 中：根据勾股定理得到：
OO12 AO12 AO2 (
b2 1 a2 R)2 ( 3 a)2 R2 b2 1 a2 2
第二部分：柱体的外接球半径 【计算步骤】 第一步：计算底面的外接圆的半径。 第二步：计算直柱体的外接球的半径。 直柱体的外接球的球心：上下底面的外接圆圆心连线的中点为球心。如下图所示：
第3页共8页
其中： O1 为下底面的外接圆的圆心， O2 为上底面的外接圆的圆心， O 为 O1O2 的中点（直柱体外接球的球心）； r 为上下底面的外接圆的半径， R 为直柱体的外接球的半径。
2
训练：求下列图形的外接圆半径。
（Ⅰ）在 ABC 中： AB AC ， AB 3 ， AC 4 ； （Ⅱ）在 ABC 中： AB AC 3 ， BC 2 5 ； （Ⅲ）在正 ABC 中： AB 3 ；
3 （Ⅳ）在 ABC 中， AB 2 ， BC 3， AC 2 ； （Ⅴ）在矩形 ABCD 中： AB 6 ， BC 3 ； （Ⅵ）在正方形 ABCD 中： AB 2 。
根据勾股定理得到： R2 r 2 ( h )2 r 2 h2 R r 2 h2 。
2
4
4
【训练一】：已知：在直三棱柱 ABC A1B1C1 中： AB AC ， AB AC 2 ， AA1 2 。 求解：直三棱锥 ABC A1B1C1 的外接球的半径。
【训练二】：已知：在正三棱柱 ABC A1B1C1 中： AB 3 ， BB1 2 3 。 求解：直三棱锥 ABC A1B1C1 的外接球的半径。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高考数学专题突破：外接球模型模板一：422r h R += 一、题型描述几何体的外接球问题：题目中涉及几何体外接球体，或者球内接几何体，再或者说成球面上有几个点围成几何体，这类题型称之为几何体的外接球问题。
二、模法讲解以下这幅图，大家应该都能看明白吧！一个底面半径为，高为的圆柱，求它的外接球半径。
那么问题来了？422r h R +=这个式子怎么来的。
那么这个式子有何妙用？1、如果我们对圆柱上下底面对应位置处，取相同数量的点，比如都取三个点，如图所示：我们可以得到（直）三棱柱，它的外接球其实就是这个圆柱的外接球，所以说直棱柱的外接球求半径符合这个模型。
在这里棱柱的高就是公式中h的，而棱柱底面外接圆的半径则是公式中的r（至于怎么求外接圆半径可以用正弦定理。
2、我们再继续进行，如果我把刚刚那个三棱柱上面的两点去掉，我将得到三棱锥，如图：这个三棱锥的特点是AA1⊥底面ABC，即有一根侧棱⊥底面的锥体，依然符合这个模型。
那条竖直棱AA1就是公式中的h，而底面ABC的外接圆半径是公式中的r。
3、题目还喜欢这么干：面PAD垂直面ABCD。
它非常符合圆柱外接球模型！我们知道，这里的r为PAD的外接圆半径，h为AB或者CD为的长。
接着看，当我对第二幅图中的三棱柱 ABC-A1B1C1只去掉C1这个点，会得到什么呢？没错！这就是刚刚那个四棱锥放倒了！它的特点是：底面A1B1AB⊥CAB侧面，出题的时候则不会这么仁慈，就会像上一幅图那样，有一个侧面⊥矩形底面的四棱锥！圆柱外接球模型——适用于：①圆柱-------r,h自带②直棱柱-------r:底面外接圆半径；h:直棱柱的高③一根侧棱⊥底面的锥体-------r:底面外接圆半径；h:垂直于底面的那条侧棱④一个侧面⊥矩形底面的四棱锥-------r:垂直底面的侧面的外接圆半径；h:垂直于那个侧面的底边长那么接下来第二步就是找到，求出，而又怎么求呢？用正弦定理。
可以说正弦定理求外接圆半径这种方法咱们基本上就在高一学的时候提及过，根本就没用过它！告诉你，几乎整个高考也就此处求外接球题型可以用它来求求那个了。
讲解如图：模板二：R 2=（R-h ）2+r 2先看以下这幅图：一个底面半径为r ，高为h 的圆锥，求它的外接球半径。
所以，你该明白今天讲解的模型公式就是：hR h 222r +=当然，有同学会问圆锥要是“矮胖”一些，即扁一些怎么办？这时候外接球球心不会在圆锥外部吗？——是的，矮胖的圆锥，外接球球心确实在圆锥外部，但是推导后的外接球半径公式依然是这个。
1、我们在上述圆锥底面边缘等距离取若干个点，与上顶点构成——正棱锥（高考常考正三、正四棱锥）。
（图示举例为正三棱锥，等距离取n 个点情况是一样的）这时，我们知道，这个正棱锥的外接球就是这个圆锥的外接球！所以，求正棱锥的外接球半径等，符合这个模型。
在这里正棱锥的高就是公式中的，而正棱锥底面外接圆的半径则是公式中的（至于怎么求外接圆半径？我们继续。
你会问，那在圆锥底面边缘随便取几个点，不等距不是也可以吗？——是的，也可以！也符合这个模型。
关键是，随便取点得到的也叫普通锥体，我们是很难判断这个锥体是取自圆锥，或者说能补成一个圆锥的。
2、这里面我们看看，什么样的棱锥符合圆锥外接球模型。
其实，不难发现，只要锥体的上顶点在底面外接圆圆心正上方或者说垂线上，就可以。
那么，我们怎么知道普通锥体，上顶点是否在底面外心正上方呢？ 所以说，考试考的往往不是随便编出来的，往往是这样的：【例题1】（2012·唐山统考）一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的表面积为（ ）A. 38B.43C.316 D.23看俯视图，我们可以了解，这个三棱锥上顶点在底面的投影正好是底面直角三角形的斜边中点上。
我们知道直角三角形的外接圆心就是斜边中点！换句话说，本题三棱锥上顶点就是在底面外接圆圆心正上方。
它符合圆锥外接球模型！所以，上顶点在直角三角形底面投影为斜边中点的三棱锥，也符合这个模型 如图——三棱锥S-ABC ，S 在底面投影恰好为直角三角形ABC 斜边中点：在这里三棱锥的高是公式中的h ，底面斜边长的一半是公式中的r 。
让我们总结一下：圆锥外接球模型——适用于：hR h 222r +=①圆锥-------r,h 自带②正棱锥-------r:底面外接圆半径；h:正棱锥的高③“底面为直角三角形+上顶点在底面投影为斜边中点”的三棱锥-------r:底面斜边长的；h:三棱锥的高一、单选题1.（2013•辽宁）已知三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的半径为（）A. B. C. D.2.（2014•湖南）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（）A. 1B. 2C. 3D. 43.正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（）A. B. 16π C. 9π D.4.已知是球的球面上两点，，为该球面上的动点，若三棱锥体积的最大值为，则球的体积为（）A. B. C. D.5.将边长为2的正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，则三棱锥C﹣ABD的外接球表面积为（）A. 16πB. 12πC. 8πD. 4π6.已知边长为的菱形ABCD中，∠BAD=60°，沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD，则四面体的外接球的表面积为（）A. 25πB. 26πC. 27πD. 28π7.如图所示的几何体中，四边形ABCD是边长为的正方形，矩形ADD1A1所在的平面垂直于平面ABCD，且AA1=2，则该几何体ABCD﹣A1D1的外接球的体积是（）A. B. C. D.8.三棱锥P﹣ABC的四个顶点都在球O的球面上，已知PA，PB，PC两两垂直，PA=1，PB+PC=4，当三棱锥的体积最大时，球心O到平面ABC的距离是（）A. B. C. D. ﹣9.某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（）A. 4πB. πC. πD. 20π10.已知A，B，C，D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD=2AB=6则该球的表面积为( )A. 16B. 24C. 32D. 4811.已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为（）A. 4πB. 12πC.D.12.已知三棱锥S﹣ABC，△ABC是直角三角形，其斜边AB=8，SC⊥平面ABC，SC=6，则三棱锥的外接球的表面积为（）A. 64πB. 68πC. 72πD. 100π13.在平行四边形ABCD中，，，若将其沿AC折成直二面角D﹣AC﹣B，则三棱锥D﹣ACB的外接球的表面积为（）A. 16πB. 8πC. 4πD. 2π14.已知菱形ABCD的边长为3，∠B=60°，沿对角线AC折成一个四面体，使得平面ACD⊥平面ABC，则经过这个四面体所有顶点的球的表面积为（）A. 15πB.C. πD. 6π15.三棱锥P﹣ABC中，底面△ABC满足BA=BC，，P在面ABC的射影为AC的中点，且该三棱锥的体积为，当其外接球的表面积最小时，P到面ABC的距离为（）A. 2B. 3C.D.16.如图，在四边形ABCD中，AB=BC=2，∠ABC=90°，DA=DC= ．现沿对角线AC折起，使得平面DAC⊥平面ABC，此时点A，B，C，D在同一个球面上，则该球的体积是（）A. B. C. D. 12π17.某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（）A. 4πB. πC. πD. 20π18.一个几何体的三视图如图所示，已知这个几何体的体积为，则这个几何体的外接球的表面积为（）A. 8πB. 24πC. 48πD. 64π19.己知球的直径SC=4，A，B是该球球面上的两点．AB=2，∠ASC=∠BSC=45°，则棱锥S﹣ABC的体积为（）A. B. C. D.20.三棱锥P﹣ABC中，底面△ABC满足BA=BC，，P在面ABC的射影为AC的中点，且该三棱锥的体积为，当其外接球的表面积最小时，P到面ABC的距离为（）A. 2B. 3C.D.21.某几何体的三视图如图，若该几何体的所有顶点都在一个球面上，则该球面的表面积为（）A. 4πB. πC. πD. 20π22.三棱锥P﹣ABC中，底面△ABC满足BA=BC，，P在面ABC的射影为AC的中点，且该三棱锥的体积为，当其外接球的表面积最小时，P到面ABC的距离为（）A. 2B. 3C.D.23.一个棱长都为a的直三棱柱的六个顶点全部在同一个球面上，则该球的表面积为( )A. B. C. D.24.已知四面体的四个顶点都在球的球面上，若平面，，且，,则球的表面积为( )A. B. C. D.25.在平行四边形ABCD中，，，若将其沿AC折成直二面角D﹣AC﹣B，则三棱锥D﹣ACB的外接球的表面积为（）A. 16πB. 8πC. 4πD. 2π26.若三棱锥S﹣ABC的底面是以AB为斜边的等腰直角三角形，AB=2，SA=SB=SC=2，则该三棱锥的外接球的表面积为（）A. B. C. D.27.一个底面积为1的正四棱柱的顶点都在同一球面上，若此球的表面积为20π，则该四棱柱的高为（）A. B. 2 C. 3 D.28.若一个几何体的三视图如图所示，则这个几何体的外接球的表面积为（）A. 34πB.C.D. 114π二、填空题29.（2012•辽宁）已知正三棱锥P﹣ABC，点P，A，B，C都在半径为的球面上，若PA，PB，PC两两垂直，则球心到截面ABC的距离为________．30.（2013•福建）已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．31.（2017•新课标Ⅱ）长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为________．32.（2017•新课标Ⅰ卷）已知三棱锥S﹣ABC的所有顶点都在球O的球面上，SC是球O的直径，若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S﹣ABC的体积为9，则球O的表面积为________．33.已知某一多面体内接于球构成一个简单组合体，如果该组合体的正视图、俯视图、均如图所示，且图中的四边形是边长为2的正方形，则该球的表面积是________．34.已知S、A、B、C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=1，BC= ，则球O的表面积等于________．35.设三棱柱的侧棱垂直于底面，所有棱的长都为3，顶点都在一个球面上，则该球的表面积为________．36.正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为________．37.若体积为8的正方体的各个顶点均在一球面上，则该球的体积为________．（结果保留π）38.轴截面是正三角形的圆锥的表面积与它的外接球的表面积的比是________．39.正四棱锥的体积为，则该正四棱锥的内切球体积的最大值为________．40.四棱锥P﹣ABCD底面是一个棱长为2的菱形，且∠DAB=60°，各侧面和底面所成角均为60°，则此棱锥内切球体积为________．41.已知三棱锥A﹣BCD中，AB⊥面BCD，△BCD为边长为2的正三角形，AB=2，则三棱锥的外接球体积为________．42.在三棱锥A﹣BCD中，侧棱AB、AC、AD两两垂直，△ABC，△ACD，△ADB的面积分别为，，，则三棱锥A﹣BCD的外接球的体积为________43.已知三棱锥A﹣BCD中，AB=AC=BC=2，BD=CD= ，点E是BC的中点，点A在平面BCD上的射影恰好为DE的中点，则该三棱锥外接球的表面积为________．44.已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC=3，PB=2 ，PC= ，则三棱锥P﹣ABC外接球的表面积为________．45.如图所示，三棱锥P﹣ABC中，△ABC是边长为3的等边三角形，D是线段AB的中点，DE∩PB=E，且DE⊥AB，若∠EDC=120°，PA= ，PB= ，则三棱锥P﹣ABC的外接球的表面积为________．46.已知如图所示的三棱锥D﹣ABC的四个顶点均在球O的球面上，△ABC和△DBC所在的平面互相垂直，，则球O的表面积为________．47.已知空间四边形ABCD中，AB=BD=AD=2，BC=1，CD= ，若二面角A﹣BD﹣C的取值范围为[ ，]，则该几何体的外接球表面积的取值范围为________．48.已知一个正方体的所有顶点在一个球面上．若球的体积为，则正方体的棱长为________49.已知球的表面积为，则球的内接圆锥（球心在圆锥内部）体积的最大值为________．50.如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，若该几何体的各个顶点在某一个球面上，则该球面的表面积为________．答案解析一、单选题1.【答案】C【解析】【解答】解：因为三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，所以三棱柱的底面是直角三角形，侧棱与底面垂直，侧面B1BCC1，经过球的球心，球的直径是其对角线的长，因为AB=3，AC=4，BC=5，BC1= ，所以球的半径为：．故选C．【分析】通过球的内接体，说明几何体的侧面对角线是球的直径，求出球的半径．2.【答案】B【解析】【解答】解：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r，则8﹣r+6﹣r= ，∴r=2．故选：B．【分析】由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r．3.【答案】A【解析】【解答】解：设球的半径为R，则∵棱锥的高为4，底面边长为2，∴R2=（4﹣R）2+（）2，∴R= ，∴球的表面积为4π•（）2= ．故选：A．【分析】正四棱锥P﹣ABCD的外接球的球心在它的高PO1上，记为O，求出PO1，OO1，解出球的半径，求出球的表面积．4.【答案】D【解析】【解答】由题意可知= ，故答案为：D.【分析】三棱锥O-ABC中，由∠AOB=60°，则三角形AOB的面积一定，要使其体积达到最大值，则将AOB作为底面，点C到d面AOB的距离即高达到最大值R时才行。