(完整word版)金属学与热处理(哈尔滨工业大学_第二版)课后习题答案
《金属学与热处理》(第二版)课后习题答案(20200628181724)
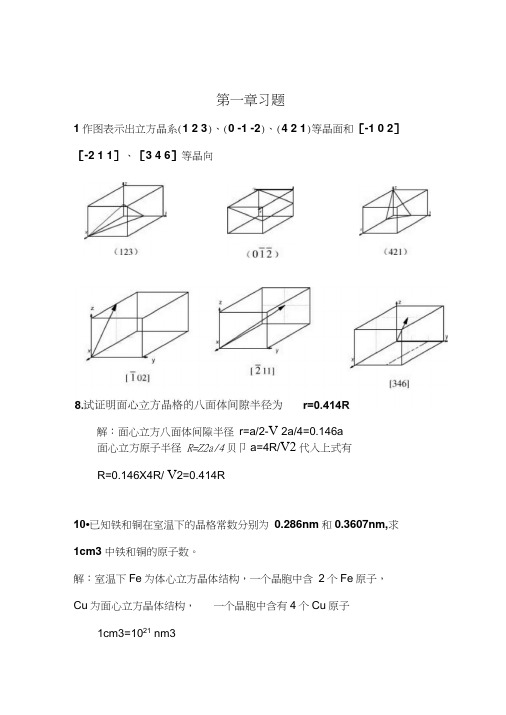
第一章习题1作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2] [-2 1 1]、[3 4 6]等晶向面心立方原子半径 R=Z2a/4贝卩a=4R/V2代入上式有R=0.146X4R/ V 2=0.414R10•已知铁和铜在室温下的晶格常数分别为 0.286nm 和0.3607nm,求 1cm3中铁和铜的原子数。
解:室温下Fe 为体心立方晶体结构,一个晶胞中含 2个Fe 原子, Cu 为面心立方晶体结构,一个晶胞中含有4个Cu 原子1cm3=1021nm3 解:面心立方八面体间隙半径 r=a/2-V 2a/4=0.146a令1cm3中含Fe的原子数为N Fe,含Cu的原子数为N Cu,室温下一个Fe的晶胞题解为V F e, 一个Cu晶胞的体积为V皿贝SN Fe=1021/V Fe=1021/(0.286)3=3.5x1018N cu=1021/V cu=1021/(0.3607)3=2.8X101811一个位错环能不能各个部分都是螺型位错或者刃型位错,试说明之。
解:不能,因为位错环上各点的位错运动方向是不一样的,而柏氏矢量的方向是确定的。
15•有一正方形位错线,其柏式矢量如图所示,试指出图中各段线的性能,并指出任性位错额外串排原子面所在的位置。
AD、BC段为刃型位错;DC、AB段为螺型位错AD段额外半原子面垂直直面向里BC段额外半原子面垂直直面向外第二章习题1•证明均匀形核时,形成临界晶粒的△ Gk与其体积V之间的关系(1)为△ G k = V/2△ G v证明:由均匀形核体系自由能的变化可知,形成半径为r k的球状临界晶粒,自由度变化为W —斗咖。
+忸9(2)对(2)进行微分处理,有4 *d(AG)川一§ 叼"J <f(4nr/(y)—" + " dr K心此0= --Kr k SG x3 + 4心口x2 ’ 即<7二3 2⑶将(3)带入(1),有AG t=-VAG v+^^S2(4)V=-K^ = ^S由于,即3V=r k S (5)将(5)带入(4)中,则有3V VAG k=-VAG v+ —AG, = -AG.匚iiW2•如果临界晶核是边长为a的正方形,试求其△ Gk和a的关系为什么形成立方晶核的△ G k比球形晶核要大?3•为什么金属结晶时一定要有过冷度,影响过冷度的因素是什么,固态金属融化时是否会出现过热,为什么?答:由热力学可知,在某种条件下,结晶能否发生,取决于固相的自由度是否低于液相的自由度,即?G二GS-GLvO ;只有当温度低于理论结晶温度Tm时,固态金属的自由能才低于液态金属的自由能,液态金属才能自发地转变为固态金属,因此金属结晶时一定要有过冷度。
《金属学与热处理》课后答案完整版.docx
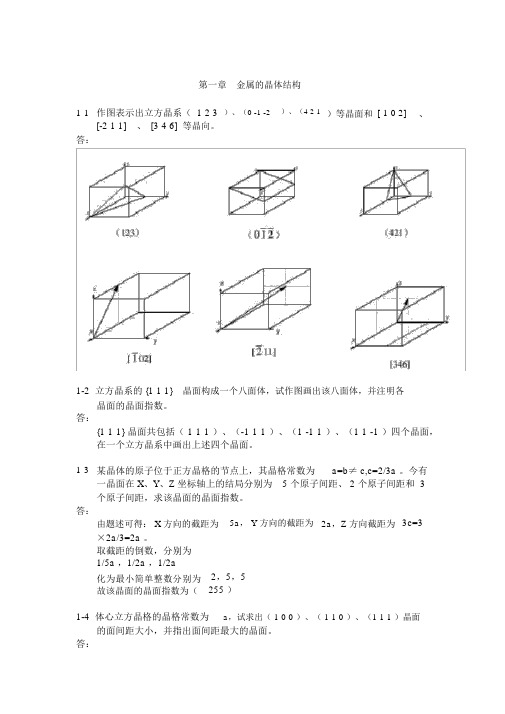
第一章金属的晶体结构1-1作图表示出立方晶系( 1 2 3[-2 1 1]、[3 4 6]等晶向。
)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、答:1-2 立方晶系的 {1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1} 晶面共包括( 1 1 1 )、(-1 1 1 )、(1 -1 1 )、(1 1 -1 )四个晶面,在一个立方晶系中画出上述四个晶面。
1-3某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠ c,c=2/3a 。
今有一晶面在 X、Y、Z 坐标轴上的结局分别为 5 个原子间距、 2 个原子间距和 3个原子间距,求该晶面的晶面指数。
答:由题述可得: X 方向的截距为×2a/3=2a 。
取截距的倒数,分别为1/5a ,1/2a ,1/2a5a, Y 方向的截距为2a,Z 方向截距为3c=3化为最小简单整数分别为故该晶面的晶面指数为(2,5,5 255 )1-4 体心立方晶格的晶格常数为a,试求出( 1 0 0 )、( 1 1 0 )、(1 1 1 )晶面的面间距大小,并指出面间距最大的晶面。
答:H( 1 0 0) ==a/2 H( 1 1 0) ==√2a/2H)==√3a/6(111面间距最大的晶面为( 1 1 0 )1-5 面心立方晶格的晶格常数为a,试求出( 1 0 0 )、( 1 1 0 )、(1 1 1 )晶面的面间距大小,并指出面间距最大的晶面。
答:H( 1 0 0) ==a/2H( 1 1 0) ==√2a/4H( 1 1 1) ==√3a/3面间距最大的晶面为( 1 1 1 )注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时 H=2、面心立方晶格晶面间距:当指数不全为奇数是H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
金属学与热处理(哈尔滨工业大学 - 第二版)课后习题答案 - 附总

金属学与热处理(哈尔滨工业大学 - 第二版)课后习题答案 -附总第六章1. 试用多晶体的塑性变形过程说明金属晶粒越细强度越高、塑性越好的原因是什么?2.答:由 Hall-Petch 公式可知,屈服强度σs 与晶粒直径平方根的倒数 d v2呈线性关系。
在多晶体中,滑移能否从先塑性变形的晶粒转移到相邻晶粒主要取决于在已滑移晶粒晶界附近的位错塞积群所产生的应力集中能否激发相邻晶粒滑移系中的位错源,使其开动起来,从而进行协调性的多滑移。
由τ=nτ0知,塞积位错数目n越大,应力集中τ越大。
位错数目n与引起塞积的晶界到位错源的距离成正比。
晶粒越大,应力集中越大,晶粒小,应力集中小,在同样外加应力下,小晶粒需要在较大的外加应力下才能使相邻晶粒发生塑性变形。
在同样变形量下,晶粒细小,变形能分散在更多晶粒内进行,晶粒内部和晶界附近应变度相差较小,引起的应力集中减小,材料在断裂前能承受较大变形量,故具有较大的延伸率和断面收缩率。
另外,晶粒细小,晶界就曲折,不利于裂纹传播,在断裂过程中可吸收更多能量,表现出较高的韧性。
2.金属材料经塑性变形后为什么会保留残留内应力?研究这部分残留内应力有什么实际意义?金属材料经塑性变形后为什么会保留残留内应力?研究这部分残留内应力有什么实际意义?答:残余内应力存在的原因1)塑性变形使金属工件或材料各部分的变形不均匀,导致宏观变形不均匀; 2)塑性变形使晶粒或亚晶粒变形不均匀,导致微观内应力;3)塑性变形使金属内部产生大量的位错或空位,使点阵中的一部分原子偏离其平衡位置,导致点阵畸变内应力。
实际意义:可以控制材料或工件的变形、开裂、应力腐蚀;可以利用残留应力提高工件的使用寿命。
3.何谓脆性断裂和塑性断裂,若在材料中存在裂纹时,试述裂纹对脆性材料和塑性材料断裂过程中的影响。
答:塑性断裂又称为延性断裂,断裂前发生大量的宏观塑性变形,断裂时承受的工程应力大于材料的屈服强度。
在塑性和韧性好的金属中,通常以穿晶方式发生塑性断裂,在断口附近会观察到大龄的塑性变形痕迹,如缩颈。
《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]
![《金属学和热处理》崔忠圻[第二版]课后答案解析[完整版]](https://img.taocdn.com/s3/m/e4df0f3a3186bceb18e8bb02.png)
第一章金属的晶体结构之阿布丰王创作1-1 作图暗示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6]等晶向。
答:1-2 立方晶系的{1 1 1}晶面构成一个八面体,试作图画出该八面体,并注明各晶面的晶面指数。
答:{1 1 1}晶面共包含(1 1 1)、(-1 1 1)、(1 -1 1)、(1 1 -1)四个晶面,在一个立方晶系中画出上述四个晶面。
1-3 某晶体的原子位于正方晶格的节点上,其晶格常数为a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的结局分别为5个原子间距、2个原子间距和3个原子间距,求该晶面的晶面指数。
答:由题述可得:X方向的截距为5a,Y方向的截距为2a,Z方向截距为3c=3×2a/3=2a。
取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)1-4 体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/2H(1 1 1)==√3a/6面间距最大的晶面为(1 1 0)1-5 面心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面间距大小,并指出面间距最大的晶面。
答:H(1 0 0)==a/2H(1 1 0)==√2a/4H(1 1 1)==√3a/3面间距最大的晶面为(1 1 1)注意:体心立方晶格和面心立方晶格晶面间距的计算方法是:1、体心立方晶格晶面间距:当指数和为奇数是H=,当指数和为偶数时H=2、H=,当指数全为奇数是H=。
1-6 试从面心立方晶格中绘出体心正方晶胞,并求出它的晶格常数。
答:1-7 证明理想密排六方晶胞中的轴比c/a=1.633。
证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,将各原子中心相连接形成一个正四面体,如图所示:此时c/a=2OD/BC在正四面体中:AC=AB=BC=CD ,OC=2/3CE所以:OD2=CD2-OC2=BC2- OC2OC=2/3CE,OC2=4/9CE2,CE2=BC2-BE2=3/4BC2可得到OC2=1/3 BC2,OD2= BC2- OC2=2/3 BC2OD/BC=√6/3所以c/a=2OD/BC=2√6/3≈1-8 试证明面心立方晶格的八面体间隙半径r=0.414R,四面体间隙半径r=0.225R;体心立方晶格的八面体间隙半径:<1 0 0>晶向的r=0.154R,<1 1 0>晶向的r=0.633R,四面体间隙半径r=0.291R。
金属学与热处理课后重点习题

在表层细晶区形成的同时,一方面型壁的温度被高温金属液体和细晶区所释 放的结晶潜热加热而迅速升高,另一方面由于金属凝固后的收缩,使细晶区和型 壁脱离,形成一层空气层,以上都给液体金属的散热造成困难,使液体金属冷却 减慢,温度梯度变得平缓。此时,固液界面前沿过冷度减小,无法满足形核的条 件,不能形成新的晶核,结晶只能依靠靠近液相的某些小晶粒继续长大来进行, 由于垂直于型壁的方向散热最快,因此晶体沿其反方向择优生长,晶体在向液体 中生长的同时,侧面受到彼此的限制而不能生长,因此只能沿散热方向的反方向 生长,从而形成柱状晶区。
此晶区晶粒长大时彼此交叉,枝叉间的搭接牢固,裂纹不易扩展;该晶区晶 粒较大,树枝晶发达,因此显微缩孔较多,力学性能较差。 5. 为了得到发达的柱状晶区应该采取什么措施?为了得到发达的等轴晶区应
该采取什么措施?其基本原理如何? 得到柱状晶区的措施及其原理: ① 提高液态金属过热度。增大固液界面前沿液态金属的温度梯度,有利于增大
3. 体心立方晶格的晶格常数为 a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面 间距大小,并指出面间距最大的晶面。
4. 面心立方晶格的晶格常数为 a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的面 间距大小,并指出面间距最大的晶面。
金属学与热处理习题及答案

金属学与热处理习题及答案金属学与热处理习题及答案金属学是研究金属材料的结构、性质和加工工艺的学科,而热处理则是指通过加热和冷却来改变金属材料的性质和结构。
在学习金属学和热处理的过程中,习题是非常重要的一部分,通过解答习题可以加深对知识的理解和掌握。
下面将给出一些金属学与热处理的习题及答案。
习题一:金属的晶体结构1. 金属的晶体结构有哪几种?2. 铁素体和奥氏体的晶体结构分别是什么?3. 钨的晶体结构是什么?答案:1. 金属的晶体结构有面心立方结构、体心立方结构和简单立方结构。
2. 铁素体的晶体结构为体心立方结构,奥氏体的晶体结构为面心立方结构。
3. 钨的晶体结构为简单立方结构。
习题二:金属的机械性能1. 什么是屈服强度和抗拉强度?2. 强度和韧性之间的关系是什么?3. 金属的硬度和强度有什么区别?答案:1. 屈服强度是指材料在受力过程中开始发生塑性变形的应力值,抗拉强度是指材料在拉伸过程中最大的抗拉应力值。
2. 强度和韧性是互相矛盾的,一般来说,材料的强度越高,韧性越低。
3. 金属的硬度是指材料抵抗局部压痕的能力,而强度是指材料抵抗外力破坏的能力。
习题三:热处理工艺1. 什么是退火和淬火?2. 淬火的目的是什么?3. 淬火过程中的冷却介质有哪些?答案:1. 退火是将金属材料加热到一定温度,然后缓慢冷却的过程,目的是消除材料内部的应力和改善其机械性能。
淬火是将金属材料加热到一定温度,然后迅速冷却的过程,目的是使材料具有高硬度和高强度。
2. 淬火的目的是通过迅速冷却来使材料的组织发生相变,从而提高材料的硬度和强度。
3. 淬火过程中常用的冷却介质有水、油和盐溶液等。
习题四:金属的腐蚀与防护1. 什么是金属的腐蚀?2. 金属腐蚀的原因有哪些?3. 防止金属腐蚀的方法有哪些?答案:1. 金属的腐蚀是指金属在与外界介质接触时,发生化学反应而使其性能和结构受到破坏的过程。
2. 金属腐蚀的原因主要有氧化、电化学腐蚀和化学腐蚀等。
《金属学与热处理》第二版课后习题参考答案

金属学与热处理第一章习题1.作图表示出立方晶系(1 2 3)、(0 -1 -2)、(4 2 1)等晶面和[-1 0 2]、[-2 1 1]、[3 4 6] 等晶向3.某晶体的原子位于正方晶格的节点上,其晶格常数a=b≠c,c=2/3a。
今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距,2个原子间距和3个原子间距,求该晶面的晶面参数。
解:设X方向的截距为5a,Y方向的截距为2a,则Z方向截距为3c=3X2a/3=2a,取截距的倒数,分别为1/5a,1/2a,1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)4.体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的晶面间距,并指出面间距最大的晶面解:(1 0 0)面间距为a/2,(1 1 0)面间距为√2a/2,(1 1 1)面间距为√3a/3三个晶面晶面中面间距最大的晶面为(1 1 0)7.证明理想密排六方晶胞中的轴比c/a=1.633证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,成正四面体,如图所示则OD=c/2,AB=BC=CA=CD=a因△ABC是等边三角形,所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2则有(CD)2=(OC)2+(1/2c)2,即因此c/a=√8/3=1.6338.试证明面心立方晶格的八面体间隙半径为r=0.414R解:面心立方八面体间隙半径r=a/2-√2a/4=0.146a面心立方原子半径R=√2a/4,则a=4R/√2,代入上式有R=0.146X4R/√2=0.414R9.a)设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积膨胀。
b)经X射线测定,在912℃时γ-Fe的晶格常数为0.3633nm,α-Fe的晶格常数为0.2892nm,当由γ-Fe转化为α-Fe时,求其体积膨胀,并与a)比较,说明其差别的原因。
金属学与热处理课后习题答案

金属学与热处理课后习题答案Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第七章金属及合金的回复和再结晶7-1 用冷拔铜丝线制作导线,冷拔之后应如何如理,为什么答:应采取回复退火(去应力退火)处理:即将冷变形金属加热到再结晶温度以下某一温度,并保温足够时间,然后缓慢冷却到室温的热处理工艺。
原因:铜丝冷拔属于再结晶温度以下的冷变形加工,冷塑性变形会使铜丝产生加工硬化和残留内应力,该残留内应力的存在容易导致铜丝在使用过程中断裂。
因此,应当采用去应力退火使冷拔铜丝在基本上保持加工硬化的条件下降低其内应力(主要是第一类内应力),改善其塑性和韧性,提高其在使用过程的安全性。
7-2 一块厚纯金属板经冷弯并再结晶退火后,试画出截面上的显微组织示意图。
答:解答此题就是画出金属冷变形后晶粒回复、再结晶和晶粒长大过程示意图(可参考教材P195,图7-1)7-3 已知W、Fe、Cu的熔点分别为3399℃、1538℃和1083℃,试估算其再结晶温度。
答:再结晶温度:通常把经过严重冷变形(变形度在70%以上)的金属,在约1h的保温时间内能够完成超过95%再结晶转变量的温度作为再结晶温度。
≈δTm,对于工业纯1、金属的最低再结晶温度与其熔点之间存在一经验关系式:T再金属来说:δ值为,取计算。
2、应当指出,为了消除冷塑性变形加工硬化现象,再结晶退火温度通常要比其最低再结晶温度高出100-200℃。
=,可得:如上所述取T再W=3399×=℃再=1538×=℃Fe再Cu=1083×=℃再7-4 说明以下概念的本质区别:1、一次再结晶和二次在结晶。
2、再结晶时晶核长大和再结晶后的晶粒长大。
答:1、一次再结晶和二次在结晶。
定义一次再结晶:冷变形后的金属加热到一定温度,保温足够时间后,在原来的变形组织中产生了无畸变的新的等轴晶粒,位错密度显着下降,性能发生显着变化恢复到冷变形前的水平,称为(一次)再结晶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章1•作图表示出立方晶系(1 2 3)、(0 -1-2)、(4 2 1)等晶面和[-1 02]、3•某晶体的原子位于正方晶格的节点上,其晶格常数今有一晶面在X、Y、Z坐标轴上的截距分别是5个原子间距,2个原子间距和3个原子间距,求该晶面的晶面参数。
解:设X方向的截距为5a, Y方向的截距为2a,则Z方向截距为3c=3X2a/3=2a,取截距的倒数,分别为1/5a,1/2a, 1/2a化为最小简单整数分别为2,5,5故该晶面的晶面指数为(2 5 5)4体心立方晶格的晶格常数为a,试求出(1 0 0)、(1 1 0)、(1 1 1)晶面的晶面间距,并指出面间距最大的晶面解:(1 0 0)面间距为a/2, (1 1 0)面间距为"2a/2, (1 1 1)面间距为"3a/3三个晶面晶面中面间距最大的晶面为(1 1 0)7证明理想密排六方晶胞中的轴比c/a=1.633证明:理想密排六方晶格配位数为12,即晶胞上底面中心原子与其下面的3个位于晶胞内的原子相切,成正四面体,如图所示贝卩OD=c/2,AB=BC=CA=CD=a因厶ABC是等边三角形,所以有OC=2/3CE由于(BC)2=(CE)2+(BE)2有(CD)2=(OC)2+(1/2C)2,即I /T J(CU)(c)2- '3 2因此c/a=V8/3=1.6338•试证明面心立方晶格的八面体间隙半径为r=0.414R解:面心立方八面体间隙半径r=a/2-v2a/4=0.146a面心立方原子半径R二辺a/4,贝卩a=4R/\2,代入上式有R=0.146X4R/ V2=0.414R9. a )设有一刚球模型,球的直径不变,当由面心立方晶格转变为体心立方晶格时,试计算其体积膨胀。
b)经X射线测定,在912C时丫-Fe的晶格常数为0.3633nm, a -Fe的晶格常数为0.2892nm,当由丫-Fe转化为a -Fe时,求其体积膨胀,并与a)比较,说明其差别的原因。
解:a)令面心立方晶格与体心立方晶格的体积及晶格常数分别为V面、V踢与a面、a体,钢球的半径为r,由晶体结构可知,对于面心晶胞有4r=辺a 面,a 面=2辺/2r, V 面二(a 面)3= (2辺r)3对于体心晶胞有4r= \3a 体,a 体=4v3/3r, V 体二(a 体)3= (4\3/3r)3则由面心立方晶胞转变为体心立方晶胞的体积膨胀厶V为△V=2X V体-V 面=2.01r3B)按照晶格常数计算实际转变体积膨胀厶V实,有△V实=2^ V体-V 面=2x(0.2892)3-(0.3633)3=0.000425nm3实际体积膨胀小于理论体积膨胀的原因在于由丫-Fe转化为a-Fe时,Fe原子的半径发生了变化,原子半径减小了。
10. 已知铁和铜在室温下的晶格常数分别为0.286nm和0.3607nm,求1cm3 中铁和铜的原子数。
解:室温下Fe为体心立方晶体结构,一个晶胞中含2个Fe原子,Cu为面心立方晶体结构,一个晶胞中含有4个Cu原子1cm3=1021 nm3令1cm3中含Fe的原子数为N Fe,含Cu的原子数为N cu,室温下一个Fe的晶胞题解为V Fe,一个Cu晶胞的体积为V cu,则N Fe=1021/V Fe=1021/(0.286)3=3.5x1018N Cu=1021/V cu=1021/(0.3607)3=2.8X101811. 一个位错环能不能各个部分都是螺型位错或者刃型位错,试说明之。
解:不能,看混合型位错13.试计算{110}晶面的原子密度和[111]晶向原子密度。
解:以体心立方{110}晶面为例{110}晶面的面积S=a x辺a{110}晶面上计算面积S内的原子数N=2则{110}晶面的原子密度为p =N/S= v2a-2[111]晶向的原子密度p =2/v3a15•有一正方形位错线,其柏式矢量如图所示,试指出图中各段线的性能,并指出任性位错额外串排原子面所在的位置。
D f -------------------------------------- k C------ ►bAD、BC段为刃型位错;DC、AB段为螺型位错AD段额外半原子面垂直直面向里BC段额外半原子面垂直直面向外第二章1•证明均匀形核时,形成临界晶粒的△ Gk与其体积V之间的关系为△ G k = V/2 △ G v证明:由均匀形核体系自由能的变化可知,形成半径为r k的球状临界晶粒,自由度变化为ACJ JJ =―兀r* AG b+ 4眄 P(2)对(2)进行微分处理,有如G)dr0A扫远6伽口乩即售晋将(3)带入(1),有AG k=-VAG v+^^-S(4)将(5)带入(4)中,则有由于,即3V=r k S (5)2•如果临界晶核是边长为a的正方形,试求其△ Gk和a的关系为什么形成立方晶核的△ G k比球形晶核要大?i【卜明:AG——VAG v+dS=—P上式做微分处锂辛右—一3a2AG v+12ao»则g —aAG v4, , I = 1 [因此AG k=- a AG v+- aAG v 6a ta=— a'AG v4 2当形成球翅晶核时AG11="-Itr J AG +4JTr'(5> 则有◎二"■则3 2AG/ = ——JU;AG+ 4眄:鞋比&=—TIF\1G* 3 2 3当形成立方晶核时AG';=-a'AG r+6a^5,则o = 则AG =-a,SG +&?「生呢=丄见迖G£ L' 1 4 2液态金屈同总廿值就同处不变了,所以疔=鱼匣二込,则存4 2Ok=2rti 代入Af j = F JL AG,十6。
- 殳空AG, r则4 2虫G: = 4< L AG,,又远二£心込。
、所以AG;>AG^3•为什么金属结晶时一定要有过冷度,影响过冷度的因素是什么,固态金属融化时是否会出现过热,为什么?答:由热力学可知,在某种条件下,结晶能否发生,取决于固相的自由度是否低于液相的自由度,即G二GS-GLvO;只有当温度低于理论结晶温度Tm 时,固态金属的自由能才低于液态金属的自由能,液态金属才能自发地转变为固态金属,因此金属结晶时一定要有过冷度。
影响过冷度的因素:影响过冷度的因素:1)金属的本性,金属不同,过冷度大小不同; 2)金属的纯度,金属的纯度越高,过冷度越大; 3)冷却速度,冷却速度越大,过冷度越大。
固态金属熔化时会出现过热度。
原因:由热力学可知,在某种条件下,熔化能否发生,取决于液相自固态金属熔化时会出现过热度。
原因:由度是否低于固相的自由度,即G = GL-GSvO;只有当温度高于理论结晶温度Tm 时,液态金属的自由能才低于固态金属的自由能,固态金属才能自发转变为液态金属,因此金属熔化时一定要有过热度。
4. 试比较均匀形核和非均匀形核的异同点。
相同点:均匀形核与非均匀形核具有相同的临界晶核半径,非均匀形核的临界形核功也等于三分之一.不同点:非均匀形核要克服的位垒比均匀形核的小得多,在相变的形核过程通常都是非均匀形核优先进行。
核心总是倾向于以使其总的表面能和应变能最小的方式形成,因而析出物的形状是总应变能和总表面能综合影响的结果。
5. 说明晶体成长形状与温度梯度的关系(1)、在正的温度梯度下生长的界面形态:光滑界面结晶的晶体,若无其它因素干扰,大多可以成长为以密排晶面为表面的晶体,具有规则的几何外形。
粗糙界面结构的晶体,在正的温度梯度下成长时,其界面为平行于熔点等温面的平直界面,与散热方向垂直,从而使之具有平面状的长大形态,可将这种长大方式叫做平面长大方式。
(2)、在负的温度梯度下生长的界面形态粗糙界面的晶体在负的温度梯度下生长成树枝晶体。
主干叫一次晶轴或一次晶枝。
其它的叫二次晶或三次晶。
对于光滑界面的物质在负的温度梯度下长大时,如果杰克逊因子a不太大时可能生长为树枝晶,如果杰克逊因子a很大时,即使在负的温度梯度下,仍有可能形成规则形状的晶体。
6. 简述三晶区形成的原因及每个晶区的性能特点形成原因:1)表层细晶区:低温模壁强烈地吸热和散热,使靠近模壁的薄层液体产生极大地过冷,形成原因形成原模壁又可作为非均匀形核的基底,在此一薄层液体中立即产生大量的晶核,并同时向各个方向生长。
晶核数目多,晶核很快彼此相遇,不能继续生长,在靠近模壁处形成薄层很细的等轴晶粒区。
2)柱状晶区:模壁温度升高导致温度梯度变得平缓;过冷度小,不能生成新晶核,但利于细晶区靠近液相的某些小晶粒长大;远离界面的液态金属过热,不能形核;垂直于模壁方向散热最快,晶体择优生长。
3)中心等轴晶区:柱状晶长到一定程度后,铸锭中部开始形核长大---中部液体温度大致是均匀的,每个晶粒的成长在各方向上接近一致,形成等轴晶。
性能特点:1)表层细晶区:组织致密,力学性能好;2)柱状晶区:组织较致密,存在弱面,力学性能有方向性;3)中心等轴晶区:各晶粒枝杈搭接牢固,无弱面,力学性能无方向性。
7. 为了得到发达的柱状晶区应采用什么措施,为了得到发达的等轴晶区应采取什么措施?其基本原理如何?答:为了得到发达的柱状晶区应采取的措施:1)控制铸型的冷却能力,采用导热性好与热容量大的铸型为了得到发达的柱状晶区应采取的措施:材料,增大铸型的厚度,降低铸型的温度。
2)提高浇注温度或浇注速度。
3)提高熔化温度。
基本原理:基本原理:1)铸型冷却能力越大,越有利于柱状晶的生长。
2)提高浇注温度或浇注速度,使温度梯度增大,有利于柱状晶的生长。
3)熔化温度越高,液态金属的过热度越大,非金属夹杂物溶解得越多,非均匀形核数目越少,减少了柱状晶前沿液体中的形核的可能,有利于柱状晶的生长。
为了得到发达的等轴晶区应采取的措施:为了得到发达的等轴晶区应采取的措施:1)控制铸型的冷却能力,采用导热性差与热容量小的铸型材等轴晶区应采取的措施料,增大铸型的厚度,提高铸型的温度。
2)降低浇注温度或浇注速度。
3)降低熔化温度。
基本原理:基本原理:1)铸型冷却能力越小,越有利于中心等轴晶的生长。
2)降低浇注温度或浇注速度,使温度梯度减小,有利于等轴晶的生长。
3)熔化温度越低,液态金属的过热度越小,非金属夹杂物溶解得越少,非均匀形核数目越多,增加了柱状晶前沿液体中的形核的可能,有利于等轴晶的生长。
第三章1.在正温度梯度下,为什么纯金属凝固时不能呈树枝状生长,而固溶体合金却能呈树枝状成长?纯金属凝固时,要获得树枝状晶体,必需在负的温度梯度下;在正的温度梯度下,只能以平面状长大。
而固溶体实际凝固时,往往会产生成分过冷,当成分过冷区足够大时,固溶体就会以树枝状长大。
2.何谓合金平衡相图,相图能给出任一条件下的合金显微组织吗?合金平衡相图是研究合金的工具,是研究合金中成分、温度、组织和性能之间关系的理论基础,也是制定各种热加工工艺的依据。
