课时1《实数的概念》基础训练
人教版七年级数学下册实数第1课时实数及其性质同步练习

人教版七年级数学下册实数第1课时实数及其性质同步练习第1课时实数及其性质基础训练知识点1 无理数1.下列各数中为无理数的是()A.-1B.3.14C.πD.02.(2016·宜昌)下列各数:1.414,,-,0,其中是无理数的为()A.1.414B.C.-D.03.下列语句正确的是()A.0.101 001 000 1是无理数B.无限小数不能转化成分数C.无理数分为正无理数﹨零﹨负无理数D.无限不循环小数是无理数4.下列说法中正确的是()A﹨的平方根是±3B﹨1的立方根是±1C﹨=±1D﹨是5的平方根的相反数知识点2 实数及其分类5.下列实数中,属于有理数的是()A.-B.C.πD.6.实数0是()A.有理数B.无理数C.正数D.负数7.把下列各数填入相应的大括号内:-7,0.32,,3.1,0,,,0.101 001 000 1…(相邻两个1之间0的个数逐次加1),,-. 有理数:{,…};无理数:{,…};正实数:{,…};实数:{,…}.8.下列说法正确的是()A.正实数和负实数统称实数B.正数﹨零和负数统称有理数C.带根号的数和分数统称实数D.无理数和有理数统称实数知识点3 实数的性质9.(2016·随州)-的相反数是()A.-B.C.D.-10. 如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是()A.1B. 1.4C.D.11.在实数范围内,下列判断正确的是()A.若|x|=|y|,则x=yB.若x>y,则x2>y2C.若|x|=()2,则x=yD.若=,则x=y易错点对分数的定义理解不准确12.下列说法正确的是()A.是分数B.是分数C.是分数D.是分数提升训练考查角度1 利用实数的性质进行计算13.按要求计算:(1)的算术平方根;(2)3.14-π的相反数﹨绝对值﹨倒数.考查角度2 利用实数的性质求值14.已知a,b,c,d,e,f为实数,且a,b互为倒数,c,d互为相反数,e的绝对值为,f的算术平方根是8,求ab++e2+的值.参考答案1.【答案】C2.【答案】B3.【答案】D4.【答案】A解:本题主要考察平方根﹨算术平方根﹨立方根的概念,∵=9,9的平方根是±3,∴A正确.5.【答案】D6.【答案】A7.解:有理数:-7,0.32,,3.1,0,…;无理数:,,0.101 001 000 1…(相邻两个1之间0的个数逐次加1),,-,…;正实数:0.32,,3.1,,,0.101 001 000 1…(相邻两个1之间0的个数逐次加1),,…;实数:-7,0.32,,3.1,0,,,0.101 001 000 1…(相邻两个1之间0的个数逐次加1), ,-,….8.【答案】D9.【答案】C10.【答案】C解: 本题考察了数轴上的点与全体实数的一一对应的关系.∵正方形的边长为1,对角线为,由圆的定义知|AO|=,∴A 表示数为,故选C11.【答案】D12.【答案】D解:虽然中带有根号,但是=-2,实质上是一个负整数,因此是分数.本题易错之处在于学生误认为具有“分数”形式的数就是分数.13.解:(1)的算术平方根为.(2)3.14-π的相反数为π-3.14,绝对值为π-3.14,倒数为. 14.解:因为a,b互为倒数,所以ab=1.因为c,d互为相反数,所以c+d=0.因为|e|=,所以e=±.因为=8,所以f=64.当e=时,原式=×1++()2+=;当e=-时,原式=×1++(-)2+=.综上,原式=.。
2019年春七年级数学下册实数第1课时实数的概念同步练习(新版)新人教版

6.3 第1课时 实数的概念知识点 1 无理数的定义 1.下列说法正确的是( ) A .无限小数是无理数 B .有根号的数是无理数 C .无理数是开方开不尽的数D .无理数包括正无理数和负无理数 2.任何一个有理数都可以写成________________的形式,反过来,任何________________都是有理数.3.下列各数中:-14,3.14159,-π,π5,0,0.3,15,5.2·01·,2.121122111222…,其中无理数有________________________.知识点 2 实数的定义与分类 4.能够组成全体实数的是( ) A .自然数和负数 B .整数和分数 C .有理数和无理数D .正数和负数 5.下列说法正确的是( ) A .正实数和负实数统称实数 B .正数、零和负数统称为有理数 C .带根号的数和分数统称实数 D .无理数和有理数统称为实数6.按大小分,实数可分为________、________、________三类. 7.把下列各数分别填入相应的数集里.-13π,-2213,7,327,0.324371,0.5,39,-0.4,16,0.8080080008… 无理数集合{ …}; 有理数集合{ …}; 分数集合{ …}; 负实数集合{ …}.知识点 3 实数与数轴的关系8.和数轴上的点成一一对应关系的数是( ) A .自然数 B .有理数 C .无理数 D .实数9.如图6-3-1,数轴上的A ( )A .点AB .点BC .点CD .点D知识点 4 实数的相反数、绝对值 10.2的相反数是( )A .- 2 B. 2 C.12D .211.若m ,n 互为相反数,则式子|m -5+n |=________. 12.在数轴上表示-6的点到原点的距离为________. 13.求下列各数的相反数和绝对值.(1)-2; (2)-364; (3)π-3.14.求下列各式中的x . (1)|x |=35; (2)|x |=17.15.下列各组数中互为相反数的是( ) A .5和(-5)2B .-|-5|和-(-5)C .-5和3-125 D .-5和1516.实数a 对应的点在数轴上的位置如图6-3-2所示,则a ,-a ,1a的大小关系为( )图6-3-2A.1a <a <-a B .-a <1a<aC .a <1a <-a D.1a<-a <a17.已知a 为实数,则下列四个数中一定为非负数的是( )A .a B.3a C .|-a | D .-|-a |18.如图6-3-3,数轴上A ,B 两点表示的数分别为2和5.1,则A ,B 两点之间表示整数的点共有( )图6-3-3A .6个B .5个C .4个D .3个19.3-2的相反数是________,绝对值是________.20.有九个数:0.1427,(-0.5)3,3.1416,121,327,2.5,227,-2π,0.2020020002…,若无理数的个数为x ,整数的个数为y ,非负数的个数为z ,则x +y +z =________.21.如图6-3-4,A 是硬币圆周上一点,硬币与数轴相切于原点O (点A 与点O 重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A ′重合,则点A ′对应的实数是________.图6-3-422.已知实数a ,b 在数轴上的对应点的位置如图6-3-5所示,试化简:(a -b )2-|a +b |.图6-3-523.已知实数a ,b ,c ,d ,e ,f ,且a ,b 互为倒数,c ,d 互为相反数,e 的绝对值为2,f 的算术平方根是8,求12ab +c +d 5+e 2+3f 的值.24.先阅读下面的文字,再解答问题.大家知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部地写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,将这个数减去其整数部分,差就是小数部分.已知:10+3=x+y,其中x是整数,且0<y<1,求x-y的值.教师详解详析1.D [解析] A 项不正确,无限不循环小数是无理数.B 项不正确,有根号的数不一定是无理数,如4,38等.C 项不正确,π及类似1.010010001…(两个1之间0的个数逐次加1)的数也是无理数.2.有限小数或无限循环小数 有限小数或无限循环小数3.-π,π5,2.121122111222…4.C 5.D 6.正实数 0 负实数7.解:无理数集合{-13π,7,39,-0.4,0.8080080008…,…};有理数集合{-2213,327,0.324371,0.5,16,…};分数集合{-2213,0.324371,0.5,…};负实数集合{-13π,-2213,-0.4,…}.8.D [解析] ∵任何实数都可以用数轴上的点来表示,数轴上的任何一点都表示一个实数,∴和数轴上的点成一一对应关系的数是实数. 故选D . 9.B [解析] ∵3≈1.732, ∴-3≈-1.732.∵点A ,B ,C ,D 表示的数分别为-3,-2,-1,2,∴与数-3表示的点最接近的是点B.故选B . 10.A11. 5 [解析] 由题意m ,n 互为相反数,可知m +n =0,则|m -5+n|= 5.12. 6 [解析] 数轴上表示-6的点到原点的距离为-6的绝对值,|-6|= 6. 13.解:(1)-2的相反数为2,绝对值为||-2= 2. (2)-364的相反数为364=4,绝对值为⎪⎪⎪⎪-364=364=4.(3)π-3的相反数为3-π,因为π>3,所以绝对值为||π-3=π-3.14.解:(1)x =±35.(2)x =±17.15.B [解析] 只有符号不同的两个数互为相反数,它们的和为0,由此可判定选项.A 中(-5)2=5,两个数相等,故错误;B 中-|-5|=-5,-(-5)=5,-5与5互为相反数,故正确;C 中3-125=-5,两个数相等,故错误;D 中-5和15既不是相反数,也不是倒数,故错误.故选B .16.A [解析] 采用特殊值法来解决.不妨设a =-12,则-a =12,1a =-2.因为-2<-12<12,所以1a<a <-a.故选A .17.C [解析] 选项A 中的a 可以表示任何实数.选项B 中的3a 的符号与a 相同,所以也可以表示任何实数.选项C 中的|-a|表示-a 的绝对值,根据绝对值的意义,可知|-a|为非负数.选项D 中的-|-a|表示|-a|的相反数,由于|-a|为非负数,所以-|-a|为非正数.故选C .18.C [解析] 因为1<2<2,5<5.1<6,所以A ,B 两点之间表示整数的点有表示2,3,4,5的点,共有4个.故选C .19.2- 3 3- 2 [解析] 3-2的相反数是-(3-2)=-3+2=2-3.3-2是一个正实数,正实数的绝对值等于它本身.20.12 [解析] 无理数有 2.5,-2π,0.2020020002…,所以x =3.整数有121,327,所以y =2.非负数有0.1427,3.1416,121,327, 2.5,227,0.2020020002…,所以z=7,所以x +y +z =3+2+7=12.21.π [解析] 将硬币沿数轴正方向滚动一周,点A 恰好与数轴上的点A′重合,则点A 转过的距离是圆的周长,即π,因而点A′对应的实数是π.22.解: 根据数轴可得出:a -b >0,a +b <0,∴(a -b )2-|a +b|=(a -b)+(a +b)=2a. 23.解:因为a ,b 互为倒数,所以ab =1. 因为c ,d 互为相反数,所以c +d =0. 因为e 的绝对值为2,所以e =±2,所以e 2=(±2)2=2.因为f 的算术平方根是8,所以f =64,所以3f =364=4,所以12ab +c +d 5+e 2+3f =12+0+2+4=612.24.解:由1<3<2,得11<10+3<12.由x 是整数,且0<y<1,得x =11, y =10+3-11=3-1,从而x -y =11-(3-1)=12- 3.。
(完整版)实数知识点和练习
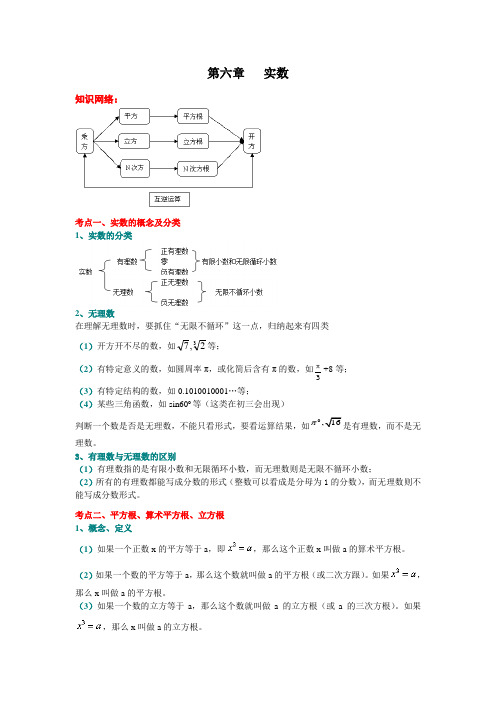
第六章实数知识网络:考点一、实数的概念及分类1、实数的分类2、无理数在理解无理数时,要抓住“无限不循环”这一点,归纳起来有四类,7等;(1)开方开不尽的数,如32π+8等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等(这类在初三会出现)是有理数,而不是无判断一个数是否是无理数,不能只看形式,要看运算结果,如0,16理数。
3、有理数与无理数的区别(1)有理数指的是有限小数和无限循环小数,而无理数则是无限不循环小数;(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数),而无理数则不能写成分数形式。
考点二、平方根、算术平方根、立方根1、概念、定义(1)如果一个正数x的平方等于a,即,那么这个正数x叫做a的算术平方根。
(2)如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
如果,那么x叫做a的平方根。
(3)如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
如果,那么x叫做a的立方根。
2、运算名称(1)求一个正数a 的平方根的运算,叫做开平方。
平方与开平方互为逆运算。
(2)求一个数的立方根的运算,叫做开立方。
开立方和立方互为逆运算。
3、运算符号(1)正数a 的算术平方根,记作“a ”。
(2)a(a ≥0)的平方根的符号表达为。
(3)一个数a 的立方根,用表示,其中a 是被开方数,3是根指数。
4、运算公式4、开方规律小结(1)若a ≥0,则a 的平方根是a ±,a 的算术平方根a ;正数的平方根有两个,它们互为相反数,其中正的那个叫它的算术平方根;0的平方根和算术平方根都是0;负数没有平方根。
实数都有立方根,一个数的立方根有且只有一个,并且它的符号与被开方数的符号相同。
正数的立方根是正数,负数的立方根是负数,0的立方根是0。
(2)若a<0,则a 没有平方根和算术平方根;若a 为任意实数,则a 的立方根是。
初中数学实数基础训练1含答案

实数基础训练1一.选择题(共16小题)1.下列实数中,()是无理数.A.﹣3.1416B.C.﹣D.2.矩形的面积为18,一边长为,则另一边长为()A.B.C.D.243.与是同类二次根式的是()A.B.C.D.4.当x为下列何值时,二次根式有意义()A.x≠2B.x>2C.x≤2D.x≥2 5.﹣8的立方根是()A.2B.﹣2C.4D.﹣46.若+n2+2n+1=0,则m n=()A.B.C.2D.﹣27.2的平方根是()A.±4B.4C.±D.8.若最简二次根式与最简二次根式是同类二次根式,则x的值为()A.x=0B.x=1C.x=2D.x=﹣2 9.若在实数范围内有意义,则x的取值范围是()A.x<﹣2B.x>﹣2C.x≤﹣2D.x≥﹣2 10.估计+1的值在()A.2到3之间B.3到4之间C.4到5之间D.5到6之间11.﹣27的立方根是()A.3B.﹣3C.±3D.﹣3 12.估计的运算结果应在()A.3到4之间B.4到5之间C.5到6之间D.6到7之间13.下列二次根式中,是最简二次根式的是()A.B.C.D.14.下列二次根式中属于最简二次根式的是()A.B.C.(a>0,b>0)D.15.下列计算正确的是()A.×=B.=2C.+=D.=﹣5 16.=()A.﹣4B.4C.﹣8D.8二.填空题(共11小题)17.当x______时,二次根式在实数范围内有意义.18.已知a=2+,b=2﹣,则ab(a+b)=______.19.实数a、b在数轴上位置如图,化简:|a+b|+=______.20.写出一个满足<a<的整数a的值为______.21.代数式+2的最小值是______.22.计算的结果是______.23.若a、b为实数,且(a+)2+=0,则a b的值______.24.有理化分母:=______.25.已知的小数部分是a,的整数部分是b,则a+b=______.26.的小数部分是______.27.若,则x2+2x+1=______.三.解答题(共3小题)28.(π﹣3.14)0+()﹣1﹣|﹣3|29.计算:﹣14+|﹣2|﹣(π﹣3.14)0+÷30.实数a、b、c在数轴上的位置如图所示,求代数式|a|﹣|a+b|+|c﹣a|+|b﹣c|的值.实数基础训练1参考答案与试题解析一.选择题(共16小题)1.解:A、﹣3.1416是有限小数,属于有理数,故本选项不合题意;B、是无理数,故本选项符合题意;C.,是整数,属于有理数,故本选项不合题意;D.是分数,属于有理数,故本选项不合题意.故选:B.2.解:∵矩形的面积为18,一边长为,∴另一边长为=3,故选:C.3.解:的被开方数是2.A、原式=3,其被开方数是3,与的被开方数不同,它们不是同类二次根式,故本选项不符合题意.B、该二次根式的被开方数是6,与的被开方数不同,它们不是同类二次根式,故本选项不符合题意.C、原式=,其被开方数是3,与的被开方数不同,它们不是同类二次根式,故本选项不符合题意.D、原式=2,其被开方数是2,与的被开方数相同,它们是同类二次根式,故本选项符合题意.故选:D.4.解:根据二次根式有意义的条件可得:2﹣x≥0,解得:x≤2.故选:C.5.解:﹣8的立方根为﹣2,故选:B.6.解:∵+n2+2n+1=0,∴+(n+1)2=0,∴m﹣2=0,n+1=0,∴m=2,n=﹣1,∴m n=2﹣1=.故选:A.7.解:∵(±)2=2,∴2的平方根为±,故选:C.8.解:根据题意,得x+4=3x,解得x=2.故选:C.9.解:由题意,得x+2≥0,解得x≥﹣2.故选:D.10.解:∵2<3,∴3<+1<4,故选:B.11.解:﹣27的立方根是﹣3,故选:B.12.解:∵9<15<16,∴3<<4.故选:A.13.解:A、被开方数里含有能开得尽方的因数8,故本选项错误;B、符合最简二次根式的条件;故本选项正确;C、被开方数里含有分母;故本选项错误.D、被开方数里含有能开得尽方的因式a2;故本选项错误;故选:B.14.解:(A)原式=2,故A不符合题意;(B)原式=6,故B不符合题意;(C)不是最简二次根式,故C不符合题意;故选:D.15.解:∵=,故选项A正确;∵=3,故选项B错误;∵==3,故选项C错误;∵=5,故选项D错误;故选:A.16.解:∵82=64,∴=8.故选:D.二.填空题(共11小题)17.解:由题意,得x+1≥0.则x≥﹣1.故答案是:≥﹣1.18.解:a+b=2++2﹣=4,ab=(2+)(2﹣)=1,则ab(a+b)=4×1=4,故答案为:4.19.解:由题意可知:a<0<b,∴a+b<0,a﹣b<0,∴原式=﹣(a+b)﹣(a﹣b)=﹣a﹣b﹣a+b=﹣2a,故答案为:﹣2a20.解:∵1<<2,4<<5,a为整数,∴2≤a<5,∴满足<a<的整数a的值可以为2,故答案为:2(答案不唯一).21.解:∵≥0,∴+2≥2,即的最小值是2.故答案为:2.22.解:原式=2﹣3=﹣.故答案为:﹣.23.解:∵(a+)2+=0,∴(a+)2=0,=0,解得,a=﹣,b=2,则a b=(﹣)2=3,故答案为:3.24.解:原式==+,故答案为:+25.解:∵2<<3,2<<3,∴a=﹣2,b=2,a+b=﹣2+2=,故答案为.26.解:∵4<<5,∴的小数部分是﹣4,故答案为:﹣4.27.解:原式=(x+1)2,当x=﹣1时,原式=()2=2.三.解答题(共3小题)28.解:(π﹣3.14)0+()﹣1﹣|﹣3|=1+2﹣3+2=229.解:﹣14+|﹣2|﹣(π﹣3.14)0+÷=﹣1+2﹣﹣1+=030.解:由数轴可知,a<0,a+b<0,c﹣a>0,b﹣c<0,∴|a|﹣|a+b|+|c﹣a|+|b﹣c|=﹣a+a+b+c﹣a﹣b+c =﹣a+2c.。
完整版)实数练习题基础篇附答案

完整版)实数练习题基础篇附答案实数练题一、判断题(1分×8=8分)1.3不是9的算术平方根。
(×)2.2的平方根是根号2,它的算术平方根也是根号2.(√)3.-2没有实数平方根。
(×)4.-0.5不是0.25的一个平方根。
(×)5.2的平方根是a。
(×)6.6根是4.(√)7.-10不是1000的一个立方根。
(×)8.-7是-343的立方根。
(√)9.无理数可以用数轴上的点表示出来。
(√)10.有理数和无理数统称实数。
(√)二、选择题(3分×5=15分)11.列说法正确的是(B)A、1是0.5的一个平方根B、正数有两个平方根,且这两个平方根之和等于它们的和C、7的平方根是7D、负数有一个平方根12.如果y=0.25,那么y的值是(C)A、0.0625B、-0.5C、0.5D、±0.513.如果x是a的立方根,则下列说法正确的是(A)A、-x也是a的立方根B、-x是-a的立方根C、x是-a的立方根D、x等于a14.√3、22/7、-3、3343、3.1416都是无理数,它们的个数是(C)A、1个B、2个C、3个D、4个15.与数轴上的点建立一一对应的是(C)A、全体有理数B、全体无理数C、全体实数D、全体整数16.如果一个实数的平方根与它的立方根相等,则这个数是(A)A、0B、正实数且等于1C、负实数且等于-1D、1三、填空题(1分×30=30分)2.100的平方根是10,10的算术平方根是3.3.±3是√9的平方根,-3是√9的平方根;(-2)^2的算术平方根是2.4.正数有两个平方根,它们分别是正数和负数;负数没有实数平方根。
5.-125的立方根是-5,±8的立方根是2,27的立方根是3.6.正数的立方根是正数;负数的立方根是负数;0的立方根是0.7.2的相反数是-2,-π≈-3.14.8.比较下列各组数大小:⑴ <⑵ 3-64=2.5>1.5⑶ π≈3.14<3.5⑷ 2322>2000四、解下列各题。
中考数学总复习第1课时实数基础过关训练新人教版(new)

第1课时实数知能优化训练中考回顾1.(2017福建中考)3的相反数是()A.-3B.-C D.3答案:A2.(2017青海西宁中考)在下列各数中,比—1小的数是()A.1 B。
—1C.—2D.0答案:C3.(2017天津中考)计算(—3)+5的结果等于()A.2B.-2C。
8 D.—8答案:A4.(2017四川成都中考)《九章算术》中注有“今两算得失相反,要令正负以名之",意思是:今有两数若其意义相反,则分别叫做正数与负数。
若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为()A。
零上3 ℃B。
零下3 ℃C.零上7 ℃D。
零下7 ℃答案:B5.(2017天津中考)据《天津日报》报道,天津市社会保障制度更加成熟完善,截至2017年4月末,累计发放社会保障卡12 630 000张,将12 630 000用科学记数法表示为()A.0.126 3×108B.1.263×107C。
12。
63×106D。
126。
3×105答案:B6。
(2017青海西宁中考)市民惊叹西宁绿化颜值暴涨,2017年西宁市投资25 160 000元实施生态造林绿化工程建设项目。
将25 160 000用科学记数法表示为。
答案:2。
516×1077.(2017新疆中考)计算:-|-|++(1—π)0。
解:原式=2-+2+1=3+模拟预测1.在0,1,—2,-3.5这四个数中,是负整数的是()A.0B.1C.—2 D。
—3。
5解析:-2是负整数,故选C.答案:C2。
若x=(-3),则x的倒数是()A.-BC。
-2 D。
2解析:因为x=(—3)=-,所以x的倒数是-2.故选C.答案:C3.对于-(-8),有下列理解:①可表示—8的相反数;②可表示-1与—8的乘积;③可表示-8的绝对值;④运算结果等于8。
其中错误的个数是()A。
0 B。
1C。
2 D.3答案:A4。
如图,数轴上A,B两点对应的实数分别为1和,若点A关于点B的对称点为C,则点C所表示的实数是()A。
人教版七年级下册《6.3第1课时实数的概念》同步练习(含答案)
6.3实数第1课时实数的有关概念关键问答①无理数有几种常见的表现形式?②数轴上的每一点都可以表示一个什么样的数?1.①2017·滨州下列各数中是无理数的是()A. 2B.0 C.12017D.-12.②如图6-3-1,半径为1个单位长度的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr),把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,则点A表示的数是________,属于__________(填“有理数”或“无理数”).图6-3-1命题点1无理数[热度:90%]3.③下列说法正确的是()A.无理数就是无限小数B.无理数就是带根号的数C.无理数都是无限不循环小数D.无理数包括正无理数、0和负无理数易错警示③(1)无理数的特征:无理数的小数部分位数无限且不循环,不能表示成分数的形式.(2)常见的无理数有三种表现形式:化简后含π的数;有规律的无限不循环小数,如:1.3131131113…;含有根号且开方开不尽的数,如5,36.4.④在下列各数:0.51525354…,0,0.2,3π,227,9,39,13111,27中,是无理数的有________________________.方法点拨④一个数不是有理数就是无理数,识别一个数是不是有理数,只需看其是不是整数或分数即可.5.有一个数值转换器,原理如图6-3-2所示:当输入的x 为256时,输出的y 是________.图6-3-26.⑤在1,2,3,…,100这100个自然数的算术平方根和立方根中,无理数共有多 少个?方法点拨⑤分别找出1~100这100个自然数的算术平方根和立方根中有理数的个数,即可得出无理数的个数.命题点 2 实数的概念与分类 [热度:95%] 7.⑥下列说法中,正确的是( ) A .正整数、负整数统称整数 B .正数、0、负数统称有理数C .实数包括无限小数与无限不循环小数D .实数包括有理数与无理数 易错警示⑥实数包括有理数和无理数,即有限小数、无限循环小数、无限不循环小数. 8.⑦有下列说法:①两个无理数的和还是无理数;②无理数与有理数的积是无理数;③有理数与有理数的和不可能是无理数;④无限小数是无理数;⑤不是有限小数的数不是有理数.其中正确的有( )A .0个B .1个C .2个D .3个 解题突破⑦两个无理数的和或差不一定是无理数.9.⑧实数13,24,π6中,分数有( )A .0个B .1个C .2个D .3个 方法点拨⑧分数是两个整数作商,不能整除的数. 10.下列说法错误的是( ) A.14是有理数 B.2是无理数 C .-3-27是正实数 D.22是分数11.在数轴上,表示实数2与10的点之间的整数点有________个;表示实数2与10之间的实数点有________个.12.将下列各数填在相应的集合里: 3512,π,3.1415926,-0.456,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),0,511,-321,(-13)2,0.1.有理数集合:{_____________________________________________…};无理数集合:{_____________________________________________…};正实数集合:{_____________________________________________…};整数集合:{_______________________________________________…}.命题点3实数与数轴[热度:98%]13.下列说法中正确的是()A.每一个整数都可以用数轴上的点表示,数轴上的每一个点都表示一个整数B.每一个有理数都可以用数轴上的点表示,数轴上的每一个点都表示一个有理数C.每一个无理数都可以用数轴上的点表示,数轴上的每一个点都表示一个无理数D.每一个实数都可以用数轴上的点表示,数轴上的每一个点都表示一个实数14.⑨如图6-3-3,数轴上的A,B,C,D四个点表示的数中,与-3最接近的是()图6-3-3A.点A B.点B C.点C D.点D解题突破⑨-3介于哪两个连续的整数之间?这两个连续的整数中哪个整数的平方与3的差的绝对值小?15.2018·宁晋县期中如图6-3-4,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是()图6-3-4A.π-1 B.-π-1C.-π-1或π-1 D.-π-1或π+116.⑩在同一数轴上表示2的点与表示-3的点之间的距离是________.方法点拨⑩数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数.17.⑪如图6-3-5所示,按下列方法将数轴的正半轴绕在一个圆(该圆的周长为3个单位长度,且在圆周的三等分点处分别标上了数字0,1,2)上.先让原点与圆周上0所对应的点重合,再将数轴的正半轴按顺时针方向绕在该圆周上,使数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,这样数轴的正半轴上的整数就与圆周上的数字建立了一种对应关系.图6-3-5(1)圆周上数字a与数轴上的数字5对应,则a=__________;(2)数轴绕过圆周100圈后,一个整数点落在圆周上数字2所对应的位置,这个整数是________.模型建立⑪数轴绕过圆周n圈(n为正整数)后,一个整数落在圆周上数字2所对应的位置,这个整数是3n+2.18.阅读下面的文字,解答问题.大家都知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,所以将2减去其整数部分,差就是其小数部分.(1)你能求出5+2的整数部分和小数部分吗?(2)已知10+3=x +y ,其中x 是整数,且0<y <1,请求出x -y 的相反数.19.⑫定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作是分母为1的有理数;反之为无理数.如2不能表示为两个互质的整数的商,所以2是无理数.可以这样证明:设2=a b ,a 与b 是互质的两个整数,且b ≠0,则2=a 2b 2,a 2=2b 2.因为b 是整数且不为0,所以a 是不为0的偶数.设a =2n (n 是整数),所以b 2=2n 2,所以b 也是偶数,这与a ,b 是互质的两个整数矛盾,所以2是无理数.仔细阅读上文,求证:5是无理数.方法点拨⑫从结论的反向出发,经推理,推得与基本事实、定义、定理或已知条件相矛盾的结果,这样的方法称为反证法.典题讲评与答案详析1.A 2.-2π无理数 3.C4.0.51525354…,3π,39,27[解析] 因为0是整数,0.2可化成分数,9=3,是整数,13111,227是分数,所以这五个数都是有理数.0.51525354…,3π,39,27都是无理数.5.2[解析] 由题图中所给的程序可知,把256取算术平方根,结果为16,因为16是有理数,所以再取算术平方根,结果为4,是有理数.再取4的算术平方根,结果为2,是有理数.再取算术平方根,结果为2,2是无理数,所以y= 2.6.解:∵12=1,22=4,32=9,…,102=100,∴1,2,3,…,100这100个自然数的算术平方根中,有理数有10个,∴无理数有90个.∵13=1,23=8,33=27,43=64,53=125,且64<100,125>100,∴1,2,3,…,100这100个自然数的立方根中,有理数有4个,∴无理数有96个,∴1,2,3,…,100这100个自然数的算术平方根和立方根中,无理数共有90+96=186(个).7.D[解析] 正整数、负整数、0统称为整数;有理数分为正有理数、0和负有理数;有理数包括无限循环小数和有限小数;实数包括有理数和无理数.8.B[解析] 两个无理数的和不一定是无理数,如2和-2;无理数与有理数的积也不一定是无理数,如2和0;有理数与有理数的和一定是有理数;无限不循环小数是无理数;有限小数和无限循环小数是有理数.9.B [解析] 分数是两个整数作商,不能整除的数,因此只有13是分数.10.D [解析]A 项,14=12是有理数,故选项正确;B 项,2是无理数,故选项正确;C 项,-3-27=3是正实数,故选项正确;D 项,22是无理数,故选项错误.故选D.11.2 无数12.有理数集合:{3512,3.1415926,-0.456,0,511,(-13)2,…};无理数集合:{π,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),-321,0.1,…};正实数集合:{3512,π,3.1415926,3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1),511,(-13)2,0.1,…};整数集合:{3512,0,(-13)2,…}.13.D [解析] 实数与数轴上的点具有一一对应的关系. 14.B15.C [解析]∵圆的直径为1个单位长度,∴此圆的周长=π,∴当圆向左滚动时点A ′表示的数是-1-π;当圆向右滚动时点A ′表示的数是π-1.16.2+3 [解析] 在同一数轴上表示2的点与表示-3的点之间的距离是2+||-3=2+ 3.17.(1)2 (2)302 [解析] (1)∵数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,∴圆周上的数字a 与数轴上的数字5对应时,a =2.(2)∵数轴上1,2,3,4,…所对应的点分别与圆周上1,2,0,1,…所对应的点重合,∴圆周上的数字0,1,2与数轴的正半轴上的整数0,1,2,3,4,5,6,7,8,…每3个一组分别对应,∴数轴绕过圆周100圈后,一个整数点落在圆周上数字2所对应的位置,这个整数是302.18.解:(1)∵4<5<9,∴2<5<3,∴5的整数部分是2,小数部分是5-2,∴5+2的整数部分是2+2=4,小数部分是5-2.(2)∵3的整数部分是1,小数部分是3-1,∴10+3的整数部分是10+1=11,小数部分是3-1,∴x=11,y=3-1,∴x-y的相反数是y-x=3-12.19.证明:设5=ab,a与b是互质的两个整数,且b≠0,则5=a2b2,a2=5b2.因为b是整数且不为0,所以a不为0且为5的倍数.设a=5n(n是整数),所以b2=5n2,所以b也为5的倍数,这与a,b是互质的两个整数矛盾,所以5是无理数.【关键问答】①无理数有三种常见的表现形式:一是含有根号且开方开不尽的数;二是化简后含π的数;三是人为创造的一些无限不循环小数.②数轴上的每一点都可以表示一个实数.。
人教版 数学七年级下册课时练 第六章 实数 6.3 第1课时 实数的概念
人教版 数学七年级下册 第六章 实数6.3 实数第1课时 实数的概念1.(教材P57,习题6.3,T1改编)下列说法正确的是( C )A .带根号的数一定是无理数B .无限小数一定是无理数C .无理数一定是无限小数D .无理数是开平方或开立方开不尽的数2.(2019·湖南邵阳中考)下列各数中,属于无理数的是( C ) A.13 B .1.414 C. 2 D. 43.(2018·湖北咸宁中考)写出一个比2大比3小的无理数(用含根号的式子表示)__5(答案不唯一)__.4.下列说法中,正确的是( C )A .无理数包括正无理数、零和负无理数B .无限小数都是无理数C .正实数包括正有理数和正无理数D .实数可以分为正实数和负实数两类5.把下列各数填在相应的大括号内:0,8,-3827,16,-27,-2,3,227,π4,0.101 001 000 1…(每两个1之间依次多一个0).自然数集合:{0,16,…};有理数集合:⎩⎨⎧⎭⎬⎫0,-3827,16,-2,227,…;正数集合:{8,16,3,227,π4,0.101 001 000 1…(每两个1之间依次多一个0),…};整数集合:{}0,16,-2,…;非负整数集合:{}0,16,…;无理数集合:{8,-27,3,π4,0.101 001 000 1…(每两个1之间依次多一个0),…}.6.(2019·湖北宜昌中考)如图,A,B,C,D是数轴上的四个点,其中最适合表示无理数π的点是( D)A.点A B.点BC.点C D.点D7.如图,O是原点,实数a,b,c在数轴上对应的点分别为A,B,C,则下列结论错误的是( B)A.a-b>0 B.ab<0C.a+b<0 D.b(a-c)>08.(2019·安徽合肥蜀山区期末)如图,将面积为3的正方形放在数轴上,以表示实数1的点为圆心,正方形的边长为半径作圆,交数轴于点A,B,则点A表示的数为__1-3__.易错点对无理数的概念理解不清而致错9.(2019·湖北黄冈期末)在实数:3.141 59,364,0.4.6.,1.010 010 001…(每两个1之间依次多1个0),π,227中,无理数有( B)A.1个B.2个C .3个D .4个10.已知点A 为数轴上表示实数2-1的点,将点A 沿数轴平移3个单位得到点B ,则点B 表示的实数为__2-4或__2+2__. 11.(2019·福建泉州惠安一模)任何一个无限循环小数都可以写成分数的形式.我们以无限循环小数0.5·为例说明如下:设0.5·=x ,由0.5·=0.555…可知,10x =5.555…,所以10x -x =5,解方程得x =59,于是,0.5·=59.请你把0.2·7·写成分数的形式:__311__.12.先阅读材料,再回答问题.因为12+1=2,且1<2<2,所以12+1的整数部分为1; 因为22+2=6,且2<6<3,所以22+2的整数部分为2; 因为32+3=12,且3<12<4,所以32+3的整数部分为3.(1)20的整数部分是__4__,小数部分是__20-4__;(2)以此类推,n 2+n (n 为正整数)的整数部分是__n __,请说明理由.解:(2)n ,理由如下:因为n 2<n 2+n <(n +1)2,即n <n 2+n <n +1,所以n 2+n 的整数部分为n .。
实数的基础训练
实数的基础训练(一)1、下列各式3π,π2-,03)(+π,1+π中无理数的个数是 。
2、面积为3的正方形的边长为 。
(如果是有理数写出这个有理数,如果不是有理数,写出它的近似值保留两个有效数字)3、已知a 为非0的有理数,b 为无理数,下列命题正确的是( )①b a +是无理数; ②b a -是无理数; ③ab 是无理数; ④ba是无理数。
A 、①②③④ B 、①② C 、①③ D 、①③④4、π的整数部分为 ,小数部分为 。
5、将下列各数填入适当的横线上:2,722,..21.2-,03)(+π,π,3.14159,4.121121112…。
有理数 , 无理数 。
6、在长方形ABCD 中,∠DAE=∠CBE=45°,AD=1,则AE 、BE 的长是有理数吗?△ABE 的面积是有理数吗?7、有一个直角三角形的两边是3cm 和4cm 则第三边的长度是有理数吗?如果是求出这个有理数,如果不是求出近似值。
(保留到小数点后1位)实数的基础训练(二)1、下列说法正确的是( ) A 、5是25的算术平方根。
B 、±4是16的算术平方根; C 、—6是()26-的算术平方根;D 、0.01是0.1的算术平方根。
2、81的算术平方根是 。
3、若2-a 有意义,则a 的最小整数值是 。
4、如果032=++-b a 则a b 的值为 。
5、若322+-+-=x x y 则y x -= 。
6、计算下列各题(1)121 (2)36.0± (3)36225(4)25.04112484+-7、已知x x x y 82112+-+-=求654-+y x 的算术根。
8、已知△ABC 的三边长分别为a 、b 、c 满足096432=+-+-+-c c b a ,试判断△ABC 的形状,并求出△ABC 的周长。
9、若5+11的小数部分为a ,5—11的小数部分为b ,求b a +的值。
实数的基础训练(三)1、实数4的平方根是 。
沪教版(上海)七年级第二学期12.1实数的概念基础训练(含答案)
1 / 5沪教版七年级第二学期12.1基础训练一、单选题1.下列实数是无理数的是( )AB .﹣1C .227D .3.14 2的结果在哪两个整数之间( )A .2和3B .3和4C .4和5D .5和6 3,227,2π中,无理数有( ) A .1个 B .2个C .3个D .4个 4.已知面积为8的正方形的边长为x ,那么下列对x 的大小的估计正确的是( ) A .13x << B .23x << C .34x << D .45x <<. 5.下列说法中正确的是( )A .无限小数都是无理数B .无理数都是无限小数C .无理数可以分为正无理数、负无理数和零D .两个无理数的和、差、积、商一定是无理数6)A .0和1之间B .1和2之间C .2和3之间D .3和4之间 7.在实数1, 3.14,03-中,无理数是( ) A .13 B. C . 3.14- D .0 8.设a 为正整数,且a<a+1,则a 的值为( )A .5B .6C .7D .89.实数a 在数轴上的位置如图所示,则a 2.5-=( )A .a 2.5-B .2.5a -C .a 2.5+D .a 2.5--10.下列数据:﹣52,0.21212121|﹣2|π,2.003003003⋯(相邻两个3之间有2个0),60.12345..(小数部分由相继的正整数组成),属于无理数的个数为( )A .6个B .5个C .3个D .4个 11.3184900精确到十万位的近似值为( )A .3.18×106B .3.19×106C .3.1×106D .3.2×106二、填空题12.设a 、b 均为有理数,且满足等式4=2b a ,则ab =_____.13.是一个无限不循环小数,它的小数点后百分位上的数字是__________. 14.在0,1,π,227-这些数中,无理数是___________ .15的点是 .16.已知m ,n 是两个连续整数,且m <n ,则m +n =_____.17_____.18.求23201312222+++++的值,可令:23201312222S =+++++,则3 / 523201422222S =++++,因此2014221S S -=-仿照以上推理,计算出23201613333+++++=__________.三、解答题 19.把下列各数分别填在表示它所属的括号里:,1,2019, 3.1,3---(1)无理数{_____…}(2)整数:{_____…}(3)分数:{_____…}20.把下列各数分别填在相应的集合里: -2.4,3,113-,227,0.333…,-(2.28),3.14,2--,1.010010001…(相邻两个1之间0的个数增加1),2015π-.(1)正有理数集合{ ……}(2)整数集合{ ……}(3)负分数集合{ ……}(4)无理数集合{ ……}21.将下列各数填入相应的集合中. 10.6,,8, 2.2,809,0.101,2,89.9,0.1010010001,0.4,9,032π--+-- 正数集合:{ ...}; 分数集合:{ ...}; 整数集合:{ ...}; 非正数集合:{ ...};自然数集合:{ ...}; 有理数集合:{ ...}. 22.把下列各数分别填在相应的集合中:60,5,3.141 592 6,227234.101 001 000 1…(相邻两个1之间依次多1个0).1 / 5 参考答案1.A2.C3.B4.B5.B6.C7.B8.B9.B10.C11.D 12.-213.614.π15.B16.517.403518.2017312- 190,2019,﹣2 ﹣13,﹣3.1 20.(1) {223,,0.333,3.147 ……}; (2){3,|2|-- ……};(3) {12.4,1,(2.28)3--- ……}; (4){ 1.010010001…(相邻两个1之间0的个数增加1),2015π-……}.21.略22.略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时1 实数的概念
知识点1 无理数的定义
1.(2018广东广州中考)四个数,
12中,是无理数的是 ( )
B.1
C.12
D.0
2.(2018广东汕头潮阳实验学校期中),,46π-是 ( )
A.0
B.1
C.2
D.3
3.给出下列说法:①无限小数都是无理数;②无理数都是无限小数;③带根号的数都是无理数;④两个无理数的和还是无理数.其中错误的是 .(填序号) 知识点2 实数的定义及分类
4.下列说法正确的是 ( )
A.正实数和负实数统称实数
B.正数、0和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
5.把下列各数分别填入相应的集合中.
1,,7
π-,-0.2121121112…(每两个2之间依次多一个1).
有理数集合:{ …};
无理数集合:{ …};
负实数集合:{ …}.
知识点3 实数与数轴的关系
6.(2017湖北武汉英格实验中学模拟)给出下列结论:①数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.
其中正确的是 ( )
A.①②
B.②③
C.③④
D.②③④
7.(2018山东淄博张店区二模)如图,若数轴上的点A,B 分别于实数-1,1对应,用圆规在数轴上画点C,则与点C 对应的实数是 ( )
A.2
B.3
C.4
D.5
知识点4 实数范围内的绝对值、相反数、倒数
8.(2018江苏苏州吴江区一模3 ( ) A.33 B.-3333 9.(2018吉林模拟2的倒数是 ( ) 2222
327-的倒数是 ,绝对值是 .
11.(2017河南洛阳孟津期中)设a 是最小的自然数,b 是最大的负整数,c 是绝对值最小的实数,求a+b+c 的值.、
12.28(27)a b +-与互为相反数,33a b 的值.
参考答案
1.A
解析:无限不循环小数叫做无理数.由此可知0,1,
12
是有理数是无理数.故选A.
2.C
解析513,所以4,6π是无理数,,-0.125,,所以无理数有2个.故选C.
名师点睛:无理数有三种形式:(1)开方开不尽的数,如
等;(2)与π有关的数,如2
π等;(3)构造型无理数,如0.101001…(每两个1之间依次多一个0)等. 3.①③④
解析:若无限小数不循环,则是无理数,若无限小数循环,则是有理数,所以①错误;因为无限不循环小数叫做无理数,所以无理数都是无限小数,所以②正确;带根号
的数不都是无理数,=2,2是有理数,,所以③错误;两个无
理数的和不一定是无理数,+(-与都是无理数,但它们的和是有理数,所以④错误.
4.D
5.解析:有理数集合:{,1,7
…};
无理数集合:π,-0.2121121112…(每两个2之间依次多一个1),…};
负实数集合:{,-1.414,-0.2121121112…(每两个2之间依次多一个1),…}.
名师点睛:对实数进行分类时,应先对某些数进行计算或化简,然后根据最后结果进行分类,不能仅看到用根号表示的数就认为一定是无理数.
6.B
解析:数轴上的点既能表示无理数,也能表示有理数,故①错误;易知②③正确;有
理数有无限个,无理数有无限个,故④错误.故选B.
7.B
解析:∵数轴上的点A,B分别与实数-1,1对应,∴AB=-1(1)
--=2.由题图,知BC=AB=2,∴与点C对应的实数是1+2=3.故选B.
8.C
9.B
10.-1
3
3
解析:的倒数是-1
3
,-3的绝对值是3,的倒数是-
1
3
,
绝对值是3.
11.解析:因为a是最小的自然数,所以a=0.因为b是最大的负整数,所以b=-1. 因为c是绝对值最小的实数,所以c=0,
所以a+b+c=0+(-1)+0=-1.
12.依题意,2
(27)
b-=0,∴a+8=0,b-27=0,∴a=-8,b=27,
=-2-3=-5.。
