spss正交试验设计
采用SPSS软件对正交试验设计结果进行分
采用SPSS软件对正交试验设计结果进行分析（1）将P268例题4数据编辑到Excel里，如图1所示。
图1 P268例题4数据（2）打开SPSS软件，Excel里（P268例题4）的数据导入到SPSS软件（也可以直接复制后粘贴到SPSS）中，见图2所示。
图2 P268例题4数据导入SPSS软件（3）点击【分析】【一般线性模型】【单变量】，如图3、图4所示。
图3图4（4）将“得率”导入【因变量】，将“A”、“B”、“C”主因素导入【固定因子】，如图5所示。
注意：由于“D”、“E”两列属于空列，千万不能导入到【固定因子】里面，否则SPSS软件无法进行正确的分析。
图5（5）点击【模型】，选择【设定】，将左边A、B、C三因素以主效应的类型导入到右边【模型】框里面，如图6所示。
点击【继续】退出【模型】。
图6（6）点击【两两比较】，将左框的A、B、C三个“因子”选中并导入到右框【两两比较检验】里面，如图7所示。
点击【继续】退出【两两比较】。
图7（7）如图8所示，点击【确定】。
图8（8）点击【确定】后，得到分析结果【查看器】，如图9所示。
图9 查看器所显示的结果（9）【主体间效应的检验】中显示的就是方差分析的结果，如图10所示。
图10 方差分析结果（10）在【主体间效应的检验】中选中需要的数据并列出方差分析表，如表1所示。
（11）由表1可知，A因素各水平间存在极显著差异，B、C两因素各水平间差异不显著，需对A因素各水平间进一步进行多重比较。
详见图11。
图11 A因素各水平间的多重比较结果（q法）【思考题】1.图11展示的是α=0.05水平下的显著性情况，如何将α=0.01水平下的显著性情况列出来？2.图11中多重比较的结果是采用的“子集”的形式进行表达，需要转化为“字母标记法”，如何转化？。
SPSS软件在正交试验设计、结果分析中的应用
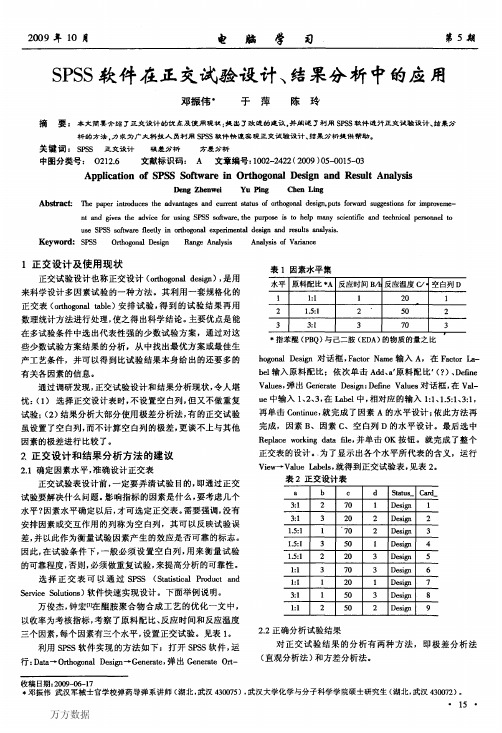
Ｐ Ｏ．０９１９ Ｏ．０００ Ｏ．０９９ ０．０１６ ０．０００ ０．０１６
综合表６、７，可以得出：Ｂ。均数最大（８．３３３），且Ｂ３与 Ｂ，、Ｂ：之间存在显著性的差异（Ｐ＜０．０５），Ｂ。、Ｂ：之间不存在 显著性的差异（Ｐ＝Ｏ．０９９＞０．０５）
同理，可以从另外的几张表格中分析可以得到：Ａ：均数 最大（９．０６７），且Ａ。、Ａ：、Ａ，之间均存在显著性差异；Ｃ：均 数最大（１０．３００），Ｃ。、Ｃ：、Ｃ，之间也都存在显著性差异。
总结论：中华芦荟丛生芽诱导的最佳培养基为：
Ａ２８１Ｃ２，即６一ＢＡ：２．０ｒａｇ／Ｌ：ＮＡＡ：０．３ｒａｇ／Ｌ：
· １６ ·
万方数据
２００９年１０月
电脑学 习
第５期
一个用ＶＢＡ编写的Ｑｕｉｎｅ
蓝鹰‘
刘松
摘 要：本文介绍了一个在ｗｏｒｄ
Ｗｏｒｄ
递归定理
中图分类号：ＴＰ３１１．１
文献标识码： Ａ 文章编号：１００２－２４２２（２００９）０５－００１７－－０１
Ａ ＶＢＡ Ｑｕｉｎｅ
Ｌａｎ Ｙｔｎｇ
Ａｂｓｔｒａｃｔ：Ｉｎ ｔｈｉｓ ｐａｐｅｒ，ａ ＶＢＡ Ｑｕｉｎｅ ｉｓ ｐｒｅｓｅｎｔｅｄ．
Ｋｅｙｗｏｒｄ：Ｑｎｌ．ｅ ＶＢＡ Ｗｏｒｄ
Ｒｅｃｕｒｓｉｏｎ Ｔｈｅｏｒｅｍ
２００９年１０月
电脑学 习
第５期
ＳＰＳＳ软件在正交试验设计、结果分析中的应用
邓振伟’
于萍 陈玲
摘 要：本文简要介绍了正交设计的优点及使用现状：提出了改进的建议．并阐述了利用ＳＰＳＳ软件进行正交试验设计、结果分
析的方法。力求为广大科技人员利用ＳＰＳＳ软件快速实现正交试验设计、结果分析提供帮助。
关键词：ＳＰＳＳ 正交设计 极差分析
SPSS软件在正交试验设计、结果分析中的应用
SPSS软件在正交试验设计、结果分析中的应用SPSS软件在正交试验设计、结果分析中的应用随着科学技术的飞速发展，正交试验设计在科学研究中的应用越来越广泛。
作为一种系统化的试验设计方法，正交试验设计在优化实验条件、提高实验效率、探索因素间相互作用等方面具有独特的优势。
而SPSS软件作为一种功能强大的统计分析工具，因其简单易学、数据处理能力强等特点，被广泛应用于正交试验设计及结果分析中。
本文将介绍SPSS软件在正交试验设计中的应用，并探讨其在结果分析中的优势。
一、SPSS软件在正交试验设计中的应用1. 正交试验设计的建立正交试验设计包括确定试验因素、确定水平数以及构建正交表格等步骤。
SPSS软件可以帮助实验者进行正交设计的建立。
首先，通过SPSS软件的数据管理功能，可以方便地建立试验因素、水平数等信息的数据框架。
然后，通过使用SPSS的数据编辑功能，可以轻松地输入试验因素的水平值。
最后，SPSS软件提供了正交试验设计模块，可以自动生成正交表格，并计算出试验所需的实验组合数。
通过SPSS软件的帮助，实验者可以快速、方便地完成正交试验设计的建立。
2. 数据的收集和整理正交试验设计所得到的数据需进行收集和整理，以便后续的结果分析。
SPSS软件提供了强大的数据处理功能，可以帮助实验者对数据进行收集和整理。
首先，SPSS软件提供了数据输入模块，可以方便地将实验数据输入到软件中。
其次，SPSS软件提供了数据清洗和转换的功能，可以对异常数据进行筛选和删除，并进行数据的转化、归一化等操作。
通过SPSS软件，实验者可以高效地对实验数据进行整理和准备，为后续的结果分析打下良好的基础。
3. 结果的分析与解释正交试验设计通过多因素的对比和交叉设计，可以更全面地了解各因素对实验结果的影响。
而SPSS软件作为一种统计分析工具，具备强大的数据分析能力，可以对正交试验设计所得到的数据进行有效的结果分析。
首先，SPSS软件提供了多种统计方法，如方差分析、回归分析等，可以对试验结果进行综合分析和比较。
SPSS的正交实验设计课件
结果如下：
因素C的多重比较结果，表显示的是两两水平比较，其中1-2的 P值为0.104，大于0.05，说明因素C的水平1和2之间没有显著 差异，水平1和3以及水平2和3的P值分别为0.015和0.034，都 小于0.05，说明因素C的这两组水平之间有显著差异。
结果如下：
检验结果表明：因素A和因素B的P值分别为0.071和0.136 ，都大于0.05，那么这两个因素对实验结果y的作用不显著 ；因素C 的P值为0.028，小于0.05，说明因素C显著。
最优组合先选择因素C最好，因为该因子对试验结果影响显著，操 作步骤如下：
step1，在“Aanalyze”菜单“General Linear Model”中选择Univariate命令；在 弹出的Univariate对话框中，选择“y”变量，使之添加到Dependent Variable框中 ，选择“a”、“b”变量，“c“变量使之添加到Fixed Factor框中；
结果如下：
由以上3个表发现，对于c变量来 说，水平3最好；而因素a和b没有 显著影响，故可随意选择，而最 优组合的选择取决于实验结果y的 取值方向，即实际中y是越大越好 ，还是越小越好，对于本题来说y 是越大越好，则最优组合为： a3B2c3（参考）
7
ቤተ መጻሕፍቲ ባይዱ
3
1
3
2
57
8
3
2
1
3
62
9
3
3
2
1
64
正交实验方差分析
例1 无重复正交实验的方差分析 说明：三因素正交表L9（34） 1、“L”是正交表的代号，L的下标“9”表示表的行数，
利用SPSS软件实现药学实验中正交设计的方差分析
利用SPSS软件实现药学实验中正交设计的方差分析利用SPSS软件实现药学实验中正交设计的方差分析一、引言药学实验中正交设计是一种常用的实验设计方法，可以有效地降低误差和提高实验的精确度。
方差分析是统计学中常用的一种方法，可以用于分析不同因素对实验结果产生的影响。
本文旨在介绍如何利用SPSS软件实现药学实验中正交设计的方差分析，并解释如何解读分析结果。
二、正交设计的基本概念正交设计是指通过合理的选取试验因素的水平和组合方式，使得每个试验因素的主效应与交互效应之间相互独立，从而实现在有限试验条件下获得尽可能多的信息。
正交设计的特点是可以同时考察多个因素的效应，并减少试验数目，节省时间和成本。
三、SPSS软件的使用SPSS是一种非常强大的统计分析工具，可以用于数据的录入、整理、分析和可视化展示。
在进行正交设计的方差分析时，首先需要将实验数据录入到SPSS软件中，然后按照正交设计的分组方式进行数据整理和分析。
四、数据录入和整理在SPSS软件中，将实验数据录入到一个数据表格中，每个试验因素作为一个独立的变量，每个因素的不同水平分别作为变量的取值。
然后将所有的结果数据作为一个单独的变量，与试验因素的变量进行对应。
完成数据录入后，可以进行数据的整理，例如删除缺失值、处理异常值等。
五、方差分析模型的建立在SPSS软件中，可以通过“分析”-“一元方差分析”来建立方差分析模型。
在模型建立时，需要选择适当的模型类型，例如单因素方差分析、双因素方差分析等，根据实验设计的具体要求进行选择。
六、方差分析结果的解读方差分析的结果可以通过SPSS软件进行自动计算和解释。
在解读结果时，主要关注F值和P值。
F值表示组间变异与组内变异的比值，用于判断因素对实验结果的影响是否显著。
P值表示假设检验的结果，如果P值小于显著性水平（通常为0.05），则可以拒绝原假设，说明因素对实验结果的影响是显著的。
七、方差分析图的绘制在SPSS软件中，可以通过“图表”-“散点图”来绘制方差分析图。
SPSS用于正交试验优化设计及其方差分析
SPSS用于正交试验优化设计及其方差分析试验优化设计，指在最优化思想的指导下，进行最优设计的一种优化方法，从不同的优良性出发，合理设计试验方案，有效控制试验干扰，科学处理试验数据，全面进行优化分析，直接实现优化目标。
正交试验设计是试验优化的常用技术，在农业试验、工业优化、商业优化等方面应用已久。
主要优点是能在多试验条件中选出代表性强的少数试验方案，通过对这些少数试验方案结果的分析，从中找出最优方案或最佳生产工艺条件，并可以得到比试验结果本身给出的还要多的有关各因素的信息。
SPSS软件不仅具有包括数据管理、统计分析、图表分析、输出管理等在内的基本统计功能，而且用它处理正交试验设计中的数据程序简单，分析结果明了。
【实施正交试验设计的步骤】1、明确试验目的，确定考核指标明确通过正交试验想要解决什么问题，确定用来衡量试验效果的评价指标，并详细描述出评定该指标的原则标准、测定指标的方法重要信息。
2、挑因素，选水平有依据的选择引起指标变化的影响因素，因素在试验中的各种状态称为因素的水平。
尽量选择适用于人为控制的和调节的影响因素，最后列出因素水平表。
3、选择合适的正交表在能够安排下试验因素和交互作用前提下，尽可能选用较小的正交表，以减少试验次数和成本的消耗。
4、进行表头设计表头设计即将试验因素安排到所选正交表的各列中去的过程。
正交表中的任意一列的位置是一样的，可以任意变换，因此不考虑交互作用的情况下可直接将所有因素安排在任意一列；如果考虑交互作用，则必须按照交互作用列表的规定进行配列；为避免混杂，那些主要因素重点考察的因素涉及交互作用较多的因素，应优先安排；特别注意，尽可能安排空列，用于反映试验误差，并以此作为衡量试验因素产生的效应是否可靠的标志。
5、排出试验方案表头设计完成后，将所选正交表中各列的不同数字换成对应因素的相应水平，形成试验方案。
试验方案中的试验号并不意味着实际进行试验的顺序，一般需同时进行，若条件不允许，为排除外界环境干扰，应使试验序号随机化。
利用SPSS的正交设计
Orthogonal experimental design 1.定义是利用一套规格化的“正交表”，将实验因素、各水平之间的组合均匀搭配、合理安排，用较少的、有代表性的处理组合数，提供充分有用信息的一种高效、快速的多因素实验设计方法。
2. 因素和水平因素factor：实验结果或观察指标的影响因素。
水平level：各因素的不同状态。
3. 主效应和交互作用主效应main effect—每个因素对观察指标的作用。
交互作用interaction—一些因素取不同水平时对另一些因素的作用。
两个因素间的交互作用，称为一级交互作用，记为A×B。
三个因素间的交互作用，称为二级交互作用，记为A×B×C。
三个因素以上的交互作用统称为高级交互作用。
经验证明，二级交互作用大多可以忽略，高级交互作用则全部可以忽略。
L n (m k ) L 4 (2 3 ) 是指最多可以安排3个两水平的因素作4次实验的正交表。
实验次数因素及其水平 A B C 第一次第二次第三次第四次A1 A1 A2 A2 B1 B2 B1 B2 C1 C2 C2 C1 L 8 (2 7 ) 实验次数因素及其水平A B C 第一次第二次第三次第四次第五次第六次第七次第八次A1 A1 A1 A1 A2 A2 A2 A2 B1 B1 B2 B2 B1 B1 B2 B2 C1 C2 C1 C2 C1 C2 C1 C2 （1）安排某个因素（2）安排某种交互作用（3）空列（做误差用）L 4 (2 3 ) 列号列号 1 2 3 1 2 3 2 1 L 8 (2 7 ) 列号列号1 2 3 4 5 6 7 1 2 3 2 1 5 6 7 4 7 6 1 7 4 5 2 3 6 5 4 3 2 1 根据分析需要，选用合适的正交表，将各个因素安排在正交表的各列的过程，称为表头设计。
表头设计原则：根据因素个数、水平数合理安排主效应和因素之间的交互作用。
利用SPSS进行方差分析以及正交试验设计
利用SPSS进行方差分析以及正交试验设计方差分析是一种常见的统计方法，用于比较两个或多个组之间的差异。
正交试验设计是一种实验设计方法，能够同时考虑多个因素对结果的影响。
本文将利用SPSS进行方差分析和正交试验设计的步骤介绍，并讨论如何解读分析结果。
首先，我们将介绍方差分析的步骤。
方差分析的基本思想是比较组间和组内的变异程度。
假设我们有一个因变量和一个自变量，自变量有两个或多个水平。
下面是方差分析的步骤：1.导入数据：将数据导入SPSS软件，并确保每个变量都已正确标记。
2.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"方差"，再选择"单因素"。
3.设置因变量和自变量：在弹出的对话框中，将需要进行方差分析的因变量拖放到因素列表框中，然后将自变量也拖放到因素列表框中。
4.点击"设定"按钮：点击"设定"按钮，设置方差分析的参数，例如是否需要进行正态性检验、多重比较等。
然后点击"确定"。
5.查看结果：SPSS将输出方差分析的结果，包括各组之间的F值、p值等统计指标。
可以根据p值判断各组之间是否存在显著差异。
接下来，我们将介绍正交试验设计的步骤。
正交试验设计是一种多因素独立变量的实验设计方法，可以在较小的实验次数内获得较高的信息量。
下面是正交试验设计的步骤：1.设计矩阵：根据研究目的和独立变量的水平，构建正交试验的设计矩阵。
2.导入数据：将设计矩阵导入SPSS软件，并将每个变量的水平标注为自变量。
3.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"一般线性模型"，再选择"多元方差分析"。
4.设置因变量和自变量：在弹出的对话框中，将因变量拖放到因子列表框中，然后将自变量也拖放到因子列表框中。
5.点击"设定"按钮：点击"设定"按钮，设置正交试验设计的参数，例如交互作用是否显著、多重比较等。
spss正交设计
Spss正交设计1问题提出：很多朋友才接触或长期没有接触正交试验，用起来很是头疼，甚至很是复杂的设计正交表搞的晕晕！本问主要介绍spss软件设计正交表！为什么选择者spss软件作为正交表设计软件，主要因为spss统计分析功能齐全、强大,当完成正交设计后可继续对正交表资料进行统计分析；另一点spss在全世界所公认软件之一。
因此通过图文并茂的方式来介绍正交设计。
2设计步骤2.1 举例做三因素三水平的例题来设计正交表，见表1。
表1 正交试验因素水平设计表水平因素A温度(℃)B时间(h)CpH1 60 0.5 6.02 70 1 7.03 80 1.5 8.02.2 spss设计图11双击spss图标后见上图1界面。
2 将出现图2的接口。
在此接口输入数据，见图3。
在图3中左下角点击变量视图可直接改变“VAR00001”、“VAR00002”、“VAR00003”为温度、时间、pH，最终结果见图4。
图2 图3图4 图53点击图2中的“数据”菜单，下拉菜单中有“设计正交”继续点击“生成”，最终弹出对话框，如图5.在1画红线的地方输入“温度”，红线2出灰色“添加”按钮变成黑色，点击“添加”将使温度添加到右边空白处，如图6.点击图6中红线温度，图5中的红线3“定义值”由灰变黑，点击“定义值”将出现图7，在图7中填写温度数值：60、70、80，然后点击“继续”，返回图8，按照上面步骤继续添加时间、pH 值。
图7 图84在图5中红线4填写正交表名称，点击确认则生成图9正交表。
图9鸣谢:此文章的完成是在我女朋友监督下所作,感谢她的鼓励!可有很多不足,希 望大家指正!。
spss与正交实验及结果分析
一、SPSS简介SPSS是世界上最早的统计分析软件，1984年SPSS总部首先推出了世界上第一个统计分析软件微机版本SPSS/PC+，开创了SPSS微机系列产品的开发方向，极大地扩充了它的应用范围，并使其能很快地应用于自然科学、技术科学、社会科学的各个领域，世界上许多有影响的报刊杂志纷纷就SPSS的自动统计绘图、数据的深入分析、使用方便、功能齐全等方面给予了高度的评价与称赞。
SPSS的基本功能包括数据管理、统计分析、图表分析、输出管理等等。
SPSS统计分析过程包括描述性统计、均值比较、一般线性模型、相关分析、回归分析、对数线性模型、聚类分析、数据简化、生存分析、时间序列分析、多重响应等几大类，每类中又分好几个统计过程，比如回归分析中又分线性回归分析、曲线估计、Logistic回归、Probit回归、加权估计、两阶段最小二乘法、非线性回归等多个统计过程，而且每个过程中又允许用户选择不同的方法及参数。
SPSS也有专门的绘图系统，可以根据数据绘制各种图形。
SPSS 的分析结果清晰、直观、易学易用，而且可以直接读取EXCEL及DBF数据文件，现已推广到多种各种操作系统的计算机上，它和SAS、BMDP并称为国际上最有影响的三大统计软件。
SPSS输出结果虽然漂亮，但不能为WORD等常用文字处理软件直接打开，只能采用拷贝、粘贴的方式加以交互。
这可以说是SPSS软件的缺陷。
二、方差分析例如 某高原研究组将籍贯相同、年龄相同、身高体重接近的30名新战士随机分为三组，甲组为对照组，按常规训练，乙组为锻炼组，每天除常规训练外，接受中速长跑与健身操锻炼，丙组为药物组，除常规训练外，服用抗疲劳药物，一月后测定第一秒用力肺活量(L)，结果见表。
试比较三组第一秒用力肺活量有无差别。
对照组为组一，锻炼组为组二，药物组为组三。
第一步：打开SPSS软件第二步：由数据视图切换为变量视图修改变量名称第三步：输入数据第四步：点击“分析” -- --比较均值 -- -- --单因素AVOVA, 如下所示：第五步：点击两两比较进行设置（选择“LSD”，选择“S-N-K”，点击继续）→点击选项（选择“描述性”，选择“方差同质性检验”，点击继续）→确定。
利用SPSS软件实现药学实验中正交设计的分析
利用SPSS软件实现药学实验中正交设计的分析一、概述正交设计，作为一种高效、系统的实验设计方法，在药学实验领域得到了广泛应用。
其核心思想是通过合理安排实验因素与水平，使得所有实验点都能够在多维因素空间中均匀分布，从而全面、有效地考察各因素对实验结果的影响。
正交设计不仅可以减少实验次数，提高实验效率，还能确保实验结果的可靠性和准确性。
在药学实验中，正交设计常被用于优化药物制剂的处方、工艺参数、质量控制等方面。
通过正交设计，研究人员可以系统地分析各种因素对药物性质、稳定性、生物利用度等的影响，为药物的研发和生产提供科学依据。
SPSS软件作为一款强大的统计分析工具，为药学实验中的正交设计分析提供了便利。
SPSS软件内置了丰富的统计分析模块，包括正交设计分析所需的方差分析、回归分析等。
通过SPSS软件，研究人员可以轻松地导入实验数据，进行正交设计分析，并生成详细的实验结果报告。
本文旨在介绍如何利用SPSS软件实现药学实验中正交设计的分析。
通过本文的阐述，读者将了解正交设计的基本原理、SPSS软件在正交设计分析中的应用方法以及案例分析等内容。
通过学习和实践，读者将能够熟练掌握SPSS软件在药学实验正交设计分析中的应用技巧，为药学研究和生产提供有力支持。
1. 正交设计在药学实验中的应用概述在药学实验中，正交设计作为一种高效的实验设计方法，被广泛应用于多个领域。
正交设计通过正交表来安排多因素多水平的实验，旨在找到影响实验结果的关键因素，并得出最优的实验方案。
在药学研究中，正交设计的应用主要体现在药物配方优化、药物剂型设计以及药物提取工艺研究等方面。
在药物配方优化方面，正交设计能够协助科研人员确定药物配方中各成分的最佳比例，以提高药物的疗效和稳定性。
通过正交设计的多因素组合设计，可以快速筛选出最佳组合方案，并对方案进行优化调整。
正交设计在药物剂型设计方面也发挥着重要作用。
利用正交设计，科研人员可以对不同的剂型因素进行组合，以获得最佳的药物剂型。
SPSS软件在正交试验设计_结果分析中的应用
SPSS软件在正交试验设计_结果分析中的应用正交试验设计是一种常用于实验研究中的设计方法，可以帮助研究者有效地分析和推断实验结果。
SPSS是一种常用的统计分析软件，可以提供数据管理、统计分析和结果展示的功能，因此在正交试验设计的结果分析中有着重要的应用。
在正交试验设计的结果分析中，SPSS可以提供以下几个主要的应用功能：1. 数据的导入与整理：SPSS可以将实验结果数据导入软件中进行统计分析。
首先，研究者需要将实验参数和结果数据整理成统一格式的数据文件，常见的格式包括Excel、CSV等。
然后，通过SPSS的数据导入功能，可以将数据文件导入到SPSS软件中进行后续的统计分析。
2.描述统计分析：在正交试验设计中，研究者通常关注各个因素对结果的影响程度。
SPSS可以提供各种描述统计方法，如平均值、标准差、频数等，帮助研究者了解各个变量之间的基本情况。
通过描述统计结果，可以初步判断各个因素之间的差异以及对结果变量的贡献程度。
3.方差分析：正交试验设计通常涉及到多个因素和多个水平，因此需要进行方差分析来判断各个因素的显著性。
SPSS可以提供单因素和多因素方差分析的功能，通过检验各个因素的F值和p值，可以判断各个因素的显著性。
此外，还可以进行多重比较分析，得出不同因素水平之间的差异以及交互作用的影响。
4.回归分析：在正交试验设计中，研究者可能还关注各个因素对结果变量的预测能力。
通过回归分析，可以建立因素与结果变量之间的线性关系模型，进一步研究各个因素对结果的影响程度。
SPSS提供了线性回归分析和多元线性回归分析的功能，通过回归系数和显著性检验，可以确定各个因素对结果变量的预测能力。
5.结果可视化和报告生成：SPSS还可以帮助研究者将分析结果可视化，比如通过绘制图表、制作图形化报告等，以便更直观地展示实验结果。
研究者可以选择合适的图表类型，并通过SPSS的可视化功能进行设计和生成。
此外，SPSS还提供报告生成的功能，可以根据分析结果自动生成报告文档，简化结果的总结和分享过程。
《2024年SPSS软件在正交试验设计、结果分析中的应用》范文
《SPSS软件在正交试验设计、结果分析中的应用》篇一一、引言正交试验设计是一种多因素、多水平的实验方法，它通过设计正交表来安排试验，以达到高效、准确地获取试验结果的目的。
随着科技的发展，数据处理和分析的难度逐渐增大，因此需要借助专业的统计软件进行辅助分析。
SPSS软件作为一款功能强大的统计分析软件，在正交试验设计及结果分析中发挥着重要作用。
本文将详细介绍SPSS软件在正交试验设计、结果分析中的应用。
二、SPSS软件在正交试验设计中的应用1. 试验设计在正交试验设计中，SPSS软件可以通过其内置的正交表生成器来生成正交表。
用户可以根据试验的具体需求，选择合适的因素数和水平数，生成相应的正交表。
这样，用户就可以根据正交表来安排试验，使得试验结果更加准确、可靠。
2. 数据分析在正交试验中，SPSS软件可以方便地收集和整理试验数据。
通过SPSS软件的数据导入功能，用户可以将试验数据导入到软件中，并进行清洗、整理和转换等操作。
这样，用户就可以得到一个清晰、规范的数据集，为后续的统计分析提供基础。
三、SPSS软件在正交试验结果分析中的应用1. 极差分析极差分析是正交试验结果分析中的一种常用方法。
通过SPSS 软件的极差分析功能，用户可以计算各因素的水平均值和极差值，从而确定各因素对试验结果的影响程度。
这样，用户就可以根据极差分析的结果，找出最优的水平组合，为生产实践提供指导。
2. 方差分析方差分析是正交试验结果分析中的另一种重要方法。
通过SPSS软件的方差分析功能，用户可以计算各因素对试验结果的方差贡献率，从而确定各因素的显著性水平。
这样，用户就可以了解各因素对试验结果的影响程度和重要性，为进一步优化试验方案提供依据。
3. 回归分析回归分析是一种常用的数据分析方法，可以用来研究变量之间的关系。
在正交试验中，通过SPSS软件的回归分析功能，用户可以建立各因素与试验结果之间的回归模型，从而了解各因素对试验结果的影响规律。
正交试验设计的spss分析
上机操作6：正交试验设计的spss分析习题：有一混合水平的正交试验，A因素为葡萄品种，A1、A2、A3、A4，B因素为施肥期，有B1、B2，C因素为施肥量，有C1、C2，重复三次，采用L8(4×24)正交表，试验结果如下表，试进行分析解：1.定义变量，输入数据：在变量视图中写入变量名称“产量”、“区组”、“施肥量”、“施肥期”、“品种”“处理”，宽度均为8，小数均为0。
并在数据视图依次输入变量。
2．分析过程：（1）正态分布检验：工具栏“图形”——“P-P图”，在“变量”中放入“产量”，“检验分布”为“正态”，“确定”。
（2）方差齐性检验：a.工具栏“分析”——“比较均值”——“单因素ANOVA”。
b.在“因变量”中放入“产量”，在“固定因子”中放入“品种”。
c.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
d.“确定”。
工具栏“分析”——“比较均值”——“单因素ANOVA”。
e.在“因变量”中放入“产量”，在“固定因子”中放入“施肥期”。
f.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
g.“确定”。
在“因变量”中放入“产量”，在“固定因子”中放入“施肥量”。
h.点击“选项”，在“统计量”中点击“方差同质性检验”，“继续”。
i.“确定”。
在“因变量”中放入“产量”，在“固定因子”中放入“处理”。
点击“选项”，在“统计量”中点击“描述性”和“方差同质性检验”，“继续”。
j.“确定”。
（3）显著性差异检验：a.工具栏“分析”——“常规线性模型”——“单变量”。
b.在“因变量”中放入“产量”，在“固定因子”中分别放入“施肥期”、“施肥量”、“品种”“区组”。
c.点击“模型”，“定制”，将“施肥期”、“施肥量”、“品种”、“区组”放入“模型”下。
在“建立项”中选择“主效应”，“继续”。
d.点击“两两比较”，将“施肥期”、“施肥量”、“品种”放入“两两比较检验”中，点击“假定方差齐性”中的“Duncan”。
SPSS软件在正交试验设计、结果分析中的应用
SPSS软件在正交试验设计、结果分析中的应用SPSS软件在正交试验设计与结果分析中的应用一、引言正交试验设计是一种经典的统计方法，用于研究多个因素对于实验结果的影响。
该方法将实验因素进行有序的组合，既能减少试验次数，又能避免因素之间的相互影响。
而SPSS软件作为统计分析领域中的瑞士军刀，拥有强大的数据处理和分析功能，为研究者提供了便利的工具。
本文将探讨SPSS软件在正交试验设计与结果分析中的应用。
二、正交试验设计的基本原理正交试验设计遵循一定的规则和原则。
首先，需要明确要研究的因素，这些因素可以是实验操作，也可以是实验条件。
其次，确定各个因素的水平，水平的选择要充分考虑实验的目的和研究对象。
然后，在确定因素和水平的基础上，构建正交试验设计表，以便按照设计表中的规则进行试验。
最后，根据试验结果，进行数据分析和结果解释。
三、SPSS软件在正交试验设计中的应用1. 设计试验方案SPSS软件提供了一系列的数据输入工具和试验设计模块，可以帮助研究者轻松地构建正交试验设计。
通过SPSS软件，可以灵活地选择因素和水平，并生成正交试验设计表。
同时，SPSS软件还提供了随机分组和重复设计等功能，以满足实验设计的要求。
2. 数据输入与整理SPSS软件支持多种数据输入方式，可以通过导入Excel表格、文本文件等格式的数据，或者直接在软件中手动输入数据。
在正交试验设计中，往往涉及大量的数据输入，SPSS软件的数据输入功能可以帮助研究者快速、准确地输入数据。
同时，SPSS软件还提供了数据整理和清理功能，可以对异常值、缺失值等进行处理，使得数据更加可靠。
3. 数据分析与解释SPSS软件的数据分析功能非常强大，可以进行多元方差分析、协方差分析、回归分析、相关分析等多种统计分析方法。
在正交试验设计中，可以使用SPSS软件进行多因素方差分析，以确定各个因素对实验结果的影响。
同时，SPSS软件还提供了图表制作功能，可以直观地展示分析结果。
SPSS的正交实验设计
2021/5/9
19
一个较好的方法即进行正交实验，它对每一因素的各水 平安排的实验次数是一样的，其次任两个因素之间又 是交叉分组的全面实验。
要安排一个正交实验，只要选用相应的正交表去安排实 验就可以了。
2021/5/9
2
正交实验方差分析
例1 无重复正交实验的方差分析
为提高某化工产品的转化率，选择了三个有关的因素，反应 温度（A），反应时间（B），用碱量（C），选取的水平 如下:(检验水平为0.1)
4(空)
转化率y
1
1
1
1
1
31
2
1
2
2
2
54
3
1
3
3
3
38
4
2
1
2
3
53
5
2
2
3
1
49
6
2
3
1
2
42
7
3
1
3
2
57
8
3
2
1
3
62
9
3
3
2
1
64
2021/5/9
4
正交实验方差分析
例1 无重复正交实验的方差分析 说明：三因素正交表L9（34） 1、“L”是正交表的代号，L的下标“9”表示表的行数，
表示要做9个不同条件的试验； 2、圆括号中的指数“4”表示表的列数，在试验中表示用
➢ step3，接步骤1对话框，单击options，在弹出的对话框中， 将a、b、c选到display means for中，点击continue，点击 ok。
2021/5/9
18
结果如下：
因素C的多重比较结果，表显示的是两两水平比较，其中1-2的 P值为0.104，大于0.05，说明因素C的水平1和2之间没有显著 差异，水平1和3以及水平2和3的P值分别为0.015和0.034，都 小于0.05，说明因素C的这两组水平之间有显著差异。
利用SPSS_进行方差分析以及正交试验设计
position-related consumption of civil servants has been swept by finance, consumer, regardless of cost, extravagance and waste in the civil service position-related consumption, abuse, corruption and embezzlement, corruption is important. Then, under the conditions of market economy, how to reform the existing civil duty consumption management, explores a source to prevent and curb the post consumption corruption way, is currently a major issue faced by honest work. Recently, I conducted research on this issue, this problem on some humble opinions. First, the existing public servants ' duty consumption the main problems seen from the investigation and reasons, in recent years, public servants ' duty consumption caused by the abuses and not a person of integrity, is one of the major problems in the party in Government, its operation order have a negative effect on the party and Government organs, seriously damaging the image of the party and the Government, undermining the relationship between party and the masses, effect, opening up and economic construction. From I County in recent years of governance situation see, positions consumption in the produced of "two not" phenomenon rendering four a features: a is positions consumption system lost has due of binding, right is greater than rules, and right is greater than method of phenomenon more highlight; II is in positions consumption in the Camera Obscura operation, using terms, will positions consumption into has personal consumption, will corporate points to into personal points to, makes positions consumption in some aspects has into positions enjoy and self-dealing of means; three is to positions consumption for name, fraud, false impersonator, Trend of negative corruption phenomena such as corruption and misappropriation; four palaces, follow the fashion, rivalries, wasteful, and post consumption became a symbol of showing off their individual capacities. Caused by public servants ' duty consumption of many "two" phenomenon in which people reflect the biggest problems are: (a) the official car problems. Mainly in three aspects: one is the larger buses cost expenditure. According to statistics, until November 2003, XX County township Department bus 159 cars, which department owns the bus 145 vehicles, and showed an increasing trend. Financial expenses cost per bus per year to 35,000 yuan, and in fact every cost up to 50,000 yuan. Some units also hiring temporary drivers and expenditure on wages and subsidies. Necessary to "keep a car", but also "dependants", leading to larger expenses. Second, gongchesiyong breed unhealthy tendencies. Some people believe that now some bus drivers use one-third, one-third leading private one-third used for official purposes. Some public servants, especially leading officials motoring, cars for private purposes, violating the self-discipline regulations, and even lead to traffic accidents. According to statistics from related departments, since 2004, the correct investigation in our County serves nearly 30 cars for private purposes, only the first half of this year, cars for private purposes orleaders driving a vehicle accident caused by road accidents, 1, 1 people killed and direct economic losses amounting to more than 100,000 yuan. Third, high efficiency and low cost of the bus. Surveys show that, the operating costs of taxis for the 8200/... Is a fundamental priority of the reform, it is a difficult problem that must be solved in the reform process. Clearly, the post consumption averages three years before as a base and fine-tuned on the basis of this single practices must be improved. Improvements to adhere to three principles: first, under the existing policy provisions approved for public servants ' duty consumption standards, calibration, is not contrary to policy. Second, according to the local financial situation and people's sustainability, public servants ' duty consumption standards approved, both financial reach, and people passing through. Third, according to the operational needs of civil servants responsible for authorized public servants ' duty consumption standards, both high and low positions, but also the nature of the work and the workload. In reform of method Shang, approved civil servants positions consumption standard to "big unified, and small dispersed" suitable, that most positions consumption project should according to policy provides proposed unified standard, consider to ranks, and units and the work task of differences sex, unified of standard should has elastic of and dynamic of, makes regions, and units in implementation unified standard Shi has must of flexible disposal right; but since set of standard must after financial, and audit, sector audit approved Hou to implementation. (C) reform package. Public servants ' duty consumption elasticity of consumption to limit consumption, turning mess into kitchen after dinner, follow the civil servant with a how to use personal title subsidies, or how to manage a personal duty consumption use of subsidies. Therefore, we must establish and perfect with public servants ' duty consumption monetization reform support of the series of governance systems such as the civil service examination of responsibility, system, low fault investigation system, the report said. While other measures to keep up. Discipline inspection and supervision organs, financial, auditing departments should strengthen supervision and inspection of public servants ' duty consumption monetization reform progress, to strengthen the reform of public servants ' duty consumption monetization system, measures to develop and monitor the implementation of inspection, not consumption as required, even shifting consumer behavior to stop, serious cases to deal with. Three ideas, public servants ' duty consumption monetization reform of politics, the economy and the deepening of the reform, public servants ' duty consumption as somewhere between a reform also demonstrated its importance and urgency. First of all, civil servants especially party and Government leaders and public servants ' duty consumption there are big drawbacks. NPC deputies and CPPCC members and the broad masses are concerned about. Secondly, the一、SPSS 简介SPSS 是世界上最早的统计分析软件，1984年SPSS 总部首先推出了世界上第一个统计分析软件微机版本SPSS/PC+，开创了SPSS 微机系列产品的开发方向，极大地扩充了它的应用范围，并使其能很快地应用于自然科学、技术科学、社会科学的各个领域，世界上许多有影响的报刊杂志纷纷就SPSS 的自动统计绘图、数据的深入分析、使用方便、功能齐全等方面给予了高度的评价与称赞。
SPSS并不适合进行正交表的生成
SPSS并不适合进行正交表的生成SPSS是IBM公司推出的一系列用于统计学分析运算、数据挖掘、预测分析和决策支持任务的软件产品及相关服务的总称。
由于其操作简单，已经在我国的社会科学、自然科学的各个领域发挥了巨大作用。
该软件还可以应用于经济学、数学、统计学、物流管理、生物学、心理学、地理学、医疗卫生、体育、农业、林业、商业等各个领域。
但事实上，该软件有它的局限性，这里从SPSS与正交试验的契合上予以说明。
从正交表的设计上来说明。
所谓正交试验设计就是利用一种规格化的表——正交表来合理地安排试验，利用数理统计的原理科学地分析试验结果、处理多因素试验的科学方法。
这种方法的优点是能够通过代表性很强的少数次试验，摸清各个因素对试验指标的影响情况，确定出因素的主次顺序，找出较好的生产条件或优参数组合。
经验证明，正交试验设计是一种解决多因素试验问题的卓有成效的方法。
正交表是正交设计的基本工具，它是根据均衡分散的思想，运用组合数学理论在拉丁方和正交拉丁方的基础上构造的一种表格。
鉴于正交表具有以上特点，这也就无形中规定了它应当有的一些固定化格式，比如说，最后的正交表当是“固定”的、“唯一”的，它的唯一性表现在，它是按照一定的渐进顺序依次排列，而不是混乱的，如下表4.1所示的L8(27)正交表，从序列号1开始一直到8，我们现实将“1”这个因素排列完毕，然后再去排列“2”和“3”，这也是我们在日常生产工作中所遵循的一种默认格式，这就方便了我们依次将试验进行到底，不致于将某个试验项遗漏。
表1用SPSS软件生成的正交表恰恰就不满足上面所说的特点，我们通过例子来予以说明。
【例】兔毛纤维集合体手感柔软、保暖性好，其很多方面的性能与羊绒类似，但兔毛纤维卷曲小，鳞片张角小且紧覆毛干，表面光滑，摩擦系数小，抱合力差，造成其可纺性差。
现将其按照混纺比70:30和腈纶混纺成纱。
研究不同的纺纱方法、温湿度条件对成纱强度的影响，不考虑因素之间的交互作用。