第二章 电阻电路的等效变换
第2章 电阻电路的等效变换总结

Req
def
∑R
k=1
n
k
8
i
+ u1 - + u2 R1
R2
+ un Rn
i 等效 + u -
+ u -
Req
(3)串联电阻的分压 uk = Rk i = Rk u < u Req 表明:电压与电阻成 正比,因此串联电阻 电路可作分压电路。
2018年10月15日星期一
p1 : p2 : : pn = G1 : G2 : : Gn 总功率 p = Gequ2 = Gequ2 = (G1+ G2+ + Gn ) u2
= G1u2 + G2u2 + + Gnu2 = p1 + p2 + + pn 表明
①电阻并联时,各电 阻消耗的功率与电 阻大小成反比;
=
C
B
2018年10月15日星期一
5
例如:
1 i
A R1 R3 1 i R5 R4 + u 1'
B
+ us -
R
+ u 1'
i4
R2
+ u5 -
+ us -
R
Req
• 欲求电流 i、电压 u和 uS 的功率等,可以用 Req 替代端子 1-1' 以右的部分,使问题得到简化。
注意:(1-1' 以右)虚线框内的电路是不同的。 如果需要计算 i4 和 u5 ,就必须回到原电路(A),
2018年10月15日星期一
利用已求得的 i 和 u 进一步计算。
2018年10月15日星期一
电路分析基础-第2章电阻电路的等效变换课件

3.元件与电流源的串联:等效为电流源。
1i + 元件 u iS
1+ i iS
u
2–
– 2
1i
+
R
1+ i iS
u iS
u
2–
1i +
+ uS
u iS –
– 2 1+ i
iS
u
2–
– 2
三、 实际电源的两种模型及其等效变换
实际电压源、实际电流源两种模型可以进行等效变换,所谓 的等效是指端口的电压、电流在转换过程中保持不变。
Req=( R1+ R2 +…+Rn) = Rk
结论 串联电路的等效电阻等于各分电阻之和。
等效:对外部电路(端钮 以外)效果相同。
2.串联电阻上电压的分配
R1
Rk
Rn
+
_ u1
i
+
+ uk _ u
+
un _ uk
_
Rk i
Rk
u Req
Rk u u Req
表明 电压与电阻成正比,因此串联电阻电路可作分压电路。
应用举例
例:2-3 如图所示电路,已知输入电压US =32V,求电压U0。
解: I 1
I 1
+ 1 32V
-
1 2
5 + 1 U0
1 15 -
+ 32V
Ω-
R2 5 +
R1 R3
1 15
U0 -
R1
1+1+ 11 2
5 2
R2
R3
1+ 2+ 12 1
第2章电阻电路的等效变换习题及答案
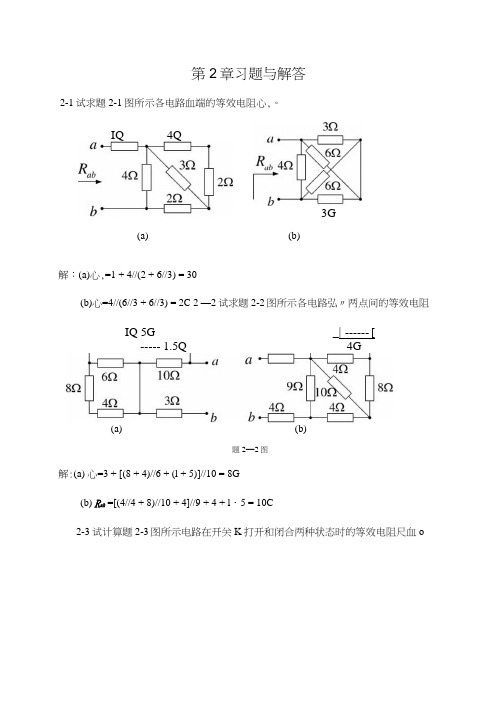
第2章习题与解答2-1试求题2-1图所示各电路血端的等效电阻心,。
解:(a)心,=1 + 4//(2 + 6//3) = 30(b)心=4//(6//3 + 6//3) = 2C 2 —2试求题2-2图所示各电路弘〃两点间的等效电阻IQ 5G_| ------ [ ----- 1.5Q 4G(a)(b)题2—2图解:(a) 心=3 + [(8 + 4)//6 + (l + 5)]//10 = 8G(b) R ah =[(4//4 + 8)//10 + 4]//9 + 4 + l ・5 = 10C2-3试计算题2-3图所示电路在开关K 打开和闭合两种状态时的等效电阻尺血oIQ 4Q3G(b)(a)题2—3图 解:(a)开关打开时心=(8 + 4)//4 = 3。
开关闭合时^,=4/74 = 20(b)开关打开时 R ah =(6 + 12)/7(6+12) = 90开关闭合时心=6//12 + 6//12 = 8。
2—4试求题2—4图(a)所示电路的电流/及题2—4图(b)所示电路的电压U 。
解:(a)从左往右流过1G 电阻的电流为I] =21/(1 + 6//12 + 3//6)二21/(l+4 + 2) = 3A 从上往下流过3 O 电阻的电流为I.= —x3 = 2A3 + 6 从上往下流过120电阻的电流为I p =—^-x3 = lA12 + 6 所以1 =【3叫2 = 1 A⑹从下往上流过6V 电压源的电流为"击莎1Q + O1V3Q 6Q(a)12Q6Q题2—4图从上往下流过两条并联支路的电流分别为2A所以U = 2x2-lx2=2V2 — 5试求题2 — 5图所示各电路ab端的等效电阻R ah,其中/?] = = 1。
2Q题2-5图解:(a)如图,对原电路做厶-丫变换后,得一平衡电桥所以心,=(*+*)//(1 + 1)= *°(b)将图中的两个Y形变成△形,如图所示2.5Q5Q 白804Q 4QT50T T2Q即得所以陰=L269G2 —6计算题2 —6图所示电路中弘b两点间的等效电阻。
第02章电阻电路的等效变换(丘关源)

(6)恒压源并联任何元件其两端电压不变;
恒流源串联任何元件其流出电流不变;
a a
+ us
-
+ +
-
对外等效
us
-
b
c
b c
对外等效
is
+
-
d
is
d
(1-30)
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解:
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS=+uS1 …-uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件:uS=uS1=uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
(1-21)
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS=+uS1-uS2
R=R1 + R2
(1-22)
二、理想电流源的串联和并联
电路原理(邱关源)习题解答第二章课件-电阻电路的等效变换练习

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻84R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA u i s 10100212===V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
邱关源《电路》第五版 第二章 电阻电路的等效变换

a
10
10 10 10
b
10
Rab=5
b
10
§2-3 电阻的串联和并联 求解等效电阻时必须注意:
* 首先搞清对何处等效;
* 分清串、并联关系;
* 可改画电路,原则是电阻相互联接关系不能改 变,但电阻位置可变,尽量缩短无阻支路,逐 步等效,逐步化简。 * 等电位点可以短路,电流为零的支路可以开路。 特别注意电路中有无平衡电桥电路。
-
2
§2-5 电压源、电流源的串联和并联 4. 电流源与任意支路串联
iS R i + 1
+
uS
iS + u
1
u
-
2 iS
1
-2
+
u
-
2
§2-5 电压源、电流源的串联和并联 5. 举例
【例1】化简电路。
iS1 =1A
-ห้องสมุดไป่ตู้
+
uS1=2V
1
+
uS2=2V
R1=1
iS2=1A
R2=1
2
§2-6 实际电源的两种模型及其等效变换
2
2
iS
iS iS1 iS2 iSn
iS1 iS 1 iS2 iSn
显然只有电流源 电流相等时,才允 2 许串联。
iS iS1 iS2 iSn
§2-5 电压源、电流源的串联和并联 3. 电压源与任意支路并联
+
uS
i R 1
+
uS
1 iS i
-
2 1
2
+
uS
i
3 R3 i3
i1
第二章电阻电路的等效变换2015
§ 2-2 电路的等效变换
电路等效:两个内部结构完全不同的二端网络,如果它 们端口上的对外的伏安关系相同,这两个网络是 等效的。
电路等效条件:端口对外具有相同的伏安关系。
电路等效变换的目的:化简电路、方便计算。
一个无源二端电阻网络可以用一电阻来等效。
I
I
+
无 等效 +
U_
源
U_
R等效 R等效= U / I
– 1
u31 R31
– i2
i3 +
2 +
R23 u23
3 –
+ i1Y 1 –
u12Y
– i2Y R2 2
+
R1
u31Y
u23Y
R3 i3Y +
3–
等效变换条件:
i1 = i1Y i2 = i2Y i3 = i3Y
u12 = u12Y u23 = u23Y u31 = u31Y
由Y :
R 12
1k
R
§ 2-4 电阻的Y形联结与形联结的等效变换
三端无源网络:
°பைடு நூலகம்°
无 源
°
+
–
i1 1
+ i1Y 1 –
u12 R12
– i2 2
+
u31 R31
R23 u23
i3 + 3
–
形联结
u12Y
– i2Y R2 2
+
R1
u31Y
u23Y
R3 i3Y +
3–
Y形联结
←→Y等效变换的条件:
+ i1 u12 R12
+
电路-第2章习题-电阻电路的等效变换
2-1、求电路的入端电阻R AB 。
R= 2//2+4//6AB答案 3.4Ω2-2、求各电路的入端电阻R AB。
(6//6+9)//102-3、求各电路的入端电阻R AB。
→解:(a)(3//6+1)//6=2Ω(b) 等效电路如图所示:即2-4、试求下图所示电路中的电流I。
答案-1.1A2-5、求图示电路中的电流i。
答案:- 0.1A2-6、电路如图所示,求B点的电位V B。
解:该电路图可以改变成如下图所示的形式2-7、电路如图所示,求电流I和电压U AB。
解:原电路可以等效变换为如下电路152-8、电路如图所示,求AB端的等效电阻R AB。
解:在AB端外加电源,使u、i对二端电路来说是关联参考方向。
由图可得:得到2-9、求图 (a) 和 (b) 所示两电路的输入电阻。
2-10、用电源等效变换法求图示电路中负载R L 上的电压U 。
12A5ΩR L+ -14V +-4Ω14-2Ω 2Ω2Ω2-11、化简为一个等效的电压源支路。
(a) (b) (c) (d)其中111R U I S S =,222R U I S S =,21S S S I I I +=,)(2121R R R R R S +=,S S S I R U =。
恒流源与恒压源的串联和并联两种情况(1) (2)2-12、化简图示电路。
(a) (b) (c) (d)2-13、在图(a )所示电路中,已知V 12=S U ,Ω=31R ,A 5=S I ,Ω=62R ,试求2R 支路中的电流2I 。
(a) (b) (c)解: 3)5312(633)(12112=++=++=S S I R U R R R I A10;2-14、在图示电路中,N为一个实际的直流电源。
当开关S断开时,电压表读数为V1。
试求该直流电源N的电压源模型与电流源模型。
当开关S闭合时,电流表读数为A解:等效电路如图:,2-15、电路如图所示。
已知Ω=61R ,Ω=1.02R ,98.0=α,Ω=53R ,V U 9.4=。
第2章电阻电路的等效变换习题及参考答案
精心整理第2章习题与解答2-1试求题2-1图所示各电路ab 端的等效电阻ab R 。
(a) (b)题2-1图解:(a )14//(26//3)3ab R =++=Ω(b 2-2解:(a (b 2-3(a)(b)解:(a (b 2-4(a) (b)题2-4图解:(a )从左往右流过1Ω电阻的电流为从上往下流过3Ω电阻的电流为36I 32A 36=⨯=+ 从上往下流过12Ω电阻的电流为126I 31A 126=⨯=+ 所以312I I -I =1A =(b )从下往上流过6V 电压源的电流为66I 4A 1.5===(1+2)//(1+2) 从上往下流过两条并联支路的电流分别为2A所以U 22-12=2V =⨯⨯2-5试求题2-5图所示各电路ab 端的等效电阻ab R ,其中121R R ==Ω。
(a) (b)题2-5图解:(a(b 即得所以ab R 2-6解:(a 所以ab R (b 所以ab R 2-7U 及总电压ab U 题2-7图解:将图中的Y 形变成△形,如图所示所以(32.5//526//2)//2655510ab R =++=+=Ω回到原图已知128I I +=348I I +=1310840I I +=245240I I +=联立解得1 2.4I A =2 5.6I A =32I A =46I A =所以121054U I I V =-+=2-8试求题2-8图所示电路的输入电阻in R 。
(a)(b)题2-8图解:(a )如图所示,在电路端口加电压源U ,求I 所以21(1)in U R R R Iμ==+- (b )如图所示,在电路端口加电压源U ,求I12R R U 2-(b 2-62-题2-11图解:先化简电路,如图所示43Ω所以有41(2933i i +-=3i A = 2-12题2-12图所示电路中全部电阻均为1Ω,试求电路中的电流i 。
题2-12图解:先求电路右边电阻块的等效电阻ab R ,如图所示将中间的Y 形化成△形。
电路 第五版高等教育出版社 原著邱关源第2章 电阻电路的等效变换PPT课件
B
i
+ 等效 u
-
C
i
+ u
-
对A电路中的电流、电压和功率而言,满足:
B
A
C
A
6
明确
①电路等效变换的条件: 两电路具有相同的VCR;
②电路等效变换的对象: 未变化的外电路A中的电压、电流和功率; (即对外等效,对内不等效)
③电路等效变换的目的: 化简电路,方便计算。
I4
3 2R
19
从以上例题可得求解串、并联电路的一般步骤: ①求出等效电阻或等效电导; ②应用欧姆定律求出总电压或总电流; ③应用欧姆定律或分压、分流公式求各电阻上的电
流电压
以上的关键在于识别各电阻的串联、并联关系!
例3 求: Rab , Rcd
cd 6 5 a
R a b(5 5 )/1 / 5 6 1Ω 2 R cd (1 5 5 )/5 /4 Ω
标题添加
点击此处输入相 关文本内容
点击此处输入 相关文本内容
2
重点: 1. 电路等效的概念; 2. 电阻的串、并联; 3. 电阻的Y— 变换; 4. 电压源和电流源的等效变换;
3
2.1 引言
线性电路
由线性时不变元件构成的电路
线性电阻电路
仅由电源和线性电阻构成的电路
简称:电阻电路
分析方法
①欧姆定律和基尔霍夫定律是分析 电阻电路的依据;
7
2.3 电阻的串联和并联
1.电阻串联
①电路特点
R1
Rk
Rn
i + u1 _ + u k _ + un _
+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返华回东理上工页大学下 页
(4) 功率
p1=G1u2, p2=G2u2,…, pn=Gnu2
p1: p2 : … : pn= G1 : G2 : … :Gn
总功率 p=Gequ2 = (G1+ G2+ …+Gn ) u2 =G1u2+G2u2+ …+Gnu2
表明
=p1+ p2+…+ pn
(1) 电阻并连时,各电阻消耗的功率与电阻大小成反比
Y接: 用电流表示电压
i1∆ =u12∆ /R12 – u31∆ /R31 i2∆ =u23∆ /R23 – u12∆ /R12 (1)
i3∆ =u31∆ /R31 – u23∆ /R23
u12Y=R1i1Y–R2i2Y
u23Y=R2i2Y – R3i3Y
(2)
u31Y=R3i3Y – R1i1Y
i1Y+i2Y+i3Y = 0
返华东回理上工页大学下 页
2.2 电路的等效变换
1. 两端电路(网络)
任何一个复杂的电路, 向外引出两个端钮,
称为二端网络。如果二端网络从一个端子流入的
电流等于从另一端子流出的电流,则称为一端口
网络。
i i
N端网络—任何只有N个引出端子与外 部电路相连接的部分电路。
华东理工大学
外特性—网络端子处的端电压与端电流之间的关 系(VCR曲线或VCR方程)。即对外电路而言 的VAR曲线。
1. 电阻串联( Series Connection of Resistors )
(1) 电路特点
R1
Rk
Rn
i
+ u1 _ + U k _ + un _
+
u
_
(a) 各电阻顺序连接,流过同一电流 (KCL);
(b) 总电压等于各串联电阻的电压之和 (KVL)。
u = u1 + ⋅ ⋅ ⋅ + uk + ⋅ ⋅ ⋅ + un
(2) 等效电阻消耗的功率等于各并连电阻消耗功率的总 和
华东理上工页大学下 页
电路中有电阻的串联,又有电阻的
3. 电阻的串并联 并联,这种连接方式称电阻的串并
联。
例 计算各支路的电压和电流。
6Ω
i1 5 Ω
i1 5 Ω
+
165V
-
i2 6 Ω i3
+
18 Ω
4Ω i4
165V
i5 -
12 Ω
i2
i3
k =1
结论: 串联电路的总电阻等于各分电阻之和。
返华回东理上工页大学下 页
(3) 串联电阻的分压
uk
=
Rk i =
Rk
u Req
=
Rk Req
u<u
说明电压与电阻成正比,因此串连电阻电路可作分压
电路
例
两个电阻的分压:
i º ++
u-1 R1 u_ u+2 R2
u1
=
R1 R1 + R2
u
u2
=
− R2 R1 + R2
简记方法:
RΥ = ∆相邻电阻乘积
∑ R∆
∆变Y
华东理上工页大学下 页
特例:若三个电阻相等(对称),则有
R∆ = 3RY
注意
外大内小
R12 R1
R2
R31 R3
R23
(1) 等效对外部(端钮以外)有效,对内不成立。 (2) 等效电路与外部电路无关。 (3) 用于简化电路
华东理上工页大学下 页
例 桥 T 电路
1kΩ 1kΩ 1kΩ
E
1kΩ R
1/3kΩ 1/3kΩ
1/3kΩ
R
E
1kΩ
1kΩ
3kΩ i
R E
3kΩ 3kΩ
华东理上工页大学下 页
例 计算90Ω电阻吸收的功率
1Ω
4Ω
+ 20V 90Ω
i
9Ω 9Ω 9Ω
-
1Ω
9Ω
1Ω
+ 20V
-
i1
90Ω 10Ω
1Ω
4Ω 3Ω
R eq
=1+
10 10
× 90 + 90
这点上二者是相同的,等效的。因为为了达到 日行千里之目的,用白马和用黑马之间无任何区别。
等效电路 — 如果两个端点一一对应的n端 网络N和N´具有相同的外特性,则二者相 互等效,并互称为等效电路。
华东理工大学
设N与N´分别为二个无源二端网络, 当u = f (i)与u' = f (i')相同时, N与N ′是等效的。
返华回东理上工页大学下 页
例
+ 12V_
I1 I2 R I3 R
+
+
2R U_1 2R U_2 2R
I4 求:I1 ,I4 ,U4
+
2R U_4
解 ① 用分流方法做
I1
=
12 R
I4
=
−
1 2
I3
=
−
1 4
I2
=
−
1 8
I1
=
−
1 8
12 R
=
−
3 2R
U4 = −I4 × 2R = 3 V
②用分压方法做
= 10 Ω
+
3Ω
3Ω i = 20 / 10 = 2 A
型电阻= Y相邻电阻两两乘积之和 Y型不相邻电阻
R 31
=
R1R2
+
R2 R3 R2
+ R3R1
Y变∆
华东理工大学
上页 下页
类似可得到由∆型→ Y型的变换条件:
R1
=
R 12
R12 R 31 + R 23 + R 31
R2
=
R 12
R 23 R12 + R 23 + R 31
R3
=
R 12
R 31 R 23 + R 23 + R 31
i a ●粗略地讲两者等效是指两者具有
N
u
相同的电气性能; ●从物理意义上讲,两者等效是指在其
b
端口处,对任一同一个外电路而言能 有同样的电路效果,即当加有同样端
i′
a′
电压时,两端子电流一样,或反之; ●从数学概念上讲(即是上述的定义),
N’
u′ 即两者端口处对外电路而言具有
b′
完全相同的数学模型(VAR方程), 或说两者的外特性曲线相重合。
5Ω
a
5Ω
a
15Ω b
20Ω
缩短无电阻支路
15Ω b
7Ω
6Ω
6Ω
7Ω 6Ω 6Ω
Rab=10Ω
4Ω
a
15Ω b
10Ω
4Ω
a
15Ω b
7Ω 3Ω
华东理上工页大学下 页
例
40Ω
º
40Ω
30Ω
40Ω
º 40Ω
R º
30Ω
R
30Ω 30Ω 30Ω
º 30Ω
R = (40∥40+30∥30∥30) = 30Ω
u
注意方向 !
º
返华回东理上工页大学下 页
(4) 功率
p1=R1i2, p2=R2i2,…, pn=Rni2 p1: p2 : … : pn= R1 : R2 : … :Rn
总功率 表明
p=Reqi2 = (R1+ R2+ …+Rn ) i2 =R1i2+R2i2+ …+Rni2 =p1+ p2+…+ pn
i3Y
=
u31Y R2 − u23Y R1 R1R2 + R2 R3 + R3R1
i3∆ =u31∆ /R31 – u23∆ /R23
根据等效条件,比较式(3)与式(1),得Y型→∆型的变换
条件:
R12
=
R1R2
+
R2 R3 R3
+
R3 R1
R 23
=
R2 R1
+ R2R3 R1
+
R3 R1
简记方法:
华东理上工页大学下 页
2. ∆—Y 变换的等效条件
1 + i1∆
u12∆ R12
– R3u1 31∆
– i2 ∆ 2+
R23 u23∆
i3 ∆+ –3
1 +i1Y –
u12Y – i2Y R2
2+
R1 u31Y R3 i3Y +
u23Y – 3
等效条件: i1∆ =i1Y ,
i2 ∆ =i2Y , i3 ∆ =i3Y ,
华东理工大学
2.4 电阻的星形联接与三角形联接的
等效变换 (∆—Y 变换)
c
1. 电阻的∆ ,Y连接
R1
R2
包含
1
a
b
R3
R4
1d
R12
R31
R1
R2
R3
三端 网络
2
R23
3
2
3
∆ 型网络
Y型网络
华东理上工页大学下 页
∆ ,Y 网络的变形:
π 型电路 (∆ 型)
T 型电路 (Y、星 型)
这两个电路当它们的电阻满足一定的关系时, 能够相互等效
ik
=
Gk Geq
i
