含有圆的组合图形的面积(方与圆)
外圆内方圆的面积公式

外圆内方圆的面积公式在数学的奇妙世界里,各种图形的面积计算总是引人入胜。
今天,咱们就来好好探讨一下外圆内方圆的面积公式。
首先,咱们得弄清楚啥是外圆内方圆。
简单说,就是一个大圆里面套着一个正方形,正方形的四个顶点都在圆上。
这种组合图形在实际生活和数学问题中可不少见呢!那怎么来计算它的面积呢?咱们分开来看。
先说说圆的面积。
圆的面积公式大家应该都不陌生,那就是 S =πr²,这里的 S 表示圆的面积,π是圆周率,约等于 314159,r 呢则是圆的半径。
再看看正方形。
要计算正方形的面积,就得先知道它的边长。
对于外圆内方的情况,这个正方形的对角线长度正好就是圆的直径。
假设圆的半径是 r,那么直径就是 2r。
因为正方形的对角线把正方形分成了两个全等的等腰直角三角形,根据勾股定理,正方形的边长 a 就可以算出来啦,a²+ a²=(2r)²,也就是 2a²= 4r²,所以 a²= 2r²,那么正方形的面积就是 S 正= a²= 2r²。
接下来,咱们就可以算出外圆内方圆的面积啦。
外圆内方圆的面积=圆的面积正方形的面积,也就是 S =πr² 2r²=(π 2)r² 。
为了更好地理解这个公式,咱们来举个例子。
假设圆的半径 r 是 5 厘米,那么圆的面积就是 314×5²= 785 平方厘米,正方形的面积是2×5²= 50 平方厘米,外圆内方圆的面积就是(314 2)×5²= 285 平方厘米。
可能有人会问了,这个公式有啥用呢?用处可大啦!比如说在建筑设计中,要设计一个圆形花坛中间有一个正方形的雕塑底座,知道了花坛的半径,就能很快算出除去雕塑底座所占面积后,还能用来种花的面积有多少。
在制作圆形的糕点,中间要放上一个方形的夹心,也能通过这个公式算出周边糕点部分的面积。
苏教版五年级下《圆的组合图形面积的计算》

苏教版五年级下《圆的组合图形面积的计算》《苏教版五年级下〈圆的组合图形面积的计算〉》在我们的数学学习中,图形的面积计算一直是一个重要的部分。
当我们遇到圆与其他图形组合而成的复杂图形时,如何准确、快速地计算出它们的面积,就成为了一项具有挑战性但又十分有趣的任务。
今天,就让我们一起来探索苏教版五年级下《圆的组合图形面积的计算》。
首先,我们要明确什么是圆的组合图形。
简单来说,就是由圆和其他常见图形(如三角形、矩形、梯形等)组合在一起形成的新图形。
比如,一个半圆和一个矩形拼在一起,或者一个圆里面挖去了一个三角形。
那为什么要学习圆的组合图形面积的计算呢?这是因为在我们的日常生活和实际应用中,很多物体的形状并不是简单的单一图形,而是由多种图形组合而成的。
比如,一个圆形花坛周围有一圈矩形的小路,要计算这条小路的面积,就需要用到圆的组合图形面积的计算方法。
接下来,让我们看看计算圆的组合图形面积的基本思路。
第一步,要仔细观察图形,把组合图形分解成我们熟悉的基本图形。
这就像是把一个复杂的大问题分解成一个个小问题,逐个解决。
第二步,分别计算出各个基本图形的面积。
对于圆的面积,我们都知道公式是 S =πr²,其中π通常取 314,r 是圆的半径。
而对于三角形的面积公式是 S = 1/2 ×底 ×高,矩形的面积是 S =长 ×宽,梯形的面积是 S =(上底+下底)×高 ÷ 2 。
第三步,再根据图形的组合方式,把各个基本图形的面积进行相加或者相减,就能得到组合图形的面积。
举个例子,假设有一个图形是由一个正方形和一个半圆组成的。
正方形的边长是 8 厘米,半圆的直径等于正方形的边长。
我们先分别计算正方形和半圆的面积。
正方形的面积= 8×8 = 64 平方厘米。
半圆的半径= 8÷2 = 4 厘米,半圆的面积= 1/2×314×4²= 2512 平方厘米。
圆的组合图形的面积

假设有一个半径为5cm的圆 和一个底边长为8cm、高为 6cm的三角形,相交部分面
积为18.84cm^2。
05 圆的组合图形面积计算的 扩展应用
Байду номын сангаас
在几何图形设计中的应用
图案设计
圆的组合图形可以用于各种图案 设计,如地板、墙纸、纺织品等,
为设计提供丰富的视觉效果和创 意灵感。
建筑设计
在建筑设计中,圆的组合图形可以 用于外观设计、室内装饰和景观规 划,增加建筑的艺术感和美感。
微积分是通过微积分学中的定 积分概念,将不规则图形的面 积转化为求曲线下面积的问题 进行求解。
03 圆的组合图形面积计算
圆与圆的重叠
总结词
计算重叠部分的面积
详细描述
当两个或多个圆重叠时,需要分别计算各个圆的面积,并从总面积中减去重叠 部分的面积。重叠部分的面积可以通过计算重叠部分的弧长和半径来得出。
04 圆的组合图形面积计算实 例
实例一:圆与圆的重叠面积计算
总结词
计算重叠部分的面积
详细描述
当两个圆部分重叠时,需要计算重叠部分的面积。可以通 过计算两个圆的面积,然后减去两个圆不相交部分的面积 来实现。
公式
重叠部分的面积 = 两个圆的面积 - 不相交部分的面积
示例
假设有两个半径分别为3cm和5cm的圆,重叠部分面积为 12.56cm^2。
实例二:圆与矩形的组合面积计算
计算圆与矩形相交部分的面积
输入 标题
详细描述
当圆与矩形相交时,需要计算相交部分的面积。可以 通过计算矩形和圆的面积,然后减去矩形与圆不相交 部分的面积来实现。
总结词
公式
假设有一个半径为4cm的圆和一个长为8cm、宽为 6cm的矩形,相交部分面积为25.12cm^2。
常见组合图形面积计算实例
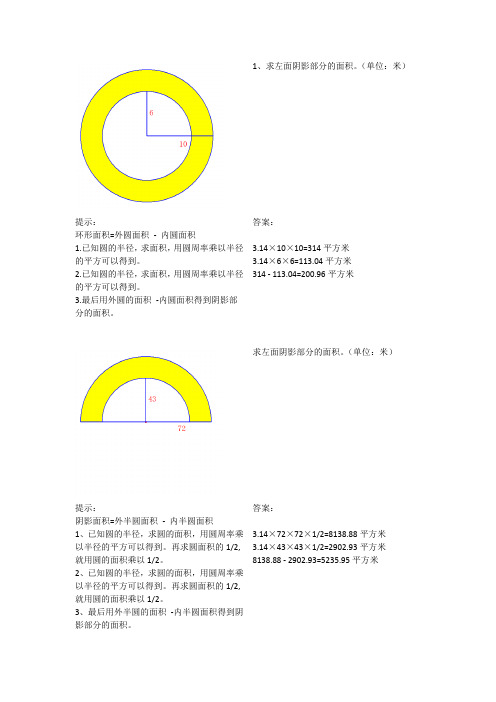
1、求左面阴影部分的面积。
(单位:米)提示:环形面积=外圆面积-内圆面积1.已知圆的半径,求面积,用圆周率乘以半径的平方可以得到。
2.已知圆的半径,求面积,用圆周率乘以半径的平方可以得到。
3.最后用外圆的面积-内圆面积得到阴影部分的面积。
答案:3.14×10×10=314平方米3.14×6×6=113.04平方米314 - 113.04=200.96平方米求左面阴影部分的面积。
(单位:米)提示:阴影面积=外半圆面积-内半圆面积1、已知圆的半径,求圆的面积,用圆周率乘以半径的平方可以得到。
再求圆面积的1/2,就用圆的面积乘以1/2。
2、已知圆的半径,求圆的面积,用圆周率乘以半径的平方可以得到。
再求圆面积的1/2,就用圆的面积乘以1/2。
3、最后用外半圆的面积-内半圆面积得到阴影部分的面积。
答案:3.14×72×72×1/2=8138.88平方米3.14×43×43×1/2=2902.93平方米8138.88 - 2902.93=5235.95平方米求左面阴影部分的面积。
(单位:米)提示:阴影部分面积可以用正方形的面积减去圆形的面积。
1、求正方形面积已知正方形的边长,求面积,用边长乘以边长可以得到。
2、求圆面积已知圆的直径,求面积,先用直径除以2得到半径,再用圆周率乘以半径的平方可以得到。
3、求阴影面积,用正方形面积减去圆的面积答案:1、正方形面积32×32=1024平方米2、圆面积32÷2=16米3.14×16×16=803.84平方米3、阴影面积1024- 803.84=220.16平方米求左面阴影部分的面积。
(单位:米)提示:阴影部分面积可以三角形面积减去右空白面积。
三角形面积是长方形面积的一半,右空白面积是长方形面积与半圆面积差的一半。
长方形的长就是圆的直径,宽是圆的半径。
六年级上册数学第五单元集体备课表格式教案(新审定人教版)

六年级上册数学第五单元集体备课表格式教案(新审定人教版)第五单元《圆》集体备课教案六年级上册设计者:施教者:教学内容含有圆的组合图形的面积(环形)课型新授课教学目标 1、让学生结合具体情境认识组合图形的特征,掌握计算组合图形的面积的方法,并能准确掌握和计算简单组合图形的面积。
2、通过自主合作,培养学生独立思考、合作探究的意识。
一、探索交流,解决问题 4.导入新课:这节课我们一起来探讨环形的知识。
(板书课题:圆环的面积) 二、创设情境,认识圆环 1.师:我们来欣赏一组美丽的图片。
课件出示圆形花坛、圆形水池外的圆形甬路、奥运五环标志、光盘…… 2.同学们,你们从图中发现了什么?(它们都是环形的) 3.教师拿出环形光盘说明:像这样的图形,我们称它为圆环或环形。
你还知道生活中有哪些环形的物体?它们给我们的生活带来了怎样的变化?三、学习新知 1.画一画,剪一剪,发现环形特点。
(1)画一画。
让学生在硬纸板上用同一个圆心分别画一个半径为10厘米和5厘米的圆。
(2)剪一剪。
指导学生先剪下所画的大圆,再剪下所画的小圆。
3.课件出示例2。
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。
圆环的面积是多少?四、巩固练习,拓展提高完成教材68页做一做第2、题。
板书设计或要点圆环的面积圆环面积=外圆面积-内圆面积 S环=πR2-πr2或S环=π×(R2-r2)第五单元《圆》集体备课教案六年级上册设计者:施教者:教学内容含有圆的组合图形的面积(方与圆)课型新授课教学目标 1、让学生结合具体情境认识组合图形的特征,掌握计算组合图形的面积的方法,并能准确掌握和计算简单组合图形的面积。
2、通过自主合作,培养学生独立思考、合作探究的意识。
教学重点组合图形的认识及面积计算、图形分析教学难点组合图形的认识及面积计算、图形分析教具学具圆规、直尺教学内容个人修改设计一、探索交流,解决问题上一节课我们一起来探讨环形的知识。
五年级下圆环及圆的组合图形的面积

注意事项:计 算时要考虑圆 与矩形或三角 形是否相切, 以及圆心是否 在矩形或三角
形内部
举例说明:给 出具体例子, 展示如何计算 组合图形面积
计算方法:先分别求出圆和圆环的面积,再根据组合图形的特点进行计算
注意事项:考虑圆与圆环的相对位置,注意圆心与半径的确定
举例说明:通过具体例子展示组合图形面积的计算过程
培养空间思维和 逻辑推理能力
圆的组合图形在艺术领域的应用:在艺术设计中,圆环和圆的组合图形被广泛应用于 各种艺术作品的创作中,如雕塑、绘画等,以增加作品的美感和视觉效果。
理解问题的背景和要求 分析问题中的已知条件和未知条件 运用圆的组合图形的面积公式计算面积 结合实际,考虑实际情况,确定最终解决方案
实际应用中,要考 虑到实际情况,如 圆环的大小、位置 等。
结论:组合图形的面积计算需要灵活运用圆的面积公式和圆环的面积公式,同时要注意图形 的特点与计算方法的结合。
定义:由两个 或两个以上的 圆组成的图形
计算方法:先 计算每个圆的 面积,再根据 组合图形的特 点进行相加或
相减
注意事项:确 保每个圆的半 径和位置都正 确,避免计算
错误
举例:通过具 体例子展示多 个圆的组合图 形面积计算过
力
圆环和圆相切:使用圆环面积公式和圆面积公式计算 圆环和圆相交:分解为多个图形,分别计算面积再相加 圆和圆外其他图形组合:分解为多个图形,分别计算面积再相加 圆内嵌套其他图形:使用分割法,将图形分割成多个部分,分别计算面积再相加
掌握圆环和圆的 面积计算方法
理解图形组合的 解题思路
学会运用辅助线、 分割法等技巧
计算面积时,需要 考虑到圆环的内外 半径及高。
在组合图形中,需 要考虑圆与其他图 形的关系及相互作 用。
圆的组合图形的面积计算

答:光盘的面积是32π平方厘米。
如果我们用S 表示圆环的面积,R 表示大圆的 圆环
半径,r 表示小圆的半径。圆环的面积公式可以怎 么表达?
S =πR²-πr² 圆环
或 S 圆环=π(R²-r²)
一扇窗户由一个正方形和一个半圆形组合而成 (如右图)。这扇窗户的面积是多少平方米?
圆的组合图形的面积计算
五年级数学·(下册)
复习 平面图形的面积计算公式
长方形面积 = 长×宽
三角形面积 =底×高÷2
正方形面积 =边 长×边长
梯形面积 =( 上底+下底)×高÷2
平行四边形面积 = 底×高
圆的面积 s=πr²
r
求下面各圆的面积。
(1)r=7dm
π×7²= 49 π(dm²)
(2)d=1.2m
π×112÷2-π×5.5²÷2
面积之和
16
24
涂色部分的面积=长方形的面积+半圆的面积 16÷2=8(毫米)……圆的半径
24×16+ π×82÷2
14
面积之差
涂色部分的面积=半圆的面积-三角形的面积 14×2=28(毫米)……三角形的底
π×142÷2-28×14÷2
计算组合图形的面积我们可以分几步走?
1.看 2.想 3.算
看组合图形是由哪些基本图形组合而成的。
想组合图形的面积是这些基本图形的面积之和 还是面积之差。
找到数据之间的相互联系,正确地运用公式进 行计算。
课后作业
课后作业
感谢您的莅临指导
长方形面积:8×4=32(cm2)
= 9π÷2
半圆面积: π×42找÷2到数据之间)
(完整版)圆的组合图形面积及答案

圆的组合图形面积姓名:【知识与方法】要解决与圆有关的题目,需要注意以下几点:1、熟练掌握有关圆的概念和面试公式:圆的面积= 圆的周长=扇形的面积= 扇形的弧长=(n是圆心角的度数)2、掌握解题技巧和解题方法:加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。
例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
店上联校枣臻小学导案
年级六备课时间课型新授主备人李红梅审核人课时
备课内容含有圆的组合图形的面积(方与圆)
教学目标
1.让学生结合具体情境,认识组合图形的特征,掌握计算“外方内圆”和“外圆内方”的图形面积的方法。
2.通过自主合作,培养独立思维,合作探究的意识。
教学
重难
点
组合图形的认识及面积计算、图形分析
教法
指导
引导学生小组合作交流,讨论总结规律方法。
教具
运用
圆规、直尺、多媒体课件
导学流程
一、知识铺垫
生活中我们经常能看到圆形的物体,还常常看到圆和其他图
形组成的图形,像这样有几个简单的图形组合而成的图形叫组合
图形。
组合图形在日常生活中有着广泛的应用,
二、自主探究
1.实践操作
(1)这两种设计有什么联系和区别?
左边的雕窗外面是方的里面是圆的;右边的雕窗外面是
( )的里面是( )的。
都是由( )和( )这两个图形组
成的。
我们可以将上述特征分别概括地称为外( )内
( )、外( )内( )。
(2)用学具组合出这两个图形。
二次备课及
备课诠释
导学流程
2.解决问题
3.回顾反思,理解算法
(1)如果两个圆的半径都是r,结果又是怎样的?结合左图我们一起来算一算。
(2)右图中正方形和圆之间部分的面积怎样算呢?
三、课堂达标
1.圆的周长是6
2.8厘米,求正方形的面积。
2.圆的半径是4分米,求圆和正方形之间部分的面积。
3.求阴影部分面积。
4.正方形的边长是10厘米,求阴影部分的面积。
板书设计
方与圆的面积
d=a r=
左图外方内圆右图外圆内方
S
正
-S圆=2r2-3.14r2=0.86r2 S圆-S正=3.14r2-×2=1.14r2
教后反思
店上联校枣臻小学学案
年级六科目数学课型新授课学习主人学习时间课时
学习内容含有圆的组合图形的面积(方与圆)
学习目标
1.让学生结合具体情境,认识组合图形的特征,掌握计算“外方内圆”和“外圆内方”的图形面积的方法。
2.通过自主合作,培养独立思维,合作探究的意识。
学习
重难
点
组合图形的认识及面积计算、图形分析
学法
指导
小组合作交流,讨论总结规律方法学具
运用
学案
学习流程
一、知识铺垫
生活中我们经常能看到圆形的物体,还常常看到圆和其他图形组成的图形,像这样有几个简单的图形组合而成的图形叫组合图形。
组合图形在日常生活中有着广泛的应用,
二、自主探究
1.实践操作
(1)这两种设计有什么联系和区别?
左边的雕窗外面是方的里面是圆的;右边的雕窗外面是( )的里面是
( )的。
都是由( )和( )这两个图形组成的。
我们可以将上述特征分别概括地称为外( )内( )、外( )内
( )。
(2)用学具组合出这两个图形。
学习流程
2.解决问题
3.回顾反思,理解算法
(1)如果两个圆的半径都是r,结果又是怎样的?结合左图我们一起来算一算。
(2)右图中正方形和圆之间部分的面积怎样算呢?
三、课堂达标
1.圆的周长是6
2.8厘米,求正方形的面积。
2.圆的半径是4分米,求圆和正方形之间部分的面积。
3.求阴影部分面积。
4.正方形的边长是10厘米,求阴影部分的面积。
