圆的证明与计算
圆的相关证明与计算(复习讲义)(原卷版)-中考数学重难点题型专题汇总
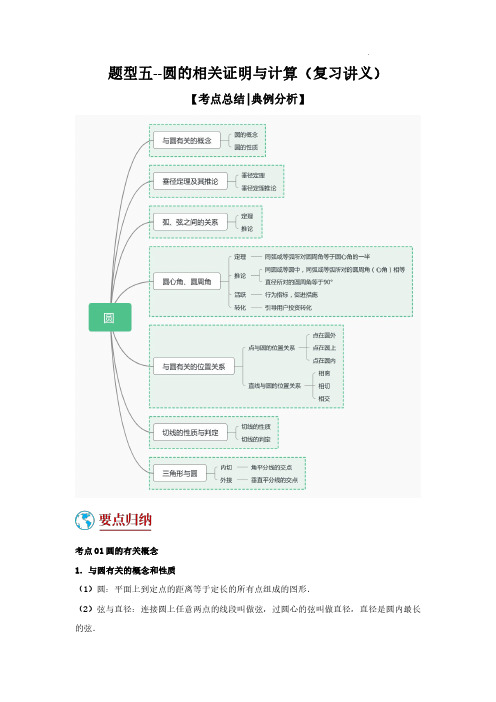
题型五--圆的相关证明与计算（复习讲义）【考点总结|典例分析】考点01圆的有关概念1．与圆有关的概念和性质（1）圆：平面上到定点的距离等于定长的所有点组成的图形．（2）弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦．（3）弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧．（4）圆心角：顶点在圆心的角叫做圆心角．（5）圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角．（6）弦心距：圆心到弦的距离．考点02垂径定理及其推论1．垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形．2．推论（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧．考点03圆心角、弧、弦的关系1．定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等．圆心角、弧和弦之间的等量关系必须在同圆等式中才成立．2．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．考点04圆周角定理及其推论1．定理一条弧所对的圆周角等于它所对的圆心角的一半．2．推论（1）在同圆或等圆中，同弧或等弧所对的圆周角相等．（2）直径所对的圆周角是直角．考点05与圆有关的位置关系1．点与圆的位置关系设点到圆心的距离为d．(1)d<r⇔点在⊙O内；(2)d=r⇔点在⊙O上；(3)d>r ⇔点在⊙O 外．判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可．2．直线和圆的位置关系位置关系相离相切相交图形公共点个数0个1个2个数量关系d>r d=r d<r考点06切线的性质与判定1．切线的性质（1）切线与圆只有一个公共点．（2）切线到圆心的距离等于圆的半径．（3）切线垂直于经过切点的半径．利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题．2．切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）．（2）到圆心的距离等于半径的直线是圆的切线．（3）经过半径外端点并且垂直于这条半径的直线是圆的切线．切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径．考点07三角形与圆1.三角形外接圆外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等．2．三角形的内切圆内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等．1.如图，点,,,,A B C D E 在O 上，,42AB CD AOB =∠=︒，则CED ∠=（）A．48︒B．24︒C．22︒D．21︒2.如图，A，B，C 是半径为1的⊙O 上的三个点，若，∠CAB＝30°，则∠ABC 的度数为（）A．95°B．100°C．105°D．110°3.如图，AB 是⊙O 的直径，AC，BC 是⊙O 的弦，若20A ∠=︒，则B Ð的度数为（）A．70°B．90°C．40°D．60°4.如图，Rt ABC 中，90ACB ∠=︒，AC =3BC =．点P 为ABC ∆内一点，且满足22PA PC +2AC =．当PB 的长度最小时，ACP ∆的面积是（）A．3B．C．4D．25.如图，已知在⊙O 中， AB BCCD ＝＝，OC 与AD 相交于点E．求证：（1）AD∥BC（2）四边形BCDE 为菱形．6.如图，A，B 是O 上两点，且AB OA =，连接OB 并延长到点C，使BC OB =，连接AC．（1）求证：AC 是O 的切线．（2）点D，E 分别是AC，OA 的中点，DE 所在直线交O 于点F，G，4OA =，求GF 的长．7.如图，Rt ABC 中，90ABC ∠=︒，以点C 为圆心，CB 为半径作C ，D 为C 上一点，连接AD 、CD ，AB AD =，AC 平分BAD ∠．（1）求证：AD 是C 的切线；（2）延长AD 、BC 相交于点E，若2EDC ABC S S = ，求tan BAC ∠的值．8.如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．9.如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．10.如图，已知点C 是以AB 为直径的圆上一点，D 是AB 延长线上一点，过点D 作BD 的垂线交AC 的延长线于点E ，连结CD ，且CD ED =．（1）求证：CD 是O 的切线；（2）若tan 2DCE ∠=，1BD =，求O 的半径．11.如图，AB 是⊙O 的直径，C 为⊙O 上一点，连接AC，CE⊥AB 于点E，D 是直径AB 延长线上一点，且∠BCE＝∠BCD．（1）求证：CD 是⊙O 的切线；（2）若AD＝8，BE CE=12，求CD的长．12.如图，△ABC内接于⊙O，AB为⊙O的直径，AB＝10，AC＝6，连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．13.如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO并延长，与⊙O 交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．=CD =DB ，连接AD，过点D作14.如图，AB为⊙O的直径，C、D为⊙O上的两个点，ACDE⊥AC交AC的延长线于点E．（1）求证：DE是⊙O的切线．（2）若直径AB＝6，求AD的长．15.如图，AB是半圆O的直径，C，D是半圆O上不同于A，B的两点，AD＝BC，AC与BD相交于点F．BE是半圆O所在圆的切线，与AC的延长线相交于点E．（1）求证：△CBA≌△DAB；（2）若BE＝BF，求证：AC平分∠DAB．16.如图，AB为⊙O的直径，C为⊙O上一点，AD与过C点的直线互相垂直，垂足为D，AC 平分∠DAB．（1）求证：DC为⊙O的切线．（2）若AD＝3，DC=3，求⊙O的半径．17.如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作⊙O的切线交AC于点E．（1）求证：DE⊥AC；（2）若⊙O的半径为5，BC＝16，求DE的长．。
2024年云南省人教版九年级中考数学二轮复习课件专题四 圆的证明与计算(35张PPT)
∴∠ODF=30°.∴∠DOF=60°.
∵AB⊥DC,∴DF=FC.
∵BF=OF,AB⊥DC,
∴S△CFB=S△CFO=S△DFO.
×
∴S 阴影部分=S 扇形 BOD=
= π.
[典型例题2] (2023北京)如图所示,圆内接四边形ABCD的对角线AC,BD
交于点E,BD平分∠ABC,∠BAC=∠ADB.
∵CP与☉O相切,∴OC⊥PC.∴∠PCB+∠OCB=90°.
∵AB⊥DC,∴∠PAD+∠ADF=90°.∴∠PCB=∠PAD.
(2)若☉O的直径为4,弦DC平分半径OB,求图中阴影部分的面积.
(2)解:如图②所示,连接 OD,
∵弦 DC 平分半径 OB,∴BF=OF.
在 Rt△ODF 中,OF= OD.
∵AC为☉O的直径,∴∠ABC=90°.
∵BD是∠ABC的平分线,∴∠ABD=∠DBE=45°.
∴∠DOC=2∠DBE=90°.
∵AC∥DE,∴∠ODE=90°,即OD⊥DE.
∵OD是☉O的半径,∴DE是☉O的切线
(2)探究线段BE,CE,DE之间有何数量关系?写出你的结论,并证明.
2
(2)解:DE =CE·BE.证明如下:
2
又∵
2
=
,∴ =
.解得 CE=
2
.
2
2.如图所示,☉O的半径为1,A,P,B,C是☉O上的四个点,
∠APC=∠CPB=60°.
(1)判断△ABC的形状,并说明理由.
解:(1)△ABC是等边三角形.理由如下:
∵∠APC=∠CPB=60°,
涉及圆的证明与计算问题
涉及圆的证明与计算问题圆的证明与计算是中考必考点，也是中考的难点之一。
纵观全国各地中考数学试卷，能够看出，圆的证明与计算这个专题内容有三种题型：选择题、填空题和解答题。
一、与圆有关的概念1．圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心，定长称为半径。
圆的半径或直径决定圆的大小，圆心决定圆的位置。
2．圆心角：顶点在圆心上的角叫做圆心角。
圆心角的度数等于它所对弧的度数。
3.圆周角：顶点在圆周上，并且两边分别与圆相交的角叫做圆周角。
4.外接圆和外心：经过三角形的三个顶点可以做一个圆，这个圆叫做三角形的外接圆。
外接圆的圆心，叫做三角形的外心。
外心是三角形三条边垂直平分线的交点。
外心到三角形三个顶点的距离相等。
5．若四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个圆叫做这个四边形的外接圆。
6.和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。
内心是三角形三个角的角平分线的交点。
内心到三角形三边的距离相等。
二、与圆有关的规律1.圆的性质：（1）圆具有旋转不变性；（2）圆具有轴对称性；（3）圆具有中心对称性。
2.垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。
3．推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．4．在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦心距也相等。
在同圆或等圆中，如果两条弧相等，那么他们所对的圆心角相等，所对的弦相等，所对的弦心距也相等。
在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角相等，所对的弧相等，所对的弦心距也相等。
5.在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．7．圆内接四边形的特征①圆内接四边形的对角互补；②圆内接四边形任意一个外角等于它的内对角。
三、点和圆、线和圆、圆和圆的位置关系1.点和圆的位置关系①点在圆内⇔点到圆心的距离小于半径②点在圆上⇔点到圆心的距离等于半径③点在圆外⇔点到圆心的距离大于半径2.直线与圆有3种位置关系如果⊙O的半径为r，圆心O到直线l的距离为d，那么d<；①直线l和⊙O相交⇔rd=；②直线l和⊙O相切⇔rd>。
圆的证明与计算PPT
(7)切线长定理: 线段相等、垂直关系、角相等及全等。 2、圆中几个关键元素之间的相互转化:
弧、弦、圆心角、圆周角等都可以通过相等来互相转化.这在圆中的证明和 计算中经常用到.
二、考题形式分析：
主要以解答题的形式出现，近两年来，此题考查形 式由原来的单图题演变成双图题;
第一小问也由原来的切线的证明，转变成应用圆中 简单性质进行计算和证明; 第二问则在第一问的基础上进行深化和运用，考查 学生灵活运用所学圆的相关知识解决线段长，面积、线 段比、三角函数的有关问题的能力。
圆的证明与计算
（双图题）专题探究
华科附中初三备课组 主讲人：常静
一、圆中的有关知识点：
1、圆中的重要定理: (1)圆的定义:主要是用来证明四点共圆. (2)垂径定理:主要是用来证明——弧相等、线段相等、垂直关系等等. (3)三者之间的关系定理: 主要是用来证明— —弧相等、线段相等、圆心角相等. (4)圆周角性质定理及其推论: 主要是用来证明——直角、角相等、弧相等. (5)切线的性质定理:主要是用来证明——垂直关系. (6)切线的判定定理: 主要是用来证明直线是圆的切线.
原创例题2：
来源：课本九年级上册86页例2
第一问考查：
利用弦切角 找特殊直角三 角形
构题的出发点：
以切割线为背景合理 运用圆的有关性质和 勾股定理建立方程进 行计算。
第二问考查：（基本策略）
看见等弧找等弦；看见直径找直角； 看见三角函数找直角三角形； 看见切割线找相似 目标线段旁有特殊角的情况下，作垂 线构造直角三角形。
（3）如图（3）：若CK⊥AB于K，则：①CK=CD；BK=DE； 1 CK= 2 BE=DC；AE+AB=2AK=2AD; ②⊿ADC∽⊿ACB AC2=AD•AB
圆的证明与计算范文
圆的证明与计算范文圆是几何中的基本图形之一，它是平面上所有点与固定点之间距离保持不变的集合。
下面将从不同的角度对圆的性质进行证明，并介绍一些常见的圆的计算方法。
一、圆的性质及证明1.圆的定义证明对于平面上的一个点O以及一个长度r，定义集合E为与O的距离为r的点的集合。
我们要证明E是一个圆。
证明：（1）任意取平面上的一点A，若A∈E，证明OA=r。
假设A∈E，则OA的长度等于A与O的距离，即OA=r。
因此，E是以O为圆心，长度为r的圆。
（2）任意取平面上的一点B，若OB=r，证明B∈E。
假设OB=r，则OB的长度等于B与O的距离，即OB=BO=r。
因此，B∈E。
由（1）和（2）可得，对于平面上的一个点O以及一个长度r，定义集合E为与O的距离为r的点的集合是一个圆。
2.圆心角的证明圆心角是指圆上两条射线所夹的角，它的度数等于弧所对的圆周角的度数。
我们要证明圆心角的度数等于所对弧的度数。
证明：任意取圆上两点A和B，以圆心O为顶点，连接OA和OB两条射线。
延长AO和OB分别与圆交于点C和D，则∠AOB是圆心角，∠ACB是所对弧所对的圆周角。
（1）∠AOB的度数等于所对弧AD的度数。
由于AD是圆上的弧，所以∠ACO是所对弧AD的圆周角。
根据圆周角的性质，∠ACO的度数等于所对弧AD的度数。
（2）∠ACB的度数等于所对弧AD的度数。
同样根据圆周角的性质，∠ACB的度数等于所对弧AD的度数。
由（1）和（2）可得，圆心角∠AOB的度数等于所对弧AD的度数。
通过证明，我们可以得出圆心角的度数等于所对弧的度数这一结论。
二、圆的计算在实际应用中，我们有时需要计算圆的周长、面积以及部分圆的面积。
以下是圆的计算公式：1.周长的计算2.面积的计算3.部分圆的面积的计算对于已知圆的半径r和所对的圆心角θ，部分圆的面积计算公式为：A=(πr²×θ)/360，其中A表示部分圆的面积，r表示半径，θ表示圆心角。
圆的证明与计算
《圆的证明与计算》一、重要考点：考点（一）垂径定理及推论：1、垂径定理：垂直于弦的直径，并且平分弦所对的2、推论：平分弦（不是直径）的直径，并且平分弦所对的垂径定理及其推论可概括为：过圆心垂直于弦一直线平分弦知二推三平分弦所对的优弧平分弦所对的劣弧【名师提醒：1、圆中常作的辅助线是过圆心作弦的线２、垂径定理常用作计算，在半径r、弦长a、弦心距d和弓形高h中已知两个可求另外两个】考点（二）、圆心角、弧、弦之间的关系：定理：在中，两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别【名师提醒：注意：该定理的前提条件是“在同圆或等圆中”】考点（三）圆周角定理及其推论：圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中，如果两个圆周角那么它们所对的弧推论2、半圆（或直径）所对的圆周角是900的圆周角所对的弦是【名师提醒：作直经所对的圆周角是圆中常作的辅助线】考点（四）切线的性质和判定：⑴性质定理：圆的切线垂直于经过切点的【名师提醒：根据这一定理，在圆中遇到切线时，常用连接圆心和切点，即可的垂直关系】⑵判定定理：经过半径的且这条半径的直线式圆的切线【名师提醒：在切线的判定中，当直线和圆的公共点标出时，用判定定理证明。
当公共点未标出时，可证圆心到直线的距离d=r来判定相切,即“有公共点连半径，无公共点作垂直”】O D C B A O ED CB A FOE D C B A考点（五）、切线长定理切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角 考点（六）、弧长和扇形面积 1、圆周长C ＝2πR ；2、弧长180Rn L π=２、圆面积：2R S π=； 2、扇形面积：3602R n S π=扇形二、考题形式：主要以解答题的形式出现,第1问主要是判定切线；第2问主要是与圆有关的计算：①求线段长（或阴影面积）；②求线段比；③求角度的三角函数值（实质还是求线段比）。
圆中的相关证明与计算
圆中的相关证明与计算圆是平面上到一个给定点的距离恒定的所有点的集合。
通过研究圆的性质和相关的定理，我们可以了解圆的性质和概念，并可以进行相关的证明和计算。
以下是一些关于圆的相关证明和计算的例子：1.圆的半径与直径的关系证明：首先，我们知道直径是通过圆心并且两端点在圆上的线段。
现在我们要证明直径是半径的两倍。
证明：假设圆的半径为r，直径为d。
根据直径的定义，我们知道直径是通过圆心的，并且它的两个端点在圆上。
所以直径d可以看作是两个半径r的长度相加，即d=r+r=2r。
所以我们可以得出结论：直径等于半径的两倍。
即d=2r。
2.圆周率的计算：周长的计算公式为：C=2πr，其中r为圆的半径。
面积的计算公式为：A=πr^2，其中r为圆的半径。
例如，如果一个圆的半径为5厘米，则它的周长为：C=2π*5=10π≈31.42厘米；面积为：A=π*5^2=25π≈78.54平方厘米。
3.弦和半径的垂直关系证明：在圆中，连接圆周上的两点的线段称为弦。
现在我们要证明如果一个弦与半径相交，那么这个弦就是半径的垂直平分线。
证明：假设在圆中有一个弦AB，如果它与半径OC相交于点M，我们要证明AM=MB。
根据圆的性质，半径OC与弦AB相交于点M，则角OMC是直角，因为OC是半径，所以OM=MC。
又由于弦AB与半径OC相交于点M，所以AM=MC，MB=MC。
综上所述，AM=MB，即弦AB是半径OC的垂直平分线。
通过以上证明和计算，我们可以更深入地了解圆的性质和相关的定理。
圆是几何学中重要的概念之一，它在各种数学和科学领域中都有广泛的应用。
希望以上内容对您有所帮助。
圆中的计算和证明
1、如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD。
（1）求证：AD＝AN；（2）若AB＝24，ON＝1，求⊙O的半径。
2、在⊙O中，AB为直径，点C为圆上一点，将劣弧AC沿弦AC翻折交AB于点D，连结CD。
（1）如图1，若点D与圆心O重合，AC＝2，求⊙O的半径r；（2）如图2，若点D与圆心O不重合，∠BAC＝25°，求出∠DCA的度数。
知识点（圆相关概念和性质）知识点一：垂径定理1．垂径定理：于弦的直径这条弦且这条弦所对的。
2．推论（1）：①平分（）的垂直于弦且弦所对的；②弦的经过且弦所对的两条弧；③弦所对的一条的直径弦且平分弦所对的另一条弧。
推论（2）：圆的两条弦所夹的弧。
知识点二：圆心角、弧、弦、弦心距间的关系1．定理：在或中，相等的圆心角所对的相等，所对的相等，相等。
2．推论：同圆或等圆中，如果①两个相等，②两条相等，③两条相等，④两条弦的中有一组量相等，那么它们所对应的其余各组量都分别相等。
知识点三：圆周角定理及其推论1．定理：在同圆或等圆中，或所对的相等，都等于这条弧所对的的。
2．推论①：同弧或等弧所对的相等；同圆或等圆中，相等的圆周角所对的弧是。
推论②：或所对的是直角；是直角（90°的）所对的弧是，所对的弦是。
推论③：若三角形一边上的中线等于这边的一半，那么这个三角形是。
知识点四：圆内接四边形性质定理1．概念：所有顶点都在同一个圆上的四边形叫做圆内接四边形。
2．定理：圆内接四边形的对角，并且任何一个外角都等于它的。
知识点五：直线与圆的位置关系直线和圆的位置关系相交相切相离公共点个数圆心到直线的距离d与半径r的关系公共点名称直线名称知识点六：圆的切线1．切线的性质（1）切线性质定理：圆的切线垂直于过切点的直径。
拓展：①经过圆心且垂直于切线的直线必经过切点；②经过切点且垂直于切线的直线必经过圆心；③切线与圆只有一个公共点；④圆心到切线的距离等于半径。
第40讲 与圆有关的计算与证明题 课件(共74张ppt) 2024年中考数学总复习专题突破.ppt
复习讲义
（2）若 = 5 ， cos ∠ =
4
，求 的长.
5
∘
解： ∵ ∠ = 90∘ ， ∴ ∠ + ∠ = 90 .
由（1）知， = 2 = 10 ， ∠ = 90∘ ，
∴ ∠ + ∠ = 90∘ .
图3
∴ ∠ = ∠.
4
.
5
∴ cos = cos ∠ =
复习讲义
（2）若 = 10 ， = 12 ， = 2 ，求 ⊙ 的半径．
思路点拨 由（1）知 ⊥ ，因此可在 Rt △
中利用勾股定理列方程求解.
解： ∵ = ， ⊥ ， ∴ = =
1
2
= 6.
图1
∴ = 2 − 2 = 102 − 62 = 8.
∴ = 6 .
目录导航
9
第40讲 与圆有关的计算与证明题
复习讲义
2.（2022·鄂尔多斯）如图3，以 为直径的
⊙ 与 △ 的边 相切于点 ，且与 边
交于点 ，点 为 的中点，连接 ， ，
.
（1）求证： 是 ⊙ 的切线.
1.（2022·衡阳）如图2， 为 ⊙ 的直径，过圆上一
点 作 ⊙ 的切线 交 的延长线于点 ，过点
作 // 交 于点 ，连接 ．
（1）直线 与 ⊙ 相切吗？请说明理由.
图2
目录导航
7
第40讲 与圆有关的计算与证明题
复习讲义
解：直线 与 ⊙ 相切.
， 的点，连接 ， ，点 在 的延长线
上，且 ∠ = ∠ ，点 在 的延长线上，
陕西中考圆的证明与计算(2023版)
陕西中考圆的证明与计算（2023版）知识总结1．切线的性质：垂直于过切点的半径．（连半径，得垂直）2．切线的判定：（1）定义法：和圆只有一个交点的直线是圆的切线；（2）距离法：到圆心距离等于半径的直线是圆的切线；证明d =r 即可，常用于已知数据的计算，比如动圆相切问题．（3）判定定理：经过半径外端且垂直于这条半径的直线是圆的切线．换个说法：⎧⎨⎩有交点：连半径,证垂直无交点：作垂直,证半径，多用于几何证明．多数情况为有交点，重点考虑如何证垂直：①证明和已知垂线平行；②证明夹角为直角．3．常见相切图（1）角分+等腰得平行：点C 在以AB 为直径的圆O 上，AH ⊥CH ，且AC 平分∠HAB ．【证明】连接OC，则OC=OA，∴∠OCA=∠OAC，又∠OAC=∠HAC，∴∠OCA=∠HAC，∴OC∥AH，∴OC⊥CH，∴CH是圆O的切线．（2）证明和已知直角相等．证明△PCO≌△PAO，可得∠PCO=∠PAO=90°．（3）证明夹角为直角．（弦切角定理）如图，若∠BAC=∠D，则AB是圆O切线．如图，连接AO并延长交圆O于点P，则∠P=∠D=∠BAC，∵∠P+∠PAC=90°，∴∠BAC+∠PAC=90°，即AB⊥AP，∴AB是圆O的切线．1．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC 于点E．（1）求证：DE＝AE；（2）若AD＝8，DE＝5，求BC的长度．2．如图，在Rt△ABC中，∠ABC＝90°，以BC为直径的⊙O交AC于点E，⊙O的切线DE交AB于点D．（1）求证：DA＝DB；（2）连接BE，OD，交点为F，若cos A＝，BC＝6，求OF的长．3．如图，AB是⊙O的直径，经过⊙O上一点D，作⊙O的切线EF，交AB的延长线于点F，AE⊥EF，交BD的延长线于点C．（1）求证：AB＝AC．（2）若⊙O的半径为3，，求BF的长．4．如图，AB为⊙O的直径，C、E为⊙O上的两点，过点E的切线交CB的延长线于点D，且CD⊥DE，连接CE，AE．（1）求证：∠ABC＝2∠A；（2）若⊙O半径为，AB：BD＝5：1，求AE的长．5．已知：如图，AB为⊙O的直径，CD与⊙O相切于点C，交AB延长线于点D，∠D＝30°，连接AC、BC，CE平分∠ACB交⊙O于点E，过点B作BF⊥CE，垂足为F．（1）求证：CA＝CD；（2）若AB＝12，求线段BF的长．6．已知：如图，⊙O过正方形ABCD的顶点A，B，且与CD边相切于点E．点F是BC与⊙O的交点，连接OB，OF，AF，点G是AB延长线上一点，连接FG，且∠G+∠BOF＝90°．（1）求证：FG是⊙O的切线；（2）如果正方形边长为8，求⊙O的半径．7．如图，在△AOB中，以点O为圆心的⊙O与AB相切于点D，延长AO交⊙O于点C，连接CD，过点A作AF⊥BO，交BO的延长线于点H，交⊙O于点F，∠B＝∠C．求证：（1）AF∥CD；（2）AH2＝OH⋅BH．8．如图，AB是⊙O的直径，已知点D是弧BC的中点，连接DO并延长，在延长线上有一点E，连接AE，且∠E＝∠B．（1）求证：AE是⊙O的切线；（2）连接AC，若AC＝6，CF＝4，求OE的长．9．如图，AB是⊙O的直径，C在AB的延长线上，⊙O与CD相切于点D，过点A作AE ⊥CD，垂足为E．（1）求证：AD平分∠EAC．（2）若BC＝3，，求⊙O的半径以及线段ED的长．10．如图，AB是⊙O的直径，点D是直径AB上不与A，B重合的一点，过点D作CD⊥AB，且CD＝AB，连接BC交⊙O于点F，在CD上取一点E，使EF＝EC．（1）求证：EF是⊙O的切线；（2）当D是OA的中点时，AB＝4，求BF的长．11．如图，△ABC内接于⊙O，AB＝AC，过点A作BC平行线AM，连接BO并延长，交AM于点D，连接AO、CO．（1）求证：AM是⊙O的切线；（2）若BC＝10，AD＝8，求⊙O的半径．12．如图，已知△ABC的边AB所在的直线是⊙O的切线，切点为B，AC经过圆心O并与圆交于点D、C，E为AB延长线上一点，连接CE交⊙O于点F，且∠BCE＝∠ACB．（1）求证：CE⊥AB；（2）若⊙O的半径是6，AB＝8，求EF的长．13．如图，在△ABC中，∠C＝90°，以FB为直径作⊙O，⊙O与直角边AC相切，切点为E．（1）求证：∠DBE＝∠EBA；（2）若AB＝10，DB＝4，求EB的长．14．如图，已知AB是⊙O的直径，C是⊙O上一点，OD⊥BC，垂足为D，连接AD，过点A作⊙O的切线与DO的延长线相交于点E．（1）求证：∠B＝∠E；（2）若⊙O的半径为4，OE＝6，求AD的长．15．如图，AB是⊙O的直径，点D、E均在⊙O上，连接AD、BD、BE、DE，过点D作⊙O的切线，交AB的延长线于点C．（1）求证：∠DEB＝∠CDB；（2）若BD＝DE＝6，BE＝9.6，求⊙O的半径．16．如图，△ABC是⊙O的内接三角形，BC为⊙O的直径，点E是⊙O上一点，连接OE 并延长交过点C的切线CD于点D，∠B＝∠D．（1）求证：OD∥AC；（2）延长EO交AB于点F，AF＝2，⊙O的直径为2，求OD的长．17．如图，已知△ABC的外接圆直径是AB，点O是圆心，点D在⊙O上，且＝，过点D作⊙O的切线，与CA、CB的延长线分别交于点E、F．（1）求证：AB∥EF；（2）若⊙O的半径为5，BC＝8，求DF的长度．18．如图，AB为⊙O的直径，C为⊙O上一点，AD⊥CE，垂足为D，AC平分∠DAB．（1）判定直线CE与⊙O的位置关系，并说明你的理由；（2）若AD＝3，AC＝4，求圆的半径．19．如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点恰好为BC的中点D，与AC边的交点为F，过点D作DE⊥AC于点E．（1）求证：直线DE是⊙O的切线；（2）若AB＝5，tan∠ACB＝2，求弦AF的长度．20．如图，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D．过点D作DE⊥AC，垂足为E，延长CA交⊙O于点F．（1）求证：DE是⊙O的切线；（2）若tan B＝，⊙O的半径为5，求线段CF的长．21．如图，AB为⊙O的直径，OD为⊙O的半径，⊙O的弦CD与AB相交于点F，⊙O的切线CE交AB的延长线于点E，EF＝EC．（1）求证：OD垂直平分AB；（2）若⊙O的半径长为3，且BF＝BE，求OF的长．22．如图，AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，BD⊥CD，DB的延长线与⊙O交于点E．（1）求证：∠ABE＝2∠A；（2）若，BD＝4，求BE的长．23．如图，在△ABC中，AC＝AB，以AB为直径的⊙O交BC于点D，过点D作ED⊥AC 点E，交AB延长线于点F．（1）求证：EF是⊙O的切线；（2）若DF＝4，tan∠BDF＝，求AC的长．24．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且∠DCF＝∠CAD．（1）求证：CF是⊙O的切线；（2）若直径AD＝10，cos B＝，求FD的长．25．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CAD＝∠CDE；（2）若CD＝6，tan∠BAD＝，求⊙O的半径．26．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为⊙O的直径，过点A作AE ⊥CD，与CD的延长线交于点E，且DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若⊙O的半径为5，CD＝6，求AD的长．27．如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是的中点，过点B的切线与AC的延长线交于点D．①求证：BD⊥AD；②若AC＝9，tan∠ABC＝，求⊙O的半径．28．如图，△ABC中，∠C＝90°，点O在AB上，⊙O经过点A，且与BC相切于点D．（1）求证：AD平分∠BAC；（2）若AC＝6，cos∠BAC＝，求⊙O的半径．29．如图，AB是⊙O的直径，点C为⊙O上一点，CD平分∠ACB，交AB于点E，交⊙O 于点D，延长BA到点P，使得PE＝PC．（1）求证：PC与⊙O相切；（2）若⊙O的半径3，PC＝4，求CD的长．30．如图，AB是⊙O的直径，点C、D是⊙O上两点，CE与⊙O相切，交DB延长线于点E，且DE⊥CE，连接AC，DC．（1）求证：∠ABD＝2∠A；（2）若DE＝2CE，AC＝8，求⊙O的半径．31．如图，AB是⊙O的直径，AC是弦，且OD⊥AC于点E，OD交⊙O于点F，连接CF、BF，若∠BFC＝∠ODA．（1）求证：AD是⊙O的切线：（2）若AB＝10，AC＝8，求AD的长．32．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，连接OD，过点D作⊙O的切线DE，交AC于点E，延长CA交⊙O于点F，连接BF．（1）求证：DE⊥AC；（2）若⊙O的直径为5，cos C＝，求CF的长．33．如图，在⊙O中，PA是直径，PC是弦，PH平分∠APB且与⊙O交于点H，过H作HB⊥PC交PC的延长线于点B．（1）求证：HB是⊙O的切线；（2）若HB＝4，BC＝2，求⊙O的半径．34．如图，AB是⊙O的直径，点D在直径AB上（D与A，B不重合），CD⊥AB，且CD＝AB，连接CB，与⊙O交于点F，在CD上取一点E，使得EF＝EC．（1）求证：EF是⊙O的切线；（2）若D是OA的中点，AB＝4，求CF的长．35．如图，四边形ABCD是⊙O的内接四边形，且对角线BD为直径，过点A作⊙O的切线AE，与CD的延长线交于点E，已知DA平分∠BDE．（1）求证：AE⊥DE；（2）若⊙O的半径为5，CD＝6，求AD的长．36．如图，在Rt△ACD中，∠ACD＝90°，点O在CD上，作⊙O，使⊙O与AD相切于点B，⊙O与CD交于点E，过点D作DF∥AC，交AO的延长线于点F，且∠OAB＝∠F．（1）求证：AC是⊙O的切线；（2）若OC＝3，DE＝2，求DF的长．37．如图，在Rt△ABC中，∠ACB＝90°，点D是AB的中点，以CD为直径作⊙O，与BC交于点E，过点E作⊙O的切线EF，交AB于点F．（1）求证：EF⊥AB；（2）若⊙O的半径是，cos∠ACD＝，求DF的长．38．如图，⊙O是△ABC的外接圆，＝，过点A作AD∥BC交⊙O于点D，连接CD，延长DA到点E，连接CE，∠D＝∠E．（1）求证：CE是⊙O的切线；（2）若CE＝8，AE＝5，求⊙O半径的长．39．如图，BD为⊙O的直径，∠ABE＝∠BCA，过点A的直线与⊙O分别交于点E，C，与BD交于点F，连接BE，BC．（1）求证：AB为⊙O的切线．（2）若∠A＝∠ABE，BE＝5，BC＝8，求⊙O的半径．40．如图，AB是⊙O的直径，AE是⊙O的切线，点C为直线AE上一点，连接OC交⊙O 于点D，连接BD并延长交线段AC于点E．（1）求证：∠CDE＝∠CAD；（2）若CD＝4，tan B＝，求⊙O的半径．。
圆的证明与计算练习(2024年中考真题)
圆的证明与计算练习(2024年中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。
(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD 中,AD <AC ,ADC BAD ∠<∠,延长AD 至点E ,使AE =AC ,延长BA 至点F ,连结EF ,使AFE ADC ∠=∠.(1)若60O AFE ∠=,CD 为直径,求ABD ∠的度数.(2)求证:①EF ∥BC ②EF =BD .4.(24年辽宁中考)如图,O 是ABC 的外接圆,AB 是O 的直径,点D 在 BC 上, AC BD=,E 在BA 的延长线上,CEA CAD ∠=∠．(1)如图1,求证:CE 是O 的切线(2)如图2,若2CEA DAB ∠=∠,8OA =,求 BD的长．5.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E, AD BD=.(1)求证：△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ，,60D ABC ∠=∠=︒．(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求 AC 的长．8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E ．O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=．(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积．9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论．如图,已知ABC ,CA CB =,O 是ABC 的外接圆,点D 在 O 上(AD BD >),连接AD ,BD ,CD ．【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系．(用含α的式子表示)10.(24年赤峰中考)如图,ABC 中,90ACB ∠=︒,AC BC =,O 经过B,C 两点,与斜边AB 交于点E,连接CO 并延长交AB 于点M,交O 于点D,过点E 作EF CD ∥,交AC 于点F ．(1)求证:EF 是O 的切线;(2)若BM =,1tan2BCD ∠=,求OM 的长．11.(24年绥化中考)如图1,O 是正方形ABCD 对角线上一点,以O 为圆心,OC 长为半径的O 与AD 相切于点E ,与AC 相交于点F ．(1)求证:AB 与O 相切．(2)若正方形ABCD 1,求O 的半径．(3)如图2,在(2)的条件下,若点M 是半径OC 上的一个动点,过点M 作MN OC ⊥交 CE于点N ．当:1:4CM FM =时,求CN 的长．12.(24年河北中考)已知O 的半径为3,弦MN =,ABC 中.90,3,ABC AB BC ∠=︒==在平面上,先将ABC 和O 按图1位置摆放(点B 与点N 重合,点A 在O 上,点C 在O 内),随后移动ABC ,使点B 在弦MN 上移动,点A 始终在O 上随之移动,设BN x =．(1)当点B 与点N 重合时,求劣弧 AN 的长.(2)当OA MN ∥时,如图2,求点B 到OA 的距离,并求此时x 的值.(3)设点O 到BC 的距离为d ．①当点A 在劣弧 MN上,且过点A 的切线与AC 垂直时,求d 的值.②直接写出d 的最小值．13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题:如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系．(提示:分别作AB 和BC 边上的高．)【得出结论】sin sin sin a b c A B C==．【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C ==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C ===(R 为ABC 外接圆的半径)．请利用图1证明:2sin sin sin a b c R A B C ===．【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒．求过A,B,D 三点的圆的半径．14.(24年苏州中考)如图,ABC 中,AB =,D 为AB 中点,BAC BCD ∠=∠cos4ADC ∠=.O 是ACD 的外接圆．(1)求BC 的长(2)求O 的半径．15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为 CB 上一点,且 AC CE=．(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积．16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点．(1)求证:AB 与半圆O 相切(2)连接OA ．若4CD =,2CF =,求sin OAC ∠的值．17.(24年甘肃武威中考)如图,AB 是O 的直径, BCBD =,点E 在AD 的延长线上,且ADC AEB ∠=∠．(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值．18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E ．(1)求证:DE BE⊥(2)若AB =,5BE =,求O 的半径．19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、．(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径．20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =．点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF ．(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径．21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠．(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长．22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是»AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠．(1)求证:AD 是O 的切线．(2)若4,BE AD ==,求O 的半径长．23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F ．(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长．24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明:点D 为 BC上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系,并说明理由;②若ABC 为锐角三角形,求DF 的取值范围．25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD ．(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长．26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD ．(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径．27.(24年四川达州中考)如图,BD 是O 的直径．四边形ABCD 内接于O ．连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F ．(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E ．若3CD DE =,求cos ABC ∠的值．28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是 AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G ．(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM ．①求证:AM 是O 的切线;②若6DG =,5DF =,求O 的半径．29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠．(1)如图1,若1BE =,CE =,求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥．(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F ．(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N ．求证:MN 是O 的切线．31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===．以点A 为圆心,以AD 为半径作 DE交AB 于点E ,以点B 为圆心,以BE 为半径作 EF 所交BC 于点F ,连接FD 交 EF于另一点G ,连接CG ．(1)求证：CG 为 EF所在圆的切线(2)求图中阴影部分面积．(结果保留π)32.(24年青海中考)如图,直线AB 经过点C,且OA OB =,CA CB =．(1)求证:直线AB 是O 的切线;(2)若圆的半径为4,30B ∠=︒,求阴影部分的面积．圆的证明与计算练习答案1.(24年湖北中考)【答案】(1)略(2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解(2)2π5.(24年安徽中考)【答案】(1)略(2)6.(24年新疆中考)【答案】(1)略(2)4CE =.7.(24年江西中考)【答案】(1)见解析(2)2π8.(24年呼伦贝尔中考)【答案】(1)略(2)43π9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在 BC上时,2sin2CD AD BD α⋅=-.当D 在 AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略(2)OM =11.(24年绥化中考)【答案】(1)证明略(3)512.(24年河北中考)【答案】(1)π(2)点B 到OA 的距离为2;3(3)①3d =;②2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:3AB =;推广证明:见解析;拓展应用:6R =．14.(24年苏州中考)【答案】(1)4BC =(2)O 的半径为47715.(24年乐山中考)【答案】(1)略(2)3π493-16.(24年武汉中考)【答案】(1)略(2)4517.(24年甘肃武威中考)【答案】(1)略(2)7tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略(2)19.(24年盐城中考)【答案】(1)略(2)25620.(24年广西中考)【答案】(1)略(2)略(3)1021.(24年四川广安中考)【答案】(1)略(2)1422.(24年四川南充中考)【答案】(1)略(2)23.(24年四川泸州中考)【答案】(1)证明略(2)4524.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;②DF 的取值范围为532DF <<．25.(24年四川宜宾中考)【答案】(1)略(2)CD =553DE =．26.(24年内蒙古通辽中考)【答案】(1)证明略(2)327.(24年四川达州中考)【答案】(1)证明略(2)5528.(24年四川遂宁中考)【答案】(1)证明略(2)①证明略,②O 的半径为203．29.(24年包头中考)【答案】(1)3(2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1(2)略31.(24年山东枣庄中考)【答案】(1)略(2)3343π-32.(24年青海中考)【答案】(1)详见解析(2) 83S π=阴影。
初中三：圆的证明与计算
圆的证明与计算【高频核心考点】1，圆周角定理以及垂径定理，如下图所示∵ AB 为直径且AB ⊥CD∴ CE=DE ，弧BC=弧BD ，弧AC=弧AD 注：运算中主要运用勾股定理。
2，圆的切线长定理，如下图所示∵ PA，PB 为⊙O 的两条切线∴ PA=PB ，且PO 垂直平分AB 同理可证：EC=EA ，FC=FB3，相交弦定理 切割线定理 割线定理结论： PA ·PB=PC ·PD PA 2=PB ·PC PB ·PA=PD ·PC4，切割线延伸： 切割线互垂（角平分线）：结论：tan A DB BC CDAD CD AC∠===结论：∠ABD=∠CBD ，DB 2=BC ·BE ，AD 2=AE ·ABOFE DC BA【精题精讲精练】◆例1：《角平分线模型》1，如图，在Rt ABC∆中，90C∠=︒，AD平分BAC∠交BC于点D，O为AB上一点，经过点A，D的O⊙分别交AB，AC于点E，F，连接OF交于点G.（1）求证：BC是O⊙的切线；（2）设AB x=，AF y=，试用含,x y的代数式表示线段AD的长；（3）若8BE=，5sin13B=，求DG的长.2，如图1，在△ABC中，AB=AC，⊙O是△ABC的外接圆，过点C作∠BCD=∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF=AC，连接AF.（1）求证：ED=EC；（2）求证：AF是⊙O的切线；（3）如图2，若点G是△ACD的内心，BC·BE=25，求BC的长.AD【变式练习】已知：如图，△ABC 内接于⊙O ，AB 为直径，∠CBA 的平分线交AC 于点F ，交⊙O 于点D ，DE ⊥AB 于点E ，且交AC 于点P ，连结AD. （1）求证：2AC DE =；（2）若tan∠CBD =12，AP·AC=5，求AC 的长； （3）若65AD =，⊙O 的半径为152，延长DE 交⊙O 于点M ，且DP ：DM=1：3，求CM 的长.◆例2：《母子型相似》1，如图,AB 为⊙O 的直径,C,D 为圆上的两点,OC∥BD，弦AD ，BC 相交于点E.(1)求证：弧AC=弧CD ；(2)若CE=1，EB=3，求⊙O 的半径；(3)在(2)的条件下,过点C 作⊙O 的切线,交BA 的延长线于点P,过点P 作PQ∥CB 交⊙O 于F,Q 两点(点F 在线段PQ 上)，求PQ 的长。
与圆有关的计算和证明解题技巧
与圆有关的计算和证明解题技巧
与圆有关的计算和证明是数学中一个重要的部分，它涉及到许多基本的数学概念和技巧。
以下是一些与圆有关的计算和证明的解题技巧：
1. 确定圆心和半径：在解决与圆有关的问题时，首先需要确定圆心和半径。
圆心是圆的中心点，而半径是从圆心到圆周的距离。
知道这些信息可以帮助你找到圆的方程，或者解决与圆有关的问题。
2. 使用圆的性质：了解并利用圆的性质是解决与圆有关问题的关键。
例如，圆的对称性、切线的性质、弦的性质等。
3. 利用勾股定理：勾股定理是一个非常重要的数学定理，它可以帮助你解决与圆有关的问题。
特别是当涉及到弦、切线、半径等时，勾股定理是非常有用的。
4. 使用圆的方程：圆的方程是解决与圆有关问题的另一个重要工具。
通过圆的方程，你可以找到圆心和半径，或者找到与圆有关的特定点的坐标。
5. 利用三角函数：在解决与圆有关的问题时，三角函数是非常有用的工具。
例如，当涉及到角度、弧长等时，三角函数可以帮助你找到解决方案。
6. 利用几何推理：几何推理是解决与圆有关问题的另一个重要技巧。
通过观察和推理，你可以找到解决问题的方法。
7. 练习和反思：最后，要提高解决与圆有关问题的能力，你需要不断地练习和反思。
通过练习，你可以熟悉各种问题类型和解题技巧，而反思则可以帮助你发现自己的弱点并加以改进。
希望这些技巧能帮助你更好地理解和解决与圆有关的问题！。
圆的计算与证明范文
圆的计算与证明范文圆是数学中一种重要的几何形状，由于其特殊的性质和广泛的应用，圆的计算和证明一直是几何学习的重点内容之一、本文将对圆的计算和证明进行详细介绍。
一、圆的定义与性质圆的定义：平面上的一个点集合，到该点距离相等的所有点构成的图形，称为圆。
圆的性质：1.圆上的任意一点到圆心的距离都相等。
2.圆心到圆上任意一点的线段称为半径，圆上任意两点之间的线段称为弦。
3.圆的直径是通过圆心的一条弦，且等于弦长的两倍。
4.圆的周长是圆上任意一段弧长与半径的乘积，即C=2πr，其中C 为周长，r为半径。
5.圆的面积是半径平方乘以π，即A=πr²，其中A为面积，r为半径。
二、圆的计算根据圆的性质，可以进行以下计算：1.已知圆的半径，计算周长和面积。
以半径为4cm的圆为例，周长和面积的计算公式为：C=2πr=2π×4=8π≈25.13cm（取π≈3.14），A=πr²=π×4²=16π≈50.27cm²。
2.已知圆的周长，计算半径和面积。
以周长为10cm的圆为例，半径的计算公式为：r=C/2π=10/(2π)≈1.59cm，面积的计算公式为：A=πr²=π×(1.59)²≈7.97cm²。
3.已知圆的面积，计算半径和周长。
以面积为20cm²的圆为例，半径的计算公式为：r=√(A/π)=√(20/π)≈2.52cm，周长的计算公式为：C=2πr=2π×2.52≈15.86cm。
三、圆的证明1.圆心角的证明圆心角是指圆心所对的弧所对应的角，圆心角的证明如下：（步骤一）连接弧所对应的两条半径。
（步骤二）在弧所对应的两条半径上分别取任意一点，分别连接这两点与圆心的直线。
（步骤三）观察三角形圆心角，可以发现它们是共边共顶点的相似三角形，根据相似三角形的性质可知，它们的对应角相等。
（步骤四）由于圆上任意两点之间的弦所对应的圆心角相等，因此可以得出结论：圆上任意两点之间的弦所对应的圆心角相等。
圆的概念 公式及推导完整版
〖圆的定义〗几何说：平面上到定点的距离等于定长的所有点组成的图形叫做圆。
定点称为圆心，定长称为半径。
轨迹说：平面上一动点以一定点为中心，一定长为距离运动一周的轨迹称为圆周，简称圆。
集合说：到定点的距离等于定长的点的集合叫做圆。
〖圆的相关量〗圆周率：圆周长度与圆的直径长度的比叫做圆周率，值是3.14159265358979323846…，通常用π表示，计算中常取3.1416为它的近似值。
圆弧和弦：圆上任意两点间的部分叫做圆弧，简称弧。
大于半圆的弧称为优弧，小于半圆的弧称为劣弧。
连接圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径。
圆心角和圆周角：顶点在圆心上的角叫做圆心角。
顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。
内心和外心：过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心。
和三角形三边都相切的圆叫做这个三角形的内切圆，其圆心称为内心。
扇形：在圆上，由两条半径和一段弧围成的图形叫做扇形。
圆锥侧面展开图是一个扇形。
这个扇形的半径成为圆锥的母线。
〖圆和圆的相关量字母表示方法〗圆—⊙半径—r 弧—⌒直径—d扇形弧长／圆锥母线—l 周长—C 面积—S〖圆和其他图形的位置关系〗圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r。
直线与圆有3种位置关系：无公共点为相离；有两个公共点为相交；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点。
以直线AB与圆O为例（设OP⊥AB于P，则PO是AB到圆心的距离）：AB与⊙O相离，PO＞r；AB与⊙O相切，PO＝r；AB与⊙O相交，PO＜r。
两圆之间有5种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交。
两圆圆心之间的距离叫做圆心距。
两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r。
2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)
2024年中考数学复习重难点题型训练—圆的相关证明与计算（含答案解析）类型一基本性质有关的1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．(1)求证：直线PE是⊙O的切线；(2)若⊙O的半径为6，∠P=30°，求CE的长．【答案】(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，可得BD=CD=12BC=6，在Rt△CDE中，即得CE的长是3．本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．(1)求证：CE与⊙O相切；(2)若AD=4，∠D=60°，求线段AB，BC的长．【答案】(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，60°，即得AB=3BD=23，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=2AB= 6，又△AOC是等腰直角三角形，OA=OC=2，得AC=22，故CF=AC2−AF2=2，从而BC=BF+CF=6+2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．3.（2021·山东临沂市·中考真题）如图，已知在⊙O中，＝＝，OC与AD相交于点AB BC CDE．求证：（1）AD∥BC（2）四边形BCDE为菱形．【答案】（1）见解析；（2）见解析【分析】（1）连接BD ，根据圆周角定理可得∠ADB=∠CBD ，根据平行线的判定可得结论；（2）证明△DEF ≌△BCF ，得到DE=BC ，证明四边形BCDE 为平行四边形，再根据 BCCD =得到BC=CD ，从而证明菱形．【详解】解：（1）连接BD ，∵ AB BCCD ==，∴∠ADB=∠CBD ，∴AD ∥BC ；（2）连接CD ，∵AD ∥BC ，∴∠EDF=∠CBF ，∵ BCCD =，∴BC=CD ，∴BF=DF ，又∠DFE=∠BFC ，∴△DEF ≌△BCF （ASA ），∴DE=BC ，∴四边形BCDE 是平行四边形，又BC=CD ，∴四边形BCDE 是菱形．【点睛】本题考查了垂径定理，圆周角定理，弧、弦、圆心角的关系，全等三角形的判定和性质，菱形的判定，解题的关键是合理运用垂径定理得到BF=DF ．4.（2021·四川南充市·中考真题）如图，A ，B 是O 上两点，且AB OA =，连接OB 并延长到点C ，使BC OB =，连接AC ．（1）求证：AC 是O 的切线．（2）点D ，E 分别是AC ，OA 的中点，DE 所在直线交O 于点F ，G ，4OA =，求GF 的长．【答案】（1）见解析；（2）【分析】（1）先证得△AOB 为等边三角形，从而得出∠OAB=60°，利用三角形外角的性质得出∠C=∠CAB=30°，由此可得∠OAC=90°即可得出结论；（2）过O 作OM ⊥DF 于M ，DN ⊥OC 于N ，利用勾股定理得出AC=30°的直角三角形的性质得出DN ，再根据垂径定理和勾股定理即可求出GF 的长．【详解】（1）证明：∵AB=OA ，OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°，∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线；（2）∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点，∴OE//BC ，DC=过O 作OM ⊥DF 于M ，DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中，∠C=30°，∴DN=12DC=∴OM=3连接OG ，∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定，熟练掌握相关的知识是解题的关键．5.（2021·安徽中考真题）如图，圆O 中两条互相垂直的弦AB ，CD 交于点E ．（1）M 是CD 的中点，OM ＝3，CD ＝12，求圆O 的半径长；（2）点F 在CD 上，且CE ＝EF ，求证：AF BD ⊥．【答案】（1）35；（2）见解析．【分析】（1）根据M 是CD 的中点，OM 与圆O 直径共线可得OM CD ⊥，OM 平分CD ，则有6MC =，利用勾股定理可求得半径的长；（2）连接AC ，延长AF 交BD 于G ，根据CE EF =，AE FC ⊥，可得AF AC =，12∠=∠，利用圆周角定理可得2D ∠=∠，可得1D ∠=∠，利用直角三角形的两锐角互余，可证得90AGB ∠=︒，即有AF BD ⊥．【详解】（1）解：连接OC ，∵M 是CD 的中点，OM 与圆O 直径共线∴OM CD ⊥，OM 平分CD ，90OMC ∴∠=︒12CD = 6MC ∴=．在Rt OMC △中．OC ===∴圆O 的半径为（2）证明：连接AC ，延长AF 交BD 于G ．CE EF = ，AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理，圆周角定理，直角三角形的两锐角互余，勾股定理等知识点，熟练应用相关知识点是解题的关键．∠是 AD所对的圆周角，6.（2021·浙江中考真题）如图，已知AB是⊙O的直径，ACD∠=︒．30ACD∠的度数；（1）求DABAB=，求DF的（2）过点D作DE AB⊥，垂足为E，DE的延长线交⊙O于点F．若4长．【答案】（1）60︒；（2）23【分析】（1）连结BD ，根据圆周角性质，得B ACD ∠=∠；根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算，即可得到答案；（2）根据含30°角的直角三角形性质，得12AD AB =；根据垂径定理、特殊角度三角函数的性质计算，即可得到答案．【详解】（1）连结BD ，30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径，90ADB ∴∠=︒，9060DAB B ∴∠=︒-∠=︒（2）90ADB ∠=︒ ，30B ∠=︒，4AB =∴122AD AB ==60DAB ∠=︒ ，DE AB ⊥，且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=．【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识；解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质，从而完成求解．7.（2021·湖南中考真题）如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．【答案】（1）见解析；（2）5CE =．【分析】（1）连接OD ，由点D 是 BC的中点得OD ⊥BC ，由DE//BC 得OD ⊥DE ，由OD 是半径可得DE 是切线；（2）证明△ODE 是等腰直角三角形，可求出OE 的长，从而可求得结论．【详解】解：（1）连接OD 交BC 于点F ，如图，∵点D 是 BC的中点，∴OD ⊥BC ，∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切；（2）∵AC 是O 的直径，且AB=10,∴∠ABC=90°，152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得，OE =∴5CE OE OC =-=．【点睛】此题主要考查了切线的判定与性质的综合运用，熟练掌握切线的判定与性质是解答此题的关键．8.（2021·湖南张家界市·中考真题）如图，在Rt AOB 中，90∠=︒ABO ，30OAB ∠=︒，以点O 为圆心，OB 为半径的圆交BO 的延长线于点C ，过点C 作OA 的平行线，交O 于点D ，连接AD ．（1）求证：AD 为O 的切线；（2）若2OB =，求弧CD 的长．【答案】（1）见解析；（2）23π【分析】（1）连接OB ，先根据直角三角形的性质得到∠AOB=60°，再运用平行线的性质结合已知条件可得60AOD ∠=︒，再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可；（2）先求出∠COD ，然后再运用弧长公式计算即可．【详解】（1）证明：连接OD∵30OAB ∠=︒，90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线；（2）∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=．【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点，掌握圆的切线的证明方法成为解答本题的关键．9.（2020•齐齐哈尔）如图，AB 为⊙O 的直径，C 、D 为⊙O 上的两个点，AC=CD =DB ，连接AD ，过点D 作DE ⊥AC 交AC 的延长线于点E ．（1）求证：DE 是⊙O 的切线．（2）若直径AB ＝6，求AD 的长．【分析】（1）连接OD ，根据已知条件得到∠BOD =13×180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．【解析】（1）证明：连接OD，=CD =DB ，∵AC∴∠BOD=13×180°＝60°，=DB ，∵CD∴∠EAD＝∠DAB=12∠BOD＝30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∵∠DAB＝30°，AB＝6，∴BD=12AB＝3，∴AD=62−32=33．10.（2020•深圳）如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝10，BC＝6，求CD的长．【分析】（1）证明：连接AC、OC，如图，根据切线的性质得到OC⊥CD，则可判断OC∥AD，所以∠OCB＝∠E，然后证明∠B＝∠E，从而得到结论；（2）利用圆周角定理得到∠ACB＝90°，则利用勾股定理可计算出AC＝8，再根据等腰三角形的性质得到CE＝BC＝6，然后利用面积法求出CD的长．【解析】（1）证明：连接AC、OC，如图，∵CD为切线，∴OC⊥CD，∴CD⊥AD，∴OC∥AD，∴∠OCB＝∠E，∵OB＝OC，∴∠OCB＝∠B，∴∠B＝∠E，∴AE＝AB；（2）解：∵AB为直径，∴∠ACB＝90°，∴AC=102−62=8，∵AB＝AE＝10，AC⊥BE，∴CE＝BC＝6，∵12CD•AE=12AC•CE，∴CD=6×810=245．11.（2020•陕西）如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°．连接AO并延长，交⊙O于点D，连接BD．过点C作⊙O的切线，与BA的延长线相交于点E．（1）求证：AD∥EC；（2）若AB＝12，求线段EC的长．【分析】（1）连接OC，由切线的性质可得∠OCE＝90°，由圆周角定理可得∠AOC＝90°，可得结论；（2）过点A作AF⊥EC交EC于F，由锐角三角函数可求AD＝83，可证四边形OAFC是正方形，可得CF＝AF＝43，由锐角三角函数可求EF＝12，即可求解．【解析】证明：（1）连接OC，∵CE与⊙O相切于点C，∴∠OCE＝90°，∵∠ABC＝45°，∴∠AOC＝90°，∵∠AOC+∠OCE＝180°，∴∴AD∥EC（2）如图，过点A作AF⊥EC交EC于F，∵∠BAC＝75°，∠ABC＝45°，∴∠ACB＝60°，∴∠D＝∠ACB＝60°，∴sin∠ADB=AB AD==83，∴AD=∴OA＝OC＝43，∵AF⊥EC，∠OCE＝90°，∠AOC＝90°，∴四边形OAFC是矩形，又∵OA＝OC，∴四边形OAFC是正方形，∴CF＝AF＝43，∵∠BAD＝90°﹣∠D＝30°，∴∠EAF＝180°﹣90°﹣30°＝60°，∵tan∠EAF=EF AF=3，∴EF=3AF＝12，∴CE＝CF+EF＝12+43．类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．(1)求证：∠D=∠EBC；(2)若CD=2BC，AE=3，求⊙O的半径．【答案】(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．13.（2022·北部湾）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E，延长BA交⊙O于点F.（1）求证：DE是⊙O的切线（2）若AE DE=23，AF=10，求⊙O的半径.【答案】（1）证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线（2）解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD=CD，即OD是△ABC的中位线，∵AC是⊙O的直径，∴∠CFA=90°，∵DE⊥AB，∴∠BED=90°，∴∠CFA=∠BED=90°，∴DE∥CF，∴BE=EF，即DE是△FBC的中位线，∴CF=2DE，∵AE DE=23，∴设AE=2x，DE=3k，CF=6k，∵AF=10，∴BE=EF=AE+AF=2k+10，∴AC=BA=EF+AE=4k+10，在Rt△ACF中，由勾股定理，得AC2=AF2+CF2，即(4k+10)2=102+(6k)2，解得：k=4，∴AC=4k+10=4×4+10=26，∴OA=13，即⊙O的半径为13.【知识点】平行线的判定与性质；等腰三角形的性质；圆周角定理；切线的判定；三角形的中位线定理【解析】【分析】（1）连接OD ，根据等腰三角形的性质可得∠C=∠ODC ，∠B=∠C ，则∠B=∠ODC ，推出OD ∥AB ，由平行线的性质可得∠ODE=∠DEB=90°，即DE ⊥OD ，据此证明；（2）连接CF ，由（1）知OD ⊥DE ，则OD ∥AB ，易得OD 是△ABC 的中位线，根据圆周角定理可得∠CFA=90°，根据垂直的概念可得∠BED=90°，则DE ∥CF ，推出DE 是△FBC的中位线，得CF=2DE ，设AE=2x ，DE=3k ，CF=6k ，则BE=EF=2k+10，AC=BA=4k+10，根据勾股定理可得k 的值，然后求出AC 、OA ，据此可得半径.14.（2021·江苏无锡市·中考真题）如图，四边形ABCD 内接于O ，AC 是O 的直径，AC 与BD 交于点E ，PB 切O 于点B ．（1）求证：PBA OBC ∠=∠；（2）若20PBA Ð=°，40ACD ∠=︒，求证：OAB CDE V V ∽．【答案】（1）见详解；（2）见详解【分析】（1）由圆周角定理的推论，可知∠ABC=90°，由切线的性质可知∠OBP=90°，进而即可得到结论；（2）先推出20OCB OBC ∠=∠=︒，从而得∠AOB=40°，继而得∠OAB=70°，再推出∠CDE=70°，进而即可得到结论．【详解】证明：（1）∵AC 是O 的直径，∴∠ABC=90°，∵PB 切O 于点B ，∴∠OBP=90°，∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒，∴PBA OBC ∠=∠；（2）∵20PBA Ð=°，PBA OBC ∠=∠，∴20OBC ∠=︒，∵OB=OC ，∴20OCB OBC ∠=∠=︒，∴∠AOB=20°+20°=40°，∵OB=OA ，∴∠OAB=∠OBA=(180°-40°)÷2=70°，∴∠ADB=12∠AOB=20°，∵AC 是O 的直径，∴∠ADC=90°，∴∠CDE=90°-20°=70°，∴∠CDE=∠OAB ，∵40ACD ∠=︒，∴40ACD AOB ∠=∠=︒，∴OAB CDE V V ∽．【点睛】本题主要考查圆的性质以及相似三角形的判定定理，掌握圆周角定理的推论，相似三角形的判定定理，切线的性质定理，是解题的关键．15.（2020•衢州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝10，AC ＝6，连结OC ，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．【分析】（1）利用垂径定理以及圆周角定理解决问题即可．（2）证明△AEC∽△BCA，推出CE AC=AC AB，求出EC即可解决问题．【解析】（1）证明：∵AE＝DE，OC是半径，=CD ，∴AC∴∠CAD＝∠CBA．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE，∴OC⊥AD，∴∠AEC＝90°，∴∠AEC＝∠ACB，∴△AEC∽△BCA，∴CE AC=AC AB，∴CE6=610，∴CE＝3.6，∵OC=12AB＝5，∴OE＝OC﹣EC＝5﹣3.6＝1.4．16.（2020•铜仁市）如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D 是直径AB延长线上一点，且∠BCE＝∠BCD．（1）求证：CD是⊙O的切线；（2）若AD＝8，BE CE=12，求CD的长．【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【解析】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD是⊙O的切线；（2）解：∵∠A＝∠BCE，∴tanA=BC AC=tan∠BCE=BE CE=12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC=CD AD=12，∵AD＝8，∴CD＝4．17.（2020•衡阳）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【分析】（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；（2）连接DE，根据圆周角定理得到∠ADE＝90°，根据相似三角形的性质得到AC=325，根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论．【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AE AD=AD AC，108=8AC，∴AC=325，∴CD=AD2−AC2==245，∵OD⊥BC，AC⊥BC，∴△OBD∽△ABC，∴OD AC=BD BC，∴5325=BD BD+245，∴BD=1207．18.（2020•遵义）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交BC 于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【解析】（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BA=BF BD，∴BD2＝BF•BA＝2×6＝12．∴BD＝23．19.（2019•陕西）如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．【分析】（1）根据切线的性质得到∠OAP＝90°，根据圆周角定理得到∠BCD＝90°，根据平行线的性质和判定定理即可得到结论；（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．【解析】（1）证明：∵AP是⊙O的切线，∴∠OAP＝90°，∵BD是⊙O的直径，∴∠BCD＝90°，∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO，∴DC∥AP；（2）解：∵AO∥BC，OD＝OB，∴延长AO交DC于点E，则AE⊥DC，OE=12BC，CE=12CD，在Rt△AOP中，OP=62+82=10，由（1）知，△AOP∽△CBD，∴DB OP=BC OA=DC AP，即1210=BC6=DC8，∴BC=365，DC=485，∴OE=185，CE=245，在Rt△AEC中，AC=AE2+CE2==20（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC 是O 的切线：（2）若2,33OA BE OD ==，求DA 的长．【答案】（1）见解析；（2）910【分析】（1）连接OC ，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC 是圆O 的切线；（2）根据已知得到OA=2DA ，证明△DCO ∽△DEB ，得到DO CO DB EB =，可得DA=310EB ，即可求出DA 的长．【详解】解：（1）如图，连接OC ，由题意可知：∠ACB 是直径AB 所对的圆周角，∴∠ACB=90°，∵OC ，OB 是圆O 的半径，∴OC=OB ，∴∠OCB=∠ABC ，又∵∠DCA=∠ABC ，∴∠DCA=∠OCB ，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC ⊥DC ，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB+===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．21.（2021·江苏扬州市·中考真题）如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ．（1）试判断CD 与B 的位置关系，并说明理由；（2）若AB =，60BCD ∠=︒，求图中阴影部分的面积．【答案】（1）相切，理由见解析；（2）π-【分析】（1）过点B 作BF ⊥CD ，证明△ABD ≌△FBD ，得到BF=BA ，即可证明CD 与圆B 相切；（2）先证明△BCD 是等边三角形，根据三线合一得到∠ABD=30°，求出AD ，再利用S △ABD -S 扇形ABE 求出阴影部分面积．【详解】解：（1）过点B 作BF ⊥CD ，∵AD ∥BC ，∴∠ADB=∠CBD ，∵CB=CD ，∴∠CBD=∠CDB ，∴∠ADB=∠CDB ，又BD=BD ，∠BAD=∠BFD=90°，∴△ABD ≌△FBD （AAS ），∴BF=BA ，则点F 在圆B 上，∴CD 与圆B 相切；（2）∵∠BCD=60°，CB=CD ，∴△BCD 是等边三角形，∴∠CBD=60°∵BF ⊥CD ，∴∠ABD=∠DBF=∠CBF=30°，∴∠ABF=60°，∵AB=BF=，∴AD=DF=tan30AB ⋅︒=2，∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-．【点睛】本题考查了切线的判定，全等三角形的判定和性质，等边三角形的判定和性质，扇形面积，三角函数的定义，题目的综合性较强，难度不小，解题的关键是正确做出辅助线．22.（2020•上海）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC 于点D．（1）求证：∠BAC＝2∠ABD；（2）当△BCD是等腰三角形时，求∠BCD的大小；（3）当AD＝2，CD＝3时，求边BC的长．【分析】（1）连接OA．利用垂径定理以及等腰三角形的性质解决问题即可．（2）分三种情形：①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD．③若DB＝DC，则D与A重合，这种情形不存在．分别利用三角形内角和定理构建方程求解即可．（3）如图3中，作AE∥BC交BD的延长线于E．则AE BC=AD DC=23，推出AO OH=AE BH=43，设OB＝OA＝4a，OH＝3a，根据BH2＝AB2﹣AH2＝OB2﹣OH2，构建方程求出a即可解决问题．【解析】（1）证明：连接OA．A∵AB＝AC，=AC ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠BAD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC+∠C+∠BDC＝180°，∴8∠ABD＝180°，∴∠C＝3∠ABD＝67.5°．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠C ＝4∠ABD ，∵∠DBC+∠C+∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23，∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ，∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =∴BC ＝2BH =23.（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC是O的切线：（2）若2,33OA BEOD==，求DA的长．【答案】（1）见解析；（2）9 10【分析】（1）连接OC，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC是圆O的切线；（2）根据已知得到OA=2DA，证明△DCO∽△DEB，得到DO CODB EB=，可得DA=310EB，即可求出DA的长．【详解】解：（1）如图，连接OC，由题意可知：∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∵OC，OB是圆O的半径，∴OC=OB，∴∠OCB=∠ABC，又∵∠DCA=∠ABC，∴∠DCA=∠OCB，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC⊥DC，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB +===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．(1)求证：BF与⊙O相切；(2)若AP=OP，cosA=45，AP=4，求BF的长．【答案】(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD，然后利用等腰三角形的性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE= 90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．25.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD ，∠BDC =∠BAD ．(1)求证：CD 是⊙O 的切线．(2)若tan∠BED =23，AC =9，求⊙O 的半径．【答案】（1）连接OD ，由圆周角定理得出∠ADB =90°，证出OD ⊥CD ，由切线的判定可得出结论；(2)证明△BDC∽△DAC ，由相似三角形的性质得出CD AC =BC CD =BD DA =23，由比例线段求出CD 和BC 的长，可求出AB 的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.（2021·山东菏泽市·中考真题）如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．【答案】（1）见解析；（2）=2BG 【分析】（1）连接OE ，证明OE ⊥EF 即可；（2）由3sin 5F =证得4sin 5G =，运用正弦的概念可得结论．【详解】解：（1）证明：连接OE ，如图，∵OA=OE∴∠OAE=∠OEA ．∵EF=PF ，∴∠EPF=∠PEF∵∠APH=∠EPF ，∴∠APH=∠EPF ，∴∠AEF=∠APH ．∵CD ⊥AB ，∴∠AHC=90°．∴∠OAE+∠APH=90°．∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF ．∵OE 是O 的半径∴EF 是圆的切线，（2）∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =，则5FG x=由勾股定理得，4FH x=由（1）得，OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =，即45OE OE BG =+∵8OE =∴8485BG =+解得，2BG =【点睛】此题主要考查了圆的切线的判定，勾股定理和解直角三角形等知识，熟练掌握切线的判定是解答此题的关键．27.（2022·黔东南）（1）请在图中作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹，不写作法）；的中点，过点B的（2）如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE切线与AC的延长线交于点D.①求证：BD⊥AD；②若AC=6，tan∠ABC=34，求⊙O的半径.【答案】（1）解：如下图所示（2）解：①如下图所示，连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角，∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示，连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理；三角形的外接圆与外心；切线的性质；解直角三角形；作图-线段垂直平分线【解析】【解答】（1）∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点，半径为交点到任意顶点的距离，∴做AB、AC的垂直平分线交于点O，以OB为半径，以O为圆心做圆即可得到△ABC 的外接圆；【分析】（1）利用尺规作图分别作出AC，AB的垂直平分线，两垂直平分线交于点O，然后以点O为圆心，OB的长为半径画圆即可.（2）①连接OC，OB，利用切线的性质可证得OB⊥BD，利用圆周角定理可证得∠COE=2∠CAE，由点B是弧CE的中点，可推出∠CAE=∠BOE，利用平行线的判定定理可证得AD∥OB，由此可证得结论；②连接CE，利用同弧所对的圆周角相等，可证得∠ABC=∠AEC，利用直径所对的圆周角是直角，可推出∠ACE=90°；再利用解直角三角形求出CE的长，利用勾股定理求出AE的长.28.（2022·鄂州）如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB=∠OAC，过点O作BC的平行线交PC的延长线于点D.（1）试判断PC与⊙O的位置关系，并说明理由；（2）若PC＝4，tanA＝12，求△OCD的面积.【答案】（1）解：PC与⊙O相切，理由如下：∵AB是圆O的直径，∴∠ACB=90°，∴∠OCB+∠OCA=90°，∵OA=OC，∴∠OCA=∠OAC，∵∠PCB=∠OAC，∴∠PCB=∠OCA，∴∠PCB+∠OCB=∠OCA+∠OCB=90°，即∠PCO=90°，∴PC与⊙O相切（2）解：∵∠ACB=90°，tanA=12，∴BC AC=12，∵∠PCB=∠OAC，∠P=∠P，∴△PBC∽△PCA，∴PC PA=PB PC=BC CA=12，∴PA=8，PB=2，∴AB=6，∴OC=OB=3，∴OP=5，∵BC∥OD，∴△PBC∽△POD，∴PB OP=PC PD，即25=4PD，∴PD=10，∴CD=6，∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质；圆周角定理；切线的判定；相似三角形的判定与性质；锐角三角函数的定义【解析】【分析】（1）由圆周角定理得∠ACB=90°，根据等腰三角形的性质可得∠OCA=∠OAC，结合∠PCB=∠OAC得PCB=∠OCA，结合∠OCB+∠OCA=90°可得∠PCO=90°，据此证明；（2）根据三角函数的概念可得BC AC=12，易证△PBC∽△PCA，根据相似三角形的性质可得PA、PB，然后求出AB、OP，证明△PBC∽△POD，根据相似三角形的性质可得PD，由PD-PC=CD可得CD，然后根据三角形的面积公式进行计算.29.（2022·毕节）如图，在△ABC中，∠ACB=90∘，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F.（1）求证：BF=BD；（2）若CF=1，tan∠EDB=2，求⊙O直径.【答案】（1）证明：连接OE，如下图所示：∵AC为圆O的切线，∴∠AEO=90°，∵AC⊥BC，∴∠ACB=90°，∴OE∥BC，∴∠F=∠DEO，又∵OD=OE，∴∠ODE=∠DEO，∴∠F=∠ODE，∴BD=BF.（2）解：连接BE，如下图所示：由(1)中证明过程可知：∠EDB=∠F，。
中考数学复习《圆的证明与计算》经典题型及测试题(含答案)
中考数学复习《圆的证明与计算》经典题型及测试题（含答案）阅读与理解圆的相关知识的考查是中考数学中的一个重要内容，圆作为一个载体，常与三角形、四边形结合，考查切线的性质及判定、相似三角形的性质与判定、解直角三角形、求阴影面积等．解题时要先分析题干中的条件，然后从图象中挖掘隐含条件，最后再解题．类型一切线的判定判定一条直线是圆的切线，首先看圆的半径是否过直线与圆的交点，有半径则证垂直；没有半径，则连接圆心与切点，构造半径证垂直．例1 (2016·黄石)如图，⊙O的直径为AB，点C在圆周上(异于A，B)，AD⊥CD.(1)若BC＝3，AB＝5，求AC的值；(2)若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．【分析】（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得AC的长即可；（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得⊥OCA=⊥CAD，即可得到OC⊥AD，由于AD⊥CD，那么OC⊥CD，由此得证．【自主解答】（1）解：⊥AB是⊥O直径，C在⊥O上，⊥⊥ACB=90°，又⊥BC=3，AB=5，⊥由勾股定理得AC=4；（2）证明：⊥AC是⊥DAB的角平分线，⊥⊥DAC=⊥BAC，又⊥AD⊥DC，⊥⊥ADC=⊥ACB=90°，⊥⊥ADC⊥⊥ACB，⊥⊥DCA=⊥CBA，又⊥OA=OC，⊥⊥OAC=⊥OCA，⊥⊥OAC+⊥OBC=90°，⊥⊥OCA+⊥ACD=⊥OCD=90°，⊥DC是⊥O的切线．变式训练1．(2017·白银) 如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．解：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB==，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．类型二切线的性质已知某条直线是圆的切线，当圆心与切点有线段连接时，直接利用切线的性质：圆的切线垂直于过切点的半径；当圆心与切点没有线段相连时，则作辅助线连接圆心与切点，再利用切线的性质解题．例2 (2016·资阳) 如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连接BD.(1)求证：∠A＝∠BDC；(2)若CM平分∠ACD，且分别交AD，BD于点M，N，当DM＝1时，求MN的长．【分析】(1)连接OD，由切线的性质可得∠CDB＋∠ODB＝90°，由AB是直径，可得∠ADB＝90°，进而可得∠A＋∠ABD＝90°，进而求得∠A＝∠BDC；(2)由角平分线及三角形外角性质可得∠A＋∠ACM＝∠BDC＋∠DCM，即∠DMN＝∠DNM，再根据勾股定理求得MN的长．【自主解答】(1)如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，∴∠BDC＋∠ODB＝90°.∵AB是⊙O的直径，∴∠ADB＝90°，∴∠A＋∠ABD＝90°.∵OB＝OD，∴∠OBD＝∠ODB，∴∠A＋∠ODB＝90°，∴∠A＝∠BDC.(2)∵CM平分∠ACD，∴∠DCM＝∠ACM.∵∠A＝∠BDC，∴∠A＋∠ACM＝∠BDC＋∠DCM.即∠DMN＝∠DNM.∵∠ADB＝90°，DM＝1，∴DN＝DM＝1，∴MN＝变式训练2．(2017·长沙)如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E，=（1）求证：OA=OB；（2）已知AB=4，OA=4，求阴影部分的面积．解：（1）连接OC，∵AB与⊙O相切于点C∴∠ACO=90°，由于=，∴∠AOC=∠BOC，∴∠A=∠B∴OA=OB，（2）由（1）可知：△OAB是等腰三角形，∴BC=AB=2，∴sin∠COB==，∴∠COB=60°，∴∠B=30°，∴OC=OB=2，∴扇形OCE的面积为：=，△OCB的面积为：×2×2=2=2﹣π∴S阴影类型三圆与相似的综合圆与相似的综合主要体现在圆与相似三角形的综合，一般结合切线的判定与性质综合考查，求线段长或半径．一般的解题思路是利用切线的性质构造角相等，进而构造相似三角形，利用相似三角形对应边成比例求出所求线段或半径．例3 (2017·兰州) 如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD，∠D=∠BAF．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2，求EF的长．【分析】（1）由BC是⊙O的直径，得到∠BAF+∠FAC=90°，等量代换得到∠D+∠AOD=90°，于是得到结论；（2）连接BF，根据相似三角形的判定和性质即可得到结论．【自主解答】解：（1）∵BC是⊙O的直径，∴∠BAF+∠FAC=90°，∵∠D=∠BAF，∠AOD=∠FAC，∴∠D+∠AOD=90°，∴∠OAD=90°，∴AD是⊙O的切线；（2）连接BF，∴∠FAC=∠AOD，∴△ACE∽△OCA，∴，∴，∴AC=AE=，∵∠CAE=∠CBF，∴△ACE∽△BFE，∴，∴=，∴EF=．变式训练3．(2016·丹东)如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.(1)求证：∠BDC＝∠A；(2)若CE＝4，DE＝2，求AD的长．(1)证明：如图，连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，即∠ODB＋∠BDC＝90°，∵AB为⊙O的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°. ∴∠BDC＝∠ADO.∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A.(2)解：∵CE⊥AE，∴∠E＝90°，∴DB∥EC，∴∠DCE＝∠BDC.∵∠BDC＝∠A，∴∠A＝∠DCE.∵∠E＝∠E，∴△AEC∽△CED，∴∴CE2＝DE·AE，即16＝2(2＋AD)，∴AD＝6.。
圆的证明与计算(精编版)
圆的证明与计算(精编版)圆的证明与计算《圆的证明与计算》专题讲解圆的证明与计算是中考中的一类重要的问题，此题完成情况的好坏对解决后面问题的发挥有重要的影响，所以解决好此题比较关键。
圆的有关证明一、圆中的重要定理:(1)圆的定义:主要是用来证明四点共圆.(2)垂径定理:主要是用来证明――弧相等、线段相等、垂直关系等等.(3)三者之间的关系定理: 主要是用来证明――弧相等、线段相等、圆心角相等. (4)圆周角性质定理及其推轮: 主要是用来证明――直角、角相等、弧相等. (5)切线的性质定理:主要是用来证明――垂直关系. (6)切线的判定定理: 主要是用来证明直线是圆的切线. (7)切线长定理: 线段相等、垂直关系、角相等.2.圆中几个关键元素之间的相互转化:弧、弦、圆心角、圆周角等都可以通过相等来互相转化.这在圆中的证明和计算中经常用到.二、考题形式分析：主要以解答题的形式出现,第1问主要是判定切线；第2问主要是与圆有关的计算：①求线段长（或面积）；②求线段比；③求角度的三角函数值（实质还是求线段比）。
知识点一：判定切线的方法：（1）若切点明确，则“连半径，证垂直”。
常见手法有：全等转化；平行转化；直径转化；中线转化等；有时可通过计算结合相似、勾股定理证垂直；（2）若切点不明确，则“作垂直，证半径”。
常见手法：角平分线定理；等腰三角形三线合一，隐藏角平分线；总而言之，要完成两个层次的证明：①直线所垂直的是圆的半径（过圆上一点）；②直线与半径的关系是互相垂直。
在证明中的关键是要处理好弧、弦、角之间的相互转化,要善于进行由此及彼的联想、要总结常添加的辅助线.例：方法一：若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1 如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.圆的证明与计算例2 如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD.求证：PA与⊙O相切. 证明一：作直径AE，连结EC. ∵AD是∠BAC的平分线，∴∠DAB=∠DAC. ∵PA=PD，∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB，∴∠1=∠B. 又∵∠B=∠E，∴∠1=∠E∵AE是⊙O的直径，∴AC⊥EC，∠E+∠EAC=900.∴∠1+∠EAC=900. 即OA⊥PA.∴PA与⊙O相切.证明二：延长AD交⊙O于E，连结OA，OE. ∵AD是∠BAC的平分线，⌒，⌒ ∴BE=CE∴OE⊥BC.∴∠E+∠BDE=900. ∵OA=OE，∴∠E=∠1. ∵PA=PD，∴∠PAD=∠PDA. 又∵∠PDA=∠BDE, ∴∠1+∠PAD=900即OA⊥PA. ∴PA与⊙O相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用.圆的证明与计算例3 如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M 求证：DM与⊙O相切.例4 如图，已知：AB是⊙O的直径，点C在⊙O上，且∠CAB=300，BD=OB，D在AB的延长线上.求证：DC是⊙O的切线例5 如图，AB是⊙O的直径，CD⊥AB，且OA2=OD·OP. 求证：PC是⊙O的切线.圆的证明与计算例6 如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E，交CD于F. 求证：CE与△CFG的外接圆相切.分析：此题图上没有画出△CFG的外接圆，但△CFG是直角三角形，圆心在斜边FG的中点，为此我们取FG的中点O，连结OC，证明CE⊥OC即可得解.证明：取FG中点O，连结OC.∵ABCD是正方形，∴BC⊥CD，△CFG是Rt△ ∵O是FG的中点，∴O是Rt△CFG的外心. ∵OC=OG，∴∠3=∠G，∵AD∥BC，∴∠G=∠4.∵AD=CD，DE=DE，∠ADE=∠CDE=450，∴△ADE≌△CDE（SAS）∵∠2+∠3=900, ∴∠1+∠2=900.即CE⊥OC.∴∠4=∠1，∠1=∠3.∴CE与△CFG的外接圆相切方法二：若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”(一般用于函数与几何综合题）例1：如图，AB=AC，D为BC中点，⊙D与AB切于E点. 求证：AC与⊙D相切.分析：说明：证明一是通过证明三角形全等证明DF=DE的，证明二是利用角平分线的性质证明DF=DE的，这类习题多数与角平分线有关.圆的证明与计算例2：已知：如图，AC，BD与⊙O切于A、B，且AC∥BD，若∠COD=900. 求证：CD是⊙O的切线.证明一：连结OA，OB，作OE⊥CD，E为垂足.∵AC，BD与⊙O相切，∴AC⊥OA，BD⊥OB. ∵AC∥BD，∴∠1+∠2+∠3+∠4=1800. ∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900. ∵∠4+∠5=900. ∴∠1=∠5.∴Rt△AOC∽Rt△BDO. ∴ACOC. OBODACOC. OAOD∵OA=OB，∴又∵∠CAO=∠COD=900，∴△AOC∽△ODC，∴∠1=∠2.又∵OA⊥AC，OE⊥CD, ∴OE=OA. ∴E点在⊙O上. ∴CD是⊙O的切线.证明二：连结OA，OB，作OE⊥CD于E，延长DO交CA延长线于F.∵AC，BD与⊙O相切，∴AC⊥OA，BD⊥OB. ∵AC∥BD，∴∠F=∠BDO. 又∵OA=OB，∴△AOF≌△BOD（AAS）圆的证明与计算∴OF=OD. ∵∠COD=900，∴CF=CD，∠1=∠2. 又∵OA⊥AC，OE⊥CD，∴OE=OA. ∴E 点在⊙O上. ∴CD是⊙O的切线.证明三：连结AO并延长，作OE⊥CD于E，取CD中点F，连结OF.∵AC与⊙O相切，∴AC⊥AO. ∵AC∥BD，∴AO⊥BD.∵BD与⊙O相切于B，∴AO的延长线必经过点B. ∴AB是⊙O的直径.∵AC∥BD，OA=OB，CF=DF，∴OF∥AC，∴∠1=∠COF.∵∠COD=900，CF=DF，∴OF1CD CF. 2∴∠2=∠COF. ∴∠1=∠2.∵OA⊥AC，OE⊥CD，∴OE=OA. ∴E点在⊙O上. ∴CD是⊙O的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A、O、B三点共线.圆的证明与计算课后练习：（1）如图，AB是⊙O的直径，BC⊥AB，AD∥OC交⊙O于D点，求证：CD为⊙O的切线；A（2）如图，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于D，点E为BC的中点，连结DE，求证：DE是⊙O的切线.（3）如图，以等腰△ABC的一腰为直径作⊙O，交底边BC于D，交另一腰于F，若DE⊥AC于E（或E为CF中点），求证：DE是⊙O的切线.（4）如图，AB是⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C，求证：CD是⊙O的切线.圆的证明与计算知识点二：与圆有关的计算计算圆中的线段长或线段比，通常与勾股定理、垂径定理与三角形的全等、相似等知识的结合，形式复杂，无规律性。
中考数学一轮复习专题解析—圆的证明与计算
中考数学一轮复习专题解析—圆的证明与计算复习目标1.了解圆的定义及点与圆的位置关系。
2.掌握圆的基本性质。
3.掌握圆中复杂证明及两圆位置关系中证明。
考点梳理一、圆的有关概念1. 圆的定义如图所示，有两种定义方式：①在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆．固定的端点O叫做圆心，以O为圆心的圆记作①O，线段OA叫做半径；①圆是到定点的距离等于定长的点的集合．2.与圆有关的概念①弦：连接圆上任意两点的线段叫做弦；如上图所示线段AB，BC，AC都是弦．①直径：经过圆心的弦叫做直径，如AC是①O的直径，直径是圆中最长的弦．①弧：圆上任意两点间的部分叫做圆弧，简称弧，如曲线BC、BAC都是①O中的弧，分别记作BC，BAC．①半圆：圆中任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆，如AC是半圆．①劣弧：像BC这样小于半圆周的圆弧叫做劣弧．①优弧：像BAC这样大于半圆周的圆弧叫做优弧．①同心圆：圆心相同，半径不相等的圆叫做同心圆．①弓形：由弦及其所对的弧组成的图形叫做弓形．①等圆：能够重合的两个圆叫做等圆．①等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．⑪圆心角：顶点在圆心的角叫做圆心角，如上图中①AOB，①BOC是圆心角．⑫圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角，如上图中①BAC、①ACB都是圆周角．例1．已知：如图所示，在①O中，弦AB的中点为C，过点C的半径为OD．(1)若AB＝23，OC＝1，求CD的长；(2)若半径OD＝R，①AOB＝120°，求CD的长.【答案】解：①半径OD经过弦AB的中点C，①半径OD①AB．(1)①AB＝3AC＝BC3①OC＝1，由勾股定理得OA＝2．①CD＝OD－OC＝OA－OC＝1，即CD ＝1.(2)①OD①AB ，OA ＝OB ， ①①AOD ＝①BOD ．①①AOB ＝120°，①①AOC ＝60°． ①OC ＝OA·cos①AOC ＝OA·cos60°＝12R ， ①1122CD OD OC R R R =-=-=．二、圆的有关性质 1.圆的对称性圆是轴对称图形，经过圆心的直线都是它的对称轴，有无数条．圆是中心对称图形，圆心是对称中心，又是旋转对称图形，即旋转任意角度和自身重合． 2.垂径定理①垂直于弦的直径平分这条弦，且平分弦所对的两条弧．①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．如图所示：在图中(1)直径CD ，(2)CD①AB ，(3)AM ＝MB ，(4)C C A B =，(5)AD BD =．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三．注意：(1)(3)作条件时，应限制AB 不能为直径． 3.弧、弦、圆心角之间的关系①在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；①在同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．4.圆周角定理及推论①圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．①圆周角定理的推论：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．例2．如图所示，AB＝AC，O是BC的中点，①O与AB相切于点D，求证：AC与①O相切．【答案】证明：连接OD，作OE①AC，垂足为E，连结OA．①AB与①O相切于点D，①OD①AB．①AB＝AC，OB＝OC，①①1＝①2，①OE＝OD．①OD为①O半径，①AC与①O相切．三、与圆有关的位置关系1.点与圆的位置关系如图所示．d表示点到圆心的距离，r为圆的半径．点和圆的位置关系如下表：点与圆的位置关系d与r的大小关系点在圆内d＜r点在圆上d＝r点在圆外d＞r(1)圆的确定：①过一点的圆有无数个，如图所示．①过两点A、B的圆有无数个，如图所示．①经过在同一直线上的三点不能作圆．①不在同一直线上的三点确定一个圆．如图所示．(2)三角形的外接圆经过三角形三个顶点可以画一个圆，并且只能画一个．经过三角形三个顶点的圆叫做三角形的外接圆．三角形外接圆的圆心叫做这个三角形的外心．这个三角形叫做这个圆的内接三角形．三角形的外心就是三角形三条边的垂直平分线交点．它到三角形各顶点的距离相等，都等于三角形外接圆的半径．如图所示．2.直线与圆的位置关系①设r为圆的半径，d为圆心到直线的距离，直线与圆的位置关系如下表．①圆的切线．切线的定义：和圆有唯一公共点的直线叫做圆的切线．这个公共点叫切点．切线的判定定理：经过半径的外端．且垂直于这条半径的直线是圆的切线．友情提示：直线l是①O的切线，必须符合两个条件：①直线l经过①O上的一点A；①OA①l．切线的性质定理：圆的切线垂直于经过切点的半径．切线长定义：我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长．切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分这两条切线的夹角．①三角形的内切圆：与三角形各边都相切的圆叫三角形的内切圆，三角形内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形，三角形的内心就是三角形三个内角平分线的交点．3.三角形外心、内心有关知识比较4.圆与圆的位置关系在同一平面内两圆作相对运动，可以得到下面5种位置关系，其中R、r为两圆半径(R≥r)．d为圆心距．①相切包括内切和外切，相离包括外离和内舍．其中相切和相交是重点．①同心圆是内含的特殊情况．①圆与圆的位置关系可以从两个圆的相对运动来理解．①“r1－r2”时，要特别注意，r1＞r2．四、正多边形和圆1.正多边形的有关概念正多边形的外接圆(或内切圆)的圆心叫正多边形的中心．外接圆的半径叫正多边形的半径，内切圆的半径叫正多边形的边心距，正多边形各边所对的外接圆的圆心角都相等，这个角叫正多边形的中心角，正多边形的每一个中心角都等于360 n °．要点诠释：通过中心角的度数将圆等分，进而画出内接正多边形，正六边形边长等于半径．2.正多边形的性质任何一个正多边形都有一个外接圆和一个内切圆，这两圆是同心圆．正多边形都是轴对称图形，偶数条边的正多边形也是中心对称图形，同边数的两个正多边形相似，其周长之比等于它们的边长(半径或边心距)之比． 3.正多边形的有关计算定理：正n 边形的半径和边心距把正n 边形分成2n 个全等的直角三角形． 正n 边形的边长a 、边心距r 、周长P 和面积S 的计算归结为直角三角形的计算．360n a n =°，1802sin n a R n =°，180cos n r R n=°， 2222n n a R r ⎛⎫=+ ⎪⎝⎭，n n P n a =，1122n nnn n S a r n P r ==．五、圆中的计算问题 1.弧长公式：180n Rl π=，其中l 为n°的圆心角所对弧的长，R 为圆的半径． 2.扇形面积公式：2360n R S π=扇，其中12S lR =扇．圆心角所对的扇形的面积，另外12S lR =扇．3.圆锥的侧面积和全面积：圆锥的侧面展开图是扇形，这个扇形的半径等于圆锥的母线长，弧长等于圆锥底面圆的周长．圆锥的全面积是它的侧面积与它的底面积的和．1．（2022·四川省宜宾市第二中学校九年级）如图，CD 为O 的直径，弦AB CD ⊥，垂足为E ，1CE =，6AB =，则O 的半径为（ ）A．3B．4C．5D．无法确定【答案】C【分析】连接OA，由垂径定理得AE=3，设OA=OC=x，根据勾股定理列出方程，进而即可求解．【详解】连接OA，①CD为O的直径，弦AB CD⊥，AB=3，①AE=12设OA=OC=x，则OE=x-1，①()222x x-+=，解得：x=5，13①O的半径为5．故选C．2．（2022·河南九年级期末）如图，AD为①O的直径，6cmAD=，DAC ABC∠=∠，则AC的长度为（）A．2B．22C．32D．33【答案】C【分析】连接CD，由圆周角定理可知90∠=∠可知AC CD=，由∠=︒，再根据DAC ABCACD勾股定理即可得出AC的长．【详解】解：连接CD，AD是O的直径，∴∠=︒，ACD90∠=∠，DAC ABC∠=∠，ABC ADC∴∠=∠，DAC ADC∴CD AC=，∴=，AC CD又222AC CD AD+=，22∴=，2AC ADAD=，6∴=AC故选：C．3．（2022·全国九年级课时练习）O的半径为10cm，弦//AB CD．若==，则AB和CD的距离为（）AB CD12cm,16cmA．2cm B．14cm C．2cm或14cm D．2cm或10cm 【答案】C【分析】分AB、CD在圆心的同侧和异侧两种情况求得AB与CD的距离．构造直角三角形利用勾股定理求出即可．【详解】当弦AB和CD在圆心异侧时，如图1，过点O作OE①AB于点E，反向延长OE交CD于点F，连接OA，OC，①AB①CD，①OF①CD，①AB=12cm，CD=16cm，①AE=6cm，CF=8cm，①OA=OC=10cm，①在Rt①AOE中，由勾股定理可得；8EO cm，在Rt①COF中，由勾股定理可得：6OF===cm，①EF=OF+OE=8+6=14cm．当弦AB和CD在圆心同侧时，如图2，过点O作OF①CD，垂足为F，交AB于点E，连接OA，OC，①AB①CD，①OE①AB，①AB=12cm，CD=16cm，①AE=6cm，CF=8cm，①OA=OC=5cm，在Rt①AOE中，由勾股定理可得：2222=-=-=cm，1068EO OA AE在Rt①COF中，由勾股定理可得：2222=-=-=cm，OF OC CF1086①EF=OE﹣OF=8﹣6=2cm；故选C．4．（2022·全国九年级课时练习）如图，在ABC中，10,8,6===，经过AB AC BC点C且与边AB相切的动圆与,CB CA分别相交于点E，F，则线段EF长度的最小值是（）A．42B．4.75C．5D．4.8【答案】D【分析】设EF的中点为O，①O与AB的切点为D，连接OD，连接CO，CD，则有OD①AB，由勾股定理逆定理知，ABC是直角三角形，OC+OD=EF，而OC+OD≥CD，只有当点O在CD上时，OC+OD=EF有最小值为CD的长，即当点O在直角三角形ABC的斜边AB的高上CD时，EF=CD有最小值，由直角三角形的面积公式知求出CD的长即可．【详解】解：设EF的中点为O，①O与AB的切点为D，连接OD，连接CO，CD，①10,8,6===，AB AC BC①AC2+BC2=AB2，①ABC 是直角三角形，①ACB =90°， ①EF 是①O 的直径， ①OC +OD =EF ， ①①O 与边AB 相切， ①OD ①AB ， ①OC +OD ≥CD ，即当点O 在直角三角形ABC 的斜边AB 的高上时，OC +OD =EF 有最小值， 此时最小值为CD 的长， ①CD =864.810AC BC AB ⋅⨯==， ①EF 的最小值为4.8． 故选D ．5．（2020·沭阳县怀文中学九年级月考）有下列说法：①直径是圆中最长的弦；①等弧所对的弦相等；①圆中90°的角所对的弦是直径；①相等的圆心角对的弧相等；①平分弦的直径垂直于弦；①任意三角形一定有一个外接圆．其中正确的有（ ） A ．2个 B ．3个C ．4个D ．5个【答案】B 【分析】根据直径的定义对①进行判断；根据圆心角、弧、弦的关系对①①进行判断；根据圆周角定理对①进行判断；根据垂径定理对①进行判断；根据三角形外接圆的定义对①进行判断． 【详解】解：①直径是圆中最长的弦；故①正确，符合题意；①能够重合的弧叫做等弧，等弧所对的弦相等；故①正确，符合题意； ①圆中90°的圆周角所对的弦是直径；故①错误，不符合题意；①在同圆或等圆中，相等的圆心角所对的弧相等；故①错误，不符合题意； ①平分弦（弦不是直径）的直径垂直于弦；故①错误，不符合题意； ①任意三角形一定有一个外接圆；故①正确，符合题意； 其中正确的有①①①， 故选：B ．6．（2022·厦门海沧实验中学九年级开学考试）四边形ABCD 中，ACD △是边长为6的等边三角形，ABC 是以AC 为斜边的直角三角形，则对角线BD 的长的取值范围是（ ） A ．33BD <≤+B ．36BD << C ．63BD <≤+D ．3BD <≤【答案】C 【分析】由①ABC 是以AC 为斜边的直角三角形可知点B 在以AC 为直径的圆上，然后结合点到圆上点的距离求出对角线BD 长度的取值范围． 【详解】①①ABC 是以AC 为斜边的直角三角形， ①点B 在以AC 为直径的圆上，如图中①O ，连接OD 并延长，交①O 于点E 和点B ，①等边①ACD的边长为6，①AC=BE=6，OB=OE=OA=OC=3，OD①AC，①①COD=90°，①OD=2222CD OC-=-=，6333①BD=OD+OB=333+，△是边长为6的等边三角形，ACD当B与,A C重合时，BD最小6=①对角线BD的长度的取值范围为6＜BD≤333+．故选：C．7．（2022·河南九年级期末）如图，在ABC∠=︒，30Rt△中，90ACB∠=︒，3ABCAB=，将ABCRt△绕直角顶点C顺时针旋转，当点A的对应点A'落在AB边上时，停止转动，则点B经过的路径长为__．3【分析】首先根据勾股定理计算出BC 长，再根据等边三角形的判定和性质计算出60ACA ∠'=，进而可得60BCB ∠'=，然后再根据弧长公式可得答案．【详解】解：30B ∠=，3AB =，①ACB=90° ①1322AC AB ==，60A ∠=，①22332BC AB AC =-=AC A C ='，AA C ∴'是等边三角形， 60ACA ∴∠'=，60BCB ∴∠'=，∴弧长3360321802l ππ⋅⋅==， 故答案为：32π． 8．（2022·河南九年级期末）如图，在ABC 中，90ACB ∠=︒，60B ∠=︒，以AC 为直径做半圆交AB 于点D ，若1BC =，则图中阴影部分的面积为__．3π+【分析】连接OD ，CD ，根据圆周角定理得到90ADC ∠=︒，解直角三角形求得AC =CD OC OD =，32AD =，60COD ∠=︒，然后根据扇形的面积和三角形的面积公式即可得到结论． 【详解】解：连接OD ，CD ，在ABC 中，90ACB ∠=︒，60B ∠=︒， ①9030A B ∠=︒-∠=︒， 又①1BC =， ①22BA BC ==，①AC =AC 为O 的直径，90ADC ∴∠=︒，12OA AC =，又①30A ∠=︒，12CD AC ∴==①32AD ， ①30A ∠=︒，260COD A ︒∴∠=∠=，∴阴影部分的面积()()ABC AOD AOD COD COD S S S S S S ∆∆=++--+△半圆扇形扇形 122ABC ACD COD S S S S ⎛⎫=+-+ ⎪⎝⎭△△半圆扇形22601111321222360222ππ⎛⋅ =⨯⋅-+⨯⨯⎪⎝⎭38π+=， 故答案为：38π+．9．（2022·河南九年级期末）如图，在ABC 中，AB BC =，以AB 为直径的①O 交BC 于点D ，交AC 于点F ，过点C 作//CE AB ，且CAD CAE ∠=∠． （1）求证：AE 是①O 的切线； （2）若5AB =，4=AD ，求CE 的长．【答案】（1）见解析；（2）2 【分析】（1）利用平行线的性质，圆的性质和等腰三角形的性质，证明AEC △和ADC 全等即可得到结论；（2）由勾股定理求出2CD =，根据全等三角形的性质可得出答案． 【详解】（1）证明：AB BC =，BAC BCA ∴∠=∠，//CE AB ，BAC ACE ∴∠=∠，ACB ACE ∴∠=∠，在AEC △和ADC 中，CAD CAE AC ACACB ACE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ADC AEC ASA ∴≅△△，ADC E ∴∠=∠， AB 是O 的直径，90ADB ADC ∴∠=∠=︒，90E ∴∠=︒，//AB CE ，180BAE E ∴∠+∠=︒，90BAE ∴∠=︒，AE ∴是O 的切线；（2）解：90ADB ∠=︒，5AB =，4=AD ，3BD ∴==，532CD BC BD ∴=-=-=，①ADC AEC ≅△△，2CE CD ∴==．10．（2022·安庆市第四中学九年级）如图，①O 是①ABC 的外接圆，FH 是①O 的切线，切点为F ，FH ①BC ，连结AF 交BC 于E ，①ABC 的平分线BD 交AF 于D ，连结BF ．（1）求证：AF平分①BAC；（2）若EF＝4，DE＝3，求AD的长．【答案】（1）证明见详解；（2）AD =214．【分析】（1）连结OF，由FH是①O的切线，可得OF①FH，由FH∥BC，可得OF垂直平分BC，根据垂径定理可得BF FC=，根据圆周角性质可得①1=①2即可；（2）根据①ABC的平分线BD，可得①4=①3，可证①FDB=①FBD，可得BF=FD，再证①BFE①①AFB，根据性质可得BF AFFE BF=，再求BF=DF= 7，可求494FA=，即可求AD．【详解】（1）证明：连结OF，①FH是①O的切线，①OF①FH，①FH∥BC，①OF垂直平分BC，①BF FC=，①①1=①2，①AF平分①BAC，（2）解①①ABC 的平分线BD 交AF 于D ， ①①4=①3，①1=①2，①①1+①4=①2+①3，①①5=①2，①①1+①4=①5+①3 ，①①FDB =①FBD ，①BF =FD ，在①BFE 和①AFB 中，①①5=①2=①1，①AFB =①EFB ， ①①BFE ①①AFB ， ①BF AF FE BF=， ①2BF FE FA =⋅， ①2BF FA FE= ， ①BF =DF =EF +DE =7，①274944FA ==， ①AD=AF -DF =4974-=214．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以圆为背景的证明、动态探究题1.如图，在Rt△ABC中，∠ABC=90°，点M是AC的中点，以AB为直径作⊙O 分别交AC，BM于点D，E.（1）求证：MD=ME（2）填空：①若AB=6，当AD=2DM时，DE=___________；②连接OD，OE，当∠A的度数为____________时，四边形ODME是菱形.2.如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P 作⊙O的切线PA，PB，切点分别为点A，B．（1）连接AC，若⊙APO=30°，试证明⊙ACP是等腰三角形；（2）填空：①当DP= cm时，四边形AOBD是菱形；②当DP=________cm时，四边形AOBP是正方形．3.如图，AB是半圆O的直径，点P是半圆上不与点A，B重合的一个动点，延长BP到点C，使PC＝PB，D是AC的中点，连接PD，PO．（1）求证：△CDP≌△POB;（2）填空：①若AB＝4，则四边形AOPD的最大面积为_________________;②连接OD，当∠PBA的度数为________时，四边形BPDO是菱形．4.如图，在⊙O中，AB是⊙O的直径，AC是⊙O的弦，过点C作⊙O的切线交BA的延长线于点P，连接BC.（1）求证：∠PCA=∠B;（2）已知∠P=40°,AB=12cm,点Q在优弧AC上，从点A开始以πcm/s的速度逆时针运动到点C停止（点Q与点A、C不重合），设运动时间为ts.①当t=________时，以点A、Q、B、C为顶点的四边形面积最大。
②当t=________时，△ABQ与△ABC全等。
5.如图，在Rt△ABC中，∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线交BC于点E,连接OE,⊙O的半径为3。
（1）求证：OE∥AB;（2）①当BC=_________时，四边形ODEC是正方形。
②当BC=_________时，AD=3DE.6.如图，AD是⊙O的直径，AD=2BD,点C是上的不与A、D重合的动点，连接BC、BA、AC.（1）求∠ACB的度数；（2）填空：已知⊙O半径为4，①当的长为___________时，四边形OBDC是菱形。
②当的长为___________时，四边形ABDC是矩形。
7.如图，在△ABC中AB=AC,以AB为直径的⊙O交BC于点D，交AC于点E，过点D作DF⊥AC,垂足为点F.（1）求证：DF为⊙O的切线。
（2）若过点A且与BC平行的直线交BE延长线于点G,连接CG,设⊙O的半径为5.①当CF=_________时，四边形ABCG是菱形。
4时，四边形ABCG的面积是__________.②当BC=58.如图，在Rt△ABC中，∠BAC=90°，∠C=30°，以边AC上一点O为圆心，OA为半径作圆，恰好经过边BC的中点D，并与边AC相交于另一点F. （1）求证：BD是⊙O的切线；（2）若AB=3，点E是半圆AmF上一动点，连接AE、AD、DE.填空：①当的长度是_________时，四边形ABDE是菱形；②当的长度是_________时，△ADE是直角三角形。
9.如图，⊙O是△ABC的外接圆，AB为直径，过点O的直线OM∥BC,交AC于点M。
（1）∠AMO的度数是________。
（2）延长OM交⊙O于点E,过点E作⊙O的切线，交BC的延长线于点F，连接FM并延长，交AB于点G.①试判断四边形CFEM的形状，并说明理由；②若AG=2，CM=3，则四边形CFEM的面积是__________.圆的证明计算题1.如图，AB为⊙O的直径，OP⊥AB交⊙O于点D,PM切⊙O于点M，AM交OP于点N,过点B作PM的平行线交⊙O于点C.（1）求证：PM=PN；3OD，求弦BC的长.（2）若AB=4,DP=22..如图，已知AB是⊙O的直径，过点O作OP，交弦AC于点D，交⊙O于点E，且使∠PCA=∠ABC.（1）求证：PC是⊙O的切线.（2）若∠P=60°，PC=2，求PE的长.3..如图，点E在以AB为直径的⊙O上，点C是弧BE的中点，过点C作CD垂直于AE，交AE的延长线于点D，连接BE交AC于点F.（1）求证：CD是⊙O的切线；4，BF=15,求AC的长.（2）若cos∠CAD=54..如图，已知△ABC内接于⊙O，且AB=AC，直径AD交BC于点E，F是OE 上的一点，使CF∥BD．（1）求证：BE=CE；（2）试判断四边形BFCD的形状，并说明理由；（3）若BC=8，AD=10，求CD的长5.如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB ＝15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．（1）求证：CD是半圆O的切线；3-6，求EF和半径OA的长．（2）若DH=36..如图AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D.（1）求证；DB=DE.（2）若AB=12,BD=5,求⊙O的半径.7..如图△ABC中，∠C=90°，点D是AB边上一点，以CD为直径的⊙O交BC 于点E，连接AE，交CD于点P,交⊙O于另一点F,连接DF，∠CAE=∠ADF. （1）求证：AB是⊙O的切线.（2）若PF:PC=1:2,AF=5,求PC的长.8..如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交AC，BC于点D，E，点F在AC的延长线上，且∠CBF=12∠CAB．（1）求证：直线BF是⊙O的切线；（2）若AB=5，sin∠CBFBC和BF的长．9..如图，在△ACE中，CA=CE，∠CAE=30°，⊙O经过点C，且⊙O的直径AB 在线段AE上．（1）试说明CE是⊙O的切线；（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；（3）设点D是线段AC上任意一点（不含端点），连接OD，当12CD+OD 的最小值为6时，求⊙O的直径AB的长．A10.如图，在⊙O中，AB是直径，AC是弦，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E,连接BD.（1）求证DE是⊙O的切线；（2）若AD=2BD,CE=1,求⊙O的半径.11.如图，PA、PB切⊙O于A、B，C是线段PB上的点，且OC∥PA，CD⊥PA，垂足为点D.（1）求证：OC=AD；（2）若⊙O的半径为3，PA=9,求OC的长.12.如图，△ABC内接于⊙O,BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD,∠D=∠BAF.（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2,求EF的长.13.如图，直线PA交⊙O于A、B两点，AE是⊙O的直径，C是圆上一点，且AC平分∠PAE，CD⊥PA于点D.（1）求证：CD是⊙O的切线；（2）若CD+AD=6,AE=10，求线段AB的长；.14.如图，△ABC中，AB=AC，以AB为直径的圆O交BC于点E，交AC于点F.作EH⊥AC,垂足为点H.(1)求证：EH是⊙O的切线；(2)连接OH，若CH=1,OH=7,求⊙O的半径.15.如图，以AB为直径的圆交△ABC的边AC于点D，∠CBD=∠BAC.（1）求证：BC 是⊙O 的切线； （2）若AE=6，tan ∠BAC=32，tan ∠BEC=35,求圆的直径.圆的基本概念与定理1.如图，E 为正方形ABCD 的边CD 的中点，经过A ，B ，E 三点的⊙O 与边的值为__________．2.如图，点D 为边AC 上一点，点O 为边AB 上一点，AD =DO ．以O 为圆心，OD 长为半径作半圆，交AC 于另一点E ，交AB 于F ，G 两点，连接EF ．若∠BAC =22°，则∠EFG =______．P F OBAADECOG B3.如图，⊙O 的直径AB 与弦CD 相交于点E ，若AE =5，BE =1，CD =42，则∠AED =___________．4.如图，半圆O 的直径AB=7，两弦AC ，BD 相交于点E ，弦CD=，且BD=5，则DE 等于_________．5.如图，半圆的直径AB 的长为10，弦AC 的长为6，AD 平分∠BAC 交半圆于D ，连接CD ，则CD 的长为____________．6.如图，在平面直角坐标系中，点A 的坐标为（3，0），以点A 为圆心，以2为半径在第一象限内作半圆，点P 是半圆上一动点，PQ ⊥OP 交y 轴于点Q ，则OQ 长度的最小值是_____________．27CDA BO xyQPOAEACDB O EDCBA7.如图，AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F .若∠ACF ＝65°，则∠E 的度数是____________．8.如图，BC 是⊙O 的直径，点A 、D 分别在CB 、BC 的延长线上，且AB ＝BC ＝CD ，点P 是圆上任意一点（不与点B 、C 重合），则tan ∠APB ·tan ∠DPC 的值为_____________．9.如图，⊙O 中，BC 是弦，AD 过圆心O ，AD ⊥BC ，E 是⊙O 上一点，F 是AE 延长线上一点，EF ＝AE ，连接CF ．若AD ＝9，BC ＝6，则线段CF 长度的最小值是_____________．CADEFHO ABCODPAECQ10.如图，AB 是⊙O 的直径，点P 在AB 的延长线上，BP ＝OB ＝2，点Q 在⊙O 上，连接PQ 交⊙O 于点C ，若PC ＝CQ ，则弦AQ 的长为_____________． 11.如图，⊙O 的直径AB 与弦CD 互相垂直，垂足为E ，AB ＝4，CD ＝23，动点P 从B 点出发，沿劣弧BD 运动到D 点，AF ⊥CP 于F ，则线段AF 的中点M 所经过的路径长为__________，线段AF 所扫过的图形面积为__________．12.如图，AB 是⊙O 的直径，AD 、BC 是⊙O 的切线，P 是⊙O 上一动点，若ABCD O EPFMDAPOAD ＝3，AB ＝4，BC ＝6，则△PDC 的面积的最小值是_____________．13.如图，⊙O 的直径AB 与弦CD 相交于点E ，AE ＝1，BE ＝5，∠AEC ＝45°，则CD 的长为_____________．14.如图，⊙O 的内接四边形ABCD 两组对边的延长线分别相交于点E 、F ，则若∠E ＝α，∠F ＝β，∠A ＝______________．（用含α、β的代数式表示）15.如图，AB 、AC 、AE 是⊙O 的弦，CD ⊥AB 于D ，AC 平分∠BAE 的外角，若AD ＝3，AE ＝2，则BD ＝_____________．新 初中数学 命题解题群 340 529 648ABOEDCABODC EFABCD EO ABFDCE O16. AB 是⊙O 的直径，C 是⊙O 上一点，D 是直径AB 上一点，DF ∥AC ，交BC 于E ，交⊙O 于F ，若AB ＝13，AC ＝5，DEEF＝54，则CF 的长是__________17如图，AB 是⊙O 的直径，CB 、CD 是O 的切线，切点分别为B 、D ，且CB ＝AB ，连接AC 、BD 交于点E ，则 AEEC的值为_____________．18.如图，正方形ABCD 的边长为2，点E 在边AD 上（不与A 、D 重合），点F 在边CD 上，且∠EBF ＝45°，若△ABE 的外接圆⊙O 与CD 边相切，则△BEF 的面积为_____________．ABCDOE ADBCEFOTHANKS !!!致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求欢迎您的下载，资料仅供参考。