抽样分布习题
抽样分布习题及答案

抽样分布习题及答案抽样分布习题及答案抽样分布是统计学中一个重要的概念,它描述了从总体中抽取样本后,样本统计量的分布情况。
在实际应用中,我们经常需要利用抽样分布来进行统计推断,因此对于抽样分布的理解和掌握是十分必要的。
本文将介绍一些常见的抽样分布习题,并提供相应的答案。
1. 问题:某公司有1000名员工,其中400人是女性。
现从中随机抽取100人,求抽取样本中女性人数的抽样分布。
解答:在这个问题中,我们可以将女性的出现看作是一个二项分布的实验,成功的概率为0.4。
因此,抽取样本中女性人数的抽样分布是一个二项分布。
根据二项分布的性质,我们可以计算出不同女性人数的概率。
2. 问题:某电商平台有1000个用户,他们的购买金额服从均值为100元,标准差为20元的正态分布。
现从中随机抽取50个用户,求抽取样本的平均购买金额的抽样分布。
解答:在这个问题中,样本的平均购买金额的抽样分布是一个服从均值为100元,标准差为20/√50元的正态分布。
根据正态分布的性质,我们可以计算出不同平均购买金额的概率。
3. 问题:某城市的居民年收入服从均值为50000元,标准差为10000元的正态分布。
现从中随机抽取200个居民,求抽取样本的平均年收入的抽样分布。
解答:在这个问题中,样本的平均年收入的抽样分布是一个服从均值为50000元,标准差为10000/√200元的正态分布。
根据正态分布的性质,我们可以计算出不同平均年收入的概率。
4. 问题:某医院每天接诊的患者数服从均值为50人,标准差为10人的泊松分布。
现从中随机抽取30天,求抽取样本的平均每天接诊的患者数的抽样分布。
解答:在这个问题中,样本的平均每天接诊的患者数的抽样分布是一个服从均值为50人,标准差为10/√30人的正态分布。
根据正态分布的性质,我们可以计算出不同平均每天接诊的患者数的概率。
通过以上几个习题的解答,我们可以看到不同问题中抽样分布的情况是不同的,需要根据具体的问题来确定抽样分布的类型和参数。
统计学习题答案 第4章 抽样与抽样分布

第4章抽样(chōu yànɡ)与抽样分布——练习题(全免(quán miǎn))1. 一个(yīɡè)具有个观察(guānchá)值的随机样本抽自于均值等于20、标准差等于(děngyú)16的总体。
⑴给出的抽样分布(重复抽样)的均值和标准差⑵描述x的抽样分布的形状。
你的回答依赖于样本容量吗?⑶计算标准正态统计量对应于的值。
⑷计算标准正态z统计量对应于的值。
解: 已知 n=64,为大样本,μ=20,σ=16,⑴在重复抽样情况下,x的抽样分布的均值为a. 20, 2b. 近似正态c. -2.25d. 1.502 . 参考练习4.1求概率。
⑴x<16;⑵x>23;⑶x>25;⑷.x落在16和22之间;⑸x<14。
解: a. 0.0228 b. 0.0668 c. 0.0062 d. 0.8185 e. 0.00133. 一个具有个观察值的随机样本选自于、的总体。
试求下列概率的近似值:解: a. 0.8944 b. 0.0228 c. 0.1292 d. 0.96994. 一个具有个观察值的随机样本选自于和的总体。
⑴你预计x的最大值和最小值是什么?⑵你认为x至多偏离多么远?⑶为了回答b你必须要知道 吗?请解释。
解:a. 101, 99 b. 1 c. 不必5.考虑一个包含的值等于0,1,2,…,97,98,99的总体。
假设x的取值的可能性是相同的。
则运用计算机对下面的每一个值产生500个随机样本,并对于每一个样本计算x。
对于每一个样本容量,构造x的500个值的相对频率直方图。
当n值增加时在直方图上会发生什么变化?存在什么相似性?这里和。
解:趋向正态6.美国(měi ɡuó)汽车联合会(AAA)是一个(yīɡè)拥有90个俱乐部的非营利联盟,它对其成员提供旅行、金融(jīnróng)、保险以及与汽车相关的各项服务。
数理统计习题集-抽样分布
k
β(c + 1, 82 − c) p
知 F (c, p) 为 p 的减函数, 故应有 p = 0.9. 因此, 等价于求
c
cmin = min c F (c, 1) =
82 0.9k0.182−k ⩾ 0.95, p ∈ [0, 1] k
k=0
借计算器求得 cmin = 78.
♢
题 11. 设某电子元件的寿命 ( 单位: 小时 ) 服从参数 λ = 0.0015 的指数分布 E(λ), 测试 6 个元件后问:
(1) 求样本的分布.
n
(2) 求 Xi 的分布律.
i=1
3
(3) 指出下列样本的函数中哪些是统计量,哪些不是统计量,为什么?
T1 = X1 + · · · + X5)/5; T2 = X5 − E[X1]
T3 = X5 − p;
T4 = max(X1, · · · , X5).
(4) 如果一个样本观测值为 (0, 1, 0, 1, 1),写出其样本均值、样本方差和经验分布函数.
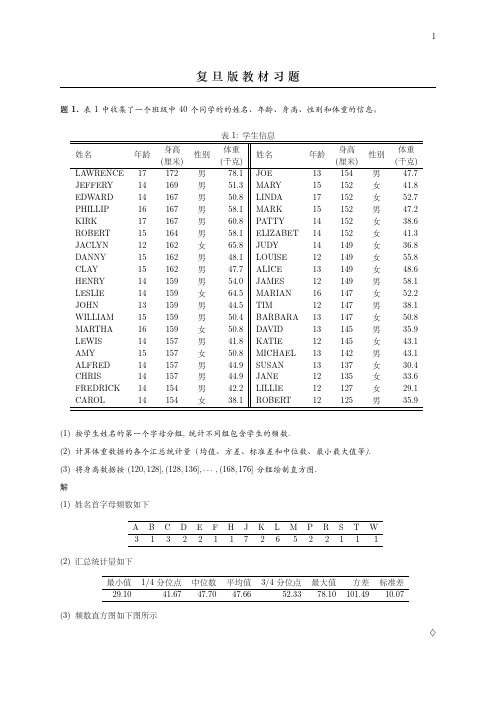
ABCDEFHJKLMPRSTW 3 1 3 2 2 1 17 2 6 5 2 21 1 1
(2) 汇总统计量如下
最小值 1/4 分位点 中位数 平均值 3/4 分位点 最大值 方差 标准差
29.10
41.67 47.70 47.66
52.33 78.10 101.49 10.07
(3) 频数直方图如下图所示 ♢
解 样本均值
1
m
1m
X
=
n1
+···
+ nm
(xini)
i=1
=
n
(xini)
i=1
抽样分布习题

抽样分布习题1.抽样分布是指( C )A 一个样本各观测值的分布B 总体中各观测值的分布C 样本统计量的分布D 样本数量的分布2.根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的均值为( A )。
A μ B x C 2σ D n 2σ3.根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的方差为( D )。
A μ B x C 2σ D n 2σ4.从一个均值μ=10,标准差σ=0.6的总体中随机选取容量为n=36的样本。
假定该总体并不是很偏的,则样本均值x 小于9.9的近似概率为( A )。
A 0.1587B 0.1268C 0.2735D 0.63245.假设总体服从均匀分布,从此总体中抽取容量为36的样本,则样本均值的抽样分布( B )A 服从非正态分布B 近似正态分布C 服从均匀分布D 服从2χ分布6.从服从正态分布的无限总体中分别抽取容量为4,16,36的样本,当样本容量增大时,样本均值的标准差( C )A 保持不变 B 增加 C 减小D 无法确定7. 总体均值为50,标准差为8,从此总体中随机抽取容量为64的样本,则样本均值的抽样分布的均值和标准误差分布为( B )。
A 50,8B 50,1C 50,4D 8,88.某大学的一家快餐店记录了过去5年每天的营业额,每天营业额的均值为2500元,标准差为400元。
由于在某些节日的营业额偏高,所以每日营业额的分布是右偏的,假设从这5年中随机抽取100天,并计算这100天的平均营业额,则样本均值的抽样分布是( B )。
A 正态分布,均值为250元,标准差为40元B 正态分布,均值为2500元,标准差为40元C 右偏分布,均值为2500元,标准差为400元D 正态分布,均值为2500元,标准差为400元9. 某班学生的年龄分布是右偏的,均值为22,标准差为4.45,如果采取重复抽样的方法从该班抽取容量为100的样本,则样本均值的抽样分布是( A )A 正态分布,均值为22,标准差为0.445B 分布形状未知,均值为22,标准差为4.45C 正态分布,均值为22,标准差为4.45D 分布形状未知,均值为22,标准差为0.44510.在一个饭店门口等待出租车的时间是左偏的,均值为12分钟,标准差为3分钟,如果从饭店门口随机抽取100名顾客并记录他们等待出租车的时间,则该样本均值的分布服从( A )A 正态分布,均值为12分钟,标准差为0.3分钟B 正态分布,均值为12分钟,标准差为3分钟C 左偏分布,均值为12分钟,标准差为3分钟D 左偏分布,均值为12分钟,标准差为0.3分钟11. 某厂家生产的灯泡寿命的均值为60小时,标准差为4小时,如果从中随机抽取30只灯泡进行检查,则样本均值( D )A 抽样分布的标准差为4小时B 抽样分布近似等于总体分布C 抽样分布的中位数为60小时D 抽样分布近似等同于正态分布,均值为60小时12.假设某学校学生的年龄分布是右偏的,均值为23岁,标准差为3岁。
抽样分布习题 答案

抽样分布习题答案抽样分布习题答案随着统计学的发展,抽样分布成为了统计推断的重要基础。
在统计学中,我们经常需要从总体中抽取一部分样本,然后通过对样本的分析来推断总体的特征。
而抽样分布则是描述样本统计量的分布情况的概率分布。
在这篇文章中,我们将回答一些关于抽样分布的习题,帮助读者更好地理解和应用这一概念。
1. 假设某个总体的均值为μ,标准差为σ,从该总体中抽取样本容量为n的简单随机样本。
则样本均值的抽样分布的均值为多少?标准差为多少?答案:样本均值的抽样分布的均值为总体均值μ,标准差为总体标准差σ除以样本容量n的平方根,即σ/√n。
这意味着随着样本容量的增加,样本均值的抽样分布的标准差将减小,从而更加接近总体均值。
2. 假设某个总体服从正态分布,均值为μ,标准差为σ。
从该总体中抽取样本容量为n的简单随机样本,计算样本均值。
当n足够大时,样本均值的抽样分布将近似服从什么分布?答案:当样本容量n足够大时,样本均值的抽样分布将近似服从正态分布。
这是由于中心极限定理的适用,即当样本容量足够大时,样本均值的抽样分布将趋于正态分布,无论总体的分布形态如何。
3. 假设某个总体服从正态分布,均值为μ,标准差为σ。
从该总体中抽取样本容量为n的简单随机样本,计算样本标准差。
当n足够大时,样本标准差的抽样分布将近似服从什么分布?答案:当样本容量n足够大时,样本标准差的抽样分布将近似服从正态分布。
这是由于当样本容量足够大时,样本标准差的抽样分布可以通过中心极限定理近似为正态分布。
4. 假设某个总体的比例为p,从该总体中抽取样本容量为n的简单随机样本,计算样本比例。
样本比例的抽样分布的均值和标准差分别为多少?答案:样本比例的抽样分布的均值为总体比例p,标准差为√(p(1-p)/n)。
这意味着当样本容量足够大时,样本比例的抽样分布将近似服从正态分布,均值为总体比例p,标准差为√(p(1-p)/n)。
通过以上习题的解答,我们可以看到抽样分布在统计推断中的重要性。
习题课3抽样分布

一、主要内容 二、重、难点 三、典型例题
一、主要内容
1. 数理统计的一些基本概念:总体、样本、 抽样、简单随机抽样、统计量 2、三大抽样分布的定义及相关性质 3、三大抽样分布的定义及相关性质
二 重点、难点
1、三大抽样分布的定义及相关性质 2三大抽样分布的定义及相关性质
三、典型例题
1.填空、选择题
1 2
2
)
2
cov( X 1, X 1 ) cov( X 1, X 2 )]
2
1 ( 2 0) 2 2 2
D(X 1 X)=D( X 1) D( X)-2cov(X 1 , X )=
2
1 1 2 2 2 2 2 2
1 1 同理 cov( X 2 , X ) 2 , D(X 2 X)= 2 2 2 cov( X 1 X , X 2 X ) cov( X 1 , X 2 ) cov( X 1 , X ) cov( X , X 2 ) cov( X , X ) 0
2 (n 1), 2 (9)
7 S12 故 4
2 9 S 2 (7), 2 5
即得结论 练习题 (2)
(n 1) S 2 (n 1) S 2 2 (n 1), 故D( ) 2(n 1) 2 2 (n 1) 2 2 4 2 2 所以, 4 D( S ) 2(n 1), 则D( S ) n 1
n1
2 ( X X ) i i 1
n1
n1 1
2 (n1 1) (n1 1) S X
2
2
2 2 (n1 1)S X
则 同理
E ( ( X i X ) ) E (
抽样分布习题及答案

抽样分布习题及答案1. 题目:从一个容器中随机取出30个样本,每个样本的体积服从正态分布,均值为150,标准差为10。
计算样本均值的抽样分布的标准差。
解答:我们知道,样本均值的抽样分布的标准差(也称为标准误差)可以通过总体标准差除以样本容量的平方根来计算。
标准误差 = 总体标准差/ √样本容量在本题中,总体标准差为10,样本容量为30,代入公式可得:标准误差= 10 / √30 ≈ 1.83因此,样本均值的抽样分布的标准差约为1.83。
2. 题目:某电视台进行了一项调查,随机抽取了500名观众,其中有380人表示喜欢该电视节目。
根据该样本数据,计算其样本比例的抽样分布的标准差。
解答:样本比例的抽样分布的标准差可以通过以下公式计算:标准误差= √((样本比例 × (1 - 样本比例)) / 样本容量)在本题中,样本比例为380/500 = 0.76,样本容量为500,代入公式可得:标准误差= √((0.76 × (1 - 0.76)) / 500) ≈ 0.018因此,样本比例的抽样分布的标准差约为0.018。
3. 题目:某商品的包装袋上注明每袋重量服从正态分布,均值为500克,标准差为10克。
为了确定该注明是否准确,随机抽取了100袋该商品,计算抽取样本的平均重量的抽样分布的标准差。
解答:抽取样本的平均重量的抽样分布的标准差可以通过总体标准差除以样本容量的平方根来计算。
标准误差 = 总体标准差/ √样本容量在本题中,总体标准差为10克,样本容量为100,代入公式可得:标准误差= 10 / √100 = 1因此,抽取样本的平均重量的抽样分布的标准差为1克。
4. 题目:某超市进行了一次促销活动,随机抽取了50个顾客进行调查,得知他们购买的平均金额为200元,标准差为50元。
计算该样本的平均金额的抽样分布的标准差。
解答:样本的平均金额的抽样分布的标准差可以通过总体标准差除以样本容量的平方根来计算。
样本及抽样分布习题

第六章 样本及抽样分布习题( 附注: 以下各章的习题中 2211(),1ni i S X X n ==--∑都表示样本方差,不在赘述。
)1.填空题:⑴ 设来自总体X 的一个样本观察值为:2.1,5.4,3.2,9.8,3.5,则样本均值 = ,样本方差 = ;⑵ 在总体)16,5(~N X 中随机地抽取一个容量为36的样本,则均值X 落在4与6之间的概率 = ;⑶ 设某厂生产的灯泡的使用寿命),1000(~2σN X (单位:小时),抽取一容量为9的样本,得到100,940==s x ,则(940)P X <= .[4] 设71,,X X 为总体)5.0,0(~2N X 的一个样本,则=>∑=)4(712i iXP ;[5] 设61,,X X 为总体)1,0(~N X 的一个样本,且cY 服从2χ分布,这里,26542321)()(X X X X X X Y +++++=,则=c .2.设321,,X X X 是总体),(~2σμN X 的一个样本,其中μ已知而0>σ未知,则以下的函数:⑴ 321X X X ++; ⑵ μ33+X ; ⑶ 1X ;⑷ 22X μ;⑸321ii Xσ=∑;⑹ }max{i X ;⑺3X +σ 中哪些为统计量?为什么?3.在总体)3.6,52(~2N X 中随机地抽取一个容量为36的样本,求样本均值X 落在50.8与53.8之间的概率.4.设n X X ,,1 是总体~(8)X P 的一个样本,X 与2S 分别为其样本均值与样本方差,求X D X E ,与2ES .5. 设51,,X X 是总体)4,12(~N X 的一个样本,求: ⑴ 样本均值与总体均值之差的绝对值大于1的概率; ⑵ },15),,{max(51>X X P }10),,{min(51<X X P .6.设41,,X X 是来自正态总体)4,0(N 的样本,证明统计量Y 服从)2(2χ分布,这里 243221)43(01.0)2(05.0X X X X Y -+-=.7.设921,,,X X X 是来自正态总体X 的样本,∑==61161i i X Y ,∑==97231i i X Y ,922271()2i i S X Y ==-∑, SY Y Z )(221-=,证明统计量Z 服从自由度为2的t 分布.8.已知)(~n t X ,求证),1(~2n F X .*9.设),(~2σμN X ,n X X X 221,, 是总体X的容量为2n 的样本,其样本均值为∑==ni i X n X 2121,试求统计量∑=+-+=ni i n i X X X Z 12)2(的数学期望及方差.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抽样分布习题
1.抽样分布是指( C )
A 一个样本各观测值的分布
B 总体中各观测值的分布
C 样本统计量的分布
D 样本数量的分布
2.根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的均值为( A )。
A μ B x C 2σ D n 2
σ
3.根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的方差为( D )。
A μ B x C 2σ D n 2
σ
4.从一个均值μ=10,标准差σ=0.6的总体中随机选取容量为n=36的样本。
假定该总体并不是很偏的,则样本均值x 小于
9.9的近似概率为( A )。
A 0.1587
B 0.1268
C 0.2735
D 0.6324
5.假设总体服从均匀分布,从此总体中抽取容量为36的样本,则样本均值的抽样分布( B )
A 服从非正态分布
B 近似正态分布
C 服从均匀分布
D 服从2χ分布
6.从服从正态分布的无限总体中分别抽取容量为4,16,36的样
本,当样本容量增大时,样本均值的标准差( C )A 保持不变 B 增加 C 减小D 无法确定
7. 总体均值为50,标准差为8,从此总体中随机抽取容量为64的样本,则样本均值的抽样分布的均值和标准误差分布为( B )。
A 50,8
B 50,1
C 50,4
D 8,8
8.某大学的一家快餐店记录了过去5年每天的营业额,每天营业额的均值为2500元,标准差为400元。
由于在某些节日的营业额偏高,所以每日营业额的分布是右偏的,假设从这5年中随机抽取100天,并计算这100天的平均营业额,则样本均值的抽样分布是( B )。
A 正态分布,均值为250元,标准差为40元
B 正态分布,均值为2500元,标准差为40元
C 右偏分布,均值为2500元,标准差为400元
D 正态分布,均值为2500元,标准差为400元
9. 某班学生的年龄分布是右偏的,均值为22,标准差为4.45,如果采取重复抽样的方法从该班抽取容量为100的样本,则样本均值的抽样分布是( A )
A 正态分布,均值为22,标准差为0.445
B 分布形状未知,均值为22,标准差为4.45
C 正态分布,均值为22,标准差为4.45
D 分布形状未知,均值为22,标准差为0.445
10.在一个饭店门口等待出租车的时间是左偏的,均值为12分钟,标准差为3分钟,如果从饭店门口随机抽取100名顾客并记录他们等待出租车的时间,则该样本均值的分布服从( A )
A 正态分布,均值为12分钟,标准差为0.3分钟
B 正态分布,均值为12分钟,标准差为3分钟
C 左偏分布,均值为12分钟,标准差为3分钟
D 左偏分布,均值为12分钟,标准差为0.3分钟
11. 某厂家生产的灯泡寿命的均值为60小时,标准差为4小时,如果从中随机抽取30只灯泡进行检查,则样本均值( D )
A 抽样分布的标准差为4小时
B 抽样分布近似等于总体分布
C 抽样分布的中位数为60小时
D 抽样分布近似等同于正态分布,均值为60小时
12.假设某学校学生的年龄分布是右偏的,均值为23岁,标准差为3岁。
如果随机抽取100名学生,下列关于样本均值抽样分布描述不正确的是(AD )
A 抽样分布的标准差等于3
B 抽样分布近似服从正态分布
C 抽样分布的均值近似为23
D 抽样分布为非正态分布
13.从均值为200,标准差为50的总体中抽取容量为100的简单随机样本,样本均值的数学期望是(B )
A 150
B 200
C 100
D 250 14.假设总体比例为0.55,从此总体中抽取容量为100的样本,则样本比例的标准差为( B )
A 0.01
B 0.05
C 0.06
D 0.55
15. 假设总体比例为0.4,采取重复抽样的方法从此总体中抽取一个容量为100的简单随机样本,则样本比例的期望是( B )
A 0.3
B 0.4
C 0.5
D 0.45
16. 样本方差的抽样分布服从( B )
A 正态分布B2χ分布 C F分布 D 未知
17. 大样本的样本比例的抽样分布服从( A )
A 正态分布
B t分布
C F分布
D 2χ分布
18. 大样本的样本比例之差的抽样分布服从( A )
A 正态分布
B t分布
C F分布
D 2χ分布。
