Abel和对有界变差函数及ω-型单调函数的逼近

合集下载

有界变差函数有界变差函数

i =1
称 V ( , f ) 为 f 关于分划 D 的变差。 D
若存在常数 M，使对一切分划 D ，都有
V ( , f ) £ M ，则称 f (x 为 [ , b 上的有 D ) a ]
界变差函数。令
V ( f ) = sup V ( , f ) D ，
D b a
。
将 D , D 2 合并起来得 [ , b 的一个分划 a ] 1
D1 : a = x < x <L x = y < y <L< y = b < n 0 1 0 1 m ，于是由 D f ) £ V b ( f ) 及 V ( , a V ( , f ) = V ( 1 , f ) + V ( 2 , f ) D D D c b b e 得 V ( f ) + V ( f ) - 2 £ V ( f ) ， a c a 由 e 的任意性立得 c b b V ( f ) + V ( f ) £ V ( f ) 。 a c a
e > 0
D1 : a = x < 1 ，可以找到分划 x < L < x = c 0 n 及分划 D2 : c = y < y < L < y = b ，使得 0 1 m
b V ( 1 , f ) ³ V c ( f ) - e ，V D , f ) ³V ( f ) -e D ( 2 a c
n
V ( , f ) = å f ( x ) - f ( x -1 ) | D | i i
i 1 = i 0
£ å f ( x ) - f ( x -1 ) | + | f ( ) - f ( i 0 ) | | i c x i

abel dirichlet准则

Abel Dirichlet 准则是数学分析中的一条重要定理，它主要用于研究傅立叶级数的收敛性。

这个定理是由两位著名数学家Niels Henrik Abel 和Peter Gustav Lejeune Dirichlet在19世纪提出的，它在数学分析领域具有重要的地位。

1. 定理内容Abel Dirichlet 准则主要用于研究傅立叶级数在某一点的收敛性。

具体而言，如果一个函数在某一点连续，那么它的傅立叶级数在这一点就收敛于这个函数的函数值。

这个定理对于理解傅立叶级数的性质和应用具有重要意义。

2. 定理证明证明 Abel Dirichlet 准则的过程比较复杂，需要运用数学分析中的一系列技巧和方法。

需要利用傅立叶级数的定义和性质，结合级数的收敛性理论，推导出在某一点连续的函数的傅立叶级数在这一点收敛的条件。

需要运用数学分析中的一些基本定理和工具，如Cauchy准则、Abel变换等，来对函数和级数进行分析和运算，最终得出结论。

3. 定理应用Abel Dirichlet 准则在数学分析和工程领域有着广泛的应用。

在数学分析中，它被用来研究函数的性质和级数的收敛性，深化对傅立叶级数的理解。

在工程领域，它被应用于信号处理、图像处理等领域，用于分析和处理周期信号和周期性数据，为工程问题的建模和求解提供了重要的数学工具。

4. 定理意义Abel Dirichlet 准则的提出和证明，填补了傅立叶级数理论中的一些空白，为数学分析领域的发展作出了重要贡献。

它不仅对于傅立叶级数的理论研究具有重要意义，而且在实际问题的建模和求解中具有重要的应用价值。

它丰富了数学理论体系，拓展了数学在工程领域的应用，为学科交叉和理论与应用的结合提供了有力支持。

在总结中，Abel Dirichlet 准则作为数学分析中的一条重要定理，在傅立叶级数理论的研究和应用中具有重要地位。

它的提出和证明，填补了傅立叶级数理论中的一些空白，为数学分析领域的发展作出了重要贡献，并且在工程领域具有重要的应用价值。

阿贝尔分部求和公式地推广及应用

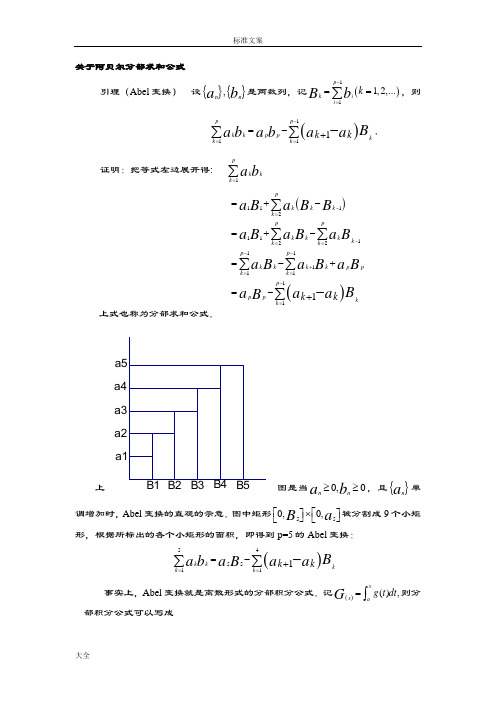
关于阿贝尔分部求和公式引理（Abel 变换）设{}{},n n a b 是两数列，记()111,2,...p k i i k b B -===∑，则()1111p p kkppkk k k k Ba b a b a a -===-+-∑∑．证明：把等式左边展开得: 1p k k k a b =∑()()11121112211111111pk k k k ppk k k k k k p p k k pk k p k k p p p kk k k a a B B B a a a B B Ba a a B B B Ba a a B -=-==--+==-==+-=+-=-+=-+∑∑∑∑∑-∑上式也称为分部求和公式．图是当0,0n n a b ≥≥，且{}n a 单上调增加时，Abel 变换的直观的示意．图中矩形550,0,a B ⎡⎡⎤⎤⨯⎦⎦⎣⎣被分割成9个小矩形，根据所标出的各个小矩形的面积，即得到p=5的Abel 变换：()5455111kkkk k k k Ba b a a a B ===-+-∑∑事实上，Abel 变换就是离散形式的分部积分公式．记()(),xx ag t dt G =⎰则分部积分公式可以写成B5B4a5a4B3B2a2B1a1a3()()()()()()bbaaf xg x dx G x df x f b G b =-⎰⎰．将数列的通项类比于函数，求和类比于求积分，求差类比于求微分，1k a +－k a 对应于()df x ，则两者是一致的．三阿贝耳分部求和公式的推广及应用（一）关于数论方面的推广和应用定理 1 设1x ≥，()b n 是一个数论函数， ()()n xB x b n ≤=∑．再设()a x 是区间12,x x ⎡⎤⎣⎦上的连续可微函数，21>0.x x ≥那么有()()12n n n x x a b <≤∑＝()()22x x a B ＿()()11x x a B ＿()()21'x B x a x dx x ⎰．证明：设1n ＝1x ⎡⎤⎣⎦，2n ＝2x ⎡⎤⎣⎦．我们有（约定()0B ＝0）12(n)b(n)n a x x <≤∑=()()12<n nnx n a b ≤∑=()(){}()2111n n B n B n a n n =+--∑=－()()111Ba n n +＿()()(){}21111n n B n a n a n n -=++-∑+()()22B a n n=－()()111Ba n n +()()21111'n nn n B n a x dx n -+=+-+∑⎰()()22B a n n＝－()()111Ba n n +-()()211'nB x a x dx n+⎰＋()()22B a n n 此外还有()()111'n B x a x dx x +⎰＝()()(){}1111.B a a n n x +- ()()22'x B x a x dx n =⎰()()(){}222.B a a n x n -注意到()1B x ＝()1B n ，()2B x ＝()2B n ，由以上三式即得公式成立．由阿贝耳求和公式可知，如果我们知道了数论函数()n b 的均值()B x 的渐进公式，那么，对于满足适当条件的函数()x a ，数论函数()()n a b n 的均值的渐进公式有可能通过定理公式得到。

abel变换公式(二)

abel变换公式(二)Abel变换公式1. Abel变换的定义Abel变换是一种积分变换，用来将一个函数的导数转换为函数本身。

Abel变换的一维形式定义如下：F(r)=2∫f∞r(x)√x2−r2dx (1)其中，f(x)是函数f的连续可导函数，r是变量。

2. Abel变换公式Abel变换公式（第一型）根据定义，利用分部积分法，可以得到Abel变换公式（第一型）：∫F ∞0(r)g(r)dr=−∫f∞(r)G(r)dr (2)其中，F(r)和f(r)是函数f的Abel变换和逆变换，G(r)和g(r)是函数g的Abel变换和逆变换。

Abel变换公式（第二型）根据定义，将r换为x，可以得到Abel变换公式（第二型）：f(r)=−1π∫F′(x)√x2−r2∞r(3)其中，F′(x)表示F(x)的导数。

3. Abel变换公式的应用举例拉普拉斯方程的极坐标解根据拉普拉斯方程的极坐标形式：1 r ∂∂r(r∂u∂r)+1r2∂2u∂θ2=0 (4)我们可以使用Abel变换来求解上述方程。

定义函数F(r)=r∂u∂r，则方程(4)可以转换为：∂F ∂r +1r∂u∂θ=0 (5)对方程(5)应用Abel变换公式（第一型）(2)，得到：∫(∂F∂r+1r∂u∂θ)∞0g(r)dr=−∫F∞(r)G(r)dr (6)通过求解式(6)，可以得到F(r)的表达式。

进一步，通过Abel变换公式（第二型）(3)，可以得到u的表达式，从而求解出拉普拉斯方程的极坐标解。

X射线透射薄膜的衍射模型在X射线透射薄膜的衍射研究中，可以使用Abel变换来描述出射角θ对应的衍射强度分布。

定义函数F(θ)=I(θ)sin(θ)，其中I(θ)是射线通过薄膜后的衍射强度。

根据定义，可以推导出：I(θ)=−1π∫F′(φ)sin(φ)πθdφ (7)式(7)给出了射线透射薄膜的衍射强度与衍射角度的关系。

结论通过对Abel变换的介绍和相关公式的解释，我们可以看到Abel 变换在不同领域中具有广泛的应用。

Abel变换的应用

=
n（［
n
+
1） 2 ］
k=1
k=1
6
6
6
2
1. 2 Abel 变换在级数中的应用
利用 Abel 变换可以推导出判断数项级数收敛性与函数项级数一致收敛性的狄利克雷判别法与阿
贝尔判别法，相关结论与例题见文［3］．下面利用 Abel 变换的思想，证明一些级数收敛问题．
∞
∞
例 3 {λn} 为单调增加并趋向于正无穷的正数序列，∑λkak 收敛，证： ∑ak 收敛．
1 ．
2
收稿日期： 2018－05－22 作者简介：周蕊（ 1983－），女（汉族），河北承德人，东北大学秦皇岛分校数学与统计学院讲师，博士，主要研究方向：组合数学．通讯作者：徐大树（ 1998－），男（汉族），江苏连云港人，东北大学秦皇岛分校数学与统计学院学生，主要研究方向：分析学．
数列极限、级数敛散性和函数项级数一致收敛性等问题．
m
∑ Abel 变换的形式如下：设有两个序列｛ ak｝，｛ bk｝，为了求 akbk，引入： bk = Sk － Sk－1（ k = 1，2，…， k=1
m
m－1
∑ ∑ m），其中规定 S0 = 0．这样 ak bk = （ ak － ak+1） Sk + amSm．
第1期
周蕊等： Abel 变换的应用
23
k
∑ 记 Sk =
xi ，Sk +
为{xi }
k i=
1
中所有正数的和，Sk －
为{xi }
k i=
1
中所有负数的和，则有：
Sn
= 0．
i=1

双调和Abel—Poisson算子对有界变差函数的逼近

１主要结果
定理１设ｆ ∈ Ｂ，Ｖ则
，，ｒ
１ｃ …ⅢｃＩｃ … ６ ≤
。
，一， ≤
．
其中
（｛一． ‘ 厂＋一 ∞ ≠’ ￡。－＋一‘ ∞ 厂一Ｏ）ｆ￣厂一 ‘ 一，－（。￡ｔｘ）
收稿日期：０６１ — ８２０—２１
其中０＜＜７ｃ．
（３）
下面分别来估计ｆ和Ｉ．先估计ｆ，。首设
ｒｙ
（，一Ｊ２ｒ￡ｄ， ≤ Ｙ＜７ｒ）ＩＰ（，ｔ）０ｃ，ｏ
则显然有ｌ（，７ ≤ ，ｒ３）ｌ分部积分即得
ｔｔｆＰｒｄｆｄ，—ｇｃ）Ｊｒｄｃ≤ｃ・，— ｇ。ｔｃｌｒ－，ｇｆｇｃｃｃ）— ｇｃｌ，Ｉｔ￣４，ｔｒ８：）ｌｃｃ
维普资讯
１６７
杭州师范学院学报（自然科学版）
２００７焦
（）－表示厂在［，］上的全变差，口厂口６［］表示口的整数部分．
２定理的证明
由于ｌ２ｒ）：１故Ｐ（，ｄｔｔ，
维普资讯
第６卷第３期
２００７年５月
杭州师范学院学报（自然科学版）
ＪｕｎｌｆａｇｈｕＴａｈｒＣｌｇ（ａｕａＳｉｎｅＥｉｏ）ｏｒａｏｎｚｏｅｃｅｓｏｌｅＮｔｒｌｃｃｄｔｎＨｅｅｉ
ｒ）如下，
Ａ２厂，，（ｒ）一ｌｔ＋）（，）ｔｆ（Ｐ２ｒ￡ｄ，

幂级数的阿贝尔(Abel)定理(最全)word资料

幂级数的阿贝尔（Abel）定理当幂级数中的变量 x 取定某一个值时，它就成为一个常数项级数。

若收敛，则称为幂级数（1）的收敛点；若发散，则称为幂级数（1）的发散点。

幂级数（1）的收敛点的全体称为它的收敛域，发散点的全体称为它的发散域。

例如：幂级数是一个公比为 x 的等比级数，显然当 | x | < 1 时，该级数收敛，当 |x |≥1 时，该级数发散，当故该级数的收敛域为（－1，1），发散域为，可见它的收敛域是一个关于原点对称的区间，由下面的定理可知，这个结论对于一般的幂级数（1）也是成立的。

定理1 阿贝尔（Abel）定理①若幂级数（1）在（≠0）处收敛，则对于满足不等式 | x | < | | 的一切 x ，幂级数（1）绝对收敛。

②若幂级数（1）在处发散，则对于满足不等式| x | > | | 的一切 x ，幂级数（1）发散。

证：①设是幂级数（1）的收敛点，即级数收敛，根据级数收敛的必要条件知又因收敛数列必有界，故存在常数 M > 0，使于是，对于级数（1）为一般项，有由条件 | x | < | | ，即，可知等比级数，再由比较判别法知收敛，故幂级数绝对收敛。

②用反证法：假设有一点（| | > | |）使幂级 a 数（1）在该点处收敛，那么由本定理1中的①知，幂级数（1）在处绝对收敛，这与条件相矛盾，定理证毕。

例1：设在点= 3 处收敛，问此级数在点=－2.5 与点=3.5自是否收敛？解：因为| |＝|－2.5| =2.5 < | | =3，而在点=3 处收敛，故由阿贝尔定理知，该级数在点＝－2.5 处也收敛，而该级数在点＝3.5处的敛散性不能确定。

第二部分函数项级数和含参变量广义积分第十九章函数项级数.幂级数§1.函数项级数的一致收敛1. 讨论下列函数序列在所示区间的一致收敛性2(1)();(2)(),01;(3)()sin(),();(4)()(1),01;(5)(),01;1(6)()ln ,0 1.n n n n n n n n n f x x f x x x x x f x ni l x l ii x f x x x x nxf x x nx x xf x x n n=-∞<<+∞=-≤≤=-<<-∞<<+∞=-≤≤=≤≤+=<<解：（1）显然()||().n f x x n =→→∞因为22()||().111|()|||1n n f x x n n f x x n n =→→∞-=<=对任给的0,ε>取1N ε⎡⎤=⎢⎥⎣⎦，当n N >时，恒有01|()|||n f x x n ε-<<故()n f x 在(,)-∞+∞内一致收敛。

Fejér和对ω-型单调函数的逼近

（ｌ：（。当 ∈ ｉ时Ｊ一厂Ｉ：（）ｅ和共函类逼阶厂Ｊ０一，ｆＬ１，厂（Ｊ０））ｐｌ）；ｊ对轭数的近，而Ｆ臼
ＺｇｕｄＡ证明得到：厂∈Ｌｐ（＜ａ１时，ｙｍｎ当ｉ０ａ ≤ ）其逼近阶能一致达到Ｉ（）ｌ．Ｏ（一）Ｊ７一厂Ｊｚ一ｎ。叫．ｃ
关于ｚ一致成立，中（，）为厂的连续模．其厂￡
文［］引入型单调函数，了如下推广：２作定理Ｃ若厂∈ ｃ一兀兀［，］Ｎ＾一兀兀，Ｕ［，］贝
ｓ：；Ｏ１［，．）三厂（）Ｌ詈＼］：ｚ（ｎ骞（）Ｊ；三－／詈（）ｚ厂二），ｆ一￣＼（厂／
近来一些作者对Ｆｕｉｒｏｒ级数逼近某些函数类问题作了许多研究＂ｅ．
文［］引进单调型函数，功地去掉了因子ｌｇ，到：６成ｏｎ得
收藕日期：０７０ —０２０ —９２．
基金项目：州师范学院科研基金项目（０３２）温２０Ｙ４．
Ｖ０．．１６Ｎｏ６
ＮＯ．２７ｒ００
文章编号：０８９０（０７０ —０３－０１０－４３２０）６４０５
Ｆｊｒ对Ｏ型单调函数的逼近ｅ６和Ｊ一
叶秀芳
（州大学瓯江学院，江温州３５３）温浙２０５
作者简介：秀芳（９５）女，江平阳人，师，士，要从事函数逼近论研究．叶１７一，浙讲硕主

第五章第四节 4.4 有界变差函数

b a
第四节有界变差函数四. 有界变差函数的性质性质1 性质若 f 是 [a, b]上的有界变差函必为有界函数。数，则 f 必为有界函数。
第四节有界变差函数证明：若不然，则存在 {xn} [a, b]。使 | f (xn ) | →∞ ，由 f 是有界变差函数知 Vab ( f ) < ∞。对任意 n，作 [a, b] 的分划 n : a < xn < b，则
第四节有界变差函数从 θ ′(x x0 ) = 0 a.e.我们还看到另一个事实，一个非常值的函数可以有几乎处处等于0的导数，这样的函数称为奇异函数，即下面的定义6 设 f 是 [a, b]上的有限函数，若在 [a, b]上 f ′(x) = 0 a. e.，且 f 不恒为常数，则称 f 为 [a, b]上的奇异函数奇异函数。奇异函数
n→∞ a
b
证毕。
≤ f (b) f (a).
第四节有界变差函数应该注意到定理5与牛顿-莱布尼兹公式的差别，此处严格不等式样可能成立的，例如，若 x0 ∈(a, b),(x) =θ (x x0 )，则
b
′(x) = 0 a.e.。于是 ∫ ′(x)dx = 0，但 a (b) = 1，(a) = 0，故 (b) (a) = 1，
k =1 ∞ k =1 ∞ k =1 ∞
∑{ f ' (x) S'
k=1
∞
nk
(x)} < ∞ a.e.
第四节有界变差函数进而，级数的通项趋于0，即
lim ( f ' (x) S'nk (x)) = 0 a.e.，
k →∞
∞
也即
∑f '
证毕。

泛函分析之期末考习题解答-实变函数与泛函分析概要第二册

泛函分析之期末考习题解答-实变函数与泛函分析概要第⼆册赋范线性空间E E 局部紧证：→不妨设E 为实n 维赋范线性空间，则E 与R n 拓扑同构⽽R n 中任意有界闭集是紧的，由紧集上的连续函数定理知E 的任意有界闭⼦集是紧的，即E 局部紧←设E ⽆限维但任意有界闭⼦集是紧的S 是E 中的单位球⾯：S={x:||x||=1}则S 是E 中的紧集由⾥斯定理：x1∈S,?x2∈S,ST,||x2-x1||≥1/2,?x3∈S,ST,||x3-xi||≥1/2,(i=1.2)……类推，由E ⽆限维，故可取S 中的⼀个系列元素x1,x2…xk…ST，||xk-xl||≥1/2,显然｛xk｝⽆收敛⼦列，⽭盾X 是完备的距离空间，T:X→X,?x,y ∈X,ρ(Tx,Ty)≤θρ(x,y),0≤θ<1,则T 中存在唯⼀不动点x`,ST,Tx`=x`,&&x`可⽤迭代法求出证：x0∈X,Set,x1=Tx0,…，xn+1=xn…则ρ(x1,x2)≤θρ(x0,x1)…ρ(xn,xn+p)≤（θn +θn+1+…+θn +p ）ρ(x0,Tx0)=θn ρ(x0,Tx0)/(1-θ)→0则{xn}是基本点列，⼜因为X 完备，故{xn}收敛于某x`∈Xρ(Tx,Ty)≤θρ(x,y)知T 连续，xn+1=xn 令n→∞得x`=Tx`即x`是不动点设另有不动点y`∈X,则ρ(x`,y`)≤θρ(x`,y`)得ρ(x`,y`)=0即x`=y`闭图像定理：T 是E 到E1的闭算⼦，E，E1都是B 空间，则T 有界证：E,E1是B 空间，则E ⊕E1也是B 空间，||(x,y)||=||x||+||y||设G 是E ⊕E1的闭⼦空间，则G 也是B 空间定义：T`：G→E,T`(x,Tx)=x,则T 为双射再者由||T`(x,Tx)||=||x||≤||x||+||Tx||=||(x,Tx)||知T`有界故T`有有界逆算⼦T~,则?x ∈E,(x,Tx)=T~x→||(x,Tx)||≤||T~||||x||→||Tx|||T~||≤||x||即T 有界P669.(a)略(b)提⽰：设A={多项式全体}，每个函数都有傅⽴叶展开式11.(a)略(b)提⽰：同胚即找双射，距离之间存在双射，要连续的17.证明第三节例题六的空间L ∞[a,b]是完备的距离空间证：取基本点列｛x n ｝∈L ∞[a,b]ε>0,?N ∈Ν,m,n≥N 时||x m -x n ||<ε故?[a,b]中的Lebesgue 集{Emn}ST||x m -x n ||=SUP{x m -x n |x ∈[a,b]/Emn}Set E=∪Emn ?[a,b],则x ∈[a,b]/E，m,n≥N 时|x m -x n |≤SUP{x m -x n |x ∈[a,b]/E}≤||x m -x n ||<ε故x ∈[a,b]/E 时，{xn}是实基本列，必收敛于某实数x显然x 可测，令m→∞则n≥N 时|x-x n |<ε在x ∈[a,b]/E 成⽴x-x n ∈L ∞[a,b]故x ∈L ∞[a,b]&&|x-x n |≤SUP{x-x n |x ∈[a,b]/E}≤ε即x n 按L ∞[a,b]的距离收敛于x，即L ∞[a,b]完备34.证明lp 中的⼦集A 准紧的充要条件是：(a)?k>0,ST,?x={ξ1,ξ2…ξn…}∈A,∑∞1||p n ξ(b)?ε>0,?N>0,ST,m>N 时，?x ∈A,∑∞1||p n ξ<ε(a).证：→A 准紧，则A 全有界，则A 有界可分（对应定理4.1，4.2）←?k>0,ST,?x={ξ1,ξ2…ξn…}∈A,∑∞1||p n ξ由准紧的定义，A 中每个点列必含有收敛⼦列，故A 准紧注：A 准紧的充要条件是A 有界+A 等度连续(b).命题与（a）等价P1241.V[a,b]是定义在[a,b]的有界变差函数全体，线性运算与C[a,b]相同，定义范数：||x||=|x(a)|+V a b (x),证明V[a,b]按||·||是不可分B 空间证:V[a,b]是线性空间，易证范数满⾜范数公理，故只要证完备性即可取V[a,b]中的基本列｛xn(t)｝，?ε>0,?N ∈Ν,m,n≥N 时||x m -x n ||<ε易知xn(t)⼀致收敛，令Lim xn(t)=x(t)，以下证其是有界变差函数设Δt>0,因为xn 右连续（有界变差的条件之⼀）且|x(t)-x(t+Δt)|≤|x(t)-xn(t)|+|xn(t)-xn(t+Δt)|+|x(t+Δt)-xn(t+Δt)|故x 右连续。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

２００８年４月
Ａｐ，２８ｒ００
Ａｂｌ对有界变差函数及一ｅ和型单调函数的逼近
叶秀芳，杨闻善２
（．温州大学瓯江学院，浙江温州３５３；２浙江师范大学数理学院，浙江金华３１０）１２０５．２０４
定理ｉ设０－ ≤１ｃ４，则
．
关于，（，），Ｘ逼近ｆ（）．ｘ的偏差，Ｉａｎｏ．Ｎｔｓｎ曾证明了如下定理：Ｅａ
Ｉ１ｒｓ＂０一）ｏ＿，（）ｅｒ＋（，＿＜－￣ｃａ１．＜１ｉ，
” ”１Ｉ＿Ｄ）．ｌ（ｒ ’ ｏｒ１ｇ）＿（ｌｒ１＋，２
）ｇ是，ｓｎ上的单调函数，则称，是Ｉ２＇Ｏ型单调函数，￣ｆ一ＪＣ记
２定义和定理及证明
定义１设，是实直线Ｒ上的一个区间，ｆ定义在，上，ｃｔ是某个连续模，若存在某个ｏ）（常数Ｃ４Ｆ（）（）Ｅ￣ｘ＝，＋ｃ
摘要：究了Ａｅ和对有界变差函数及其共轭函数的逼近，其逼近结果用有界变差函数的局部全变研ｂｌ ≤１函１
差来刻画；并由Ａｂｌｅ和对有界变差函数及其共轭函数的逼近结果推出了Ａｂｌｅ和对Ｌｐａｏｉ（
数类的逼近阶，同时又得出了Ａｅ和对（一ｂｌ１型单调函数及其共轭函数的逼近估计；另外也指出了俞国９
Ｉ，７））（Ｉ３ｎ）（（一，３，，．Ｚ：ｖ
其中）＝一＿ｆ．）］
定理４若ｆｃ一，】ｇ．，］则 ∈ ［万ｎ［，万
Ｓｘｆ．（）ｆ－
，
，
一

，
，
（＝－［，Ｏ￣詈詈ｘ（，＋］）ｎ．喜１
维普资讯
第２９卷第２期
Ｖ＿９．０２Ｎｏ２ｌ
温州大学学报・自然科学版
ＪｕｒａｆＷｅｈｏｎｌｏｎｚｏｕＵｎｉｒｉｙ・ａｕｒｌＳｃｅｅｖｅｓｔＮｔａｉｎｃｓ
维普资讯
２
温州大学学报・自然科学版（０８第２卷第２２０）９期
∑（ｉｘｂｏｘ＂ｏ，１ｓｎ－．ｓ），＿．）ｎｃｎｒ（＜＿，＜
记（）其分示为７，，积表为．，
一
ｆ，＝ｃ（ｆ，一（）一Ｊ）（ｆ二ｒｘｒ＋一）［，
为ｆＭ∞ ；（＝０＜１时， ∞特 ∈ ，当ｆｔ（＿））将，记为Ｍ，称，的，并中函数，上为，
的一型单调函数．
文献４【在证明Ｍ是，ｏ＜＜）集的】，（＿１＿真子过程中指出：数函
，（）：
』ｓ，∈ 】ｆｉ［ｏｎ．／ｆ，
１０，＝０
维普资讯
叶秀芳等：Ａｅ和对有界变差函数及．ｂｌ型单调函数的逼近
３
在［，】一上不是１单调函但它一调函事实这个函也不一单．型数，是２型单数．上，数是１型调函
有关三角多项式算子对有界变差函数和Ｃ一Ｏ型单调函数的逼近问题的研究结果主要有：
定理２若ｆ∈Ｂ［，，则Ｖ一】
Ｉ，［＋，。喜ｇ，。（））（一（）】（，＋一）Ｉ，
其中ｇ（＝ｆｘ）ｘ）（＋ｔ＋ｆ（ —ｔ一ｆ（ｆｘ）ｘ＋Ｏ一厂（）一０．）定理３若ｆ∈ＢＶ一，＂。［ｌ，则ｔ】
收稿日期：２０ —０ｌ０７１一５基金项目：温州师范学院２０年度科学研究基金（０３４０３２０Ｙ２）作者简介：叶秀芳（９５）１７一，女，浙江平阳人，讲师，硕士，研究方向：函数逼近论
（）式的Ａｂｌ是：１ｅ和
●
詈喜ｃ＋ｓ０－＇＋（。ｎ，ｒ）ｓｉ（＜似似－１＜
记为ｆ（，）ｒＸ，其积分表示为
ｆ，＝厂＋二ｒＳ（）ｒ￡（（Ｏ＋））１ＣｔＺ一２ｒ
（）式的Ａｂｌ是：２ｅ和
级数记为
ｆ～＋（。＋ｉ）（鲁喜ｃｎｘｓｓ）艇似
它的共轭级数为
（－）
（２
∑（ｓｎ－ｎｓ）ｉｘｂｏｘｎｎｃ
ｎ：ｌ
如果（）是函数ｇｘ的Ｆｕｉ级数，那么就说ｇｘ是ｆｘ的共轭函数，并记ｇｘ＝ｆｘ．２（）ｏｒｒｅ（）（）（）（）
华丈中的错误之处．
关键词：Ａｂｌ；有界变差函数；（一ｅ和１型单调函数；逼近９
中图分类号：Ｏ１４７文献标识码：Ａ文章编号：１０ —３５２０）２００ —７０６０７（０８０．０１０
１预备知识设ｃ一，】周期２一，】实续函空间，于‘ ｃ一，，ｏｒｒ［是为的［上的连数对厂［】其Ｆｕｅ ∈ ｉ