2014九年级数学上学期专题复习训练卷四 新人教版
安徽省淮南市潘集区2014届九年级数学上学期期末联考试题 新人教版

某某省某某市潘集区2014届九年级上学期期末联考数学试题 新人教版题号一二三四五六七八总分1516 17 18 19 20 21 22 23 得分一.选择题(本题共10小题,每小题4分,满分40分) 1.16的算术平方根是( ) A .4 B .4±C .2 D .2±xx 1-有意义,那么x 的取值X 围是( ) A .x ≥≠1C.x>0D .x ≥0且x ≠13.在下列图形中既是轴对称图形又是中心对称图形的是( ) ①线段,②角,③等边三角形,④圆,⑤平行四边形,⑥矩形. A. ③④⑥ B. ①③⑥ C. ④⑤⑥ D. ①④⑥4. 下列一元二次方程中,有两个不相等的实数根的方程是( )A .2x 3x 10-+=B .2x 10+=C .2x 2x 10-+=D .2x 2x 30++=2x kx 60--=的一个根为x=3,则实数k 的值为( )A .1B .-1C .2D .-26.如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB 宽为8cm ,水面最深地方的高度为2cm ,则该输水管的半径为( ) A .3cmB .4cmC .5cm D .6cm7.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( ) A .6,32 B .32,3 C .6,3 D .62,328. 已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为()A. 15π cm 2B. 30πcm 2C. 60πcm 2D. 391cm 29.下列事件为必然事件的是( )A .小王参加本次数学考试,成绩是150分B .某射击运动员射靶一次,正中靶心C .打开电视机,CCTV 第一套节目正在播放新闻D .口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球10.若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为( ) A .12B .34 C .13 D .14二.填空题(本题共4小题,每小题5分,满分20分)x x x x -⋅+=-+44)4)(4(成立的条件是_____。
九年级数学上学期专题复习训练卷四 新人教版(1)

专题复习训练卷四图形的认识(时间:60分钟满分:100分)一、填空题(每题2分,共20分)1. 下列说法中,正确的是( ).A. 经过三个点一定可以作圆B. 任意一个圆一定有内接三角形,并且只有一个内接三角形C. 任意一个三角形一定有一个外接圆,并且只有一个外接圆D. 三角形的外心到三角形各边的距离都相等2. 点P在⊙O内,OP=2 cm,若⊙O的半径是3 cm,则过点P的最短弦的长度为( ).A. 1 cmB. 2 cmC. 5 cmD. 2 5 cm3.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( ).A.4m B.6m C.8m D.10m(第3题) (第4题)4.如图,AB是⊙O的直径,若∠C=26°,则∠ABD等于( ).A.36° B.38° C.52° D.64°5.如图,P是⊙O外一点,PA、PB切⊙O于点A、B,点C在优弧AB上,若∠P=68°,则∠ACB等于( ).A.22° B.34° C.56° D.68°(第5题) (第6题)6.如图,⊙O中,AB、AC是弦,O在∠BAC的内部,∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系中,正确的是( ).A. θ=α+βB. θ=2α+2βC. α+β+θ=180°D. α+β+θ=360°7.如图,⊙O的直径AB长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则CD的长为().A. 7B.(第7题) (第8题)8.如图,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=3R.其中,使得BC=R 的有( ).A. ①②B. ①③④C. ②③④D. ①②③④9. 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且OA与平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( ).A. 0≤x≤ 2B. -2≤x≤ 2C. -1≤x≤1D. x> 2(第9题)10.如图,C、D是以线段AB为公共弦的两条圆弧的中点,AB=4,E、F分别是线段CD、AB 上的动点,设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( ).(第10题)二、选择题(每题3分,共24分)11.如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是 .(第11题) (第12题)12.已知:如图,⊙O 的半径为3cm ,B 为⊙O 外一点,OB 交⊙O 于点A ,AB =OA ,动点P 从点A 出发,以cm/s 的速度在⊙O 上按逆时针方向运动一周回到点A 立即停止.当点P 运动的时间为______s 时,BP 与⊙O 相切.13.已知∠BAC =45°,一动点O 在射线AB 上运动(点O 与点A 不重合),设OA =x ,如果半径为1的⊙O 与射线AC 只有一个公共点,那么x 的取值范围是______.14.两圆的直径分别是17-和17+,圆心距为d ,当两圆相交时,d 的整数值为______. 15.如图,两个半圆,大半圆中,长为16cm 的弦AB 平行于直径CD ,且与小半圆相切,则图中阴影部分的面积为______cm 2.(第15题) (第16 题) 16.如图,已知圆柱体底面圆的半径为π2,高为2,AB 、CD 分别是两底面的直径,AD 、BC 是母线.若一只小虫从点A 出发,从侧面爬行到点C ,则小虫爬行的最短路线的长度是______.(结果保留根式)17.芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图(1),他在边长为1的正方形ABCD 内作等边三角形BCE ,并与正方形的对角线交于点F 、G ,制成如图(2)的图标.则图标中阴影部分图形AFEGD 的面积=__________.(第17题)18.如图,ΔABC 内接于⊙O ,∠B =90º,AB =BC ,D 是⊙O 上与点B 关于圆心O 成中心对称的点,P 是BC 边上一点,连结AD 、DC 、AP .已知AB =8,CP =2,Q 是线段AP 上一动点,连结BQ 并延长交四边形ABCD 的一边于点R ,且满足AP =BR ,则BQQR的值为_______________.(第18题)三、 解答题(每题8分,共56分)19. 小明家的房前有一块矩形的空地,空地上有三棵树A 、B 、C ,小明想建一个圆形花坛,使三棵树都在花坛的边上.(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹); (2)若△ABC 中AB =8米,AC =6米,∠BAC =90°,试求小明家圆形花坛的面积.(第19题)20. 如图,在△ABC 中,AB =AC ,以BC 为直径的半圆O 与边AB 相交于点D ,切线DE ⊥AC ,垂足为点E .求证:(1)△ABC 是等边三角形; (2)AE =13CE .(第20题)21. 如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.(1)试探究AE与⊙O的位置关系,并说明理由;(2)已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O 的半径r的一种方案:①你选用的已知数是__________;②写出求解过程(结果用字母表示).(第21题)22. 如图,PA、PB是半径为1的⊙O的两条切线,点A、B分别为切点,∠APB=60°,OP与弦AB交于点C,与⊙O交于点D.(1)在不添加任何辅助线的情况下,写出图中所有的全等三角形;(2)求阴影部分的面积(结果保留π).(第22题)BC.23.如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=12(1)求∠BAC的度数;(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形;(3)若BD=6,CD=4,求AD的长.(第23题)24. 我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).请你用上面的思想和方法对下面关于圆的问题进行研究:(1)如图(1),在圆O所在平面上,放置一条..直线(和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?(2)如图(2),在圆O所在平面上,请你放置与圆O都相交且不同时经..直线....过圆心...的两条和(与圆O分别交于点A、B,与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之.(3)如图(3),其中AB是圆O的直径,AC是弦,D是ABC的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.(1) (2)(3)(第24题)25. 小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图(1)),它的侧面边缘上有两条圆弧(如图(2)),其中顶部圆弧AB的圆心O1在竖直边缘AD上,另一条圆弧BC的圆心O2在水平边缘DC的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计,π取3.141 6).(1)计算出弧AB所对的圆心角的度数(精确到0.01度)及弧AB的长度(精确到0.1 cm);(2)计算出遮雨罩一个侧面的面积(精确到1cm2);(3)制做这个遮雨罩大约需要多少平方米的玻璃钢材料(精确到0.1平方米)?(1)(2)(第25题)附加题(共10分,不计入总分)26.如图(1),在直角坐标系xOy中,O是坐标原点,点A在x正半轴上,OA=cm,点B 在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t s(0<t<6).(1)求∠OAB的度数.(2)以OB为直径的⊙O‘与AB交于点M,当t为何值时,PM与⊙O‘相切?(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t 值.(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.(1)(第26题)专题复习训练卷四1. C2. D 3.A 4.D 5.C 6. B 7.B 8. D 9. A 10. C 11.(-1,1) 12.1或5 13.0<x <1或2x14.2 15.32 16.2217. 18.1和121319. (1)用尺规作出两边的垂直平分线作出圆⊙O 即为所求做的花园的位置.如下图:(第19题)(2)∵ ∠BAC =90°,AB =8米,AC =6米, ∴ BC =10米.∴ △ABC 外接圆的半径为5米.∴ 小明家圆形花坛的面积为25π平方米. 20. (1)连接OD . ∵ 切线DE ⊥AC , ∴ OD ∥AC . ∴ ∠BDO =∠A .由OB =OD 得∠OBD =∠ODB , ∴ ∠OBD =∠A . ∴ BC =AC . 又 AB =AC ,∴ △ABC 是等边三角形. (2)连接CD ,则CD ⊥AB . ∴ D 是AB 中点.∵ AE =AD -cos ∠A =12AD ,∵ AE =14AB =14AC ,∴ EC =3AE . ∴ AE =13CE .21. (1)AE 与⊙O 相切.理由略. (2)①选择a ,b ,c ,或其中2个 ②解答举例: 若选择a ,b ,c . 由CD ∥OA ,aa +c =bb +r,得r =bc a.若选择a ,b .在Rt △OCE 中,由勾股定理,得a 2+r 2=(b +r )2,得r =a 2-b 22b.22. (1)△ACO ≌△BCO ,△APC ≌△BPC ,△PAO ≌△PBO (2)∵ PA 、PB 为⊙O 的切线,∴ PO 平分∠APB ,PA =PB ,∠PAO =90°. ∴ PO ⊥AB .∴ 由圆的对称性可知:S 阴影=S 扇形AOD .∵ 在Rt △PAO 中,∠APO =12∠APB =12×60°=30°,∴ ∠AOP =90°-∠APO =60°. ∴ S 阴影=S 扇形AOD =60×π×12360=π6.23.(1)连结OB 和OC .(第23题)∵OE⊥BC,∴BE=CE.∵OE=12 BC,∴∠BOC=90°.∴∠BAC=45°.(2)∵AD⊥BC,∴∠ADB=∠ADC=90°.由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,∠BAG=∠BAD,∠CAF=∠CAD. ∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°.∴∠GAF=∠BAG+∠CAF+∠BAC=90°.∴四边形AFHG是正方形.(3)由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.设AD的长为x,则BH=GH-GB=x-6,CH=HF-CF=x-4.在Rt△BCH中,BH2+CH2=BC2,∴(x-6)2+(x-4)2=102.解得x1=12,x2=-2(不合题意,舍去).∴AD=12.24. (1)弦、弧、弓形、求弓形的面积等.(2)情形1:如图(1),AB为弦,CD为垂直于弦AB的直径.结论:略(垂径定理的结论之一).证明:略情形2:如图(2),AB为弦,CD为弦,且AB与CD在圆内相交于点P.结论:PA ·PB =PC ·PD .证明:略.(3)若点C 和点E 重合,则由圆的对称性,知点C 和点D 关于直径AB 对称. 设∠BAC =x ,则∠BAD =x ,∠ABC =90°-x .又D 是ABC 的中点,所以2∠CA D =∠CAD +∠ACD =180°-∠ABC , 即2·2x =180°-(90°-x ).解得x =∠BAC =30°.所以当∠BAC =30°时,点C 与点E 重合.(1)(2)(第24题)26. 由题意知BE =60,AE =50,连接O 1B ,设弧AB 的半径为R .在Rt △O 1BE 中,由勾股定理得R 2=602+(R -50)2.解得 R =61. 由sin ∠BO 1E =BE R =6061,得∠BO 1E ≈79.61° ∴ 弧AB 的长=79.61180×π×61≈84.8(cm). (2)扇形O 1AB 的面积=12×84.8×61≈2 586.4(cm 2). 扇形O 2BC 的面积=14×π×402=400π≈1 256.6(cm 2).梯形O 1BO 2D 的面积=12×(29+40)×60=2 070(cm 2).∴ 遮雨罩一个侧面的面积=扇形O 1AB 的面积+梯形O 1BO 2D 的面积-扇O 2BC 形的面积=2 586.4+2 070-1 256.6≈3 400(cm 2)(3)遮雨罩顶部的面积=84.8×180=15 264(cm 2).∴ 遮雨罩的总面积=3 400×2+15 264=22 064(cm 2)≈2.2(m 2). 制做这个遮雨罩大约需要2.2平方米玻璃钢材料.26.(1)在Rt △AOB 中,OB =12,OA =,AB =24,∴ ∠OAB =30°.(2)如图(1),连接OP ,OM .当PM 与⊙O ‘相切时,有∠PM O ‘=∠PO O ′=90°,△PM O ′≌△PO O ′(第26题(1))由(1)知∠OBA =60°.∵ O ‘M = O ‘B ,∴ △O ‘BM 是等边三角形.∴ ∠B O ‘M =60°.可得∠O O ‘P =∠M O ‘P =60°.∴ OP = 6.又 OP =t ,∴ t =.即t =3时,PM 与⊙O ‘相切.(3)如图(2),过点Q 作QE ⊥x 于点E .∵ ∠BAO =30°,AQ =4t ,∴ QE =21AQ =2t .(第26题(2))由勾股定理得AE =t.∴ OE =OA -AE = t .∴ 点Q 的坐标为( t ,2t ).S △PQR = S △OAB -S △OPR -S △APQ -S △BRQ =)212(32213121221t t -⋅⋅-⋅⋅ )32312(2212)32312(21t t t t -⋅-⋅-- =372336362+-t t =318)3(362+-t (60<<t ).当t =3时,S △PQR 最小=318.(4)分三种情况:如图(3).(第26题(3))①当AP =AQ 1=4t 时,∵ OP +AP =,∴ t +4t =12.∴ t =12-18.②当PQ 2=AQ 2=4t 时,过点Q2作Q2D⊥x轴于点D,∴PA=2AD=4t.即2 t+4 t =12.∴t=2.③当PA=PQ3时,过点P作PH⊥AB于点H.AH=18-3t,AQ3=2AH=36-6t.得36-6t=4t,∴t=3.6.综上所述,当t=2,3.6,12 -18时,△APQ是等腰三角形.。
2014届中考九年级模拟四数学试卷

第9题图 EF O A B C 212014届中考九年级模拟四数学试卷 一、选择题(每题4分,共40分)1.右图是一个表示“众志成城,奉献爱心”的图标,图标中两圆的位置关系是( ) A .外离 B .内含 C .外切 D .内切 2.下列说法错误的是( ) A .必然事件发生的概率为1 B .不确定事件发生的概率为0.5 C .不可能事件发生的概率为0 D .随机事件发生的概率介于0和1之间4.一元二次方程0412=++x x 根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .只有一个实数根D .无法确定 5.下列计算正确的是( )A.= B .325=-C3= D3=-[来 6.用配方法解方程x2+4x+1=0,配方后的方程为( )A .(x +2)2=3B .(x-2)2=3C .(x―2)2=5D .(x+2)2=57.如图,在正方形ABCD 中,AB=4,点O 在AB 上,OB=1,P 是BC 上一动点,连接OP 将线段OP 绕点O 逆时针旋转90°得到线段OQ.要使点Q 恰好落在AD 上,则BP 的长是( ) A .1 B .2 C .3 D .48.如图,A,B,C,D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O C D O ---路线作匀速运动.设运动时间为(),()t s APB y ∠=︒,则下列图象中表示y 与t 之间函数关系最恰当的是( )9.如图,四边形OABC 为菱形,点B 、C 在以点O 为圆心的⌒EF 上,若OA=1,∠1=∠2,则扇形OEF 的面积为( )第7题图第8题图D C B 第10题图A. 6πB. 4πC. 3πD. 32π10.Rt △ABC 中,已知∠C =90°,∠B =50°,点D 在边BC 上,BD =2CD .把△ABC 绕着点D 逆时针旋转m (0<m <180)度后,如果点B 恰好落在初始Rt △ABC 的边上, 那么m =( ) A .50° B .80° C .80° 或 120° D .50°或 120° 二、填空题(每题5分,共30分)11.在平面直角坐标系中,点P (2,-3)关于原点对称的点的坐标是12. 一个半径为6cm 的扇形纸片,与一个半径为2cm 的圆形纸片刚好能组合成圆锥体,则圆锥的侧面积等于 cm2.13. 当x 取某一范围的实数时,代数式22)13()16(-+-x x 的值是一个常数,该常数是_______.14.如图,在矩形ABCD 中,AB=1,AD=2,将AD 绕点A 顺时针旋转,当点D 落在BC 上点D`时,则∠15.如图⊙P 与两坐标轴分别交于点A (0,2)、B (0,6)、C (-3,0)和D(-4,0),双曲线k y x =过圆心P ,则k=_______. 16.如图,在平面直角坐标系中,⊙O 的半径为5,点P 为直线y=-x+4上的一点,过点P 作⊙O 的切线PC 、PD ,切点分别为C 、D ,若PC ⊥PD ,则点P 的坐标为 . 三、解答题(共80分) 17.计算(每小题4分,共8分)(1)0)21()12(8+-+; (2)241221348+⨯-÷18.解方程(每小题4分,共8分)(1)73)12(2=+-x (2)x2+4x +2=0;19.(本题满分8分)已知关于x 的一元二次方程x2-2 3 + m=0 有两个不相等的实数根. (1)求实数m 的取值范围;第14题图 第16题图(2)在(1)的条件下,化简:|m-3|+(4-m)2 =0 .20.(本题满分10分)如图,在平面直角坐标系中,AOB ∆的顶点A (2-,0)、 B (1-,1).将AOB ∆绕点O 顺时针旋转︒90后,点A 、B 分别落在'A 、 'B(1)在图中画出旋转后的''OB A ∆;(确认无误后请用水笔描黑) (2)求点A 旋转到点'A 所经过的弧形路线长.21.(本题满分10分)如图,已知点E 在△ABC 的边AB 上,∠C =90°, ∠BAC 的平分线交BC 于点D ,且D 在以AE 为直径的⊙O 上. (1)求证:BC 是⊙O 的切线; (2)已知∠B =30°,⊙O 的半径为6,求线段AD 的长.(第21题图)B22.(本题满分10分)减负提质“1+5”行动计划是我市教育改革的一项重要举措.某中学“阅读与演讲社团”为了了解本校学生的每周课外阅读时间,采用随机抽样的方式进行了问卷调查,调查结果分为“2小时内”、“2小时—3小时”、“3小时—4小时”、“4小时以上”四个等级,分别用A、B、C、D表示,根据调查结果绘制成了如图所示的两幅不完整的统计图,由图中所给出的信息解答下列问题:(1)求出x的值,并将不完整的条形统计图补充完整;(2)在此次调查活动中,初三(1)班的两个学习小组内各有2人每周课外阅读时间都是4小时以上,现从这4人中任选2人参加学校的知识抢答赛,用列表法或画树状图的方法求选出的2人来自不同小组的概率.23.(本题满分12分)对于平面直角坐标系x O y中的点P和⊙C,给出如下定义:若⊙C 上存在两个点A,B,使得∠APB=60°,则称P为⊙C 的好点.如图,等边DEF∆的三个顶点刚好在坐标轴上,其中D点坐标为(0,4).(1)求等边DEF∆内切圆的半径r;(2)当⊙O的半径为2时,请直接判断点D和点E是否是⊙O的的好点?点D ,点E (填“是”或“否”);若直线DE上的点P(m,n)是⊙O的好点,则m的取值范围是;(3)若线段EF上的所有点都是⊙O的好点,求⊙O的半径r的取值范围.24.(本题满分14分)已知,如图①,在平行四边形ABCD中,AB=12,∠DAB=60°,AD ⊥BD,以AD为斜边在平行四边形ABCD的内部作Rt△AED,∠EAD=30°∠AED=90°.(1)求△AED的面积;(2)若△AED以每秒2个单位长度的速度沿DC向右平行移动,得到△A0E0D0,当A0D0与BC重合时停止运动.设移动时间为t秒,△A0E0D0与平行四边形ABCD重叠部分的面积为S,请求出S与t之间的函数关系式,并注明t的取值范围;(3)如图②,当△AED停止运动后得到△BEC,将△BEC绕点C按顺时针方向旋转α(0°<α<180°),在旋转过程中,B的对应点为B1,E的对应点为E1,设直线B1E1与直线BE交于点P、与直线CB交于点Q,是否存在这样的α,使△BPQ为等腰三角形?若存在,求出α的度数;若不存在,请说明理由.备用图。
人教版数学九年级上册专项训练4课件

►雨水打在窗户上,发出嘀嗒,嘀嗒的声响。这天空好似一个大筛子, 正永不疲倦地把银币似的雨点洒向大地。远处,被笼罩在雨山之中的 大楼,如海市蜃楼般忽隐忽现,让人捉摸不透,还不时亮起一丝红灯, 给人片丝暖意。 ►七月盛夏,夏婆婆又开始炫耀她的手下——太阳公公的厉害。太阳 公公接到夏婆婆的命令,以最高的温度炙烤着大地,天热得发了狂, 地烤得发烫、直冒烟,像着了火似的,马上要和巧克力一样融化掉。 公路上的人寥寥无几,只有汽车在来回穿梭奔跑着。瓦蓝瓦蓝的天空 没有一丝云彩,一些似云非云、似雾非雾的灰气,低低地浮在空中, 使人觉得憋气不舒服。外面的花草树木被热得打不起精神来,耷拉着 脑袋。
C.338π-3
D. 33+π
2
2.如图,正方形 ABCD 内接于⊙O,AB=4,则图中阴影部分的面积是( B )
A.4π-16 C.16π-32
B.8π-16 D.32π-16
3
3.【山东济南中考】如图,在菱形 ABCD 中,E 是 BC 的中点,以点 C 为圆心、 CE 长为半径作弧,交 CD 于点 F,连接 AE、AF.若 AB=6,∠B=60°,则阴影部分 的面积为( A )
A.9 3-3π C.18 3-9π
B.9 3-2π D.18 3-6π
4
4.【吉林中考】如图,在扇形 OAB 中,∠AOB=90°.D、E 分别是半径 OA、OB
︵ 上的点,以 OD、OE 为邻边的□ODCE 的顶点 C 在AB上.若 OD=8,OE=6,则阴
影部分图形的面积是_____2_5_π_-__4_8_____.(结果保留 π)
5
类型 2 等积变形法求阴影部分的面积 5.如图,AB 是⊙O 的直径,CD 是弦,∠BCD=30°,OA=2,则阴影部分的 面积是( B )
人教版2014年中考九年级数学模拟试题(四)

2014年九年级数学一轮试题满分:120分 时间:120分钟注意事项:1.本试题分卷Ⅰ和卷Ⅱ两部分,卷Ⅰ为选择题42分;卷Ⅱ为非选择题78分. 2. 答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束,试题和答题卡一并收回. 3. 第Ⅰ卷每题选出答案后,都必须用2B 铅笔把答题卡上对应题目的答案标号【ABCD 】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案. 4. 考试时,不允许使用科学计算器.第Ⅰ卷(选择题 共42分)一、选择题(本题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的。
)1. -6是6的( ) A .算术平方根 B .倒数 C .绝对值 D .相反数2. PM 2.5是指大气中直径0000025.0≤米的颗粒物,将0.0000025用科学记数法表示为 2.5×10-n (n 是正整数),则n 的值为( ) A .5 B .6 C .7 D .83. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )A. 10° B. 20° C. 25° D.30°4. 下列运算正确的是( )A .3x 2+4x 2=7x 4B .2x 3∙3x 3=6x 3 C.(a +2) 2=a 2+4 D .x 6÷x 3=x 3 5. 已知xy >0,化简二次根式2x y x -的正确结果为( )A .yB .y -C .y -D .y --6. 化简112+--x x x 的结果是( ) A.x -11 B. x x --112 C. 112--x x D.11-x 7. 如图是某几何体的三视图,则该几何体的体积是( )A. 318B. 354C. 3108D. 32168. 不等式组⎩⎨⎧>+≤-- ,x x x x 3427)1(3的解集是( ) A .-2<x <4 B .x <4或x ≥-2 C .-2≤x <4 D .-2<x ≤49. 在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所 示:A .1.70,1.65B .1.70,1.70C .1.65,1.70D .3,410. 如图,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CE 交AD 于E ,点F 是AB 的中点,则S △AEF ∶S 四边形BDEF 为( )A .3∶4B .1∶2C .2∶3D .1∶310题图 12题图 13题图 11. “服务他人,提升自我”,五一学校积极开展四德教育服务活动,来自初三的5名同学(3男2女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是( )A .16B .15C .25D .3512. 如图,AB 是⊙O 的直径,∠AOC =110°,则∠D=( )A .25°B .35°C .55°D .70° 13. 如图,在平面直角坐标系中,抛物线221x y =经过平移得到抛物线x x y 2212-= ,其对称轴与两段抛物线弧所围成的阴影部分的面积为( )A .2B .4C .8D .1614. 如图,已知A 、B 是反比例函数(0,0)ky k x x=>>上的两点,BC x 轴,交y 轴于C ,动点P 从坐标原点O 出发,沿O A B C →→→匀速运动,终点为C ,过运动路线上任意一点P 作PM x ⊥轴于M ,PN y ⊥轴于N ,设四边形OMPN 的面积为S ,P 点运动的时间为t ,则S 关于t 的函数图象大致是( )第Ⅱ卷(非选择题 共78分)注意事项:1.请用钢笔或圆珠笔直接答在试卷上. 2.答卷前将密封线内的项目填写清楚.二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上。
新人教版九年级上第四次月考试卷
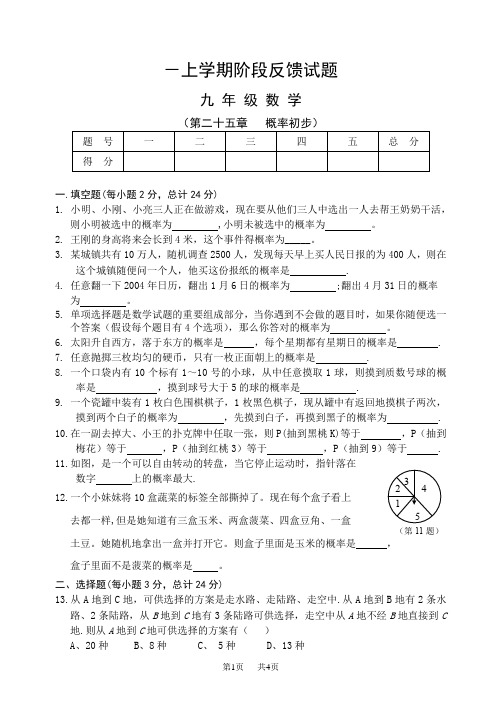
12 345 (第11题)-上学期阶段反馈试题九 年 级 数 学题 号 一 二 三 四 五 总 分 得 分一.填空题(每小题2分,总计24分)1. 小明、小刚、小亮三人正在做游戏,现在要从他们三人中选出一人去帮王奶奶干活,则小明被选中的概率为 ,小明未被选中的概率为 。
2. 王刚的身高将来会长到4米,这个事件得概率为_____。
3. 某城镇共有10万人,随机调查2500人,发现每天早上买人民日报的为400人,则在这个城镇随便问一个人,他买这份报纸的概率是 .4. 任意翻一下2004年日历,翻出1月6日的概率为 ;翻出4月31日的概率为 。
5. 单项选择题是数学试题的重要组成部分,当你遇到不会做的题目时,如果你随便选一个答案(假设每个题目有4个选项),那么你答对的概率为 。
6. 太阳升自西方,落于东方的概率是 ,每个星期都有星期日的概率是 .7. 任意抛掷三枚均匀的硬币,只有一枚正面朝上的概率是 .8. 一个口袋内有10个标有1~10号的小球,从中任意摸取1球,则摸到质数号球的概率是 ,摸到球号大于5的球的概率是 .9. 一个瓷罐中装有1枚白色围棋棋子,1枚黑色棋子,现从罐中有返回地摸棋子两次,摸到两个白子的概率为 ,先摸到白子,再摸到黑子的概率为 . 10.在一副去掉大、小王的扑克牌中任取一张,则P(抽到黑桃K)等于 ,P (抽到梅花)等于 ,P (抽到红桃3)等于 ,P (抽到9)等于 . 11.如图,是一个可以自由转动的转盘,当它停止运动时,指针落在数字 上的概率最大. 12.一个小妹妹将10盒蔬菜的标签全部撕掉了。
现在每个盒子看上去都一样,但是她知道有三盒玉米、两盒菠菜、四盒豆角、一盒土豆。
她随机地拿出一盒并打开它。
则盒子里面是玉米的概率是 , 盒子里面不是菠菜的概率是 。
二、选择题(每小题3分,总计24分)13.从A 地到C 地,可供选择的方案是走水路、走陆路、走空中.从A 地到B 地有2条水路、2条陆路,从B 地到C 地有3条陆路可供选择,走空中从A 地不经B 地直接到C 地.则从A 地到C 地可供选择的方案有( )A 、20种B 、8种C 、 5种D 、13种图25—A —2 14.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( ) A 、154 B 、31 C 、51 D 、152 15.下列事件发生的概率为0的是( )A 、随意掷一枚均匀的硬币两次,至少有一次反面朝上;B 、今年冬天黑龙江会下雪;C 、随意掷两个均匀的骰子,朝上面的点数之和为1;D 、一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域。
2014年中考数学模拟四试题
初中毕业生学业(升学)统一考试模拟四数学一、选择题(本大题共15小题,每小题3分,共45分.每小题选项中只有一个选项正确,请把你认为正确的选项填涂在相应的答题卡上)1.若23(2)0m n -++=,则2m n +的值为( )A .4-B .1-C .0D .42.2008北京奥运会火炬传递的路程约为13.7万公里.近似数13.7万是精确到( ) A .十分位 B .十万位 C .万位 D .千位3.某县为发展教育事业,加强了对教育经费的投入,2008年投入3 000万元,预计2010年投入5 000万元.设教育经费的年平均增长率为x ,根据题意,下面所列方程正确的是( ) A .23000(1)5000x +=B .230005000x =C .23000(1)5000x +=%D .23000(1)3000(1)5000x x +++=4.有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为( ) A .8人 B .9人C .10人D .11人5.已知方程20x bx a ++=有一个根是(0)a a -≠,则下列代数式的值恒为常数的是( )A .abB .ab C .a b + D .a b - 6.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( )7.把抛物线y =x 2+bx +c 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为 y =x 2-3x +5,则( )A .b =3,c =7B .b =6,c =3C .b =-9,c =-5D .b =-9,c =21 8.函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是( ) A .1k > B .1k < C .1k >- D .1k <-9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( )A. (4 cmB. 9 cmC.D. cm10.已知圆锥的母线长是5cm ,侧面积是15πcm 2,则这个圆锥底面圆的半径是( )A .1.5cmB .3cmC .4cmD .6cm 11.观察下列几何体,主视图、左视图和俯视图都是..矩形的是( )12.在正方形网格中,ABC △的位置如图所示,则cos B ∠的值为( )A .12BCD13.正方形ABCD 在坐标系中的位置如图所示,将正方形ABCD绕D 点顺时针方向旋转90后,B 点的坐标为( )A .(22)-,B .(41),C .(31),D .(40), 14.右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于该班40名同学一周参加体育锻 炼时间的说法错误..的是( ) A .极差是3 B .中位数为8C .众数是8D .锻炼时间超过8小时的有21人 15.在盒子里放有三张分别写有整式1a +、2a +、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是( ).A . 13B . 23C . 16D . 34二、填空题(本大题共5小题,每小题5分,共25分)16.计算:2933a a a -=-- . 17.写出含有字母x 、y 的五次单项式 (只要求写出一个).18.三角形的每条边的长都是方程2680x x -+=的根,则三角形的周长是 . 19.搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②,图③的方式串起来搭建,则串7顶这样的帐篷需要 根钢管.ABDC89107锻炼时间(小时)(第5题图)20.如图,AB 为⊙O 的弦,⊙O 的半径为5,OC ⊥AB 于点D ,交⊙O 于点C ,且CD =l ,则弦AB 的长是 . 三、解答题(本大题共7个小题,各小题分值见题号后,共80分)21.(本题8分)解不等式组12(1)532122x x x --⎧⎪⎨-<+⎪⎩≤,并把解集在数轴上表示出来.22.(本题8分)已知30x y -=,求 的值.23.(本题10分)如图,已知: ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC ∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.24.(本题12分)如图,已知CD 是△ABC 中AB 边上的高,以CD 为直径的⊙O 分别交CA 、CB 于点E 、F ,点G 是AD 的中点.求证:GE 是⊙O 的切线.25.(本题12分)阅读对人成长的影响是很大的.希望中学共有1500名学生,为了了解学生课外阅读的情况,就“你最喜欢的图书类别”(只选一项)随机调查了部分学生,并将调查结果统计后绘制成如下统计表和条形统计图.请你根据统计图表提供的信息解答下列问题: (1)这次随机调查了 名学生;(3分) (2)把统计表和条形统计图补充完整;(6分)(3)随机调查一名学生,恰好是最喜欢文学类图书的概率是多少?(3分))(2222y x y xy x y x -⋅+-+A B CE F G)26.(本题14分)已知关于x 的一元二次方程22(21)0x m x m +-+=有两个实数根1x 和2x .(1)求实数m 的取值范围;(6分)(2)当22120x x -=时,求m 的值.(8分)27.(本题16分)某物流公司的快递车和货车每天往返于A 、B 两地,快递车比货车多往返一趟.下图表示快递车距离A 地的路程y (单位:千米)与所用时间x (单位:时)的函数图象.已知货车比快递车早1小时出发,到达B 地后用2小时装卸货物,然后按原路、原速返回,结果比快递车最后一次返回A 地晚1小时.(1) 请在下图中画出货车距离A 地的路程y (千米)与所用时间x (时)的函数图象;(3分) (2) 求两车在途中相遇的次数(直接写出答案);(3分)(3) 求两车最后一次相遇时,距离A 地的路程和货车从A 地出发了几小时.(10分)。
2014届九年级数学上学期第二次月考试题 (新人教版 第80套)
湖北省十堰市茅箭区实验学校2014届九年级上学期第二次月考数学试题 新人教版一、选择题(本大题共10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是正确的)1.下列各式中,正确的是( )A .3=- B.3=- C3=± D3=± 2.下列一元二次方程有两个相等实数根的是( ) A. 032=+x B. 022=+x x C. 0)1(2=+x D. 0)1)(3(=-+x x 3.下列图形中,是中心对称图形但不是轴对称图形的是( )4.如图,若AB 是⊙0的直径,CD 是⊙O 的弦,∠ABD=58°, 则∠BCD=( )A. 116°B. 32°C. 58°D. 64°5.袋中有红球4个,白球若干个,它们只有颜色上的区别。
从袋中随机地取出一个球,如果取到白球的可能性较大,那么袋中白球的个数可能是( )A. 3个B. 不足3个C. 4个D. 5个或5个以上 6.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( ) A.5π B. 4π C.3π D.2π 7.若两个相似三角形的面积之比为1:4,则它们的周长之比为( ) A. 1:2 B. 1:4 C. 1:5 D. 1:168.若A (1,413y -),B (2,45y -),C (3,41y )为二次函数245y x x =+- 的图象上的三点,则1,y 2,y 3y 的大小关系是( )A .123y y y << B .213y y y << C .312y y y <<D .132y y y <<9.如左图,AB 是半圆直径,半径OC ⊥AB 于点O ,AD 平分∠CAB 分别交OC 于点E ,交弧BC 于点D ,连结CD 、OD ,给出以下四个结论:①S △A EC=2S △DEO ;②AC=2CD ;③线段OD 是DE 与DA 的比例中项;④.其中正确结论的序号( )A. ①④B. ①②④C. ①③④D. ③④10.如右图,已知二次函数y=ax 2+bx+c 的图象过A (-3,0),对称轴为直线x=-1,下列结论:①b2>4ac ;②2a+b=0;③a-b+c=0;④5a<b ;⑤a-b>m(am+b)(m ≠-1)其中正确的结论有( )A .1个B .2个C .3个D .4个二、填空题(本题共6小题,每小题3分,共18分)11.若二次根式2x -4有意义,则x 的取值范围是_______________.12.某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片,如果全班有x 名学生,根据题意,列出方程为_________________. 13.已知⊙O 的半径为5,圆心O 到直线AB 的距离为2,则⊙O 上有且只有_________ 个点到直线AB 的距离为3。
2014年中考数学复习基础训练4
2014年中考数学复习基础训练4 D子 _________ 枚.(用含n 的代数式表示)三、解答题一(本大题共3小题,每小题5分,共15分) 17、解不等式组⎩⎨⎧>+<-01231x x 18、解不等式组:12(31)5xxx x ⎧-<⎪⎨⎪--≥-⎩ 19、解不等式组:23 6 (23)......23x x x x +≤+⎧⎪⎨++>⎪⎩①②,并把解集在数轴上表示出来。
四、解答题二(本大题共3小题,每小题8分,共24分) 20、某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.已知小敏5月1日前不是该商店的会员.(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?(2)请帮小敏算一算,所购买商品的价格在什么范围内时,采用方案一更合算?21、今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A 、B 两水库各调出14万吨水支援甲、乙两地抗旱.从A 地到甲地50千米,到乙地30千米;从B 地到甲地60千米,到乙地45千米.⑴设从A 水库调往甲地的水量为x 万吨,完成下表 甲 乙 总计 Ax 14 B 14 总计151328⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)调入地水量调出地22、为庆祝建党90周年,某学校欲按如下规则组建一个学生合唱团参加我市的唱红歌比赛。
规则一:合唱团的总人数不得少于50人,且不得超过55人。
规则二:合唱团的队员中,九年级学生占合唱团总人数的12,八年级学生占合唱团总人数14,余下的为七年级学生。
请求出该合唱团中七年级学生的人数。
五、解答题三(本大题共3小题,每小题9分,共27分)23、我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼.有关成本、销售额见下表:(1) 2011年,王大爷养殖甲鱼20亩,桂鱼10亩.求王大爷这一年共收益多少万元?(收益=销售额-成本)(2) 2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2011年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?(3) 已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg.根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每载装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需全部饲料比原计划减少了2次.求王大爷原定的运输车辆每次可装载饲料多少kg?24、某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元. (1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?25、今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环保意识,节约用水,某校数学教师编造了一道应用题:月用水量(吨)单价(元/吨)不大于10吨1.5部分大于10吨不2大于m吨部分(20≤m≤50)大于m吨部分 3为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:(1)若某用户六月份用水量为18吨,求其应缴纳的水费;(2)记该户六月份用水量为x吨,缴纳水费y元,试列出y关于x的函数式;(3)若该用户六月份用水量为40吨,缴纳消费y元的取值范围为70≤y≤90,试求m的取值范围。
2014九年级人教版数学模拟试题及答案
2014九年级人教版数学模拟试题及答案xx为大家整理的2014九年级人教版数学模拟试题及答案的文章,供大家学习参考!更多最新信息请点击初三考试网一、选择题(共10小题,每小题3分,满分30分)1.(2014年四川巴中)﹣的相反数是( )A.﹣B.C. ﹣5D. 5分析:根据只有符号不同的两个数互为相反数,可得一个数的相反数.解:﹣的相反数是,故选:B.点评:本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.(2014年四川巴中)2014年三月发生了一件举国悲痛的空难事件﹣﹣马航失联,该飞机上有中国公民154名.噩耗传来后,我国为了搜寻生还者及找到失联飞机,在搜救方面花费了大量的人力物力,已花费人民币大约934千万元.把934千万元用科学记数法表示为( )元.A.9.34×102B. 0.934×103C. 9.34×109D. 9.34×1010分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|﹣1 B. m≥﹣1 C. m>﹣1且m≠1 D. m≥﹣1且m≠1分析:根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.解:根据题意得:,解得:m≥﹣1且m≠1.故选D.点评:本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.5.(2014年四川巴中)如图,两个大小不同的实心球在水平面靠在一起组成如图所示的几何体,则该几何体的左视图是( )A.两个外切的圆B. 两个内切的圆C. 两个内含的圆D. 一个圆分析:根据左视图是从左面看得到的视图,圆的位置关系解答即可.解:从左面看,为两个内切的圆,切点在水平面上,所以,该几何体的左视图是两个内切的圆.故选B.点评:本题考查了三视图的知识,左视图是从物体的左面看得到的视图.6.(2014年四川巴中)今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000.其中说法正确的有( )A.4个B. 3个C. 2个D. 1个分析:总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.解:这4万名考生的数学中考成绩的全体是总体;每个考生的数学中考成绩是个体;2000名考生的中考数学成绩是总体的一个样本,样本容量是2000.故正确的是①④.故选C.点评:本题考查了总体、个体、样本、样本容量的概念,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.7.(2014年四川巴中)下列汽车标志中既是轴对称图形又是中心对称图形的是( )A. B. C. D.分析:根据轴对称图形与中心对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.如果一个图形绕某一点旋转180°后能够与自身重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.解:A、是轴对称图形,不是中心对称图形.故本选项错误;B、不是轴对称图形,也不是中心对称图形.故本选项错误;C、是轴对称图形,也是中心对称图形.故本选项正确;D、是轴对称图形,不是中心对称图形.故本选项错误.故选C.点评:考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.8.(2014年四川巴中)在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )A. B. C. D.分析:根据题意作出直角△ABC,然后根据sinA= ,设一条直角边BC为5x,斜边AB为13x,根据勾股定理求出另一条直角边AC的长度,然后根据三角函数的定义可求出tan∠B.解:∵sinA= ,∴设BC=5x,AB=13x,则AC= =12x,故tan∠B= = .故选D.点评:本题考查了互余两角三角函数的关系,属于基础题,解题的关键是掌握三角函数的定义和勾股定理的运用.9.(2014年四川巴中)已知直线y=mx+n,其中m,n是常数且满足:m+n=6,mn=8,那么该直线经过( )A.第二、三、四象限B.第一、二、三象限C.第一、三、四象限D.第一、二、四象限分析:根据m+n=6,mn=8,可得出m与n为同号且都大于0,再进行选择即可. 解:∵mn=8>0,∴m与n为同号,∵m+n=6,∴m>0,n>0,∴直线y=mx+n经过第一、二、三象限,故选B.点评:本题考查了一次函数图象在坐标平面内的位置与m、n的关系.解答本题注意理解:直线y=mx+n所在的位置与m、n的符号有直接的关系.m>0时,直线必经过一、三象限.m0时,直线与y轴正半轴相交.n=0时,直线过原点;n0,故得abc>0.B.根据图知对称轴为直线x=2,即 =2,得b=﹣4a,再根据图象知当x=1时,y0;D.把二次函数y=ax2+bx+c化为顶点式,再求出平移后的解析式即可判断.解:A.由开口向下,可得a0,故得abc>0,故本选项错误;B.根据图知对称轴为直线x=2,即 =2,得b=﹣4a,再根据图象知当x=1时,y=a+b+c=a﹣4a+c=﹣3a+c0,故本选项错误;D.y=ax2+bx+c= ,∵ =2,∴原式= ,向左平移2个单位后所得到抛物线的解析式为,故本选项错误;故选:B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、选择题(每题3分,共24分)
11.如图,一圆弧过方格的格点A、B、C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是.
(第11题) (第12题)
12.已知:如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以cm/s的速度在⊙O上按 逆时针方向运动一周回到点A立即停止.当点P运动的时间为______s时,BP与⊙O相切.
请你根据所构造的图形提出一个结论,并证明之.
(3)如图(3),其中AB是圆O的直径,AC是弦,D是的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
(1) (2)
(3)
(第24题)
25.小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图(1)),它的侧面边缘上有两条圆弧(如图(2)),其中顶部圆弧AB的圆心O1在竖直边缘AD上,另一条圆弧BC的圆心O2在水平边缘DC的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的 问题(玻璃钢材料的厚度忽略不计,π取3.141 6).
(2)扇形O1AB的面积= ×84.8×61≈2 586.4(cm2).
扇形O2BC的面积=×π×402=400π≈1 256.6(cm2).梯形O1BO2D的面积=×(29+40)×60=2 070(cm2).
∴ 遮雨罩一个侧面的面积=扇形O1AB的面积+梯形O1BO2D的 面积-扇O2BC形的面积=
所以当∠BAC=30°时,点C与点E重合.
(1)
(2)
(第24题)
26.由题意知BE=60,AE=50,
连接O1B,设弧AB的半径为R.
在Rt△O1BE中,由勾股定理得R2=602+(R-50)2.
解得R=61.
由sin∠BO1E==,得∠BO1E≈79.61°
∴ 弧AB的长=×π×61≈84.8(cm).
(第19题)
20.如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.求证:
(1)△ABC是等边三角形;
(2)AE=CE.
(第20题)
21.如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
(1)试探究AE与⊙O的位置关系,并说明理由;
专题复习训练卷四 图形的认识
(时间:60分钟 满分:100分)
一、填空题(每题2分,共20分)
1.下列说法中,正确的是().
A.经过三个点一定可以作圆
B.任意一 个圆一定有内接三角形,并且只有一个内接三角形
C.任意一个三角形一定有一个外接圆,并且只有一个外接圆
D.三角形的外心到三角形各边的距离都相等
∴(x-6)2+(x-4)2=102.
解得x1=12,x2=-2(不合题意,舍去).
∴AD=12.
24. (1)弦、弧、弓形、求弓形的面积等.
(2)情形1:如图(1),AB为弦,CD为垂直于弦AB的直径.
结论:略(垂径定理的结论之一).
证明:略
情形2:如图(2),AB为弦,CD为弦,且AB与CD在圆内相交于点P.
∴D是AB中点.
∵AE=AD-cos∠A=AD,
∵AE=AB=AC,
∴EC=3AE.
∴AE=CE.
21. (1)AE与⊙O相切.理由略.
(2)①选择a,b,c,或其中2个
②解答举例:
若选择a,b,c.
由CD∥OA,= ,得r=.
若选择a,b.
在Rt△OCE中,由勾股定理,得a2+r2=(b+r)2,得r=.
∴S阴影=S扇形AOD==.
23.(1)连结OB和OC.
(第23题)
∵OE⊥BC,
∴BE=CE.
∵OE= BC,
∴∠BOC=90°.
∴∠BAC=45°.
(2)∵AD⊥BC,
∴∠ADB=∠ADC=90°.
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,∠BAG=∠BAD,∠CAF=∠CAD.
∴∠BAG+∠CAF=∠BAD+∠CAD=
∠BAC=45°.
∴∠GAF=∠BAG+∠CAF+∠BAC=
90°.
∴四边形AFHG是正方形.
(3)由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.
设AD的长为x,则BH=GH-GB=x-6,
CH=HF-CF=x- 4.
在Rt△BCH中,BH2+CH2=BC2,
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图(1),在圆O所在平面上,放置一条直线(和圆O分别交 于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?
(2)如图(2),在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线和(与圆O分别交于点A、B,与圆O分别交于点C、D).
∴BC=10米.
∴ △ABC外接圆的半径为5米.
∴ 小明家圆形花坛的面积为25π平方米.
20. (1)连接OD.
∵ 切线DE⊥AC,
∴OD∥AC.
∴ ∠BDO=∠A.
由OB=OD得∠OBD=∠ODB,
∴ ∠OBD=∠A.
∴BC=AC.
又AB=AC,
∴ △ABC是等边三角形.
(2)连接CD,则CD⊥AB.
2 586.4+2 070-1 256.6≈3 400(cm2)
2.点P在⊙O内,OP=2 cm,若⊙O的半径是3 cm,则过点P的最短弦的长度为().
A.1 cmB.2 cm
C.cm D.2cm
3.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16 m,则拱高CD为( ).
A.4mB.6mC.8mD.10m
(第3题)(第4题)
4.如图 ,AB是⊙O的直径,若∠C=26°,则
(1)在不添加任何辅助线的情况下,写出图中所有的全等三角形;
(2)求阴影部分的面积(结果保留π).
(第22题)
23.如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,OE= BC.
(1)求∠BAC的度数;
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形;
结论:PA·PB=PC·PD.
证明:略.
(3)若点C和点E 重合,则由圆的对称性,知点C和点D关于直径AB对称.
设∠BAC=x,则∠BAD=x,
∠ABC=90°-x.
又D是的中点,所以2∠CA D=∠CAD+∠ACD=180°-∠ABC,
即2·2x=180°-(90°-x).
解得x=∠BAC=30°.
(第18题)
三、解答题(每题8分,共56分)
19.小明家的房前有一块矩形的空地,空地上有三棵 树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.
(1)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);
(2)若△ABC中AB=8米, AC=6米,∠BAC=90 °,试求小明家圆形花坛的面积.
A.θ=α+βB.θ=2α+2β
C.α+β+θ=180°D.α+β+θ=360°
7.如图,⊙O的直径AB长为10, 弦AC长为6,∠ACB的平分线交⊙O于D,则CD的长为().
A. 7 B. C. D. 9
(第7题) (第8题)
8.如图,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB 的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120 °;④DC=R.其中,使得BC=R的有().
22. (1)△ACO≌△BCO,△APC≌△BPC,△PAO≌△PBO
(2)∵PA、PB为⊙O的切线,
∴PO平分∠APB,PA=PB,∠PAO=90°.
∴PO⊥AB.
∴ 由圆的对称性可知:S阴影=S扇形AOD.
∵ 在Rt△PAO中,∠APO=∠APB=×60°=30°,
∴ ∠AOP=90°-∠APO=60°.
13.已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC只有一个公共点,那么x的取值范围是______.
14.两圆的直径分别是 和 ,圆心距为d,当两圆相交时,d的整数值为______.
15.如图,两个半圆,大半圆中,长为16cm的弦AB平行于直径CD,且与小半圆相切,则图中阴影部分的面积为______cm2.
(第17题)
18.如图,ΔABC内接于⊙O,∠B=90º,AB=BC,D是⊙O上与点B关于圆心O成中心对称的点,P是BC边上一点,连结AD、DC、AP.已知AB=8,CP=2,Q是线段AP上一动点,连结BQ并延长交四边形ABCD的一边于点R,且满足AP=BR,则
的值为 _______________.
∠ABD等于( ).
A.36°B.38°C.52°D.64°
5.如图,P是⊙O外一点,PA、PB切⊙O于点A、B,点C在优弧AB上,若∠P=68°,则∠ACB等于( ).
A.22°B.34°C.56 °D.68°
(第5题)(第6题)
6.如图,⊙O中,AB、AC是弦,O在∠BAC的内部,∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系中,正确的是().
A.①②B.①③④
C.②③④D.①②③④
9.如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且OA与平行的直线与⊙O有公共点,设OP=x,则x的取值范围是().
A. 0≤x≤B.-≤x≤
C.-1≤x≤1 D.x>
(第9题)
10.如图,C、D是以线段AB为公 共弦的两条圆弧的中点,AB=4,E、F分别是线段CD、AB上的动点,设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是().
