初三数学培优资料
初三数学培优资料1

初三数学培优资料1(共44页) -本页仅作为预览文档封面,使用时请删除本页-初三数学培优资料第一讲:一元二次方程的根一、内容提要1.一元二次方程ax2+bx+c=0(a≠0)的实数根,是由它的系数a, b, c的值确定的.求根公式是:x=a acb b24 2-±-. (b2-4ac≥0)2.根的判别式①实系数方程ax2+bx+c=0(a≠0)有实数根的充分必要条件是:b2-4ac≥0.②有理系数方程ax2+bx+c=0(a≠0)有有理数根的判定是:b2-4ac是完全平方式⇔方程有有理数根.③整系数方程x2+px+q=0有两个整数根⇔p2-4q是整数的平方数.3.设x1, x2是ax2+bx+c=0的两个实数根,那么①ax12+bx1+c=0 (a≠0,b2-4ac≥0), ax22+bx2+c=0 (a≠0, b2-4ac≥0);②x1=aacbb242-+-,x2=aacbb242---(a≠0, b2-4ac≥0);③韦达定理:x1+x2=ab-, x1x2=ac(a≠0, b2-4ac≥0).4.方程整数根的其他条件整系数方程ax2+bx+c=0 (a≠0)有一个整数根x1的必要条件是:x1是c的因数.特殊的例子有:C=0⇔x1=0 , a+b+c=0⇔x1=1 ,a-b+c=0⇔x1=-1.二、例题例1.已知:a, b, c是实数,且a=b+c+1.求证:两个方程x2+x+b=0与x2+ax+c=0中,至少有一个方程有两个不相等的实数根.例2.已知首项系数不相等的两个方程:(a-1)x2-(a2+2)x+(a2+2a)=0和 (b-1)x2-(b2+2)x+(b2+2b)=0 (其中a,b为正整数)有一个公共根. 求a, b的值.例3. 已知:m, n 是不相等的实数,方程x2+mx+n=0的两根差与方程y2+ny+m=0的两根差相等.求:m+n 的值.例4. 若a, b, c 都是奇数,则二次方程ax 2+bx+c=0(a ≠0)没有有理数根.例5.求证:对于任意一个矩形A ,总存在一个矩形B ,使得矩形B 与矩形A 的周长比和面积比都等于k(k ≥1).例6. k 取什么整数值时,下列方程有两个整数解?①(k 2-1)x 2-6(3k -1)x+72=0 ; ②kx 2+(k 2-2)x -(k+2)=0.三、练习1. 写出下列方程的整数解:① 5x 2-3x=0的一个整数根是___.② 3x 2+(2-3)x -2=0的一个整数根是___.③ x 2+(5+1)x+5=0的一个整数根是___.2. 方程(1-m )x 2-x -1=0 有两个不相等的实数根,那么整数m 的最大值是____.3. 已知方程x 2-(2m -1)x -4m+2=0 的两个实数根的平方和等于5,则m=___.4. 若x ≠y ,且满足等式x 2+2x -5=0 和y 2+2y -5=0.那么yx 11 =___.(提示:x, y 是方程z 2+5z -5=0 的两个根.)5. 如果方程x 2+px+q=0 的一个实数根是另一个实数根的2倍,那么p, q 应满足的关系是:___________.6. 若方程ax 2+bx+c=0中a>0, b>0, c<0. 那么两实数根的符号必是______.7. 如果方程mx 2-2(m+2)x+m+5=0 没有实数根,那么方程(m -5)x 2-2mx+m=0实数根的个数是( ).(A)2 (B )1 ( C )0 (D )不能确定8. 当a, b 为何值时,方程x 2+2(1+a)x+(3a 2+4ab+4b 2+2)=0 有实数根?9.10.9. 两个方程x 2+kx -1=0和x 2-x -k=0有一个相同的实数根,则这个根是( )(A)2 (B )-2 (C )1 (D )-110.已知:方程x 2+ax+b=0与x 2+bx+a=0仅有一个公共根,那么a, b 应满足的关系是:_________11. 已知:方程x 2+bx+1=0与x 2-x -b=0有一个公共根为m ,求:m ,b 的值.12. 已知:方程x 2+ax+b=0的两个实数根各加上1,就是方程x 2-a 2x+ab=0的两个实数根.试求a, b 的值或取值范围.13. 已知:方程ax 2+bx+c=0(a ≠0)的两根和等于s 1,两根的平方和等于s 2, 两根的立方和等于s 3.求证:as 3+bs 2+cs 1=0.14. 求证:方程x 2-2(m+1)x+2(m -1)=0 的两个实数根,不能同时为负.(可用反证法)15. 已知:a, b 是方程x 2+mx+p=0的两个实数根;c, d 是方程x 2+nx+q=0的两个实数根. 求证:(a -c )(b -c)(a -d)(b -d)=(p -q)2.16. 如果一元二次方程的两个实数根的平方和等于5,两实数根的积是2,那么这个方程是:__________.17. 如果方程(x -1)(x 2-2x+m)=0的三个根,可作为一个三角形的三边长,那么实数m 的取值范围是 ( )(A ) 0≤m ≤1 (B )m ≥43 (C )43<m ≤1 (D )43≤m ≤118. 方程7x 2-(k+13)x+k 2-k -2=0 (k 是整数)的两个实数根为α,β且0<α<1,1<β<2,那么k 的取值范围是( )(A )3<k<4 (B)-2<k<-1 (C) 3<k<4 或-2<k<-1 (D )无解第二讲:未知数比方程个数多的方程组解法一、内容提要1、在一般情况下,解方程或方程组,未知数的个数总是与方程的个数相同的,但也有一些方程或方程组,所含的未知数的个数多于方程的个数,包括在列方程解应用题时,引入的辅助未知数.2、解这类方程或方程组,一般有两种情况:一是依题意只求其特殊解,如整数解,或几个未知数的和(积)等,无需求出所有的解;二是在实数范围内,可运用其性质,增加方程或不等式的个数. 例如,利用取值范围,非负数的性质等.二、例题解析:例1. 在实数范围内,解下列方程或方程组: ①0211122=++--+-y x x x ; ②x 2+xy+y 2-3x -3y+3=0; ③⎩⎨⎧=-=++4222z xy z y x例2. 一个自然数除以4余1,除以5余2,除以11余4,求适合条件的最小自然数.例3. 有甲,乙,丙三种货物.若购买甲3件,乙7件,丙1件共需元;若购买甲4件,乙10件,丙1件共需元.问购买甲、乙、 丙各1件共需几元?例4. 甲、乙两车分别从A、B两站同时出发,相向而行,当甲车走完全程的一半时,乙车距A 站24公里;当乙车走完全程的一半时,甲车距B站15公里.求A、B两站的距离.三、巩固练习:1. 甲,乙,丙,丁,戊做一件工程,甲,乙,丙合作需小时,甲,丙戊合作需5小时,甲,丙,丁合作需6小时,乙,丁,戊合作需4小时.问五人合作需几小时?2. 服装厂向百货商店购买甲、乙两种布,共付元,售货员收款时发现甲、乙两种布单价对调了,退给厂方元,厂方把这元又买了甲、乙两种布各1尺.问服装厂共买布几尺?3. 两只船分别从河的两岸同时对开,速度保持不变,第一次相遇时,距河的一岸700米,继续前进到达对岸后立即返回,第二次相遇时,距河的另一岸400米,求河的宽.4. 游泳运动员自闽江逆流而上,在解放大桥把水壶丢失,继续前游20分钟才发现,于是返回追寻,在闽江大桥处追到,已知两桥相距1000米,求水流的速度.5. 已知长方形的长和宽均为整数,且周长的数值与面积的数值相等.问这长方形的长和宽各是多少?6. 有一队士兵,若排成3列纵队,则最后一行只有1人;若排成5列纵队,则最后一行只有7. 人;排成7列纵队,则最后一行只有6人.问这队士兵最少是几人?7. 求下列方程的实数解:①0-+xx+-y1=13122+② 5x 2+6xy+2y 2-14x -8y+10=0③ (x 2+1)(y 2+4)=8xy④ 052312=+-+-+y x y x8. 一件工程,如果甲单独完成所需的时间是乙,丙合做,完成这件工程所需时间的a 倍;如果乙单独完成所需的时间是甲,丙合做,完成这件工程所需时间的b 倍.(其中b>a>1),那么丙单独完成所需的时间是甲,乙合做,完成这件工程所需时间的多少倍?9. 甲,乙两车从东站,丙,丁两车从西站,同时相向而行.甲车行120公里遇丙车,再行20公里遇丁车;乙车在离西站126公里处遇丙车,在中途遇丁车.求东西两站的距离.10. 三辆车A ,B ,C 从甲到乙.B 比C 迟开5分钟,出发后20分钟追上C ;A 比B 迟开10分钟,出发后50分钟追上C.求A 出发后追上B 的时间.11. 学生若干人住宿,如果每间4人,有20人没房住;如果每间8人,则有一间不满也不空.求学生人数.12.一只船从甲码头顺水航行到乙码头用5小时,由乙码头逆水航行到甲码头需7小时。
初三数学培优资料
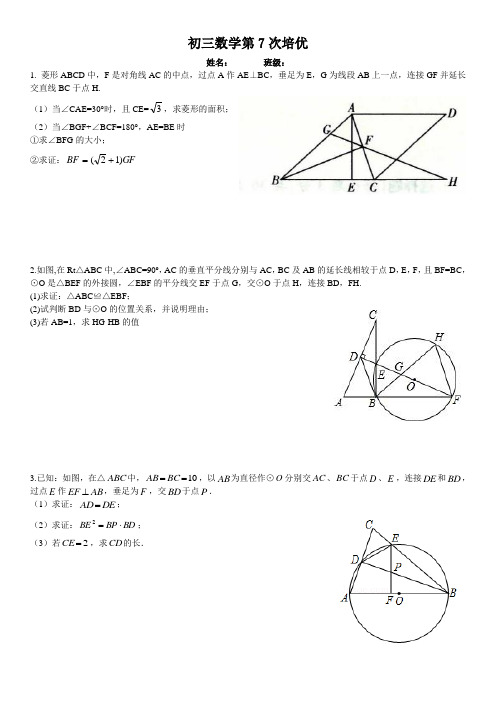
初三数学第7次培优 姓名: 班级:1. 菱形ABCD 中,F 是对角线AC 的中点,过点A 作AE ⊥BC ,垂足为E ,G 为线段AB 上一点,连接GF 并延长交直线BC 于点H.(1)当∠CAE=30°时,且CE=3,求菱形的面积;(2)当∠BGF+∠BCF=180°,AE=BE 时①求∠BFG 的大小;②求证:GF BF )12(+=2.如图,在Rt △ABC 中,∠ABC=90º,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相较于点D ,E ,F ,且BF=BC ,⊙O 是△BEF 的外接圆,∠EBF 的平分线交EF 于点G ,交⊙O 于点H ,连接BD ,FH.(1)求证:△ABC ≌△EBF ;(2)试判断BD 与⊙O 的位置关系,并说明理由;(3)若AB=1,求HG·HB 的值3.已知:如图,在△ABC 中,10==BC AB ,以AB 为直径作⊙O 分别交AC 、BC 于点D 、E ,连接DE 和BD ,过点E 作AB EF ⊥,垂足为F ,交BD 于点P .(1)求证:DE AD =;(2)求证:BD BP BE ⋅=2;(3)若2=CE ,求CD 的长.4.定义:用函数的最值来判定参数的取值范围,这种方法称为“最值判定法”例如:当21≤≤-x 时,0≤+a x 恒成立,求a 的取值范围。
可令y=x+a ,因为y 随x 的增大而增大,所以当x 取最大值2时,对应的y 取最大值2+a ,由02≤+a ,得2-≤a 。
(1)①对于反比例函数x y 2-=,当1-y ,)0(0≤>≤<时a a x 恒成立,求a 的取值范围。
②当2≥x 时,32≤--b x 恒成立,求b 的最小值。
(2)若当11≤≤-x 时,不等式x ax x ≤-+-32恒成立,求实数a 的取值范围。
(3)若当11≤≤-x 时,二次函数y=3)1(2--+-x a x 有最大值a ,求实数a 的值。
初三数学培优

一、补成三角形1.补成三角形 例1.如图1,已知E 为梯形ABCD 的腰CD 的中点;证明:△ABE 的面积等于梯形ABCD 面积的一半。
2.补成等腰三角形例2 如图2.已知∠A =90°,AB =AC ,∠1=∠2,CE ⊥BD ,求证:BD=2CE3.补成直角三角形例3.如图3,在梯形ABCD 中,AD ∥BC ,∠B +∠C =90°,F 、G 分别是AD 、BC 的中点,若BC =18,AD =8,求FG 的长。
4.补成等边三角形例4.图4,△ABC 是等边三角形,延长BC 至D ,延长BA 至E ,使AE =BD ,连结CE 、ED 。
证明:EC =ED二、补成特殊的四边形1.补成平行四边形例5.如图5,四边形ABCD 中,E 、F 、G 、H 分别是AB 、CD 、AC 、BD的中点,并且E 、F 、G 、H 不在同一条直线上,求证:EF 和GH 互相平分。
2.补成矩形例6.如图6,四边形ABCD 中,∠A =60°,∠B =∠D =90°,AB =200m ,CD =100m ,求AD 、BC 的长。
图图63.补成菱形例7.如图7,凸五边形ABCDE 中,∠A=∠B =120°,EA =AB =BC =2,CD =DE =4,求其面积4.补成正方形例8.如图8,在△ABC 中,AD ⊥BC 于D ,∠BAC =45°,BD =3,DC =2。
求△ABC 的面积。
5.补成梯形例9.如图9,已知: G 是△ABC 中BC 边上的中线的中点,L 是△ABC 外的一条直线,自A 、B 、C 、G 向L 作垂线,垂足分别为A 1、B 1、C 1、G 1。
求证:GG 1=41(2AA 1+BB 1+CC 1)。
图7图8图9。
初三数学培优资料

一、解答题1.如图所示,圆O 是ABC 的外接圆,BAC ∠与ABC ∠的平分线相交于点I ,延长AI 交圆O 于点D ,连结BD DC 、.(1)求证:BD DC DI ==;(2)若圆O 的半径为10cm ,120BAC ∠=︒,求BDC 的面积.2.如图,已知D,E 分别为△ABC 的边AB,BC 上两点,点A,C,E 在⊙D 上,点B,D 在⊙E 上.F 为弧BD 上一点,连接FE 并延长交AC 的延长线于点N ,交AB 于点M,,1)若∠EBD 为α,请将∠CAD 用含α的代数式表示;,2)若EM=MB ,请说明当∠CAD 为多少度时,直线EF 为⊙D 的切线;,3)在(2)的条件下,若3MN MF的值.3.四边形ABCD 为平行四边形,AC 为对角线,∠BAC =60°,CE 、BF 分别∠ACB 、∠ABC 的角平分线,CE 、BF 相交于G ;(1)求∠CGF 的度数;(2)求证:BE+CF =BC ;(3)若BE :CF =1:2,EG =7ABCD 的面积.5.已知如图平面直角坐标系中,点O是坐标原点,矩形ABCO是顶点坐标分别为A,3,0,,B,3,4,,C,0,4).点D在y轴上,且点D的坐标为(0,,5),点P是直线AC上的一动点.,1)当点P运动到线段AC的中点时,求直线DP的解析式(关系式);,2)当点P沿直线AC移动时,过点D,P的直线与x轴交于点M.问在x轴的正半轴上是否存在使△DOM与△ABC 相似的点M?若存在,请求出点M的坐标;若不存在,请说明理由;,3)当点P沿直线AC移动时,以点P为圆心、R,R,0)为半径长画圆.得到的圆称为动圆P.若设动圆P的半径,过点D作动圆P的两条切线与动圆P分别相切于点E,F.请探求在动圆P中是否存在面积最小的四边形长为AC2DEPF?若存在,请求出最小面积S的值;若不存在,请说明理由.4.我们规定:有一组邻边相等,且这组邻边的夹角为60°的凸四边形叫做“准筝形”.如图1,四边形ABCD中,若AB=AD,∠A=60°,则四边形ABCD是“准筝形”,,1)如图2,CH是△ABC的高线,∠A=45°,∠ABC=120°,AB=2.求CH,,2)在(1)条件下,设D是△ABC所在平面内一点,当四边形ABCD是“准筝形”时,请直接写出四边形ABCD的面积;,3)如图3,四边形ABCD中,BC=2,CD=4,AC=6,∠BCD=120°,且AD=BD,试判断四边形ABCD是不是“准筝形”,并说明理由.参考答案1.(1)证明见解析(2)【解析】(1)证明:AI 平分BAC ∠BAD DAC BD DC ∴∠=∠∴=, BI 平分ABC ABI CBI ∠∴∠=∠,BAD DAC DBC DAC ∠=∠∠=∠,BAD DBC ∴∠=∠,又DBI DBC CBI DIB ABI BAD ∠=∠+∠∠=∠+∠,DBI DIB BDI ∴∠=∠∴,为等腰三角形BD ID BD DC DI ∴=∴==,(2)解:当120BAC ∠=︒时,ABC 为钝角三角形,∴圆心O 在ABC 外,连结OB OD OC 、、,2120DOC BOD BAD ∴∠=∠=∠=︒,60DBC DCB ∴∠=∠=︒,∴BDC 为正三角形.又知10cm OB =,2sin 602102BD OB ∴=︒=⨯⨯=224BDC S ∴==答:BDC 的面积为2.(1)根据角平分线的性质、圆周角定理、三角形的外角定理即得结论;(2)连结OB OD OC 、、,证得BDC 为正三角形,先根据三角函数求得BD 的长,在根据等边三角形的面积公式即可求出结果.2.(1)3902α-;(2)45°;(3) 【解析】分析:,1)根据同圆的半径相等和等边对等角得:∠EDB=∠EBD=α,∠CAD=∠ACD,∠DCE=∠DEC=2α,再根据三角形内角和定理可得结论;,2)设∠MBE=x ,同理得:∠EMB=∠MBE=x ,根据切线的性质知:∠DEF=90°,所以∠CED+∠MEB=90°,同理根据三角形内角和定理可得∠CAD=45°,,3)由(2)得:∠CAD=45°;根据(1)的结论计算∠MBE=30°,证明△CDE 是等边三角形,得求,根据三角形内角和及等腰三角形的判定得:详解:(1)连接CD,DE,在⊙E 中,∵ED=EB,∴∠EDB=∠EBD=α,∴∠CED=∠EDB+∠EBD=2α,在⊙D 中,∵DC=DE=AD,∴∠CAD=∠ACD,∠DCE=∠DEC=2α,△ACB 中,∠CAD+∠ACD+∠DCE+∠EBD=180°, ∴∠CAD=018032α-=03902α-, ,2)设∠MBE=x,∵EM=MB,∴∠EMB=∠MBE=x,当EF 为⊙D 的切线时,∠DEF=90°,∴∠CED+∠MEB=90°,∴∠CED=∠DCE=90°,x,△ACB 中,同理得,∠CAD+∠ACD+∠DCE+∠EBD=180°,∴2∠CAD=180°,90∴=90∴,∴∠CAD=45°,,3)由(2)得:∠CAD=45°,由(1)得:∠CAD=018032MBE -∠, ∴∠MBE=30°,∴∠CED=2∠MBE=60°,∵CD=DE,∴△CDE 是等边三角形,∴Rt △DEM 中,∠∴△ACB 中,∠NCB=45°+30°=75°,△CNE 中,∠CEN=∠BEF=30°,∴∠CNE=75°,∴∠CNE=∠NCB=75°,∴∴MNMF =NE EM MF +点睛:本题考查三角形内角和定理、三角形的外角的性质、等腰三角形的性质和判定等知识,解题的关键是学会利用三角形角之间的关系确定边的关系,学会构建方程解决问题,属于中考常考题型.3.(1)60°;(2)见解析;(3)【解析】【分析】(1)由角平分线的性质和三角形内角和定理可求解;(2)在BC 边上截取CN =CF ,连接GN ,由“SAS”可证△CGN ≌△CG ,可得∠CGN =∠CGF =60°,可得∠BGN =∠BGE ,由“ASA”可证△BGN ≌△BGE ,可得BE =BN ,可得结论;(3)设BE =a ,CF =2a ,AE =c ,AF =b ,由相似三角形的性质列出方程组,求出7854a c b c ⎧=⎪⎪⎨⎪=⎪⎩,通过证明△ABF ∽△GEB ,可得EG BG BE AF AB BF==,可求c 的值,可得AB ,AC ,BC 的值,即可求平行四边形ABCD 的面积.【详解】解:(1)∵∠BAC =60°,∴∠ABC+∠ACB =120°,∵CE 、BF 分别∠ACB 、∠ABC 的角平分线,∴∠GBC+∠GCB =12×120°=60°, ∴∠BGC =120°,∴∠CGF =60°;故答案为:60°.(2)在BC 边上截取CN =CF ,连接GN ,如图所示:在△CGN 和△CGF 中,CN CF NCG FCG CG CG =⎧⎪∠=∠⎨⎪=⎩,∴△CGN ≌△CGF (SAS ),∴∠CGN =∠CGF ,GF =GN∵∠BGC =120°,∠CGF =60°,∴∠BGN =60°,∠EGF =120°,∴∠BGE =360°﹣120°﹣120°﹣60°=60°,∴∠BGN =∠BGE ,在△BGN 和△BGE 中,BGN BGE BG BGGBN GBE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△BGN ≌△BGE (ASA ),∴BE =BN ,EG =GN∴EG =GN =GF∵BC =BN+CN =BE+CF ,∴BE+CF =BC ;(3)如图,延长CE ,DA 交于点H ,延长BF 交AD 于点P ,过点B 作BM ⊥AC 于M ,∵BE :CF =1:2,∴设BE =a ,CF =2a ,由(2)可知BC =BE+CF =a+2a =3a ,∵四边形ABCD 是平行四边形∴AD ∥BC∴∠H =∠BCE ,∠APB =∠FBC ,∵CE 、BF 分别∠ACB 、∠ABC 的角平分线∴∠ACE =∠BCE ,∠ABF =∠CBF∴∠H =∠ACE ,∠APB =∠ABF∴AH =AC ,AP =AB ,设AE =c ,AF =b ,∴AB =c+a ,AC =b+2a ,∵AH ∥BC∴△AHE∽△BCE∴AH BC AE BE=∴3 AC a AE a=∴b+2a=3c①∵AH∥BC∴△APF∽△CBF∴32 AP BC a AF CF a==∴32 ABb=∴c+a=32b②由①②组成方程组2332b a cc a b+=⎧⎪⎨+=⎪⎩解得:7854a cb c ⎧=⎪⎪⎨⎪=⎪⎩∴AB=158c,AC=3c,由(2)可知FG=EG=∵∠EGB=∠BAC=60°,∠ABF=∠GBE,∴△ABF∽△GEB,∴EG BG BEAF AB BF==781548cBGBG GF c c==+∴BG=c=8∴a=7,b=10∴AB=15,AC=24,BC=21,∵∠BAC=60°,BM⊥AC∴AM =12AB =152,BM =2,∴S ▱ABCD =2S △ABC =2×12×2×24=故答案为:【点睛】本题考查了平行四边形的性质,全等三角形的判断与性质,相似三角形的判断与性质. 属于四边形综合题,利用相似三角形的性质列出方程组是解决本题的关键.4.(1)y=143x,5;(2)若△DOM 与△CBA 相似,则点M 的坐标为(154,0)或(203,0,,,3,√22914【解析】试题分析:(1)只需先求出AC 中点P 的坐标,然后用待定系数法即可求出直线DP 的解析式.(2)由于,DOM 与,ABC 相似,对应关系不确定,可分两种情况进行讨论,利用三角形相似求出OM 的长,即可求出点M 的坐标.(3)易证S △PED =S △PFD .从而有S 四边形DEPF =2S △PED =DE .由,DEP=90°得DE 2=DP 2﹣PE 2=DP 2﹣.根据“点到直线之间,垂线段最短”可得:当DP,AC 时,DP 最短,此时DE 也最短,对应的四边形DEPF 的面积最小.借助于三角形相似,即可求出DP,AC 时DP 的值,就可求出四边形DEPF 面积的最小值.解:(1)过点P 作PH,OA ,交OC 于点H ,如图1所示.,PH,OA ,,,CHP,,COA.,==.,点P是AC中点,,CP=CA.,HP=OA,CH=CO.,A(3,0)、C(0,4),,OA=3,OC=4.,HP=,CH=2.,OH=2.,PH,OA,,COA=90°,,,CHP=,COA=90°.,点P的坐标为(,2).设直线DP的解析式为y=kx+b,,D(0,﹣5),P(,2)在直线DP上,,,,直线DP的解析式为y=x﹣5.(2),若,DOM,,ABC,图2(1)所示,,,DOM,,ABC,,=.,点B坐标为(3,4),点D的坐标为(0.﹣5),,BC=3,AB=4,OD=5.,=.,OM=.,点M在x轴的正半轴上,,点M的坐标为(,0),若,DOM,,CBA,如图2(2)所示,,,DOM,,CBA,,=.,BC=3,AB=4,OD=5,,=.,OM=.,点M在x轴的正半轴上,,点M的坐标为(,0).综上所述:若,DOM与,CBA相似,则点M的坐标为(,0)或(,0).(3),OA=3,OC=4,,AOC=90°,,AC=5.,PE=PF=AC=.,DE、DF都与,P相切,,DE=DF,,DEP=,DFP=90°.,S△PED=S△PFD.,S四边形DEPF=2S△PED=2×PE•DE=PE•DE=DE.,,DEP=90°,,DE2=DP2﹣PE2.=DP2﹣.根据“点到直线之间,垂线段最短”可得:当DP,AC时,DP最短,此时DE取到最小值,四边形DEPF的面积最小.,DP,AC,,,DPC=90°.,,AOC=,DPC.,,OCA=,PCD,,AOC=,DPC,,,AOC,,DPC.,=.,AO=3,AC=5,DC=4﹣(﹣5)=9,,=.,DP=.,DE2=DP2﹣=()2﹣=.,DE=,,S四边形DEPF=DE=.,四边形DEPF面积的最小值为.点评:本题考查了相似三角形的判定与性质、用待定系数法求直线的解析式、切线长定理、勾股定理、垂线段最短等知识,考查了分类讨论的思想.将求DE的最小值转化为求DP的最小值是解决第3小题的关键.另外,要注意“,DOM与,ABC相似”与“,DOM,,ABC“之间的区别.5.(1)见解析;(2)2【解析】【分析】(1)连接OB,由OP⊥OA,得∠A+∠APO=90°;由CP=CB,得∠CBP=∠CPB;再由OA=OB,得∠A=∠OBA,而∠CPB=∠APO,整理变形可得∠OBC=90°,即BC是⊙O 的切线;(2)设BC=x,则PC=x,在Rt△OBC中,由勾股定理可得关于x的方程52+x2=(x+3)2,解方程即可求出CB的长;(3)作CD⊥BP于D,由PC=PB,得PD=BD=12PB,易证△AOP∽△PCD,则由1210 9S S =,可得209AOPPCDSS=,即22209OACD=,由此可求CD的长,再在Rt△BCD中,按照正切定义求出tan∠CBP即可.【详解】(1)证明:连接OB,如图,∵OP⊥OA,∴∠AOP=90°,∴∠A+∠APO=90°,∵CP=CB,∴∠CBP=∠CPB,而∠CPB=∠APO,∴∠APO=∠CBP,∵OA=OB,∴∠A=∠OBA,∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,∴OB⊥BC,∴BC是⊙O的切线;(2)解:设BC=x,则PC=x,在Rt△OBC中,OB=OA=5,OC=CP+OP=x+3,∵OB2+BC2=OC2,∴52+x2=(x+3)2,解得x =83, 即BC 的长为83; (3)解:如图,作CD ⊥BP 于D ,∵PC =PB ,∴PD =BD =12PB, ∵∠PDC =∠AOP =90°,∠APO =∠CPD ,∴△AOP ∽△PCD , ∵12109S S =, ∴209AOP PCD S S =, ∴22209OA CD =, ∵OA =4,∴CD=5, ∴tan ∠CBP =CD BD =2.【点睛】本题考查了圆的切线的判定、勾股定理、锐角三角函数和圆中的计算问题,对于(1),连接OB ,证明OB ⊥BC 是判定圆的切线的常用方法;对于(2),关键是根据勾股定理列出方程;而对于(3),解题的关键是作CD ⊥BP 于D,综合利用等腰三角形的性质、相似三角形的判定及性质、锐角三角函数的有关知识去分析求解.6.(1)证明见解析;(2)52 BE=【解析】试题分析:(1)连接OA,OB,由圆周角定理得出∠AOB=2,ACB=90°,由等腰直角三角形的性质得出∠OAB=,OBA=45°,求出∠OAE=,OAB+,BAE=90°,即可得出结论;,2,过点A作AF⊥CD于点F,由AB=AD,得到∠ACD=∠ACB=45°,在Rt△AFC中可求得AF,3,在Rt△AFD中求得DF,1,所以AB,AD,,CD= CF+DF=4,再证明△ABE∽△CDA,得出BE AB DA CD=,即可求出BE的长度;试题解析:,1)证明:连结OA,OB,∵∠ACB=45°,∴∠AOB=2∠ACB= 90°,∵OA=OB,∴∠OAB=∠OBA=45°,∵∠BAE=45°,∴∠OAE=∠OAB+∠BAE=90°,∴OA⊥AE,∵点A在⊙O上,∴AE是⊙O的切线.,2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°,∵AB=AD,∴AB=AD∴∠ACD=∠ACB=45°,在Rt△AFC中,∵AC=∠ACF=45°,∴AF=CF=AC ·sin ∠ACF =3,∵在Rt △AFD 中, tan ∠ADC=3AF DF =, ∴DF =1,∴AB AD ==且CD = CF +DF =4,∵四边形ABCD 内接于⊙O ,∴∠ABE =∠CDA ,∵∠BAE =∠DCA ,∴△ABE ∽△CDA , ∴BE AB DA CD =,= ∴52BE =,7.,1,252524π+,,2)证明见解析;(3,354, 【解析】【分析】(1)连接OD ,由AB 是直径知,ACB =90°,结合CD 平分,ACB 知,ABD =,ACD =45°,从而知,AOD =90°,根据曲边三角形的面积=S 扇形AOD +S △BOD 可得答案;,2)由,AOD =90°,即OD ,AB ,根据DE ,AB 可得OD ,DE ,即可得证;,3)勾股定理求得BC =8,作AF ,DE 知四边形AODF 是正方形,即可得DF =5,由,EAF =90°,,CAB =,ABC 知tan,EAF =tan,CBA ,即EF AC AF BC=,求得EF 的长即可得. 【详解】解:(1)如图,连接OD ,,AB 是直径,且AB =10,,,ACB=90°,AO=BO=DO=5,,CD平分,ACB,,,ABD=,ACD=12,ACB=45°,,,AOD=90°,则曲边三角形的面积是S扇形AOD+S△BOD=2905360π⨯+12×5×5=252524π+,故答案为252524π+,,2)由(1)知,AOD=90°,即OD,AB,,DE,AB,,OD,DE,,DE是,O的切线;,3,,AB=10,AC=6,,BC过点A作AF,DE于点F,则四边形AODF是正方形,,AF=OD=FD=5,,,EAF=90°,,CAB=,ABC,,tan,EAF=tan,CBA,,EF ACAF BC=,即658EF=,,EF=154,,DE=DF+EF=154+5=354,8.(1)(5,0);(2)y=﹣5x+4;(3)①﹣1≤b≤24≤t.【解析】【分析】(1)根据“l变换点”的定义,分别画出图形,即可解决问题;(2)根据“l变换点”的定义,得到对称点的坐标,根据待定系数法即可得到结论;(3)①根据“l变换点”的定义,画出图形,求出b的最大值以及最小值即可解决问题;②如图6中,设点E 关于y 轴的对称点为E 1,E 1关于直线y=的对称点为E′,易知当点N 在⊙E 上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y 轴相切或相交时满足条件,想办法求出点E′的坐标即可解决问题.【详解】解:(1)如图1,点P (1,0)关于y 轴的对称点(﹣1,0),再关于直线x =2的对称点P 1(5,0);(2)点Q (2,1)关于y 轴的对称点(﹣2,1),设过点(﹣2,1)和(3,2)的直线的解析式为y=kx+b ,2132k b k b -+=⎧⎨+=⎩, 解得k=﹣15,b=75, ∴y =﹣15x +75, ,点(﹣2,1)和(3,2)关于直线l 对称,,直线l 过点(﹣2,1)和(3,2)连线的中点且与直线y =15x +75垂直, ,点(﹣2,1)和(3,2)连线的中点为(12,32), ,设直线l 的解析式为y =﹣5x +n , ,32=﹣5×12+n , 解得:n =4,,直线l 的解析式为:y =﹣5x +4;(3),如图4中,由题意b=12M1M′,由此可知,当M1M′的值最大时,可得b的最大值,,直线OM′的解析式为y=3x,∴tan∠M′OD=3,,MM′O=,M′OD=30°,,OM=2,易知,OM,OM′时,MM′的值最大,最大值为4,,b的最大值为2,如图5中,易知当点M在x轴的正半轴上时,可得b的最小值,最小值为﹣1,综上所述,满足条件的b取值范围为﹣1≤b≤2;,设E(t,0),如图6中,设点E关于y轴的对称点为E1,E1关于直线y+1的对称点为E′,易知当点N在,E上运动时,点N′在,E′上运动,由此可见当,E′与y轴相切或相交时满足条件.连接E 1E ′交直线y+1于K ,易知直线E 1E ′的解析式为y,由1y y x ⎧=+⎪⎨=⎪⎩,解得14x y ⎧=⎪⎪⎨+⎪=⎪⎩, ,K(4t -,14+), ,KE 1=KE ′,,E, 当,E ′与y 轴相切时,=2,解得t4, 综上所述,满足条件的t4≤t.【点睛】本题考查圆综合题、一次函数的应用、二元一次方程组的应用、轴对称变换等知识,解题的关键是灵活运用所学知识解决问题,学会利用图形,寻找特殊位置解决问题,学会用转化的思想思考问题,属于中考压轴题.9.四边形ABCD)四边形ABCD 是“准筝形”.理由见解析.【解析】整体分析:(1),设BH=x,分别在,AHC 和,BHC 中得到HC 与x 和AH 之间的关系;(2,因为“准筝形”的形状不确定,所以需要分类讨论,①AB=AD=2,∠BAD=60°,作CG 垂直BD 的延长线于点G ,AK ⊥BD 于K ,证△CBG ≌△CBH,求GC,AK 的长,分别求出S △ABD =S △CBD 即可;②BC=CD=2,∠BCD=60°,用与,相似的方法求解;,AD=CD,∠ADC=60°,作DM ⊥AC 于M,分别求S △ABC ,S △ADC ,,3,延长BC 至点E ,使CE=CD=4,连结DE,用SSS 证△ACD ≌△BED ,得到△ABD 是等边三角形.解:(1)如图2,1,设BH=x,∵∠ABC=120°,CH 是△ABC 的高线,∴∠BCH=30°,∴又∵∠A=45°,∴HA=HC,∵AB=2,解得:∴,2)在(1)条件下,四边形ABCD 的面积是:①如图2,2,AB=AD=2,∠BAD=60°,作CG 垂直BD 的延长线于点G ,则BD=2, 易得:∠CBG=60°=∠CBH,在△CBG 和△CBH 中,∵∠CGB=∠CHB,∠CBG=∠CBH ,CB=CB,∴△CBG ≌△CBH,AAS,,∴作AK ⊥BD 于K ,则易得:∴S △ABD =12△CBD =12∴S 四边形ABCD②如图∠BCD=60°,作CG 垂直BD 的延长线于点G ,则易得:∴S △BCD =12△ABD =12∴S 四边形ABCD③如图∠ADC=60°,作DM ⊥AC 于M,易得:32∴S △ABC =12S △ADC =1232∴S 四边形ABCD,3)四边形ABCD 是“准筝形”,理由:如图3,延长BC 至点E ,使CE=CD=4,连结DE,∵∠BCD=120°,∴∠DCE=60°,∴△DCE 是等边三角形,∴ED=CD=4,∠CDE=60°,∵BC=2,CE=CD=4,AC=6,∴AC=EB,在△ACD和△BED中,∵AD=BD,AC=EB,CD=ED,∴△ACD≌△BED,SSS,,∴∠ADC=∠BDE,∴∠ADB=∠CDE=60°,∴△ABD是等边三角形,∴AB=AD,∠BAD=60°,∴四边形ABCD是“准筝形”,。
初三数学培优教材(培训学校专用)

2016年初二升初三暑期培优教材(数学)第一讲 一元二次方程【学习目标】1、学会根据具体问题列出一元二次方程,培养把文字叙述的问题转换成数学语言的能力。
2、了解一元二次方程的解或近似解。
3、增进对方程解的认识,发展估算意识和能力。
【知识要点】1、一元二次方程的定义:只含有一个未知数的整式方程,并且都可以化为02=++c bx ax (a 、b 、c 、为常数,0a ≠)的形式,这样的方程叫做一元二次方程。
(1)定义解释:①一元二次方程是一个整式方程;②只含有一个未知数;③并且未知数的最高次数是2。
这三个条件必须同时满足,缺一不可。
(2)02=++c bx ax (a 、b 、c 、为常数,0a ≠)叫一元二次方程的一般形式,也叫标准形式。
(3)在02=++c bx ax (0a ≠)中,a ,b ,c 通常表示已知数。
2、一元二次方程的解:当某一x 的取值使得这个方程中的c bx ax ++2的值为0,x 的值即是一元二次方程02=++c bx ax 的解。
3、一元二次方程解的估算:当某一x 的取值使得这个方程中的c bx ax ++2的值无限接近0时,x的值即可看做一元二次方程02=++c bx ax 的解。
【经典例题】例1、下列方程中,是一元二次方程的是 ①042=-y y ; ②0322=--x x ; ③312=x ; ④bx ax =2;⑤x x 322+=; ⑥043=+-x x ; ⑦22=t ; ⑧0332=-+xx x ;⑨22=-x x ;⑩)0(2≠=a bx ax 例2、(1)关于x 的方程(m -4)x 2+(m+4)x+2m+3=0,当m__________时,是一元二次方程,当m__________时,是一元一次方程.(2)如果方程ax 2+5=(x+2)(x -1)是关于x 的一元二次方程,则a__________.(3)关于x 的方程135)32(12=+-++x x m m m 是一元二次方程吗?为什么?例3、把下列方程先化为一般式,再指出下列方程的二次项系数,一次项系数及常数项。
九数大培优全一册(学用)

九年级数学大培优第二十六章反比例函数第19讲反比例函数知识导航1.反比例函数的定义和解析式;2.反比例函数的图象和性质;3.反比例函数与方程及不等式;4.反比例函数与神奇的几何性质;5.反比例函数与直线y=a或x=a;6.反比例函数与全等相似;7.反比例函数与图形变换;8.反比例函数与定值及最值.ʌ板块一ɔ反比例函数的定义和解析式方法技巧根据定义解题1.定义:一般地,形如y=k x(k为常数,kʂ0)的函数,叫做反比例函数,其中x是自变量,y是函数.自变量x的取值范围是不等于0的一切实数;2.解析式:y=k x(kʂ0)或x y=k(kʂ0)或y=k x-1(kʂ0).▶题型一根据定义判断反比例函数ʌ例1ɔ下列函数:①y=x2;②y=2x;③y=-2x;④y=12x;⑤y=1x+2;⑥y=1x-2;⑦x y=2;⑧y= 2x-1,⑨y=2x2.其中y是x的反比例函数的有(填序号).▶题型二根据定义确定k值或解析式ʌ例2ɔ(1)反比例函数y=-32x,化为y=k x的形式,相应的k=;(2)函数y=k x中,当x=2时,y=3,则函数的解析式为.362▶题型三根据定义确定待定系数的值ʌ例3ɔ(1)如果函数y=x2m+1是关于x的反比例函数,则m的值为;(2)若函数y=(m+2)x m2-5(m为常数)是关于x的反比例函数,求m的值及函数的解析式.针对练习11.下列函数中,为反比例函数的是()A.y=x3B.y=13xC.y=1x-3D.y=1x22.反比例函数y=-32x化为y=k x的形式后,相应的k= 32.3.若关于x的函数y=(m2-4)x m2-m-7是反比例函数,求m的值.ʌ板块二ɔ反比例函数的图象和性质方法技巧抓住反比例函数的性质并结合图象解题一般地,对于反比例函数y=kx(kʂ0),由函数图象,并结合解析式,我们可以发现:1.图象分布当k>0时,x,y(同号或异号),函数图象为第象限的两支曲线;当k<0时,x,y(同号或异号),函数图象为第象限的两支曲线.因此反比例函数的图象也叫做双曲线.2.对称性若点(a,b)在反比例函数的图象上,则点,,也在此图象上,故反比例函数的图象关于直线,对称,关于点00成中心对称.3.增减性当k>0时,在每一个象限内,y随x的增大而;当k<0时,在每一个象限内,y随x的增大而.▶题型一反比例函数的增减性ʌ例1ɔ在反比例函数y=1-8m x的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,y1>y2,则m的取值范围是()A.m>18B.m<18C.mȡ18D.mɤ1818ʌ例2ɔ已知反比例函数y=-6x.(1)画出这个反比例的图象;(2)当-6ɤx<-2时,y的取值范围是;(3)当|y|ȡ3时,x的取值范围是.九年级数学 大培优▶题型二 反比例函数的图象的对称性ʌ例3ɔ 如图,直线y =a x (a ʂ0)与双曲线y =k x(k ʂ0)交于A ,B 两点,试说明A ,B 两点关于原点对称.▶题型三 反比例函数的图象与系数的关系ʌ例4ɔ 如图,反比例函数①y =k 1x ,②y =k 2x ,③y =k 3x ,④y =k 4x的部分图象如图所示,则k 1,k 2,k 3,k 4的大小关系是.▶题型四 反比例函数中k 的几何意义如图,过双曲线上任意一点P 作x 轴,y 轴的垂线段P M ,P N ,则所得的矩形P M O N 的面积S =P M ㊃P N =|y |㊃|x |=|x y|=|k |,即在反比例函数y =k x(k ʂ0)的图象上任取一点向两坐标轴作垂线段,则两垂线段与两坐标轴所围成的矩形的面积等于|k |,且这个面积的值与取点的位置无关.特别地,S әP M O =S әP N O =12|k |.ʌ例5ɔ 如图,平行于x 轴的直线A B 与双曲线y =k 1x 和y =k 2x(k 1>k 2)在第一象限内交于A ,B 两点,若S әO A B =2,求k 1-k 2的值.1212ʌ例6ɔ 如图,直线y =-12x 与双曲线y =k x(k <0)交于A ,B 两点,且点A 的横坐标为-4.(1)求k 的值;(2)过原点的另一直线交双曲线y =k x(k <0)于P ,Q 两点,点P 在第二象限.若A ,B ,P ,Q 四点组成的四边形面积为24,求点P 的坐标.148128针对练习21.对于反比例函数y =3x ,下列说法正确的是( )A.图象经过点(1,-3)B .图象在第二㊁四象限C .y 随x 的增大而减小 D.x <0时,y 随x 增大而减小2.在同一平面直角坐标系内画出函数y =k x +1和函数y =k x(k ʂ0)的图象大致是( )3.反比例函数y =a 2-a +1x(a 为常数)的图象上有三个点(x 1,y 1),(x 2,y 2),(x 3,y3),其中x 1<x 2<0<x 3,则y 1,y 2,y3的大小关系是 y 2<y 1<y 3 .4.如图,点A 是反比例函数y =k x(x <0)的图象上一点,过点A 作A B ʅx 轴于点B ,点P 是y 轴负半轴上一点,әA B P 的面积为1,求k 的值.12|5.点A (a ,y 1),B (2a ,y2)是反比例函数y =k x(k >0)的图象上的两点.(1)比较y 1与y 2的大小关系;(2)若A ,B 两点在一次函数y =-43x +b 位于第一象限的图象上(如图所示),分别过A ,B 两点作x 轴的垂线,垂足分别为点C ,D ,连接O A ,O B ,且S әO A B =8,求a 的值;(3)在(2)的条件下,如果3m =-4x +24,3n =32x,求使得m >n 的x 的取值范围.k xk x k a k 2a43x 43a 8343a 83a 1243a 83a 43x 323x43x 323x九年级数学 大培优ʌ板块三ɔ 反比例函数与方程㊁不等式方法技巧根据直线与双曲线的交点并结合图象解题▶题型一 反比例函数与方程ʌ例1ɔ 如图,直线y =-x +5与双曲线y =4x 交于A ,B 两点.(1)求A ,B两点的坐标;(2)将直线A B 向左平移n 个单位长度,若平移后的直线A B 与双曲线有唯一公共点,求n 的值.4ʌ例2ɔ 直线y =2x +4与反比例函数y =6x的图象交于A ,B 两点,直线y =m (m >0)与直线A B 相交于点M ,与反比例函数的图象相交于N ,若MN =4,求m 的值.426x6642426m 43▶题型二 反比例函数与不等式ʌ例3ɔ 如图,一次函数y =-x +4与反比例函数y =m x (m >0,x >0)的图象交于A ,B 两点,与x 轴,y轴分别相交于C ,D 两点.如果点A 的横坐标为1,利用函数图象求关于x 的不等式4-x <m x的解集.33▶题型三 反比例函数与数形结合比较大小ʌ例4ɔ 如图,直线y =2x +4与反比例函数y =k x 的图象相交于A (-3,a )和B 两点.(1)求A ,B 两点的坐标;(2)直接写出不等式k xɤ2x +4的解集.ʌ例5ɔ 如图,双曲线y =k x (k >0)与直线y =-12x +4相交于A ,B 两点.(1)当k =6时,求点A ,B 的坐标;(2)在双曲线y =k x (k >0)的同一支上有三点C (x 1,y 1),D (x 2,y 2),P (x 1+x 22,y0),请你借助图象,直接写出y 0与y 1+y 22的大小关系;(3)点M (x 1,y 1),N (x 2,y2)是双曲线y =6x (x >0)上任意两点,s =y 1+y 22,t =12x 1+x 2,试比较s 与t 的大小.备用图1221221221221221212212ʌ例6ɔ 当1ɤx ɤ4时,直线y =-2x +b 与双曲线y =4x 只有一个公共点,则b 的取值范围是 4269 .44=42-4242九年级数学 大培优针对练习31.如图,在平面直角坐标系中,直线A B :y 1=x +m 与双曲线C :y2=k x 相交于A (2,5),B 两点.(1)求点B 的坐标;(1)当y 1>y2时,x 的取值范围是;(2)当x <2时,y2的取值范围是.2.如图,一次函数y 1=x +1的图象与反比例函数y 2=k x (k 为常数,且k ʂ0)的图象都经过点A (m ,2).(1)求点A 的坐标及反比例函数的表达式;(2)结合图象直接写出当x >0时,比较y 1和y 2的大小;(3)直接写出不等式4x -2ɤx +1的解集.23.如图,一次函数y 1=x +5的图象与反比例函数y 2=k x 的图象交于A ,B 两点.当x >1时,y 1>y2;当0<x <1时,y 1<y2.(1)直接写出反比例函数y 2的解析式;6(2)过点D (t ,0)(t >0)作x 轴的垂线,分别交双曲线y 2=k x和直线y 1=x +5于P ,Q 两点.若P Q=备用图3P D 时,求t 的值.666ʌ板块四ɔ 反比例函数与神奇的几何性质方法技巧根据反比例函数k 的意义,结合全等㊁相似或参数思想㊁根系关系,可得出反比例函数一些重要几何性质,在解题中可运用这些重要性质,从而大大提高解题效率.性质一 如图,直线A B :y =m x +n 交x 轴于点A ,交y 于点B ,交双曲线k x于C ,D 两点.求证:A C =B D.图1图2k xn m n mC MD F D N CE ʑB C B D A D A C C D B D =C D A C性质应用ʌ例1ɔ 如图,直线y =x +6交x 轴于点A ,交y 轴于点B ,交双曲线y =k x于点C ,D ,若C D =2(A C +B D ),则k 的值为.16O 16性质二 如图1,A ,B 为双曲线y =k x上任意两点,A C ʅy 轴于点C ,B D ʅx 轴于点D ,直线AC ,BD 交于点E .求证:①A B ʊC D ; ②A C A E =B D B E.图112|A E C E B E D E A C A E B DB E九年级数学 大培优变式1:如图2,A C ʅx 轴于点C ,B D ʅy 轴于点D ,A C ,B D 交于点E .求证:①A B ʊCD ; ②A C AE =B D B E.图2变式2:如图3,A ,B 为双曲线y =k x 上任意两点,A C ʅy 轴于点C ,B D ʅx 轴于点D ,直线AC ,B D交于图3点E .求证:①A B ʊC D ; ②A C A E =B D B E.ʌ例2ɔ 如图,双曲线y =k x经过矩形O A B C 边A B 的中点F ,交B C于点E ,且四边形O E B F 的面积为2,则k =.12ʌ例3ɔ 如图,点P 为双曲线y =8x(x >0)上一点,P A ʅx 轴于点A ,P Bʅy 轴于点B ,P A ,P B 分别交双曲线y =k x (x >0)于C ,D 两点,若S әP C D =1,则k =.888128a k 88216性质三 如图,直线A B 与双曲线y =k x只有唯一公共点A ,且A B 与y 轴不平行,A B 交x 轴于点B ,连接O A .求证:O A =A B.k a222性质四 如图,直线y =m x 交双曲线y =k x于A ,B 两点,点P 为双曲线上一点,直线P A ,P B 分别交x轴于M ,N 两点.求证:P M =P N .ʌ例4ɔ (2018十堰中考)如图,直线y =-x 与反比例函数y =k x的图象交于A ,B 两点,过点B 作B Dʊx 轴,交y 轴于点D ,直线A D 交反比例函数y =k x 的图象于另一点C ,求C B C A的值.212212121313针对练习41.如图,点A ,B 分别是双曲线y =4x 和y =2x第一象限分支上的点,且A B ʊy 轴,B C ʅy 轴于点C ,则A B ㊃B C = 2 .2.如图,直线y =-3x +b 与y 轴交于点A ,与双曲线y =k x在第一象限交于B ,C 两点,且A B ㊃A C =4,则k = 3 .2332334333九年级数学 大培优3.如图,әO A C 的顶点A 在双曲线y =9x上,点C 在x 轴上,O A 交双曲线y=1x 于点B ,直线A C 与双曲线y =9x只有唯一公共点,且A C 与y 轴不平行,则S әA B C =.992339a2x 181212391323234.如图1,直线y =-2x +6交x 轴于点B ,交y 轴于点A ,直线A B 与双曲线y =k x(k <0)交于C ,D 两点,C E ʅx 轴于点E ,D F ʅx 轴于点F .(1)若k =-8,求C D 的长;(2)求C E -D F 的值;(3)如图2,P 是双曲线y =k x (k <0)上第二象限上一动点,P G ʅx 轴于G ,交双曲线y =k 2x(k <0)于M ,PH ʅy 轴于H ,交y =k 2x(k <0)于N ,请直接写出MN 的最小值为(用含k 的式子表示).图1 图2552212ʌ板块五ɔ 反比例函数与直线x =a 或y =a方法技巧此类问题一般可用a 表示相关点的坐标,从而表示出相关线段长,将几何问题坐标化.解题时注意情况不明时需分类讨论.ʌ例1ɔ 如图,在平面直角坐标系x O y 中,直线y =2x +n 与x 轴,y 轴分别交于点A ,B ,与双曲线y =4x在第一象限内交于点C (1,m ),过x 轴正半轴上的点D (a ,0)作平行于y 轴的直线l ,分别与直线和双曲线y =4x 交于点P ,Q ,且点P 不与点Q 重合.(1)求m 和n 的值;(2)当a >1,P Q =2Q D 时,求әA P Q 的面积;(3)连接C Q ,当C P =C Q 时,求a 的值.44412,4a 4a针对练习51.如图,直线l :y =32x +3与双曲线y =k x 在第一象限内交于点A (a ,6).(1)求双曲线的解析式;(2)直线x =t (t >0且t ʂ2)分别交直线l ,双曲线y =k x 于C ,D 两点,连接A D ,若A C =A D ,请直接写出t 的值.323221232123213412362134362134362ʌ板块六ɔ 反比例函数与全等及勾股定理方法技巧利用全等㊁相似将线段关系转化为坐标关系,实现 几何问题坐标化 .▶题型一 反比例函数与全等ʌ例1ɔ 如图,点A 是双曲线y =8x在第一象限上的一动点,连接A O 并延长交另一分支于点B ,以A B为斜边作等腰R t әA B C ,随着点A 的运动,点C 的位置也不断地变化,但始终在一函数图象上运动,则这个函数的解析式为 8 .ʌ例2ɔ (2018原创题)如图,点A (2,4),B 均为双曲线y =k x 在第一象限上的点,且øA O B =45ʎ,求点B 的坐标.13881326263九年级数学 大培优▶题型二 反比例函数与勾股定理ʌ例3ɔ 如图,矩形A B C O 的顶点B (10,8),点A ,C 在坐标轴上,E 是B C 边上一点,将әA B E 沿A E折叠,点B 刚好与O C 边上的点D 重合,过点E 的反比例函数y =k x(k >0)的图象与边A B 交于点F ,求点F的坐标.154154针对练习61.如图,A (2,3)是双曲线y =k x(x >0)上的一点,P 为x 轴正半轴上一点,将点A 绕点P 顺时针旋转90ʎ,恰好落在双曲线上的另一点B ,求点P的坐标.2.如图,已知点A (2,2),P (0,a )是y 轴上一点,连接P A ,将线段P A 绕点P 逆时针旋转90ʎ得线段P A ᶄ,若线段P A ᶄ与反比例函数y =-3x(x <0)的图象有公共点,求a 的取值范围.333.如图,直线y =3x -3交坐标轴于A ,B 两点,将әA O B 沿A B 翻折得到әA C B ,点D 在A C 的延长线上,且C D =4A C ,反比例函数y =k x的图象经过点D ,求k 的值.ʌ板块七ɔ 反比例函数与图形变换方法技巧图形变换的本质是点的变换,解题的关键是根据变换规律,将变换后的关键点的坐标表示出来,再根据条件建立关系式.ʌ例1ɔ 平面直角坐标系中,点A (-2,0),B (0,3),点P 为第二象限内一点.(1)如图,将线段A B 绕点P 旋转180ʎ得线段C D ,点A 与点C 对应,试画出图形;(2)若(1)中得到的点C ,D 恰好在同一个反比例函数y =k x的图象上,求直线B C 的解析式;(3)若点Q (m ,n )为第四象限的一点,将线段A B 绕点Q 顺时针旋转90ʎ得到线段E F ,其中点A 与点E 对应,若点E ,F 恰好在同一个反比例函数的图象上,直接写出m ,n 之间的关系式为 m =-5n .备用图3232九年级数学 大培优ʌ例2ɔ 已知点A (a ,m )在双曲线y =8x 上且m <0,过点A 作x 轴的垂线,垂足为点B .(1)如图1,当a =-2时,P (t ,0)是x 轴上的动点,将点B 绕点P 顺时针旋转90ʎ至点C .①若t =1,直接写出点C 的坐标;②若双曲线y =8x经过点C ,求t 的值;(2)如图2,将图1中的双曲线y =8x(x >0)沿y 轴折叠得到双曲线y =-8x (x <0),将线段O A 绕点O 旋转,点A 刚好落在双曲线y =-8x(x <0)上的点D (d ,n )处,求m 和n 的数量关系.8828x 针对练习71.在平面直角坐标系中,点A (a ,0)为x 轴上一动点,点M 的坐标为(1,-1),点N 的坐标为(3,-4),连接AM ,MN ,点N 关于直线AM 的对称点为点N ᶄ.(1)若a =2,在图1中画出线段MN 关于直线AM 的对称图形MN ᶄ(保留作图痕迹),直接写出点N ᶄ的坐标为 21;(2)若a >0,连接A N ,A N ᶄ,当点A 运动到øN ᶄA N =90ʎ时,点N ᶄ恰好在双曲线y =k x上(如图2),求k 的值;(3)点A 在x 轴上运动,若øN ᶄMN =90ʎ,此时a 的值为 465.65731-71x 4(6ʌ板块八ɔ 反比例函数与定值㊁最值方法技巧通过采取解析法求定值,建立二次函数模型求最值.▶题型一 反比例函数与定值ʌ例1ɔ 如图,点C (6,1),D (1,6)在双曲线y =6x的图象上.点T 在双曲线第一象限上(不同于C ,D ),直线T C ,T D分别交y 轴于E ,F ,则O F -O E 的值是 5 .6666166▶题型二 反比例函数与最值ʌ例2ɔ 如图,双曲线y =2x的第一象限的分支上一动点P ,点A (-2,-2),B (2,2),则P A -P B 的值为4 .22222222ʌ例3ɔ 如图,在平面直角坐标系中,直线A B :y 1=x +m 与双曲线C :y2=k x 相交于A ,B 两点,其中点A (2,5),A C ʅy 轴于点C .(1)求直线与双曲线的解析式;(2)直接写出x <2时,反比例函数值y 2的取值范围;(3)点E 为点B 下方直线A B 上一动点,直线E F ʅA B ,分别与直线A B ,双曲线C 及y 轴交于E ,F ,G 三点,求E F ㊃F G 的最大值.10101052325232253222253232494324946712494九年级数学 大培优针对练习81.如图,若直线y =-x +m 与反比例函数y =4x(x >0)的图象相交于两个不同点E ,F (点E 在点F 的左边),与y 轴相交于点M .(1)m的取值范围为;(2)求M E ㊃M F 的值.44224=2x 22.如图,已知反比例函数y =k x 和一次函数y =32x +6的图象有一个交点为P (-2,m ).(1)求反比例函数解析式;(2)若过点P 的直线l 与反比例函数y =k x的图象只有一个交点,求直线l 的解析式;(3)点Q 是双曲线在第四象限这一分支上的动点,过点Q 作直线,使其与双曲线y =k x只有一个公共点,且与x 轴,y 轴分别交于点C ,D ,直线y =32x +6与x 轴,y 轴分别交于点A ,B ,求四边形A BCD 面积的最小值.32663232x 3266666t 6t 66262121212t 12A 121242第20讲实际问题与反比例函数知识导航1.根据实际问题列反比例函数关系式或确定函数图象;2.反比例函数的应用.ʌ板块一ɔ根据实际问题列反比例函数关系式或确定函数图象方法技巧解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.▶题型一坐标与距离ʌ例1ɔ某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.下图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为()A.I=2RB.I=3RC.I=6RD.I=-6Rʌ例2ɔ某小学部课外兴趣小组的同学每人制作一个面积为1m2的矩形学具进行展示.设矩形的宽为x m,长为y m.那么这些同学所制作的矩形长y(m)与宽x(m)之间的函数关系的图象大致是()A.针对练习11.如果等腰三角形的底边长为x,底边上的高为y,则它的面积为定值S时,x与y的函数关系为()A.y=S xB.y=S2xC.y=2S xD.y=x2S2.在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:l x)之间成反比例函数关系,部分数据如下表所示:光照度E/l x0.511.522.53光敏电阻阻值R/Ω603020151210则光敏电阻值R与光照度E的函数表达式为R=30E.九年级数学 大培优ʌ板块二ɔ 反比例函数的应用方法技巧1.根据题意,建立反比例函数模型解题;2.正确认识图象,找到关键的点,运用好数形结合的思想.ʌ例1ɔ 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y (毫克/百毫升)与时间x (时)的关系可近似地用二次函数y =-200x 2+400x 刻画;1.5小时后(包括1.5小时)y 与x 可近似地用反比例函数y =k x(k >0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几小时血液中的酒精含量达到最大值?最大值为多少?②当x =5时,y =45,求k 的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于酒后驾驶 ,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.22522511ʌ例2ɔ 某校园艺社计划利用已有的一堵长为10m 的墙,用篱笆围一个面积为12m 2的矩形园子.(1)如图,设矩形园子的相邻两边长分别为x (m ),y (m ).①求y 关于x 的函数表达式;②当y ȡ4m 时,求x 的取值范围;(2)小凯说篱笆的长可以为9.5m ,洋洋说篱笆的长可以为10.5m.你认为他们俩的说法对吗为什么?1265651212x针对练习21.当温度不变时,某气球内的气压p (k P a )与气体体积V (m 3)的函数关系如图所示,已知当气球内的气压p >120k P a 时,气球将爆炸,为了安全起见,气球的体积V 应( )A.不大于45m 3B .大于45m 3C .不小于45m 3 D.小于45m 32.为预防流感盛行,对教室进行 薰药消毒 .已知药物在燃烧及释放过程中,室内空气中每立方米含药量y (毫克)与燃烧时间x (分钟)之间的关系如图所示(即图中线段O A 和双曲线在A 点及其右侧的部分),根据图象所示信息,解答下列问题:(1)直接写出y 与x 之间的函数关系式及自变量的取值范围;(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?23150231503.(2018㊃乐山)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (ħ)与时间x (h )之间的函数关系,其中线段A B ,B C 表示恒温系统开启阶段,双曲线的一部分C D 表示恒温系统关闭阶段.请根据图中信息解答下列问题:(1)求这天的温度y 与时间x (0ɤx ɤ24)的函数关系式;(2)求恒温系统设定的恒定温度;(3)若大棚内的温度低于10ħ时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害200200九年级数学 大培优第二十七章 相似第21讲 相似三角形的判定知识导航1.相似多边形;2.平行线分线段成比例定理;3.相似三角形的判定方法.ʌ板块一ɔ 平行线分线段成比例定理方法技巧1.在利用平行线分线段成比例定理时,注意对应线段的位置;2.由平行线+中点得线段中点,利用中位线解题.▶题型一 运用平行线分线段成比例定理探究线段关系ʌ例1ɔ 如图,已知直线A B ʊC D ʊE F ,A F 与B E 交于点G ,且A G =2,G D =1,D F =5,求B C C E的值.A D FBC C E 35ʌ例2ɔ 如图,P 是▱A B C D 的边B C 的延长线上任意一点,A P 分别交B D 和C D 于点M 和N .求证:AM 2=MN ㊃MP .AM MN B M DMAM MN M P AM▶题型二 平行线等分线段定理证线段中点ʌ例3ɔ 如图,在正方形A B C D 中,点E 在对角线B D 上,连接A E ,D F ʅB D ,且D F =B E ,F B 与A C交于点M .求证:D E =2C M .针对练习11.如图,直线l 1,l 2,l 3分别交直线l 4于A ,B ,C 三点,交直线l 5于点D ,E ,F ,且l 1ʊl 2ʊl 3,已知D E ʒD F =3ʒ8,A C =24.(1)求B C的长;(2)当A D =4,C F =20时,求B E 的长.3815258522.如图,A B 是☉O 的直径,C D 是弦,A E ʅC D ,B F ʅC D ,垂足分别为点E ,F .(1)求证:D E =C F ;(2)若B F =1,A E =2,E F =4,求A B 的长.223.如图,在正方形A B C D 中,点E 在D A 的延长线上,A E =A B ,点F 在C D 上,M 为A F 的中点,过点M 作MN ʅM C 交B E 于点N .求证:MN =M C .九年级数学 大培优ʌ板块二ɔ 作平行线构造X 型相似方法技巧1.作平行线是构造三角形相似的基本方法,利用平行线对比例式进行转化.2.通常引入参数求比值或计算线段的长.▶题型一 延长平行线段构X 型相似ʌ例1ɔ 如图,▱A B C D 中,A B =2,A D =3,øA B C =60ʎ,A E ʅB C ,垂足为点E .F 为C D 的中点,D E与B F 相交于点P .(1)求E P D P 的值;(2)求B P 的长.1213ʑMN =32213131414B 132▶题型二 作平行线构X 型相似,证线段关系ʌ例2ɔ 如图,在әA B C 中,A B =A C ,D 为B C 上一点,点E ,F 在A D 上,A E =E F =12B E ,øB E D =øB A C .(1)求证:A E =F C ;(2)求证:B D =2C D .1212▶题型三 作平行线构X 型相似,求比值ʌ例3ɔ 如图,øC A B =90ʎ,A C =A B ,D 是A C 的中点,A F ʅB C 分别交B D ,B C 于点E ,F .A G ʅD B交B C 于点G .求D E A G的值.121▶题型四 利用角平分线+平行线构X 型相似ʌ例4ɔ 如图,在әA B C 中,A B =A C =5,B C =6,øA B C 的平分线交A C 于点D ,C E ʅB C 交B D 的延长线于点E ,求B D D E的值.265661148114011181183针对练习21.如图,在▱A B C D 中,M 为A B 的中点,DM ,D B 与A C 分别相交于点P ,Q .(1)求A P P Q的值;(2)若D B ʅB C ,B C =5,P Q =1.求P M 的长.121322D B 2+B C 221122121213DM 2162.如图,在әA B C 中,D 是B C 的中点,点F 在A C 上,F C =2A F ,B F 交A D 于点E .(1)求证:A E =E D ;(2)若A B =A D ,求B F A C的值.1212B F B M 23B F A C 233.如图,A D 为әA B C 的角平分线,点E 在A B 边上,C E 交A D 于点F ,C F =C D ,若A F =3F D ,E F =3,求C D 的长.34九年级数学 大培优ʌ板块三ɔ 作平行线构造A 型相似方法技巧1.求部分线段与整体线段的比的问题,往往构A 型相似求解;2.过线段端点或分点作平行线构双A (X )图或A X 型图;3.三条平行线构成X 型㊁A 型图中隐藏关系式:1a +1b =1c;4.等腰三角形中作腰的平行线构造新的等腰三角形.▶题型一 直接或间接作平行线构造A 型图求比值.ʌ例1ɔ 如图,在әA B C 中,点E 为线段B C 的中点,点D 在线段A C 上,B D 交A E 于点F .若B F =3F D ,求A F A E的值.12B 141212▶题型二 直接或间接作平行线构造A 型图转化比.ʌ例2ɔ 如图,在әA C B 中,点D 为边A C 的中点,点E 为B D 上任意一点,延长C E 交A B 于点M ,延长A E 交B C 于点N ,连接MN .求证:MN ʊA C .B NB C ▶题型三 直接或间接作平行线构造双A 型解题ʌ例3ɔ 如图,在R t әA B C 中,øA C B =90ʎ,C D ʅA B ,垂足为点D ,M 是C D 的中点,E F ʅA B ,垂足为点F .若E F =4,C E =3.2,求A E 的长.4432▶题型四1a+1b=1c型问题ʌ例4ɔ如图,A BʊC D,B D与A C交于点G,过点G作A B的平行线分别交B C,A D于点H,E.(1)求证:1A B+1C D=1G H;(2)过点H作H FʅA D,垂足为点F,若F G=2,A B=3,求C D的长.1111 A B 1C D1G H121 3112针对练习31.如图,点D是әA B C的边C B的延长线上一点,点F在A C上,D F交A B于点E,若B D=B E,C D=4A E,A C=5,求A F的长.152.如图,四边形A B C D中,A DʊB C,A FʊC D交B C于点F,E是A B上一点,A E=A D,E C交A F于点M.求证:C M㊃B F=A B㊃M E.3.如图,在әA B C中,点P是A B上一点,A P=4,B P=6,点M是P C的中点,øA C P=øP B M.(1)求A C 的长;(2)过点A作A DʊP C交B C的延长线于点D,B M的延长线交A D于点N.若N D=33,øC A D=30ʎ,求C D的长.1243336323F2+F D227九年级数学 大培优ʌ板块四ɔ 边边边法证明三角形相似方法技巧网格中或非网格中可计算出三边或算出三对对应边的比值,常用三边对应成比例证三角形相似.▶题型一 网格中的相似三角形ʌ例1ɔ 已知әA B C 中,A B =25,A C =45,B C =6.如图,是由100个边长为1的小正方形组成的10ˑ10的正方形网格.设顶点在这些小正方形顶点的三角形为格点三角形.请在网格中画一个与әA B C 相似且对应边的比最大的格点三角形,并加以证明.0204102,1021022102100272+122329210111111102▶题型二 非网格相似三角形ʌ例2ɔ 已知正方形A B C D ,点E ,F 分别在边A D ,C D 上,且A E =E D ,C F =3D F .(1)求证:әA B E ʐәE B F ;(2)连接A C 与B E ,B F 分别相交于点M ,N ,求证:B C B N =AM MN.52AMMN 针对练习41.如图,是由81个边长为1的小正方形组成的9ˑ9的正方形网格.设顶点在这些小正方形顶点的三角形为格点三角形.(1)请你计算出әA B C各边的长;(2)请在网格中画一个与әA B C 相似且与әA B C 三边对应垂直的对应边比值最大的格点三角形,并加以证明(A ,B ,C 的对应点分别为A 1,B 1,C 1).2256262=623262351111112.如图,在四边形A B C D 中,点E 在B D 上,且A B A E =B C E D =A C A D.B C =4,øB A E =30ʎ,求C D 的最小值.12ʌ板块五ɔ 边角边法证三角形相似方法技巧1.旋转型㊁子母型图常运用两边对应成比例,其夹角相等证相似;2.求形如a +n mb 的最值,常通过构 边角边 相似去求解.▶题型一 旋转型相似ʌ例1ɔ 如图1,在R t әA B C 中,øC =90ʎ,A B =15,B C =9,点P ,Q 分别在边B C ,A C 上,C P =3x ,C Q=4x (0<x <3),把әP C Q 绕点P 旋转,得到әP D E ,点C ,Q 的对应点分别为点D ,E .(1)如图1,若点D 落在线段P Q 上,且A D 平分øC A B ,求x 的值;(2)如图2,当点E 落在边A B 上且Q E ʊC B 时,求C D 的长.图1 图212412693535185▶题型二 将a 2=b c 型问题转化为 子母型 相似问题.ʌ例2ɔ 如图,在әP E F 中,P E =P F ,O 为E F 的中点,G 为P F 上一点,øP E G =27ʎ,N 为O G 的中点,P N ʅE G ,垂足为点M ,若øM O N =18ʎ,N G 2=NM ㊃N P .求øF 的度数.九年级数学大培优针对练习51.如图,P是正方形A B C D边B C上一点,点M在边C D上,B M与A P交于点Q,B P2=P Q㊃P A.(1)求证:C M=B P;(2)若P为B C中点,求øP Q C的度数.2.如图,在正方形A B C D中,点E,F分别在边B C,C D上,连接A F交B D于点H,E C=2DH.(1)求证:øE A F=45ʎ;(2)求证:AH=E H.23.如图,在等腰直角三角形A B C中,A C=B C,点E在边B C上,以A E为边作正方形A E MN,E M交A B于点F.(1)求证:B MʅA B;(2)若C E=2B E,求A E E F的值.2222221415E F A E15ʌ板块六ɔ 角角判定法证三角形相似方法技巧1.共角的两个三角形优先考虑用角角判定法证三角形相似;2.用反A 型相似证明a b =c d 型等式;3.善于发现或构造一线三等角型相似;4.共角且一对角互补的两个不相似三角形,构造等腰三角形转化为相似三角形.▶题型一 用角角判定法证明三角形相似ʌ例1ɔ 如图,D 是әA B C 边B C 的中点,点M 在A B 上,øA C M =øB .(1)求证:A C 2=AM ㊃A B ;(2)点O 在A D 边上,且A O =2O D ,过点O 作E F ʊM C ,分别交A B ,A C 于点E ,F ,若A E =6,E M =1,求A F ㊃A C 的值.▶题型二 构造等角,运用角角法证相似求边长ʌ例2ɔ 如图,点D 在A B 上,A B =3B D =12,点E 在B C 的延长线上,D E =2A C ,øA C B +øB D E =180ʎ,øB =60ʎ,求A C 的长.12123221213131▶题型三 一线三等角问题ʌ例3ɔ 如图,在әA B P 中,A P =A B ,O 为A B 上一点,O A =2,O B =1,A Q ʊB P ,且øQ O P =øB ,求A Q ㊃B P 的值.A Q O E232313x Q F O B1九年级数学 大培优针对练习61.如图,A B =A C ,øB A C =90ʎ,D 为边A B 上任意一点,A E ʊB C ,øC D E =45ʎ,求证:C D D E=2.222.如图,әA B C 中,A B =A C =15,B C =24,D ,E 分别是B C ,A B 上的点,øA D E =øB ,当әB D E 为直角三角形时,求B D 的长.1215125421162142143.如图,点E ,F 分别在线段A C ,B C 上,øF E C =øB ,øA C B =60ʎ,C H 平分øA C B 交E F 于点H .(1)求证:B C A C =E H H F;(2)若E C =43,H C =5,求B C A C的值.E H H F E M F N1212B C A C E C F C B C A C E H H F 12E 2312F =3x =3M -3x MH HN E M F N ,15-3x 23x03-1073C 754.如图,正方形A B C D 中,B C =4,对角线A C ,B D 交于点O ,P 是O B 的中点,N 在线段C D 上(不与C ,D 两点重合),P M ʅP N 交B C 于点M .求B M +13DN 的值.1213P E P D 1313D 12B 13ʌ板块七ɔ 作垂线构造三角形相似方法技巧作垂线构造直角三角形相似转化比或用比例式列方程求边.▶题型一 利用对顶角相等,作垂线构造直角三角形相似ʌ例1ɔ 如图,B D 为әA B C 的高,点E 在A B 边上,øB E C =60ʎ,B E =2C D ,C E 与B D 相交于点F .求B FF C的值.32333▶题型二 利用同角或等角的补角相等,作垂线构造直角三角形相似ʌ例2ɔ 如图,在R t әA B C 中,øB A C =90ʎ,A D ʅB C ,垂足为点D ,点O 是A C 边中点,连接B O 交A D 于点F ,O E ʅOB 交BC 边于点E .若A C A B =n ,求O F O E的值.▶题型三 利用角平分线作垂线构造直角三角形相似ʌ例3ɔ 如图,在әA B C 中,øB A C =60ʎ,A B =6,A C =4,A D 平分øB A C 交B C 于点D .求B D 的长.121233233323535322657▶题型四 面积问题作高构造直角三角形相似ʌ例4ɔ 如图,在әA B C 中,øC =45ʎ,点D ,E ,F 分别在边B C ,A C ,A B 上,A B =B D =2A E ,连接E F交A D 于点G ,øA G F =45ʎ,若A D =4,F G =32,求әA F G 的面积.1234九年级数学 大培优针对练习71.如图,在әA B C 中,øA C B =90ʎ,点E 在A C 上,A C =2B C =4C E .C D ʅB E 交B E 于点F ,交A B 于点D .求B D A D的值.12122.如图,在R t әA B C 中,øA B C =90ʎ,A B =6,D 为A C 的中点,过点A 作A E ʊB C ,连接B E ,øE B D=øC B D ,B D =5,求B E 的长.2452543.如图,B ,C ,E 三点在一条直线上,әA B C 与әD C E 均为等边三角形,D B 与A C ,A E 分别相交于点H ,F ,连接F C .(1)求证:әAH B ʐәF H C ;(2)若B F =2F E ,求B C C E的值.M N B C E C32324.如图,在四边形A B C D 中,øA B C =øA D C =90ʎ,A B =A D =2B C =2C D ,E 为C D 上一点,B F ʅA E交A D 于点F .求B F A E的值.12535383858545ʌ板块八ɔ用相似法证明线段相等方法技巧1.证明a=b的方法技巧之一:若a c=b c,则a=b;2.证明a=b的方法技巧之二:若a c=b d,c=d,则a=b.▶题型一双A双X并排型ʌ例1ɔ如图,D,E分别是әA B C的边A B,A C上的点,D EʊB C,D C交B E于点O,直线A O分别交D E,B C于点M,N.求证:B N=N C.▶题型二普通型相似ʌ例2ɔ如图,D为R tәA C B斜边A B的中点,点M在A C上,点N在B C的延长线上,øMDN=90ʎ.(1)求证:øC A B=øMN D.(2)如图2,分别过点M,N作直线A B的垂线,垂足分别为点G,H.求证:A G=DH.针对练习81.如图,在等边әA B C中,点E在C A的延长线上,点D在B C的延长线上,A E=C D,延长D A交B E 于点F.(1)求证:øE A F=øA B E;(2)过点E作E GʊF C交A D于点G.求证:E F=A G.。
人教版九年级数学上下册培优讲义机构辅导资料(共30讲)
九年级讲义目录专题01 二次根式的化简与求值阅读与思考二次根式的化简与求值问题常涉及最简根式、同类根式,分母有理化等概念,常用到分解、分拆、换元等技巧.有条件的二次根式的化简与求值问题是代数变形的重点,也是难点,这类问题包含了整式、分式、二次根式等众多知识,又联系着分解变形、整体代换、一般化等重要的思想方法,解题的基本思路是:1、直接代入直接将已知条件代入待化简求值的式子. 2、变形代入适当地变条件、适当地变结论,同时变条件与结论,再代入求值.数学思想:数学中充满了矛盾,如正与负,加与减,乘与除,数与形,有理数与无理数,常量与变量、有理式与无理式,相等与不等,正面与反面、有限与无限,分解与合并,特殊与一般,存在与不存在等,数学就是在矛盾中产生,又在矛盾中发展.=x , y , n 都是正整数)例题与求解【例1】 当x =时,代数式32003(420052001)x x --的值是( ) A 、0 B 、-1 C 、1 D 、20032-(绍兴市竞赛试题)【例2】 化简(1(ba b ab b -÷-- (黄冈市中考试题)(2(五城市联赛试题)(3(北京市竞赛试题)(4(陕西省竞赛试题)解题思路:若一开始把分母有理化,则计算必定繁难,仔细观察每题中分子与分母的数字特点,通过分解、分析等方法寻找它们的联系,问题便迎刃而解.思想精髓:因式分解是针对多项式而言的,在整式,分母中应用非常广泛,但是因式分解的思想也广泛应用于解二次根式的问题中,恰当地作类似于因式分解的变形,可降低一些二次根式问题的难度.【例3】比6大的最小整数是多少?(西安交大少年班入学试题)解题思路:直接展开,计算较繁,可引入有理化因式辅助解题,即设x y==想一想:设x=求432326218237515x x x xx x x--++-++的值. (“祖冲之杯”邀请赛试题)的根式为复合二次根式,常用配方,引入参数等方法来化简复合二次根式.【例4】 设实数x ,y 满足(1x y =,求x +y 的值.(“宗泸杯”竞赛试题)解题思路:从化简条件等式入手,而化简的基本方法是有理化.【例5】 (1的最小值.(2的最小值.(“希望杯”邀请赛试题)解题思路:对于(1)的几何意义是直角边为a ,b 的直角三角形的斜边长,从构造几何图形入手,对于(2),设y =,设A (x ,0),B (4,5),C (2,3)相当于求AB +AC 的最小值,以下可用对称分析法解决.方法精髓:解决根式问题的基本思路是有理化,有理化的主要途径是乘方、配方、换元和乘有理化因式.【例6】 设2)m a =≤≤,求1098747m m m m m +++++-的值.解题思路:配方法是化简复合二次根式的常用方法,配方后再考虑用换元法求对应式子的值.能力训练A级1.化简:7()3“希望杯”邀请赛试题)2.若x y x y+=-=,则xy=_____(北京市竞赛试题)3.+(“希望杯”邀请赛试题)4.若满足0<x<y=x,y)是_______(上海市竞赛试题)5.2x-3,则x的取值范围是()A.x≤1B. x≥2C. 1≤x≤2D. x>06)A.1B C. D. 5(全国初中数学联赛试题)7.a,b,c为有理数,且等式a+=成立,则2a+999b+1001c的值是()A.1999 B. 2000 C. 2001D. 不能确定(全国初中数学联赛试题)8、有下列三个命题甲:若α,β是不相等的无理数,则αβαβ+-是无理数;乙:若α,β是不相等的无理数,则αβαβ-+是无理数;丙:若α,β其中正确命题的个数是()A.0个B.1个C.2个D.3个(全国初中数学联赛试题)9、化简:(1(2(3(4(天津市竞赛试题)(5(“希望杯”邀请赛试题)10、设52x=,求代数式(1)(2)(3)(4)x x x x++++的值.(“希望杯”邀请赛试题)117x=,求x的值.12、设x x ==(n 为自然数),当n 为何值,代数式221912319x xy y ++的 值为1985?B 级1.已知3312________________x y x xy y ==++=则. (四川省竞赛试题)2.已知实数x ,y 满足(2008x y =,则2232332007x y x y -+--=____(全国初中数学联赛试题)3.已知42______1x x x ==++2x 那么. (重庆市竞赛试题)4.a =那么23331a a a ++=_____. (全国初中数学联赛试题)5. a ,b 为有理数,且满足等式14a +=++则a +b =( )A .2B . 4C . 6D . 8(全国初中数学联赛试题)6. 已知1,2a b c ===,那么a ,b ,c 的大小关系是( ).Aa b c << B . b <a <c C . c <b <c D . c <a <b(全国初中数学联赛试题)7.=) A . 1a a -B .1a a - C . 1a a+ D . 不能确定 8. 若[a ]表示实数a 的整数部分,则等于( )A .1B .2C .3D . 4(陕西省竞赛试题)9. 把(1)a - )A .B C. D .(武汉市调考题)10、化简:(1 (“希望杯”邀请赛试题)(210099++(新加坡中学生竞赛试题)(3(山东省竞赛试题)(4 (太原市竞赛试题)11、设01,x << 1≤<.(“五羊杯”竞赛试题)12的最大值.13、已知a , b , c为有理数,证明:222a b c a b c ++++为整数.专题02 从求根公式谈起阅读与思考一元二次方程是解数学问题的重要工具,在因式分解、代数式的化简与求值,应用题,各种代数方程,几何问题、二次函数等方面有广泛的应用.初学一元二次方程,需要注意的是: 1、熟练求解解一般形式的一元二次方程,因式分解法是基础,它体现了“降次求解”的基本设想,公式法具有一般性,是解一元二次方程的主要方法,对于各项系数较大的一元二次方程,可以先从分析方程的各项系数特征入手,通过探求方程的特殊根来求解,常用的两个结论是:① 若0=++c b a ,则方程20(0)ax bx c a ++=≠必有一根为1. ② 若0=+-c b a ,则方程20(0)ax bx c a ++=≠必有一根为1-.2、善于变形解有些与一元二次方程相关的问题时,直接求解常给解题带来诸多不便,若运用整体思想,构造零值多项式,降次变形等相关思想方法,则能使问题获得简解.思想精髓一元二次方程的求根公式为1,22b x a-±=这个公式形式优美,内涵丰富:① 公式展示了数学的抽象性,一般性与简洁美; ② 公式包含了初中阶段所学过的全部六种代数运算;③ 公式本身回答了解一元二次方程的全部的三个问题,方程有没有实数根?有实根时共有几个?如何求出实根?例题与求解例1 阅读下列的例题解方程: 2||20x x --=解:①当x ≥0时,原方程化为220x x --=,解得122,1x x ==-(舍)① 当0<x 时,原方程化为220x x +-=,解得11=x (舍),22-=x 请参照例题解方程:2|3|30x x ---=,则方程的根是____(晋江市中考试题)解题思路:通过讨论,脱去绝对值符号,把绝对值方程转化为一般的一元二次方程求解.例2 方程2|1|(42)x x -=-+的解的个数为( )A 、1个B 、2个C 、3个D 、4个(全国初中数学联赛试题)解题思路:通过去绝对值,将绝对值方程转化为一元二次方程求解.例3 已知m ,n 是二次方程2199970x x ++=的两个根,求22+19986)(20008)m m n n +++(的值.(“祖冲之杯”邀请赛试题)解题思路:若求出m ,n 值或展开待求式,则计算繁难,由方程根的定义可得关于m ,n 的等式,不妨从变形等式入手.反思:一元二次方程常见的变形方法有:①把20(0)ax bx c a ++=≠变形为2ax bx c =--②把20(0)ax bx c a ++=≠变形为2ax bx c +=-③把20(0)ax bx c a ++=≠变形为cax b x+=- 其中①②体现了“降次”代换的思想;③则是构造倒数关系作等值代换. 例4 解关于x 的方程:2(1)(21)30m x m x m -+-+-=解题思路:因未指明关于x 的方程的类型,故首先分01=-m 及1-m ≠0两种情况,当1-m ≠0时,还考虑就24b ac -的值的三种情况加以讨论.例5 已知三个不同的实数a ,b ,c 满足3=+-c b a ,方程012=++ax x 和02=++c bx x ,有一个相同的实根,方程02=++a x x 和02=++b cx x 也有一个相同的实根,求a ,b ,c 的值.解题思路:这是一个一元二次方程有公共根的问题,可从求公共根入手.方法指导:公共根问题是一元二次方程常见问题,解这类问题的基本方法是: ①若方程便于求出简单形式的根,则利用公共根相等求解. ②设出公共根,设而不求,消去二次项.例6 已知a 是正整数,如果关于x 的方程32(17)(38)560x a x a x +++--=的根都是整数,求a 的值及方程的整数根.(全国初中数学联赛试题) 解题思路:本题有两种解法,由方程系数特点发现1为隐含的根,从而将试题进行降次处理,或变更主元,将原方程整理为关于a 的较低次数的方程.能力训练 A 级1、已知方程062=+-q x x 可以配成()72=-p x 的形式,那么262=+-q x x 可以配成______________的形式.(杭州市中考试题)2、若分式22221x x x x --++的值为0,则x 的值等于____.(天津市中考试题)3、设方程2199319940,x x +-=和2(1994)1993199510x x -⋅-=的较小的根分别为α,β,则βα⋅=___.4、方程2|45|62x x x +-=-的解应是____(上海市竞赛试题) 5、方程23(1)1x x x ++-=的整数解的个数是____.A 、2个B 、3个C 、4个D 、5个(山东省选拔赛试题)6、若关于x 的一元二次方程22(1)5320m x x m m -++-+=的常数项为0,则m 的值等于( ) A 、1 B 、2 C 、1或2 D 、0(德州市中考试题)7、已知a , b 都是负实数,且1110a b a b+-=-,那么ba 的值是( )A 、12+ B 、12- C 、12- D 、12+- (江苏省竞赛试题)8、方程2||10x x --=的解是( )A 、12± B 、12- C 、12±或12- D 、12-± 9、已知a 是方程2199910x x -+=的一个根,求22199919981a a a -++的值.10、已知2410a a ++=且42321322a ma a ma a--=++,求m 的值. (荆州市竞赛试题)11、是否存在某个实数m ,使得方程220x mx ++=和220x x m ++=有且只有一个公共根?如果存在,求出这个实数m 及两方程的公共实根;如果不存在,请说明理由.12、已知关于x 的方程2(4)(8)(8012)320k k x k x ----+=的解都是整数,求整数k 的值.B 级1、已知α、β是方程2(2)10x m x +-+=的两根,则22(1)(1m )m ααββ++++的值为___ 2、若关于x 的方程20x px q ++=与20x qx p ++=只有一个公共根,则1999(p q)+=___3、设a , b 是整数,方程20x ax b ++=,则b a +=_________(全国通讯赛试题)4、用[]x 表示不大于x 的最大整数,则方程22[]30x x --=解的个数为( )A 、1个B 、2个C 、3个D 、4个 5、已知1||1a a-=,那么代数式1||a a +=( )A 、2 B 、2- C 、 D 6、方程||3||20x x x -+=的实根的个数为( )A 、1个B 、2个C 、3个D 、4个7、已知2519910x x --=,则代数式42(2)(1)1(1)(2)x x x x -+----的值为( )A 、1996B 、1997C 、1998D 、19998、已知三个关于x 的一元二次方程2220,0,0ax bx c bx cx a cx ax b ++=++=++=恰有一个公共实根,则222a b c bc ca ab++的值为( ) A 、0 B 、1 C 、2 D 、3(全国初中数学联赛试题)9、已知x =,求4322621823815x x x x x x --++-+的值. (“祖冲之杯”邀请赛试题)10、设方程2|21|40x x ---=,求满足该方程的所有根之和.(重庆市竞赛试题)11、首项系数不相等的两个二次方程222(1)(2)(2)0a x a x a a --+++= ①及222(1)(2)(2)0b x b x b b --+++= ②(其中a , b 为正整数)有一个公共根,求b ab aa b a b --++的值.(全国初中数学联赛试题)12、小明用下面的方法求出方程30=的解,请你仿照他的方法求出下面另外两个方程的解,专题04 根与系数关系阅读与思考根与系数的关系称为韦达定理,其逆定理也成立,是由16世纪的法国数学家韦达所发现的.韦达定 理形式简单而内涵丰富,在数学解题中有着广泛的应用,主要体现在: 1.求方程中字母系数的值或取值范围; 2.求代数式的值;3.结合根的判别式,判断根的符号特征; 4.构造一元二次方程; 5.证明代数等式、不等式.当所要求的或所要证明的代数式中的字母是某个一元二次方程的根时,可先利用根与系数的关系找 到这些字母间的关系,然后再结合已知条件进行求解或求证,这是利用根与系数的关系解题的基本思路,需要注意的是,应用根与系数的关系的前提条件是一元二次方程有两个实数根,所以,应用根与系数的关系解题时,必须满足判别式△≥0.例题与求解【例1】设关于x 的二次方程22(4)(21)10m x m x -+-+=(其中m 为实数)的两个实数根的倒数和为s ,则s 的取值范围是_________.【例2】 如果方程2(1)(2)0x x x m --+=的三个根可以作为一个三角形的三边长,那么,实数m 的取值范围是_________.A .01m ≤≤B .34m ≥C .314m <≤D .314m ≤≤【例3】已知α,β是方程2780x x -+=的两根,且αβ>.不解方程,求223βα+的值.【例4】 设实数,s t 分别满足22199910,99190s s t t ++=++=并且1st ≠,求41st s t++的值.【例5】(1)若实数,a b 满足258a a +=,258b b +=,求代数式1111b a a b --+--的值; (2)关于,,x y z 的方程组32236x y z axy yz zx ++=⎧⎨++=⎩有实数解(,,)x y z ,求正实数a 的最小值;(3)已知,x y 均为实数,且满足17xy x y ++=,2266x y xy +=,求432234x x y x y xy y ++++的值.【例6】 ,,a b c 为实数,0ac <0++=,证明一元二次方程20ax bx c ++=有大于1的根.能力训练A 级1.已知m ,n 为有理数,且方程20x mx n ++=有一个根是52-,那么m n += .2.已知关于x 的方程230x x m -+=的一个根是另一个根的2倍,则m 的值为 . 3.当m = 时,关于x 的方程228(26)210x m m x m -+-+-=的两根互为相反数; 当 时,关于x 的方程22240x mx m -+-=的两根都是正数;当 时,关于m 的方程23280x x m ++-=有两个大于2-的根.4.对于一切不小于2的自然数n .关于x 的一元二次方程22(2)20x n x n -+-=的两根记为,n n a b (2)n ≥则223320072007111(2)(2)(2)(2)(2)(2)a b a b a b +++=------ .5.设12,x x 是方程222(1)(2)0x k x k -+++=的两个实根,且12(1)(1)8x x ++=,则k 的值为( )A .31-或B .3-C .1D .12k ≥的一切实数 6.设12,x x 是关于x 的一元二次方程22x x n mx ++-=的两个实数根,且1210,30x x x <-<,则 ( ) A .12m n >⎧⎨>⎩ B .12m n >⎧⎨<⎩ C .12m n <⎧⎨>⎩ D .12m n <⎧⎨<⎩7.设12,x x 是方程220x x k +-=的两个不等的实数根,则22122x x +-是( )A .正数B .零C .负数D .不大于零的数8.如图,菱形ABCD 的边长是5,两对角线交于O 点,且AO ,BO 的长分别是关于x 的方程22(21)30x m x m +-++=的根,那么m 的值是( )A .3-B .5C .53-或D .53-或9.已知关于x 的方程:22(2)04m x m x --=. (1)求证:无论m 取什么实数值,方程总有两个不相等的实数根;(2)若这个方程的两个根是12,x x ,且满足212,x x =+求m 的值及相应的12,x x .10.已知12,x x 是关于x 的一元二次方程2430kx x +-=的两个不相等的实数根. (1)求k 的取值范围;(2)是否存在这样的实数k ,使12123222x x x x +-=成立?若存在,求k 的值;若不存在,说明理由.11.如图,已知在△ABC 中,∠ACB =90°,过C 点作CD ⊥AB 于D ,设AD =m ,BD =n ,且AC 2:BC 2=2:1;又关于x 的方程012)1(24122=-+--m x n x 两实数根的差的平方小于192,求整数m 、n 的值.DBAC12.已知,m n 是正整数,关于x 的方程2()0x mnx m n -++=有正整数解,求,m n 的值.B 级1.设1x ,2x 是二次方程032=-+x x 的两根,则3212419x x -+= .2.已知1ab ≠,且有25199580a a ++=及28199550b b ++=则ab= . 3.已知关于x 的一元二次方程2610x x k -++=的两个实数根是12,x x ,且221224x x +=,则k = .4.已知12,x x 是关于x 的一元二次方程22x ax a ++=的两个实数根,则1221(2)(2)x x x x --的最大值为 .5.如果方程210x px ++=(p >0)的两根之差为1,那么p 等于( )A .2B .4CD 6.已知关于x 的一元二次方程2210x mx m -+-=的两个实数根分别是12,x x ,且22127x x +=,则212()x x -的值是 ( )A .1B .12C .13D .257.在Rt △ABC 中,∠C =90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,a 、b 是关于x 的方程0772=++-c x x 的两根,那么AB 边上的中线长是 ( ) A .23 B .25C .5D .2 8.设213a a +=,213b b +=且a b ≠,则代数式2211a b+的值为( ) A .5 B .7 C .9 D .119.已知,a b 为整数,a b >,且方程233()40x a b x ab +++=的两个根,αβ满足关系式(1)(1)(1)(1)ααββαβ+++=++.试求所有整数点对(,)a b .10.若方程2310x x ++=的两根,αβ也是方程620x px q -+=的两根,其中,p q 均为整数,求,p q 的值.11.设,a b 是方程2310x x -+=的两根,c ,d 是方程2420x x -+=的两根,已知a b c dM b c d c d a d a b a b c+++=++++++++.求证:(1)222277a b c d M b c d c d a d a b a b c +++=-++++++++; (2)33334968a b c d M b c d c d a d a b a b c+++=-++++++++.12.设m 是不小于1-的实数,使得关于x 的一元二次方程222(2)310x m x m m +-+-+=有两个不相等实数根12,x x .(1)若22126x x +=,求m 的值;(2)求22121211mx mx x x +--的最大值.13.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.专题06 转化与化归----特殊方程、方程组阅读与思考特殊方程、方程组通常是指高次方程(组)(次数高于两次)、结构巧妙而富有规律性的方程、方程组.降次与消元是解特殊方程、方程组的基本策略,而降次与消元的常用方法是: 1、因式分解; 2、换元; 3、平方; 4、巧取倒数;5、整体叠加、叠乘等.转化是解各类特殊方程、方程组的基本思想,而化归的途径是降次与消元,而化归的方向是一元二次方程,这也可以说是“九九归宗”.例题与求解【例1】已知方程组⎩⎨⎧=+=+233522y x y x 的两组解是),(11y x 与),(22y x ,则1221y x y x +的值是_______ (北京市竞赛题)解题思路:通过消元,将待求式用同一字母的代数式表示,运用根与系数的关系求值.【例2】方程组⎩⎨⎧=+=+2363yz xz yz xy 的正整数解的组数是( )A .1组B .2组C .3组D .4组解题思路:原方程组是三元二次,不易消元降次,不妨从分析常数的特征入手.【例3】 解下列方程:(1) 42)113(1132=+-++-x xx x x x ; (“祖冲之杯”邀请赛试题) (2)121193482232222=+-++-++x x x x x x x x ; (河南省竞赛试题) (3) 1)1998()1999(33=-+-x x ; (山东省竞赛试题) (4) 222222)243()672()43(+-=+-+-+x x x x x x (“祖冲之杯”邀请赛试题) 解题思路:注意到方程左边或右边项与项的结构特点、内在联系,利用换元法求解.【例4】 解下列方程组:(1) ⎪⎪⎩⎪⎪⎨⎧=++=-+-+;612,331y y x y x y x (山东省竞赛试题)(2) ⎩⎨⎧=++=++;2454,144)53)(1(2y x x y x x x (西安市竞赛试题)(3) ⎩⎨⎧+-=+-=.23,23232232y y y x x x x y (全苏数学奥林匹克试题) 解题思路:观察发现方程组中两个方程的特点和联系,用换元法求解或整体处理.【例5】 若关于x 的方程xkx x x x x k 1122+=---只有一个解(相等的解也算一个).试求k 的值与方程的解.(江苏省竞赛试题)【例6】 方程02006322=+++-y x xy x 的正整数解有多少对?解题思路:确定主元,综合利用整除及分解因式等知识进行解题.能力训练A 级1.方程1)1(3)1(222=+-+xx x x 的实数根是_____________. 2.()()()22222224367243+-=+-+-+x xx x x x ,这个方程的解为x =_________________.3.实数z y x ,,满足⎩⎨⎧=+-+-=,0223,362z xy y x y x 则zy x +2的值为_______________.(上海市竞赛题) 4. 设方程组⎪⎩⎪⎨⎧=++=++=++0,0,01222b ax x a x bx bx ax 有实数解,则.________1=++b a(武汉市选拔赛试题)5.使得()()()()7823142222+-++=--x x x x x x 成立的x 的值得个数为( )A .4个B .3个C .2个D .1个(“五羊杯”竞赛试题)6.已知方程组⎩⎨⎧=-=+1,22z xy y x 有实数根,那么它有( )A .一组解B .二组解C .三组解D .无数组解(“祖冲之杯”邀请赛试题) 7.设a a 312=+,b b 312=+且b a ≠,则代数式2211b a +的值为( )A .5B .7C .9D .11 8.已知实数y x ,满足20,922=+=++xy y x y x xy ,则22y x +的值为( )A .6B .17C .1D .6或179.已知关于y x ,的方程组⎩⎨⎧=-+=-222)(3,p y x p xy p y x 有整数解()y x ,,求满足条件的质数p .10.已知方程组⎩⎨⎧=+-=++-01,022y x a y x 的两个解为⎩⎨⎧==,,11y y x x ⎩⎨⎧==,,22y y x x 且21,x x 是两个不等的正数.(1)求a 的取值范围;(2)若116832212221--=-+a a x x x x ,试求a 的值.(南通市中考试题)11.已知b a ,是方程012=--t t 的两个实根,解方程组⎪⎩⎪⎨⎧+=++=+.1,1y ayb x x b ya x(“祖冲之杯”邀请赛试题)12.已知某二次项系数为1的一元二次方程的两个实数根为q p ,,且满足关系式()⎩⎨⎧=+=++,6,5122pq q p p q p 试求这个一元二次方程.(杭州市中考试题)B 级1.方程组⎪⎩⎪⎨⎧==++++=++43251z y x z y x z y x 的解是___________________.2.已知x x x x x 71357139722=+-+++,则x 的值为______________.(全国初中数学联赛试题)3.已知实数00,y x 是方程组⎪⎩⎪⎨⎧+==11x y xy 的解,则._________00=+y x (全国初中数学联赛试题)4.方程组⎪⎩⎪⎨⎧=+=3411,9y xxy 的解是_________________. (“希望杯”邀请赛试题)5.若二元二次方程组()⎩⎨⎧+-==-12,122x k y y x 有唯一解,则k 的所有可能取值为______________. (《学习报》公开赛试题)6.正数654321,,,,,x x x x x x 同时满足1165432=x x x x x x ,2265431=x x x x x x ,3365421=x xx x x x ,4465321=x x x x x x ,6564321=x x x x x x ,9654321=x xx x x x . 则654321x x x x x x +++++的值为________.(上海市竞赛试题)7.方程06623=+--x x x 的所有根的积是()A .3B .-3C .4D .-6E .以上全不对(美国犹他州竞赛试题)8.设y x ,为实数,且满足()()()()⎩⎨⎧=-+--=-+-,1119991,111999133y y x x 则=+y x ( ) A .1 B .-1 C .2 D .-2(武汉市选拔赛试题)9.已知⎪⎩⎪⎨⎧=++=++=,3,2,1222z y x z y x xyz 则111111-++-++-+y zx x yz z xy 的值为( )A .1B .21-C .2D .32-10.对于实数a ,只有一个实数值x 满足等式012211112=-++++-+-+x a x x x x x ,试求所有这样的实数a 的和.(江苏省竞赛试题)11.解方程a x x x x =--+-+1212,其中0>a ,并就正数a 的取值,讨论此方程解的情况.(陕西省竞赛试题)12.已知c b a ,,三数满足方程组⎩⎨⎧=+-=+,4828,82c c ab b a 试求方程02=-+a cx bx 的根. (全国初中数学联赛试题)13.解下列方程(组):(1)()1639322=-+x x x ; (武汉市竞赛试题)(2)()()()6143762=+++x x x ;(湖北省竞赛试题)(3)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+,414,414,414222222x z z z y y y x x (加拿大数学奥林匹克竞赛试题)专题08 二次函数阅读与思考二次函数是初中代数的重要内容,既有着应用非常广泛的丰富性质,又是进一步学习的基础,主要知识与方法有:1.二次函数解析式c bx ax y ++=2的系数符号,确定图象的大致位置.2.二次函数的图象是一条抛物线,抛物线的形状仅仅与a 有关,a b 2-与(ab2-,a b ac 442-)决定抛物线对称轴与顶点的位置.3.二次函数的解析式通常有下列三种形式: ①一般式:c bx ax y ++=2; ②顶点式n m x a y +-=2)(:;③交点式:))((21x x x x a y --=,其中1x ,2x 为方程02=++c bx ax 的两个实根. 用待定系数法求二次函数解析式,根据不同条件采用不同的设法,可使解题过程简捷.例题与求解【例1】 二次函数c bx ax y ++=2的图象如图所示,现有以下结论:①0>abc ;②c a b +<;③024>++c b a ;④b c 32<;⑤()()1≠+>+m b am m b a .其中正确的结论有( )A . 1个B . 2个C . 3个D . 4个 (天津市中考试题)解题思路:由抛物线的位置确定a ,b ,c 的符号,解题关键是对相关代数式的意义从函数角度理解并能综合推理.【例2】 若二次函数c bx ax y ++=2(a ≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),则c b a S ++=的值的变化范围是( )A .0<S <1B . 0<S <2C . 1<S <2D . -1<S <1 (陕西省竞赛试题) 解题思路:设法将S 表示为只含一个字母的代数式,求出相应字母的取值范围,进而确定S 的值的变化范围.【例3】 某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示的坐标系下经过原点O 的一条抛物线(图中标出的数据为已知条件). 在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面3210米,入水处距池边的距离为4米,同时,运动员在距水面高度5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会失误.(1)求这条抛物线的解析式;(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为533米.此次跳水会不会失误?并通过计算说明理由. (河北省中考试题) 解题思路:对于(2),判断此次跳水会不会失误,关键时求出距池边的水平距离为533米时,该运动员与跳台的垂直距离.【例4】 如图,在直角坐标xOy 中,二次函数图象的顶点坐标为C (4,3-),且在x 轴上截得的线段AB 的长为6.(1)求二次函数的解析式;(2)在y 轴上求作一点P (不写作法),使PA +PC 最小,并求P 点坐标;(3)在x 轴的上方的抛物线上,是否存在点Q ,使得以Q ,A ,B 三点为顶点的三角形与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由. (泰州市中考试题) 解题思路:对于(1)、(2),运用对称方法求出A ,B ,P 点坐标;对于(3),由于未指明对应关系,需分类讨论.【例5】 如图,已知边长为4的正方形截去一个角后成为五边形ABCDE ,其中AF =2,BF =1.试在AB 上求一点P ,使矩形PNDM 有最大面积. (辽宁省中考试题) 解题思路:设DN =PM =x ,矩形PNDM 的面积为y ,建立y 与x 的函数关系式. 解题的关键是:最值点不一定是抛物线的顶点,应注意自变量的取值范围.PMF E DNCBA【例6】 将抛物线33:211+-=x y c 沿x 轴翻折,得抛物线2c ,如图所示.(1)请直接写出抛物线2c 的表达式.(2)现将抛物线1c 向左平移m 个单位长度,平移后得到的新抛物线的顶点为M ,与x 轴的交点从左到右依次为A ,B ;将抛物线2c 向右也平移移m 个单位长度,平移后得到的新抛物线的顶点为N ,与x 轴的交点从左到右依次为D ,E .①当B ,D 是线段AE 的三等分点时,求m 的值;②在平移过程中,是否存在以点A ,N ,E ,M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由. (江西省中考试题) 解题思路:把相应点的坐标用m 的代数式表示,由图形性质建立m 的方程. 因m 值不确定,故解题的关键是分类讨论.能力训练A 级1.已知抛物线9)2(2++-=x a x y 的顶点在坐标轴上,则a 的值为__________.2.已知抛物线c bx x y ++=2与y 轴交于点A ,与x 轴正半轴交于B ,C 两点,且BC =2,ABC S ∆=3,则b =____________. (四川省中考试题)3.已知二次函数c bx ax y ++=2的图象如图所示. (1)这个二次函数的解析式是y =_________; (2)当x =________时,3=y ;(3)根据图象回答,当x _______时,0>y . (常州市中考试题) 4.已知二次函数的图象经过原点及点(21-,41-),且图象与x 轴的另一交点到原点的距离为1,则该二次函数的解析式为_______________. (安徽省中考试题) 5.二次函数c bx ax y ++=2与一次函数c ax y +=在同一坐标系中的图象大致是( )A B C D6.由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数c bx x y ++=2的图象过点(1,0)……求证:这个二次函数的图象关于直线2=x 对称,根据现有信息,题中的二次函数图象不具有的性质是( )A .过点(3,0)B .顶点是(2,-2)C .在x 轴上截得的线段长度是2D .与y 轴的交点是(0,3) (盐城市中考试题) 7.如图,抛物线c bx ax y ++=2与两坐标轴的交点分别是A ,B ,E ,且△ABE 是等腰直角三角形,AE =BE ,则下列关系式不能总成立的是( ) (大连市中考试题)A .0=bB . 2c S ABE =∆ C .1-=ac D .0=+c a第7题图 第8题图 8.如图,某中学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距地面4米处高各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )A .9.2米B .9.1米C .9米D .5.1米 (吉林省中考试题)9.如图,是某防空部队进行射击训练时在平面直角坐标系中的示意图. 在地面O ,A 两个观测点测得空中固定目标C 的仰角分别为α和β,OA =1千米,tan α=289, tan β=83,位于O 点正上方35千米D点处的直升机向目标C 发射防空导弹,该导弹运行到达距地面最大高度3千米时,相应的水平距离为4千米(即图中E 点).(1)若导弹运行为一抛物线,求抛物线的解析式;(2)说明按(1)中轨道运行的导弹能否击中目标的理由.(河北省中考试题)10.如图,已知△ABC 为正三角形,D ,E 分别是边AC 、BC 上的点(不在顶点),∠BDE =60°. (1)求证:△DEC ∽△BDA ;(2)若正三角形ABC 的边长为6,并设DC =x ,BE =y ,试求出y 与x 的函数关系式,并求BE 最短时,△BDE 的面积.CEDBA11.如图,在平面直角坐标系中,OB ⊥OA 且OB =2OA ,点A 的坐标是(-1,2). (1)求点B 的坐标;(2)求过点A ,O ,B 的抛物线的解析式;(3)连结AB ,在(2)中的抛物线上求出点P ,使ABO ABP S S ∆∆=.(陕西省中考试题)12.如图,在平面直角坐标系中,抛物线n mx x y ++=2经过点A (3,0),B (0,-3)两点,点P 是直线AB 上一动点,过点P 作x 轴的垂线交抛物线于点M .设点P 的横坐标为t ;(1)分别求直线AB 和这条抛物线的解析式;(2)若点P 在第四象限,连结BM ,AM ,当线段PM 最长时,求△ABM 的面积;(3)是否存在这样的点P ,使得以点P ,M ,B ,O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由. (南宁市中考试题)B 级1.已知二次函数c x x y +-=62的图象顶点与坐标原点的距离为5,则c =________.2.如图,四边形ABCD 是矩形,A ,B 两点在x 的正半轴上,C ,D 两点在抛物线x x y 62+-=上.设OA 的长为m (0<m <3).矩形ABCD 的周长为l ,则l 与m 的函数解析式为__________________.(昆明市中考试题)第2题图 第3题图 第4题图3.如图,在⊙O 的内接△ABC 中,AB +AC =12,AD ⊥BC ,垂足为D (点D 在边BC 上),且AD =3,当AB 的长等于________时, ⊙O 的面积最大,最大面积为___________.4.如图,已知二次函数)0(21≠++=a c bx ax y 与一次函数)0(2≠+=k m kx y 的图象相交于点A (-2,4),B (8,2),则能使21y y >成立的x 的取值范围时______________. (杭州市中考试题) 5.已知函数c bx ax y ++=2的图象如下图所示,则函数c ax y +=的图象只可能是( )(重庆市中考试题)A B C D6.已知二次函数c bx ax y ++=2的图象如图所示,则下列6个代数式:ab ,ac ,c b a ++,c b a +-,b a +2,b a -2中,其值为正的式子个数为 ( )A .2个B .3个C .4个D .4个以上 (全国初中数学联赛试题)7.已知抛物线c bx ax y ++=2(a ≠0)的对称轴是2=x ,且经过点P (3,0)则c b a ++的值为( ) A .-1 B .0 C .1 D .2 8.已知二次函数c bx ax y ++=2(0>a )的对称轴是2=x ,且当0,,2321===x x x π时,二次函数y 的值分别时321,,y y y ,那么321,,y y y 的大小关系是( )A . 321y y y >>B . 321y y y <<C . 312y y y <<D . 312y y y >>9.已知抛物线4)343(2++-=x m mx y 与x 轴交于两点A ,B ,与y 轴交于C 点,若△ABC 是等腰三角形,求抛物线的解析式. (“新世纪杯”初中数学竞赛试题) 10.如图,已知点M ,N 的坐标分别为(0,1),(0,-1),点P 是抛物线241x y =上的一个动点. (1)判断以点P 为圆心,PM 为半径的圆与直线1-=y 的位置关系; (2)设直线PM 与抛物线241x y =的另一个交点为Q ,连结NP ,NQ ,求证:∠PNM =∠QNM . (全国初中数学竞赛试题)11.已知函数122--=x x y 的图象与x 轴相交于相异两点A ,B ,另一抛物线c bx ax y ++=2过点A ,B ,顶点为P ,且△APB 是等腰直角三角形,求a ,b ,c 的值. (天津市竞赛试题)12.如图1,点P 是直线22:--=x y l 上的点,过点P 的另一条直线m 交抛物线2x y =于A ,B 两点.(1)若直线m 的解析式为2321+-=x y ,求A ,B 两点的坐标; (2)如图2,①若点P 的坐标为(-2,t ),当PA =AB 时,请直接写出点A 的坐标;②试证明:对于。
九年级数学培优满分讲义内容(23专题23个word文档150多页)
15直线与圆的位置关系一 16直线与圆的位置关系二 17与圆相关的比例线段
18圆与圆的位置关系 19平面几何的定值问题 20平面几何的最值问题
21分而治之 22数形结合 23顺思逆想
内容截图:
15直线与圆的位置关系一16直线与圆的位置关系二17与圆相关的比例线段
九年级数学培优满分讲义内容(23专题23个word文档150多页)
1、转化与化归一般
5、最优化 6、是偶然还是必然 7、三角函数 8、旋转变换
9、平行线分线段成比例 10、从全等到相似 11、相似三角形的性质
初三数学培优辅导资料
OAB初三数学培优辅导资料(三)一、选择题(每题3分,共30分)1、已知⊙O 的半径为13,弦AB 长为24,则点O 到AB 的距离是( ) A.6 B.5 C.4 D.32、用半径为3cm ,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )3、如图,平行四边形ABCD 的顶点A 、B 、D 在⊙0上,顶点C 在⊙O 直径BE 上,连接AE ,∠E =36°,则∠ADC 的度数是( )A .44°B . 54°C .72°D .53°第3题 第5题 第6题 第7题4、已知⊙O 的面积为2π,则其内接正三角形的面积为( ) A. 33 B. 36 C. 332D. 3625、扇形AOB 的半径为1,∠AOB =90°,以AB 为直径画半圆.则图中阴影部分面积为( ) A .14π B .π12- C .12D .1142π+6、如图,以AB 为直径的⊙O 与弦CD 相交于点E ,且AC =2,AE =,CE =1.则弧BD 的长是( )A.39π B. 239π C.33π D. 233π7、如图,在平面直角坐标系中,⊙P 的圆心坐标是(3,a )(a >3),半径为3,函数y =x 的图象被⊙P 截得的弦AB 的长为,则a 的值是( )A.4B. 32C. 32D. 338、已知⊙O 的直径CD =10cm ,AB 是⊙O 的弦,AB ⊥CD ,垂足为M ,且AB =8cm ,则AC 的长为( )A . 2πcmB . 1.5cmC . πcmD . 1cmA. 25B. 45C. 25或45D. 23或439、如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为( )A. πcm.B. 2πcm.C.3πcmD. 4πcm.10、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则P A+PB的最小值为()A.B.1C.2 D.2第9题第10题第11题二、填空题(每题4分,共24分)11、如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是.12、直径为10cm的⊙O中,弦AB=5cm,则弦AB所对的圆周角是.13、如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2cm,∠BCD=22°30′,则⊙O的半径为cm.14、在⊙O中,AB是⊙O的直径,AB=8cm,==,M是AB上一动点,CM+DM的最小值是cm.15、如图,在扇形OAB中,∠AOB=90°,点C是上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为.第13题第14题第15题第16题16、如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是.三、简答题(共66分)17、(本题6分)如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,求折痕AB的长.18、(本题8分)如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD 与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.19、(本题8分)如图,A、B是圆O上的两点,∠AOB=120°,C是AB弧的中点.(1)求证:AB平分∠OAC;(2)延长OA至P使得OA=AP,连接PC,若圆O的半径R=1,求PC的长.20、(本题10分)如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,求AD的长.21.(本题10分)如图,Rt △ABC 的边BC 位于直线l 上,AC =3,∠ACB =90o ,∠A =30o ,若△RtABC 由现在的位置向右无滑动地翻转,当点A 第3次落在直线上l 时,求点A 所经过的路线的长。
九年级数学全年级培优资料
第1讲 一元二次方程的解法考点·方法·破译1.掌握一元二次方程根的定义并能应用根的定义解题;2.掌握一元二次方程的四种解法,并能灵活应用各种解法解方程; 3.会应用一元二次方程解实际应用题。
经典·考题·赏析【例1】下列关于x 的方程中,一定是一元二次方程的是( )A .(m -2)x 2-2x -1=0B .k 2x +5k +3=0C 21203x --= D .22340x x+-= 【解法指导】A 、B 选项中的二次系数可以为0,不是;D 的分母中含字母,不符合.故选C .【变式题组】1.(威海)若关于x 的一元二次方程x 2+(k +3)x +k =0的一个根是-2,则另一个根是___________.【例2】如果m 、n 是两个不相等的实数,且满足m 2-2m =1,n 2-2n =1,那么代数式2m 2+4n 2-4n +1998=___________. 【解法指导】本题要运用整体代入法,根据一元二次方程根的定义运用整体代入法降次.解:由题意,2m 2=4m +2,4n 2=8n +2,则原式=(4m +2)+(8n +2)-4n +1998=(4m +4n )+4+1998,又由根与系数关系得m +n =2,∴原式=2010.【变式题组】2.(南昌)若3a 2-a -2=0,则5+2a -6a 2=___________.3.(烟台)设a 、b 是方程x 2+x -2009=0的两个实数根,则a 2+2a +b 的值为( ) A .2006 B .2007 C .2008 D .2009【例3】关于x 的一元二次方程(m -3)x 2+4x +m 2-9=0有一个根为0,m 的值为___________. 【解法指导】方法1:将x =0代入;方法2:有一个根为0,则常数项为0.解:依题意m 2-9=0,∴m =±3,根据方程是一元二次方程得m ≠3,综合知m =-3. 【变式题组】4.(庆阳)若关于x 的方程x 2+2x +k -1=0的一个根是0,则k =___________.5.(东营)若关于x 的一元二次方程(m -1)x 2+5x +m 2-3m +2=0的常数项为0,则m 的值等于( )A .1B .2C .1或2D .0【例4】(连云港)解方程:x 2+4x -1=0. 【解法指导】解:解法一:∵a =1,b =4,c =-1,∴x .即x =-2∴原方程的根为1222x x =-=-解法二:配方,得(x +2)2=5,直接开平方,得2x -=,∴原方程的根为1222x x =-=-【变式题组】6.(清远)方程x 2=16的解是( )A .x =±4B .x =4C .x =-4D .x =16 7.(南充)方程(x -3)(x +1)=x -3的解是( )A .x =0B .x =3C .x =3或x =-1D .x =3或x =0 8.(咸宁)方程3x (x +1)=3x +3的解为( )A .x =1B .x =-1C .x 1=0,x 2=-1D .x 1=1,x 2=-19.(温州)我们已经学习了一元二次方程的四种解法:因式分解法、开平方法、配方法和公式法.请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程. ①x 2-3x +1=0;②(x -1)2=3;③x 2-3x =0;④x 2-2x =4.【例5】(山西)解方程:6x 2-x -12=0 【解法指导】为便于配方可先化二次项系数为1,解:方程两边都除以6,移项得x 2-16x =2,配方得x 2-16x +(-112)2=2+(-112)2,(x -112)2=289144=(1712)2,即x -112=±1712,∴x 1=32,x 2=43-. 【变式题组】10.(仙桃)解方程:x 2+4x +2=0.11.(武汉)解方程:x 2-3x -1=0.12.(山西)解方程:x 2-2x -3=0.演练巩固·反馈提高01.(宁德)方程x 2-4x =0的解是___________. 02.(十堰)方程(x +2)(x -1)=0的解为___________. 03.(大兴安岭)方程(x -5)(x -6)=x -5的解是( )A .x =5B .x =或x =6C .x =7D .x =5或x =704.(太原)用配方法解方程x 2-2x -5=0时,原方程应变形为( )A .(x +1)2=6B .(x -1)2=6C .(x +2)2=9D .(x -2)2=905.(云南)一元二次方程5x 2-2x =0的解是( )A .1220,5x x ==B .1250,2x x ==- C .1250,2x x == D .1220,5x x ==-06.(黄石)已知a 、b 是关于x 的一元二次方程x 2+nx -1=0的两实数根,则式子b aa b+的值是( )A .n 2+2B .-n 2+2C .n 2-2D .-n 2-2 07.(毕节)有一人患了流感,经过两轮传染后共有121人患了流感,那么每轮传染中平均一个人传染的人数为( )A .8人B .9人C .10人D .11人08.(台州)用配方法解一元二次方程x 2-4x =5的过程中,配方正确的是( )A .(x +2)2=1B .(x -2)2=1C .(x +2)2=9D .(x -2)2=909.(义乌)解方程x 2-2x -2=0.10.(兰州)用配方法解一元二次方程:2x 2+1=3x .11.(新疆)解方程:(x -3)2+4x (x -3)=0.12.(梧州)解方程:(x -3)2+2x (x -3)=0.13.(长春)解方程:x 2-6x +9=(5-2x )2.14.(上海)解方程:21220y x x xy -=⎧⎪⎨--=⎪⎩①②培优升级·奥赛检测01.(鄂州)已知α、β为方程x 2+4x +2=0的两个实根,则α3+14β+50=___________. 02.已知x 是一元二次方程x 2+3x -1=0的实数根,那么代数式235(2)362x x x x x -÷+---的值为___________.03.(苏州)若x 2-x -2=0).ABCD04.(全国联赛)已知三个关于x 的一元二次方程ax 2+bx +c =0,bx 2+cx +a =0,cx 2+ax +b =0,恰有一个公共实数根,则222a b c bc ca ab++的值为( ).A .0B .1C .2D .3 05.(全国联赛)已知实数x 、y 满足:42423x x-=,y 4+y 2=3,则444y x +的值为( ).A .7BCD .506.(全国联赛)已知m ,n ,且(7m 2-14m +a )(3n 2-6n -7)=8,则a 的值等于( ).A .-5B .5C .-9D .907.(毕节)三角形的每条边的长都是方程x 2-6x +8=0的根,则三角形的周长是___________. 08.(滨州)观察下列方程及其解的特征:⑴12x x +=的解为x 1=x 2=1;⑵152x x +=的解为x 1=2,x 2=12;⑶1103x x +=的解为x 1=3,x 2=13;…… 解答下列问题: ⑴请猜想:方程1265x x +=的解为________;⑵请猜想:关于x 的方程1x x +=________的解为x 1=a ,x 2=1a (a ≠0);⑶下面以解方程1265x x +=为例,验证⑴中猜想结论的正确性.解:原方程可化为5x 2-26x =-5.(下面请大家用配方法写出解此方程的详细过程)09.(泸州)如图,P 1(x 1,y 1),P 2(x 2,y 2),…P n (x n ,y n )在函数4y x=(x >0)的图象上,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…△P n A n -1A n 都是等腰直角三角形,斜边OA 1、A 1A 2、A 2A 3、…A n -1A n 都在x 轴上.⑴求P 1的坐标;⑵求y 1+y 2+y 3+…+y 10的值.第2讲根的判别式及根与系数的关系考点·方法·破译1.掌握一元二次方程根的判别式的运用,能兼顾运用的条件;2.理解掌握一元二次方程的根与系数关系,并会运用根与系数关系求对称式的值.经典·考题·赏板【例1】(成都)若关于x的一元二次方程有两个不相等的实数根,则k的取值范围是()A.k>-1 B. C.k<1 D.【解法指导】由题意得【变式题组】1.(十堰)下列方程中,有两个不相等实数根的是()A. B. C. D.2.(潍坊)关于x的方程有实数根,则整数a的最大值是()A.6 B.7 C.8 D.9【例2】(荆州)关于x的方程只有一解(相同解算一解),则a的值为()A.a=0 B.a=2 C.a=1 D.a=0或a=2【解法指导】本题考查方程的有关知识,关于x的方程只有一解,有两种情况,①该方程是一元一次方程,此时a=0;②该方程是一元二次方程,方程有两个相等的实数根,,解得a=2.故选D.【变式题组】3.(成都)设是一元二次方程的两个实数根,则的值为_________.4.(南通)设是一元二次方程的两个实数根,则,则a=______【例3】(包头)关于x的一元二次方程的两个实数根分别是,且=7,则的值是()A.1 B.12 C.13 D.25【解法指导】本题考查一元二次方程根与系数的关系及根的判别式,要注意所求的值必须满足.由题意知:又∵,而当m=5时,原方程的判别式,此时方程无解,不合题意舍去.,故选C.【变式题组】5.(潍坊)已知关于x的一元二次方程的两个实数根是,则k的值是()A.8 B.-7 C.6 D.56.(鄂州)设是关于x的一元二次方程的两实根,当a为何值时,有最小值?最小值是多少?【例4】(兰州)已知关于x的一元二次方程.(1)如果此方程有两个不相等的实数根,求a的取值范围;(2)如果此方程的两个实数根为,且满足,求a的值.【解法指导】 解:(1).∵方程有两个不相等的实数根,.(2)由题意得:【变式题组】7.(绵阳)已知关于x 的一元二次方程x 2 + 2(k -1)x + k 2-1 = 0有两个不相等的实数根.(1)求实数k 的取值范围; (2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.【例5】 (中山)已知关于x 的方程.(1)求证:方程有两个不相等的实数根.(2)当m 为何值时,方程的两根互为相反数?并求出此时方程的解.【解法指导】 证明方程有两个不相等的实数根,一般要把化为完全平方加正常数的形式.(1)证明:因为△=)12(4)2(2--+m m =4)2(2+-m 所以无论m 取何值时, △>0,所以方程有两个不相等的实数根.(2)解:因为方程的两根互为相反数,所以021=+x x ,根据方程的根与系数的关系得02=+m ,解得2-=m ,所以原方程可化为052=-x ,解得51=x ,52-=x【变式题组】8.(中山)已知一元二次方程.(1)若方程有两个实数根,求m 的值;(2)若方程的两个实数根为,且+,求m 的值.【例6】 设实数s ,t 分别满足,并且st ≠1,求的值.【解法指导】 本题要观察s,t 的共同点,应用方程的思想,把它们看做一个一元二次方程的两根,应用根与系数关系求值. 解:∵s ≠0,∴第一个等式可以变形为:,又∵st ≠1,∴t 是一元二次方程x 2 + 99x + 19 = 0的两个不同的实根,于是,有,即st + 1 =-99s ,t = 19s .∴演练巩固·反馈提高01.(东营)若n (n ≠0)是关于x 的方程的根,则m+n 的值为A.1B.2C.-1D.-202.(株洲)定义:如果一元二次方程20(0)ax bx c a ++=≠满足0a b c ++=,那么我们称这个方程为“凤凰”方程. 已知20(0)ax bx c a ++=≠ 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是A .a c =B .a b =C .b c =D . a b c ==03.(崇左)一元二次方程的一个根为-1,则另一个根为 .04.(贺州)已知关于x 的一元二次方程有两个不相等的实数根,则实数m 的取值范围是 .05.(上海)如果关于x 的方程20x x k -+=(k 为常数)有两个相等的实数根,那么k = .1、 06.(泰安)关于x 的一元二次方程02)12(22=-+++-k x k x 有实数根,则k 的取值范围是 .07.(淄博)已知关于x 的方程014)3(222=--+--k k x k x . (1)若这个方程有实数根,求k 的取值范围; (2)若这个方程有一个根为1,求k 的值;(3)若以方程014)3(222=--+--k k x k x 的两个根为横坐标、纵坐标的点恰在反比例函数xmy =的图象上,求满足条件的m 的最小值.08.已知关于x 的一元二次方程(1)若方程有两个相等的实数根,求m 的值; (2)若方程的两个实数根之积等于,求的值.02=--m x x09.(孝感)已知关于x 的一元二次方程22(21)0x m x m +-+=有两个实数根1x 和2x . (1)求实数m 的取值范围;(2)当22120x x -=时,求m 的值.10.(鄂州)关于x 的方程04)2(2=+++kx k kx 有两个不相等的实数根. (1)求k 的取值范围.(2)是否存在实数k ,使方程的两个实数根的倒数和等于0?若存在,求出k 的值;若不存在,说明理由 11.(北京)已知:关于x 的一元二次方程2(32)220(0)mx m x m m -+++=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中12x x <).若y 是关于m 的函数,且212y x x =-,求这个函数的解析式;(3)在(2)的条件下,结合函数的图象回答:当自变量m 的取值范围满足什么条件时,2y m ≤.12.(淄博)已知12,x x 是方程220x x a -+=的两个实数根,且1223x x +=- (1)求12,x x 及a 的值; (2)求32111232x x x x -++的值.培优升级·奥赛检测01.(全国联赛)设213a a +=,213b b +=,且a b ≠,则代数式2211a b+的值为 ( )A 5. B7. C 9. D.11.02.(延边预赛)已知m 是方程的一个根,则代数式的值等于( )A .2016 B.2017 C.2018 D.201903.如果a 、b 都是质数,且,那么的值为( )A . B. C. D 或204.(全国竞赛)已知实数,且满足的值为( )A .23 B.-23 C.-2 D.-1305.(全国竞赛)设是关于x 的方程的两个实数根,则的最大值为___________06.已知是方程的两个实数根,则07.(全国联赛)对于一切不小于2的自然数n ,关于x 的一元二次方程的两个根记作,则__08.已知关于x的方程:.(1)求证:无论m取什么实数值,这个方程总有两个相异实根;(2)若这个方程的两个实根为,满足,求m的值及相应的.09.(全国竞赛)设m是不小于-1的实数,使得关于x的方程有两个不相等的实数根,(1)若,求m的值;(2)求的最大值.第3讲 一元二次方程的应用考点方法破译1.能灵活应用一元二次方程的四种解法解方程; 2.会建立一元二次方程模型解实际应用题. 经典考题赏析【例l 】 (南平)有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为( )A .8人B .9人C .10人D .11人【解法指导】 构建一元二次方程模型求解.设每轮传染中平均一个人传染的人数为x,第一轮被传染人数为x ,患流感人数为x+l ;第二轮被传染人数为x(x+1),所以l+x+x(x+1)=100,解得x=9.应选B . 【变式题组】 1.(甘肃)近年来,全国房价不断上涨,某县2010年4月份的房价平均每平方米为3600元,比2008年同期的房价平均每平方米上涨了2000元,假设这两年该县房价的平均增长率为x ,则关于x 的方程为 .2.(襄樊)为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为10m 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学培优资料(第8周)
姓名 班级 学号
1、如图,已知AOB OA OB ∠=,,点E 在OB 边上,四边形AEBF 是矩形.请你只用无刻度的直尺在图中画出AOB ∠的平分线(请保留画图痕迹).
2、如图,在宽为20m ,长为32m 的矩形地面上修筑同样宽
的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m 2,求道路的宽.
解:设道路宽为x 米根据题意,可列出方程为
整理得
A
B
F E O
解得(舍去),
答:道路宽为2米。
3、西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元.该经营户要想每天盈利200元,应将每千克小型西瓜的售价降多少元? 解:设降价x 元,那么多售出40×(x /0.1)=400x 千克
(3-x -2)×(200+400x )-24=200
整理得:400x ²-200x +24=0
50x ²-25x +3=0
解得x =0.2或x =0.3
所以降价0.2元或0.3元就可以获得利润200元
4、已知关于x 的方程03)12(22=-+++k x k x 有实数根,求k 的取值范围.
解:因为03)12(22=-+++k x k x 有实数根
所以△=(2k +1)2-4(k 2-3)
=4k 2+4k +1-4k 2+12
=4k +13≥0
所以 k 413-≥ 5、如图,已知△ABD ,△BCE ,△ACF 都是等边三角形.
(1)求证:四边形ADEF 是平行的四边形;
(2)△ABC 满足什么条件时,四边形ADEF 是菱形?说明理由.
证明:∵△ABD ,△BCE 是等边三角形
∴∠DBA=∠EBC=60度
∴∠DBA -∠EB A =∠EBC -∠EB A 即∠DBE=∠ABC
∵DB=BA EB=BC
∴△DBE≌△ABC
∴DE=AC=FA
同理AD=EF
∴四边形DAFE 是平行四边形(两组对边分别相等的四边形是平行四边形)
(2) AB=AC
6、类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD 是“等对角四边形”,∠A ≠∠C ,∠A=70°,∠B=80°.求∠C ,∠D 的度数.
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD (如图2),其中∠ABC=∠ADC ,AB=AD ,此时她发现CB=CD 成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形“ABCD 中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC 的长.
解答:
解:(1)如图1
∵等对角四边形ABCD,∠A≠∠C,
∴∠D=∠B=80°,
∴∠C=360°﹣70°﹣80°﹣80°=130°;
(2)①如图2,连接BD,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD,
②不正确,
反例:如图3,∠A=∠C=90°,AB=AD,
但CB≠CD,
(3)(Ⅰ)如图4,当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,
∵∠ABC=90°,∠DAB=60°,AB=5,
∴AE=10,
∴DE=AE﹣AD=10﹣4═6,
∵∠EDC=90°,∠E=30°,
∴CD=2,
∴AC===2
(Ⅱ)如图5,当∠BCD=∠DAB=60°时,过点D作DE⊥AB于点E,DF⊥BC于点F,
∵DE⊥AB,∠DAB=60°AD=4,
∴AE=2,DE=2,
∴BE=AB﹣AE=5﹣2=3,
∵四边形BFDE是矩形,
∴DF=BE=3,BF=DE=2,
∵∠BCD=60°,
∴CF=,
∴BC=CF+BF=+2=3,
∴AC===2.。
