大学物理第五版热力学习题课
天津大学物理化学教研室《物理化学》(第5版)笔记和课后习题(含考研真题)详解-热力学第一定律(圣才出
或
dU=δQ＋δW
2．焦耳实验 虽然焦耳实验的设计是不精确的，但是并不影响“理想气体的热力学能仅仅是温度的函 数”这一结论的正确性。
3．体积功的定义和计算 由于系统体积的变化而引起的系统与环境交换的能量称为体积功，其定义式为：
δW=－pambdV （1）气体向真空膨胀时，pamb=0，得出
W=0 （2）恒外压过程体积功
W= －pamb(V2－V1)= －pambΔV （3）对于理想气体恒压变温过程
3 / 52
圣才电子书
十万种考研考证电子书、题库视频学习平台
W= －pambΔV= －nRΔT
（4）可逆过程体积功
Wr
=
−
V2 V1
pambdV
（5）理想气体恒温可逆过程体积功
Wr
=−
V2 V1
pambdV
= nRT ln(V1
V2 ) = nRT ln( p2
p1)
（6）可逆相变体积功
W=－pdV
三、恒容热、恒压热及焓 1．恒容热（QV） 指系统进行恒容且无非体积功的过程中与环境交换的热，它与过程的ΔU 在量值上相等。 而ΔU 只取决于始、末状态，故对一个微小的恒容且无非体积功的过程有如下关系：
=定值)、恒容过程(V=定值)、绝热(系统与环境之间无热交换)过程、循环过程等。
4．功 系统得到环境所作的功时，W＞0；系统对环境作功时，W＜0。功是途径函数，单位为 J。 （1）体积功（W）：系统因其体积发生变化反抗环境压力(pamb)而与环境交换的能量，
定义式为W = −pambdV ；
（2）非体积功（W ）：除了体积功以外的一切其他形式的功，如电功、表面功等。
焓为广度量，是状态函数，单位为 J。
大学物理上册（第五版）重点总结归纳及试题详解第五章热力学基础
⼤学物理上册（第五版）重点总结归纳及试题详解第五章热⼒学基础第五章热⼒学基础⼀、基本要求1．掌握功、热量、内能的概念，理解准静态过程。
2．掌握热⼒学第⼀定律，能分析、计算理想⽓体等值过程和绝热过程中功、热量、内能的改变量。
3．掌握循环过程和卡诺循环等简单循环效率的计算。
4．了解可逆过程和不可逆过程。
5．理解热⼒学第⼆定律及其统计意义，了解熵的玻⽿兹曼表达式及其微观意义。
⼆、基本内容1. 准静态过程过程进⾏中的每⼀时刻，系统的状态都⽆限接近于平衡态。
准静态过程可以⽤状态图上的曲线表⽰。
2. 体积功pdV dA = ?=21V V pdV A功是过程量。
3. 热量系统和外界之间或两个物体之间由于温度不同⽽交换的热运动能量。
热量也是过程量。
4. 理想⽓体的内能2iE RT ν=式中ν为⽓体物质的量，R 为摩尔⽓体常量。
内能是状态量，与热⼒学过程⽆关。
5. 热容定体摩尔热容 R i dT dQ C V m V 2)(,== 定压摩尔热容 R i dT dQ C p mp 22)(,+== 迈耶公式 R C C m V m p +=,, ⽐热容⽐ ,,2p m V mC i C iγ+==6．热⼒学第⼀定律A E Q +?=dA dE dQ +=（微分形式）7．理想⽓体热⼒学过程主要公式（1）等体过程体积不变的过程，其特征是体积V =常量。
过程⽅程： =-1PT 常量系统对外做功： 0V A =系统吸收的热量：()(),21212V V m iQ vC T T v R T T =-=-系统内能的增量：()212V iE Q v R T T ?==-（2）等压过程压强不变的过程，其特征是压强P =常量。
过程⽅程： =-1VT 常量系统对外做功：()()212121V P V A PdV P V V vR T T ==-=-?系统吸收的热量： (),2112P P m i Q vC T v R T T ??=?=+-系统内能的增量： ()212iE v R T T ?=-（3）等温过程温度不变的过程，其特征是温度T =常量。
大学物理习题课答案课件
E
M M mol
CJ
根 据 根 据 热 力 学 定 律 Q =E+A 可 知 A=-E 623J
(负 号 表 示 外 界 做 功 ）
练习十八 热力学基础（二）
1. 用公式 ECVT
(式中CV为定体摩尔热容量，视为常量，v为气体摩尔数)计算理想气体内能增量
时，此式
[(A) ]
所以Q2
1 n
Q1
4．已知1 mol的某种理想气体(其分子可视为刚性分子)，在等压过程中温度上升1 K，内
能增加了20.78 J，则气体对外作功为_____8_._3__1_J_____， 气体吸收热量为_____2_9__.0__9_J_____．
等压过程：E=n i RT i R 20.78J ,
2
2
Cp
Cv
R
i 2
R
R
20.78
8.31
29.09
Qp nC pT 29.09J
Qp E A p
A p 8.31J
6．一定量的某种理想气体进行如图所示的循环过程．已知气体在状态A的温度为TA＝ 300 K，求
(1) 气体在状态B、C的温度； (2) 各过程中气体对外所作的功； (3) 经过整个循环过程，气体从外界吸收的总热量(各过程吸热的代数和)．
Q =A+ΔE =200 J．
1
2
B
V (m 3) 3
2. 热力学第二定律表明：
(A) 不可能从单一热源吸收热量使之全部变为有用的功．
(B) 在一个可逆过程中，工作物质净吸热等于对外作的功．
(C) 摩擦生热的过程是不可逆的．
(D) 热量不可能从温度低的物体传到温度高的物体．
［C ］
《大学物理》热力学基础 自学练习题
《大学物理》热力学基础 自学练习题9-1下列表述是否正确?为什么?并将错误更正． （1）A E Q ∆+∆=∆ （2）⎰+=V p E Q d（3）121Q Q -≠η （4）121Q Q -<不可逆η 解：(1)不正确，A E Q +∆=(2)不正确， ⎰+=V p E Q d Δ(3)不正确，121Q Q -=η (4)不正确，121Q Q -=不可逆η 9-2 V p -图上封闭曲线所包围的面积表示什么?如果该面积越大，是否效率越高?答：封闭曲线所包围的面积表示循环过程中所做的净功．由于1Q A 净=η，净A 面积越大，效率不一定高，因为η还与吸热1Q 有关．9-3 如题7-3图所示，有三个循环过程，指出每一循环过程所作的功是正的、负的，还是零，说明理由．解：各图中所表示的循环过程作功都为0．因为各图中整个循环分两部分，各部分面积大小相等，而循环方向一个为逆时针，另一个为顺时针，整个循环过程作功为0．题7-3图9-4 用热力学第一定律和第二定律分别证明，在V p -图上一绝热线与一等温线不能有两 个交点．题7-4图解：1.由热力学第一定律有A E Q +∆= 若有两个交点a 和b ，则 经等温b a →过程有0111=-=∆A Q E 经绝热b a →过程012=+∆A E 022<-=∆A E从上得出21E E ∆≠∆，这与a ,b 两点的内能变化应该相同矛盾．2.若两条曲线有两个交点，则组成闭合曲线而构成了一循环过程，这循环过程只有吸热，无放热，且对外做正功，热机效率为%100，违背了热力学第二定律． 9-5 一循环过程如题7-5图所示，试指出： (1)ca bc ab ,,各是什么过程； (2)画出对应的V p -图；(3)该循环是否是正循环?(4)该循环作的功是否等于直角三角形面积?(5)用图中的热量ac bc ab Q Q Q ,,表述其热机效率或致冷系数． 解：(1) a b 是等体过程bc 过程：从图知有KT V =，K 为斜率 由vRT pV = 得KvR p =故bc 过程为等压过程 ca 是等温过程(2)V p -图如题57'-图题57'-图(3)该循环是逆循环(4)该循环作的功不等于直角三角形面积，因为直角三角形不是V p -图中的图形．(5) abca bc abQ Q Q Q e -+=题7-5图 题7-6图9-6 两个卡诺循环如题7-6图所示，它们的循环面积相等，试问： (1)它们吸热和放热的差值是否相同； (2)对外作的净功是否相等； (3)效率是否相同?答：由于卡诺循环曲线所包围的面积相等，系统对外所作的净功相等，也就是吸热和放热的差值相等．但吸热和放热的多少不一定相等，效率也就不相同． 9-7 评论下述说法正确与否?(1)功可以完全变成热，但热不能完全变成功；(2)热量只能从高温物体传到低温物体，不能从低温物体传到高温物体．(3)可逆过程就是能沿反方向进行的过程，不可逆过程就是不能沿反方向进行的过程． 答：(1)不正确．有外界的帮助热能够完全变成功；功可以完全变成热，但热不能自动地完全变成功； (2)不正确．热量能自动从高温物体传到低温物体，不能自动地由低温物体传到高温物体．但在外界的帮助下，热量能从低温物体传到高温物体．(3)不正确．一个系统由某一状态出发，经历某一过程达另一状态，如果存在另一过程，它能消除原过程对外界的一切影响而使系统和外界同时都能回到原来的状态，这样的过程就是 可逆过程．用任何方法都不能使系统和外界同时恢复原状态的过程是不可逆过程．有些过程 虽能沿反方向进行，系统能回到原来的状态，但外界没有同时恢复原状态，还是不可逆过程． 9-8 热力学系统从初平衡态A 经历过程P 到末平衡态B ．如果P 为可逆过程，其熵变为 ：⎰=-BA AB T Q S S 可逆d ，如果P 为不可逆过程，其熵变为⎰=-B A A B T Q S S 不可逆d ，你说对吗？哪一个表述要修改，如何修改？答：不对．熵是状态函数，熵变只与初末状态有关，如果过程P 为可逆过程其熵变为：⎰=-BA AB TQ S S 可逆d ，如果过程P 为不可逆过程，其熵变为⎰>-BA AB TQ S S 不可逆d9-10 如题7-10图所示，一系统由状态a 沿acb 到达状态b 的过程中，有350 J 热量传入系统，而系统作功126 J ．(1)若沿adb 时，系统作功42 J ，问有多少热量传入系统?(2)若系统由状态b 沿曲线ba 返回状态a 时，外界对系统作功为84 J ，试问系统是吸热还是放热?热量传递是多少?题7-10图解：由abc 过程可求出b 态和a 态的内能之差 A E Q +∆=224126350=-=-=∆A Q E Jabd 过程，系统作功42=A J26642224=+=+∆=A E Q J 系统吸收热量ba 过程，外界对系统作功84-=A J30884224-=--=+∆=A E Q J 系统放热9-11 1 mol 单原子理想气体从300 K 加热到350 K ，问在下列两过程中吸收了多少热量?增加了多少内能?对外作了多少功? (1)体积保持不变； (2)压力保持不变． 解：(1)等体过程由热力学第一定律得E Q ∆=吸热 )(2)(1212V T T R iT T C E Q -=-=∆=υυ 25.623)300350(31.823=-⨯⨯=∆=E Q J 对外作功 0=A(2)等压过程)(22)(1212P T T R i T T C Q -+=-=υυ 吸热 75.1038)300350(31.825=-⨯⨯=Q J )(12V T T C E -=∆υ 内能增加 25.623)300350(31.823=-⨯⨯=∆E J对外作功 5.4155.62375.1038=-=∆-=E Q A J 9-12 一个绝热容器中盛有摩尔质量为mol M ，比热容比为γ的理想气体，整个容器以速度v 运动，若容器突然停止运动，求气体温度的升高量(设气体分子的机械能全部转变为内能)．解：整个气体有序运动的能量为221mu ，转变为气体分子无序运动使得内能增加，温度变化2V 21mu T C M m E =∆=∆ )1(211212mol V 2mol -==∆γu M RC u M T 9-13 0.01 m 3氮气在温度为300 K 时，由0.1 MPa(即1 atm)压缩到10 MPa ．试分别求氮气经等温及绝热压缩后的(1)体积；(2)温度；(3)各过程对外所作的功． 解：(1)等温压缩 300=T K 由2211V p V p = 求得体积 3211210101.0101-⨯=⨯==p V p V 3m 对外作功21112ln lnp pV p V V VRT A == 01.0ln 01.010013.115⨯⨯⨯⨯=31067.4⨯-=J(2)绝热压缩R C 25V =57=γ 由绝热方程 γγ2211V p V p = γγ/12112)(p V p V =1121/12112)()(V p pp V p V γγγ==3411093.101.0)101(-⨯=⨯=m 由绝热方程γγγγ---=22111p T p T 得K 579)10(30024.04.1111212=⨯==--T p p T T γγγγ热力学第一定律A E Q +∆=，0=Q 所以 )(12molT T C M MA V --= RT M MpV mol =，)(2512111T T R RT V p A --= 35105.23)300579(25300001.010013.1⨯-=-⨯⨯⨯⨯-=A J9-14 理想气体由初状态),(11V p 经绝热膨胀至末状态),(22V p ．试证过程中气体所作的功为12211--=γV p V p A ，式中γ为气体的比热容比.答：证明： 由绝热方程C V p V p pV ===γγγ2211 得γγVV p p 111= ⎰=21d V V V p A⎰-----==21)11(1d 11121111V V r V V V p v v V p A γγγγγ]1)[(112111---=-γγV V V p 又 )(1111211+-+----=γγγγV V V p A112221111--=+-+-γγγγγV V p V V p所以 12211--=γV p V p A9-15 1 mol 的理想气体的T-V 图如题7-15图所示，ab 为直线，延长线通过原点O ．求ab 过程气体对外做的功．题7-15图解：设KV T =由图可求得直线的斜率K 为 02V T K =得过程方程 V V T K 02=由状态方程 RT pV υ= 得 VRTp υ=ab 过程气体对外作功⎰=02d V v V p A⎰⎰⎰====00000020002202d 2d 2d V V V v V V RTV V RT VV V T V R V V RT A9-16 某理想气体的过程方程为a a Vp ,2/1=为常数，气体从1V 膨胀到2V ．求其所做的功．解：气体作功⎰=21d V v V p A⎰-=-==-2121)11()(d 2121222V V V V V V a V a V V a A 9-17 设有一以理想气体为工质的热机循环，如题7-17图所示．试证其循环效率为1112121---=p p VV γη 答：等体过程吸热 )(12V 1T T C Q -='υ)(1221V 11RV p R V p C Q Q -='= 绝热过程 03='Q 等压压缩过程放热 )(12p 2T T C Q -='υ )(12P 22T T C Q Q --='=υ )(2212P RV p R V p C -= 循环效率 121Q Q -=η )1/()1/(1)()(1121212221V 2212p 12---=---=-=p p V p V p C V p V p C Q Q ννγηη题7-17图 题7-19图****************************************************************************** 9-1 一系统由图示的状态a 经acd 到达状态b ，系统吸收了320J 热量，系统对外作功126J 。
大学物理-热学习题课(ppt模板)
（二）热力学 1、功、热量、内能 W PdV (过程量)
Q Mc T2 T1 (过程量) M E T CVm T2 T1 (状态量)
2、热力学第一定律及其应用 等值过程 Q, E 和 W 的计算 见附表
附表：
Q
等温 过程 等压 过程 等体 过程
V2 M RT ln V1 M CP,m T M CV ,m T
（2）从状态B到达状态C，气体的熵变为 TC dQ TC C pdT TC 5 R 9 SBC C p ln ln TB T TB T TB 2 2
2.5 8.31 1.504 31.25 J K
1
得 T 274.37K
熵变：0C 冰
0C 水
dQ 1 S1 dQ T T 1 1 m2 L 12.23J K T 0C 的水 274.37 K 的水 m2 c2 dT dQ S 2 T T T 1 m2 c 2 ln 0.21J K T1
T2 卡诺逆循环 T1 T2
Q1
Q1
4、热力学第二定律的两种表述
克劳修斯 “热量不能自动的 从低温物体传向高温物体” 开尔文 “其唯一效果是热全部转 变为功的过程是不可能的” 5、可逆过程和不可逆过程 ★6、熵的计算与熵增加原理
dQ S 2 S1 T 可逆
三、计算 1、孤立系统中 m1 0.5kg, T1 276K
的水，和 m2 0.01kg, T2 273K 的冰 混合后冰全部融化 求（1）达到平衡时的温度 3 1 （2）系统的熵变（ L 334 10 J kg ） 解：平衡时温度为 T
m1c1 T1 T m2 L m2 c2 T T2
《大学物理学》热力学基础练习题
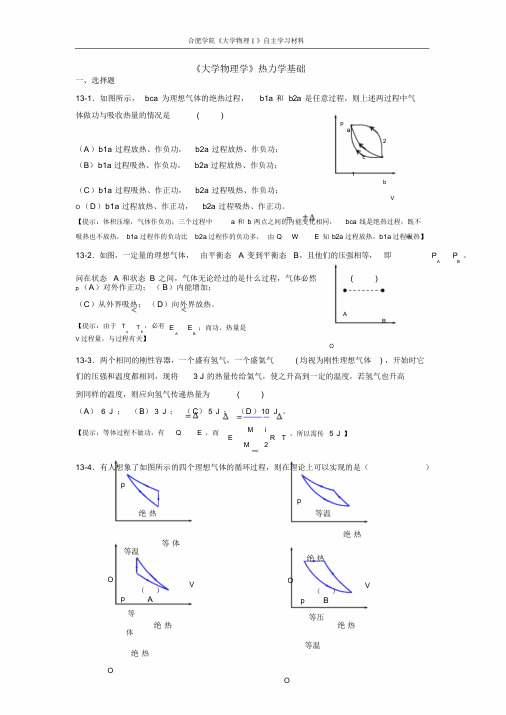
合肥学院《大学物理Ⅰ》自主学习材料《大学物理学》热力学基础一、选择题13-1．如图所示，bca 为理想气体的绝热过程，b1a 和b2a 是任意过程，则上述两过程中气体做功与吸收热量的情况是( )pa2（A）b1a 过程放热、作负功，b2a 过程放热、作负功；c（B）b1a 过程吸热、作负功，b2a 过程放热、作负功；1b（C）b1a 过程吸热、作正功，b2a 过程吸热、作负功；VO （D）b1a 过程放热、作正功，b2a 过程吸热、作正功。
【提示：体积压缩，气体作负功；三个过程中 a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b1a 过程作的负功比b2a 过程作的负功多，由Q W E 知b2a 过程放热，b1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态 A 变到平衡态B，且他们的压强相等，即P P 。
A B问在状态 A 和状态 B 之间，气体无论经过的是什么过程，气体必然( )p （A）对外作正功；（B）内能增加；（C）从外界吸热；（D）向外界放热。
AB【提示：由于T T ，必有A B E E ；而功、热量是A BV 过程量，与过程有关】O13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气( 均视为刚性理想气体) ，开始时它们的压强和温度都相同，现将 3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为( )（A） 6 J ；（B）3 J ；（C）5 J ；（D）10 J 。
【提示：等体过程不做功，有Q E ，而M iE R TM 2mol，所以需传 5 J 】13-4．有人想象了如图所示的四个理想气体的循环过程，则在理论上可以实现的是（）pp绝热等温绝热等体等温绝热Op 等（）AV Op（）B等压V 绝热绝热体等温绝热OOVV （）C（）D【提示：(A) 绝热线应该比等温线陡，（B）和（C）两条绝热线不能相交】热力学基础-1合肥学院《大学物理Ⅰ》自主学习材料13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J，则对外做功（）（A）2000 J ；（B）1000 J ；（C）4000 J ；（D）500 J 。
大学物理习题解答3第三章热力学
第三章热力学本章提要1．准静态过程系统连续经过的每个中间态都无限接近平衡态的一种理想过程。
准静态过程可以用状态图上的曲线表示。
2．内能系统内所有分子热运动动能和分子之间相互作用势能的和，其数学关系式为(,)E E V T=内能是态函数。
3．功功是过程量。
微分形式：VpA dd=积分形式：⎰=21dV VV pA4．热量两个物体之间或物体内各局部之间由于温度不同而交换的热运动能量。
热量也是过程量。
5．热力学第一定律热力学第一定律的数学表达式：Q E A=∆+热力学第一定律的微分表达式：d d dQ E A=+由热力学第一定律可知，第一类永动机是不可能造成的。
6．理想气体的热功转换〔1〕等体过程：d 0A = 热量增量为m m (d )d d V V MQ E C T μ,,==或m 21m 21V ,V ,MQ E E C (T T )μ=-=-〔2〕等压过程: 热量增量为(d )d d d d p Q E A E p V =+=+因m 21()V ME C T T μ∆,-=212121()()V V MA p V p V V R T T μd ==-=-⎰那么)()(21212T T R MT T R i M Q P -+-=μμ 〔3〕等温过程：d 0E =热量增量为(d )d d V Q A p V ==因2121d ln V T V V MV MA RT RT V V μμ==⎰那么2112lnln T T V pMM Q A RT RT V p μμ=== 〔4〕绝热过程：d 0Q = 根据热力学第一定路可得d d 0E A +=那么m d d d d V ,MA p V E C Tμ==-=-或221121m ()d d V V V ,V V MA E E p V C T μ=--==-⎰⎰)(112211V p V p A --=γ 在绝热过程中理想气体的p 、V 、T 三个状态参量之间满足如下关系：常量=γpV常量=-1γTV 常量=--γγT p 17．热容量等体摩尔热容量：m (d )d d d V V Q EC T T,== 等压摩尔热容量：m (d )d d d d d p p Q E VC p TT T,==+ 对于理想气体，假设分子自由度为i ，那么m 2V ,i C R = m 22P,i C R +=迈耶公式：m m p,V ,C C R =+比热容比：m m22p,V ,C i C γ+==8．焓在等压过程中，由热力学第一定律可得2121()()P Q E p V E E V V =∆+∆=-+-由于12P P P ==，上式可写为222111()()P Q E p V E pV =+-+ 如果令H E pV =+21P Q H H H =-=∆焓是一个态函数。
大学物理热学习题课
dN m 32 4 ( ) e Ndv 2kT
v2
对于刚性分子自由度 单原子 双原子 多原子
i tr
(1)最概然速率
2kT 2 RT RT vp 1.41 m
(2)平均速率
i=t=3 i = t+r = 3+2 = 5 i = t+r = 3+3 =6
6、能均分定理
8kT 8 RT RT v 1.60 m
M V RT ln 2 M mol V1
QA
绝热过程
PV 常量
M E CV T M mol
(2)由两条等温线和两条绝热线 组成的循环叫做 卡诺循环。 •卡诺热机的效率
Q0
Q2 T2 卡诺 1 1 Q1 T1
M P1V1 P2V2 A CV T M mol 1
E 0
•热机效率
A Q1 Q2
M E CV T M mol M Q C P T M mol
A Q1 Q2 Q2 1 Q1 Q1 Q1
A=P(V2-V1) 等温过程
A
E 0
Q1 Q2 •致冷系数 e W Q1 Q2
热机效率总是小于1的， 而致冷系数e可以大于1。
定压摩尔热容
比热容比
CP ( dQ )P dT i2 i
8、平均碰撞次数 平均自由程
z
2d v n
2
CV •对于理想气体：
Cp
v z
1.热力学第一定律
1 2 2d n
二、热 力 学 基 础
Q ( E2 E1 ) A dQ dE dA
准静态过程的情况下
4. 摩尔数相同的两种理想气体 一种是氦气，一种是氢气，都从 相同的初态开始经等压膨胀为原 来体积的2倍，则两种气体( A ) (A) 对外做功相同，吸收的热量 不同. (B) 对外做功不同，吸收的热量 相同. (C) 对外做功和吸收的热量都不 同. (D) 对外做功和吸收的热量都相 同. A=P(V2-V1)
大学物理化学1-热力学第一定律课后习题及答案
热力学第一定律课后习题一、是非题下列各题中的叙述是否正确？正确的在题后括号内画“√”，错误的画“⨯”。
1.在定温定压下，CO2由饱和液体转变为饱和蒸气，因温度不变，CO2的热力学能和焓也不变。
( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。
( )3. 一个系统从始态到终态，只有进行可逆过程才有熵变。
( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。
( )5. 稳定态单质的∆f H(800 K) = 0。
( )二、选择题选择正确答案的编号，填在各题后的括号内：1. 理想气体定温自由膨胀过程为：（）。
（A）Q > 0；（B）∆U < 0；（C）W <0；（D）∆H = 0。
2. 对封闭系统来说，当过程的始态和终态确定后，下列各项中没有确定的值的是：( )。
( A ) Q；( B ) Q＋W；(C ) W( Q = 0 )；( D ) Q( W = 0 )。
3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是：( )(A)绝热过程；( B)理想气体绝热过程；( C )理想气体绝热可逆过程；(D)绝热可逆过程。
4. 在隔离系统内：( )。
( A ) 热力学能守恒，焓守恒；( B ) 热力学能不一定守恒，焓守恒；(C ) 热力学能守恒，焓不一定守恒；( D) 热力学能、焓均不一定守恒。
5. 从同一始态出发，理想气体经可逆与不可逆两种绝热过程：( )。
( A )可以到达同一终态；( B )不可能到达同一终态；( C )可以到达同一终态，但给环境留下不同影响。
6. 当理想气体反抗一定的压力作绝热膨胀时，则：( )。
( A )焓总是不变；(B )热力学能总是增加；( C )焓总是增加；(D )热力学能总是减少。
7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T)，下列说法中不正确的是：（）。
大学物理（第五版）课后习题答案
面向21 世纪课程教材学习辅导书习题分析与解答马文蔚主编殷实沈才康包刚编高等教育出版社前言本书是根据马文蔚教授等改编的面向21世纪课程教材《物理学》第五版一书中的习题而作的分析与解答。
与上一版相比本书增加了选择题更换了约25的习题。
所选习题覆盖了教育部非物理专业大学物理课程教学指导分委员会制定的《非大学物理课程教学基本要求讨论稿》中全部核心内容并选有少量扩展内容的习题所选习题尽可能突出基本训练和联系工程实际。
此外为了帮助学生掌握求解大学物理课程范围内的物理问题的思路和方法本书还为力学、电磁学、波动过程和光学热物理、相对论和量子物理基础等撰写了涉及这些内容的解题思路和方法以期帮助学生启迪思维提高运用物理学的基本定律来分析问题和解决问题的能力。
物理学的基本概念和规律是在分析具体物理问题的过程中逐步被建立和掌握的解题之前必须对所研究的物理问题建立一个清晰的图像从而明确解题的思路。
只有这样才能在解完习题之后留下一些值得回味的东西体会到物理问题所蕴含的奥妙和涵义通过举一反三提高自己分析问题和解决问题的能力。
有鉴于此重分析、简解答的模式成为编写本书的指导思想。
全书力求在分析中突出物理图像引导学生以科学探究的态度对待物理习题初步培养学生―即物穷理‖的精神通过解题过程体验物理科学的魅力和价值尝试―做学问‖的乐趣。
因此对于解题过程本书则尽可能做到简明扼要让学生自己去完成具体计算编者企盼这本书能对学生学习能力的提高和科学素质的培养有所帮助。
本书采用了1996 年全国自然科学名词审定委员会公布的《物理学名词》和中华人民共和国国家标准GB3100 3102 -93 中规定的法定计量单位。
本书由马文蔚教授主编由殷实、沈才康、包刚、韦娜编写西北工业大学宋士贤教授审阅了全书并提出了许多详细中肯的修改意见在此编者致以诚挚的感谢。
由于编者的水平有限敬请读者批评指正。
编者2006 年1 月于南京目录第一篇力学求解力学问题的基本思路和方法第一章质点运动学第二章牛顿定律第三章动量守恒定律和能量守恒定律第四章刚体的转动第二篇电磁学求解电磁学问题的基本思路和方法第五章静电场第六章静电场中的导体与电介质第七章恒定磁场第八章电磁感应电磁场第三篇波动过程光学求解波动过程和光学问题的基本思路和方法第九章振动第十章波动第十一章光学第四篇气体动理论热力学基础求解气体动理论和热力学问题的基本思路和方法第十二章气体动理论第十三章热力学基础第五篇近代物理基础求解近代物理问题的基本思路和方法第十四章相对论第十五章量子物理附录部分数学公式第一篇力学求解力学问题的基本思路和方法物理学是一门基础学科它研究物质运动的各种基本规律由于不同运动形式具有不同的运动规律从而要用不同的研究方法处理力学是研究物体机械运动规律的一门学科而机械运动有各种运动形态每一种形态和物体受力情况以及初始状态有密切关系掌握力的各种效应和运动状态改变之间的一系列规律是求解力学问题的重要基础但仅仅记住一些公式是远远不够的求解一个具体物理问题首先应明确研究对象的运动性质选择符合题意的恰当的模型透彻认清物体受力和运动过程的特点等等根据模型、条件和结论之间的逻辑关系运用科学合理的研究方法进而选择一个正确简便的解题切入点在这里思路和方法起着非常重要的作用1正确选择物理模型和认识运动过程力学中常有质点、质点系、刚体等模型每种模型都有特定的含义适用范围和物理规律采用何种模型既要考虑问题本身的限制又要注意解决问题的需要例如用动能定理来处理物体的运动时可把物体抽象为质点模型而用功能原理来处理时就必须把物体与地球组成一个系统来处理再如对绕固定轴转动的门或质量和形状不能不计的定滑轮来说必须把它视为刚体并用角量和相应规律来进行讨论在正确选择了物理模型后还必须对运动过程的性质和特点有充分理解如物体所受力矩是恒定的还是变化的质点作一般曲线运动还是作圆周运动等等以此决定解题时采用的解题方法和数学工具2.叠加法叠加原理是物理学中应用非常广泛的一条重要原理据此力学中任何复杂运动都可以被看成由几个较为简单运动叠加而成例如质点作一般平面运动时通常可以看成是由两个相互垂直的直线运动叠加而成而对作圆周运动的质点来说其上的外力可按运动轨迹的切向和法向分解其中切向力只改变速度的大小而法向力只改变速度的方向对刚体平面平行运动来说可以理解为任一时刻它包含了两个运动的叠加一是质心的平动二是绕质心的转动运动的独立性和叠加性是叠加原理中的两个重要原则掌握若干基本的简单运动的物理规律再运用叠加法就可以使我们化―复杂‖为―简单‖此外运用叠加法时要注意选择合适的坐标系选择什么样的坐标系就意味着运动将按相应形式分解在力学中对一般平面曲线运动多采用平面直角坐标系平面圆周运动多采用自然坐标系而对刚体绕定轴转动则采用角坐标系等等叠加原理在诸如电磁学振动、波动等其他领域内都有广泛应用是物理学研究物质运动的一种基本思想和方法需读者在解题过程中不断体会和领悟3.类比法有些不同性质运动的规律具有某些相似性理解这种相似性产生的条件和遵从的规律有利于发现和认识物质运动的概括性和统一性而且还应在学习中善于发现并充分利用这种相似性以拓宽自己的知识面例如质点的直线运动和刚体绕定轴转动是两类不同运动但是运动规律却有许多可类比和相似之处如txddv 与tθωdd taddv 与tωαdd 其实它们之间只是用角量替换了相应的线量而已这就可由比较熟悉的公式联想到不太熟悉的公式这种类比不仅运动学有动力学也有如maF 与JαM0dvvmmtF 与0dLωJωtM 2022121dvvmmxF 与2022121dωJωJθM 可以看出两类不同运动中各量的对应关系十分明显使我们可以把对质点运动的分析方法移植到刚体转动问题的分析中去当然移植时必须注意两种运动的区别一个是平动一个是转动状态变化的原因一个是力而另一个是力矩此外还有许多可以类比的实例如万有引力与库仑力、静电场与稳恒磁场电介质的极化与磁介质的磁化等等只要我们在物理学习中善于归纳类比就可以沟通不同领域内相似物理问题的研究思想和方法并由此及彼触类旁通4微积分在力学解题中的运用微积分是大学物理学习中应用很多的一种数学运算在力学中较为突出也是初学大学物理课程时遇到的一个困难要用好微积分这个数学工具首先应在思想上认识到物体在运动过程中反映其运动特征的物理量是随时空的变化而变化的一般来说它们是时空坐标的函数运用微积分可求得质点的运动方程和运动状态这是大学物理和中学物理最显著的区别例如通过对质点速度函数中的时间t 求一阶导数就可得到质点加速度函数另外对物理量数学表达式进行合理变形就可得出新的物理含义如由tddav借助积分求和运算可求得在t1 -t2 时间内质点速度的变化同样由tddvr也可求得质点的运动方程以质点运动学为例我们可用微积分把运动学问题归纳如下第一类问题已知运动方程求速度和加速度第二类问题已知质点加速度以及在起始状态时的位矢和速度可求得质点的运动方程在力学中还有很多这样的关系读者不妨自己归纳整理一下从而学会自觉运用微积分来处理物理问题运用时有以下几个问题需要引起大家的关注1 运用微积分的物理条件在力学学习中我们会发现ta0vv和2021ttarv等描述质点运动规律的公式只是式tt0ddavvv0和式tttrdd000arv在加速度a为恒矢量条件下积分后的结果此外在高中物理中只讨论了一些质点在恒力作用下的力学规律和相关物理问题而在大学物理中则主要研究在变力和变力矩作用下的力学问题微积分将成为求解上述问题的主要数学工具2 如何对矢量函数进行微积分运算我们知道很多物理量都是矢量如力学中的r、v、a、p 等物理量矢量既有大小又有方向从数学角度看它们都是―二元函数‖在大学物理学习中通常结合叠加法进行操作如对一般平面曲线运动可先将矢量在固定直角坐标系中分解分别对x、y 轴两个固定方向的分量可视为标量进行微积分运算最后再通过叠加法求得矢量的大小和方向对平面圆周运动则可按切向和法向分解对切线方向上描述大小的物理量a 、v、s 等进行微积分运算3 积分运算中的分离变量和变量代换问题以质点在变力作用下作直线运动为例如已知变力表达式和初始状态求质点的速率求解本问题一条路径是由F m a 求得a的表达式再由式dv adt 通过积分运算求得v其中如果力为时间t 的显函数则a at此时可两边直接积分即ttta0ddvvv0但如果力是速率v 的显函数则a av此时应先作分离变量后再两边积分即tta0dd1vvvv0又如力是位置x 的显函数则aax此时可利用txddv得vxtdd并取代原式中的dt再分离变量后两边积分即xxtxa0ddvvvv0 用变量代换的方法可求得vx表达式在以上积分中建议采用定积分下限为与积分元对应的初始条件上限则为待求量5.求解力学问题的几条路径综合力学中的定律可归结为三种基本路径即1 动力学方法如问题涉及到加速度此法应首选运用牛顿定律、转动定律以及运动学规律可求得几乎所有的基本力学量求解对象广泛但由于涉及到较多的过程细节对变力矩问题还将用到微积分运算故计算量较大因而只要问题不涉及加速度则应首先考虑以下路径2 角动量方法如问题不涉及加速度但涉及时间此法可首选3 能量方法如问题既不涉及加速度又不涉及时间则应首先考虑用动能定理或功能原理处理问题当然对复杂问题几种方法应同时考虑此外三个守恒定律动量守恒、能量守恒、角动量守恒定律能否成立往往是求解力学问题首先应考虑的问题总之应学会从不同角度分析与探讨问题以上只是原则上给出求解力学问题一些基本思想与方法其实求解具体力学问题并无固定模式有时全靠―悟性‖但这种―悟性‖产生于对物理基本规律的深入理解与物理学方法掌握之中要学会在解题过程中不断总结与思考从而使自己分析问题的能力不断增强第一章质点运动学1 -1 质点作曲线运动在时刻t 质点的位矢为r速度为v 速率为vt 至t Δt时间内的位移为Δr 路程为Δs 位矢大小的变化量为Δr 或称Δ r 平均速度为v平均速率为v 1 根据上述情况则必有 A Δr Δs Δr B Δr ≠ Δs ≠ Δr当Δt→0 时有 dr ds ≠ dr C Δr ≠ Δr ≠ Δs当Δt→0 时有 dr dr ≠ ds D Δr ≠ Δs ≠ Δr当Δt→0 时有 dr dr ds 2 根据上述情况则必有 A v v v v B v ≠v v ≠ v C v v v ≠ v D v ≠v v v分析与解1 质点在t 至t Δt 时间内沿曲线从P 点运动到P′点各量关系如图所示其中路程Δs PP′ 位移大小Δr PP′而Δr r - r 表示质点位矢大小的变化量三个量的物理含义不同在曲线运动中大小也不相等注在直线运动中有相等的可能但当Δt→0 时点P′无限趋近P 点则有 dr ds但却不等于dr故选B 2 由于 Δr ≠Δs故tstΔΔΔΔr即 v ≠v 但由于 dr ds故tstddddr即 v v由此可见应选C 1 -2 一运动质点在某瞬时位于位矢rxy的端点处对其速度的大小有四种意见即1trdd 2tddr 3tsdd 422ddddtytx 下述判断正确的是 A 只有12正确B 只有2正确 C 只有23正确 D 只有34正确分析与解trdd表示质点到坐标原点的距离随时间的变化率在极坐标系中叫径向速率通常用符号vr表示这是速度矢量在位矢方向上的一个分量tddr表示速度矢量在自然坐标系中速度大小可用公式tsddv计算在直角坐标系中则可由公式22ddddtytxv求解故选D 1 -3 质点作曲线运动r 表示位置矢量v表示速度a表示加速度s 表示路程a 表示切向加速度对下列表达式即1d v /dt a2dr/dt v3ds/dt v4d v /dt a 下述判断正确的是A 只有1、4是对的B 只有2、4是对的C 只有2是对的D 只有3是对的分析与解tddv表示邢蚣铀俣萢 它表示速度大小随时间的变化率是加速度矢量沿速度方向的一个分量起改变速度大小的作用trdd在极坐标系中表示径向速率vr如题1 -2 所述tsdd在自然坐标系中表示质点的速率v而tddv表示加速度的大小而不是切向加速度a 因此只有3 式表达是正确的故选D 1 -4 一个质点在做圆周运动时则有 A 切向加速度一定改变法向加速度也改变B 切向加速度可能不变法向加速度一定改变C 切向加速度可能不变法向加速度不变D 切向加速度一定改变法向加速度不变分析与解加速度的切向分量a 起改变速度大小的作用而法向分量an起改变速度方向的作用质点作圆周运动时由于速度方向不断改变相应法向加速度的方向也在不断改变因而法向加速度是一定改变的至于a 是否改变则要视质点的速率情况而定质点作匀速率圆周运动时a 恒为零质点作匀变速率圆周运动时a 为一不为零的恒量当a 改变时质点则作一般的变速率圆周运动由此可见应选B 1 -5 如图所示湖中有一小船有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动设该人以匀速率v0 收绳绳不伸长且湖水静止小船的速率为v则小船作 A 匀加速运动θcos0vv B 匀减速运动θcos0vv C 变加速运动θcos0vv D 变减速运动θcos0vv E 匀速直线运动0vv 分析与解本题关键是先求得小船速度表达式进而判断运动性质为此建立如图所示坐标系设定滑轮距水面高度为ht 时刻定滑轮距小船的绳长为l则小船的运动方程为22hlx其中绳长l 随时间t 而变化小船速度22ddddhltlltxv式中tldd表示绳长l随时间的变化率其大小即为v0代入整理后为θlhlcos/0220vvv方向沿x 轴合蛴伤俣缺泶锸娇膳卸闲〈 鞅浼铀僭硕 恃 讨论有人会将绳子速率v0按x、y 两个方向分解则小船速度θcos0vv这样做对吗1 -6 已知质点沿x 轴作直线运动其运动方程为32262ttx式中x 的单位为mt 的单位为s求1 质点在运动开始后4.0 s内的位移的大小 2 质点在该时间内所通过的路程3 t4 s时质点的速度和加速度分析位移和路程是两个完全不同的概念只有当质点作直线运动且运动方向不改变时位移的大小才会与路程相等质点在t 时间内的位移Δx 的大小可直接由运动方程得到0Δxxxt而在求路程时就必须注意到质点在运动过程中可能改变运动方向此时位移的大小和路程就不同了为此需根据0ddtx来确定其运动方向改变的时刻tp 求出0 tp 和tp t 内的位移大小Δx1 、Δx2 则t 时间内的路程21xxs如图所示至于t 4.0 s 时质点速度和加速度可用txdd和22ddtx两式计算解 1 质点在4.0 s内位移的大小m32Δ04xxx 2 由0ddtx 得知质点的换向时刻为s2pt t0不合题意则m0.8Δ021xxx m40Δ242xxx 所以质点在4.0 s时间间隔内的路程为m48ΔΔ21xxs 3 t4.0 s时1s0.4sm48ddttxv2s0.422m.s36ddttxa 1 -7 一质点沿x 轴方向作直线运动其速度与时间的关系如图a所示设t0 时x0试根据已知的v-t 图画出a-t 图以及x -t 图分析根据加速度的定义可知在直线运动中v-t曲线的斜率为加速度的大小图中AB、CD 段斜率为定值即匀变速直线运动而线段BC 的斜率为0加速度为零即匀速直线运动加速度为恒量在a-t 图上是平行于t 轴的直线由v-t 图中求出各段的斜率即可作出a-t 图线又由速度的定义可知x-t 曲线的斜率为速度的大小因此匀速直线运动所对应的x -t 图应是一直线而匀变速直线运动所对应的x–t 图为t 的二次曲线根据各段时间内的运动方程xxt求出不同时刻t 的位置x采用描数据点的方法可作出x-t 图解将曲线分为AB、BC、CD 三个过程它们对应的加速度值分别为2sm20ABABABttavv 匀加速直线运动0BCa 匀速直线运动2sm10CDCDCDttavv 匀减速直线运动根据上述结果即可作出质点的a-t 图图B 在匀变速直线运动中有2021ttxxv 由此可计算在0 2 和4 6 时间间隔内各时刻的位置分别为用描数据点的作图方法由表中数据可作0 2 和4 6 时间内的x -t 图在2 4 时间内质点是作1sm20v的匀速直线运动其x -t 图是斜率k20的一段直线图c 1 -8 已知质点的运动方程为jir222tt式中r 的单位为mt 的单位为 求 1 质点的运动轨迹2 t 0 及t 2 时质点的位矢3 由t 0 到t 2 内质点的位移Δr 和径向增量Δr 4 2 内质点所走过的路程s 分析质点的轨迹方程为y fx可由运动方程的两个分量式xt和yt中消去t 即可得到对于r、Δr、Δr、Δs 来说物理含义不同可根据其定义计算其中对s的求解用到积分方法先在轨迹上任取一段微元ds则22dddyxs最后用ssd积分求 解1 由xt和yt中消去t 后得质点轨迹方程为2412xy 这是一个抛物线方程轨迹如图a所示2 将t 0 和t 2 分别代入运动方程可得相应位矢分别为jr20 jir242 图a中的P、Q 两点即为t 0 和t 2 时质点所在位置3 由位移表达式得jijirrr24Δ020212yyxx 其中位移大小m66.5ΔΔΔ22yxr 而径向增量m47.2ΔΔ2020222202yxyxrrrr 4 如图B所示所求Δs 即为图中PQ段长度先在其间任意处取AB 微元ds则22dddyxs由轨道方程可得xxyd21d代入ds则2 内路程为m91.5d4d402xxssQP 1 -9 质点的运动方程为23010ttx 22015tty 式中xy 的单位为mt 的单位为 试求1 初速度的大小和方向2 加速度的大小和方向分析由运动方程的分量式可分别求出速度、加速度的分量再由运动合成算出速度和加速度的大小和方向解 1 速度的分量式为ttxx6010ddv ttyy4015ddv 当t 0 时vox -10 m· -1voy 15 m· -1 则初速度大小为120200sm0.18yxvvv 设vo与x 轴的夹角为α则23tan00xyαvv α123°41′ 2 加速度的分量式为2sm60ddtaxxv 2sm40ddtayyv 则加速度的大小为222sm1.72yxaaa 设a 与x 轴的夹角为β则32tanxyaaβ β-33°41′或326°19′ 1 -10 一升降机以加速度1.22 m· -2上升当上升速度为2.44 m· -1时有一螺丝自升降机的天花板上松脱天花板与升降机的底面相距2.74 m计算1螺丝从天花板落到底面所需要的时间2螺丝相对升降机外固定柱子的下降距离分析在升降机与螺丝之间有相对运动的情况下一种处理方法是取地面为参考系分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动列出这两种运动在同一坐标系中的运动方程y1 y1t和y2 y2t并考虑它们相遇即位矢相同这一条件问题即可解另一种方法是取升降机或螺丝为参考系这时螺丝或升降机相对它作匀加速运动但是此加速度应该是相对加速度升降机厢的高度就是螺丝或升降机运动的路程解1 1 以地面为参考系取如图所示的坐标系升降机与螺丝的运动方程分别为20121attyv 20221gtthyv 当螺丝落至底面时有y1 y2 即20202121gtthattvv s705.02aght 2 螺丝相对升降机外固定柱子下降的距离为m716.021202gttyhdv 解2 1以升降机为参考系此时螺丝相对它的加速度大小a′g a螺丝落至底面时有2210tagh s705.02aght 2 由于升降机在t 时间内上升的高度为2021atthv 则m716.0.。
《大学物理》热力学基础练习题及答案解析
《大学物理》热力学基础练习题及答案解析一、简答题：1、什么是准静态过程?答案：一热力学系统开始时处于某一平衡态，经过一系列状态变化后到达另一平衡态，若中间过程进行是无限缓慢的，每一个中间态都可近似看作是平衡态，那么系统的这个状态变化的过程称为准静态过程。
2、从增加内能来说，做功和热传递是等效的。
但又如何理解它们在本质上的差别呢?答：做功是机械能转换为热能，热传递是热能的传递而不是不同能量的转换。
3、一系统能否吸收热量，仅使其内能变化? 一系统能否吸收热量，而不使其内能变化?答：可以吸热仅使其内能变化，只要不对外做功。
比如加热固体，吸收的热量全部转换为内能升高温度；不能吸热使内能不变，否则违反了热力学第二定律。
4、有人认为：“在任意的绝热过程中，只要系统与外界之间没有热量传递，系统的温度就不会改变。
”此说法对吗? 为什么?答：不对。
对外做功，则内能减少，温度降低。
5、分别在Vp-图、Tp-图上，画出等体、等压、等温和绝热过程的曲线。
V-图和T6、 比较摩尔定体热容和摩尔定压热容的异同。
答案：相同点：都表示1摩尔气体温度升高1摄氏度时气体所吸收的热量。
不同点：摩尔定体热容是1摩尔气体，在体积不变的过程中，温度升高1摄氏度时气体所吸收的热量。
摩尔定压热容是1摩尔气体，在压强不变的过程中，温度升高1摄氏度时气体所吸收的热量。
两者之间的关系为R C C v p +=7、什么是可逆过程与不可逆过程答案：可逆过程：在系统状态变化过程中，如果逆过程能重复正过程的每一状态，而且不引起其它变化；不可逆过程：在系统状态变化过程中，如果逆过程能不重复正过程的每一状态，或者重复正过程时必然引起其它变化。
8、简述热力学第二定律的两种表述。
答案：开尔文表述：不可能制成一种循环工作的热机，它只从单一热源吸收热量，并使其全部变为有用功而不引起其他变化。
克劳修斯表述：热量不可能自动地由低温物体传向高温物体而不引起其他变化。
9、什么是第一类永动机与第二类永动机?答案：违背热力学第一定律（即能量转化与守恒定律）的叫第一类永动机，不违背热力学第一定律但违背热力学第二定律的叫第二类永动机。
大学物理热力学基础习题与解答 PPT
QAB
m M
CP (TB
TA )
8 V/m3
5 2
( pBVB
p AVA )
14.9 105 J
全过程：Q QBC QAB 14.9 10 5 J 由图得， TA TC
E 0
W Q E 14.9105 J
3. 图所示，有一定量的理想气体，从初状态 a
3 4
ln
4
p1V1
净热量为
Q
W
3 4
ln
4
p1V1
4. 设燃气涡轮机内的理想气体作如图所示的循环过程， 其中 1 2 ，3 4 为绝热过程；2 3 ，4 1 为 等压过程，证明此循环的效率为
1
1 p1 p2
解：在等压过程中吸热为
T3
p2
由上述二式得： T1 T4 T4 T1 T2 T3 T3 T2
从而证得循环的效率为
1
1 T1
T2
1
p1 p2
[B ]
8. 如图，一卡诺机由原来采用循环过程 a b c d a
改为采用循环过程 ab' c' da ，则循环过程 的
（A）净功增大，效率提高； （B）净功增大，效率降低； （C）净功和效率都不变； （D）净功增大，效率不变
Wabcd Wab'c' d
1 T2
T1
[D]
p a
b b
E E3 E4 1246 .5 J
2. 一定量的单原子分子理想气体，从A态出发经过等压过 程膨胀到B态，又经过绝热过程膨胀到C态，如图所示。 试求这全过程中，该气体对外所做的功、内能的增量以及 吸收的热量。
大学物理第五版-热力学习题课
RT VP 1.41 M mol
物理意义：表示分布在VP附近小区 间内的分子数最多。
4
（2）算术平均速率：分子速率的算术平均值。
ò¥
V = vf (v)dv = 1.6
RT
用于计算分子间的距离
0
M mol
（3）方均根速率：分子速率平方平均值的平方根。
v 2 v 2 f vdv
0
v2
v2 f vdv 1.73
请看例题
15
练习. 一定质量的理想气体，进行如图所示的循环过程
已知气体在状态A的温度为 300K，求：
（1）气体在状态B、C的温度
（2）各过程气体对外作的功
（3）经过整个循环过程，气体 从外界吸收的总热量
解：由图知 PA 300Pa ; PB Pc 100Pa ;
VB 3m3
VA Vc 1m3
（约80亿次）
12
第13章 提要
1、热力学第一定律及其应用 (1)准静态过程的功
V2
W = ò PdV V1
(2)热力学第一定律 Q = D E + W 微变过程 dQ = dE + dW 迈耶公式 CP,m = CV ,m + R
13
2、循环过程和卡诺循环
(1) 循环过程的特点 E 0
热机效率h =
dN N
4
m
2 KT
3
2
mv2
e 2KT
v2dv
f
v dV
3
f v : 麦克斯韦速率分布函数
dN f v NdV 速率在v~v+dv区间内的分子数
v2
f vdv
dN
速率在v1~v2区间内的分子数占分子
普通物理学第五版第7章热力学答案
目录 结束
解：
dQ = c dT = a T dT
dQ =CV dT + pdV
a
T
dT
=
C
VdT
+
RT V
dV
a
R
dT
CV R
dT T=
dV V
aT
R
CV R
lnT
=
lnV
+ 常数
V
CV
TRe
aT
R=
常数
目录 结束
7-16 声音在空气中的传播可以看作是一
绝热过程。它的速度可按公式
来的温度 T升高到T1，并吸热
Q。问活塞所在的高度 h′等
于多少？
h
目录 结束
解： pV = MMmolRT
pSh = MMmolRT
pS =
M RT Mmol h
=f
=kh
M Mmol k
=
h2 RT
Q =Δ E + A = MMmoCl V (T1
h′
T
)+
x dx
h
= MMmoCl V (T1
目录 结束
解： T1=298K V1=5×10-3 m3
T2=277K V2=6×10-3 m3
由绝热方程： T1 V1γ 1= T2 V2γ 1
T1 T2
= ( V2 V1
γ)
1
298 277
=
(
6×10-3 5×10-3
)γ 1
1.076=(1.2)γ 1
ln1.076=(γ-1)ln1.2
(γ-1)=0.4
目录 结束
解：
热学习题课(大学物理)
dN m 3/ 2 4 ( ) e N 2kT
理学院 孙秋华
m 2 v 2 kT v 2 dv
热学部分习题课 分布函数
m 3/ 2 f (v ) 4 ( ) e 2kT
v
p
m 2 v 2 kT v 2
三种速率
v v
2
2k T m 8k T m 3k T m
2.能量均分定理：在温度为T 的平衡态下，气体分子每个 1 自由度的平均动能都相等，其大小等于 2 kT 。
A
V
V2 V1
理想气体无摩擦的平衡过程
M ( E 2 E1 ) C V (T2 T1 ) M mol
pdV
2 M Q CV (T2 T1 ) pdV M mol V 1
理学院
孙秋华
热学部分习题课
热力学第一定律对理想气体四个过程的应用
过程 等容 E
M cv T M mol M cv T M mol
3
V
热学部分习题课
3 1等温过程 E 31 0
V1 M A31 Q 31 RT1 ln 3 RT1 ln 2 M mol V3
1
Q2 Q1 1 Q 31 Q12 3 RT1 ln 2 1 1 ln 2 30.1% 3 RT1
P
P2
P1
2
1
理学院 孙秋华
热学部分习题课 练习题、定容摩尔热容为CV常量的某理想气体。经历如 图所示的两个循环过程A1A2A3A1和B1B2B3B1相应的循环 效率为A和B。试比较A和B的大小。
P
P2
P1
2
1
V1
大学物理 热学习题课
1
Va 1 Tb ( ) Ta 424 K Vb
VcTb Tc 848 K Vb
1
c
bc为等压过程，据等压过程方程 Tb / Vb = Tc / Vc 得
O
d a Vb Vc Va V
cd为绝热过程，据绝热过程方程
TcVc
TdVd , (Vd Va )
1
第10章
理想气体模型
气体分子运动论
统计假设
k
PV vRT
P P 2 n 3 kT k k 2 3 T E
M i E RT 2
dN f ( v ) dv N
麦克丝韦 分布率
v2
3RT
vp
2 RT
8RT
v
z 2d 2 v n
v 1 z 2d 2 n
Nf ( v )dv
v0
v0
f ( v )dv
v d N vNf (v) d v
v0—— ∞间的分子数 v0—— ∞间的分子的速率和
v0
dN Nf ( v )dv
v0
v0
vdN vNf ( v )dv
v0
(3) 多次观察一分子的速率,发现其速率大于v0 的 几率= ———。 dN N v v 所求为v0—— ∞间的分子 f (v)dv 数占总分子数的百分比 N N v
M i RT 2 M i RT 2
吸收热量Q
M i RT 2
摩尔热容C
CV i R 2
等容 等压 等温
p/T=C V/T=C pV=C
pVγ=C1 Vγ-1T=C2 pγ-1T-γ=C3
大学物理物理-热力学课后参考答案
m
4 1
Q放
M
CP (T4
T1)
p
2
3
1 Q放 1 T4 T1
p1
Q吸
T3 T2
p2
1
4
0
V
1 2
P2 1 P1 1
T2
T1
1
T1 T2
P1 P2
3 4
P2 1 P1 1
T3
T4
1
T4 T3
P1 P2
1
1
T1
P1 P2
T2
T4
P1 P2
P1 4
VC
VC 4V1
p1
a
c p1/4 b
V1
ca
等稳
W3
P1V1
ln
V1 Vc
P1V1 ln 4
净功
3
W
W1
W2
W3
( 4
ln
4) P1V1
净热
3
Q
W
( 4
ln
4) P1V1
0.636P1V1
三、4
循环效率
算Q1Q2还是算Q1W净
两绝热，算Q只两过程，算W四过程
m 2 3 Q吸 M CP (T3 T2 )
T3
1
1 Q放 Q吸
1 T4 T1 T3 T2
1
P1 P2
Q E W AB过程做功最大 内能增加最多 吸热最多
一、6 C 热二定律
（A）热量不能自发地从低温物体传到 高温物体。
（B）热不能全部变为功而不产生其它影响。 （D）无规则运动的能量不能自发地变为有
规则运动的能量。
一、7 B W图示面积 初终态E 热一比Q
由图 W 0 对外做正功. 由图 PaVa PbVb Ta Tb E 0 Q E W W 0 吸热
物理化学上册第五版天津大学出版社第三章热力学第二定律习题答案
物理化学上册第五版天津大学出版社第三章热力学第二定律习题答案3-1 卡诺热机在 T 1=600K 的高温热源和T 2=300K 的低温热源间工作，求：（1） 热机的效率；（2）当环境作功 –W=100kJ 时，系统从高温热源Q 1及向低温热源放出的 –Q 2。
解：（1）5.0600/)300600(/)(/1211=-=-=-=T T T Q W η （2）5.0/100/11==-Q kJ Q W ，得kJ Q 2001=kJ W Q Q 10021=-=+；kJ Q W Q 100)(21=-=--3-2卡诺热机在T 1=795K 的高温热源和T 2=300K 的低温热源间工作，求：（1）热机的效率；（2）当从高温热源吸热Q 1=250 kJ 时，系统对环境作的功 -W 及向低温热源放出的 –Q 2。
解：（1）6.0750/)300750(/)(/1211=-=-=-=T T T Q W η （2）kJ kJ Q W 1502506.01=⨯==-ηkJ W Q Q 15021=-=+；kJ Q W Q 100)(21=-=--3-3 卡诺热机在T 1=900K 的高温热源和T 2=300K 的低温热源间工作，求：（1）热机的效率；（2）当向低温热源放出的 –Q 2=100kJ 时，从高温热源吸热Q 1及对环境作的功 -W 。
解：（1）6667.0900/)300900(/)(/1211=-=-=-=T T T Q W η （2）6667.0/1=-Q W （a ）W kJ Q -=-1001（b ）联立求解得：Q 1=300 kJ ；-W=200kJ3-4 试证明：在高温热源和低温热源间工作的不可逆热机与卡诺热机联合操作时，若令卡诺热机得到的功W r 等于不可逆热机作出的功 – W ，假设不可逆热机的热机效率η大于卡诺热机的热机效率ηr ，其结果必然有热量从低温热源流向高温热源，而违反热力学第二定律的克劳修斯说法。
《大学物理学》热力学基础练习题
《大学物理学》热力学基础练习题《大学物理学》热力学基础一、选择题13-1．如图所示，bcab 1a 和b 2a 功与吸收热量的情况是( )（A ）b 1a 过程放热、作负功，b 2a 过程放热、作负功；（B ）b 1a 过程吸热、作负功，b 2a 过程放热、作负功；（C ）b 1a 过程吸热、作正功，b 2a 过程吸热、作负功；（D ）b 1a 过程放热、作正功，b 2a 过程吸热、作正功。
【提示：体积压缩，气体作负功；三个过程中a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b 1a 过程作的负功比b 2a 过程作的负功多，由Q W E =+∆知b 2a 过程放热，b 1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态A 变到平衡态B 状态A 和状态B 过程，气体必然 ( )（A ）对外作正功；（B ）内能增加； （C ）从外界吸热；（D ）向外界放热。
【提示：由于A B T T <，必有A B E E <；而功、热量是 过程量，与过程有关】13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气(均视为刚性理想气体)，开始时它们的压强和温度都相同，现将3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为 ( ) （A ）6J ； （B ）3J ； （C ）5J ； （D ）10J 。
【提示：等体过程不做功，有Q E =∆，而2mol M iE R T M ∆=∆，所以需传5J 】13-4．有人想象了如图所示的四个理想气体的循）A （）B （）【提示：(A) 绝热线应该比等温线陡，（B ）和（C ）两条绝热线不能相交】13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J ，则对外做功（ ） （A ）2000J ； （B ）1000J ； （C ）4000J ； （D ）500J。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
εk
=
3 2
KT
D、内能相等。
3 ．理想气体的温度（ ）
[B]
(A)与分子的平均动能成正比；
(B)与气体的内能成正比；
(C)与分子的平均平动动能成正比；
(D)与分子的平均速度成正比。
[C]
4．下面各图所示的速率分布曲线，哪一图中的两条曲线能 是同一温度下氨气和氦气的分子速率分布曲线?
[B]
5．理想气体的定压摩尔热容大于定容摩尔热容，是因为在等压 过程中（ ）
dN N
4
m
2 KT
3
2
mv2
e 2KT
v2dv
f
v dV
f v : 麦克斯韦速率分布函数
dN f v NdV 速率在v~v+dv区间内的分子数
v2
f vdv
dN
速率在v1~v2区间内的分子数占分子
v1
N 总数的百分比
4、三种速率 （1）最概然速率（对应速率分布曲线中f(v)的最大值）
Q1
Q1
Q1
致冷系数 e = Q1 = Q2 W Q1 - Q2
提醒：
热机效率总是小于1的，而致冷系数e可以大于1。
(2)由两条等温线和两条绝热线组成的循环叫做 卡诺循环。
卡诺热机的效率
卡诺
1
Q2 Q1
1 T2 T1
3、热力学第二定律
(1)热力学第二定律的开尔文表述和克劳修斯表述 是等价的，它揭示了一切与热现象有关的实际宏 观过程都是不可逆的。
（约80亿次）
第13章 提要
1、热力学第一定律及其应用 (1)准静态过程的功
V2
W = ò PdV V1
(2)热力学第一定律 Q = DE + W 微变过程 dQ = dE + dW 迈耶公式 CP,m = CV ,m + R
2、循环过程和卡诺循环
(1) 循环过程的特点 E 0
热机效率h = W = Q1 - Q2 = 1- Q2
一个分子的平均平动动能
一个分子的平均动能 εk =
kt
i 2
KT
3 2
KT
一个系统的内能
E=
m¢ M mol
i RT 2
=
m¢ M mol
Cv,mT
一个系统内能的改变量 DE = m¢ i RDT
4、麦克斯韦速率分布率
M mol 2
在平衡态下，速率在v～v + dv区间内的分子数占分
子总数的百分比
C—A： W3 0
（3）整个过程中气体作的总功：
W W1 W2 W3 200J
对整个循环过程：
E 0
Q W E 200J
2. 1mol刚性双原子分子的理想气体，开始时处于
p1 1.01105 Pa, V1 103 m3 的状态，然后经如图所示的
直线过程I变到 p2 4.04105 Pa , V2 2103 m3 状态．后
请看例题
练习. 一定质量的理想气体，进行如图所示的循环过程
已知气体在状态A的温度为 300K，求：
（1）气体在状态B、C的温度
（2）各过程气体对外作的功
（3）经过整个循环过程，气体 从外界吸收的总热量
解：由图知 PA 300Pa ; PB Pc 100Pa ;
VB 3m3
VA Vc 1m3
V2
V3 dV 2 V V2
p3V3 p2V2
( p1,V1)
O
p3 p1
V
又
V3
V2
p2 p3
2
2 103
4.04 1.01
2
m3
1
pV 2 C
32103 m3
1
1
1 1
p2V22 pV 2 , p p2V22V 2
W2 2 1.0132102 4.04 2102 J 4.85103 J
（1）C—A为等容过程：
PA TA Pc Tc
Tc
PcTA PA
= 100K
C—B为等压过程：
VB TB Vc Tc
TB
TcVB Vc
300K
（2）各过程中气体作的功：
A—B：
W1
1 2
PA
PB
VB
Vc
400J
B—C：W2 PB Vc VB 200J
热习 力题 学课
第12章 提要
掌握两方面内容：
一、理想气体状态方程；二、理想气体的压强、能量计算
1、气态方程； 2、气体的压强
pV m RT M
(
K
=
R NA
)
n N V
P nKT
p
=
1 3
nmv 2
=
2 3
nεk
3、能量按自由度均分原理
在平衡态下，分子每个自由度平均分得能量 1 KT 2
1 1.01105 4.04105 2103 103 J
2
5 4.04 2102 1.01102 J 2.02103 J 2
(2) 在过程II中气体对外做功为：
W2
V3 pdV
V2
p
( p2 ,V2 )
p2
过程II气体内能增量为
p
( p2 ,V2 )
E2
5 2
R
T3
T2
5 2
p3V3
p2V2
5 1.0132102 4.04 2102 J O ( p1,V1) 2
p3 p1
V
6.06103 J
过程I103 J 6.06103 J 1.09104 J
( A)T1 T2，1 2
(B)T1 T2，1 2 / 2
1 KT 2d 2n 2d 2 P
(C)T1 2T2，1 2
(D)T1 2T2，1 2 / 2
[B]
2．同温度、同物质的量的H2和He两种气体，它们的 （）
A、分子的平均动能相等； B、分子的平均平动动能相等； C、总动能相等；
8．单原子分子的理想气体，其自由度i= 3 ，定
容摩尔热容Cv,m=
3 2
R，定压摩尔热容Cp,m=
5 2
R。
9、一定量的理想气体，从相同状态开始分别经过等压、
等体及等温过程，若气体在上述各过程中吸收的热量
相同，则气体对外界作功最多的过程为___等__温_______。
10. 下图为同一种气体，处于不同温度状态下的速 率分布曲线，试问（1）哪一条曲线对应的温度高？
A、膨胀系数不同；
B、膨胀时气体对外作功；
C、分子间吸引力大；
[B]
D、分子本身膨胀。
6．对于室温下的双原子分子理想气体，在等压膨胀的情况下， 系统对外界作的功与从外界吸收的热量之比等于
（A）1/3 （B）1/4
[D]
（C）2/5 （D）2/7
W= Q
Q- DE = Q
R i+ 2 R
=
2 7
2
7．理想气体的压强仅与下列哪项有关（ D ） A、气体的分子数密度； B、气体的温度； C、气体分子的平均速率； D、气体的分子数密度与温度的乘积.
（2）如果这两条曲线分别对应的是同一温度下氧气
和氢气的分布曲线，问哪条曲线对应的是氧气，哪
条对应的是氢气？
解：
vp
2kT M
f(v) T1
(1) T1 < T2
(2) 绿：氧 黑：氢
T2
v v p1 p2
v
11. 求氢在标准状态下一秒内分子的平均碰撞次数。
（已知分子直径d = 210-10m )
VP 1.41
RT M mol
物理意义：表示分布在VP附近小区 间内的分子数最多。
（2）算术平均速率：分子速率的算术平均值。
ò¥
V = vf (v)dv = 1.6
RT
用于计算分子间的距离
0
M mol
（3）方均根速率：分子速率平方平均值的平方根。
v 2 v 2 f vdv
0
p3 p1
V
内能增量为：
E1
m M
CV
,mT
5 2
R
T2
T1
p
( p2 ,V2 )
5 2
p2V2
p1V1
( p1,V1)
O
p3 p1
V
由热力学第一定律，此过程气体吸收的热量为：
Q1
W1
E1
1 2
p1
p2
V2
V1
5 2
p2V2
p1V1
又经过方程为
pV
1 2
C（常量）的过程II变到
压强 p3 p1 1.01105 Pa 的状态．求：
(1) 在过程I中气体吸的热量; (2) 整个过程气体吸的热量．
p
( p2 ,V2 )
解：(1) 在过程Ⅰ中气体对外做
功为:
W1
1 2
p1
p2
V2
V1
( p1,V1)