三角 正方形 圆 五角星 规律
04讲 找规律(一)

第4讲找规律(一)会点:应用四则运算表示数之间的关系解决一步运算规律问题;重点:掌握图形大小、颜色变化等解决图形变化规律问题;难点:根据图形形状、简繁等变化解决三阶图标规律问题。
1 图形变化规律问题的主要分类常见的图形变化规律问题主要分为:(1)图形形状的变化。
(2)图形数量的变化。
(3)图形大小的变化。
(4)图形位置的变化。
(5)图形繁简的变化。
(6)图形颜色的变化。
在这类题目中,图形的变化具有多样性,有的是单一的图形变化,有的是几种变化类型结合之后复杂的图形变化,如将图形的颜色、位置结合在一起的图形变化。
遇到这样的题目,可以分步来做,先分别观察,发现各自的规律后再结合在一起,并得到最终的变化规律。
2 图形的位置变化在图形的位置变化中,常涉及顺时针变化和逆时针变化。
顺时针变化是指与钟表的时针运动方向一致的转动;逆时针变化则是指与钟表的时针运动方向相反的转动。
3 复杂图形的找规律方法对于比较复杂的图形,有时候需要先将图形分成若干个部分,然后单独考虑每个部分的变化规律,从而将复杂的图形简单化。
第 1 关图形数量的变化1-1、找出下面图形的排列规律,并画出第四幅图。
【解析】根据前三个图形我们可以知道,图中圆的数量是依次增加,而且是每个图形在最底下增加圆圈。
第一个图就是一个图,第二个图底下的图是两个,第三个图底下的圆圈是3,由此可以推断出到第四个图的时候底下的圆圈是4个。
按照规律画上去。
1-2 、根据前面几幅图的规律,画出最后一幅图。
【解析】第一步:看图形的第一行全都是圆圈,数一数有几个呢?5个。
第二步:看到圆圈的数变成了4个,少了一个,少的那个位置画上星星。
第三步:再数圆圈的数少了两个,只有3个。
少的那两个位置在后面补上星星。
第四步:圆圈的数只有2个了,少了三个,三个位置在后面补上星星。
总结规律: 圆圈的数依次减1,而星星补圆圈缺出来的空位。
[过关检测]A 组第一题观察下面的脸谱,按照规律在空格内画出适当的图形。
中心对称和中心对称图形

中心对称和中心对称图形一、中心对称中心对称是数学中的基本概念之一,在几何学中有广泛的应用。
中心对称是指存在一个中心点,通过该中心点可以将图形分成两个部分,这两个部分相互镜像,并且对称点与中心点的距离相等。
换句话说,如果将图形绕着中心点旋转180度,那么图形还是与原图形完全重合。
二、中心对称图形中心对称图形是指具有中心对称性质的图形。
常见的中心对称图形包括正方形、圆形、五角星等。
1. 正方形正方形是一种具有中心对称性质的图形。
它有四个二等边的直角三角形组成,每个直角三角形的两条直角边都是正方形的一条边。
正方形的对称中心位于正方形的中心点,通过对称中心可以将正方形分成两个对称的部分。
2. 圆形圆形也是一种具有中心对称性质的图形。
圆形的对称中心位于圆心,通过对称中心可以将圆形分成两个对称的部分。
无论从任何角度看,圆形都具有中心对称性,因为无论如何旋转都可以使圆形与原来的位置完全重合。
3. 五角星五角星是一种常见的中心对称图形。
它由两个五边形组成,每个五边形的五个顶点与另一个五边形的对称顶点相连,形成一个具有中心对称性质的图形。
五角星的对称中心位于两个五边形的重心,通过对称中心可以将五角星分成两个对称的部分。
三、应用举例中心对称和中心对称图形在日常生活中有很多应用,下面举几个例子。
1. 建筑设计中心对称在建筑设计中得到了广泛运用。
比如,很多教堂、宫殿等建筑物采用中心对称布局,将整个建筑划分成两个对称的部分。
这样的布局不仅使建筑物更加美观,而且在视觉上给人一种稳定和和谐的感觉。
2. 服装设计中心对称也在服装设计中被广泛应用。
比如,一些裙子、外套等服装的剪裁会采用中心对称设计,使得服装的左右两侧完全对称。
这种设计不仅美观,而且方便穿着,给人带来舒适的感觉。
3. 艺术创作中心对称在艺术创作中也有重要地位。
很多绘画作品和雕塑作品都运用了中心对称来构图,使得作品更加平衡和谐。
例如,著名画家达芬奇的作品《蒙娜丽莎》就采用了中心对称的构图,使得人物形象更加生动和真实。
图形推理讲义

解 D本题属于数量类,考查图形线段个数。
图形线段数量分别为3、4、5、6、?,所以“?”处线段数应为7。
所以选择D选项。
(山西、河南、辽宁、福建、重庆、海南、青海、宁夏、内蒙古、陕西、西藏2010-46)解 C,封闭空间数4(广东2010-72)解A。
数封闭区间,偶数项都含有曲线(广东2010-70)解C。
数封闭区间(黑龙江2010-64)(2007-63)解 B.线段数:第一列+第二列=第三列-11.1.4 面(2007-64)解 C .每一行的面数和为8.1.1.5 曲直性(2009-69)请从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:解 A.直线压曲线1.1.5 元素(2004-51)A B C D解 D. 观察整套图形可以发现,图形的规律是图案是间隔着递增的,依此规律可知答案为D。
(2004-53)A B C D解 A.观察图形可以发现,四幅图案均由4个形状相同的小图构成,对照选项,A 符合这一规律,故答案为A。
(2004-54)A B C D解 D.观察图形可以发现,图案下面的斜线段逐渐递减,且变化规律为图形下半部分依次呈左下右上的顺序递减,依此规律,故答案为D。
(2004-56)A B C D解 D.观察图形可以发现,该套图中的每一个图都由上下两部分组成,上半部分的变化规律为先递增后递减,下半部分的规律为递减,由此可推知D选项正确。
(2004-57)A B C D解 A.观察图形可以发现,每个图形都是由四条或开或闭曲线相交构成,依此规律,故选A。
(2009-67)请从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:解 C.本题属于“5+1”型图形推理。
本题考查的是圆圈与五星的换算关系:一个五角星等于三个圆圈。
这样换算下来就是4,5,6,7,8,9.(2009-68)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:解A.元素种类为1,2,1,2,1,2(福建2010-64)解C题考察线条数。
五角星的绘制

五角星的绘制五角星是一种具有美学价值和象征意义的几何图形,常常被用于装饰和标识。
五角星的绘制方法多种多样,本文将以步骤清晰易懂、详细有序的方式,介绍五种常见的绘制方法。
一、通过画圆的方式绘制五角星这是最简单的一种绘制方法,步骤如下:1. 在纸上画一个圆,作为五角星的外轮廓。
2. 确定五角星的中心点,也就是圆心。
通过圆的直径可以很容易找到中心点。
3. 在中心点处垂直画一条直线,这条直线将圆分为两部分。
4. 在圆上标出五个点,这些点与圆心的距离应该相等,也就是圆的半径。
5. 从圆心开始,沿着垂直直线连接相邻的两个点,将圆分为10份。
6. 从第一个点开始,顺时针连接相邻的点,这样就得到了五角星。
7. 如果要美化五角星,可以在其对角线上加入个性化的装饰,如图所示。
这种方法的优点是简单易行、不需要使用任何专业工具,但缺点是五角星不够规整,容易出现形状不对称或不美观的情况。
二、通过图形变换的方式绘制五角星这种方法要借助数学知识,比较复杂,步骤如下:1. 在纸上画一个长方形,通过比例变换将其变成一个正方形。
2. 对正方形分别进行两次45度的旋转,这样就得到了一个菱形。
3. 在菱形上连接相邻的两个点,这样就可以得到一个五边形。
4. 在五边形上连接对角线,形成第二个五边形。
5. 这个五边形就是五角星的轮廓,去掉内部部分即可得到五角星。
这种方法的优点是五角星非常规整,形状稳定、美观大方,缺点是需要使用复杂的数学知识,不易于初学者掌握。
三、通过分段拼接的方式绘制五角星这种方法是将五角星分段进行绘制,步骤如下:1. 在纸上画一个直角三角形。
2. 将三角形的一边分为5份,分别标记为A、B、C、D、E。
3. 从三角形的顶点开始,连接点A和点C,点C和点E,点E和点B,点B和点D,点D和点A。
4. 这样就得到了五个三角形,通过拼接即可得到完整的五角星。
这种方法的优点是比较容易理解和掌握,缺点是五角星的形状不够规整、右侧的三角形容易出现变形。
五角星的多种画法
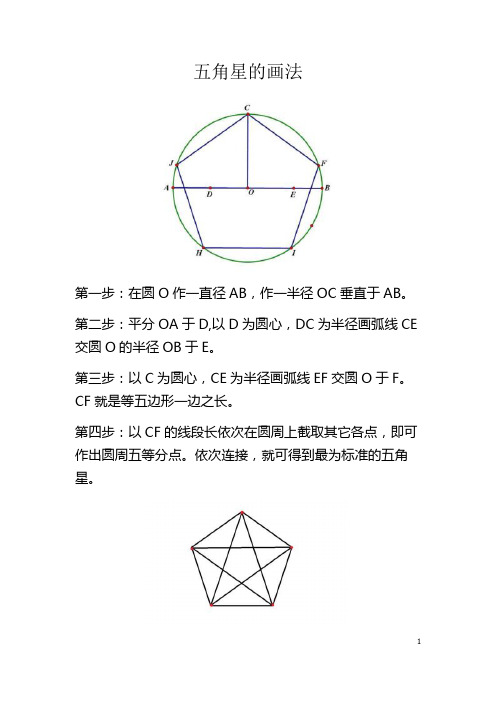
第一步:在圆O作一直径AB,作一半径OC垂直于AB。
第二步:平分OA于D,以D为圆心,DC为半径画弧线CE 交圆O的半径OB于E。
第三步:以C为圆心,CE为半径画弧线EF交圆O于F。
CF就是等五边形一边之长。
第四步:以CF的线段长依次在圆周上截取其它各点,即可作出圆周五等分点。
依次连接,就可得到最为标准的五角星。
1.先画圆A,过圆心画两条直线垂直相交;2.然后画圆A半径的中点a;3.以点a为圆心,ab为半径画弧线bc,交圆A的半径于点c;4.以点b为圆心,bc为半径画弧线交圆A于点d点e;5.以点d为圆心,bc为半径画弧交圆A于点f;6.以点f为圆心,bc为半径画弧交于点g;7.点bdfge连起来既得五角星。
正方形中的五角星在一个4*4大正方形中,可以画出标准的五角星,具体的画法步骤如下:1. 在一个平面内,画出一个4*4的大正方形,并相互连接对角线。
2.以在第二排中间两个小正方形的对角线交点为基础画直线。
3.把最下边8个小正方形看成2个中正方形,找出中心点。
4.在大正方形的上边中找到中点,以此为基础连接中正方形的中心点并延长。
5.把五角星的剩余两条边连接即可完成。
五角星的标准画法1.在白纸上,以任意一点为圆心,以任意长为半径画圆O。
2.在圆中画两条互相垂直的圆的直径AB和CD。
3.取线段OB的中点E,连接CE。
4.以点E为圆心,以CE长为半径画圆弧,交线段OA于点F。
5.连接CF,以点C为圆心,以CF长为半径在圆上依次截取相等的圆弧。
6.连接CM、CH、GN、GM、NH,就得到正五角星。
7.沿着正五角星的形状,剪下正五角星。
五角星的快速手绘方法1.在纸上画一条4cm的横向直线,在中间两厘米处点一个点,其他尺寸可以按照比例来增加或减少。
2.在横线中间画一条以它垂直的3cm的直线,并且上下各1.5cm。
3.用4cm直线把左边线和中线连接。
4.用4cm直线把右边线和中线连接。
5.用4cm直线把左上边线和左下线连接,4cm直线把右上边线和右下线连接,五星形成。
生活中的图形(一)

生活中的图形(一)引言图形是我们生活中无处不在的元素,它们存在于周围的自然界、建筑物、家具、日常用品等各个方面。
了解不同类型的图形,能够让我们更加敏锐地观察和欣赏周围的环境。
本篇文章将介绍一些常见的生活中的图形及其特点。
圆形圆形是几何学中最基本的图形之一,也是人们经常在生活中接触到的形状之一。
它具有以下特点:•圆形具有无限个对等的半径,所有半径的长度相等。
•圆形的周长是其半径的长度乘以2π。
•圆形的面积是其半径的平方乘以π。
在生活中,圆形的应用非常广泛。
例如:1.餐桌上的圆盘、杯子和碗具多为圆形,方便拿取和使用。
2.家庭中的墙壁和天花板多为方形或矩形的形状,但其中的灯具和装饰品往往是圆形的,通过照明和点缀起到美化空间的作用。
3.自然界中,花朵往往都是圆形的,它们通过鲜艳的颜色和丰富的纹理吸引昆虫传播花粉。
三角形三角形是由三条边和三个角构成的图形,它是几何学中最常见的图形之一。
三角形具有以下特点:•三角形的三条边之和等于180度。
•三角形的三个内角之和也等于180度。
•根据边的长度和角的大小,三角形可以分为等边三角形、等腰三角形和普通三角形。
在生活中,我们可以看到许多与三角形相关的事物,例如:1.厨房中的刀具,例如切菜刀、水果刀等,刀片往往是三角形的,这样可以更容易地切割食材。
2.建筑物的屋顶常常是由三角形构成的,这样的结构能够有效地抵抗风力和雨水的冲击。
3.电力塔和通信塔的结构也常常采用三角形的设计,这样可以保证塔的稳定性。
正方形正方形是一个具有四条边和四个角的图形,它是长方形的一种特殊情况。
正方形具有以下特点:•正方形的四条边的长度相等。
•正方形的四个角都是直角(90度)。
•正方形的对角线相等且互相垂直。
在我们的日常生活中,正方形是一种常见的图形,例如:1.纸张的形状就是正方形,我们常用的信纸、便签纸等都是由正方形剪切而来的。
2.电脑屏幕、手机屏幕往往具有正方形的外形,这样的设计可以方便人们查看内容。
五角星正方形三角形正方形数学题

文章标题:深度探讨:五角星、正方形、三角形数学题的解析与思考一、引言在数学领域,五角星、正方形和三角形一直是研究的热点之一。
而有关这三种图形的数学题更是常常出现在学生的课本和数学竞赛中。
本文将针对这些数学题展开深度探讨,以便读者能更全面地理解这些图形之间的关系和性质。
二、五角星、正方形、三角形的基本性质1. 五角星五角星是一种几何图形,由五条等长的线段连接而成,其内部形成一个封闭的区域。
五角星是一个中心对称的图形,具有对称性和稳定性。
在数学题中,我们经常需要计算五角星的对角线长度、面积等相关问题。
2. 正方形正方形是一种特殊的四边形,具有四条相等的边和四个直角。
正方形是正规多边形中的一种,其特点是所有角均为直角。
在数学题中,我们通常需要求解正方形的对角线长度、周长和面积等问题。
3. 三角形三角形是一种具有三条边的几何图形,其内部形成一个封闭的区域。
根据角度的不同,三角形又可以分为直角三角形、等腰三角形、等边三角形等多种类型。
在数学题中,我们会涉及到三角形的边长、角度、高度以及面积等问题。
三、数学题的解析与思考1. 五角星、正方形和三角形的关系在解决数学题时,我们常常会遇到将五角星、正方形和三角形结合在一起的题目。
给定一个正方形,要求在其上绘制一个包含五角星和三角形的图案,并计算各个图形的面积和周长。
这就需要我们深入理解这些图形的性质和关联,灵活运用相关知识来解决问题。
2. 从简到繁,由浅入深地探讨为了更好地理解这些数学题,我们可以从简单的例子开始,逐步引入更复杂的情形。
可以先从计算各个图形的周长和面积开始,然后逐步引入相关的角度和对称性等概念,最终深入探讨这些图形的数学性质和应用。
3. 个人观点与理解在我看来,五角星、正方形和三角形是数学世界中的经典图形,它们不仅具有艺术美感,更重要的是具有丰富的数学性质和广泛的应用价值。
通过学习和探索这些图形之间的关系,我们可以锻炼自己的逻辑思维和数学推理能力,为今后的学习和工作打下坚实的基础。
最全小学数学广角知识点归类

最全小学数学广角知识点归类小学数学生活知识点归类一年级一、位置一)绝对位置1、上下、前后、左右。
例如,五角星在三角形的前面(左面),正方形在圆的上面,三角形在五角星的后面(右面)。
2、小组与位置、行与列。
例如,XXX的座位是第一组第4个,XXX的座位是第四组第2个。
组就是列,组序、座序从左到右。
小猴在第一行第2个,XXX在第三行第3个,行从前往后,个从左到右。
二)相对位置例如,小鸡往下走4格,再往左走3格到企鹅处。
题:1、7后面的第3个数是()。
2、△△△▲△△○△△△△△一共有()个△,○的左边有()个△,○的右边有()个△,请把左起的第4个△涂黑。
3、XXX跟同学们一起排队,他前面有4个人,后面有7个人。
这列队伍有()人。
答案:4+7+1=12(人)二、图形的拼组1、先折后剪:从圆→扇形→三角形→正方形或长方形。
2、先剪后卷:从长方形→圆筒。
3、拼一拼:从正方体→长方体,从小正方体→长方体,从小正方体→大长方体。
4、长方体的面:它的上下、前后的面都是长方形,它的左右两个面是正方形或长方形。
题:1、用()个同样大的小正方体可以拼成一个更大的正方体。
答案:8=2³。
2、右图由()个正方形拼成。
答案:4.3、可乐的拉罐瓶是()体。
答案:圆柱。
三、认识人民币XXX发行的第五套人民币的面额:纸币:1角、2角和5角、1元、2元、5元、10元、50元、100元9种面额。
硬币:1元(第四套:1分、2分、5分)。
题:1、1元+1元8角=()。
答案:2元8角。
2、一张10元的人民币可以换成()张1元或()张5角。
人民币的单位有元、角和分。
3、一袋大米20元,一桶油15元。
妈妈带去60元钱,想买2袋大米,1桶油,够吗?60-20×2+15=5(元)。
答案:够了,还剩5元。
四、找规律一)图形的排列规律1、两种图形的排列:⑴简单排列:●▲●▲●▲●▲……规律:(AB)⑵复杂排列:●▲●●▲▲●●●▲▲▲●●●●▲▲▲▲……规律:nAB2、三种图形的排列:⑴简单排列:●▲■XXX▲■XXX▲■……规律:(ABC)⑵复杂排列:●▲■■▲●●▲■■▲●……规律:ABC CBA……⑶三角形排列:规律:(n+1)h二)数字的排列规律⑴简单排列:1 3 5 7 9……观察物体从不同方向观察物体,可以看到不同的形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角正方形圆五角星规律
1. 引言
在几何学中,我们经常会遇到各种形状,例如三角形、正方形、圆和五角星。
这些形状不仅在数学中具有重要的地位,而且在日常生活中也随处可见。
本文将介绍这些形状的特点和规律,并探讨它们之间的联系。
2. 三角形
三角形是最基本的几何形状之一,它由三条线段组成,每两条线段之间的交点称为顶点。
根据三条线段的长度,三角形可以分为不同的类型:等边三角形、等腰三角形和一般三角形。
•等边三角形:三条边的长度相等,每个角都是60度。
•等腰三角形:两条边的长度相等,两个对角也相等。
•一般三角形:三条边的长度都不相等,三个角也不相等。
三角形有许多有趣的特性,例如三角形的内角和为180度,三角形的任意两边之和大于第三边等等。
三角形在建筑、工程和艺术领域中被广泛应用。
3. 正方形
正方形是一种特殊的四边形,它的四条边长度相等且四个角都是90度。
正方形具有以下特点:
•所有边长相等:正方形的四条边长度相等,这使得它具有对称性。
•所有角度均为90度:正方形的四个角都是直角,这使得它在建筑和工程中非常实用。
•对角线相等且垂直:正方形的对角线相等且垂直于彼此,这为解决几何问题提供了便利。
正方形常用于建筑设计、城市规划和图案设计中,其对称性和稳定性使其成为一种常见的几何形状。
4. 圆
圆是一种特殊的几何形状,它由一条曲线组成,该曲线上的每个点与一个固定点之间的距离相等。
圆具有以下特点:
•半径:圆的半径是从圆心到圆上任意点的距离,所有半径长度相等。
•直径:直径是通过圆心的线段,它等于两倍的半径长度。
•弧长:弧长是圆上的一段曲线长度,它与圆心角的大小成正比。
•扇形:扇形是圆心和圆上两点之间的弧与两条辐射线所夹的区域。
圆是自然界中许多物体的基本形状,例如太阳、月亮和许多水果。
在数学中,圆也是许多重要概念的基础,例如圆的面积和周长的计算。
5. 五角星
五角星是一种具有五个尖角的几何形状,它由五条线段组成。
五角星具有以下特点:•尖角:五角星的每个角都是尖角,它们的度数为36度。
•对称性:五角星具有五重对称性,这意味着它可以通过旋转72度来重合。
•黄金分割:五角星的尖角之间的比例是黄金分割比例,即1:0.618。
五角星在许多国家的国旗、纹章和标志中被广泛使用,它具有独特的美学价值和象征意义。
6. 规律和联系
尽管三角形、正方形、圆和五角星是不同的几何形状,但它们之间存在一些规律和联系。
•内角和:三角形的内角和为180度,正方形的内角和为360度,五角星的内角和为540度。
可以看出,正方形的内角和是三角形的两倍,五角星的内角
和是正方形的1.5倍。
•对称性:正方形和五角星具有多重对称性,而三角形和圆则具有较少的对称性。
这种对称性使得正方形和五角星在设计和图案中更容易使用。
•圆的特殊性:圆是一种特殊的几何形状,它具有无限多的对称轴,而三角形、正方形和五角星只有有限数量的对称轴。
这些规律和联系展示了不同几何形状之间的相互关系,也说明了它们在数学和设计中的重要性。
7. 结论
三角形、正方形、圆和五角星是几何学中常见且重要的形状。
它们具有各自独特的特点和规律,同时也存在一些联系和共性。
了解这些形状的特点和规律,有助于我们更好地理解几何学的基础知识,并在实际生活和设计中应用它们。
几何学不仅仅是一门抽象的学科,它与我们的生活息息相关。
通过研究和理解不同几何形状的特点和规律,我们可以更好地欣赏和应用几何学在建筑、艺术和工程等领域的价值。
希望本文对你对三角形、正方形、圆和五角星的认识有所帮助,并能激发你对几何学的兴趣和探索。
让我们一起探索几何学的奥秘吧!。
