组合电路分析
组合电路分析实验报告

一、实验目的1. 掌握组合逻辑电路的基本概念和特点。
2. 学会分析组合逻辑电路的逻辑功能。
3. 熟悉逻辑门电路的原理和应用。
4. 提高实验操作能力和分析问题能力。
二、实验原理组合逻辑电路是由逻辑门电路组成的,其输出仅与当前输入有关,而与电路历史状态无关。
本实验主要涉及以下几种基本逻辑门电路:1. 与门(AND Gate):当所有输入都为1时,输出才为1。
2. 或门(OR Gate):当至少一个输入为1时,输出为1。
3. 非门(NOT Gate):将输入信号取反。
4. 异或门(XOR Gate):当输入信号不同时,输出为1。
三、实验仪器与器材1. 74LS00(四2输入与门)2. 74LS02(四2输入或门)3. 74LS04(六反相器)4. 74LS86(四2输入异或门)5. 数字逻辑实验箱6. 万用表7. 导线若干四、实验内容与步骤1. 实验一:验证与门、或门、非门、异或门的功能(1)按照实验指导书连接电路图,并检查无误。
(2)按照表1要求输入信号,观察并记录输出信号。
(3)根据观察到的输出信号,分析各门电路的逻辑功能。
表1:验证与门、或门、非门、异或门的功能| 输入信号 | 与门输出 | 或门输出 | 非门输出 | 异或门输出 || :-------: | :-------: | :-------: | :-------: | :-------: || A | B | A | A | A || 0 | 0 | 0 | 1 | 0 || 1 | 1 | 1 | 0 | 1 |2. 实验二:设计组合逻辑电路(1)设计一个组合逻辑电路,实现以下功能:当输入A为1,B为0时,输出Y为1,否则Y为0。
(2)根据设计要求,选择合适的逻辑门电路,并画出电路图。
(3)按照电路图连接实验电路,并检查无误。
(4)按照表2要求输入信号,观察并记录输出信号。
表2:设计组合逻辑电路| 输入信号 | 输出信号 || :-------: | :-------: || A | B | Y || 0 | 0 | 0 || 0 | 1 | 0 || 1 | 0 | 1 || 1 | 1 | 0 |3. 实验三:分析组合逻辑电路(1)分析实验二所设计的组合逻辑电路,确定其逻辑功能。
实验六组合逻辑电路的实验分析
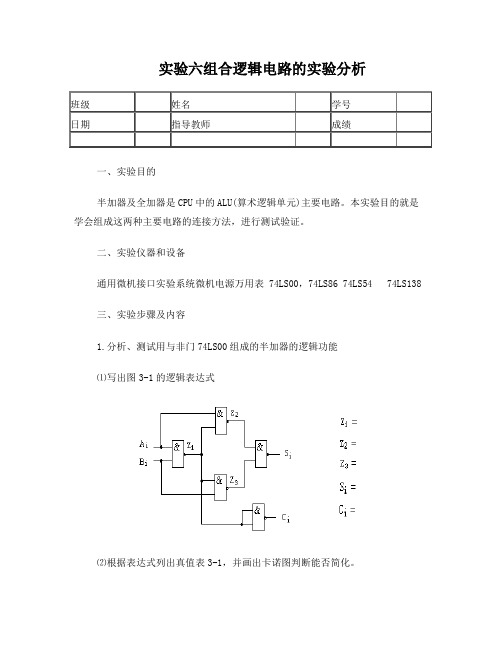
实验六组合逻辑电路的实验分析班级姓名学号日期指导教师成绩一、实验目的半加器及全加器是CPU中的ALU(算术逻辑单元)主要电路。
本实验目的就是学会组成这两种主要电路的连接方法,进行测试验证。
二、实验仪器和设备通用微机接口实验系统微机电源万用表 74LS00,74LS86 74LS54 74LS138三、实验步骤及内容1.分析、测试用与非门74LS00组成的半加器的逻辑功能⑴写出图3-1的逻辑表达式⑵根据表达式列出真值表3-1,并画出卡诺图判断能否简化。
表3-1⑶按图3-1连线,将及分别接至逻辑电平开关及,及分别接至LED电平显示电路及。
⑷给及以不同的电平,观察及的电平并记于表3-2中,同时与上表3-1比较,看两者是否一致.2.分析用一个与门(实验系统中)及一异或门(74LS86)组成半加器电路,电路如图3-2。
(1)查阅本书附录B,记下74LS86的结构和引线的排列,按图连线,测试方法同1.(3)项,将测试结果填入自拟的表格中,并验证逻辑功能。
3.分析测试用异或门、与非门和或门组成的全加器逻辑电路。
根据全加器的逻辑表达式全加和进位可知一位全加器可以用两个异或门和两个与门及一个或门组成。
1 出用上述门电路实现的全加器逻辑电路。
2 所画的原理图,选择器件,并接线。
3 进行逻辑功能测试,将测试结果填入自拟表格,判断测试是否正确。
Ai Bi Ci-1 Ci Si0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1四、实验报告要求1、整理实验数据、图表并对实验结果进行分析讨论。
2、总结组合电路的分析与测试方法。
组合逻辑电路分析

实验名称组合逻辑电路分析、设计与测试一、实验目的1.掌握组合逻辑电路的分析与测试方法;2.掌握用门电路设计组合逻辑电路的方法。
二、实验原理1.组合逻辑电路的分析与测试组合逻辑电路是最常见的逻辑电路,即通过基本的门电路(比如与门,与非门,或门,或非门等)来组合成具有一定功能的逻辑电路。
组合逻辑电路的分析,就是根据给定的逻辑电路,写出其输入与输出之间的逻辑函数表达式,或者列出真值表,从而确定该电路的逻辑功能。
组合逻辑电路的测试,就运用实验设备和仪器,搭建出实验电路,测试输入信号和输出信号是否符合理论分析出来的逻辑关系,从而验证该电路的逻辑功能。
组合逻辑电路的分析与测试的步骤通常是:(1)根据给定的组合逻辑电路图,列出输入量和中间量、输出量的逻辑表达式;(2)根据所得的逻辑式列出相应的真值表或者卡诺图;(3)根据真值表分析出组合逻辑电路的逻辑功能;(4)运用实验设备和器件搭建出该电路,测试其逻辑功能。
2.组合逻辑电路的设计与测试组合逻辑电路的设计与测试,就是根据设计的功能要求,列出输入量与输出量之间的真值表,通过化简获得输入量与输出量之间的逻辑表达式,然后根据逻辑表达式用相应的门电路设计该组合逻辑电路,然后运用实验设备与器件搭建实验电路,测试该电路是否符合设计要求。
组合逻辑电路的设计与测试的步骤通常是:(1)根据设计的功能要求,列出真值表或者卡诺图;(2)化简逻辑函数,得到最简的逻辑表达式;(3)根据最简的逻辑表达式,画出逻辑电路;(4)搭建实验电路,测试所设计的电路是否满足要求。
三、预习要求1.阅读理论教材上有关组合逻辑电路的分析与综合以及半加器等章节内容,以达到明确实验内容的目的。
2.查阅附录有关芯片管脚定义和相关的预备材料。
四、实验设备与仪器1.数字电路实验箱;2.芯片74LS00;74LS20。
五、实验内容1.半加器逻辑电路的分析与测试SC图5.5.1 半加器的逻辑电路(1) 根据图5.5.1写出中间量(1Z 、2Z 和3Z )和输出量(S 和C )关于输入量(A 和B )的逻辑表达式。
电路第03章 组合电路的分析与设计

0 0 0 1 1 =0 0 0 1 1 • 0 1 1 1 1
10 0 0 1
10 0 1 1 11 0 0 1
F
F1 A
F2 BC
F F1 F2 A BC
AB AC
注: 为使阻塞圈所代表的积项中各变量不再具有非的形式, 阻塞圈也应该围绕1重心来圈。
版权:孙文生
版权:孙文生
2. 用阻塞逻辑设计三级与非电路
解: 将函数填入卡诺图
AB CD
00
01
11
10
00 1 1
01 1 1 1 1
11
1
10 1
11
采用阻塞法化简逻辑函数
F 1 ACD BC AD BC AC CD
ACD BC AD BC AC CD
版权:孙文生
用阻塞逻辑设计三级与非电路
版权:孙文生
【应求】
例: 输入只有原变量,用最少的三级与非门实现下列函数 F(A, B,C, D) M (3,6,7,8,12,15)
1
01 1 1
1
11
11
10
11
F
(2) 求最简与或式,并变换
F A C AC AB A C AC AB A C AC AB
(3) 画出逻辑图
版权:孙文生
版权:孙文生
3.3.2 逻辑函数的两级门实现
2. 两级或非门电路的实现
求出函数的最简或与式; 对函数两次取反,再运用反演率,变成或非-或非式;
版权:孙文生
当需要用原变量标注时,在化简时应围绕1重心来圈。
版权:孙文生
积项的阻塞逻辑
阻塞逻辑:
乘积项可以用被扣除的最小项的反乘之,使积项受其控制,其 逻辑关系保持不变。
组合逻辑电路的分析

数字电子技术基础
9
竞争-冒险现象
两个输入信号同时向相反的逻辑电平跳变,
输出端可能会产生尖峰脉冲。
检测
存在 = + ′ 或 = · ′
如 = + ′ 令 = =
消除
修改逻辑设计: = + ′ +
计算机系
数字电子技术基础
(4)由真值表分析电路的逻辑功能。
计算机系
数字电子技术基础
6
实例
例1 分析图1所示电路的逻辑功能。
Bˊ
(AB ˊ) ˊ
((AˊB) ˊ(ABˊ) ˊ) ˊ
Aˊ
SH
(AˊB) ˊ
A
B
((AB) ˊ) ˊ
(AB) ˊ
CH
图1 组合逻辑电路
计算机系
数字电子技术基础
7
实例
(1)输出端的逻辑函数式
S H ((A B ) • (AB ) )
10
课堂练习
分析图2所示电路的逻辑功能。
A
B
C
Y
图2
计算机系
数字电子技术基础
11
组合逻辑电路的分析
计算机系
数字电子技术基础
1
回顾
门电路:
Y=AB
计算机系
Y=A+B
数字电子技术基础
Y=A′
2
回顾
门电路:
计算机系
数字电子技术基础
3
组合逻辑电路的特点:
任意时刻的输出仅仅取决于该时刻的输入,
与电路原来的状态无关。
功能特点:无记忆作用,输出只取决于当
前输入,与电路过去的状态无关。
C H ((AB ) )
组合逻辑电路的分析

组合逻辑电路的分析在分析组合逻辑电路时,我们可以使用真值表、卡诺图或布尔代数等方法。
下面将分别介绍这些方法的基本原理和应用。
1.真值表分析法真值表是列出电路的所有可能输入和对应输出的表格。
通过逐行检查真值表的输出列,可以确定电路的功能。
真值表分析法适用于较小规模的电路,但对于较复杂的电路可能不够实用。
2.卡诺图分析法卡诺图是一种图形表示方法,用于描述逻辑函数之间的关系。
它将所有可能的输入组合表示为一个方格矩阵,每个方格代表一个状态。
相邻的方格表示输入之间只有一个位不同。
通过合并相邻的方格,我们可以找到简化逻辑函数的最小项或最小项组合。
卡诺图分析法可以用来优化逻辑电路,减少门的数量和延迟。
3.布尔代数分析法布尔代数是一种用符号和运算规则描述逻辑函数的代数系统。
我们可以使用布尔代数的运算规则来简化和优化逻辑电路。
常见的布尔代数运算包括与运算、或运算、非运算和异或运算等。
通过应用这些运算规则,我们可以将复杂的逻辑函数简化为最小项或最小项组合,从而简化电路。
在进行组合逻辑电路的分析时,我们首先需要确定电路的输入和输出。
然后,我们可以根据电路的功能和输出要求,绘制真值表或卡诺图。
通过分析真值表或卡诺图,我们可以找到逻辑函数的最小项或最小项组合。
接下来,我们可以将这些最小项或最小项组合转化为逻辑门的输入方式。
最后,我们可以使用布尔代数的运算规则来简化逻辑函数和电路。
组合逻辑电路的分析是电路设计和优化的重要一步。
通过应用不同的分析方法,我们可以更好地理解电路的功能和性质,从而更好地设计和优化电路。
在分析组合逻辑电路时,我们需要注意电路的输入和输出要求,合理选择和配置逻辑门,以及优化电路的延迟和开销。
组合逻辑电路分析

组合逻辑电路分析
1.1 组合逻辑电路的定义
Fi fi ( X1, X 2 , X n )
输 入
X1 X2
信
号 Xn
组合逻辑 电路
( i=1,2,…,m)
F1 输 F2 出信
号 Fm
图4-1 组合逻辑电路框图
特点
由逻辑门电路组成 输出与输入之间不存在反馈回路
1.1 组合逻辑电路的定义
Y1 A Y3 Y1 Y2 A B
Y2 B Y4 A B
A
B
Y
0
0
1
0
1
0
1Leabharlann 0011
1
Y Y3 Y4
(4)该电路实现的是同或逻辑功能。
2.多输出组合逻辑电路的分析 【例4-2】已知逻辑电路如图4-3所示,分析该电路的逻辑功能。
图4-3 多输出组合逻辑电路图(来自QuartusII)
解:(1)写出所有输出逻辑函数表达式,并对其进行化简。
1.3 组合逻辑电路分析
1.单输出组合逻辑电路的分析
【例4-1】已知逻辑电路如图4-2所示,分析该电路逻辑功能。
A
Y1 Y3
Y
B
Y2
Y4
图4-2 单输出组合逻辑电路图
(2)化简逻辑电路的输出函数表达式:
Y Y3 Y4 A B A B
(3)列出真值表 表4-1 例4-1 真值表
解:(1)写出各输出的逻辑函数表达式:
1
1
0
1
1
L1
L2
L3
0
1
0
0
0
1
1
0
0
0
1
0
(3)逻辑功能说明。 该电路是一位二进制数比较器,
组合逻辑电路分析误差分析与实验结论

组合逻辑电路分析误差分析与实验结论组合逻辑电路分析实验结论:根据实验,可以轻易看出G0的波形图是有错误的,应是电线接触不良导致示波器该输出端口没有接收到信号,导致波形图为一条直线。
而其余的波形图都与真值表的对应关系一致,符合实验的内容。
组合逻辑电路分析误差分析:实验数据的误差主要是在输出结果上,在输出结果的波形图中,可以轻易看出G0的波形图是有错误的,应是电线接触不良导致示波器该输出端口没有接收到信号,此外,许多波形图中间都有白色线出现,重复实验,白色线仍然存在,可能是机器的原因,从实验过程中还可以看出有时候各输出端口信号突然消失,波形图均为一小段直线,可能是连接连续脉冲的电线接触不良导致有一小段输入信号没有接收到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.12(1)
Y Y2 Y3 A AB B AB AB AB A B
(3)分析逻辑功能 通过分析真值表可知:当A、B输入的状态不同时, 输出Y= 1;当A、B输入的状态相同时,输出Y= 0;因此, 图示电路具有异或功能,为异或门。
[例] 分析下图所示逻辑 电路的功能。 A
列真值表
分析逻辑功能
[例1] 分析下图所示逻辑 电路的功能。 A
B Y1 Y2 Y3 Y
(2)列逻辑函数真值表
输 入 A B 0 0 1 1 0 1 0 1 输出 Y 0 1 1 0
(1)写出输出逻辑函数式 解: Y 1 AB Y2 A Y1 A AB Y3 B Y1 B AB
(3)分析逻辑功能 通过分析真值表可知:当A、B输入的状态不同时, 输出Y= 1;当A、B输入的状态相同时,输出Y= 0;因此, 图示电路具有异或功能,为异或门。
[例2] 分析下图所示逻辑 电路的功能。
(2)列逻辑函数真值表 输 入 A B C 输出 Y 0 1 1 0 1 0 0
A B
C
Y1 Y
3.2 组合逻辑电路的分析及设计方法
复习导入:基本门电路
与门 (AND gate) 或门 (OR gate) 非门(NOT gate) 又称“反相器”
与非运算(NAND)
先与后非 或非运算 ( NOR )
先或后非 与或非 运算
先与后或再非
逻辑电路
组合逻辑电路 时序逻辑电路
3.2.1组合逻辑电路的分析
B Y1 Y2 Y3 Y
(2)列逻辑函数真值表
输 入 A B 0 0 1 1 0 1 0 1 输出 Y 0 1 1 0
(1)写出输出逻辑函数式 解: Y 1 AB Y2 A Y1 A AB Y3 B Y1 B AB
Y Y2 Y3 A AB B AB AB AB A B
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
(1)写出输出逻辑函数式 解: Y1 A B Y Y1 C A B C ( A B )C A B C ABC ABC ABC ABC
001 010 100 111 1 (3)分析逻辑功能 通过分析真值表可知:A、B、C 三个输入变量中,有奇数个 1 时,输出为 1,否则输出为 0。因此,图示电路为三位奇校验电路。
半加器(没有低位进位)
1.组合逻辑电路 有多个输入端、多个输出端
总结
2组合逻辑电路的分析 已知逻辑电路→输入输出变量的关系 步骤(1)逻辑电路→表达式→ (2)真值表→ (3)分析逻辑功能
作业及准备知识 作业及准备知识
第110页5.10(2) 5.11(3) 与或非逻辑符 号,功能及. 逻辑表达式
组合电路的组成特点:
由门电路构成,不含记忆单元,只存在从输 入到输出的通路,没有反馈回路。
组合逻辑电路的逻辑功能特点:
没有存储和记忆功能。
组合电路的描述方法主要有逻辑表达式、 真值表、卡诺图和逻辑图等。
分析思路:
根据给定逻辑电路,找出输出、输入间的逻辑关
系,从而确定电路的逻辑功能。
基本步骤:
根据给定逻辑图写出输出逻辑式,并进行必要的 化简。
[例3] 分析下图所示逻辑 电路的功能。
解(1)表达式
) ( A B) A AB B A A B j AB AB
(2)真值表 (3)分析逻辑功能 1位2进制加法。h-加法的和 j-进位
