matlab实验二
实验二-MATLAB-图形系统
实验二 MATLAB 图形系统一、实验目的和要求Matlab 提供了强大的图形处理功能,本次实验旨在使学生熟悉和掌握应用Matlab 实现二维图形和三维图形的绘制和控制与表现方法。
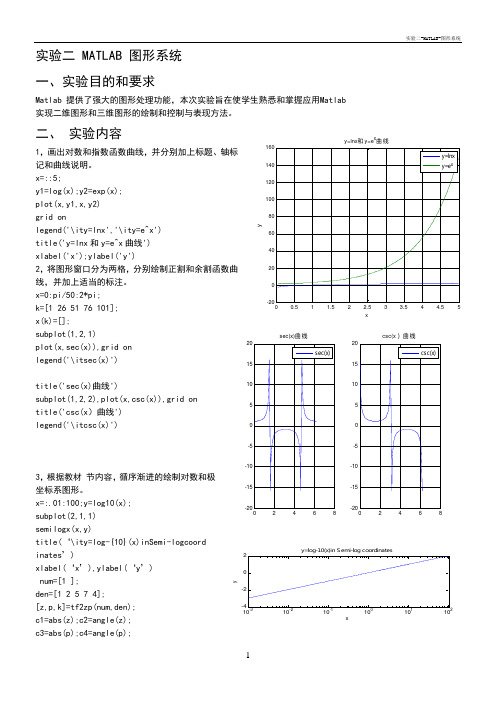
二、实验内容1,画出对数和指数函数曲线,并分别加上标题、轴标记和曲线说明。
x=::5;y1=log(x);y2=exp(x);plot(x,y1,x,y2)grid onlegend('\ity=lnx','\ity=e^x')title('y=lnx和y=e^x曲线')xlabel('x');ylabel('y')2,将图形窗口分为两格,分别绘制正割和余割函数曲线,并加上适当的标注。
x=0:pi/50:2*pi;k=[1 26 51 76 101];x(k)=[];subplot(1,2,1)plot(x,sec(x)),grid onlegend('\itsec(x)')title('sec(x)曲线')subplot(1,2,2),plot(x,csc(x)),grid ontitle('csc(x)曲线')legend('\itcsc(x)')3,根据教材节内容,循序渐进的绘制对数和极坐标系图形。
x=:.01:100;y=log10(x);subplot(2,1,1)semilogx(x,y)title(‘\ity=log-{10}(x)inSemi-logcoord inates’)xlabel(‘x’),ylabel(‘y’)num=[1 ];den=[1 2 5 7 4];[z,p,k]=tf2zp(num,den);c1=abs(z);c2=angle(z);c3=abs(p);c4=angle(p);xyy=lnx和y=e x曲线sec(x)曲线csc(x)曲线101010101010y=log-10(x)in Semi-log coordinatesxypolar(c4,c3,'bx')hold on,polar(c2,c1,'ro')gtext('极坐标系中的零极点表示')4,根据教材 节内容,绘制多峰函数和三角函数的多条曲线。
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
实验二-基于Matlab的离散控制系统仿真

实验二基于Matlab的离散控制系统仿真一、实验目的1)学习使用Matlab命令对离散控制系统进行仿真的方法。
2)学习使用Simulink工具箱对离散控制系统进行仿真的方法。
二、实验原理1. 控制系统命令行仿真一阶系统闭环传递函数为3()G ss+3请转换为离散系统脉冲传递函数并仿真。
根据要求实验有实验数据和所得图形如下:连续零极点图函数:离散函数零极点图:连续函数根轨迹图:离散函数根轨迹图:连续函数单位脉冲响应曲线:离散函数单位脉冲响应曲线:连续函数单位阶跃响应:离散函数单位阶跃响应:连续函数波特图:离散函数波特图:连续函数艾奎斯特曲线:离散函数艾奎斯特曲线:连续函数尼科尔斯曲线:离散函数尼科尔斯曲线:2. 控制系统simulink 仿真按图建立系统的Simulink 模型,对不同的输入信号进行仿真,改变参数,观察不同的仿真结果。
图1 控制系统Simulink 仿真图解答于实验内容第二问三、实验内容1) 二阶系统传递函数为225()4+25G s s s =+,请转换为零极点模型,离散系统模型(采样时间为1),以及离散零极点模型,并进行基于matlab 命令的仿真研究(求连续和离散系统的单位脉冲响应、单位阶跃响应、零极点分布图、根轨迹、波特图、奈奎斯特曲线、尼科尓斯曲线等)。
根据题意实验所得有:连续单位脉冲响应连续单位阶跃响应连续零极点分布图离散零极点分布图连续根轨迹连续波特图连续奈奎斯特曲线连续尼科尓斯曲线2)按图1建立系统的Simulink模型,对不同的输入信号进行仿真。
改变模型参数,观察不同的仿真结果。
Step输入:Ramp输入:当函数分子分别为1,10,100,500时有:经过实验可以看出分子越大超调越大,调整时间越大。
3)将上述系统离散化并基于Simulink仿真,观察仿真结果。
根据题意实验有:Step输入:Ramp输入:分子为1时:Step输入:Ramp输入:分子为250时:Step输入:Ramp输入:四、实验报告1)按照实验报告所要求的统一格式,填写实验报告;2)记录实验过程、实验结果和图表。
信号与系统MATLAB实验-实验二 Matlab中信号的运算

1、运用funtool对f(x)=sin(x)/x分别进行信号的尺度变换f(2x)、f(0.5x)和信号的移位运算f(x+1)、f(x-1)操作以及f(0.5x+1),分别记录相应波形。
f(x)=sin(x)/x f(x+1)f(2x) f(x-1)f(0.5x) f(0.5x+1)2、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式; 2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt )【实验思考】:通过不断改变dt 的取值并对比所得到的实验效果,观察当取样时间dt 为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?3、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式;2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt)【实验思考】:不断改变dt的取值并对比实验效果,当取样时间dt为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?clear alldt = 0.01;t1 = -3:dt:3;f1 = 2*(u(t1+1) - u(t1-1));figure;stairs(t1,f1);hold allgrid ont2 = -3:dt:3;f2 = u(t2+2)-u(t2-2);stairs(t2,f2)[fn, tn] = conv_cs(f1, t1, f2, t2, dt);plot(tn, fn)grid onlegend('f1', 'f2', 'f1*f2')。
实验二-MATLAB用于时域分析

实验二 MATLAB用于时域分析一、实验目的通过使用MATLAB完成系统的输出响应分析、稳定性分析、求动态性能指标以及稳态误差分析等工作。
二、实验原理在MATLAB中,可以通过单输入单输出系统的传递函数,进行系统的脉冲响应,阶跃响应以及一般输入响应等时域分析。
用到以下函数:单位阶跃响应 step(num,den,t)单位脉冲响应impluse(num,den,t)一般输入响应 y=Isim(num,den,u,t)时间t是事先定义的矢量,u为输入信号。
此外,还可以求出系统的超调量,调节时间以及稳态误差。
SIMULINK是MATLAB的一个附加组件,用来提供一个系统的建模、动态仿真及综合分析的工作平台。
SIMULINK模型可以用来模拟线性或非线性、连续或离散,或者两者混合的系统,即可用它来模拟几乎所有的动态系统。
三、实验内容通过MATLAB以及其中的SIMULINK完成系统的输出响应分析、稳定性分析、求动态性能指标以及稳态误差分析等工作。
四、实验代码1、一阶系统响应sys1=tf([100],[1 0]);sys2=tf([0.1],[1]);sys=feedback(sys1,sys2);step(sys)2、二阶系统响应wn=1t=0:0.1:12;num=[1];zeta1=0;den1=[1 2*zeta1 1];zeta3=0.3;den3=[1 2*zeta3 1];zeta5=0.5;den5=[1 2*zeta5 1];zeta7=0.7;den7=[1 2*zeta7 1];zeta9=1.0;den9=[1 2*zeta9 1];[y1,x,t]=step(num,den1,t);[y3,x,t]=step(num,den3,t);[y5,x,t]=step(num,den5,t);[y7,x,t]=step(num,den7,t);[y9,x,t]=step(num,den9,t);plot(t,y1,t,y3,t,y5,t,y7,t,y9)grid on;3、稳定性分析den=[1 1 2 24];roots(den)4、求动态性能指标t=0:0.01:2;num=[1000]';den=[1 34.5 1000];[y,x,t]=step(num,den,t);plot(t,y);maxy=max(y);yes=y(length(t));pos=100*(maxy-yes)/yesfor i=1:1:201if y(i)==maxy,n=i;endendtp=(n-1)*0.01for i=1:1:201if(y(i)<1.05&y(i)>0.95),n=i;endbreak;endts=(n-1)*0.015、稳态误差分析t=0:0.1:15;[num1,den1]=cloop([1],[1 1]);[num2,den2]=cloop([1],[1 1 0]);[num3,den3]=cloop([4 1],[1 1 0 0]);y1=impulse(num1,den1,t);y2=impulse(num2,den2,t);y3=impulse(num3,den3,t);subplot(311);plot(t,y1);subplot(312);plot(t,y2);subplot(313);plot(t,y3);er1=0-y1(length(t))er2=0-y2(length(t))er3=0-y3(length(t))6、求单位阶跃响应及其稳态误差t=0:0.1:20[num1,den1]=cloop([1],[1 1]);[num2,den2]=cloop([1],[1 1 0]);[num3,den3]=cloop([4 1],[1 1 0 0]);y1=step(num1,den1,t);y2=step(num2,den2,t);y3=step(num3,den3,t);subplot(311);plot(t,y1);subplot(312);plot(t,y2);subplot(313);plot(t,y3);er1=1-y1(length(t));er2=1-y2(length(t));er3=1-y3(length(t));7、求单位斜坡响应及其稳态误差t=0:0.1:20;t1=0:0.1:100;[num1,den1]=cloop([1],[1 1]);[num2,den2]=cloop([1],[1 1 0]);[num3,den3]=cloop([4 1],[1 1 0 0]);y1=step(num1,[den1 0],t1);y2=step(num2,[den2 0],t);y3=step(num3,[den3 0],t);subplot(311);plot(t1,y1,t1,t1);subplot(312);plot(t,y2,t,t);subplot(313);plot(t,y3,t,t);er1=t1(length(t1))-y1(length(t1))er2=t(length(t))-y2(length(t))er3=t(length(t))-y3(length(t))8、实例分析kp=[0.11 6];t=[0:0.01:1];num1=303.03*kp(1);den1=[0.00001 0.00633 0.20167 21.21*kp(1)+1];y1=step(num1,den1,t);num2=303.03*kp(2);den2=[0.00001 0.00633 0.20167 21.21*kp(2)+1];y2=step(num2,den2,t);subplot(211);plot(t,y1);subplot(212);plot(t,y2);gtext('kp=0.11');gtext('kp=6');9、SIMULINK用于系统仿真五、实验结果1、一阶系统响应2、二阶系统响应3、稳定性分析4、求动态性能指标5、稳态误差分析6、求单位阶跃响应及其稳态误差7、求单位斜坡响应及其稳态误差8、实例分析9、SIMULINK用于系统仿真六、实验总结通过本次实验实现了用MATLAB完成系统的输出响应分析、稳定性分析、求动态性能指标以及稳态误差分析等工作。
实验二 MATLAB并行计算的配置

实验二MATLAB并行计算的配置
一、实验目的
1.通过matlabpool命令启动和配置matlab并行计算池,了解matlabpool的基本使用方法。
2.能够编写parfor程序进行并行环境的测试。
3.完成课堂练习。
二、实验课时:4课时
三、实验原理
第一部分:matlab并行池的启动及matlabpool命令的基本使用
首先,通过matlabpool size命令判断是否已经启动matlabpool。
图1 matlabpool size运行结果图
如果返回0,则表示没有开启matlabpool;如果返回大于0的值,则表示已经开启matlabpool。
然后通过运行matlabpool local;命令启动默认配置,其中的local表示配置项的名称。
图2 matlabpool local运行效果图
在运行此命令时,如果是win 7或者以上版本的系统,会弹出windows安全警报对话框,我们直接点击允许访问就可以了。
图3 windows安全警报图
第二部分:编写用于自动启动matlab并行计算池的函数程序1 startmatlabpool.m如下:
程序2 closematlabpool.m代码如下:
接着,我们可以通过help parfor命令来查看parfor的基本使用方法,然后按要求完成课堂练习的编码工作。
Help parfor允许效果图
四、课堂练习
1.编写一个测试parfor的程序,要求调用以上两个函数;
2.根据下面的公式使用matlab进行计算:
五、实验报告要求
简述实验目的;写出实验内容中解答各个题目所需要的命令及实验结果;简写实验总结与心得体会。
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本科实验报告课程名称:Matlab电子信息应用实验项目:矩阵和数组的操作实验地点:电机馆跨越机房专业班级:学号:学生姓名:指导教师:2014年3月26 日一、实验目的1.掌握矩阵和数组的一般操作,包括创建、保存、修改和调用等。
2.学习矩阵和数组的加减运算与乘法。
3.掌握对数组中元素的寻访与赋值,会对数组进行一般的操作。
二、预备知识1.常用的产生特殊矩阵的函数•eye(m,n) 单位阵•rand(m,n) 随机矩阵•randn(m,n) 正态分布的随机矩阵•zeros(m,n) 零矩阵•ones(m,n) 全部元素都为1的矩阵•compan(A) 矩阵A的伴随矩阵•bankel(m,n) n维Hankel矩阵•invhilb(n) n维逆Hilbert矩阵•magic(n) n维Magic矩阵•toeplitz(m,n) Toeplitz矩阵•wilkinson(n) n维Wilkinson特征值测试矩阵•handamard(n) n维Handamard矩阵•hilb(n) n维Hilbert矩阵•kron(A,B) Kronecker张量积•pascal(n) n维Pascal矩阵•vander(A) 由矩阵A产生Vandermonde矩阵2.通过矩阵的结构变换,获得新矩阵表2 矩阵结构变化产生新矩阵L=tril(A) L主对角线及以下元素取矩阵A 的元素,其余为0L=tril(A,k) L及第k条对角线及以下元素取矩阵A的元素,其余为U=triu(A) U主对角线及以上的元素取矩阵A的元素,其余为0U=triu(A,k) U第k条对角线及以上的元素取矩阵A的元素,其余为B=rot90(A) 矩阵A逆时针旋转90°得到B B=rot90(A,k) 矩阵A逆时针旋转k*90°得到B B=fliplr(A) 矩阵A左右翻转得到BB=flipud(A) 矩阵A上下翻转得到BB=reshape(A,m, n)将矩阵A的元素重新排列,得到m*n的新矩阵(m*n 就等于A的行列式之积。
若A为3*4,则m,n可为2,6或4,3等3.数组(矩阵)操作对数组或矩阵的基本操作有插入、重新排列、提取、按列拉长、置空(去掉某行或某列)、置零、用单信下标操作一个矩阵,用逻辑数组操作一个矩阵、按指定条件求子数组,求数组的规模等.①插入通过对x进行插入运算创建矩阵A②重新排列以逆序重排A的各行形成矩阵B③提取提取A的前两行的后两列形成矩阵C④按列拉长对C按列拉长形成矩阵D⑤置空删除B的第2 列⑥置零将矩阵B的第2行第2列的元素置为1⑦用单个下标操作一个矩阵MATLAB对矩阵中的元素赋予一个序号,序号值按列从第1列第1行到第1列第2行到第2列第1行到第2列第2行,直至最后一列最后一行的顺序计数。
⑧用逻辑数组操作一个矩阵⑨按指定条件求子数组首先由条件表达式生成一个逻辑数组,然后使用系统提供的函数即可,函数在已知数组中按逻辑数组的元素值查找所需的元素下标。
三、实验内容与步骤1.用三种方法创建一个3×3矩阵,然后利用矩阵编辑器,将其扩充为4×5矩阵,并保存,试着调用它。
⑴直接输入法⑵直接利用MATLAB提供的函数创建一个3×3矩阵⑶利用MATLAB提供的“Matrix Editor”完成输入步骤1 在命令区输入A=1。
步骤2 用鼠标单击工具栏的工作区浏览器,MATLAB弹出变量浏览器,选中变量A,鼠标左键双击A,打开矩阵编辑器。
步骤3 在左下脚的两个文本框中分别输入希望得到的矩阵的行数和列数:3行3列,即得到一个3×3矩阵。
步骤4 要将上面矩阵改为一个4×5矩阵,只需改变矩阵的行数和列数即可。
如将3行3列改为4行5列,即可得到一个4×5矩阵。
若想修改其中的元素,只需用鼠标选中表格中我们想要修改的元素,将原来的元素修改为我需要的值。
步骤5 要命令区输入save data A(data为我们给变量文件起的名称,系统会自动沿设定好的路径以“.mat”格式存储文件),即可保存上面例子中创建的矩阵A。
步骤6 在命令区输入load data即可把保存在文件中的矩阵读到MATLAB的工作区的内存中来。
2.建立一个等差数列,然后由它产生一个对角阵。
步骤1 在命令区输入a=linspace(0,1.5,5)产生一个等差数列。
步骤2 在命令区输入B=diag(a)产生一个对角阵。
3.利用MATLAB的函数inv(A)求方阵A的逆矩阵。
步骤1 在命令区输入A=[1,2;5,6]得到一个2×2的方阵。
步骤2 再输入B=inv(A)求出A 的逆矩阵。
四、练习1.创建一个5×5矩阵,提取主对角线以上的部分。
>> A=magic(5)A =17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9>> triu(A)ans =17 24 1 8 150 5 7 14 160 0 13 20 220 0 0 21 30 0 0 0 92.A=rand(3),B=magic(3),C=rand(3,4),计算A×B×C>> A=rand(3);B=magic(3);C=rand(3,4);A*B*Cans =17.3808 17.3271 20.6044 11.737411.1003 9.1717 13.4321 6.667620.3142 20.2013 25.0142 15.44653.创建一个3×3矩阵,并求其转置,逆矩阵。
>> A=magic(3),A',inv(A)A =8 1 63 5 74 9 2ans =8 3 41 5 96 7 2ans =0.1472 -0.1444 0.0639-0.0611 0.0222 0.1056-0.0194 0.1889 -0.10284.用两种方法求Ax=b的解(A为4阶随机矩阵,b为4阶列向量)。
>> A=rand(4),b=[1;2;3;4],x1=A\b,x2=inv(A)*bA =0.5252 0.0196 0.5028 0.18970.2026 0.6813 0.7095 0.1934 0.6721 0.3795 0.4289 0.68220.8381 0.8318 0.3046 0.3028b =1234x1 =1.86872.6108-0.63091.5008x2 =1.86872.6108-0.63091.5008A。
5.创建一个4阶随机矩阵A,计算3>> A=rand(4),A^3A =0.3529 0.2028 0.1988 0.9318 0.8132 0.1987 0.0153 0.4660 0.0099 0.6038 0.7468 0.4186 0.1389 0.2722 0.4451 0.8462 ans =0.7294 0.9186 1.1428 1.9807 0.6355 0.7438 0.9505 1.8563 0.8965 0.9666 1.1120 1.96830.7794 0.9577 1.1558 1.92716.求100-999之间能被21整除的数的个数。
>> A=100:999;>> B=find(rem(A,21)==0);>> C=length(B)C =437. 设有矩阵A 和B⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=25242322212019181716151413121110987654321A ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=11134079423096171603B [1] 求它们的乘积C=A×B。
>> x=[11,12,13,14,15];>>A=[x-10;x-5;11,12,13,14,15;x+5;x+10];B=[3,0,16;17,-6,9;0,23,-4;9,7,0;4,13,11];>> C=A*BC =93 150 77258 335 237423 520 397588 705 557753 890 717[2] 将矩阵C 的右下角3×2子矩阵赋给D 。
>> D=C(3:5,2:3)D =520 397705 557890 7178. 求解下列方程组[1] 0523=+-x x>> solve('x^3-2*x+5=0','x')ans =-1/6*(540+12*1929^(1/2))^(1/3)-4/(540+12*1929^(1/2))^(1/3)1/12*(540+12*1929^(1/2))^(1/3)+2/(540+12*1929^(1/2))^(1/3)+1/2*i*3^(1/2)*(-1/6*(540+12*1929^(1/2))^(1/3)+4/(540+12*1929^(1/2))^(1/3))1/12*(540+12*1929^(1/2))^(1/3)+2/(540+12*1929^(1/2))^(1/3)-1/2*i*3^(1/2)*(-1/6*(540+12*1929^(1/2))^(1/3)+4/(540+12*1929^(1/2))^(1/3)) [2] ⎪⎩⎪⎨⎧=+--=-+=-+34282113321321321x x x x x x x x x>> A=[3,11,-2;1,1,-2;1,-1,1];B=[8;-4;3];x=A\Bx =1139. 求微分方程02)(2)(=+'+''y t y t y 当y(0)=0、1)0(='y 时的解。
>> dsolve('D2y+2Dy+2y=0','y(0)=0,Dy(0)=1')ans =-2*t^2+t五、实验分析从这次的练习可以看出matlab 基本可以解决全部常见的数学运算问题,并且计算的速度非常快,使用简便,通过调用函数就可以解决相应的问题十分的方便。
六、实验总结这次练习主要是对矩阵和数组进行操作,体现出了matlab 的优越性。
通过这次练习,我学会了利用matlab 解方程组,以及一些快速创建矩阵的方法,为后续的学习打下了基础。
