第二次数学实验报告Matlab 二维曲线绘图
MATLAB第二次实验

一、【实验目的】学习利用matlab作已知二维函数或三维函数的图形一、【实验任务】P791.绘制y=e x/3sin(3x) (x∈[0,4π])的图像,要求用蓝色的星号画图;并且画出其包络线y=±3e x/3的图像,用红色的点划线画图。
3.在同一图形窗口画三个子图,要求使用指令gtext、axis、legend、title、xlabel和ylabel: (1)y=xcosx, x∈(-π,π)(2)y=xtan(1/x)sin3x, x∈(π,4π)(3)y=e1/x sinx, x∈[1,8]5.绘制圆锥螺线的图像并加各种备注,圆锥螺线的参数方程为:x=tcos(π/6)ty=tsin(π/6)t (0≤t≤20π)z=2t二、【实验程序】P791.x=0:(pi/50):4*pi;y=exp(x/3).*sin(3*x);z=exp(x/3);c=-exp(x/3);plot(x,y,'b*',x,z,'r.',x,c,'r.')3.x=-pi:pi/50:4*pi;y1=x.*cos(x);y2=x.*tan(1./x).*sin(x.^3);y3=exp(1./x).*sin(x);subplot(1,3,1); plot(x,y1,'r*'),axis([-pi pi -5 5]),grid onlegend('xcosx')xlabel('x轴'),ylabel('y轴')subplot(1,3,2); plot(x,y2),axis([-pi pi -10 10]) ,grid onlegend('xtan(1/x)')xlabel('x轴'),ylabel('y轴')title('曲线y1=xcosx,y2=xtan(1/x)与y3=e^(1/x)sinx')subplot(1,3,3); plot(x,y3,'k.'),axis([1 8 -2.5 2.5]),grid onlegend('e^(1/x)sinx')xlabel('x轴'),ylabel('y轴')gtext('y1=xcosx'),gtext('y2=xtan(1/x)'),gtext('y3=e^(1/x)sinx')5.t=0:(pi/50):(20*pi);x=t.*cos(pi.*t/6);y=t.*sin (pi.*t/6);z=2.*t;plot3(x,y,z), grid onxlabel('x轴'),ylabel('y轴'),zlabel('z轴'); title('圆锥螺线');legend('x^2+y^2=z^2/4')三、【实验结果】P791.3.5.。
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
Matlab第二次实验报告
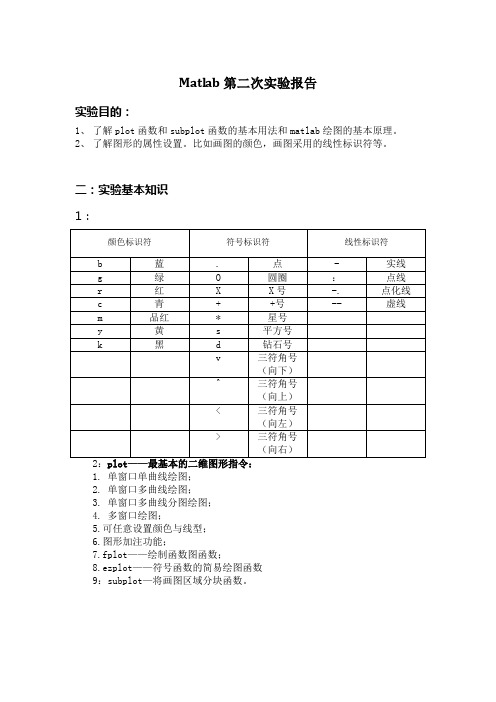
Matlab第二次实验报告实验目的:1、了解plot函数和subplot函数的基本用法和matlab绘图的基本原理。
2、了解图形的属性设置。
比如画图的颜色,画图采用的线性标识符等。
二:实验基本知识1:1. 单窗口单曲线绘图;2. 单窗口多曲线绘图;3. 单窗口多曲线分图绘图;4. 多窗口绘图;5.可任意设置颜色与线型;6.图形加注功能;7.fplot——绘制函数图函数;8.ezplot——符号函数的简易绘图函数9:subplot—将画图区域分块函数。
实验内容:将高数课本后的18个图画出上机练习程序第1——6图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1);x=-50:1:50;y=a.*x.^3;subplot(3,2,1);plot(x,y,'r');title('y=a*x^3');xlabel('X');ylabel('Y');x=0:1:50;y=sqrt(a.*x.^3);subplot(3,2,2);plot(x,y,x,-y,'r');title('y^2=a*x^3');xlabel('X');ylabel('Y');x=-3:0.1:3;y=exp(-x.^2);subplot(3,2,3);plot(x,y,'r');title('y=e^x^2');xlabel('X');ylabel('Y');x=-3:0.1:3;y=8*a^3./(x.^2+4*a^2);subplot(3,2,4);plot(x,y,'r');title('y=8*a^3./(x.^2+4*a^2)'); xlabel('X');ylabel('Y');x=0:0.01:5;y=sqrt(x.^3./(a*2.-x)); subplot(3,2,5);plot(x,y,x,-y,'r');title('y^2*(2a-x)=x^3'); xlabel('X');ylabel('Y');%t=-1:0.01:5;%x=3*a.*t./(1+t.^3);%y=3*a*t.^2./(1+t.^3);subplot(3,2,6);ezplot('x.^3+y.^3-3*3*x.*y'); %plot(x,y);title('x^3+y^3-3axy=0'); xlabel('X');ylabel('Y');输入a=3:显示结果第7——10图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0:0.1:2*pi;x=a*cos(t).^3;y=a*sin(t).^3;subplot(2,2,1);plot(x,y,'b')title('x^1.5+y^1.5=a^1.5'); xlabel('X');ylabel('Y');t=-2*pi:0.1:2*pi;x=a.*(t-sin(t));y=a.*(1-cos(t));subplot(2,2,2);plot(x,y,'b')title('°ÚÏß');xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*(1-cos(t));subplot(2,2,3);plot(p.*cos(t),p.*sin(t),'b'); title('p=a(1-cos£¨t£©)'); xlabel('X');ylabel('Y');t=0:0.01:2*pi;p=a.*t;subplot(2,2,4);plot(p.*cos(t),p.*sin(t),'b'); title('p=at');xlabel('X');ylabel('Y');输入a=1,第11题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º') figure(1);t=-2*pi:pi/100:2*pi;p=exp(a.*t);plot(p.*cos(t),p.*sin(t)); title('p=e^at');xlabel('X');ylabel('Y');输入a=0.1,显示结果:clear,clca=input('ÇëÊäÈëaµÄÖµ£º')figure(1)t=0.2*pi:pi/100:100*pi;p=a./t;plot(p.*cos(t),p.*sin(t));title('p=at');xlabel('X');ylabel('Y');输入a=1,显示结果:第13——14题图:clear,clca=input('ÇëÊäÈëaµÄÖµ£º');figure(1);t=0:pi/100:2*pi;p=(a^2.*sin(2*t)).^0.5;subplot(1,2,1);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*sin(2t)');xlabel('X');p=(a^2.*cos(2*t)).^0.5;subplot(1,2,2);plot(p.*cos(t),p.*sin(t),-p.*cos(t),-p.*sin(t),'g'); title('p^2=a^2*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第15-16题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1)t=0:pi/200:pi;p=a.*cos(3*t);subplot(1,2,1);plot(p.*cos(t),p.*sin(t),'r--');title('p=a*cos(3t)');xlabel('X');p=a.*sin(3*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'r--'); title('p=a*sin(3t)');xlabel('X');ylabel('Y');输入a=1,显示结果:第17——18题图:clear;clc;a=input('ÇëÊäÈëa:');figure(1);t=-pi:pi/200:pi;subplot(1,2,1);p=a.*sin(2*t);plot(p.*cos(t),p.*sin(t),'k-.'); title('p=a*sin(2t)');xlabel('X');ylabel('Y');p=a.*cos(2*t);subplot(1,2,2);plot(p.*cos(t),p.*sin(t),'k-.');title('p=a*cos(2t)');xlabel('X');ylabel('Y');输入a=1,显示结果:实验心得:这次实验主要是学习matlab软件的二维绘图功能:matlab软件还有丰富的图形修饰功能,如改变线条的形式和颜色;除此之外其还可以以多种形式如在一个图形中显示多个函数图形,一个figure中显示多个坐标系,还有一个程序中就可以用多个figure一起来表示不同的函数……在画图过程中你可能因为角度的区间取值不一样,画出来的图形可能跟书本上给出的图形有很大的差异,但没关系,只要你思路是对的,区间可以自己慢慢改动知道跟书本上给出的图形想接近。
实验二MATLAB绘图11页word文档

实验二MATLAB绘图一.实验目的掌握matlab二维图形和三维图形的绘制方法,并会对图形进行处理,掌握符号函数(显函数、隐函数和参数方程)的画图,掌握空间曲线和空间曲面的绘图,会对所绘图形进行加格栅,图例和标注等一些简单的处理.二.实验原理与方法(一).曲线图:Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图.命令格式为:plot(x,y,s)其中x,y分别表示所取点集的横纵坐标,s指定线型及颜色.缺省时表示画的是蓝色实线.Plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)表示将多条线画在一起.例在[0,2*pi]用红线画sin(x),用绿圈画cos(x).解:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,’r’,x,z,’g o’)所得图形如下图所示(二)符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(‘f(x)’,[a,b])表示在a<x<b绘制显函数f=f(x)的函数图ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐函数f(x,y)=0的函数图ezplot(‘x(t)’,’y(t)’,[tmin,tmax])表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图.例在[0,pi]上画y=cos(x)的图形解输入命令:ezplot(‘sin(x)’,[0,pi])例在[0,2*pi]上画t=,tx3cos=星形图siny3解输入命令:ezplot(‘cos(t).^3’,’sin(t).^3’,[0,2*pi])例在[-2,0.5],[0,2]上画隐函数0e x的图)+xysin(=解输入命令:ezplot('exp(x)+sin(x.*y)',[-2,0.5,0,2])(2) fplot格式:fplot(‘fun’,lims)表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形注意:[1] fun 必须是M 文件的函数名或是独立变量为x 的字符串.[2] fplot 函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
实验2 Matlab绘图操作

实验2 Matlab 绘图操作实验目的:1、 掌握绘制二维图形的常用函数;2、 掌握绘制三维图形的常用函数;3、 掌握绘制图形的辅助操作。
实验内容:1. 设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051,在x=0~2π区间取101点,绘制函数的曲线。
2. 已知: y x =21,cos()y x =22,y y y =⨯312,完成下列操作:(1) 在同一坐标系下用不同的颜色和线性绘制三条曲线; (2) 以子图形式绘制三条曲线;(3) 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
3.已知:ln(x x e y x x ⎧+≤⎪⎪=⎨⎪+>⎪⎩20102,在x -≤≤55区间绘制函数曲线。
4. 绘制极坐标曲线sin()a b n ρθ=+,并分析参数a 、b 、n 对曲线形状的影响。
5.在xy 平面内选择区域[][],,-⨯-8888,绘制函数z =6. 用plot 函数绘制下面分段函数的曲线。
,(),,x x f x x x x ⎧++>⎪==⎨⎪+<⎩235000507. 某工厂2005年度各季度产值(单位:万元)分别为:450.6、395.9、410.2、450.9,试绘制柱形图和饼图,并说明图形的实际意义。
8. 在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
(1).y x =-205(2)sin()cos ,sin()sin x t tt y t tπ=⎧≤≤⎨=⎩303详细实验内容:1.设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051,在x=0~2π区间取101点,绘制函数的曲线。
>> x=(0:2*pi/100:2*pi);>> y=(0.5+3*sin(x)/(1+x.^2))*cos(x); >> plot(x,y)2.已知: y x =21,cos()y x =22,y y y =⨯312,完成下列操作: (1)在同一坐标系下用不同的颜色和线性绘制三条曲线; >> x= linspace(0, 2*pi, 101);>> y1=x.*x; >> y2=cos(2x); >> y3=y1.*y2;plot(x,y1,'r:',x,y2,'b',x,y3, 'ko')(2)以子图形式绘制三条曲线;>> subplot(2,2,1),plot(x,y1)subplot(2,2,2),plot(x,y2)subplot(2,2,3),plot(x,y3)(3)分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
Matlab实验二维绘图

实验 6 二维绘图一 实验目的学习MATLAB 软件中二维绘图的方法二 实验内容与要求 1) 基本命令 格式1:plot(X,Y)说明:以X,Y 的对应元素为坐标绘二维图, 注意,X,Y 的维数要匹配. [例 1.48]>>x=0:pi/18:2*pi; %给出横坐标 >>y=()sin x ; %计算出纵坐标>>plot(x,y) %绘制图形,如图1.1所示。
问题 1.22:当X=[1,5,3,7;3,6,8,4;9,6,1,5],Y=[2,5,7,4;6,8,4,1;8,0,4,2]时,命令plot(X,Y)画出几条线,如何画出的?当X=[1,5,3,7],Y=[2,5,7,4;6,8,4,1;8,0,4,2]时,有何规律?当X=[1,5,3],Y=[2,5,7,4;6,8,4,1;8,0,4,2]时,又有何规律?格式2:plot(Y) %若Y 为m 维向量,则等价于plot(X ,Y),其中,X=1:m 。
格式3:plot(1X ,1Y ,1LineSpec ,2X ,2Y ,2LineSpec ,…)%将按顺序分别画出由3个参数定义i X ,i Y ,i LineSpec 的线条,其中,参数i LineSpec 指明了线条的类型,标记符号,和画线用的颜色. 说明:1 线型,有实线,划线,虚线,点划线,例如:’-’就表示画实线.2 线条宽度LineWidth ,取值为整数,例如,‘LineWidth ’,2就表示线宽为两个像素。
3 线条颜色,常用8种颜色,例如:‘b--’就表示蓝色划线。
4 标记类型,表示数据点标记的类型,常用13种,例如:‘*r ’就表示红色星号。
5 标记大小MarkerSize 指定标记符号的大小尺寸,取值为整数(单位为像素)。
6 标记面填充颜色‘MarkerFaceColor ’指定用于填充标记符面的颜色,颜色配比方案见表1.10,例如:‘MarkerFaceColor ’,[0,1,0]就表示标记面填绿色。
实验二(2) MATLAB绘图

实验二(2)MATLAB绘图一.实验目的1、掌握matlab二维图形的绘制方法, 会对所绘图形进行加格栅,图例和标注等一些简单的处理;2、了解对数坐标图的绘制方法;3、了解符号函数(显函数、隐函数和参数方程)的绘制方法;二.实验原理与方法(一)二维绘图:Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图.命令格式为:plot(x,y,s)其中x,y分别表示所取点集的横纵坐标,s指定线型及颜色.缺省时表示画的是蓝色实线.Plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)表示将多条线画在一起.例1:在[0,2*pi]用红线画sin(x),用绿圈画cos(x).解:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,‟r‟,x,z,‟go')(二) 符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(…f(x)‟,[a,b])表示在a<x<b绘制显函数f=f(x)的函数图ezplot(…f(x,y)‟,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax和ymin<y<ymax绘制隐函数f(x,y)=0的函数图ezplot(…x(t)‟,‟y(t)‟,[tmin,tmax])表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图.例2: 在[0,pi]上画y=sin(x)的图形解 输入命令:ezplot(…sin(x)‟,[0,pi])例3: 在[-2,0.5],[0,2]上画隐函数0)sin(=+xy e x 的图解 输入命令:ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])(2) fplot格式:fplot(…fun‟,lims)表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形注意:[1] fun 必须是M 文件的函数名或是独立变量为x 的字符串.[2] fplot 函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
国开电大 Matlab语言及其应用 实验任务:绘制二维和三维图形实验报告
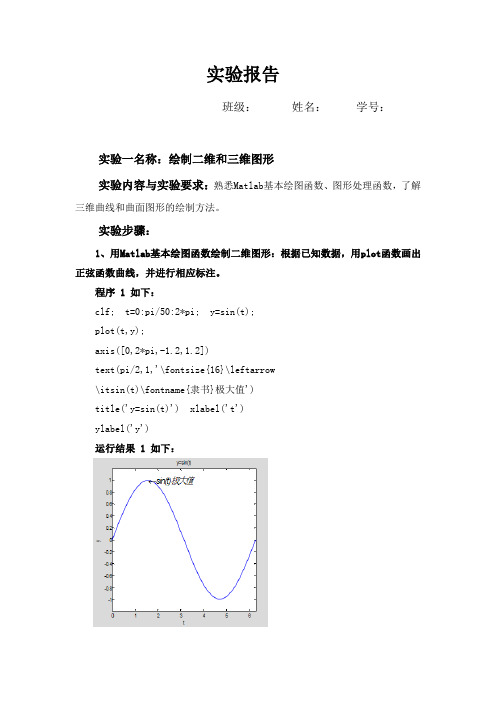
实验报告班级:姓名:学号:实验一名称:绘制二维和三维图形实验内容与实验要求:熟悉Matlab基本绘图函数、图形处理函数,了解三维曲线和曲面图形的绘制方法。
实验步骤:1、用Matlab基本绘图函数绘制二维图形:根据已知数据,用plot函数画出正弦函数曲线,并进行相应标注。
程序 1 如下:clf; t=0:pi/50:2*pi; y=sin(t);plot(t,y);axis([0,2*pi,-1.2,1.2])text(pi/2,1,'\fontsize{16}\leftarrow\itsin(t)\fontname{隶书}极大值')title('y=sin(t)') xlabel('t')ylabel('y')运行结果 1 如下:2、用三维曲线绘图基本指令plot 3绘制三维曲线图:t=0~2pi;x=sin(t);y=cos(t);z=cos(2*t);用plot3函数画出关于x,y,z的三维曲线图,并适当加标注。
程序 2 如下:t=(0:0.02:2)*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z,'b-',x,y,z, 'rd')box onlegend('链','宝石')运行结果 2 如下:3、三维网线、曲面、曲线图的比较;网线图mesh扩展形式meshz、meshc以及曲面图surf扩展形式surfl、surfc的运用;peaks曲面图和sphere球面图的绘制以及图形的透视功能。
(1)三维网线、曲面、曲线图比较:程序 3 如下:x=-4:4;y=x;[X,Y]=meshgrid(x,y);Z=X.^2+Y.^2;subplot(1,3,1);surf(X,Y,Z); //绘曲面图subplot(1,3,2);mesh(X,Y,Z); //绘网线图subplot(1,3,3);plot3(x,y,x.^2+y.^2),box on //绘曲线图运行结果 3 如下:(2)三维网线图和曲面图1)网线图mesh还有几个扩展形式:包含零平面的三维网线图: meshz用带等高线的三维网线图: meshc程序 4 如下:clf;x=-4:4;y=x;[X,Y]=meshgrid(x,y) Z=X.^2+Y.^2;subplot(121); meshc(X,Y,Z);subplot(122); meshz(X,Y,Z);运行结果 4 如下:2)曲面图surf还有几个扩展形式:带光照阴影的三维曲面图: surfl带等高线的三维曲面图: surfc程序 5 如下:clf;x=-4:4;y=x;[X,Y]=meshgrid(x,y) Z=X.^2+Y.^2;subplot(121); surfl(X,Y,Z);subplot(122); surfc(X,Y,Z);运行结果 5 如下:(3)peaks曲面图peaks曲面图是Matlab为了测试立体绘图给出的一个快捷函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学实验》报告实验名称 Matlab 二维曲线绘图
2011年 5月
一、【实验目的】
学习Matlab 绘图的运用,学会制作二维曲线,三维图形的绘画。
二、【实验任务】
P79 第3,5,9题。
1,在同一图形窗口画三个子图……
2,绘制圆锥螺线的图像并加各种标注……
3,画三维曲面z=5-x^2-y^2与平面z=3的交线。
三、【实验程序】
1.
>> clear
>> x=-pi:pi/50:4*pi;
y1=x.*cos(x);
y2=x.*tan(1./x).*sin(x.^3);
y3=exp(1./x).*sin(x);
subplot(3,1,1)
plot(x,y1,'r*'),grid on
title('y1=xcosx')
xlabel('x轴'),ylabel('y轴')
axis([-pi pi -pi pi])
gtext('y1=xcosx'),legend('y1=xcosx')
subplot(3,1,2),plot(x,y2,'b'),grid on
title('y=xtan(1/x)sin(x^3)')
gtext('y=xtan(1/x)sin(x^3)')
legend('y=xtan(1/x)sin(x^3)')
axis([pi 4*pi -2 2])
subplot(3,1,3),plot(x,y3,'y'),grid on
title('y=exp(1/x)sinx')
xlabel('x轴'),ylabel('y轴')
gtext('y=exp(1/x)sinx')
legend('y=exp(1/x)sinx')
axis([1 8 -3 3])
2.
>> clear
>> t=0:pi/50:20*pi;
x=t.*cos(pi/6.*t);
y=t.*sin(pi/6.*t);
z=2.*t;
plot3(x,y,z)
title('圆锥螺线')
xlabel('x轴'),ylabel('y轴'),zlabel('z轴')
>> t=0:pi/50:20*pi;
x=t.*cos(pi/6.*t);
y=t.*sin(pi/6.*t);
z=2.*t;
plot3(x,y,z)
title('圆锥螺线')
xlabel('x轴'),ylabel('y轴'),zlabel('z轴') 3.
>> clear
>> t=-2:0.1:2;
[x,y]=meshgrid(t);
z1=5-x.^2-y.^2+eps;
subplot(1,3,1),mesh(x,y,z1),title('曲面')
z2=3*ones(size(x));
subplot(1,3,2),mesh(x,y,z2),title('平面')
r0=abs(z1-z2)<=1;
zz=r0.*z2;yy=r0.*y;xx=r0.*x;
subplot(1,3,3)
plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'*')
title('交线')
四、【实验结果】
1.
2.
3.
五、【实验总结】
本次实验较第一次实验难了很多,第3和第5两个题目结合了C语言编程的思想,第9题与课上讲的马鞍面类似,通过模仿课上例题做出了此题。
本次的实验,使我获益匪浅,不仅对课上教授的知识有了进一步的理解,进一步掌握MATLAB的编程思想,熟悉了对plot,mesh,subplot,title,label等函数的应用,发现所有编程语言的思想想通,在此后的实验中,我不仅要加强自己独立完成实验的能力,更要加强讨论解决问题的能力,使问题的解决更加合理化,有效化。
