立体几何中存在性问题教案.docx
立体几何中的点的存在性问题
用向量法（坐标法）解决点的存在性问题点的存在问题（即探索性问题）是历年高考的热点，立体几何中，探索满足某个条件的点是否存问题，能很好的考查学生的逻辑推理能力和空间想象能能力，休现了的新课标的要求，故倍受命题人青睐。
下面结合具体例题讲解此类问题的大致类型及解题策略。
例1：如图，在正方体1111ABCD A B C D -中，E 是1DD 的中点，（1）在棱B 1C 1是否存一点G ，使得AG ⊥平面1A BE ;（2）在线段BE 上是否存一点M ，使得M-CD-A 的平面角的余弦值为25. （3）在正方形ABCD 内（含边界线段）否存一点N ，使得C 1N ⊥1A BE点评：立何几何中的点的存在问题通常使用坐标法来进得解答，此方法不需要进行复杂的作图、推理及论证，只需要通过坐标运算进行判断。
解题策略：先假设满足条件的点存在，把要成立的结论当作条件，据此列方程或解方程组，把“是否存在”问题转化为“点的坐标是否在规定范围内有解问题。
命题类型：（1）在与坐标轴平行的线段上寻求一点满点某个条件，此种类型较易，直接设出该点坐标（横、纵，竖三个坐标中，己知两个），据条件得方程即可求解；（2）在与坐标轴不平行的线段上寻求一点满点某个条件，此种类型，此点的横、纵，竖三个坐标，可能己知一个，或者都不清楚，解题时需要根据三点共线进行坐标代换。
比如：在线段AB(AB 与坐标轴不平行）上寻找一点M 满足条件f 。
具体做法：设M （x,y,z)与AM=λAB （01λ≤≤），由坐标相等概念则可将M 点的坐标全部用λ表示M （f(λ),g(λ),φ(λ)),然后根据假设的结论列方程即求得λ。
（3）在某个面上寻求一点满点某个条件，直接列方程组解决。
命题规律：所探求的点一般是线段的中点或三等分点，故此种也可先估计此点的位置，然后进行证明。
专项训练1.（2010马鞍山模拟）如图，四棱锥P—ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点.（Ⅰ）求二面角B—DE—C的平面角的余弦值；（Ⅱ）在棱PB上是否存在点F，使PB⊥平面DEF？证明你的结论.2,（2010绍兴模拟）如图，在三棱锥S-ABC中，SA=AB=AC=BC=2SB=2SC，O为BC的中点，（1）求证：SO ABC平面；（2）求异面直线SC与AB所成角的余弦值；（3）在线段AB上是否存在一点E，使得二面角B-SC-E的平面角的余弦值为15;5若存在，求BE：BA的值；若不存在，试说明理由。
立体几何中的存在性问题
立体几何中的存在性问题1、如图，在直四棱柱ABCD －A 1B 1C 1D 1中，已知DC ＝DD 1＝2AD ＝2AB ，AD ⊥DC ，AB ∥DC . (1)求证：D 1C ⊥AC 1；(2)问在棱CD 上是否存在点E ，使D 1E ∥平面A 1BD .若存在，确定点E 位置；若不存在，说明理由．2．如图所示，平面ABDE ⊥平面ABC ，△ABC 是等腰直角三角形，AC ＝BC ＝4，四边形ABDE 是直角梯形，BD ∥AE ，BD ⊥BA ，BD ＝12AE ＝2，O ，M 分别为CE ，AB 的中点．(1)求证：OD ∥平面ABC ；(2)求直线CD 和平面ODM 所成角的正弦值；(3)能否在EM 上找一点N ，使得ON ⊥平面ABDE ？若能，请指出点N 的位置，并加以证明；若不能，请说明理由．3、在如图所示的几何体中，底面ABCD 为菱形，∠BAD ＝60°，AA 1∥DD 1∥CC 1∥BE ，且AA 1＝AB ，D 1E ⊥平面D 1AC ，AA 1⊥底面ABCD . (1)求二面角D 1－AC －E 的大小；(2)在D 1E 上是否存在点P ，使得A 1P ∥平面EAC ，若存在，求D 1P PE 的值，若不存在，说明理由．立体几何中的存在性问题1、如图，在直四棱柱ABCD －A 1B 1C 1D 1中，已知DC ＝DD 1＝2AD ＝2AB ，AD ⊥DC ，AB ∥DC . (1)求证：D 1C ⊥AC 1；(2)问在棱CD 上是否存在点E ，使D 1E ∥平面A 1BD .若存在，确定点E 位置；若不存在，说明理由．2．如图所示，平面ABDE ⊥平面ABC ，△ABC 是等腰直角三角形，AC ＝BC ＝4，四边形ABDE 是直角梯形，BD ∥AE ，BD ⊥BA ，BD ＝12AE ＝2，O ，M 分别为CE ，AB 的中点．(1)求证：OD ∥平面ABC ；(2)求直线CD 和平面ODM 所成角的正弦值；(3)能否在EM 上找一点N ，使得ON ⊥平面ABDE ？若能，请指出点N 的位置，并加以证明；若不能，请说明理由．3、在如图所示的几何体中，底面ABCD 为菱形，∠BAD ＝60°，AA 1∥DD 1∥CC 1∥BE ，且AA 1＝AB ，D 1E ⊥平面D 1AC ，AA 1⊥底面ABCD . (1)求二面角D 1－AC －E 的大小；(2)在D 1E 上是否存在点P ，使得A 1P ∥平面EAC ，若存在，求D 1P PE的值，若不存在，说明理由．立体几何中的存在性问题1、如图，在直四棱柱ABCD －A 1B 1C 1D 1中，已知DC ＝DD 1＝2AD ＝2AB ，AD ⊥DC ，AB ∥DC . (1)求证：D 1C ⊥AC 1；(2)问在棱CD 上是否存在点E ，使D 1E ∥平面A 1BD .若存在，确定点E 位置；若不存在，说明理由．(1)证明 在直四棱柱ABCD －A 1B 1C 1D 1中，连接C 1D ， ∵DC ＝DD 1，∴四边形DCC 1D 1是正方形， ∴DC 1⊥D 1C .又AD ⊥DC ，AD ⊥DD 1，DC ∩DD 1＝D ， ∴AD ⊥平面DCC 1D 1， 又D 1C ⊂平面DCC 1D 1， ∴AD ⊥D 1C .∵AD ⊂平面ADC 1，DC 1⊂平面ADC 1，且AD ∩DC 1＝D ， ∴D 1C ⊥平面ADC 1，又AC 1⊂平面ADC 1，∴D 1C ⊥AC 1. (2)解 假设存在点E ，使D 1E ∥平面A 1BD . 连接AD 1，AE ，D 1E ， 设AD 1∩A 1D ＝M ， BD ∩AE ＝N ，连接MN ， ∵平面AD 1E ∩平面A 1BD ＝MN ， 要使D 1E ∥平面A 1BD ， 可使MN ∥D 1E ， 又M 是AD 1的中点， 则N 是AE 的中点． 又易知△ABN ≌△EDN ， ∴AB ＝DE .即E 是DC 的中点．综上所述，当E 是DC 的中点时， 可使D 1E ∥平面A 1BD .2．如图所示，平面ABDE ⊥平面ABC ，△ABC 是等腰直角三角形，AC ＝BC ＝4，四边形ABDE 是直角梯形，BD ∥AE ，BD ⊥BA ，BD ＝12AE ＝2，O ，M 分别为CE ，AB 的中点．(1)求证：OD ∥平面ABC ；(2)求直线CD 和平面ODM 所成角的正弦值；(3)能否在EM 上找一点N ，使得ON ⊥平面ABDE ？若能，请指出点N 的位置，并加以证明；若不能，请说明理由． (1)证明 取AC 中点F ，连接OF ，FB . ∵F 是AC 中点，O 为CE 中点， ∴OF ∥EA 且OF ＝12EA .又BD ∥AE 且BD ＝12AE ，∴OF ∥DB ，OF ＝DB ，∴四边形BDOF 是平行四边形，∴OD ∥FB . 又∵FB ⊂平面ABC ，OD ⊄平面ABC ， ∴OD ∥平面ABC .(2)解 ∵平面ABDE ⊥平面ABC ，平面ABDE ∩平面ABC ＝AB ，DB ⊂平面ABDE ，且BD ⊥BA ， ∴DB ⊥平面ABC .∵BD ∥AE ，∴EA ⊥平面ABC .2、如图所示，以C 为原点，分别以CA ，CB 所在直线为x ，y 轴，以过点C 且与平面ABC 垂直的直线为z 轴，建立空间直角坐标系．∵AC ＝BC ＝4，∴C (0,0,0)，A (4,0,0)，B (0,4,0)，D (0,4,2)，E (4,0,4)，O (2,0,2)，M (2,2,0)，∴CD →＝(0,4,2)，OD →＝(－2,4,0)，MD →＝(－2,2,2)． 设平面ODM 的法向量为n ＝(x ，y ，z )，则由n ⊥MD →，n ⊥OD →，可得⎩⎨⎧－2x ＋4y ＝0，－2x ＋2y ＋2z ＝0.令x ＝2，得y ＝1，z ＝1.∴n ＝(2,1,1)． 设直线CD 和平面ODM 所成角为θ，则sin θ＝|n ·CD →||n ||CD →|＝|(2，1，1)·(0，4，2)|22＋12＋12·02＋42＋22＝66·25＝3010.∴直线CD 和平面ODM 所成角的正弦值为3010. (3)解 当N 是EM 中点时，ON ⊥平面ABDE . 方法一 取EM 中点N ，连接ON ，CM ， ∵AC ＝BC ，M 为AB 中点， ∴CM ⊥AB .又∵平面ABDE ⊥平面ABC ，平面ABDE ∩平面ABC ＝AB ，CM ⊂平面ABC ，∴CM ⊥平面ABDE . ∵N 是EM 中点，O 为CE 中点， ∴ON ∥CM ，∴ON ⊥平面ABDE . 方法二 由(2)设N (a ，b ，c )，∴MN →＝(a －2，b －2，c )，NE →＝(4－a ，－b,4－c )． ∵点N 在ME 上，∴MN →＝λNE →， 即(a －2，b －2，c )＝λ(4－a ，－b,4－c )，∴⎩⎨⎧a －2＝λ(4－a )，b －2＝λ(－b )，c ＝λ(4－c )，解得⎩⎪⎨⎪⎧a ＝4λ＋2λ＋1，b ＝2λ＋1，c ＝4λλ＋1.∴N (4λ＋2λ＋1，2λ＋1，4λλ＋1)．∵BD →＝(0,0,2)是平面ABC 的一个法向量， ∴ON →⊥BD →，∴4λλ＋1＝2，解得λ＝1.∴MN →＝NE →，即N 是线段EM 的中点， ∴当N 是EM 的中点时，ON ⊥平面ABDE .3、在如图所示的几何体中，底面ABCD 为菱形，∠BAD ＝60°，AA 1∥DD 1∥CC 1∥BE ，且AA 1＝AB ，D 1E ⊥平面D 1AC ，AA 1⊥底面ABCD . (1)求二面角D 1－AC －E 的大小；(2)在D 1E 上是否存在一点P ，使得A 1P ∥平面EAC ，若存在，求D 1P PE 的值，若不存在，说明理由．解 (1)设AC 与BD 交于点O ，如图所示建立空间直角坐标系O －xyz ，设AB ＝2， 则A (3，0,0)，B (0，－1,0)，C (－3，0,0)，D (0,1,0)，D 1(0,1,2)，设E (0，－1，t )，t >0，则ED 1→＝(0,2,2－t )，CA →＝(23，0,0)，D 1A →＝(3，－1，－2)．∵D 1E ⊥面D 1AC ，∴D 1E ⊥CA ，D 1E ⊥D 1A ， ∴⎩⎪⎨⎪⎧ED 1→·CA →＝0，ED 1→·D 1A →＝0，解得t ＝3，∴E (0，－1,3)，∴AE →＝(－3，－1,3)，设平面EAC 的法向量为m ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧m ·CA →＝0，m ·AE →＝0，∴⎩⎨⎧23x ＝0，－3x －y ＋3z ＝0，令z ＝1，y ＝3，m ＝(0,3,1)．又平面D 1AC 的法向量ED 1→＝(0,2，－1)， ∴cos 〈m ，ED 1→〉＝m ·ED 1→|m |·|ED 1→|＝22.所以所求二面角的大小为45°. (2)假设存在点P 满足题意． 设D 1P →＝λPE →＝λ(D 1E →－D 1P →)，得D 1P →＝λ1＋λD 1E →＝(0，－2λ1＋λ，λ1＋λ)，A 1P →＝A 1D 1→＋D 1P →＝(－3，1,0)＋(0，－2λ1＋λ，λ1＋λ)＝(－3，1－2λ1＋λ，λ1＋λ)∵A 1P ∥平面EAC ，∴A 1P →⊥m ，∴－3×0＋3×(1－2λ1＋λ)＋1×λ1＋λ＝0，解得λ＝32，故存在点P 使A 1P ∥面EAC ，此时D 1P ∶PE ＝3∶2.。
立体几何中存在性问题教案
训练学生如何说明结论不成立
引发学生思考直线是怎么寻找到的，探索问题的本质
总结归纳解题思路及方法
当 数量关系变化时，如何找到点 的位置，检查学生对刚学习的解题方法的掌握程度。
提示学生并非所有的存在性问题结论都是肯定的，渗透分析法与反证法的思想，让学生去思考解决存在性问题的思路，巩固面面平行的判定与线面平行的性质
总结归纳解题思路及方法
巩固基础知识和基本思想方法，提高基本技能
检查学生对知识方法的掌握情况
四、课堂小结
通过这节课的复习，请同学们从知识与方法方面回顾一下，学习过程中遇到了什么问题需要注意哪些方面
五、作业布置
学案上的练习题
教学背景分析
教学
内容
分析
立体几何中常出现点的存在性和位置待定的问题，以“是否存在”、“是否有”、“在何位置”
等形式设问，以示结论有待于确定. 文科主要涉及到平行与垂直的位置关系的考查，其中渗透反证法与分析法的解题思路，也是高考中的常见题型。2012年北京市高考文科就考查了有关线面垂直的存在性问题，2016年北京市高考文科就考查了有关线面平行的存在性问题。
问题4：这些直线是怎么找到的
总结问题的类型及解决问题的方法：
问题5：若将题目中的已知条件 改为 ，你能判断在棱 上是否存在一点 使得 ∥平面 ， 若存在，请指出 点位置，并证明；若不存在，请说明理由.
问题6:在棱 上（除 点外）是否存在一点 使得 ∥平面 ，若存在，请指出 点位置，并证明；若不存在，说明理由.
总结问题的类型及解决问题的方法：
练习：如图，在四棱锥 中，底面 是平行四边形， 是 中点， 为线段 上一点.试确定点 在线段 上的位置，使
检测题：1、如图，在四棱锥 中，底面 是梯形， ∥ ， .在棱 上是否存在一点 使得 ∥平面 ，若存在，求出 点位置，并证明；若不存在，说明理由.
《立体几何存在性问题》
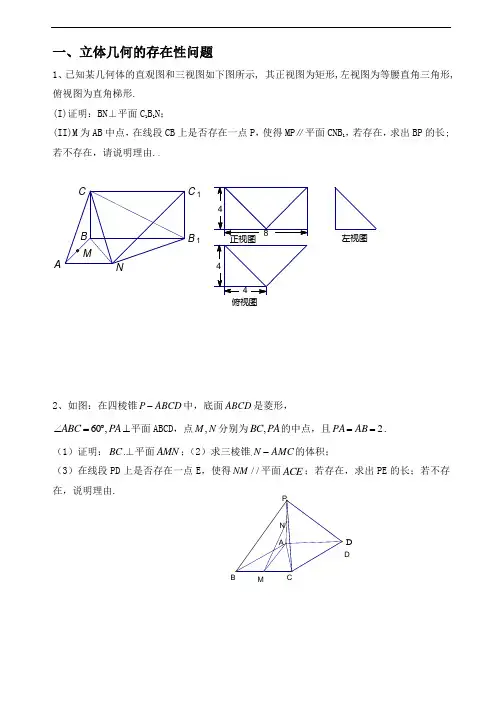
C1B1A一、立体几何的存在性问题1、已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.(I)证明：BN⊥平面C1B1N；(II)M为AB中点，在线段CB上是否存在一点P，使得MP∥平面CNB1，若存在，求出BP的长;若不存在，请说明理由.俯视图左视图2、如图：在四棱锥P ABCD-中，底面ABCD是菱形，60,ABC PA∠=︒⊥平面ABCD，点,M N分别为,BC PA的中点，且2==ABPA.（1）证明：BC⊥平面AMN；（2）求三棱锥AMCN-的体积；（3）在线段PD上是否存在一点E，使得//NM平面ACE；若存在，求出PE的长；若不存在，说明理由.M CDD3、在直三棱柱111ABC A B C -中，1CC BC =，BC AB ⊥.点N M ,分别是1CC ，C B 1的中点，G 是棱AB 上的动点.（Ⅰ）求证：⊥C B 1平面BNG ； （Ⅱ）若CG //平面M AB 1，试确定G 点的位置，并给出证明.4、如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，BC =12AD ，P A =PD ，Q 为AD 的中点．（Ⅰ）求证：AD ⊥平面PBQ ；（Ⅱ）若点M 在棱PC 上，设PM =tMC ，试确定t 的值，使得P A //平面BMQ ．PABCD Q M二、应用题综合【基本不等式】1、某单位建造一间地面面积为12m2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过a米，房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用．（1）把房屋总造价y表示成x的函数，并写出该函数的定义域.（2）当侧面的长度为多少时，总造价最底？最低总造价是多少？【导数】2、为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层，某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：C(x)＝k3x＋5(0≤x≤10)，若不建隔热层，每年能源消耗费用为8万元．设f(x)为隔热层建造费用与20年的能源消耗费用之和．(1)求k的值及f(x)的表达式．(2)隔热层修建多厚时，总费用f(x)达到最小，并求最小值．【线性规划】。
向量法探索立体几何中的存在性问题
Ｃ￡ ＝４ ． ５ｏ
一
所 以 Ａ ＿ 面 Ｐ Ｄ． Ｂｊ平 Ａ 又Ａ Ｂｃ平 面 Ｐ Ｂ， 以平 面 Ｐ ＢＪ平 面 Ｐ Ｄ Ａ 所 Ａ ＿ Ａ．
（ 以 Ａ为坐标原点 ， Ⅱ） 建立空 间直角坐标 系 Ａ— ｙ （ ｘｚ 如
图）
在平 面 Ａ Ｃ 内， Ｃ ／Ａ ＢＤ 作 Ｅ ／ Ｂ交 Ａ 于 点 Ｅ， Ｃ Ｄ 则 Ｅ￣Ａ Ｄ．
在 Ｒ ＡＣ Ｅ 中 ， Ｅ＝Ｃ ・ ｏ ５ ＝１ ｔ Ｄ Ｄ Ｄ ｃｓ 。 ， ４
Ｃ Ｅ＝Ｃ ・ ｉ ５ ：ｌ Ａ Ａ Ｄ ｓ ４ 。 设 Ｂ＝ Ｐ＝ｔ则 Ｂ（ ， ０ ， ０ ｎ ， ｔ ０， ） Ｐ（ ，
０ｔ ，）
一
由Ａ Ａ ４得Ａ ： Ｂ＋ Ｄ＝ ， Ｄ ４一ｔ所 以 Ｅ（ ３一ｔ０ ， １３ ， ０， ， ） Ｃ（ ，
ｔ０ ， ｏ， ｔＯ ， ， ）ｏ（ ４一 ，）
：
（一１１０ ， ， ，）
：（ ， ０ ４一￡ 一ｔ ， ）
面
（ ） 平 面 Ｐ Ｄ 的法 向量 为 ｎ＝（ ｙｚ ， ｉ设 Ｃ ， ，）
５‘
（ｉ在线段 Ａ ｉ ） Ｄ上是否存 在一个 点 Ｇ， 得点 Ｇ到点 Ｐ， 使
，
ｃ， Ｄ的距离都相 等？说 明理 由． 分析 ： 题 目中 的四棱锥 能够 找到三 条两两 垂直 的棱 ， 从
因此 ， 可考虑建立空间直角坐标 系 ， 利用向量表 示相关元素 ， 然后利用 向量 的运算求解结论．
向量问解：立体几何中的存在性问题
（） ２ 求二面角Ｄ－ Ｂ Ａ 的大小 ；
高版 ？ ？ ＿＿ 中 十。 擞・曩—＿
课 程 解 读
２１ ０ ２年 ７月
材 法
足点 （ ） ， 在可行域中 ， 且使 在
删
ｃｓ ｏ（
） ＝
一
一
．
ቤተ መጻሕፍቲ ባይዱ
１ 曰Ｄ卜Ｉ Ｉ ／ Ｉ ｔ
１Ｂ ： ／ ， ， Ｃ 、 Ｔ 且肘是Ｂ Ｄ的中点．
（ ） 证 ：Ｍ／ － Ｄ ； １求 Ｅ ／ ￣ Ｆ
又二面角Ｄ
Ｂ 为锐 角 ， 故二面角Ｄ－ Ｂ的大小为６ 。 Ａ ０．
（ ）假设在线段Ｅ 上存在一点Ｐ，使得Ｃ － 晰 成 的角为 ３ Ｂ Ｐ￣Ａ
本题避 开了讨论 直线斜率一ａ中。 的符号问题 ， 也无 须旋转 直 线束通过数形结合 的方法 找到 目标 函数 ＋ｙ ＝ ２仅在点 （ ， ） １０ 处 取得最小值 时 ，直线斜率 的取值 范围 ，从而巧妙解 决 了这类 线性
规 划 问 题．
０
，
—
向上 的射影 Ｉ Ｉ Ｓ ， ） Ｃ （ 取得最大值 的点在Ａ点 ， 以 Ｏ 所
解： 因为Ｅ － Ｂｊ平面Ａ Ｄ，Ｂ＿Ｂ 故 ＶＢ Ｂ Ａ Ｌ Ｄ， ２ 为原点 ， 建立如图３ 所示的空间直角坐标 ￣Ｂ ｘｚ由已知可得Ｂ ０ ００ ， ０ ２ ０ ， ， －ｙ． （ ， ， ）Ａ（ ， ， ）
Ｄ （ ， ， ）Ｃ （ ， ２０ ， （ ， ，、 了 ）Ｆ （ ， ，、 了 ）Ｍ ３Ｏ ０ ， ３ 一 ， ）Ｅ ０ ０ ／ ， ０ １ ／ ，
Ｉ ｙ≤ ２，
立体几何存在性问题
立体几何中的存在性问题1、如图,已知直三棱柱111ABC A B C -,90ACB ∠=o ,E 就是棱1CC 上动点,F 就是AB 中点 ,2==BC AC ,41=AA 、(Ⅰ)求证:CF ⊥平面1ABB ;(Ⅱ)当E 就是棱1CC 中点时,求证:CF ∥平面1AEB ;(Ⅲ)在棱1CC 上就是否存在点E ,使得二面角1A EB B --的大小就是45o ,若存在,求CE 的长,若不存在,请 说明理由、2、如图,在底面就是正方形的四棱锥P-ABCD 中,PA ⊥面ABCD,BD 交AC 于点E,F 就是PC 中点,G 为AC 上一点。
(Ⅰ)求证:BD ⊥FG;(Ⅱ)确定点G 在线段AC 上的位置,使FG//平面PBD,并说明理由;(Ⅲ)当二面角B-PC-D 的大小为23π时,求PC 与底面ABCD 所成角的正切值。
3、在四棱锥P ABCD -中,侧面PCD ⊥底面ABCD ,PD CD ⊥,E 为PC 中点,底面ABCD 就是直角梯形,//AB CD ,90ADC ∠=o ,1AB AD PD ===,2CD =、(Ⅰ)求证://BE 平面PAD ; (Ⅱ)求证:BC ⊥平面PBD ;(Ⅲ)设Q 为侧棱PC 上一点,PQ PC λ=u u u r u u u r ,试确定λ的值,使得二面角Q BD P--为45o4、如图,三棱柱111ABC A B C -中,侧面11AA C C ⊥底面ABC ,112,AA AC AC AB BC ====, 且AB BC ⊥,O 为AC 中点、 (Ⅰ)证明:1A O ⊥平面ABC ;GFE AABCD EP(Ⅱ)求直线1A C 与平面1A AB 所成角的正弦值;(Ⅲ)在1BC 上就是否存在一点E ,使得//OE 平面1A AB ,若不存在,说明理由;若存在,确定点E 的位置、5、如图,棱锥P —ABCD 的底面ABCD 就是矩形,PA ⊥平面ABCD ,PA =AD =2,BD =22、 (Ⅰ)求证:BD PAC ⊥平面; (Ⅱ)求二面角B PD C --的余弦值; (III)在线段PD 上就是否存在一点Q ,使CQ 与平面PBD 所成的角的正弦值为962,若存在,指出点Q 的位置,若不存在,说明理由、6、如图,四棱锥,,P ABCD AB AD CD AD PA ABCD -⊥⊥⊥中,底面,22PA AD CD AB ====,M PC 为的中点、(1)求证:BM PAD 平面P ;(2)在侧面PAD 内找一点N,使MN PBD ⊥平面7、如图,三棱柱ABC —A 1B 1C 1中,AA 1⊥面ABC,BC ⊥AC,BC=AC=2,AA 1=3,D 为AC 的中点、 (Ⅰ)求证:AB 1//面BDC 1;(Ⅱ)在侧棱AA 1上就是否存在点P,使得CP ⊥面BDC 1？并证明您的结论、8、 如图,四棱锥P —ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA = AD = CD = 2AB = 2,M 为PC 的中点、 (1)求证:BM ∥平面PAD ;1A BCO A 1B 1C DPABCA C 1B C 1(2)平面PAD 内就是否存在一点N ,使MN ⊥平面PBD ？ 若存在,确定N 的位置,若不存在,说明理由;9、直三棱柱A 1B 1C 1—ABC 的三视图如图所示,D 、E 分别为棱CC 1与B 1C 1的中点。
《立体几何中的存在性问题》教学设计同步培优
微课堂设计《立体几何中的存在性问题》立体几何中的存在性问题在近几年的全国卷高考中大题第二问一直都有体现，存在性问题也就是探究性问题。
存不存在，存在又如何，我们处理的总的思路是什么？立体几何中的存在问题都是先假设存在，在存在的背景下去完成这个问题。
立体几何中有许多存在性问题，主要是针对直线上是否存在一点（平面内一点）使得满足一定的位置关系（平行、垂直）或一定的角度要求（线面角、二面角）。
存在性问题解决：（1）采用先猜后证，猜中点或三等分点等等然后证明位置关系：平行多用中位线、垂直多用三线合一等；（2）采用先设后求，运用待定系数法和空间向量解决，特别运用三点共线设一般直线上一点。
一．教学目标：掌握处理立体几何中探究性问题的一般思路；二．教学重点：利用先猜后证和先设后求处理探究性问题；三．教学难点：如何猜点及设点；四．教学过程4.1例题讲解例1.如图，矩形ABCD所在平面与半圆弧CD所在平面垂直，M是CD上异于C，D的点．在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．【答案】P为AM的中点【解析】当P为AM的中点时，MC∥平面PBD．证明如下：连结AC交BD于O．因为ABCD为矩形，所以O为AC中点．连结OP，因为P为AM中点，所以MC∥OP．MC⊄平面PBD，OP⊂平面PBD，所以MC∥平面PBD．【分析】先猜后证，为什么要猜中点？根据已知条件没有比例关系，关键是连接对角线会产生中点，平行多用中位线、垂直多用三线合一。
例2.如图，在三棱锥P ABC -中，22AB BC ==，4PA PB PC AC ====，O 为AC 的中点． （1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30，求PC 与平面PAM 所成角的正弦值．【解析】（2）以O 为坐标原点，OB 的方向为x 轴正方向，建立空间直角坐标系O xyz - ．则(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23)O B A C P AP -= 取平面PAC 的法向量(2,0,0)OB =．设(,2,0)(02)M a a a -<≤，则(,4,0)AM a a =-．设平面PAM 的法向量为(,,)n x y z =．由0,0AP n AM n ⋅=⋅=得2230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩ ， 可取2(3(4),3,)n a a a =--所以22223(4)cos 23(4)3a OB n a a a -〈⋅〉=-++ ．由已知得3cos 2OB n 〈⋅〉= ．所以22223|4|3223(4)3a a a a -=-++ ． 解得4a =-(舍去)，43a = ．所以83434,,333n ⎛⎫=-- ⎪ ⎪⎝⎭ ．又(0,2,23)PC =- ，所以3cos ,4PC n 〈〉= ．所以PC 与平面PAM 所成角的正弦值为34． 【分析】本题关键在于设M 的坐标，由于M 在xoy 平面内，可以放在xoy 平面去设M 坐标，根据M 点在直线BC 上，可以得到BC 方程，从而设出M 坐标。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
教学背景分析
立体几何中常出现点的存在性和位置待定的问题，以“是否存在”、“是否有”、“在何位置”教学
等形式设问，以示结论有待于确定.文科主要涉及到平行与垂直的位置关系的考查，其中渗透反证
内容
法与分析法的解题思路，也是高考中的常见题型。
2012 年北京市高考文科就考查了有关线面垂直的分析
存在性问题，2016 年北京市高考文科就考查了有关线面平行的存在性问题。
1、进一步熟悉空间直线与直线、直线与平面和平面与平面平行的位置关系；理解并掌握线面平行和
教学
面面平行的判定定理及性质定理，会运用定理解决与平行有关的存在性问题；
目标
2、通过对例题的分析，以及对问题的探究，会把空间问题转化为平面问题，尝试用不同的方法找到
需要确定的点、线、面，初步形成解决存在性问题的思路及方法；
3、感受“线线问题、线面问题、面面问题”之间的转化，逐步体会逻辑推理的严谨性。
学生情况
学生在前面立体几何的复习过程中，基本掌握了线线、线面、面面平行的判定与性质，碰到证明问题有一定的思路，但碰到存在性问题多以猜想特殊点的方法去尝试解决，并没从深层次上思考为什么去找这个位置。
另外前面的复习过程中由于对反证法并没有过多的强调，所以在碰到结论是不存在的情况时，还不会叙述，不会写解题格式。
教学方法教学重点教学难点教学引导启发式
线线平行、线面平行、面面平行的相互转化
探索立体几何中（与平行有关的）存在性问题的解题思路，思考存在性问题的本质多媒体、几何画板课件
辅助手段
课题：立体几何中与平行有关的存在性问题
板书例题分析
设计问题 3：方法总结：问题 6：
教学步骤
教学过程
教师活动学生活动设计目的
一、热身训练
二、例题精讲判断下列命题是否正确，若不正确，请修改或
添加条件使结论成立.
①若 a / /b,b，则 a / /；
②若 a / / ,b，则 a / /b ；
③若 m / / , n / / , m, n，则 / /；
④若/ / , a，则 a / /；
⑤若/ / , m, n，则 m / / n ．
例题：如图，在四棱锥P ABCD 中，底面
ABCD 是梯形，AB∥ CD ，AB 1 CD .
2
问题 1：请指出图中的线面平行的位置关系并选
择一组证明；
问题 2：AD∥平面PBC吗为什么
问题 3：过点A能做平面PBC 的平行线吗如果
能，请在图中作出一条或两条直线并证明.
回忆、思考、小组讨论
说明或操作演示为什么不正
确，如何改正
总结证明线线、线面、面面平
行的证明方法以及相互关系
P
D
C
A B
梳理平行的相关知
识，为本节课的复
习内容作铺垫，加
强知识之间的联系
检验学生对定理的
理解程度
为例题及问题的证
明明确证明的思路
培养学生学习的自
主性
训练学生如何说明
结论不成立
学生思考， 分析解题思路， 书
写解题过程，展示学习成果
问题 4：这些直线是怎么找到的
总结问题的类型及解决问题的方法：
问题 5：若将题目中的已知条件
AB
1
CD 改
2
为 AB
1 CD ，你能判断在棱 PD 上是否存在
3
一点 E 使得 AE ∥平面 PBC ， 若存在，请指
出 E 点位置，并证明；若不存在，请说明理由
.
问题 6: 在棱 PB 上（除 B 点外）是否存在一点 E
使得 AE ∥平面 PDC ，若存在， 请指出 E 点位
置，并证明；若不存在，说明理由
.
总结问题的类型及解决问题的方法：
引发学生思考直线
是怎么寻找到的，
探索问题的本质
总结归纳解题思路
P 及方法
当 AB 与 CD 数 量
D
C
关系变化时，如何
A
B
找到点 E 的位置，
分析解题思路，书写解题过
检查学生对刚学习
程，展示学习成果
的解题方法的掌握
P
程度。
D
C
三、 课
P ABCD 中，底面
练习：如图，在四棱锥
提示学生并非所有
B
堂练习
ABCD 是平行四边形，
A
E 是 PB 中点，
F 为
的存在性问题结论
线段 DB 上一点 . 试确定点 F 在线段 DB 上的
位置，使 EF PAC
P
都是肯定的，渗透
分析法与反证法的
检测题： 1、如图，在四棱锥
P ABCD 中，底
思想，让学生去思
考解决存在性问题
E
1
CD .
面 ABCD 是梯形， AB ∥ CD ， AB
的思路，巩固面面
2
C
平行的判定与线面
D
在棱 PC 上是否存在一点
E 使得 BE ∥平面
O
平行的性质
PAD ，若存在，求出 E 点位置，并证明；若不
四、课通过这节课的复习，请同学们从知识与方法方面回顾一下，学习过程中遇到了什么问题需要注意
哪些方面
堂小结
五、作学案上的练习题
业布置。