信号与线性系统分析吴大正_第四版习题答案
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
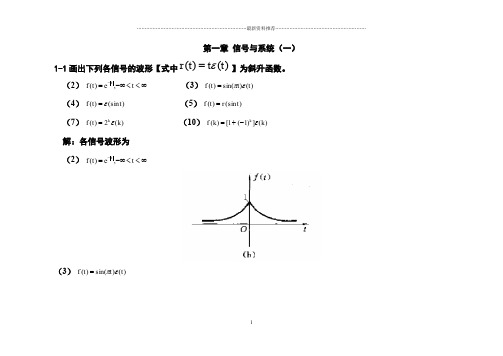
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
信号与线性系统分析习题答案_(吴大正_第四版__高等教育出版社)之欧阳音创编

第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
线性系统分析_(吴大正_第四版)习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
信号与线性系统分析(吴大正第四版)习题答案

第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)习题答案
信号与系统习题解析C1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析-(吴大正-第四版)第三章习题答案
第三章习题3.1、试求序列k 01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩,的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。
3.6、求以下差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1〕()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3〕()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5〕1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求以下差分方程所描述的离散系统的单位序列响应。
2〕()-(-2)()=y k y k f k5〕()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。
〔a〕〔c〕3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如下图,求以下卷积和。
〔1〕12()()f k f k *〔2〕23()()f k f k *〔3〕34()()f k f k *〔4〕[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、假设LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
3.16、如下图系统,试求当鼓励分别为〔1〕()()f k k ε= 〔2〕()()0.5()kf k k ε=时的零状态响应。
3.18、如下图的离散系统由两个子系统级联组成,()1=2cos4k h k π,()()2=k h k k a ε,鼓励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
〔提示:利用卷积和的结合律和交换律,可以简化运算。
〕3.22、如下图的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
信号与线性系统分析习题答案_(吴大正_第四版__高等教育出版社)之欧阳数创编
第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))(sin )(t r t f =(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
(1))()1(t t f ε- (2))1()1(--t t f ε (5))21(t f - (6))25.0(-t f(7)dtt df )( (8)dx x f t ⎰∞-)( 解:各信号波形为(1))()1(t t f ε-(2))1()1(--t t f ε (5))21(t f -(6))25.0(-t f(7)dt t df )((8)dx x f t⎰∞-)(1-7 已知序列)(k f 的图形如图1-7所示,画出下列各序列的图形。
(1))()2(k k f ε- (2))2()2(--k k f ε (3))]4()()[2(---k k k f εε (4))2(--k f (5))1()2(+-+-k k f ε (6))3()(--k f k f解:1-9 已知信号的波形如图1-11所示,分别画出)(t f 和dtt df )(的波形。
解:由图1-11知,)3(t f -的波形如图1-12(a)所示()3(t f -波形是由对)23(t f -的波形展宽为原来的两倍而得)。
将)3(t f -的波形反转而得到)3(+t f 的波形,如图1-12(b)所示。
再将)3(+t f 的波形右移3个单位,就得到了)(t f ,如图1-12(c)所示。
dtt df )(的波形如图1-12(d)所示。
1-10 计算下列各题。
(1)[]{})()2sin(cos 22t t t dtd ε+ (2))]([)1(te dt d t t δ-- (5)dt t t t )2()]4sin([2++⎰∞∞-δπ (8)dx x x t)(')1(δ⎰∞--1-12 如图1-13所示的电路,写出(1)以)(t u C 为响应的微分方程。
(2)以)(t i L 为响应的微分方程。
1-20 写出图1-18各系统的微分或差分方程。
1-23 设系统的初始状态为)0(x ,激励为)(⋅f ,各系统的全响应)(⋅y 与激励和初始状态的关系如下,试分析各系统是否是线性的。
(1)⎰+=-tt dx x xf x e t y 0)(sin )0()( (2)⎰+=t dx x f x t f t y 0)()0()()( (3)⎰+=tdx x f t x t y 0)(])0(sin[)( (4))2()()0()5.0()(-+=k f k f x k y k(5)∑=+=kj j f kx k y 0)()0()( 1-25 设激励为)(⋅f ,下列是各系统的零状态响应)(⋅zs y 。
判断各系统是否是线性的、时不变的、因果的、稳定的?(1)dtt df t y zs )()(= (2))()(t f t y zs = (3))2cos()()(t t f t y zs π=(4))()(t f t y zs -= (5))1()()(-=k f k f k y zs (6))()2()(k f k k y zs -=(7)∑==k j zs j f k y 0)()( (8))1()(k f k y zs -=1-28 某一阶LTI 离散系统,其初始状态为)0(x 。
已知当激励为)()(1k k y ε=时,其全响应为 若初始状态不变,当激励为)(k f -时,其全响应为)(]1)5.0(2[)(2k k y k ε-=若初始状态为)0(2x ,当激励为)(4k f 时,求其全响应。
第二章2-1 已知描述系统的微分方程和初始状态如下,试求其零输入响应。
(1)1)0(',1)0(),()(6)('5)(''-===++-y y t f t y t y t y(4)0)0(',2)0(),()()(''===+-y y t f t y t y2-2 已知描述系统的微分方程和初始状态如下,试求其+0值)0(+y 和)0('+y 。
(2))()(,1)0(',1)0(),('')(8)('6)(''t t f y y t f t y t y t y δ====++--(4))()(,2)0(',1)0(),(')(5)('4)(''2t e t f y y t f t y t y t y t ε====++--解:2-4 已知描述系统的微分方程和初始状态如下,试求其零输入响应、零状态响应和全响应。
(2))()(,2)0(',1)0(),(3)(')(4)('4)(''t e t f y y t f t f t y t y t y t ε---===+=++解:2-8 如图2-4所示的电路,若以)(t i S 为输入,)(t u R 为输出,试列出其微分方程,并求出冲激响应和阶跃响应。
2-12 如图2-6所示的电路,以电容电压)(t u C 为响应,试求其冲激响应和阶跃响应。
2-16 各函数波形如图2-8所示,图2-8(b)、(c)、(d)均为单位冲激函数,试求下列卷积,并画出波形图。
(1))(*)(21t f t f (2))(*)(31t f t f (3))(*)(41t f t f(4))(*)(*)(221t f t f t f (5))3()(2[*)(341--t f t f t f波形图如图2-9(a)所示。
波形图如图2-9(b)所示。
波形图如图2-9(c)所示。
波形图如图2-9(d)所示。
波形图如图2-9(e)所示。
2-20 已知)()(1t t t f ε=,)2()()(2--=t t t f εε,求)2('*)1(*)()(21--=t t f t f t y δ2-22 某LTI 系统,其输入)(t f 与输出)(t y 的关系为dx x f e t y t x t )2()(1)(2-=⎰∞--- 求该系统的冲激响应)(t h 。
2-28 如图2-19所示的系统,试求输入)()(t t f ε=时,系统的零状态响应。
2-29 如图2-20所示的系统,它由几个子系统组合而成,各子系统的冲激响应分别为求复合系统的冲激响应。
第三章习题、试求序列的差分、和。
、求下列差分方程所描述的LTI离散系统的零输入相应、零状态响应和全响应。
1)3)5)、求下列差分方程所描述的离散系统的单位序列响应。
2)5)、求图所示各系统的单位序列响应。
(a)(c)、求图所示系统的单位序列响应。
、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)、求题图所示各系统的阶跃响应。
、求图所示系统的单位序列响应和阶跃响应。
、若LTI 离散系统的阶跃响应,求其单位序列响应。
、如图所示系统,试求当激励分别为(1)(2)时的零状态响应。
、如图所示的离散系统由两个子系统级联组成,已知,,激励,求该系统的零状态响应。
(提示:利用卷积和的结合律和交换律,可以简化运算。
)、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为,,求复合系统的单位序列响应。
第四章习题求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-15利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和图4-19根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ (2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε试用时域微积分性质,求图4-23示信号的频谱。
