平面介质波导建模过程
光波导数值模拟方法

光波导数值模拟方法介质光波导是利用介质的折射率差来限制光场,从而引导和控制光波传播的一种结构,是光波导器件中的最基本构成成分。
常见的波导主要有光纤和平面波导两种,本文主要针对应用于平面集成光路的平面光波导进行讨论。
平面光波导主要有两种结构,即平板波导(二维结构)和条形波导(三维结构)两种[46], 如图2.1所示。
平板波导如图2.1a 所示,在垂直于光波传播方向(z 方向)的截面上,只在纵向(x 方向)上受到限制,而在横向上(y 方向)可以无限延伸,是完全均匀的。
而条形波导,如图2.1b ,则是在两个方向(x ,y 方向)同时受到限制。
通常实际光器件都是建立在条形波导的基础上的,平板波导由于在横向上缺乏对光的约束,只在很少情况下(如AWG 的自由传输区)才会用到。
但是从平板这种更加简单的二维结构入手,可以更方便于对波导特性的研究。
图2.1 两种平面波导结构:(a )平板波导,(b )条形波导平板光波导理论假设现有一平板波导由三种介质组成,如图2.2所示,上包层折射率为n c (x >a ),衬底折射率n s ,(x <-a ),芯层折射率n f (-a <x <a ),平板芯层厚度为2a 。
传统的射线理论认为,光线在波导中传播时,将会在上下两个界面中发生全反射,以此也可得出波导存在导波模式的最基本条件:n f >n s ,n c 。
那么,当光线入射到界面的角度满足max(sin(),sin())c f s f arc n n arc n n θ>,光线就能同时在两个界面都发生全内反射,从而被束缚在波导之中。
同时,为了使得光线能在波导中稳定传输,还必需满足光线在两个界面之间往返一次的总相位变化是2π的整数倍。
于是根据以上这些条件,就可以求出对应于某一波长(真空中波矢为k 0)的光线所需满足的入射角θ,从而求出其传播常数,即传播方向上的波矢分量,0sin f k n βθ=,以及与该传播模式对应的等效折射率0eff n k β=,在此不再赘述。
第二章-理想平板介质光波导中的光传播特性及仿真

第2章介质光波导分析方法2.1 平板介质光波导一般概念2.1 平板介质光波导一般概念波动理论法则是把平板介质光波导中的光波看作是满足波导边界条件的麦克斯韦方程组的解。
2.2 平板光波导分析的射线法振幅反射率和附加相移振幅反射率和附加相移S 波(TE 波——电矢量平行于界面)振幅反射率:光传播过程相位变化:光波不仅在介质中传播过程中相位会发生改变,在界面上反射时相位也会变化。
对于θ1 < θ1c ,界面上发生全反射,此时上式的分子和分母中第二个平方根内为负数,因此得到的振幅反射率r 为复数。
1.106分子分母同乘k )振幅反射率和附加相移振幅反射率和附加相移s 波( TE波——电矢量平行于界面) 附加相移为:p 波( TM波——磁矢量平行于界面)在界面发生全反射时引起的附加相移为:(1.145)(1.144)界面:n1、n2、n3的界面,不是入射面平板波导中的其他光场均可视为TEM 模:模式只有横向分量,而无纵导模特征方程导模特征方程入射光线两次反射后与入射光线同方向传输特征方程特征方程A、B 两点的距离为:C、D两点的距离为:光线CD 还经历了两个附加相移:分别是介质1、3 界面处全反射的附加相移ϕ3 和介质1、2 界面处全反射的附加相移ϕ2.平板光波导的特征方程:特征方程特征方程 界面处的附加相移会因入射光偏振方向的不同而有所差异,因此就能够得到两个不同模式下的特征方程电矢量平行于界面的导波式中:特征方程特征方程同样地,磁矢量平行于界面的导波TM 模的特征方程(代入ΦM2和ΦM3) :这里采用的是简单光线传播的射线理论。
实际上,从麦克斯韦方程出发,结合介质界面处的边界条件也可以推导出以上特征方程。
引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他引入的几个重要参数——都是θ的函数,得到一个光波模式的波矢就可以求解其他纵向波矢横向波矢衰减系数< n 1kn 2k << n 1k2.3 平板光波导中的TE模TE模的电磁理论求解TE模的电磁理论求解平板光波导中的TE模仅有E y由麦克斯韦方程:(2.30)TE模的电磁理论求解TE模的电磁理论求解的式子因此可以将H的分量表示为Ey代入式(2.30),可以得到关于Ey的波动方程,j = 1;2;3 表示分别是在芯层、衬底和覆盖层。
1.2-介质板波导

k k0 n2
应有K 2 k0 2 n2 2 2 0, 令 2 2 k0 2 n2 2
D ( x d ) e i D x ( x d ) ( )e x
12
(3) 边界条件和特征方程式
当x d 时, 应有E y1 E y 2 , H z1 H z 2 A(1 K
1.2 介质平板波导
1
主要内容
1.
基本波动方程和波导方程式
2.
3.
对称介质平板波导的传输模式
介质板波导中的多模群时延
2
1、波动方程和波导方程式
1)波动方程:由麦克斯韦方程组推导出
B E t E ( B ) t D 2 ( E ) E ( ) t t D ( E ) E E 0 E E
准备2
i E z H z Ex 2 ( ) K x y i H z E z Hx ( ) 2 K x y i E z H z E y 2 ( ) K y x i H z E z Hy ( ) 2 K y x K 2 k 2 2 2 2
两个平面波的传输方向与介质板的法线夹角
tan
K
在介质板上,两个平面波满足内部全反射条件, 它们对介质板入射角度是由模式传输矢量的分量β、K所决定。
21 结论:模式截止的情况与以临界角入射到介质板上的平面波相对应
3)TM模式(以TE分析类似) 3.介质板波导中的多模群时延
d dL dH K 2 k0 2 n12 2 f 0
得 令
4平面光波导工艺
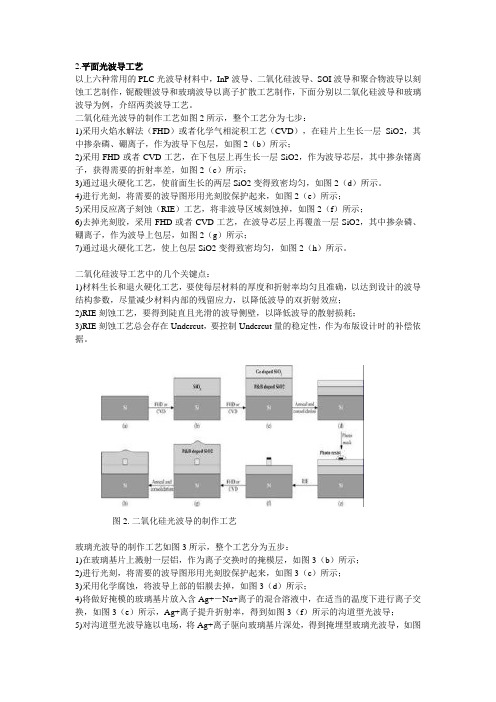
2.平面光波导工艺以上六种常用的PLC光波导材料中,InP波导、二氧化硅波导、SOI波导和聚合物波导以刻蚀工艺制作,铌酸锂波导和玻璃波导以离子扩散工艺制作,下面分别以二氧化硅波导和玻璃波导为例,介绍两类波导工艺。
二氧化硅光波导的制作工艺如图2所示,整个工艺分为七步:1)采用火焰水解法(FHD)或者化学气相淀积工艺(CVD),在硅片上生长一层SiO2,其中掺杂磷、硼离子,作为波导下包层,如图2(b)所示;2)采用FHD或者CVD工艺,在下包层上再生长一层SiO2,作为波导芯层,其中掺杂锗离子,获得需要的折射率差,如图2(c)所示;3)通过退火硬化工艺,使前面生长的两层SiO2变得致密均匀,如图2(d)所示。
4)进行光刻,将需要的波导图形用光刻胶保护起来,如图2(e)所示;5)采用反应离子刻蚀(RIE)工艺,将非波导区域刻蚀掉,如图2(f)所示;6)去掉光刻胶,采用FHD或者CVD工艺,在波导芯层上再覆盖一层SiO2,其中掺杂磷、硼离子,作为波导上包层,如图2(g)所示;7)通过退火硬化工艺,使上包层SiO2变得致密均匀,如图2(h)所示。
二氧化硅波导工艺中的几个关键点:1)材料生长和退火硬化工艺,要使每层材料的厚度和折射率均匀且准确,以达到设计的波导结构参数,尽量减少材料内部的残留应力,以降低波导的双折射效应;2)RIE刻蚀工艺,要得到陡直且光滑的波导侧壁,以降低波导的散射损耗;3)RIE刻蚀工艺总会存在Undercut,要控制Undercut量的稳定性,作为布版设计时的补偿依据。
图2. 二氧化硅光波导的制作工艺玻璃光波导的制作工艺如图3所示,整个工艺分为五步:1)在玻璃基片上溅射一层铝,作为离子交换时的掩模层,如图3(b)所示;2)进行光刻,将需要的波导图形用光刻胶保护起来,如图3(c)所示;3)采用化学腐蚀,将波导上部的铝膜去掉,如图3(d)所示;4)将做好掩模的玻璃基片放入含Ag+-Na+离子的混合溶液中,在适当的温度下进行离子交换,如图3(e)所示,Ag+离子提升折射率,得到如图3(f)所示的沟道型光波导;5)对沟道型光波导施以电场,将Ag+离子驱向玻璃基片深处,得到掩埋型玻璃光波导,如图3(g)所示。
平面介质光波导和耦合模理论ppt课件

0neff n3
n3 neff n2
n2 neff n1
M=1
M=0
ppt精选版
TE0
27
3、截止波长
如果某个模式在衬底出现辐射则称该模式截止,
由截止条件 k0n2 带入公式2.2.5a得到kx,带入
2.2.6a可得
k0d
n12n22
marctan
n22n32 n12n22
TEm模式的截止波长
2.2.0.3
BOHMOr HOH
ppt精选版
P-媒质极化强度,M-磁化强度 -媒质电导率,o、o-自由空 间的介电常数和磁导率
19
波动方程的推导思路:
1、光波导材料为不导电的均匀、各向同性,J=0,
=0,r为常数 2、对公式2.2.0.1前2个式子做旋度处理,并利用后两式
结果,可以得到
2E
n2
2
xa
xa 2.2.4
ax
式中
k
2 x
2
n
2 1
k
2 o
a
2 2
2
n
2 2
k
2 o
a
2 3
2
n
2 3
k
2 o
2.2.5a 2.2.5b 2.2.5c
kx---x方向的波数, a2、a3---分别为衬底层、覆盖层中电场沿X方向的 衰减常数,k0---真空中的波数,---场量在Z方向的传播常数 注:上式中省略了exp(-j z)
辐射模式 k 0 n 3 k 0 pn pt2 精 选版 0 k 0 n 3 2.2.8 26
平面光波导的模式及传播常数小结
sin c
n3 n1
n2 ≥ n3, s ≥ c
电信传输原理及应用第四章 介质光波导理论_平面光波导
第4章 介质光波导理论
本征值方程
边界条件:TE模式: Ey,Hz在上下界面连续; TM模式: Hy,Ez在上下界面连续。 本征值方程:
第4章 介质光波导理论
第4章 介质光波导理论
第4章 介质光波导理论
第4章 介质光波导理论
场分布特点
禁区: 导模:
β>n1k0 n1k0> β> n2k0
χ21>0,传播场; χ22, χ20<0,消逝场 衬底辐射模: n1k0> β> n3k0 χ23<0,消逝场; χ22, χ20>0,传播场 辐射模: n3k0> β> 0 χ21, χ22 ,χ20 > 0,传播场
第4章 介质光波导理论
第4章 介质光波导理论
平面光波导中的波动法分析
波导场方程:
∂ Ey
2
∂x
2 j
2
+ χ Ey = 0
2 j 2 0 2 j 2
χ =k n −β
场分量:TE模式: Ey,Hx,Hz: (2-2-1)-(2-2-3)
TM模式: Hy,Ex,Ez: (2-2-4)-(2-2-6)
第4章 介质光波导理论
第4章 介质光波导理论
几何光学分析
光线轨迹:锯齿形折线 约束光线条件: 上界面全反射: θ10>θc10=arcsin(n0/n1) 下界面全反射: θ12>θc12=arcsin(n2/n1) 相位匹配:上下两次反射经 历相移为2π整数倍
介质波导法

介质波导法介质波导法是一种在介质中传播电磁波的方法。
在介质波导中,电磁波通过界面反射来限制在介质内传播。
这种波导结构在许多应用中都得到广泛应用,如光纤通信和微波技术等。
介质波导法涉及到一些关键的概念,例如全内反射和波导模式。
首先,全内反射是指当光线从光密介质射入光疏介质时,当入射角大于临界角时,光线将完全被反射,不再继续传播到光疏介质中。
这种特性是光纤通信中的核心机制之一。
波导模式是介质波导的电磁场分布的一种特定形式。
它是波导中电磁场的准静态解决方案,且具有特定的传播常数。
波导模式的特点是只有特定的频率和传播常数下才能在波导中传播。
这些模式通过波导的物理尺寸和介质参数来确定。
介质波导的设计和分析可以使用一些数学方法和物理原理。
其中,麦克斯韦方程组是描述电磁波的重要工具,它们将电场和磁场之间的关系进行了描述。
此外,电磁波的传播可以使用亥姆霍兹方程进行建模,该方程描述了电磁波在波导中的传播行为。
在实际的介质波导应用中,波导结构的设计和特性分析是非常重要的。
例如,在光纤通信中,波导的损耗和色散特性是需要进行详细研究的。
波导损耗是指光能量在波导中传输时的衰减,这会导致信号的衰减和干扰。
波导色散是因为介质的色散特性而导致信号在波导中传播速率随着频率的变化而变化。
为了实现较低的波导损耗和色散特性,波导的结构和材料选择也是需要仔细考虑的。
例如,在光纤通信中,选择较低损耗和较低色散的材料非常重要。
传统的光纤一般由硅或玻璃制成,这些材料具有低损耗和较低色散特性,使其成为光纤通信中的首选。
除了光纤通信,介质波导法还在微波技术中得到广泛应用。
例如,微波集成电路中的传输线和器件常常使用介质波导结构来实现信号的传输和分配。
在微波波导中,微波信号的传播速率和功率耗散也是需要考虑的因素。
总而言之,介质波导法是一种广泛应用于光纤通信和微波技术等领域的方法。
通过对介质波导的设计和分析,我们可以实现优化的波导结构,从而实现更高效、低损耗的信号传输。
第4章-介质波导
Ae
be
e r
A
g
b
ar
x y z
a
n1 n2 plane l of f incidence i id
a e a cos e a r a cos r a g a cos g b e br bg b Poyntingvector S E H
2 n1 cos g 1 2 sin 2 e n2 Eg 2n1 cos e Ee n1 cos e n 2 cos g
rTE
2 2 2 Er n1 cos e n 2 n1 sin e 2 2 Ee n1 cos e n 2 2 n 1 sin e
r cs e e
e
e
cc r
导波模
两个界面处全内反射 nf > ns > nc
2ΦS
17
nc nf ns
h
z
nc
z=h
cc
s
c e
radiation mode
x
y n=0
nf
ns
e
h
cc
r
substrate mode
h
s
2ΦC
e
h
e
cc r
rcs e
1
4.1 光的反射和折射
TE-Wave
He Ee ke e r Hr Er kr
n1 < n2
He
ke
TM-Wave
kr Er
Hr
n1 n2
x y z
Ee
e r
n1 n2
g
Eg
Hg kg
g
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
©2013 COMSOL
1 |
DIELECTRIC SLAB WAVEGUIDE
Solved with COMSOL Multiphysics 4.3b
The analytic solution is found by assuming that the electric field along the direction of propagation varies as Ez = E(y)exp(-ikxx), where E(y) = C1cos(kyy) inside the dielectric slab, and E(y) = C0exp(−α(|y| − (hslab/2)) in the cladding. Because the electric and magnetic fields must be continuous at the interface, the guidance condition is t slab α = k y tan k y --------- 2 where ky and α satisfy k y = k core – k cladding – α
Figure 1: The guided modes in a dielectric slab waveguide have a known analytic solution.
Model Definition
A dielectric slab of thickness hslab = 1 μm and refractive index ncore = 1.5 forms the core of the waveguide, and sits in free space with ncladding = 1. Light polarized out of the plane of propagation, of wavelength λ = 1550 nm, is perfectly guided along the axis of the waveguide structure, as shown in Figure 1. Here, only the TE0 mode can propagate. The structure varies only in the y direction, and it is infinite and invariant in the other two directions.
Name lambda0 n_core n_claddin g h_core h_claddin g w_slab k_core k_claddin g f0 GEOMETRY 1 Expression 1550[nm] 1.5 1 1[um] 7[um] 5[um] 2*pi[rad]*n_core/lambda0 2*pi[rad]*n_cladding/ lambda0 c_const/lambda0 Description Wave length Refractive index, core Refractive index, cladding Thickness, core Thickness, cladding Slab width Wave number, core Wave number, cladding Frequency
1 In the Model Builder window, under Model 1 click Geometry 1. 2 In the Geometry settings window, locate the Units section. 3 From the Length unit list, choose µm.
Model Library path: Wave_Optics_Module/Verification_Models/
dielectric_slab_waveguide
Modeling Instructions
MODEL WIZARD
1 Go to the Model Wizard window. 2 Click the 2D button. 3 Click Next. 4 In the Add physics tree, select Optics>Wave Optics>Electromagnetic Waves, Frequency Domain (ewfd). 5 Click Add Selected. 6 Click Next.
2 2 2 2
with kcore = 2πncore/λ and kcladding = 2πncladding/λ. It is possible to find the solution to the above two equations via the Newton-Raphson method, which is used whenever COMSOL Multiphysics detects a system of nonlinear equations, the only requirement being that of an adequate initial guess. This model considers a section of a dielectric slab waveguide that is finite in the x and y directions. Because the fields drop off exponentially outside the waveguide, the fields can be assumed to be zero at some distance away. This is convenient as it makes the boundary conditions in the y direction irrelevant, assuming that they are imposed sufficiently far away. Use Numerical Port boundary conditions in the x direction to model the guided wave propagating in the positive x direction. These boundary conditions require first solving an eigenvalue problem that solves for the fields and propagation constants at the boundaries.
Rectangle 1
1 Right-click Model 1>Geometry 1 and choose Rectangle. 2 In the Rectangle settings window, locate the Size section. 3 In the Width edit field, type w_slab. 4 In the Height edit field, type h_core. 5 Locate the Position section. From the Base list, choose Center. 6 Click the Build Selected button.
Results and Discussion
Figure 2 shows the results. The numerical port boundary condition at the left side excites a mode that propagates in the x direction and is perfectly absorbed by the numerical port on the right side. The analytic and numerically computed propagation constants agree.
©2013 COMSOL3来自|DIELECTRIC SLAB WAVEGUIDE
Solved with COMSOL Multiphysics 4.3b
7 Find the Studies subsection. In the tree, select Custom Studies>Empty Study. 8 Click Finish.
GLOBAL DEFINITIONS
Parameters
1 In the Model Builder window, right-click Global Definitions and choose Parameters. 2 In the Parameters settings window, locate the Parameters section. 3 In the table, enter the following settings:
4 |
D I E L E CT R I C SL A B WAVE G UI D E
©2013 COMSOL
Solved with COMSOL Multiphysics 4.3b
Rectangle 2
1 In the Model Builder window, right-click Geometry 1 and choose Rectangle. 2 In the Rectangle settings window, locate the Size section. 3 In the Width edit field, type w_slab. 4 In the Height edit field, type h_cladding. 5 Locate the Position section. From the Base list, choose Center. 6 Click the Build All button. 7 Click the Zoom Extents button on the Graphics toolbar.
