湘教版七年级上册第一章有理数部分知识点思维导图归纳
初中数学七年级上册思维导图

1.⼤于0的数叫做正数。
2.在正数前⾯加上负号“-”的数叫做负数。
3.整数和分数统称为有理数。
七年级上册数学知识点思维导图+考点梳理,考前必看!(附打印版)01有理数4.⼈们通常⽤⼀条直线上的点表示数,这条直线叫做数轴。
5.在直线上任取⼀个点表示数0,这个点叫做原点。
6.⼀般的,数轴上表示数a的点与原点的距离叫做数a的绝对值。
7. 由绝对值的定义可知:⼀个正数的绝对值是它本身;⼀个负数的绝对值是它的相反数;0的绝对值是0。
8.正数⼤于0,0⼤于负数,正数⼤于负数。
9.两个负数,绝对值⼤的反⽽⼩。
10.有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)绝对值不相等的异号两数相加,取绝对值较⼤的加数的负号,并⽤较⼤的绝对值减去较⼩的绝对值,互为相反数的两个数相加得0。
(3)⼀个数同0相加,仍得这个数。
11.有理数的加法中,两个数相加,交换交换加数的位置,和不变。
12.有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
13.有理数减法法则:减去⼀个数,等于加上这个数的相反数。
14.有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值向乘。
任何数同0相乘,都得0。
15.有理数中仍然有:乘积是1的两个数互为倒数。
16.⼀般的,有理数乘法中,两个数相乘,交换因数的位置,积相等。
17. 三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
18. ⼀般地,⼀个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
19.有理数除法法则:除以⼀个不等于0的数,等于乘这个数的倒数。
20.两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何⼀个不等于0的数,都得0。
21. 求n个相同因数的积的运算,叫做乘⽅,乘⽅的结果叫做幂。
在an 中,a叫做底数,n叫做指数。
22.根据有理数的乘法法则可以得出:负数的奇次幂是负数,负数的偶次幂是正数。
显然,正数的任何次幂都是正数,0的任何次幂都是0。
初一上册数学思维导图第一单元图片

初一上册数学思维导图第一单元图片_初一数学思维导图第一章有理数1 正数和负数(1)正数大于0 的数;负数小于0 的数;(2)0 既不是正数,也不是负数;(3)在同一个问题中,分别用正数和负数表示的量具有相反的意义;(4)-a 不一定是负数,+a 也不一定是正数;(5)自然数0 和正整数统称为自然数;(6)a>0 ? a 是正数;a<0 ? a 是负数;a ≥0 ? a 是正数或0 ? a 是非负数;a≤0 ? a 是负数或0 ? a 是非正数.2 有理数(1)正整数、0、负整数、正分数、负分数都可以写成分数的形式,这样的数称为有理数;(2)正整数、0、负整数统称为整数;(3)有理数的分类? ?正整数?正有理数?正分数? ? 有理数?零? ?负整数?负有理数? ?负分数?正整数?整数?零? ? ? 有理数? ?负整数? ?正分数?分数? ?负分数?(4)数轴规定了原点、正方向、单位长度的一条直线;(即数轴的三要素)(5)一般地,当a 是正数时,则数轴上表示数a 的点在原点的右边,距离原点a 个单位长度;表示数-a 的点在原点的左边,距离原点a 个单位长度;(6)两点关于原点对称一般地,设a 是正数,则在数轴上与原点的距离为a 的点有两个,它们分别在原点的左右,表示-a 和a,我们称这两个点关于原点对称;(7)相反数只有符号不同的两个数称为互为相反数;(8)一般地,a 的相反数是-a;特别地,0 的相反数是0;(9)相反数的几何意义数轴上表示相反数的两个点关于原点对称;(10)a、b 互为相反数?a+b=0 ;(即相反数之和为0)(11)a、b 互为相反数?a ? ?1 b或b ? ?1 ;(即相反数之商为-1)a(12)a、b 互为相反数?|a|=|b|;(即相反数的绝对值相等)(13)绝对值一般地,在数轴上表示数a 的点到原点的距离叫做a 的绝对值;(|a|≥0)(14)一个正数的绝对值是其本身;一个负数的绝对值是其相反数;0 的绝对值是0;(a ? 0) ?a (15)绝对值可表示为a ? ? 0 (a ? 0) ? ? ? a (a ? 0) ?a aa a(16)?1? a ? 0 ;? ?1 ? a ?0 ;(17)有理数的比较在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序。
湘教版七年级数学第一单元《有理数》知识清单

新课标湘教版数学七年级(上)知识要点概括第一章有理数1.(1)正数:大于零的数;(2)负数:小于零的数(在正数前面加上负号“—”的数);注意:①0既不是正数也不是负数,它是正负数的分界点;②对于正数和负数,不能简单理解为带“+”号的数是正数,带“—”号的数是负数;③字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
④正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.有理数的概念⑴正整数、0、负整数统称为整数;⑵正分数和负分数统称为分数;⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数;②有限小数和无限循环小数都可化成分数,都是有理数;③-a不一定是负数,+a也不一定是正数;3.有理数的分类⑴按有理数的定义分类⑵按性质符号来分正整数正整数整数 0 正有理数负整数正分数有理数有理数 0 (0不能忽视)正分数分数负有理数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数⑤0是整数不是分数。
4. 规定了原点,正方向,单位长度的直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸的直线;⑵原点、正方向、单位长度是数轴的三要素,三者缺一不可;⑶同一数轴上的单位长度要统一。
(4)数轴一般取右(或向上)为正方向,数轴的原点的选定,正方向的取向,单位长度大小的确定都是根据实际需要规定的。
5.数轴上的点与有理数的关系⑴所有的有理数都可以用数轴上的点来表示,正有理数可用原点右侧的点表示,负有理数可用原点左侧的点表示,0用原点表示。
⑵所有的有理数都可以用数轴上的点表示出来,但数轴上的点不都表示有理数,也就是说,有理数与数轴上的点不是一一对应关系。
七年级数学上册思维导图

⎪思维导图 ⎪⎪ ⎩分数 ⎪按性质符号分⎪⎨0 ⎪负有理数 ⎪ ⎪ ⎩ ⎧相反数 — —只有符号不同的两个数,叫做互为相反数 ⎪ ⎪绝对值 — — 叫做数a 的绝对值 ⎪ ⎪ 有理数⎨相关概念⎨ ⎪ ⎪ 把一个数表示乘a ⨯ 10 n 的形式(其中1 ≤ a < 10, ⎪⎩ n 是正整数),这种记数方法叫做科学记数法 ⎧ ⎪⎪有理数的减法法则 ⎪ ⎪ ⎪有理数的除法法则 ⎪ ⎪ ⎪ ⎪⎩乘方的运算符号法则 ⎪运算⎨ ⎧ ⎧加法交换律 ⎪交换律⎨ ⎪ ⎩乘法交换律⎪ ⎪运算律⎪结合律⎧加法结合律 ⎪ ⎪ ⎪ ⎩乘法结合律⎪ ⎪分配律 ⎪ ⎪ ⎪ ⎪⎧第一章 有理数⎪ ⎪ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎧ ⎧整数 ⎪ ⎪按定义分⎨ ⎪ ⎪分类⎨ ⎧正有理数 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 一般地,数轴上表示数a 的点与原点的距离, ⎪ ⎪ ⎪ ⎪ ⎪倒数 — —乘积是1的两个数互为倒数 ⎪ ⎪ 求n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂 ⎪ ⎪乘方 — — ⎪ ⎪ 相同的因数叫做底数,相同因数的个数叫做指数 ⎪ ⎪ ⎪ ⎪科学记数法 — — ⎪ ⎪ ⎪ ⎧有理数的加法法则 ⎪ ⎪ ⎪ ⎪ ⎪法则⎨有理数的乘法法则 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎩ ⎩⎧ ⎪定义 — —由数或字母的积组成的式子 ⎪ ⎪单项式⎨ ⎪ ⎪ ⎧定义 — —几个单项式的和 ⎪ ⎪项 — —组成多项式的每个单项式 多项式⎨ 整 ⎪ 加 ⎪ 作为合并后项的系数 整式的加减⎨ ⎪ ⎪去括号⎨ ⎪括号外因数为负 — — ⎪ ⎪ ⎧去括号 ⎪ ⎪ ⎪步骤⎪ ⎪ ⎪⎩合并同类项⎩ ⎨ ⎩ ⎩ 第二章 整式的加减思维导图⎧用字母表示数 ⎪ ⎪ ⎪ ⎪ 系数 — —单项式中的数字因数 ⎪ ⎪ ⎪ ⎩次数 — —单项式中所有字母的指数的和 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪常数项 — —不含字母的项 式 ⎪ ⎪ 的 ⎪ ⎪次数 — —多项式中次数最高项的次数 ⎪ ⎧同类项 — —所含字母相同并且相同字母的指数也相同 减 ⎪ ⎪⎪ ⎪ 把同类项的系数相加,所得的结果 ⎪ ⎪合并同类项 — — ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧括号外因数为正 — — ⎪ ⎪ ⎪去括号后原括号内各项的符号与原来的符号相同 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪去括号后原括号内各项的符号与原来的符号相反 ⎪ ⎪ ⎪ ⎩⎪ ⎪方程的解:使方程中等号左右两边相等的未知数的值 ⎧⎪性质1:等式两边加(或减)同一个数(或式子),结果仍相等 ⎪等式的性质⎨ 一 ⎪ ⎪去括号 一 ⎪ ⎨ 程 ⎪ ⎪系数化为1 ⎪一次方程 ⎪⎨列:根据题目中的数量关系、相等关系、倍数关系以及若干倍多或少 ⎪ ⎪ ⎩ ⎩ ⎨ ⎩ ⎩第三章第四章 一元一次方程思维导图⎧ ⎧方程:含有未知数的等式 ⎪ ⎪ ⎪ ⎪一元一次方程:只含有一个未知数(元),未知数的次数都是1, ⎪ ⎪⎪等号两边都是整式 ⎪一元一次方程⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪解方程:求方程的解的过程 ⎪ ⎪ ⎪ ⎪ ⎪性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等 ⎪⎧去分母 元 ⎪ ⎪ ⎪ ⎪ 次 ⎪解一元一次方程的步骤⎪移项 方 ⎪ ⎪⎪ ⎪合并同类项 ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎧审:弄清题意,分清已知量和未知量,明确各数量间的关系 ⎪ ⎪ ⎪ ⎪设:设未知数,并且用含未知数的代数式表示与所列方程有关的数量 ⎪ ⎪ ⎪列一元 ⎪ ⎪解应用题 ⎪一个数字列方程 ⎪ ⎪ ⎪解:解所列的方程,求出未知数的值以及题目中所要求的相关数量的值 ⎪ ⎪ ⎪验:检验所求的解是否符合题意,是否符合实际意义第五章第六章几何图形初步思维导图⎧从正面看 ⎪立体图形⎨从不同的方向看立体图形⎨从左面看 ⎪ ⎪ ⎪从上面看 ⎩ ⎪ ⎪ ⎪立体图形的平面展示图⎪ ⎧ ⎧ ⎪ ⎪ 直线⎪ ⎪ ⎨特点 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪线⎨ ⎧表示方法 射线⎨ ⎪⎪ ⎪ ⎪ ⎪ 特点⎩ ⎪ 线段 段最短⎨基本事实:两点之间线 ⎪平面图形⎨ ⎪ ⎪线段的中点⎪ ⎪ ⎪ ⎪ ⎧定义 ⎪ ⎪ ⎪ ⎪表示方法 ⎪ ⎪ ⎪角⎪⎨ ⎧互余⎪ ⎪两角的特殊关系 ⎨ ⎪⎩ ⎩角的度量 ⎪ ⎧表示方法 ⎪ ⎪ ⎪基本事实:两点确定一⎪ 条直线 ⎪ ⎪ ⎪特点 ⎪ ⎪ ⎪比较方法⎪ ⎪ ⎪ ⎪ ⎩线段的和、差与画法 ⎪ ⎪ ⎧ ⎧ ⎪ ⎪常见的立体图形 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ 几何图形初步⎨ ⎧表示方法 ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪⎪ ⎪两点之间的距离 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪比较大小的方法 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩互补 ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩。
七年级数学第一章有理数思维导图
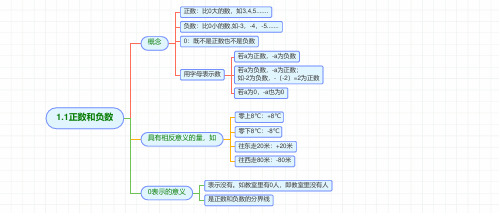
1.1正数和负数概念正数:比0大的数,如3,4,5.......负数:比0小的数,如-3,-4,-5.......0:既不是正数也不是负数用字母表示数若a为正数,-a为负数若a为负数,-a为正数;如-2为负数,-(-2)=2为正数若a为0,-a也为0具有相反意义的量,如零上8℃:+8℃零下8℃:-8℃往东走20米:+20米往西走80米:-80米0表示的意义表示没有。
如教室里有0人,即教室里没有人是正数和负数的分界线1.2有理数1.2.1有理数按意义分整数正整数负整数分数正分数负分数按性质符号分正有理数正整数正分数负有理数负整数负分数1.2.2数轴有原点、正方向、单位长度的一条直线任何有理数都能找到一个点与之对应,右边的数大于左边的数两点间距离:右边点对应的数减左边点对应的数1.2.3相反数只有符号不相同的两个数字互为相反数,a的相反数记为-a0的相反数是0,正数的相反数为负,负数的相反数为正一个数和它的相反数关于原点对称互为相反数的两个数相加等于01.2.4绝对值数轴上表示数a的点与原点的距离叫做数a 的绝对值,写为|a|互为相反数的两个数:绝对值相等两个负数,绝对值大的反而小,绝对值小的反而大若a>0,则|a|=a;若a<0,则|a|=-a;|0|=01.3有理数的加减法1.3.1加法同号两数相加:取相同的符号,绝对值相加;如-3+(-4)=-7异号两数相加:谁绝对值大,就取谁的符号;再用大绝对值减小绝对值;如-5+3=-2互为相反数的两数相加得0,任何数加0等于它本身1.3.2减法减去一个数,等于加上这个数的相反数;即a-b=a+(-b)如:5-(-3)=5+3=8加减混合相反数结合法:互为相反数的两个数相加等于0同分母结合法:把含相同分母的数或可通分的数结合在一起有带分数时先拆分为整数和分数,再结合分数和小数混合时统一为分数或统一为小数同号结合法:把符号相同的加数相结合(-23)-(-18)+(-15)-(+1)+(+23)原式=-23+(+18)+(-15)+(-1)+(+23)=(-23-25-1)+(18+23)=-7凑整法:把和为整数的加数相结合(+6.6)+(-5.2)-(-3.8)+(-2.6)-(+4.8)原式=(+6.6)+(-5.2)+(+3.8)+(-2.6)+(-4.8)=(6.6-2.6)+(-5.2-4.8)+3.8=-2.2分组结合法2-3-4+5+6-7-8+9…+66-67-68+69原式=(2-3-4+5)+(6-7-8+9)+…+(66-67-68+69)=0先拆项后结合(-2-4-6-8...-100)+(1+3+5+7 (99)原式=(-2+1)+(-4+3)+......+(-100+99)=-501.4有理数的乘除法1.4.1乘法两数相乘,同号得正,异号得负,并把绝对值相乘任何数乘0得0多个有理数相乘1.4.2除法除以一个数等于乘以这个数的倒数两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个非0数,等于0;0不能作除数只要一个因数为0则积为0如果因数都不是0,则结果符号根据负数的个数来定:奇负偶正1.5.1有理数的乘方求n个相同因数的积的运算,叫做乘方在aⁿ中,a 叫做底数,n 叫做指数。
初中数学七年级上册思维导图

初中数学七年级上册思维导图一、数的认识1. 整数自然数:0, 1, 2, 3,正整数:1, 2, 3,负整数:1, 2, 3,整数:自然数和负整数的统称2. 分数真分数:分子小于分母的分数假分数:分子大于或等于分母的分数分数的基本性质:分子分母同时乘以或除以同一个非零整数,分数的值不变3. 小数小数的表示方法:整数部分和小数部分小数的性质:小数点向右移动一位,相当于乘以10;小数点向左移动一位,相当于除以10二、数的运算1. 整数的运算加法:将两个整数相加减法:将一个整数从另一个整数中减去乘法:将两个整数相乘除法:将一个整数除以另一个非零整数2. 分数的运算加法:将两个分数的分子相加,分母保持不变减法:将一个分数的分子从另一个分数的分子中减去,分母保持不变乘法:将两个分数的分子相乘,分母相乘除法:将一个分数的分子乘以另一个分数的分母,分母乘以另一个分数的分子3. 小数的运算加法:将两个小数的小数部分相加,整数部分相加减法:将一个小数的小数部分从另一个小数的小数部分中减去,整数部分相减乘法:将两个小数相乘除法:将一个小数除以另一个非零小数三、方程与不等式1. 方程一元一次方程:ax + b = 0(a, b为常数,x为未知数)方程的解:使方程成立的未知数的值2. 不等式一元一次不等式:ax + b > 0 或 ax + b < 0(a, b为常数,x 为未知数)不等式的解集:满足不等式的未知数的值的集合四、函数与图形1. 函数定义:函数是一种特殊的关系,每个输入值对应唯一的输出值表示方法:函数关系可以用函数表达式、函数图像、函数表格等方式表示2. 图形直线:一次函数的图像抛物线:二次函数的图像双曲线:反比例函数的图像五、统计与概率1. 统计数据的收集与整理:收集数据、整理数据、制作统计图表数据的分析与解释:分析数据、得出结论、解释结论2. 概率概率的定义:某个事件发生的可能性概率的计算:根据事件发生的次数和总次数计算概率初中数学七年级上册思维导图六、几何图形的认识1. 点、线、面点:没有长度、宽度和高度的几何元素线:只有长度没有宽度和高度的几何元素面:具有长度和宽度的几何元素2. 平面图形三角形:由三条线段组成的闭合图形四边形:由四条线段组成的闭合图形圆:由一个点到平面上所有点的距离相等的点的集合3. 空间图形立方体:由六个正方形面组成的立体图形圆柱:由两个平行圆面和一个侧面组成的立体图形圆锥:由一个圆面和一个侧面组成的立体图形七、几何图形的性质1. 三角形的性质内角和定理:三角形的内角和等于180度等腰三角形的性质:底角相等,底边上的高、中线、角平分线互相重合直角三角形的性质:直角边上的高、中线、角平分线互相重合2. 四边形的性质平行四边形的性质:对边平行且相等,对角相等,对角线互相平分矩形的性质:四个角都是直角,对边平行且相等,对角线互相平分且相等菱形的性质:四个角都是直角,对边平行且相等,对角线互相垂直平分3. 圆的性质圆的周长公式:C = 2πr(r为圆的半径)圆的面积公式:A = πr²圆的性质:圆心到圆上任意一点的距离都相等八、几何图形的计算1. 三角形的计算三角形的周长:三条边的长度之和三角形的面积:底乘以高除以22. 四边形的计算四边形的周长:四条边的长度之和四边形的面积:根据不同类型的四边形使用相应的公式计算3. 圆的计算圆的周长:2πr圆的面积:πr²九、综合应用1. 解决实际问题利用数学知识解决生活中的实际问题,如计算面积、周长、体积等运用几何知识解决空间布局问题,如设计家具布局、建筑平面图等2. 数学建模将实际问题抽象为数学模型,如建立函数模型、方程模型等利用数学模型解决问题,如预测趋势、优化资源配置等初中数学七年级上册思维导图十、数学思维与方法1. 逻辑推理演绎推理:从一般到特殊的推理过程归纳推理:从特殊到一般的推理过程类比推理:通过比较不同事物之间的相似性进行推理2. 数学建模实际问题抽象:将实际问题转化为数学问题建立模型:选择合适的数学模型来描述问题模型求解:利用数学方法求解模型,得到问题的解答3. 解决问题的策略分析问题:明确问题的目标和已知条件寻找规律:通过观察、实验、推理等方式寻找解决问题的规律制定计划:根据规律制定解决问题的步骤和方法执行计划:按照计划逐步解决问题检验结果:验证解答的正确性,对结果进行评估和反思十一、数学实验与探究1. 数学实验通过实际操作和观察,验证数学结论的正确性培养学生的动手能力和观察能力培养学生的探究精神和创新意识2. 数学探究提出问题:发现问题并提出有意义的数学问题收集信息:查阅资料、进行调查、进行实验等,获取解决问题的信息分析信息:对收集到的信息进行分析和整理提出假设:根据分析结果提出可能的解答或解决方案实验验证:通过实验或推理验证假设的正确性得出结论:根据实验结果或推理结果得出结论十二、数学交流与合作1. 数学交流表达观点:清晰地表达自己的数学观点和思考倾听他人:耐心倾听他人的数学观点和思考互相讨论:与他人进行数学问题的讨论和交流共享资源:分享自己的数学知识和经验,互相学习2. 数学合作分工合作:在解决问题或完成数学任务时,进行合理的分工和合作互相支持:在合作过程中互相支持和帮助共同解决问题:共同面对问题,共同寻找解决方案分享成果:分享合作成果,互相学习和借鉴初中数学七年级上册思维导图一、数与代数1. 实数(1)有理数:包括整数和分数,整数又分为正整数、0和负整数,分数分为正分数和负分数。
七年级上册数学思维导图第一章

七年级上册数学思维导图第一章1. 引言本导图旨在帮助七年级学生理解数学思维导图的概念和用途。
数学思维导图是一种图形化的表达方式,可以帮助学生整理和归纳数学知识,提高数学学习效果。
本导图将介绍数学思维导图的基本概念和使用方法,并提供一些实例帮助学生更好地理解。
2. 数学思维导图的定义数学思维导图是一种将数学概念、方法和问题用图形的方式进行组织和展示的工具。
它通过使用不同颜色和形状的节点和线条,将相关的概念和关系连接在一起,形成一个有机的整体。
数学思维导图可以帮助学生更直观地理解数学概念,提高记忆和应用能力。
3. 数学思维导图的原则在使用数学思维导图时,有一些原则需要注意:•简洁性:导图应尽量简洁明了,避免过多的文字和图形,以减少学生的认知负荷。
•逻辑性:导图应按照逻辑顺序进行组织,将相关内容放在一起,便于理解和记忆。
•层次性:导图可以分层展示不同的概念和关系,从整体到细节逐步展开。
•联系性:导图应突出不同概念之间的联系和关系,通过线条和箭头表示。
4. 数学思维导图的使用方法数学思维导图的使用方法非常灵活,可以根据具体需求进行调整。
下面介绍一种常见的使用方法:步骤一:确定中心主题首先,在导图的中心位置写下主题或问题,这是整个导图的核心。
步骤二:添加分支接下来,在主题周围画几个分支,每个分支代表一个相关的概念或问题。
通过线条将分支与主题连接起来。
步骤三:增加分支的分支在每个分支的旁边再画几个小分支,代表子概念或问题。
同样使用线条将它们与主要分支连接起来。
步骤四:添加关系和示例使用箭头表示不同分支之间的关系,例如,表示因果关系、相互作用关系等。
还可以在每个分支下面添加一些例子,以帮助更好地理解与应用。
步骤五:细化和完善根据需要,可以继续细化和完善导图,添加更多的分支和子分支,以及详细的说明和示例。
5. 数学思维导图的实例下面是一个关于数学运算的思维导图示例:- 主题:数学运算- 分支:加法- 子分支:带进位加法- 子分支:不带进位加法- 分支:减法- 子分支:借位减法- 子分支:不借位减法- 分支:乘法- 子分支:竖式乘法- 子分支:列式乘法6. 总结数学思维导图是一种有助于学生整理和归纳数学知识的图形化工具。
七年级数学思维导图PPT课件
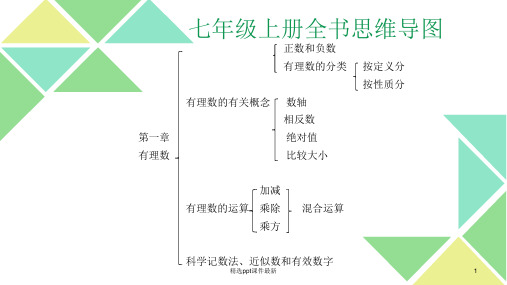
七年级上册全书思维导图
正数和负数 有理数的分类 按定义分
按性质分 有理数的有关概念 数轴
相反数 绝对值 比较大小
加减 有理数的运算 乘除
乘方
混合运算
科学记数法、近似数和有效数字
精选ppt课件最新
1
第二章 整式的加减
用字母表示数 整式 单项式
多项式
同类项 整式的加减 合并同类项
去括号规律 整式加减的运算法则
平面图形
两点之间线段最短
角的度量
角 角的比较与运算、角的平分线
余角和补角
精选ppt课件最新
4
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
精选ppt课件最新
2
第三章 一元一次方程
方程 概念 一元一次方程
等式的性质 去分号 去括号
解一元一次方程的步骤 移项 合并同类项 系数化为1
列Байду номын сангаас元一次方程解应用题
精选ppt课件最新
3
点、线、面、体
立体图形 从不同方向看立体图形
第四章
展开立体图形
几何图形
线段的大小比较
直线、射线、线段 两点确定一条直线
