调压室涌波水位计算
简单式和阻抗式调压室的水位波动计算
简单式和阻抗式调压室的水位波动计算调压室水位波动计算常用的方法有解析法和逐步积分法。
解析法较简便，可直接求出最高和最低水位，有时精度差，不能求出波动的全过程，常用以初步决定调压室的尺寸。
逐步积分法是通过逐步计算以求出最高和最低水位，其最大优点是可以求出波动的全过程和求解复杂的问题。
逐步积分法可分为图解法和列表法(数学积分法)，两者原理相同。
图解法简便，醒目，列表法较精确。
逐步积分法一般用于后期的设计阶段。
近年来随着电子计算机的发展，在工程设计中已越来越多地采用电算法，以同时解决调压井涌波、水锤压力及机组速率上升的复杂计算，特别是研究各参数的影响时，电算法更为优越。
下面我们主要介绍解析法和图解法。
电算法则在第九节中介绍。
一、水位波动计算的解析法（一）丢弃全负荷情况当丢弃全负荷后，水轮机的流量Q=0,连续性方程式(15-3）变为在水流进出调压室时，如考虑由于转弯、收缩和扩散引起的阻抗孔口水头损失K,则动力方程式(15-4)变为式中，其中为水头损失系数（为一常数）。
,其中和分别为流量流过引水道和进出调压室所引起的水头损失。
令，则，，将以上关系代入式(15-7)，两边除以,并令，则得将V=y代入式（15-6），并和式（15-8）消去dt，得再令，即Z=SX，dZ=SdX，代入上式，得系数S具有长度因次，用以表示“引水道—调压室”系统的特性。
X和Xo均为无因次的比值。
式（15-10）为变数X和的一阶线性微分方程式，积分后得积分常数C可由起始条件决定。
波动开始时，t=0，V=，即y=1,Z=,X=Xo,以y=1,X=Xo代入上式，得故（15-10）的最后解答为对于调压室的任何水位（用X表示），可用上式算出与之对应的引水道的流速V = y，也可以进行相反的计算，但不能求出流速V与水位X对于时间t的关系，因此，不能求出水位波动过程。
1.最高水位的计算欲求波动的最高水位，只需求出即可。
在水位达到最高时，V=0，即y=0，代人式(15-11)得两边取对数得式中的符号在静水位以上为负，在静水位以下为正。
调压室水力计算
调压室的水力计算1. 调压室断面计算当上游死水位，下游为最低水位，最小水位H min=188.9m，三台机满发，引水道糙率取最小值，压力管道糙率取最大值，通过水轮机的流量为57m3s⁄，则此时的引水隧洞水头损失的计算如表格1，压力钢管水头损失的计算如表格2。
引水道应选可能的最小糙率0.012，压力管道应选择可能的最大糙率0.013。
表格1引水隧洞水头损失表表格2压力钢管水头损失表F Tℎ>Lf2αgH1=Lf2αg(H0−ℎw0−3ℎwT)=45.548m2其中H0——最小水头损失，H0=188.9m；ℎw0——引水隧洞损失，ℎw0=17.802+0.296=18.098；ℎwT0——压力管道水头损失，ℎwT=3.110+2.805=5.915m；L——引水隧洞长度，12662m；g——重力加速度，g=9.81m/s2 f——引水隧洞面积，16.62m2。
α——引水道阻力系数v0=Qf=5716.619=3.43m s⁄α=ℎw0v02=18.0983.4302=1.5385为了保证大波动的稳定，一般要求调压室断面大于托马斯断面，初步分析时可取（1.0~1.1）F Tℎ，作为调压室的设计断面。
这里选取D=7.8m，则系数k为：F k=47.784k=F k/F Tℎ=1.052. 最高涌波水位计算按正常蓄水位时共用同一调压室的三台机组全部满载运行瞬时丢弃全部负荷（即流量由Q max=57减至流量Q=0）作为设计工况。
引水隧洞的糙率取尽可能的最小值（能耗少，涌波高）。
n=0.012引水道损失由表格1和表格2得：ℎw0=ℎw0程+ℎw0局=17.802+0.296=18.098mv0为时段开始时管中流速v0=Qf=3.43m s⁄；f为引水隧洞断面面积。
F为调压井断面面积，145.267m2；引水隧洞长L=12662m，g=9.81m s2⁄得引水道—调压室系统的特性系数。
λ=Lfv022gFℎw0=12662×16.62×3.4322×9.81×47.784×18.098=145.89令X0=ℎw0λ=0.124，X=zλ，则要求最高涌波水位z max，只需要求出X max=z maxλ即可。
基于MathCAD的调压室涌波计算
收稿 日期 ： ２ ０ １ ３ ￣６ － ２ ０
作 者简介： 胡 刚， 男， 湖北英山人 ， 主要从事水工设计方面工作 。
大， 而通过 Ｍａ ｔ ｈ Ｃ Ａ Ｄ的求解 函数很好地解决 了这个问题。
首 先 利 用 Ｍａ ｔ ｈ Ｃ Ａ Ｄ 的“ ｘ —Ｙ 绘 图”功 能 快 速 得 到
该方法优点是 比较简便 ， 主要通 过查 表法进 行 ； 缺点是 存在
一
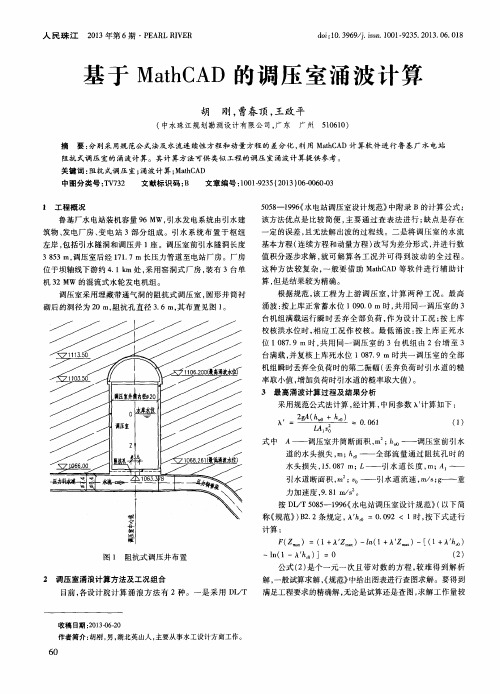
鲁基厂水 电站装 机容量 ９ ６ ＭＷ， 引水 发电系统 由引水建 筑物 、 发电厂房 、 变 电站 ３部 分组成 。引水 系统布 置于 枢纽 左岸 ， 包括引水隧洞 和调压井 １座 。调压 室前 引水隧洞长度
定 的误差 ， 且无法解 出波的过程线 。二是将调 压室的水流
０ Ｕ ． ０ ６ １
㈩ １，
Ｌ Ａ１
式 中 Ａ——调压 室井 筒断面积 ， ｍ ；
——调压 室前 引水
道 的水头损失 ， ｍ； ｈ —— 全部 流量通过 阻抗孔 时 的 水头损失 ， １ ５ ． ０ ８ ７ ｉ Ｔ Ｉ ； Ｌ —— 引水 道 长度 ， ｌ ｒ ｌ ； Ａ ． —— 引水道断 面积 ， ｍ ； —— 引水道 流速 ， ｍ／ ｓ ； ｇ ——重
人 民珠 江
２ ０ １ ３年第 ６期 ・ Ｐ Ｅ Ａ Ｒ Ｌ Ｒ Ｉ Ｖ Ｅ Ｒ
ｄ ｏ ｉ ： １ ０ ． ３ ９ ６ ９ ／ ｊ ． ｉ ｓ ｓ ｎ ． １ ０ ０ １ — ９ ２ ３ ５ ． ２ ０ １ ３ ． ０ ６ ． ０ １ ８
基 于 Ｍａ ｔ ｈ Ｃ Ａ Ｄ的调 压 室 涌 波 计 算
力加速度 ， ９ ． ８ １ ｍ／ ｓ 。
按 Ｄ ｌ ｆＴ ５ ０ ８ ５ －１ ９ ９ ６ （ 水 电站调压 室设计规 范》 （ 以下简
按规范计算阻抗式调压室涌波计算
0.8
c
一般取0.6～0.8
c
2
取阻抗孔直径：
=
10.179 h = 15.087
c0
1
c0
0
3、求λ
λ :=
2 ⋅ g ⋅ A ⋅ (h + h L⋅A ⋅ υ 2 λ ⋅ h = 0.917
w0 1 0 c0
c0
)
=
0.061
λ⋅
h <1
c0
4、求A0
Aபைடு நூலகம்
0
:=
( 1 + λ ⋅ hw0) − ln ( 1 − λ ⋅ hc0) = 3.982 ) − ln ( 1 + λ ⋅ Zmax) − A0
n := 0.014
1
d = 77.249 谢才系数：C := n1 ⋅ 4 2 h := 642⋅ Q 2 ⋅ L 5 = 1.528 C ⋅π ⋅d ⑵、喷混凝土支护段：d := 7.4
1 1 1 w01 0 1 1 1 2
1 6
L := 3084
2
n := 0.0305
2
d = 36.327 谢才系数：C := n1 ⋅ 4 2 h := 642⋅ Q 2 ⋅ L 5 = 13.405 C ⋅π ⋅d 所以，h := h + h + 0.5 = 15.432
阻抗式调压室稳定断面及最高、 阻抗式调压室稳定断面及最高 、最低涌波计算( 最低涌波计算(按规范计算) 按规范计算 )
一、稳定断面面积计算 原始恒定流量：Q := 140.1 1、Q 在调压室前水道内的水头损失h 计算，糙率取平均值 ⑴、钢筋混凝土衬砌段：d := 6.4 L := 769
0 0 w0 1 1
调压室水力计算分解
调压室的水力计算1. 调压室断面计算当上游死水位，下游为最低水位，最小水位H min=188.9m，三台机满发，引水道糙率取最小值，压力管道糙率取最大值，通过水轮机的流量为57m3s⁄，则此时的引水隧洞水头损失的计算如表格1，压力钢管水头损失的计算如表格2。
引水道应选可能的最小糙率0.012，压力管道应选择可能的最大糙率0.013。
表格1引水隧洞水头损失表表格2压力钢管水头损失表F Tℎ>Lf2αgH1=Lf2αg(H0−ℎw0−3ℎwT)=45.548m2其中H0——最小水头损失，H0=188.9m；ℎw0——引水隧洞损失，ℎw0=17.802+0.296=18.098；ℎwT0——压力管道水头损失，ℎwT=3.110+2.805=5.915m；L——引水隧洞长度，12662m；g——重力加速度，g=9.81m/s2 f——引水隧洞面积，16.62m2。
α——引水道阻力系数v0=Qf=5716.619=3.43m s⁄α=ℎw0v02=18.0983.4302=1.5385为了保证大波动的稳定，一般要求调压室断面大于托马斯断面，初步分析时可取（1.0~1.1）F Tℎ，作为调压室的设计断面。
这里选取D=7.8m，则系数k为：F k=47.784k=F k/F Tℎ=1.052. 最高涌波水位计算按正常蓄水位时共用同一调压室的三台机组全部满载运行瞬时丢弃全部负荷（即流量由Q max=57减至流量Q=0）作为设计工况。
引水隧洞的糙率取尽可能的最小值（能耗少，涌波高）。
n=0.012引水道损失由表格1和表格2得：ℎw0=ℎw0程+ℎw0局=17.802+0.296=18.098mv0为时段开始时管中流速v0=Qf=3.43m s⁄；f为引水隧洞断面面积。
F为调压井断面面积，145.267m2；引水隧洞长L=12662m，g=9.81m s2⁄得引水道—调压室系统的特性系数。
λ=Lfv022gFℎw0=12662×16.62×3.4322×9.81×47.784×18.098=145.89令X0=ℎw0λ=0.124，X=zλ，则要求最高涌波水位z max，只需要求出X max=z maxλ即可。
第十五章 调压室5
第十五章调压室第五节双室式、溢流式和差动式调压室的水位波动计算一、双室式和溢流式调压室双室式调压室适用在水电站的水头较高和水库工作深度较大的情况下，水头高则要求调压室的稳定断面小（详见本章第六节），因此竖井可以采用较小的直径。
水库的工作深度大，则要求调压室具有较大的高度，采用双室式调压室，只需要增加断面不大的竖井高度即可。
溢流式常和双室式结合使用，在上室中加设溢流堰，如图15-3(d)所示。
在丢弃负荷时，水位开始迅速上升，达到溢流堰后开始溢流，在最高水位附近保持一段时间后，才开始缓慢地下降，如图15-12所示。
由于上室的水量绝大部分是经溢流堰流出的，其重心进一步提高了，同时最高水位受溢流堰限制，因此，在相同的条件下，所需上室的容积减小了，所以，设置溢流堰能改善双室式调压室的工作条件。
图15-12 丢弃负荷后竖井及上室水位变化过程双室式调压室，只宜于做成地下结构，其上下室可做成各种形式。
图15-13为一双室式调压室的实例。
上室呈长槽形，在岩石中开挖而成，因岩石较好，顶部不加衬砌。
上室有进出口与外部相通，作为交通与通气之用。
上室的轴线和引水道的轴线不在一个铅直面上，交角27°30'。
盲肠形的下室具有圆形横断面，其轴线与引水道垂直，这样对结构较为有利；下室分两段，对称布置在引水道的两侧，这样既减小了下室的长度又使水流对称。
图15-13 双室式调压室（尺寸：m）上室的底部应在最高静水位以上，这样才能充分发挥上室的作用。
下室的顶部应在最低静水位以下，其底应在最低涌波水位以下。
上室和下室的底部应有不小于1％的坡度倾向竖井，以便放空水流；下室的顶部应有不小于1.5％的反坡，当室内水位上升时，便于空气逸出。
对下室的容积、高程和形状的设计应特别仔细，不应满足于一般计算，必要时要进行模型试验。
某水电站调压室模型试验表明：细而长的下室工作不够灵敏，当竖井水位迅速下降时，室内要形成一个较大的水面坡降后才能向竖井补水，速度迟缓，迫使竖井水位低于下室内水位，容易使引水道进入空气；当竖井水位回升时，同样要形成一个反向的水面坡降才能使室内充水，迅速上升的水位很快将洞口淹没，致使下室中遗留的空气从水底逸出，水流极不稳定，因此，下室应尽量做成粗而短或对称布置在引水道的两侧。
用随机微分方程模型求解调压室涌波
（一２ ｌ） ｚ ｎ Ｌ １
ｄ ＝一 Ｆ ｔ一
（ ５ ）
＼／ （） Ｖ ６
初始 条件 同前 ．
２ 随 机 模 型
对于给 定 的水 电站 水力单 元而 言 ， ， Ａ， ｇ和 Ｑ 都为确定 量 ． ￡ 尺， Ｆ， ｆ 引水 道糙率 ｎ受 隧洞 衬砌 材料 、 工 施 质量 、 水流 流态 、 流长期 冲蚀 的时 间效应 、 水 量测 误差等 多 种 因素 的影 响 ， 而具 有较 大 的不 确定 性 ． 因 由文献 ［］ ７假设糙 率 ｎ服从任 意三 角形分 布 ， 概率 密度 函数为 其
（ ２ ）
（） ３ （） ４
Ｑ： ＋ 警 。 Ｆ
初始条 件 （ ）： Ｑ ０ ｏ
／ ｔ
）：
ｎ
ｖ（） ２ｏ
式 中：
引水 道流 速 （ 以水库 向调 压 室方 向为 正 ） ｚ ； —— 调 压 室 瞬时 相对 水 位 （ 以库 水 位 ｚ Ｒ为 基准 ， 向
下为正 ） 凡， ， ， —— 引水 道糙 率 、 ； Ａ 长度 、 水力 半径及 断 面面积 ； —— 调 压室 断面 面积 ． Ｆ
设 Ｑｆ 为机 组满 负荷 时 的引用流量 ， ｏ Ｑ 分 别为 机组 负荷 变化前 后 的引用 流 量 ， ， 分 别 为机组 负 Ｑ ，。 ｍｏｍ・
收 稿 日期 ＿０７ ０ —０ ． ０ — ３ ３ ２ ’
基金项 目： 武汉大学水 资源与水 电工程科学国家重点实验 室开放￣
（ｏ ６ ｏｏ ２ｏ Ｂ ３ ）
作者简介 ： 朱永忠（９８ ）男 ， １６ 一 ， 江西瑞昌人 ， 副教授 ， 博士 ， 主要从事随机过程及水电站水击 和调压室涌浪的随机研究
维普资讯
调压室水位波动计算
调压室水位波动计算1.计算说明1.1 最高涌波水位计算上游库水位应取正常发电可能出现的最高水位，引水道的糙率应取可能的最小值（使水头差最小），计算工况一般按丢弃全负荷考虑。
1.2 最低涌波水位计算上游库水位应取可能的最低水位，引水道糙率取可能最大值（阻力大，供水慢）。
在初步设计阶段，设计工况采用其余机组均满负荷运行，而最后一台机组投入运行的情况，但最后加入的容量应不小于三分之一，同时应该计算库水位丢弃全负荷后水位波动的第二振幅，以检验是否低于增荷时的最低涌波水位，选择最大值作为调压室的最低涌波水位。
1.3 调压室的顶高程应为最高涌波水位加安全超高，一般为2—3米；压力钢管进口底高程应距最低涌波水位至少1米。
2.计算公式及符号说明2.1 计算最高涌波水位max max 0)1(X X In X ++-=22w gFh Lfv =λ λwo h X =0 λz X -=式中：L ——引水隧道的长度f ——引水隧道横截面面积 v ——引水道的初始速度，m/s F ——调压室横断面面积0w h ——流量为Q 时引水道的水头损失 根据此式求得λmaxmax z X -=，即可得到m ax Z ，由水库正常高水位减去m ax Z 则为水库最高涌波水位。
2.2 计算最低涌波水位2.2.1丢弃全负荷产生的第二涌波水位 )1()1(max max 22X In X X In X -+=-+ 式中X 2为负值，而X max 为正值。
2.2.2 增加负荷时的最低涌波水位62.00min/2)/1)(1)(9.0/05.0275.0(1w w h m m m h z λεεεε=---+-+=式中：m ——负荷系数，小于1.Ɛ——表示引水道—调压室系统的特性根据计算结果，由水库最低水位减去min Z 即为最低涌波水位3.水库水位波动计算由上述计算可知，最高涌波水位：66.785+1279.0=1345.785(m) 最低涌波水位：1279.0-26.178=1252.822 (m)因此考虑安全超高，则调压室的顶高程为：1345.785+3=1348.785（m ） 同时调压室进水口底板应低于最低涌波水位1米，则压力钢管进口顶高程1252.822-1=1251.822(m).表一：最高涌波水位表二：第二波动振幅表三：增加负荷最低水位。
水电站调压室涌浪水位多种计算方法比较
水电站调压室涌浪水位多种计算方法比较
陈玲;鞠小明;杨济铖
【期刊名称】《中国农村水利水电》
【年(卷),期】2013()9
【摘要】水电站调压室水位波动过程有很多较为成熟的计算方法,这些方法在实际工程设计中均有应用。
以某工程资料为实例,分别采用解析法、数值积分法和特征线法,计算调压室水位波动的最高、最低涌浪水位以及波动过程,论述了调压室水位波动过程不同计算方法之间的区别和联系,给出了具体的计算公式和方程,以及不同计算方法的适用条件和计算要求。
【总页数】4页(P158-161)
【关键词】水电站;调压室;涌浪水位;波动过程
【作者】陈玲;鞠小明;杨济铖
【作者单位】四川大学水利水电学院;四川大学水力学与山区河流开发保护国家重点实验室
【正文语种】中文
【中图分类】TV732.5
【相关文献】
1.水电站输水系统相继甩负荷下调压室涌浪叠加研究 [J], 陈胜;张健;俞晓东
2.水电站调压室涌浪最不利叠加时刻的研究 [J], 程永光;陈鉴治;杨建东
3.螺丝湾水电站调压室涌浪的试验研究 [J], 张绍春;李师贤
4.某水电站上下游双调压室涌浪计算初探 [J], 石刘宏幸; 刘慧; 彭聃
5.CFD在调压室涌浪水位模拟中的应用 [J], 刘飞;杨建东;李进平
因版权原因，仅展示原文概要，查看原文内容请购买。
水电站调压室设计规范DLT5058_1996
水电站调压室设计规范Specification for design of surge chamber of hydropowerstation中华人民共和国电力行业标准水电站调压室设计规范主编部门：电力工业部华东勘测设计研究院批准部门：中华人民共和国电力工业部中华人民共和国电力工业部关于发布《水电站调压室设计规范》电力行业标准的通知电技［1996］733号各电管局，各省、自治区、直辖市电力局，水电水利规划设计总院，各有关单位：《水电站调压室设计规范》电力行业标准，经审查通过，批准为推荐性标准，现予发布。
其编号为：DL/T5058－1996该标准自1997年5月1日起实施。
请将执行中的问题和意见告水电水利规划设计总院，并抄送部标准化领导小组办公室。
1996年10月31日目次1总则2术语、符号3调压室的设置条件及位置选择4调压室的基本布置方式、基本类型及选择5调压室的水力计算及基本尺寸的确定6抽水蓄能电站调压室的设计7调压室的结构设计、构造、观测及运行要求附录A压力水道水头损失计算公式附录B调压室的涌波计算公式附录C抽水蓄能电站水泵工况断电、导叶拒动时的调压室涌波计算方法本规范用词规定附加说明1总则1.0.1水电站调压室是压力水道系统中一项重要建筑物，为体现国家现行的技术经济政策，积极慎重地采用国内外先进技术和经验，统一调压室设计的标准、要求，特制定本规范。
1.0.2本规范适用于大、中型水利水电枢纽工程中常规水电站和抽水蓄能电站调压室设计，小型水电站的调压室设计可参照执行。
1.0.3水电站调压室设计应根据地形、地质情况、压力水道的布置、机电特性和运行条件等资料，经综合论证，做到因地制宜、经济合理、安全可靠。
1.0.4水电站调压室设计除必须遵守本规范的规定外，还应符合SDJ12—78《水利水电枢纽工程等级划分及设计标准(山区、丘陵区部分)》(试行)及补充规定、SD134—84《水工隧洞设计规范》、SDJ173—85《水力发电厂机电设计技术规范》(试行)、DL/T5057—1996《水工混凝土结构设计规范》、SDJ10—78《水工建筑物抗震设计规范》(试行)等现行的国家、行业有关标准与规定。
抽水蓄能电站调压井最低涌浪的粗略计算公式
假 定调 压室 的水 位波 动过 程可 以用 正 弦 函数 来
描 述
＝
Ａｓ ｔ ｎ ｔ ｉ ｏ
ｆ） ７
令 Ａ ＝
式（） 边对 时问 ｔ 导得 ７两 求
将 以上各 积分 值代入 并整 理得 ：
ｄ ＝ ｏ（ ｔ Ａｗｃ ＳＪ ｃ （） 、， ８
ｇ Ａ２ Ｆ ＋
一 】后 ￣ ｖ ＝ （＋ ） ｆｏ Ｏ Ｌ ２
推 导 ， 图 如 图 １所 示 ： 简
假定 水泵 流量 由 Ｑ 变至 Ｑ ，令 Ｑ ＝ ｋＱ ， ｏ ｏ 。－ ｏＱ 水 泵 断 电前 引 水 道 的 流量 值 ， 泵 断 电后 压 力 管 道 Ｑ水
逆流 的 流量 值 ，则 以调 压 井底 部 与输 水 道节 点 为研 究对象 ， 由水 流 的连续 性方 程得 ：
水 泵 突然 断 电又 偶 遇机 械 系统 故 障 的工况 。在初 步 设计 阶 段 由于 种 种 原 因没 有 条 件 对 所 有 工 况 的水 力一 械过 渡过 程 进行 数值 模 拟 汁算 时 ， 以应用 下 机 可 面从 水 力 学 的基 本 方 程 导 出 的 公 式 进 行 粗 略 的估 算 ．为输 水 系统 的布置 及 调压 井高 程 和 断面 积 提供 设 计依 据 ． ． 本 文先 以抽 水 蓄能 电 站输 水 发 电系 统采 用 单元 供 水 方 式 时上游 调 压井 的水位 波 动过 程 为模 型 进行
械 系 统 故 障 时 上 游 调 压 室 最 低 涌 浪 水 位 的 算 公 式 ， 推 广 至下 游 调 室 和 联 合 供 水 或 分 组 供 水 方 式 。 没 有 条 并 在 件 进 行 数 值 计 算 之 前 该 公 式 不 失 为 一 个 很 实 用 的 粗 略 计箅 公 式 。 关键词 调压室 流体力学 粗 略计 算 公 式
调压室涌波最高水位随机分析的显式计算方法
Method of explicit calculation for stochastic analysis of the highest water level in surge tank
ZHU Yong2zhong1 , FANG Yu2ting2 , SUO Li2sheng3 (1. College of Sciences , Hohai University , Nanjing 210098 , China ; 2. East China Yixing Pumped Storage Power Co. Ltd , Yixing 214205 , China ; 3. College of Water Conservancy and Hydropower Engineering , Hohai University , Nanjing 210098 , China)
Z1 G.
a . 确定性模型求解. 假设水轮机导叶瞬时全关 ,引水道糙率 n 取可能的最小值 n = 01012 ,利用调压室涌 波计算的解析式[4]可解得最高涌波为 45171 m. 因此 ,调压室最高水位 Z1 G = 710 m + 45171 m = 755171 m. 采用 龙格Ο库塔数值积分 ,求得最高涌波水位为 755169 m.
dV dt
=
g L
Z-
n2 L R4/ 3
V
V
(5)
dZ dt
=-
f F
V
+
m1 Qf F
(6)
初始条件同前.
2 随 机 模 型
对于给定的水电站水力单元而言 , L , R , f , F , g 和 Qf 为确定量 , 引水道糙率 n 的取值变幅很小 , 为方便
海甸峡水电站调压室稳定断面选定及其涌波计算
件 的一种可靠 措施 。调压 室稳定 断面积 的选择 涉及 较 多影响 因素 。合 适 的调 压室稳 定断 面积不但 能保
项 目名称
Ｉ
该 电站需设 上 游调压 室 。引水系 统水头 损失计算 见
表 １ 。
糙 率 取 值 混 凝 士 钢 管
ｏｏ４ ． １ ０Ｏ２ ． １
表 １ 引水 系统 水 头 损 失 计 算成 果表
ＯＯ６ ．１ ＯＯ２ ．１
ｏｏ３ ．１ ＯＯ １ ．１
用于增加负荷时的涌波计算 用于丢弃负荷时的涌波计算
作 者 简介 ： 明锋 （ ９ ９年 一） 男 ， 肃 兰 州 人 ， 王 １７ ， 甘 工程 师 。
・
４ ・ ４
科研与 管理 ２ ２ 调压 室稳定 断面面积 计算 ．
１ 概 述
海 甸峡水 电站 位 于甘肃 省 临洮 县 西 南 约 ３ ｋ ８ ｍ
的洮河 干流 上 ，是 洮 河水 能 梯 级开 发 的第 ２ １个 梯
证水 位波动 的快 速衰减 ，而且 能够 提高水 电站运 行 的稳 定性 和供 电质量 。调压 室稳定 断面积 的最优 选
择 ，拟根 据具 体情况采 用 电算 法对 引水 系统作小 波
ＴＶ ３ ． 【 献 标 识码 】 Ｂ 【 章 编 号 】 １ ７ —２ ６ （ ０ １ ２ Ｏ ４ ０ ７２５ 文 文 ６ ２ ４ ９ ２ １ ）０ —０ ４ — ３
１ ． ９ ９ ｊ ｉｓ ． ６ ２ ２ ６ ． ０ １ ０ ． １ ０ ３ ６ ／．ｓｎ １ ７ — ４ ９ ２ １ ． ３ ０ ４
科 研与管 理
水利 规划 与设计
２１ ０ １年 第 ３ 期
海甸峡水 电站 调压室稳定断 面 选 定及其 涌波计算
调压室水力计算的电算法简介
调压室水力计算的电算法简介电算法与常用的解析法和图解法相比，具有计算理论严密，简化假设少，速度快，精度高，可以计算不同类型的调压室在各种工况下的涌波全过程并可与水锤、机组转速变化联合求解等许多优点。
尤其在研究某参数对调压室水位变化过程的影响时，电算法更为便利。
进行调压室水位波动计算时，以水轮机、阀门的出流方程作为边界条件，从某种已知初始状态开始，采用四阶龙格-库塔数值积分法求解调压室水流连续方程和隧洞水流动力方程。
本节仅介绍阻抗式、简单式调压室的水位波动计算，给出IBM-PC/XT机FORTRAN语言的计算程序及计算实例。
对程序稍加修改，便可用于某些布置方式较特殊的调压室波动计算。
一、调压室水位波动的基本微分方程调压室的基本方程为：.连续方程2.动力方程式中Q——隧洞中的流量；——压力管道中的流量；F——调压室的截面积；Z——调压室水位；——上游水库水位；K——调压室阻抗水头损失系数；——调压室中的流量，以进人调压室时为正；R——隧洞的沿程损失和局部损失系数；g——重力加速度；A——隧洞的截面积；L——隧洞的长度。
如已知出流变化规律，则，可以根据四阶龙格-库塔法来逐步求解式(15-53)和式(15-54）。
二、龙格-库塔法计算公式如已知t时刻的、值，则可以根据以下公式来求t十△t时刻的、之值。
三、程序框图程序框图如图15-25所示。
图15-25 计算框图四、程序中所用符号的意义NS——调压室高程—截面曲线已知点数。
ZA (I, J)——调压室高程—截面曲线。
共I行，每行二列，分别为一个高程值及相应的调压室截面积。
ZA(I，1)为高程，ZA(I，2)为面积。
HR——上游水库水位，m。
TS——水轮机导叶或阀门关闭或开启时间，s。
KI——水流流进调压室时的阻抗系赦，即为中的系数，单位为。
K0——水流流出调压室时的阻抗系数，。
Q0——起始流量，。
QE——终止流量，。
Z——起始时调压室中的水位，m。
L——从水库到调压室处的引水隧洞长度，m。
差动式调压室甩荷时水位波动以及大井面积和有效阻抗孔面积的计算方法
& ’ B
再设
? ?
水 ! 动 ! 力 ! 学 ! 研 ! 究 ! 与 ! 进 ! 展 !!!!!!!!!" . 年第 $ 期
’ S ’S S! S 2" S 2 2 2 $ $ $ S * S * S * S 2 S * ’ ’"" ! 2 #S 2 ’S 2 $ S 2 " S 2
将上式代入式 ! " 得 B S! " ’"" ’" $"" 2 2 ’1 "2 S 2 上式也可以写成
" " " " " #" $ ) ! ( % #" 1! !- " ! " "! ", + 1 &- " * "
1 !-"! &
!
"
! " # .
! " # 上式即为水位第一 次 向 上 波 动 时 调 压 室 最 高 涌 波 水 位的计算式 * 下面推求当调压室水位上升到最高时 # 调压室第二振幅的计算公式 * ! " # #
$ $ D 6!,ED F G > H F < I : 2% * I > G < I : 27 < > L & G !!4 !!4 J J K
" % $ % # M G < I2 I G N & ’ O G P LC & H F I * + * M G < IA # ? @$ ; F G I < =* J =
! " # B
+& #则由上式得 ,* "% + &" " .$ $ " -" , 1" *
调压室水位波动计算
调压室水位波动计算1.计算说明1.1 最高涌波水位计算上游库水位应取正常发电可能出现的最高水位，引水道的糙率应取可能的最小值（使水头差最小），计算工况一般按丢弃全负荷考虑。
1.2 最低涌波水位计算上游库水位应取可能的最低水位，引水道糙率取可能最大值（阻力大，供水慢）。
在初步设计阶段，设计工况采用其余机组均满负荷运行，而最后一台机组投入运行的情况，但最后加入的容量应不小于三分之一，同时应该计算库水位丢弃全负荷后水位波动的第二振幅，以检验是否低于增荷时的最低涌波水位，选择最大值作为调压室的最低涌波水位。
1.3 调压室的顶高程应为最高涌波水位加安全超高，一般为2—3米；压力钢管进口底高程应距最低涌波水位至少1米。
2.计算公式及符号说明2.1 计算最高涌波水位max max 0)1(X X In X ++-=22w gFh Lfv =λ λwo h X =0 λz X -=式中：L ——引水隧道的长度f ——引水隧道横截面面积 v ——引水道的初始速度，m/s F ——调压室横断面面积0w h ——流量为Q 时引水道的水头损失 根据此式求得λmaxmax z X -=，即可得到m ax Z ，由水库正常高水位减去m ax Z 则为水库最高涌波水位。
2.2 计算最低涌波水位2.2.1丢弃全负荷产生的第二涌波水位 )1()1(max max 22X In X X In X -+=-+ 式中X 2为负值，而X max 为正值。
2.2.2 增加负荷时的最低涌波水位62.00min/2)/1)(1)(9.0/05.0275.0(1w w h m m m h z λεεεε=---+-+=式中：m ——负荷系数，小于1.Ɛ——表示引水道—调压室系统的特性根据计算结果，由水库最低水位减去min Z 即为最低涌波水位3.水库水位波动计算由上述计算可知，最高涌波水位：66.785+1279.0=1345.785(m) 最低涌波水位：1279.0-26.178=1252.822 (m)因此考虑安全超高，则调压室的顶高程为：1345.785+3=1348.785（m ） 同时调压室进水口底板应低于最低涌波水位1米，则压力钢管进口顶高程1252.822-1=1251.822(m).表一：最高涌波水位表二：第二波动振幅表三：增加负荷最低水位。
例析地下双室式调压井涌波水位计算
例析地下双室式调压井涌波水位计算1. 电站引水系统布置概况该电站引水系统采用一洞（管）三机的布置方式，引水系统建筑物布置在左岸，包括电站进水口、引水隧洞、调压井、压力管道等。
设计引用流量在不考虑电站综合利用（城市供水、灌区供水）流量（3.97m3/s）时为56.6m3/s，考虑电站综合利用时引用流量时为60.57m3/s。
进水口为岸塔式，底板高程1837.00m；塔顶高程为1900.00m，塔高63m。
塔前正常蓄水位EL.1895.000m，设计洪水位EL.1895.429m，校核洪水位EL.1896.301m，死水位EL.1848.000m。
引水隧洞为有压隧洞，长度1.678km，洞径4.4m；调压井为地下双室式；钢管道采用全埋管方式布置，主管长446.532m，内径4.0m，剖面上采用两平一斜段布置，为一管三机供水。
2. 计算采用基本参数（1）上游库水位正常蓄水位：1895.000m设计洪水位：1895.010m校核洪水位：1895.370m死水位：1848.000m（2）装机台数：3台（3）设计引用流量不考虑下游生态供水，仅发电，引用流量为56.6m3/s，单台机引用流量：18.867m3/s。
考虑下游生态供水，引用流量为60.57m3/s，单台机引用流量：20.19m3/s。
（4）流道参数引水隧洞断面为圆形，直径4.4m，全长1639m，含进水口段全长1678.375m。
压力管道主管、支管断面均为圆形，主管直径4m，全长447.637m，支管直径2.2m，长约30m。
3. 调压井稳定断面面积计算计算时，先计算出自水库至调压室水头损失系数α值，再计算出调压井水位波动所需最小断面面积，各项参数取值及具体计算成果详见表1。
调压井竖井断面采用圆形，根据上述托马稳定断面计算成果，调压井竖井直径初拟采用D=8m。
4. 调压井最高涌波水位计算4.1 最高涌波计算计算工况：上游水库正常蓄水位1895.000m，全部机组瞬时丢弃全部负荷。
阻抗式调压室甩负荷涌浪计算显式公式
阻抗式调压室甩负荷涌浪计算显式公式提要本文利用小参数幂渐近展开法，得出了机组甩负荷时，阻抗式调压室涌浪的第一与第二幅值的显式计算公式，该式比原理论公式适用范围广，精度良好，形式简单，便于工程应用。
关键词阻抗式调压室甩负荷涌浪公式一、引言现有文献中，水电站全弃负荷时，阻抗式调压室涌浪的第一振幅(最高涌浪)及第二振幅常分别用如下理论公式计算［1，2］：式中：分别为水电站全弃负荷后第一、第二振幅；l、f、v0为引水道长度、截面积及水体流速，h w0、k0为流量Q0流经引水道及进出调压室所引起的水头损失；F为调压室断面面积；g为重力加速度；x m1、x2、x0均为无因次的比值，s具有长度因次，用以表示“引水道－调压室”系统特性，η代表阻抗大小，η=0即为简单圆筒式调压室。
式(1)、式(2)为隐式超越方程，使用不太方便，且对于阻抗孔口较小(阻抗值较大)的调压室，公式右端对数函数的真数可能为负，导致难以计算。
本文拟利用小参数幂的渐近展开方法，求解调压室动力方程，导出甩负荷后调压室涌浪的第一、第二幅值的显示计算式。
二、调压室基本方程1.连续方程式中z为调压室水位，以水库水位为基准，向下为正；Q T为电站引用流量；v为通过瞬时流量Q时引水道的流速。
2.动力方程其中h w=αv2为通过瞬时流量Q时引水道的水头损失；α为引水道水头损失系数，β为调压室阻抗的水头损失系数。
即使水轮机引用流量Q T已知，(3)与(4)式仍为一非线性方程组，无法根据给定的初始条件求出调压室内涌浪变化的全过程。
三、甩负荷调压室涌浪水位计算当水电站丢弃全负荷后，Q T=0，式(3)化为：将之与(4)式联立，消去v后，得以下二阶动力系统方程：其中：，为忽略引水道与调压室阻抗损失的水位波动周期，式(6)反映的是在平方阻尼的情况下调压室水位波动，如令：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式中ε
= 2 λ⁄ℎ������0
= 9.134，m
=
2 3
，解得：
z������������������ = 50.44������ 所以当增加负荷时水位降到静水位下 23.74m
3.2 丢弃全负荷时产生的第二波动振幅
解之
������2 + ln(1 − ������2) = ������������������������ + ln(1 − ������������������������ )
λ
=
������������������02 2g������ℎ������0
=
2
12662 × 16.62 × 3.432 × 9.81 × 47.784 × 18.098
=
145.89
令������0
=
ℎ������0 λ
=
0.124，X
=
������������，则要求最高涌波水位������������������������ ，只需要求出������������������������
调压室的水力计算
1. 调压室断面计算
当上游死水位，下游为最低水位，最小水位������������������������=188.9m，三台机满发，引 水道糙率取最小值，压力管道糙率取最大值，通过水轮机的流量为 57������3 ⁄������，则 此时的引水隧洞水头损失的计算如表格 1，压力钢管水头损失的计算如表格 2。 引水道应选可能的最小糙率 0.012，压力管道应选择可能的最大糙率 0.013。
������������+∆������
=
������������
1 +6
(������1
+
2������2
+ 2������3
+ ������4)
������1 = ∆������������1(������, ������������, ������������)
������2
=
∆������������1
=
������ ������
=
57 16.619
=
3.43
������⁄������
α
=
ℎ������0 ������02
=
18.098 3.4302
=
1.5385
1
为了保证大波动的稳定，一般要求调压室断面大于托马斯断面，初步分析时
可取（1.0~1.1）������������ℎ，作为调压室的设计断面。这里选取 D=7.8m，则系数 k 为： ������������ =47.784
表格 1 引水隧洞水头损失表
流量 （m3/s）
平均糙率 (n=0.014)
沿程水头损失(m) 最大糙率 (n=0.016)
最小糙率 (n=0.012)
局部水头损失 (m)
57
24.231
31.649
17.802
0.296
38
10.769
14.066
7.911
0.132
19
2.692
表格 2 压力钢管水头损失表
������3
=
∆������������2
(������
+
∆������ 2
,
������������
+
������2 2
,
������������
+
���2��� 2)
������4 = ∆������������2(������ + ∆������, ������������ + ������3, ������������ + ������3)
������)
已知压力管道的流量变化规律，则调压室流量等于隧洞流量减压力管道流量，即：
������������ = ������ − ������������ 。上述方程两个未知量，Q 和 Z，采用四阶龙格库塔法进行逐步求 解。
4.2 四阶龙格库塔法计算公式
如果已知 t 时刻的������������，������������值，采用以下公式求解 t+∆t 时刻的������������+∆t，������������+∆t。
������4 = ∆������������1(������ + ∆������, ������������ + ������3 , ������������ + ������3)
������������ +∆������
=
������������
+
1 6
(������1
+
2������2
+
2������ 3
φ(������) = ln （1 + ������） − ������ + ������0
牛顿迭代公式为： φ(������)
������������+1 = ������������ − ������′(������)
取迭代初值x0 = −0.5，计算结果见下表
表格 3 迭代计算结果
k
1
2
3
������������
������,
������)
������������ ������������
=
(������������
−
������
−
������������������ |������������ ������
|
−
������������ |������|)g������
=
������2(������,
������,
+
������ 4)
������1 = ∆������������2 (������, ������������, ������������)
������ 2
=
∆������������2
(������
+
∆������ 2,
������������
+
������1 2
,
������������
+
������ 1) 2
-0.43085
-0.41928
-0.41899
由表格 3 可以看出精确到 0.001，������������������������
= ������������������������ = −0.419
λ
4 -0.41899
|z������������������ | = −λ������������������������ = 61.128m 根据《水电站调压室设计规范》调压室最高涌波水位以上的安全超高不宜小于
������2 + ln(1 − ������2) = − 0.069
������2 = 0.327 z������������������ = λ������2 =47.70m 所以当丢弃全负荷时，水位降到静水位下 47.70m
综上所述调压室的最低涌波水位应为静水位下 50.44m
根据《水电站调压室设计规范》上游调压室最低涌波水位与调压室处压力引水道
ℎ������0 = ℎ������0 程 + ℎ������0 局 = 31.649 + 0.296 = 31.945m
|z������������������ | ℎ������0
=
1
+
(√������
−
0.275√������
+
0.05⁄������
−
0.9)(1
−
������)(1
−
������⁄������0.62 )
4
4.3 程序框图
5
4.4 VBA 程序代码 定义函数������������： Public Function f1(t As Double, z As Double, q As Double) Dim a As Double a = 5 'a 为导叶直线关闭时间 If t < a Then f1 = (q - (57 - 57 * t / a)) / 47.784 Else f1 = q / 47.784 End If End Function 定义函数������������： Public Function f2(t As Double, z As Double, q As Double) Dim r As Double r = 0.0055 'r 为隧洞的沿程损失和局部损失系数 f2 = 9.81 * 16.61 * (1279 - z - r * Abs(q) * q) / 12662 End Function 调压室甩负荷时水位波动程序 Sub tyssw() Dim t As Double Dim z As Double Dim q As Double '将 t,z,q 定义为实数 Dim k1, k2, k3, k4 As Double Dim l1, l2, l3, l4 As Double '将 k1, k2, k3, k4,l1, l2, l3, l4 定义为实数 Dim dt, stoptime As Double 'dt 为时间步长，stoptime 为计算的调压室水位波动的 时间，单位（s） stoptime = 200 '计算从导叶开始关闭到 t=200s 的水位波动过程 i = 2 'i 用于计算结果计数 dt = 1 t=0 q = 57 z = 1260.9 't,q,z 稳态时的初始值 Do While t < stoptime '当时间 t 小于 stoptime 时执行以下循环过程 k1 = dt * f1(t, z, q) l1 = dt * f2(t, z, q) ' k2 = dt * f1(t + dt / 2, z + k1 / 2, q + l1 / 2) l2 = dt * f2(t + dt / 2, z + k1 / 2, q + l1 / 2) ' k3 = dt * f1(t + dt / 2, z + k2 / 2, q + l2 / 2) l3 = dt * f2(t + dt / 2, z + k2 / 2, q + l2 / 2) ' k4 = dt * f1(t + dt, z + k3, q + l3) l4 = dt * f2(t + dt, z + k3, q + l3)