邱关源电路(第五版)_第四章
《电路》邱关源第五版课后习题解答
电路习题解答第一章 电路模型和电路定律【题1】：由U A B =5V 可得：I AC .=-25A ：U D B =0：U S .=125V 。
【题2】：D 。
【题3】：300；-100。
【题4】：D 。
【题5】：()a i i i =-12；()b u u u =-12；()c ()u u i i R =--S S S ；()d ()i i R u u =--S SS 1。
【题6】：3；-5；-8。
【题7】：D 。
【题8】：P US1=50 W ；P U S 26=- W ；P U S 3=0；P I S 115=- W ；P I S 2 W =-14；P I S 315=- W 。
【题9】：C 。
【题10】：3；-3。
【题11】：-5；-13。
【题12】：4（吸收）；25。
【题13】：0.4。
【题14】：3123I +⨯=；I =13A 。
【题15】：I 43=A ；I 23=-A ；I 31=-A ；I 54=-A 。
【题16】：I =-7A ；U =-35V ；X 元件吸收的功率为P U I =-=-245W 。
【题17】：由图可得U E B =4V ；流过2 Ω电阻的电流I E B =2A ；由回路ADEBCA 列KVL 得 U I A C =-23；又由节点D 列KCL 得I I C D =-4；由回路CDEC 列KVL 解得；I =3；代入上 式，得U A C =-7V 。
【题18】：P P I I 12122222==；故I I 1222=；I I 12=； ⑴ KCL ：43211-=I I ；I 185=A ；U I I S =-⨯=218511V 或16.V ；或I I 12=-。
⑵ KCL ：43211-=-I I ；I 18=-A ；U S =-24V 。
第二章电阻电路的等效变换【题1】：[解答]I=-+9473A=0.5A；U Ia b.=+=9485V；IU162125=-=a b.A；P=⨯6125.W=7.5W；吸收功率7.5W。
电路第五版邱关源课后习题详解.pdf
%
&)
! %
’
’&&#
%
!%-&( $
% $+.&4
(!!.! 若已知显像管行偏转圈中的周期性扫描电流如题!!.图所示#现已知线圈
电 感 为-+-!A#电 阻 略 而 不 计 #试 求 电 感 线 圈 所 加 电 压 的 波 形 !
题!!.图 !!!!!!!!!!!!! 题解!!.图 !!
分析 ! 根据图示可写出#’&(的表达式#由"(’&(% ,>#>&’&(即可求解! 解 ! 电流#’&(的函数表示式为
#的约束方程为$
" %!*# %!!-’!-$#
’,(图为线性电感元件!’,(图电感元件" 和# 的约束方程为$
"
%!#-’!-!$
># >&
&# &
!! 电路同步辅导及习题全解
’/(图为线性电容元件!’/(图电容元件" 和# 的约束方程为$
#
%
!-’!-!9
>" >&
%
!-!&
>" >&
’>(图 是 理 想 电 压 源 !’>(图 的 约 束 方 程 为 $
%!!# ! 若某元件端子上的电压和电流取关联参考方向#而" %!.-/01’!--!&(*## % .123’!--!&(4!求 $ ’!(该 元 件 吸 收 功 率 的 最 大 值 * ’#(该 元 件 发 出 功 率 的 最 大 值 !
解 ! !!!!!!!!!$’&(%"’&(#’&( % !.-/01’!--!&(’.123’!--!&( % &5&123’#--!&(6
电路.邱关源-第五版-学习笔记
绪论 ..................................................................................................................................................1 第一章 电路模型和电路定律.......................................................................................................1
§1－1 电路和电路模型.........................................................................................................1 §1－2 电流和电压和参考方向.............................................................................................1 §1－3 电功率和能量.............................................................................................................1 §1－4 电路元件.....................................................................................................................2 §1－5 电阻元件.............................................
电路分析邱关源第五版----四章习题解答
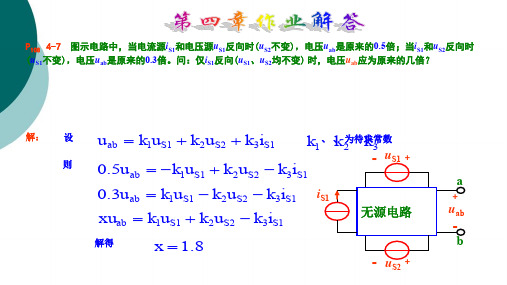
解： 设
uab k1uS1 k2uS2 k3iS1
u1 20V u2 0 i2 2A
uˆ1 0
iˆ1 I1" 1A
uˆ2
5I
" 2
20
iˆ2
I
" 2
20
1
0
I
" 2
0 i1
5I
" 2
20
2
I
" 2
2A
根据叠加定理
I1 I1' I1" 3 1 2A
I2
I
' 2
I
" 2
6V -
1'
由结点电压法得
1 8
1 2
u1
1 2
u
4
4u1 2
1
S
4A
+
2
1S 8
-u1
2u1
1 2
u1
1 5
Байду номын сангаас1 2
u
i
4 u1 2
4A
解得
i 4.364 u
6.471
(d)
- 1 S
(完整版)电路(第五版). 邱关源原著 电路教案,第4章.
第4章 电路定理● 本章重点1、叠加定理的应用及注意事项；2、替代定理的含义；3、应用戴维南、诺顿定理分析电路；4、最大功率传输定理Maximum power transfer theorem 的内容。
● 本章难点1、含有受控源电路应用叠加定理；2、求解含有受控源电路的戴维南、诺顿等效电路。
● 教学方法本章讲述了电路理论的一些重要定理，共用6课时。
采用讲授为主，自学为辅的教学方法。
为使学生能理解定理内容，并应用定理来分析问题和解决问题。
在课堂上讲述了大量例题，课下布置一定的作业，使学生能学会学懂，由于课时量偏紧，对于定理的证明要求自学。
● 授课内容4.1 叠加定理 线性函数)(x f ：)()()(2121x f x f x x f +=+ —可加性Additivity)()(x af ax f = —齐次性Homogeneity )()()(2121x bf x af bx ax f +=+—叠加性Superposition（a 、b 为任意常数Arbitrary Constant ）一、定理对于任一线性网络，若同时受到多个独立电源的作用，则这些共同作用的电源在某条支路上所产生的电压或电流等于每个独立电源各自单独作用时，在该支路上所产生的电压或电流分量的代数和。
例1：试用叠加定理计算图4-1（a ）电路中3Ω电阻支路的电流I 。
图4-1（a ）二、注意事项（1）只适用于线性电路中求电压、电流，不适用于求功率；也不适用非线性电路；（2）某个独立电源单独作用时，其余独立电源全为零值，电压源用“短路”替代，电流源用“断路”替代；（3）受控源不可以单独作用，当每个独立源作用时均予以保留； （4）“代数和”指分量参考方向与原方向一致取正，不一致取负。
例2：电路如图4-2（a ），试用叠加法求U 和x I 。
图4-2（a ）解：第一步10V 电压源单独作用时如图4-2（b ）。
_2Ω 6V2I x +_26Ω'A 3I =-6V+ "A 3I =-2Ω _'x I+_'图4-2（b ）''x x 3210I I += ⇒ 'x 2I A = （受控源须跟控制量作相应改变）'x '36V U I ==第二步3A 电流源单独作用时如图4-2（c ）。
邱关源《电路》第五版参考答案
邱关源《电路》第五版参考答案答案第一章电路模型和电路定律【题1】：由U A B =5V 可得：I AC .=-25A ：U D B =0：U S .=125V 。
【题2】：D 。
【题3】：300；-100。
【题4】：D 。
【题5】：()a i i i =-12；()b u u u =-12；()c ()u u i i R =--S S S ；()d ()i i R u u =--S SS 1。
【题6】：3；-5；-8。
【题7】：D 。
【题8】：P US1=50 W ；P U S 26=- W ；P U S 3=0；P I S 115=- W ；P I S 2 W =-14；P I S 315=- W 。
【题9】：C 。
【题10】：3；-3。
【题11】：-5；-13。
【题12】：4（吸收）；25。
【题13】：0.4。
【题14】：3123I +?=；I =13A 。
【题15】：I 43=A ；I 23=-A ；I 31=-A ；I 54=-A 。
【题16】：I =-7A ；U =-35V ；X 元件吸收的功率为P U I =-=-245W 。
【题17】：由图可得U E B =4V ；流过2 Ω电阻的电流I E B =2A ；由回路ADEBCA 列KVL 得U I A C =-23；又由节点D 列KCL 得I I C D =-4；由回路CDEC 列KVL 解得；I =3；代入上式，得U A C =-7V 。
【题18】：P P I I 12122222==；故I I 1222=；I I 12=；⑴KCL ：43211-=I I ；I 185=A ；U I I S =-?=218511V 或16.V ；或I I 12=-。
⑵KCL ：43211-=-I I ；I 18=-A ；U S =-24V 。
第二章电阻电路的等效变换【题1】：[解答]I =-+9473A =0.5 A ；U I a b .=+=9485V ； I U 162125=-=a b .A ；P =?6125. W =7.5 W；吸收功率7.5W 。
邱关源《电路》第五版 第四章 电路定理
1 + u 1
-
任何一个有源一端口网络，对外电路来说，可 以用一个电流源和电阻相并的组合来等效代替。电
1 R0=Req + + u uS =uOC 1
i
外 电 路
u uS R0i
uS uoc
R0 Req
§4-3 戴维宁定理和诺顿定理
3. 举例
【例1】电路如图，求通过电阻R3的电流I3 。
I3
4
R3 5
8
a Uoc
b 8
2
2
4 2
2 I1
+
40V
+
40V
10
+
-
2.25A 1
A 1.5A 1
B
1 0.5A 1A
US
+ Us D 4.5A 1 6
0.75A
6.75V
U AD 6 4.5V
U BC 2 3V
U 0 =2V
C 1 B 1
A 3A
+ 13.5V
1.5A
1A
2A
Us
-
6
U AD 6 9V
U BC 2 6V
U 0 =4V
iS1
+
R3
uS3
R3 iS1
中，任一支路电流
（或支路电压）都是
i iR1 R4 R2 R2 R1
i R1
R1
uS2
+ -
=
R4 i R 2 R2电路各个独立电源单
独作用时在该支路产
+
i R1
R1
R4 i R 2 R2
iR1
生的电流（或电压）
邱关源—电路—教学大纲—第四章-2
KVL 的矩阵形式。
二．特勒根定理
定理 1(又名功率守恒定理)：对于网络 N 共有 n 个结点，b 条支路，其支路电压、支路 电流向量分别为 U = [U1 L U b ] ， I = [ I1 L I b ] ，且各支路电压与电流参考方向相关联。
T T
则 U I = 0 或 I U = 0 。即
例 1：电路如图 4-30(a)所示，试求电流 I。
4Ω
a
2Ω _
b
4Ω 2Ω
d a I
I3 2Ω
b
2Ω
d
+ 1Ω 8V
_
2Ω
c (a)
I
1Ω
I2
(b)
2Ω I1
c
8V +
图 4-30
解：原电路为一不平衡桥式电路，但为仅有一个独立源单独作用的线性电阻电路，可使用互 易定理进行分析。 互易后的电路如右图所示。 此时应注意互易前后对应支路上的电压电流的 参考方向必须同时关联或非关联。在图 4-5-4(b)中可以求得：
i1 0 －1 ＋1 0 i2 = 0 0 －1 ＋1 －1 i 0 3 i 4
Ai = 0
A－―降阶关联矩阵。可见，矩阵 A 的某些列将只有一个+1，或一个-1，每一个这样的
列一定对应于与划去节点相关联的一条支路， 而且依据该列中非零元素的正负号就可以判断 该支路的方向。 同理， 根据有向图也可以列出支路电压与节点电压之间的关系。 仍以节点 3 作为参考节 点，且令 Un3=0，则各支路电压与节点电压之间的关系为：
+ uS1 _
+
u _ U
∗ ∗ 1 1
+ 9V _
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
c
44
RR IRI++
aa
uC
1A
320＋V3V
22
2200VV － bb －－ 88 I1
a点
(1 2
1 4)ua
1 20 4
1
ua ub 8V I1 1A IR I1 1 2A
uR uC ub 20 8 12V
R 12 6Ω 2
代入实验数据：
uS
＋
－
k1 k2 2
2k1 k2 1
k1 1 k2 1
iS 无源
i uS iS 3 5 2A
线性 i 网络
返回 上页 下页
5.齐性原理
线性电路中，所有激励(独立源)都增大(或减 小)同样的倍数，则电路中响应(电压或电流)也增 大(或减小)同样的倍数。
⑤含受控源(线性)电路亦可用叠加，但受控源应 始终保留。
4. 叠加定理的应用
例1 求电压源的电流及功率
2A
4
70V 10 +－
解 画出分电路图
2
I
5
返回 上页 下页
2A 4
I (1)
＋ 10
4
70V 10 +－
2
5
2 I (2） 5
2A电流源作用，电桥平衡：
I (1) 0
3A
＋－
3
u
＋
1
12V
2A
－
其余电源作用： i(2) (6 12) /(6 3) 2A
u(2) 6i(2) 6 2 1 8V u u(1) u(2) 9 8 17V
3A
＋ － 6 i (2)
＋ u(1)
6 3
1
－ 6V
＋
3＋u(2) － ＋
G2iS1 G2 G3
b1iS1
Hale Waihona Puke b2uS 2b3uS 3
i (1)
2
i(2)
2
i(3)
2
i3
(un1
uS3 )G3
( G3G2 G2 G3
)uS 2
( G2G3 G2 G3
)uS 3
3
G3iS1 G2 G3
i i i (1) (2) (3)
3
3
i i G1
(1) 2
G2
(1) 3
G3
+
is1
us3
–
三个电源共同作用
is1单独作用
i G (2) 12
i(2)
3 G3
+
+
+
–us2
us2单独作用
i G (3) 12
i(3)
3 G3
+ us3–
us3单独作用
返回 上页 下页
③功率不能叠加(功率为电压和电流的乘积，为 电源的二次函数)。
④ u, i叠加时要注意各分量的参考方向。
解 用替代：
3I ＋ 10V
1
1
1
IIx0.5R0x .5
8
0.5
– U+
－0.5I
0.50.5
I 1 0.5
1 1 I
0.5
=
– U' + 0.5 0.5
+
0.5
8 – U'' +
0.5
返回 上页 下页
I 1 0.5
– U' + 0.5 0.5
1 0.5
Uoc 0.510 10 15V
(2) 求输入电阻Req
Req 10 //10 5Ω
注意两种解法结果一致，戴维
b 宁定理更具普遍性。
返回 上页 下页
2.定理的证明
ai
a
+
A
u –
b
叠加
A
N
替代
A
+ u –
i
b
A中
a
a
独
+ u' –
+
N+
Req
u'' –
i
立 源 置
b
b
零
u' uoc
u'' Reqi
返回 上页 下页
u u' u'' uoc Reqi
ia
Req +
Uoc -
+
uN
– b
返回 上页 下页
3.定理的应用
（1）开路电压Uoc 的计算 戴维宁等效电路中电压源电压等于将外电路断
开时的开路电压Uoc，电压源方向与所求开路电 压方向有关。计算Uoc的方法视电路形式选择前 面学过的任意方法，使易于计算。
返回 上页 下页
注意 ②替代后电路必须有唯一解。
无电压源回路；
无电流源结点(含广义结点)。
22..55AA
？
＋ ＋ 22 ＋＋ 1A +
1100VV 55VV
5V5
－ －
－－ 1？.5A －
③替代后其余支路及参数不能改变。
返回 上页 下页
3. 替代定理的应用
例1
若使
Ix
1 8
I , 试求Rx
例4 封装好的电路如图，已知下列实验数据：
当 uS 1V, iS 1A 时，响应 i 2A 当 uS 1V, iS 2A 时，响应 i 1A
研究激 励和响 应关系
求 uS 3V, iS 5A 时，响应 i ？
的实验
解 根据叠加定理 i k1iS k2uS
方法
R 2/1 2Ω
u1 6 /1.2 5V I 1.5 0.5 1A
返回 上页 下页
例5 已知: uab=0, 求电阻R
ab
解 uab 0
60 25
iab icd 0
用开路替代，得：
4
0.5A
＋
30 20
42V R 10
ubd 20 0.5 10V －
返回 上页 下页
例4 用多大电阻替代2V电压源而不影响电路的工作
3A
4
I
0.5A
2 1 + 2V －
＋ 2 4V
－
+ 2V － 10 10 2
＋
I1
10V 5 2
－
解 应求电流I，先化简电路。 应用结点法得：
(
1 2
1 2
1 5)u1
10 2
2 2
6
I1 (5 2) / 2 1.5A
返回 上页 下页
1. 戴维宁定理
任何一个线性含源一端口网络，对外电路来说，
总可以用一个电压源和电阻的串联组合来等效置
换；此电压源的电压等于外电路断开时端口处的
开路电压uoc，而电阻等于一端口的输入电阻（或
等效电阻Req）。
i a
+
Au -b
Req +
Uoc -
ia + u
b
返回 上页 下页
例
a
10 10 +
第4章 电路定理
本章重点
4.1 叠加定理 4.2 替代定理 4.3 戴维宁定理和诺顿定理 4.4 最大功率传输定理 4.5* 特勒根定理 4.6* 互易定理 4.7* 对偶原理
首页
重点:
熟练掌握各定理的内容、适用范围 及如何应用。
返回
4.1 叠加定理
1. 叠加定理在线性电路中，任一支路的电流(或
1A 40
短路替代 uac 10V
cd
uR 20 110 30V R uR 30 15Ω
iR 2
iR (42 30) / 4 1 2A
返回 上页 下页
4.3 戴维宁定理和诺顿定理
工程实际中，常常碰到只需研究某一支路的电 压、电流或功率的问题。对所研究的支路来说，电 路的其余部分就成为一个有源二端网络，可等效变 换为较简单的含源支路(电压源与电阻串联或电流 源与电阻并联支路), 使分析和计算简化。戴维宁定 理和诺顿定理正是给出了等效含源支路及其计算方 法。
返回 上页 下页
例2 求电流I1
解 用替代：
3
6
5 1
6
I1 4 +
+
2 ＋
6V 3V
7V
–
－
－
4A
4 I1
2
＋
7V
－
4A
I1
7 6
2 2
4 4
15 6
2.5A
返回 上页 下页
例3 已知:uab=0, 求电阻R
解 用替代：
uab 3I 3 0 I 1A
电压)可以看成是电路中每一个独立电源单独作用
于电路时，在该支路产生的电流(或电1 压)的代数和。
2 .定理的证明
应用结点法：
G1 i2 G2 i3
is1
+
us2
–
G3
+ us3 –
(G2+G3)un1=G2us2+G3us3+iS1
返回 上页 下页
un1
G2uS 2 G2 G3
G3uS 3 G2 G3
iS1 G2 G3
或表示为：
G1 is1