辽宁省重点协作校盘锦市高级中学,本溪市高级中学,营口市高级中学等20172018学年高一下学期期末考
辽宁省重点高中协作校(沈阳二中、大连育明中学、辽师大附中、本溪高中等)2017届高三上学期期末考试英语
辽宁省重点高中协作校2017届高三上学期期末考试英语试题考生注意：1.本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分，考试时间120分钟。
2.答题前，考生在答题考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码，请认真核准条形码上的准考证号、姓名和科目。
3.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，在选涂其他答案标号，在试题卷上作答无效．．．．．．．．．。
4.本试卷主要考试内容：高中综合。
第I卷第一部分听力（共两节，满分30分）第一节（共5小题，每小题1.5分，满分7.5分）听下面5段对话。
每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。
听完每段对话后，你都有10秒钟的时间回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How old is the woman?A. 16 years oldB. 19 years oldC. 20 years old2. What does the woman do?A. A teacherB. A studentC. A doctor3. What does the man do on holiday?A. Read booB. Listen to musicC. Travel with friends4. What is the woman doing?A. Using a travel websiteB. Flying to AtlantaC. Looing for a travel agent5. What is the man’s reaction to the news?A. He feels surprised at itB. He doesn’t care about itC. He is very happy at it第二节（共15小题，每小题1.5分，满分22.5分）听下面5段对话或独白。
辽宁省重点高中排名
辽宁省重点高中排名集团标准化办公室：[VV986T-J682P28-JP266L8-68PNN]辽宁省重点高中排名1本溪市高级中学2,辽宁省实验中学3,东北育才中学4,大连第24中学5,大连育明中学6,鞍山一中7,盘锦辽河油田第一高级中学8,沈阳二中9,盘锦市高级中学10,阜新市实验中学11,抚顺二中12,丹东凤城一中13,大连八中14,丹东二中15,葫芦岛市高级中学16,锦州高中17,沈阳120中学18,本溪市第一中学19,大连一中20,丹东东港二中21,大连瓦房店高级中学22,锦州渤海大学附中23,抚顺一中24,沈阳第20中学25,大连庄河市高级中学26,鞍山八中27,抚顺清原高中28,大连开发区一中29,营口高中30,本溪县高级中学31,阜新市高级中学32,沈阳第31中学33,大连普兰店二高中34,沈阳一中35,大连辽师大附中36,辽阳一中37,鞍山三中38,锦州北镇高中39,朝阳二高40,沈阳新民高中41,鞍山钢中42,大连金州高中43,本溪桓仁县44,辽阳辽化高中45,绥中一高中46,铁岭市高中47,锦州一高中48,锦州铁中49,鞍山岫岩中学50,大连23中学51,抚顺十中52,营口大石桥市一高中53沈阳四中54,丹东四中55,朝阳北票高中56,辽中县一高中57,丹东一中58,抚顺12中59,抚顺新宾高中60,葫芦岛兴城市一高中61,沈阳翔宇中学62,丹东宽甸二高中63,朝阳凌源实验中学64,锦州凌海市一高中65,鞍山海城高中。
【NO.155】辽南协作校高二文理试卷解析
【NO.155】辽南协作校高二文理试卷解析
别的题目不解析了，就解析几个题目。
理科选择题第12题。
后面的题目我就不写了，都是没有什么难度的，答案粘贴出来。
辽南协作校共30个：抚顺二中、抚顺一中、沈阳二中、沈阳一百二十中、沈阳二十七中、沈阳三十一中、沈阳十一中、旅顺中学、大连一中、瓦房店高中、熊岳高中、海城高中、辽阳一中、营口高中、盘锦高中、辽河油田一高中、锦州中学、阜新高中、绥中高中、丹东二中、本溪高中、岫岩高中、铁岭高中、昌图高中、新宾高中、辽师大附中、阜新实验中学、鞍山八中、辽化高中、大连二十三中。
还有一个叫辽宁省重点高中协作校：
沈阳市：沈阳二中，沈阳120中学，沈阳27中，沈阳31中，沈阳11中等；
大连市：旅顺中学，大连育明中学，大连一中，瓦房店高中，辽师大附中，大连23中，大连市金州高中等；
鞍山市：鞍钢高中，海城高中，鞍山八中，岫岩高中，同泽高中，等；
抚顺市：抚顺一中，抚顺二中，新宾高中，等；
本溪市：本溪高中，本溪一中，桓仁一中，等；
丹东市：丹东二中；
锦州市：锦州中学；
营口市：大石桥高中，营口高中，熊岳高中，等；
阜新市：阜新高中，阜新实验，等；
辽阳市：辽阳一高，辽化高中，灯塔一高等；
铁岭市：铁岭高中，昌图高中，等；
朝阳市：朝阳二高，等；
盘锦市：盘锦市高，辽油一高，等；
葫芦岛市：绥中一高中，等；。
辽宁省市级重点高中协作校2016-2017学年高二上学期期
第I卷（选择题，共60分）一、单项选择题（每小题2分，共60分）读地球局部经纬网图，回答1—2题。
1、乙位于A.南半球B.东半球C.中纬度D.丙的西南方2、丙丁间的距离约为A.1150kmB.1110kmC.2220kmD.3330km读“某地等高线图”，图中等高距为100米，粗实线为河流。
回答3—4题。
3、该河流的流向是A.从西北向东南B.从东向西C.从东南向西北D.从西向东4、甲、乙两地的相对高度有可能是①380米②280米③180米④480米A. ①②B. ②③C. ①③D. ②④甲、乙两地点之间有三条道路相连。
某地理活动小组测绘了这三条道路的纵向剖面图。
读图完成5—6题。
5、甲、乙两地点间高差大致为A．80m B．110m C．170m D．220m6、若使用大型运输车从乙地运送重型机械设备至甲地，最适合行车的是A．道路① B．道路③ C．道路①和② D．道路②和③下图是亚洲东北部冬季某区域等压线分布图。
分析回答7—9题。
7、下列关于图中等压线数值的排序正确的是A．P3>P2>P1 B．P1>P2>P3 C．P2>P3>P1 D．P1>P3>P28、此时a点盛行风是A．东南风 B．西南风 C．东北风 D．西北风9、造成该岛降雪集中于P3沿线地区的主导因素是A．气压 B．纬度 C．地形 D．海陆位置2014年1月1日是中国——东盟自贸区成立四周年。
四年来双边贸易增长迅速，双方投资合作也在提速。
读中国——东盟自贸区局部图，回答10—12题。
10、图中①～④代表的四个城市，气候方面的相同点是A．气候类型一样 B．全年皆高温 C．全年盛行风向一致 D．降水季节分配一致11、该地区的主要物产不包括A．石油 B．锡 C．橡胶 D．可可12、从目前看，中国—东盟自贸区与欧盟相比,最具有潜力的是A．技术优势 B．资本优势 C．市场优势 D．人才优势读“印度示意图”，分析回答13—14题。
辽宁省协作校辽师大附中、本溪高中、沈阳二中等2017-2018学年高考物理一模试卷 Word版含解析
辽宁省协作校辽师大附中、本溪高中、沈阳二中等2017-2018学年高考物理一模试卷一、选择题（共8小题，每题6分．每题给出的四个选项中，第1-5题只有一个选项，第5-7有多个选项符合题目要求，全部选对的得6分，选对但不全的得3分，有选错的得0分）1．下列关于物理学家所做科学贡献、物理规律以及物理量的单位等说法正确的是（）A．从牛顿第一定律可演绎出“质量是物体惯性大小的量度”的结论B．开普勒经过多年的潜心研究，提出了行星运动的三大定律，并揭示了行星运动规律的力学原因C．库仑最早引入电场概念并提出用电场线表示电场D．kg•m/s2与Wb•A/m能表示同一个物理量的单位2．如图所示，在光滑水平面上，用弹簧水平连接一斜面，弹簧的另一端固定在墙上，一人站在斜面上，最初系统静止不动，后来人沿斜面加速向上运动，则（）A．最初系统静止不动时，弹簧处于压缩状态B．最初系统静止不动时，斜面共受到4个力作用C．在人沿斜面加速向上运动的过程中，弹簧处于压缩状态D．在人沿斜面加速向上运动的过程中，弹簧处于原长3．一卫星绕火星表面附近做匀速圆周运动，绕行n圈用时为t．假设宇航员在火星表面以初速度v 水平抛出一小球，经过时间t1恰好垂直打在倾角α=30°的斜面体上，已知引力常量为G，则火星的质量为（）A．B．C．D．4．两物体A、B从不同地点沿同一方向同时开始做直线运动，速度﹣时间图象如图所示．t2时刻A、B相遇，在0﹣t2时间内，下列说法错误的是（）A．A的加速度不断增大B．A、B的距离先减小，再增大，再减小C．A、B的距离先增大，再减小，再增大D．t=0时刻A在B的前方5．如图所示，将四个相同正点电荷分别放在正方形的四个顶点上．O点为该正方形对角线的交点，直线段AB通过O点且垂直于该正方形所在平面，OA＞OB，则一电子沿AB方向从A运动到B的过程中（）A．电子在A点的电势能最大B．电子在B点的电势能最小C．电子受到的电场力一定先变小后变大D．电子受到的电场力一定先变大后变小再变大6．一物体在沿斜面向上的拉力F作用下由静止开始沿斜面向上运动，如图甲所示．在物体运动过程中，其机械能E与位移x的关系图象如图乙所示，其中曲线上点A处的切线的斜率最大，则（）A．在x2处物体的速度最大B．在x1处物体所受拉力最大C．在x1﹣x3的过程中，物体的动能先增大后减小D．在0﹣x2的过程中，物体的加速度先增大后减小7．如图所示，两个倾角分别为30°和60°的光滑斜面固定于水平地面上，并处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中，两个质量均为m、电荷量均为q的带正电小滑块甲和乙分别从两个斜面顶端由静止释放，运动一段时间后，两小滑块都将飞离斜面，在此过程中（）A．甲滑块比乙滑块飞离斜面瞬间的速度小B．甲滑块比乙滑块在斜面上运动的时间长C．甲滑块比乙滑块在斜面上运动的位移小D．两滑块在斜面上运动的过程中，重力的平均功率相等8．正方形金属线圈abcd平放在粗糙水平传送带上，被电动机带动一起以速度v匀速运动，线圈边长为l，电阻为R，质量为m，有一宽度为2l的磁场垂直于传送带，磁感应强度为B，线圈穿过磁场区域的过程中速度不变，下列说法正确的是（）A．线圈进入磁场时有沿abcda方向的感应电流B．线圈进入磁场的过程中对传送带有水平向左的静摩擦力作用C．线圈进入磁场的过程中流过某一线圈导线截面的电荷量为D．线圈经过磁场区域的过程中，电动机多消耗的电能为二、非选择题（必考题）9．气垫导轨是研究与运动有关的实验的装置，也可以用来研究功能关系．如图甲所示，在气垫导轨的左端固定一轻质弹簧，轨道上有一滑块A紧靠弹簧但不连接，已知滑块的质量为m．（1）用游标卡尺测出滑块A上的挡光片的宽度，读数如图乙所示，则宽度d=cm；利用该装置探究弹簧对物块做功的大小：某同学打开气源，调节装置，使滑块可以静止悬浮在导轨上，然后用力将滑块A压紧到P点，释放后，滑块A上的挡光片通过光电门的时间为△t，则弹簧对滑块所做功为（用题中所给字母表示）；（3）利用该装置测量滑块与导轨间的动摩擦因数：关闭气源，仍将滑块A由P点释放，当光电门到P点的距离为x时，测出滑块A上的挡光片通过光电门的时间为t，移动光电门，测出多组数据（滑块都能通过光电门），并绘出x﹣图象，如图丙所示，已知该图线的斜率的绝对值为k，则可算出滑块与导轨间的动摩擦因数为．10．如图所示的实验电路可以测定电源的电动势和内电阻．电压表V1、V2可以看到理想电表，滑动变阻器用R表示．已知定值电阻阻值为R．（1）以电压表V1的示数U1为纵坐标，以电压表V1与电压表V2的示数之差U1﹣U2为横坐标，在平面直角坐标系中描点作图，得到一条直线，测出直线的斜率的绝对值为k，纵坐标截距为b，则电源电动势E=，内阻r=．以电压表V1的示数U1为横坐标，电压表V2的示数U2为纵坐标，在平面直角坐标系中描点作图，同样会得到一条直线，测出该直线的斜率为k′，纵轴截距为b′，则电源电动势为k′、b′可表示为E=，内阻r=．11．滑板是青少年喜爱的体育运动，如图所示，一位少年正在进行滑板运动．图中ABD是同一水平路面，BC是一段R=4m的圆弧路面，圆弧的最高点G与其圆心O在同一竖直线上，BC对应的圆心角为37°，该少年从A点由静止开始运动，他在AB路段单腿用力蹬地，然后冲上圆弧路段到达C 点，从C点水平抛出，其落地点与C点的水平距离为1.6m．如果该少年和滑板可视为一个质点，总质量为40kg，不计滑板与各路段之间的摩擦力以及经过B点时的能量损失．已知重力加速度g=10m/s2，cos37°=0.8，sin37°=0.6．求：（1）在C点时该少年对地面的压力；青少年在AB段所做的功．12．如图所示，在xOy平面内半径为R的圆O1与y轴相切于坐标原点O，在该圆形区域内有与y 轴平行的匀强电场和垂直于圆面的匀强磁场，一个带正电的粒子从O点以一定的速度沿x轴进入场区．若场区内只存在匀强电场或匀强磁场时，该粒子恰好做匀速直线运动，穿过地区的时间为T0；若电场、磁场都撤去，其他条件都不变，该粒子穿过场区的时间为T0．（1）求电场强度与磁感应强度的比值．若电场、磁场都存在，其他条件都不变，求该粒子穿过场区的时间．（3）若电场、磁场都存在，无数多个粒子以相同的速率向圆形场区平面内不同方向射出，其他条件都不变，用阴影表示出进入场区的粒子穿过场区时，在圆形场区内所能到达区域并求出其面积．（直接画图即可，不需要说明理由）[选修3-3]13．下列说法正确的是（）A．一个绝热容器中盛有气体，假设把气体中分子速率很大的如大于V A的分子全部取走，则气体的温度会下降，此后气体中不再存在速率大于V A的分子B．温度高的物体分子平均动能一定大，内能也一定大C．气体压强的大小跟气体分子的平均动能、分子的密集程度有关D．分子势能随着分子间距离的增大，可能先减小后增大E．热力学第二定律指出：在任何自然的过程中，一个弧立的系统的总熵不会减小14．如图所示，两个截面积都为S的圆柱形容器，右边容器高为H．上端封闭，左边容器上端是一个可以在容器内无摩檫滑动的质量为M的活塞：两容器由装有阀门的极细管道相连，容器、活塞和细管都是绝热的．开始时阀门关闭，左边容器中装有理想气体，平衡时活塞到容器底的距离为H，右边容器内为真空．现将阀门缓慢打开，活塞便缓慢下降，直至系统达到新的平衡．此时理想气体的温度增加为原来的1.4倍，已知外界大气压强为P0，求此过程中气体内能的增加量．[选修3-4]15．如图为一列在均匀介质中沿x轴正方向传播的简谐横波在某时刻的波形图，波源在O点，波速为2m/s，该时刻机械波刚好传播到x=8m处．下列说法正确的是（）A．质点P此时刻开始后的振动函数表达式为y=﹣5sinπtcmB．P点振幅比Q点振幅小C．再经过△t=41s，质点P具有正向的最大加速度D．再经过△t=4s，质点Q通过的路程是0.4mE．再经过△t=41s，坐标为的点具有y轴正向最大速度16．如图所示为一直角三棱镜截面，∠A=30°，∠C=90°，BC边长为L．一足够大的光屏MN平行于BC竖直放置．以MN为y轴建立如图所示直角坐标系，B点坐标为（﹣L，0），C点的坐标为（﹣L，L）．在0＜y＜1的范围内，一簇平行于AC的平行光射到AB面上．过AB中点的光线经AB面折射后恰好射向C点．（1）求该棱镜的折射率．求光屏上有光照射到的坐标范围．三、非选择题（选考题，请考从中任选一题作答，如果多做，则按所做的第一题计分．）[选修3-5] 17．下列说法正确的是（）A．由玻尔理论可知，氢原子的核外电子由较高能级跃迁到较低能级时，要释放一定频率的光子，同时电子的动能减小，电势能增大B．对于同一种金属来说，其极限频率恒定，与入射光的频率及光的强度均无关C．比结合能越大表示原子核中的核子结合得越牢固D．通过α粒子散射实验可以估算原子核的大小E．太阳内部发生的核反应是U+n→Ba+Kr+3n18．如图所示，半径为R、内径光滑的半圆形槽的质量为M，置于光滑的水平面上，质量为m的小球自槽口A点由静止滑下．小球开始下滑时，第一次在槽的左侧用一木桩抵住，则小球第一次通过最低点后相对最低点上升的最大高度为h1，第二次在槽的右侧用一木桩抵住，则小球第一次通过最低点后相对最低点上升的最大高度为h2，求．辽宁省协作校辽师大附中、本溪高中、沈阳二中等高考物理一模试卷参考答案与试题解析一、选择题（共8小题，每题6分．每题给出的四个选项中，第1-5题只有一个选项，第5-7有多个选项符合题目要求，全部选对的得6分，选对但不全的得3分，有选错的得0分）1．下列关于物理学家所做科学贡献、物理规律以及物理量的单位等说法正确的是（）A．从牛顿第一定律可演绎出“质量是物体惯性大小的量度”的结论B．开普勒经过多年的潜心研究，提出了行星运动的三大定律，并揭示了行星运动规律的力学原因C．库仑最早引入电场概念并提出用电场线表示电场D．kg•m/s2与Wb•A/m能表示同一个物理量的单位考点：物理学史．分析：在物理学发展的过程中，许多物理学家对科学作出了贡献，根据他们的成就进行解答即可．解答：解：A、从牛顿第二定律可演绎出“质量是物体惯性大小的量度”的结论，故A错误．B、开普勒经过多年的潜心研究，提出了行星运动的三大定律，牛顿发现万有引力定律，揭示了行星运动规律的力学原因，故B错误．C、法拉第最早引入电场概念并提出用电场线表示电场，故C错误．D、根据磁通量的定义式Φ=BS，得：1Wb=1T•m2．根据定义式B=可得：1T=1N/A•m．则1Wb=1N•m2/A•m=1N•m/A即有1Wb•A/m=1N，由牛顿第二定律F=ma知：1N=1kg•m/s2，所以kg•m/s2与Wb•A/m能表示同一个物理量的单位，故D正确．故选：D．点评：此题考查我们对常见物理学史及物理量对应单位的记忆，属于基础题，容易解答．2．如图所示，在光滑水平面上，用弹簧水平连接一斜面，弹簧的另一端固定在墙上，一人站在斜面上，最初系统静止不动，后来人沿斜面加速向上运动，则（）A．最初系统静止不动时，弹簧处于压缩状态B．最初系统静止不动时，斜面共受到4个力作用C．在人沿斜面加速向上运动的过程中，弹簧处于压缩状态D．在人沿斜面加速向上运动的过程中，弹簧处于原长考点：共点力平衡的条件及其应用；物体的弹性和弹力．专题：牛顿运动定律综合专题．分析：系统静止时，系统受力平衡，对系统整体进行受力分析可知，弹簧没有弹力，对斜面进行受力分析可知斜面的受力情况，对斜面与人整体分析，整体有沿斜面向上的加速度，可以在直角坐标系中分解成水平向右和竖直向上的分量，水平方向外力只有弹簧可以提供，进而判断弹簧处于伸长还是压缩状态．解答：解：A、系统静止时，系统受力平衡，水平方向不受力，弹簧弹力等于零，弹簧处于原长，故A错误B、系统静止时斜面受到4个力的作用，人对斜面的压力（垂直斜面向下），对斜面的摩擦力（沿斜面向下），地面对斜面的支持力（竖直向上），斜面的重力（竖直向下），故B正确；C、对斜面与人整体分析，整体有沿斜面向上的加速度，可以在直角坐标系中分解成水平向右和竖直向上的分量，水平方向外力只有弹簧可以提供，竖直方向由地面提供，所以弹簧处于伸长状态，故C错误，D错误．故选：B点评：本题的关键是对物体进行受力分析，能熟练运用整体法和隔离法，特别是在整体法的应用中二者加速度不同，要理解其意义．难度适中．3．一卫星绕火星表面附近做匀速圆周运动，绕行n圈用时为t．假设宇航员在火星表面以初速度v 水平抛出一小球，经过时间t1恰好垂直打在倾角α=30°的斜面体上，已知引力常量为G，则火星的质量为（）A．B．C．D．考点：万有引力定律及其应用．专题：万有引力定律的应用专题．分析：小球垂直落在斜面上时速度方向与竖直方向之间的夹角是α，利用速度的合成与分解可以求出火星表面附近的重力加速度g；再根据重力等于向心力，求得火星的半径．根据万有引力等于重力，求解火星的质量．解答：解：据题小球垂直落在斜面上时速度方向与竖直方向之间的夹角是α，则落在斜面上时竖直分速度为v y=vcotα=又v y=gt1解得火星表面附近的重力加速度为：g=设火星的半径为R，质量为M．一卫星绕火星表面附近做匀速圆周运动，绕行n圈用时为t，则周期为根据重力等于向心力，得：mg=m=根据万有引力等于重力，得：mg=G联立解得：M=故选：B．点评：该题把平抛运动与万有引力相结合，关键要抓住重力等于向心力、万有引力等于重力这两个基本思路，求解天体的质量．4．两物体A、B从不同地点沿同一方向同时开始做直线运动，速度﹣时间图象如图所示．t2时刻A、B相遇，在0﹣t2时间内，下列说法错误的是（）A．A的加速度不断增大B．A、B的距离先减小，再增大，再减小C．A、B的距离先增大，再减小，再增大D．t=0时刻A在B的前方考点：匀变速直线运动的图像．专题：运动学中的图像专题．分析：v﹣t图象中，倾斜的直线表示匀变速直线运动，斜率表示加速度；图象与坐标轴围成的面积表示位移大小，相遇要求在同一时刻到达同一位置．解答：解：A、v﹣t图象的斜率表示加速度，故物体A的加速度逐渐增加，故A正确；D、v﹣t图象与坐标轴围成的面积表示位移大小，故0﹣t2时间内B的位移大，A的位移小，t2时刻A、B相遇，说明开始时刻是A在B的前方，故D正确；B、C、在0﹣t1时间内，是B的速度大，故AB间距逐渐减小，追上后距离要增加；在t1﹣t2时间内是A快，故A与B的间距又重新减小，在t2时刻A、B相遇，故B正确，C错误；本题选错误的，故选：C．点评：该题考查了速度﹣时间图象相关知识点，要求同学们能根据图象判断物体的运动情况，从图中读取有用信息解题，难度不大．5．如图所示，将四个相同正点电荷分别放在正方形的四个顶点上．O点为该正方形对角线的交点，直线段AB通过O点且垂直于该正方形所在平面，OA＞OB，则一电子沿AB方向从A运动到B的过程中（）A．电子在A点的电势能最大B．电子在B点的电势能最小C．电子受到的电场力一定先变小后变大D．电子受到的电场力一定先变大后变小再变大考点：电势差与电场强度的关系；电场强度．专题：电场力与电势的性质专题．分析：两个等量同种电荷连线中点O的电场强度为零，无穷远处电场强度也为零，故从O点沿着中垂线向上到无穷远处电场强度先增大后减小，方向与中垂线平行．解答：解：在对角线上的两个等量正电荷连线中点O的电场强度为零，无穷远处电场强度也为零，故从O点沿着中垂线向上到无穷远处电场强度先增大后减小，A点电场强度竖直向上，B点电场强度竖直向下；A、B、两组对角线上的两个等量正电荷连线中点O的电场强度为零，OA上的电场线的方向向上，BO上的电场线的方向向下，上下的电场强度是对称的，由于OA＞OB，所以B点的电势高，电子带负电，所以电子在A点的电势能最大．故A正确，B错误；C、故从O点沿着中垂线向上到无穷远处电场强度先增大后减小，由于没有确定电场强度的最大点是否在A点，或在A的上边、下边，所以不能确定电子受到的电场力一定先变小后变大，还是电子受到的电场力一定先变大后变小再变大．故CD错误．故选：A．点评：本题关键是要明确两个等量同种电荷连线的中垂线上的场强分布情况和电势分布情况，沿着场强方向，电势越来越低．6．一物体在沿斜面向上的拉力F作用下由静止开始沿斜面向上运动，如图甲所示．在物体运动过程中，其机械能E与位移x的关系图象如图乙所示，其中曲线上点A处的切线的斜率最大，则（）A．在x2处物体的速度最大B．在x1处物体所受拉力最大C．在x1﹣x3的过程中，物体的动能先增大后减小D．在0﹣x2的过程中，物体的加速度先增大后减小考点：功能关系；功的计算．分析：根据功能关系：除重力以外其它力所做的功等于机械能的增量，0﹣﹣X1过程中物体机械能在增加，知拉力在做正功，机械能与位移图线的斜率表示拉力．当机械能守恒时，拉力等于零，通过拉力的变化判断其加速度以及动能的变化．解答：解：A、0～X1过程中，图象的斜率越来越大，则说明拉力越来越大；X1～X2过程中，图象的斜率越来越小，则说明拉力越来越小；在X2处物体的机械能最大，图象的斜率为零，则说明此时拉力为零；在这一过程中物体应先加速后减速，则说明最大速度一定不在X2处；故A错误；B、由图可知，X1处物体图象的斜率最大，则说明此时机械能变化最快，由E=FX可知此时所受的拉力最大；故B正确；C、X1～X2过程中，图象的斜率越来越小，则说明拉力越来越小；在X2处物体的机械能最大，图象的斜率为零，则说明此时拉力为零；在这一过程中物体应先加速后减速，故动能先增大后减小，故C正确；D、在X2处物体的机械能最大，图象的斜率为零，则说明此时拉力为零；在这一过程中物体应先加速后减速，则说明加速度先减小后增大，故D错误；故选：BC点评：本题画出了我们平时所陌生的机械能与高度的变化图象；要求我们从图象中分析物体的运动过程．要求我们能明确机械能与外力做功的关系；明确重力做功与重力势能的关系；并正确结合图象进行分析求解．7．如图所示，两个倾角分别为30°和60°的光滑斜面固定于水平地面上，并处于磁感应强度大小为B、方向垂直纸面向里的匀强磁场中，两个质量均为m、电荷量均为q的带正电小滑块甲和乙分别从两个斜面顶端由静止释放，运动一段时间后，两小滑块都将飞离斜面，在此过程中（）A．甲滑块比乙滑块飞离斜面瞬间的速度小B．甲滑块比乙滑块在斜面上运动的时间长C．甲滑块比乙滑块在斜面上运动的位移小D．两滑块在斜面上运动的过程中，重力的平均功率相等考点：带电粒子在混合场中的运动；功率、平均功率和瞬时功率．专题：带电粒子在磁场中的运动专题．分析：小滑块向下运动的过程中受到重力、支持力、垂直斜面向上的洛伦兹力，向下运动的过程中，速度增大，洛伦兹力增大，支持力减小，当支持力减到0时，离开斜面．解答：解：A、小滑块飞离斜面时，洛伦兹力与重力的垂直斜面的分力平衡，故：mgcosθ=qv m B解得：v m=所以斜面角度越小，飞离斜面瞬间的速度越大，故A错误，B、由受力分析得加速度a=gsinθ，所以甲的加速度小于乙的加速度，因为甲的最大速度大于乙的最大速度，由v m=at得，甲的时间大于乙的时间，故B正确；C、由AB的分析和x=得，甲的位移大于乙的位移，故C错误；D、由平均功率的公式P=F=．故D正确故选：BD点评：解决本题的关键知道洛伦兹力的方向和洛伦兹力的大小以及能够正确的受力分析，理清物体的运动状况．8．正方形金属线圈abcd平放在粗糙水平传送带上，被电动机带动一起以速度v匀速运动，线圈边长为l，电阻为R，质量为m，有一宽度为2l的磁场垂直于传送带，磁感应强度为B，线圈穿过磁场区域的过程中速度不变，下列说法正确的是（）A．线圈进入磁场时有沿abcda方向的感应电流B．线圈进入磁场的过程中对传送带有水平向左的静摩擦力作用C．线圈进入磁场的过程中流过某一线圈导线截面的电荷量为D．线圈经过磁场区域的过程中，电动机多消耗的电能为考点：楞次定律．专题：电磁感应与电路结合．分析：A、根据楞次定律，从而确定感应电流方向；B、根据左手定则，结合感应电流方向，确定线圈安培力方向，从而确定摩擦力方向，进而可知线圈对传送带的摩擦力方向；C、根据电量q=It=，求出通过线圈某一截面的电荷量；D、通过电流的大小，根据焦耳定律求出线圈中产生的热量．解答：解：A、根据楞次定律，可知，感应电流方向adcba，故A错误；B、感应电流方向adcba，根据左手定则，bc边的受到的安培力方向向左，则传送带对线圈有向右的静摩擦力，那么线圈对传送带有向左的静摩擦力，故B正确；C、通过线圈某一截面的电荷量q=It==，故C正确；D、根据焦耳定律得，求得线圈发热产生热量，Q=I2Rt=（）2R=，因此电动机多消耗的电能为，故D正确；故选：BCD．点评：本题综合考查了电磁感应与电路的综合，要求掌握切割产生的感应电动势公式、闭合电路欧姆定律、安培力大小公式以及焦耳定律、电量的公式等．二、非选择题（必考题）9．气垫导轨是研究与运动有关的实验的装置，也可以用来研究功能关系．如图甲所示，在气垫导轨的左端固定一轻质弹簧，轨道上有一滑块A紧靠弹簧但不连接，已知滑块的质量为m．（1）用游标卡尺测出滑块A上的挡光片的宽度，读数如图乙所示，则宽度d=0.510cm；利用该装置探究弹簧对物块做功的大小：某同学打开气源，调节装置，使滑块可以静止悬浮在导轨上，然后用力将滑块A压紧到P点，释放后，滑块A上的挡光片通过光电门的时间为△t，则弹簧对滑块所做功为（用题中所给字母表示）；（3）利用该装置测量滑块与导轨间的动摩擦因数：关闭气源，仍将滑块A由P点释放，当光电门到P点的距离为x时，测出滑块A上的挡光片通过光电门的时间为t，移动光电门，测出多组数据（滑块都能通过光电门），并绘出x﹣图象，如图丙所示，已知该图线的斜率的绝对值为k，则可算出滑块与导轨间的动摩擦因数为．考点：探究功与速度变化的关系．专题：实验题．分析：（1）先读主尺，在读游标尺，游标尺不能估读，那个对齐就读那个．由滑块A上的挡光片通过光电门的时间可得此时滑块的平均速度，由于滑块此阶段做匀速运动，故瞬时速度等于平均速度，由能量转化和守恒可得弹簧弹性势能．（3）每次都有P释放，则每次弹簧弹性势能都相同，由能量转化和守恒可得结果．解答：解：（1）主尺读数为：5mm；游标尺分度为0.05mm，第2个刻度对齐，故游标尺读数为：0.05×2mm=0.10mm，故宽度为：d=5+0.10=5.10mm=0.510cm．滑块通过光电门已经是匀速运动了，其平均速度为：，瞬时速度等于平均速度，故瞬时速度为：，此时滑块动能全部由弹簧弹性势能转化而来，故弹簧弹性势能为：．（3）每次都有P释放，则每次弹簧弹性势能都相同，由能量转化和守恒可得：。
2017-2018学年辽宁省重点协作校(营口市高级中学等)高一下学期期末考试地理试题
2017-2018学年辽宁省重点协作校（营口市高级中学等）高一下学期期末考试地理试题注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答题前，考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时，选出每小题的答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时，将答案填写在答题卡上，写在试卷上无效。
4. 考试结束，将本试卷和答题卡一并交回。
第Ⅰ卷本卷共40小题。
每小题1.5分，共60分。
在每个小题给出的四个选项中，只有一项是符合题目要求的。
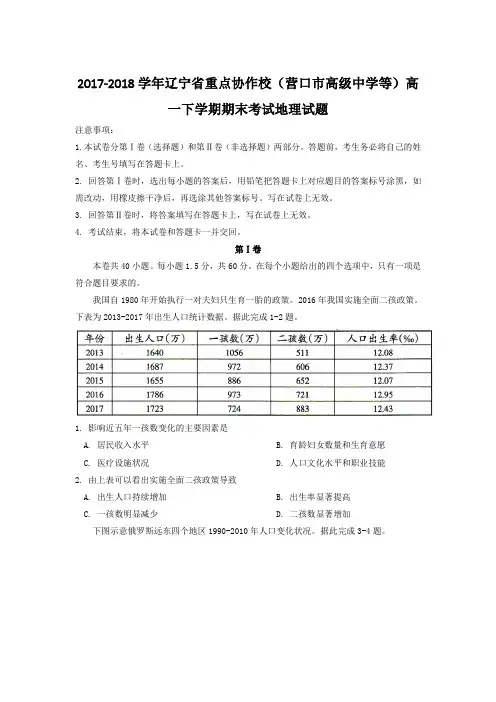
我国自1980年开始执行一对夫妇只生育一胎的政策。
2016年我国实施全面二孩政策。
下表为2013-2017年出生人口统计数据。
据此完成1-2题。
1. 影响近五年一孩数变化的主要因素是A. 居民收入水平B. 育龄妇女数量和生育意愿C. 医疗设施状况D. 人口文化水平和职业技能2. 由上表可以看出实施全面二孩政策导致A. 出生人口持续增加B. 出生率显著提高C. 一孩数明显减少D. 二孩数显著增加下图示意俄罗斯远东四个地区1990-2010年人口变化状况。
据此完成3-4题。
3. 1990-2010年期间，下列四个地区中人口净迁出人数最多的是A. ①B. ②C. ③D. ④4. 人口数量变化对远东地区带来的影响有A. 经济发展速度加快B. 环境人口容量变小C. 促进资源开发D. 劳动力数量减少杭州未来科技城(海创园)是中组部、国资委确定的全国4个未来科技城之一，位于杭州主城区西侧，往东与西湖区接壤，坐拥西溪湿地，是一片罕见的城中次生湿地。
海创园区位优越、环境优美、资源丰富、空间广阔，是浙江省重点打造的杭州城西科创产业集聚区的创新极核，阿里巴巴集团等一大批科研教育单位先后入驻。
右图为杭州未来科技城示意图。
据此完成5-6题。
5. 杭州科技城未来发展壮大的驱动力是A. 研发创新B. 政策支持C. 资金保障D. 改善环境6. 从长远考虑，对杭州未来科技城未来的发展，应注重的是A. 加大人才引进的资金投入B. 合理规划保护生态用地C. 形成完善立体交通网络D. 科技创新引领全国沟垄田间集雨技术是我国重要的田间雨水利用技术，通过提高作物根区的水分满足度，来提高农作物产量和水分利用效率。
辽宁省本溪市高级中学、盘锦市高级中学19年-20年学年高二上学期期中数学试题
2019—2020学年度上学期期中考试高二试题数学一、单项选择题：本题共10小题每题6分，共60分.1.经过点(3,0)P -且与直线:210l x y +-=垂直的直线方程为( ) A. 230x y ++= B. 230x y +-= C. 260x y -+= D. 260x y --=【答案】C 【解析】 【分析】根据直线垂直斜率乘积为1-可求得所求的直线斜率，进而利用点斜式得到直线方程. 【详解】直线l 斜率为12-，∴与l 垂直的直线的斜率为2， ∴过()3,0P -且与l 垂直的直线为：()23y x =+，即260x y -+=.故选：C .【点睛】本题考查根据直线垂直关系求解直线方程的问题，关键是明确两直线垂直斜率乘积为1-.2.圆221:2410C x y x y ++-+=与圆222:6210C x y x y +-++=的位置关系是( )A. 内切B. 相交C. 外切D. 相离【答案】C 【解析】 【分析】由圆的方程可求得两圆圆心和半径，根据圆心距1212C C r r =+可得两圆位置关系. 【详解】圆1C 方程可整理为：()()22124x y ++-=，则圆心()11,2C -，半径12r =；圆2C 方程可整理为：()()22319x y -++=，则圆心()23,1C -，半径23r =.则两圆圆心距12125C C r r ===+，∴两圆外切.故选：C .【点睛】本题考查圆与圆的位置关系的判断，关键是明确两圆位置关系需利用圆心距和两圆半径之间的关系来进行判断.3.过原点的直线l 被圆22:(1)1C x y -+=所截得的弦长为1，则直线l 的倾斜角为( )A.6π B.6π或56π C.3πD.3π或23π 【答案】D 【解析】 【分析】根据圆的方程确定圆心和半径，根据垂径定理可构造方程求得直线斜率，由斜率和倾斜角的对应关系可求得结果.【详解】由圆C 方程知，圆心()1,0C ，半径1r =. 当直线l 斜率不存在时，直线与圆相切，不合题意，∴可设直线:l y kx =，即0kx y ，则圆心C 到直线l距离d =1∴==，解得：k =∴直线l 的倾斜角为3π或23π. 故选：D .【点睛】本题考查直线倾斜角的求解，关键是能够利用垂径定理表示出直线被圆截得的弦长，从而构造方程求得直线的斜率.4.已知12(1,0),(1,0)F F -分别为椭圆2222:1(0)x y C a b a b +=>>的左、右焦点，P 为椭圆C 上一点，若12PF F △周长是6，则椭圆C 的方程是( )A. 22154x y +=B. 22143x y +=C. 22132x y +=D. 2212x y += 【答案】B 【解析】【分析】由椭圆定义和焦距可表示出12PF F ∆的周长，求得a ；根据椭圆,,a b c 关系可求得2b ，进而得到椭圆方程. 【详解】由椭圆定义知：122PFPF a +=，12PF F ∆周长1212226PF PF F F a ++=+=，2a ∴=，2413b ∴=-=，∴椭圆C 的方程为：22143x y +=.故选：B . 【点睛】本题考查椭圆标准方程的求解问题，涉及到椭圆的定义、椭圆焦点三角形周长的问题，属于基础题.5.圆221:20C x y x +-=与圆222:40C x y y ++=的公共弦长为( )A.B.C.D.【答案】B 【解析】 【分析】两圆方程作差可求得公共弦所直线方程，利用垂径定理即可求得结果.【详解】由22222040x y x x y y ⎧+-=⎨++=⎩得：20x y +=，即公共弦所在直线方程为：20x y +=. 圆1C 方程可整理为()2211x y -+=，则圆心()11,0C ，半径1r =，∴圆心1C 到20x y +=的距离d == ∴公共弦长为5==. 故选：B .【点睛】本题考查两圆相交公共弦长的求解，涉及到垂径定理的应用；关键是明确两圆相交的公共弦所在直线方程可通过两圆方程直接作差求得.6.若椭圆22:1x C y m+=的离心率为12，则椭圆C 的长轴的长为( )A.B. 2C.83 D. 2或83【答案】B 【解析】 【分析】分别讨论焦点在x 轴和y 轴两种情况下利用离心率构造方程可求得m ，由此得到长轴长.【详解】若椭圆C 焦点在x 轴上，则2114m e m -==，解得：43m =，符合题意，∴长轴长为=；若椭圆C 焦点在y 轴上，则2114m e m -==，解得：45m =，符合题意，∴长轴长为2.综上所述：椭圆C 的长轴长为2故选：B .【点睛】本题考查根据离心率求解椭圆长轴长的问题，易错点是忽略椭圆焦点位置的讨论，造成丢根的情况出现.7.若,M N 为圆22:(2)(2)3C x y -+-=上任意两点，P 为y 轴上一个动点，则MPN ∠的最大值是( ) A. 45° B. 60° C. 90° D. 120°【答案】D 【解析】 【分析】若MPN ∠最大，则只需CPN ∠最大，可知当PN 是圆C 的切线时，CPN ∠最大，根据正弦值可确定只需CP 最小时，CPN ∠最大；当CP y ⊥轴时，CP 最小，由此得到CPN ∠的最小值，从而求得结果.【详解】由圆的对称性可知，若MPN ∠最大，则只需CPN ∠最大，∴当直线PN 是圆C 的切线时，CPN ∠最大.3sin CN CPN CP ∠==CPN ∴∠最大时，CP 最小， 当CP y ⊥轴时，CP 最小，最小值为2，sin CPN ∴∠的最大值为32， ()max 60CPN ∴∠=，()max 120MPN ∴∠=.故选：D .【点睛】本题考查圆中最值问题的求解，关键是能够将所求角的最值转化为线段长度最值的求解问题，考查学生的分析和解决问题的能力.8.已知曲线224y x x =-(5)4y k x =-+有两个不同的交点，则k 的取值范围是( ) A. 20,5⎛⎤ ⎥⎝⎦B. 2(0,3⎤⎥⎦C. (0,2]D. 12(0,5⎤⎥⎦【答案】A 【解析】 【分析】将问题转化为过定点()5,4P 的直线与半圆()()()222242x y y -+-=≥有两个交点的问题，通过数形结合的方式可确定临界状态，进而求得结果.【详解】由224y x x =-()()()222242x y y -+-=≥.直线()54y k x =-+过定点()5,4P ，∴若曲线224y x x =+-与()54y k x =-+有两个不同的交点，则k 的取值范围为如下图所示的(]12,k k ，//PA x 轴，10k ∴=，()0,2B ，()5,4P ，2422505k -∴==-，k ∴的取值范围为20,5⎛⎤⎥⎝⎦. 故选：A .【点睛】本题考查根据直线与圆的交点个数求解参数范围的问题，关键是通过能够通过数形结合的方式确定临界状态；易错点是忽略y 的取值范围，将半圆误认为圆，造成求解错误.9.若直线:20()l ax y a a R +-=∈与圆22:240C x y mx +-+=至少有一个交点，则实数m 的取值范围是( ) A. (2,)+∞ B. [2,)+∞ C. (,2)-∞-D. (,2]-∞-【答案】A 【解析】 【分析】根据二元二次方程表示圆可求得m 的取值范围，由直线与圆至少有一个交点，可知直线所过定点在圆内或圆上，由此构造不等式求得m 的范围；综合上述范围可得最终结果.【详解】圆C 的方程可整理为：()2224x m y m -+=-，240m ∴->，解得：2m <-或2m >，∴圆心(),0C m ，半径24r m =-.直线l 方程可整理为：()20a x y -+=，则直线l 恒过定点()2,0. 直线l 与圆C 至少有一个交点，()2,0∴在圆C 内部或圆上， 即4440m -+≤，解得：2m ≥， 综上所述：实数m取值范围为()2,+∞.故选：A .【点睛】本题考查根据直线与圆的位置关系求解参数范围的问题，关键是能够将问题转化为点在圆内或圆上的问题；易错点是忽略二元二次方程表示圆所需的参数的范围，造成求解错误.10.已知直线1:0l mx y m -+=与直线2:10l x my +-=的交点为P ，若点Q 为直线3:30l x y -+=上的一个动点，则||PQ 的最小值为（ ） A.1B.1 C. 1-D.1【答案】B 【解析】【分析】根据两直线恒过定点及垂直关系可知交点P 的轨迹是以()0,0为圆心，1为半径的圆；根据圆上的点到直线距离的最小值为d r -可求得结果. 【详解】()110m m ⨯+-⨯=，12l l ∴⊥，直线1l 恒过定点()1,0-，直线2l 恒过定点()1,0，且12l l ⊥，P ∴点轨迹是以()0,0为圆心，1为半径的圆，min 11PQ ∴==. 故选：B .【点睛】本题考查圆上的点到直线距离的最小值的求解问题，关键是能够根据直线所过定点和垂直关系得到直线交点的轨迹，需明确圆上的点到直线距离最小值为圆心到直线距离d 减去半径r .二、填空题：本题共4小题，每小题5分共20分.11.已知椭圆222: 19x y C a +=，直线4y x =-经过椭圆C 的一个焦点，则椭圆C 的离心率为____________.【答案】45【解析】 【分析】分别讨论焦点在x 轴和y 轴两种情况，根据直线与坐标轴交点坐标确定c ，根据椭圆,,a b c 关系可求得离心率.【详解】直线4y x =-与x 轴交点为()4,0，与y 轴交点为()0,4.若椭圆C 焦点在x 4=，解得：2259a =>，45e ∴=； 若椭圆C 焦点在y 轴上，则43e =，不合题意. 综上所述：椭圆C 的离心率45e =.故答案为：45.【点睛】本题考查椭圆离心率的求解问题，关键是能够准确求解出椭圆的,a c 的值，属于基础题. 12.由直线:40l x y ++=上的任意一个点向圆22:(1)(1)1C x y +++=引切线，则切线长的最小值为___________. 【答案】1 【解析】 【分析】若要切线长最小，则只需圆心与直线上的点的连线最小，即为圆心到直线距离即可；利用点到直线距离公式可求得圆心到直线距离，代入可求得切线长的最小值. 【详解】由圆C 方程知：圆心()1,1C --，半径1r =. 设直线l 上的点为P ，过P 作圆C 切线，切点为Q .∴切线长222221PQ CP CQ CP r CP =-=-=-，若切线长PQ 最小，则只需CP 最小，CP 最小值为圆心C 到直线l 的距离，min 11422CP --+∴==min 211PQ ∴=-=.故答案为：1.【点睛】本题考查过直线上一点做圆的切线，切线长的最小值的求解问题，关键是能够将问题转化为圆心与直线上的点的连线的最小值的求解问题，进而利用点到直线距离公式求得结果.13.已知点(1,0),(3,0)M N .若直线:0l x y m +-=上存在一点P 使得0PM PN ⋅=成立，则m 的取值范围是_____________.【答案】[22,22] 【解析】 【分析】根据PM PN ⊥可确定P 点轨迹为以()2,0为圆心，1为半径的圆，利用直线l 与圆有交点可知d r ≤，由此构造不等式求得结果. 【详解】0PM PN ⋅=，PM PN ∴⊥，P ∴点轨迹是以()2,0为圆心，1为半径的圆.:0l x y m +-=上存在点P ，l ∴与以()2,0为圆心，1为半径的圆有交点，∴圆心()2,0到直线l 距离212m d -=≤，解得：2222m ≤≤即m 的取值范围为：22,22⎡⎣.故答案为：22⎡+⎣.【点睛】本题考查根据直线与圆的位置关系求解参数范围的问题；关键是能够根据平面向量数量积得到垂直关系，进而确定动点轨迹，从而将问题转化为直线与圆位置关系的求解问题.14.已知定点(3,1),(5,0)M N -，若动点(,)P x y 20=，则||||PM PN +的最小值为___________.【答案】20【解析】 【分析】根据方程的几何意义，结合椭圆定义可求得P 点轨迹方程；设椭圆右焦点为F ，将PM PN +转化为2PM a PF +-，由此可得最小值为20FM -.20=可知(),P x y 到()5,0-和()5,0的距离之和为20，根据椭圆定义可知：10a =，5c =，22275b a c ∴=-=，P ∴点轨迹方程为：22110075x y +=. 设椭圆右焦点为F ，则()5,0F ，22020PM PN PM a PF PM PF FM ∴+=+-=+-≥-（当且仅当M 在线段PF 上时取等号），()min2020PM PN∴+==故答案为：20.【点睛】本题考查椭圆上点到定点与焦点的距离之和的最小值的求解问题，涉及到动点轨迹的求解；关键是能够利用椭圆定义将问题转化为椭圆上的点到定点与焦点距离之差的最小值的求解问题，进而结合三角形三边关系得到结果.三、解答题共70分.解答应写出文字说明、证明过程或演算步骤.15.已知直线1:10l ax y a +++=与直线22(:1)30l x a y +-+=. （1）若12l l ⊥，求a 的值； （2）若12//l l ，求1l 和2l 之间的距离.【答案】（1）13；（2【解析】【分析】 （1）由垂直关系可构造方程求得结果；（2）由平行关系可构造方程求得a ，利用平行直线间距离公式可求得结果.【详解】（1）由12l l ⊥可得：210a a +-=，解得：13a =. （2）由12//l l 可得()()12321a a a a ⎧-=⎪⎨≠+⎪⎩，解得：1a =-. 则1:0l x y -=，23:02l x y -+=，∴1l 和2l 之间的距离3d ==【点睛】本题考查根据直线的垂直和平行关系求解参数值、平行直线间距离的求解；关键是明确两直线垂直则12120A A B B +=，两直线平行则12210A B A B -=且12210B C B C -≠.16.已知圆C 的圆心坐标为(3,4)，直线:2l x =被圆C 截得的弦长为（1）求圆C 的方程；（2）求圆C 关于直线2350x y +-=对称的圆D 的标准方程.【答案】（1）22(3)(4)4x y -+-=；（2）22(1)(2)4x y +++=.【解析】【分析】（1）利用垂径定理可构造方程求得半径r ，进而得到圆的方程；（2）设圆心()3,4关于直线的对称点为(),m n ，根据两点连线与直线垂直、两点连线中点在直线上可构造方程组求得(),m n ，进而得到圆的标准方程.【详解】（1）由题意可知：圆心到2x =的距离为1，∴=2r ，∴圆C 的方程为：()()22344x y -+-=.（2）设圆心()3,4关于直线2350x y +-=的对称点的坐标为(),m n ，则4213334235022n m m n ⎧-⎛⎫⋅-=- ⎪⎪⎪-⎝⎭⎨++⎪⨯+⨯-=⎪⎩，解得：12m n =-⎧⎨=-⎩， ∴圆D 的圆心为()1,2--，半径为2，∴圆D 的标准方程为：()()22124x y +++=.【点睛】本题考查根据直线被圆截得的弦长求解圆的方程、圆关于直线对称的圆的方程的求解等知识；关键是熟练应用垂径定理和点关于直线对称点的求解方法；需明确圆关于直线对称的圆的半径相同，圆心关于直线对称.17.已知直线1:40l x y +-=与直线2:270l x y -+=的交点为P ，圆22:2410C x y x y +--+=. （1）求过12,l l 的交点P ，且在两坐标轴上截距相等的直线方程；（2）过P 点做圆C 的切线，求切线方程.【答案】（1）50x y +=或40x y +-=；（2）1x =-或512550x y +-=.【解析】【分析】（1）直线方程联立可求得()1,5P -，分别讨论直线过原点和不过原点两种情况，从而求得直线方程；（2）由圆的方程可确定圆心和半径；分别讨论过P 的切线斜率存在和不存在两种情况，可知当斜率不存在时满足题意；当切线斜率存在时，利用圆心到直线距离等于半径可构造方程求得斜率，进而得到切线方程.【详解】（1）由40270x y x y +-=⎧⎨-+=⎩得：()1,5P -， ①直线过原点，则方程为：50x y +=；②若直线不过原点，设方程为()0x y a a +=≠，将点(1,5)P -代入该方程得：4a =，故直线方程为40x y +-=.综上所述：直线方程为50x y +=或40x y +-=.（2）圆C 方程可整理为：()()22124x y -+-=，则圆心()1,2C ，半径2r①当斜率不存在时，直线方程为1x =-，为圆C 的切线，满足题意；②当切线斜率存在时，设方程为()51y k x -=+，即50kx y k -++=，∴圆心到直线的距离2d ==，解得：512k =-， ∴切线方程为512550x y +-=.综上所述：切线方程为1x =-或512550x y +-=.【点睛】本题考查在坐标轴截距相等的直线方程的求解、过圆外一点圆的切线方程的求解问题；易错点是在忽略截距为零、直线斜率不存在的情况，造成丢根的情况.18.已知椭圆2222:1(0)x y C a b a b+=>>，其右焦点为2F ，直线:210l x y -+=交椭圆C 于,A B 两点，交x 轴于点D ，线段AB 中点为11(,)24M -. （1）求椭圆C 的方程；（2）设P 为椭圆C 上一点，求||PD 的最小值及取得最小值时P 点的坐标. 【答案】（1）2214x y +=；（2）3，4,33⎛⎫- ⎪ ⎪⎝⎭或4,33⎛-- ⎝⎭. 【解析】【分析】（1）利用点差法可得到224a b =，根据焦点坐标和椭圆,,a b c 关系可求得22,a b ，进而得到椭圆方程； （2）设(),P x y ，利用两点间距离公式可得()22322224PD x x x =++-≤≤，根据二次函数的性质可求得最小值，并得到取最小值时x 的取值，代入椭圆方程可求得P 点坐标.【详解】（1）设()11,A x y ，()22,B x y ， AB 中点为11,24M ⎛⎫- ⎪⎝⎭，1212112x x y y +=-⎧⎪∴⎨+=⎪⎩， 由22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩得：()()()()12121212220x x x x y y y y a b +-+-+=， 221212*********AB y y x x b b k x x a y y a -+∴==-⋅==-+，即224a b =.右焦点)2F ，22233a b b ∴-==，21b ∴=，24a =， ∴椭圆C 的方程为：2214x y +=. （2）由题意得：()1,0D -.设(),P x y ，则()221224x y x =--≤≤， ()()()2222223111222244x PD x y x x x x ∴=++=++-=++-≤≤， ∴当24332x =-=-时，min 3PD ==，此时43P ⎛- ⎝⎭或4,3P ⎛- ⎝⎭. 【点睛】本题考查椭圆标准方程的求解、椭圆上的点到定点距离的最值的求解问题，涉及到点差法和二次函数性质的应用；当求解弦中点的问题时，常采用点差法来进行求解；求解椭圆上的点到定点距离的最值问题的关键是能够将问题转化为函数最值的求解问题.19.已知动点M 在椭圆22:14y C x +=上，过点M 作y 轴的垂线，垂足为N ，点P 满足2NP NM =. （1）求点P 的轨迹方程E ；（2）已知点(0,2)A ，若直线23y kx =+与P 点轨迹交于G ，H 两点，证明：论k 取何值时，直线AG 和AH 的斜率之积均是定值，并求出该定值.【答案】（1）224x y +=；（2）定值为12-，证明见解析 【解析】【分析】（1）设P 点坐标(,)x y ,则有点M 坐标为,2x y ⎛⎫ ⎪⎝⎭，利用相关点法即可求解. （2）设()11,,G x y ()22,H x y ()120,0x x ≠≠，可得112,AG y k x -=222AH y k x -=，计算AG AH k k ⋅ 然后将直线与椭圆方程联立，消去y ，利用韦达定理求出两根之和、两根之积，代入斜率之积式子化简即可求解.【详解】（1）设P 点坐标(,)x y ,则有点M 坐标为,2x y ⎛⎫⎪⎝⎭， 因为M 在椭圆上，所以将点坐标代入椭圆， 可得22144x y += 所以点P 的轨迹方程为224x y +=（2）证明：设()11,,G x y ()22,H x y ()120,0x x ≠≠， 于是112,AG y k x -=222AH y k x -=， 121222AG AH y y k k x x --⋅=⋅()212121241639k x x k x x x x -++= 直线与圆联立22423x y y kx ⎧+=⎪⎨=+⎪⎩，于是有()224321039k x kx ++-= 由此可得1221224313291k x x k x x k ⎧-⎪+=⎪⎪+⎨⎪-⎪=⎪+⎩ 代入AG AH k k ⋅中可得，AG AH k k ⋅22224324169131393291k k k k k k --⋅-⋅+++=-+169329=-12=- 【点睛】本题考查了动点的轨迹方程，直线与圆的位置关系中定值问题，考查了计算能力，属于中档题.20.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12,3F F 分别为左右焦点，P 是椭圆C 上点，且1212,908F PF PF PF ︒∠=⋅=.（1）求椭圆C 的方程；（2）过2F 的直线l 与椭圆C 交于不同的两点,A B ，则1F AB 的内切圆的面积是否存在最大值？若存在，求出这个最大值以及此时的直线方程；若不存在，请说明理由.【答案】（1）22164x y +=；（2）存在，89π，x . 【解析】【分析】（1）根据椭圆定义和勾股定理可构造方程组得到224416a c =+，结合离心率和椭圆,,a b c 关系可求得,,a b c 的值，进而得到椭圆方程；（2）由等面积法可得21r y =-，设:l x ty =+定理表示出21y y -，得到r =max r ，进而得到内切圆面积的最大值，同时确定直线方程. 【详解】（1）由题意可知：222121212482PF PF c PF PF PF PF a⎧+=⎪⋅=⎨⎪+=⎩，()222124164PF PF c a ∴+=+=，由224416a c c e a ⎧=+⎪⎨==⎪⎩得：a c ⎧=⎪⎨=⎪⎩2224b a c ∴=-=， ∴椭圆C 的方程为：22164x y +=. （2）设()()1222,,,A x y B x y ，1F AB ∆内切圆半径r . 由等面积法可得：1AB 222211422F S F F y y a r ∆=⨯⨯-=⨯⨯，于是21r y =-. 由题意可知l 不可能是x 轴，故可设直线方程为：x ty =+联立22164x y x ty ⎧+=⎪⎨⎪=⎩得：()222380t y ++-=，12122823y y y y t ⎧+=⎪⎪∴⎨-⎪=⎪+⎩，21r y y ∴=-==令()211m t m =+≥，则()22221114412344t m m m t m m+==+++++，1m ≥，∴当1m =时，14m m +取得最小值5，max r ∴== ∴1F AB ∆内切圆的面积的最大值为：2max 89r ππ=， 此时0t =，则直线方程为x =【点睛】本题考查直线与椭圆综合应用问题，涉及到椭圆标准方程的求解、椭圆中最值问题的求解；求解最值的关键是能够将所求最值转化为关于某一变量的函数，通过函数最值的求解方法求得结果.。
辽宁省重点高中协作校2017-2018学年高一上学期期中考试地理试题 Word版含答案
2017-2018学年本溪市高级中学时间：60分钟试卷满分100分一、单项选择题：（本大题共35个小题，每小题2分，共70分）下图中M示意某行星，箭头示意行星公转方向一读图回答1～2题。
1M可能为①水星②金星③火星④木星A.①②B.②③C.③④D.①④2据图中信息可推测，与地球相比，M行星A．质量更大 B.密度更大 C．白天表面温度更高 D.体积更大读下图，完成3～4题。
3．图中包含A．l级天体系统 B．2级天体系统 C．3级天体系统 D．4级天体系统4．图中标识的天体，全部属于①太阳系②地月系③银河系④河外星系⑤总星系A.①②③ B。
②③④ C.③④⑤ D.①③⑤5．图中昼夜温差最大的是据《汉书·五行志》中记载：“西汉河平元年（公元前28年）……三月乙未，日出黄，有黑气大如钱，居日中央。
”读太阳外部结构示意图，完成6～8题。
6图中太阳的大气层甲、乙、丙分别代表A．色球层、光球层、日冕层 B.光球层、色球层、日冕层C.光球层、日冕层、色球层D.日冕层、色球层、光球层7太阳黑子和耀斑A.均发生在甲层B.分别发生在丙层和乙层C.都发生在乙层D.分别发生在甲层和乙层8下列关于太阳活动的叙述，正确的是①地球上出现的“磁暴”现象与太阳活动无关②太阳活动增强与否，对地球没有影响③太阳活动的平均周期大约是l1年④耀斑爆发时间短，释放的能量巨大A.①②B.①③C.②④D.③④9 2016年里约奥运会开幕式于2016年8月5H晚19：55分（西三区）在马拉卡纳体育场(Ma —rar,ana Stadium)举行。
小明在本溪的家中收看开幕式的时问（东八区）是A.8月5日19:55分B.8月6日19:55分C.8月6 日 6:55分D.8月5开6:55分下图中，a点位于30°N，h点位于30°S，角aoc=45°，C点位于400W经线上。
读图，完成10-11题。
10下列关于图中a、h、c三点的叙述，不正确的是A. a、b两点线速度相等B.a、h两点地方时相同C.a、b两点角速度相等D.h、c两点地方时相同ll a点经度为A.85°WB. O°C. 5°ED. 40°E下图中，阴影部分表示黑夜，非阴影部分表示白天．据此完成12～14题。
辽宁重点高中协作校(沈阳二中、大连育明中学、辽师大附中、本溪高中等)2017届高三上学期期末考试历史.doc
辽宁省重点高中协作校2017届高三上学期期末考试历史试题第I卷（选择题共48分）本卷共24小题，每小题2分，共48分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 商周时期，商人家族对其控制下的商业资源有相当程度的支配权，国家只是名义上的最高所有者。
商人与国家通过买卖的方式进行商品交换，只不过购买受到限制——主要是国家及奴隶主贵族。
这反映了商周时A.不存在工商食官现象B.官营手工业占主导地位C.商业经营权属于国家D.商业发展保持相对独立2. 齐桓公向管仲提出如何解决国家财政不足问题时，管仲回答说:“唯官山海（指：盐铁）为可耳”。
这说明管子主张A.以农为本B.积极干预经济C.开发荒山D.鼓励市场交换3. 唐代招生限文武官员五品以上子孙，宋代招生可招庶民的俊异者。
这一变化有助于A.皇权向社会基层扩展B.增强中央政府的向心力C.削弱地方官员的权力D.强化基层百姓的德行修养4. 宋代的官、职、差遣(临时任用)分开授予，“官”是确定待遇的标准；“职”指职位，如“大学士”系而“差遣”则掌握实际事务权力。
这样承担内外事可以不受官品和贿的限制。
这一做法有助于A.防止官员权力膨胀B.明确官员的职责C.提高中央行政效率D.减少吏治腐败发生5. 中国古代医术，亦称“仁术”。
医学家在行医过程中也常以“仁”的道德标准作为行医准则，如唐朝的孙思邈提出：“人命至重，有贵千金，一方济之，德逾于此”•这反映了古代中国医术A.重在教化病人的心理B.浸润了儒家文化的价值观C.以儒家思想为理论基础D.受到封建伦理道德的约束6. 明朝中后期，受心学的影响，一批知识分子跳出了宋儒的框架，他们作品中的人物由达官贵人、才子佳人、孝子贤孙转变为普普通通的市民、商贩、农民。
他们傲视封建礼教，鄙视功名利禄，敢于直言。
这反映出心学A.有利于商品经济的发展B.冲破了宋代理学的思想禁锢C.有利于民主观念的形成D.激发了个体自由主义思想发展7. 下面是清代中期山地被开垦为耕地的数额统计示意图（同期人口持续增长）。
辽宁省本溪市高级中学、盘锦市高级中学2024届物理高一第二学期期末质量检测模拟试题含解析
辽宁省本溪市高级中学、盘锦市高级中学2024届物理高一第二学期期末质量检测模拟试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。
选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题：本大题共10小题，每小题5分，共50分。
在每小题给出的四个选项中，有的只有一项符合题目要求，有的有多项符合题目要求。
全部选对的得5分，选对但不全的得3分，有选错的得0分。
1、(本题9分)-个质点做曲线运动时一定变化的物理量是A．速度B．加速度C．速率D．动能2、(本题9分)第一宇宙速度是指A．月球绕行地球的速度B．飞行器克服地球引力脱离地球的速度C．飞行器克服太阳引力脱离太阳系的速度D．飞行器在地面附近绕地球做匀速圆周运动时必须具有的速度3、(本题9分)质量为m的小球从高H处由静止开始自由下落，以地面作为参考平面．当小球的动能和重力势能相等时，重力的瞬时功率为( )A．2mg gH B．mg gH C．12mg gH D．13mg gH4、(本题9分)某物体沿一直线运动，其v－t图象如图所示，下列说法中正确的是()A．第1 s内和第2 s内物体的速度方向相反B．第1 s内和第2 s内物体的加速度方向相反C．第2 s末物体的速度和加速度都为零D．第4s内物体的速度方向和加速度方向相同5、起重机沿竖直方向以大小不同的速度两次匀速吊起质量相等货物，则两次起重机对货物的拉力和起重机的功率大小关系是（）A．拉力不等，功率相等B．拉力不等，功率不等C．拉力相等，功率相等D．拉力相等，功率不等6、(本题9分)2013年12月2日1时30分，嫦娥三号探测器由长征三号乙运载火箭从西昌卫星发射中心发射，首次实现月球软着陆和月面巡视勘察,嫦娥三号的飞行轨道示意图如图所示．假设嫦娥三号在环月段圆轨道和椭圆轨道上运动时，只受到月球的万有引力,则以下说法正确的是()A．若已知嫦娥三号环月段圆轨道的半径、运动周期和引力常量，则可以计算出月球的密度B．嫦娥三号由环月段圆轨道变轨进入环月段椭圆轨道时，应让发动机点火使其减速C．嫦娥三号在从远月点P向近月点Q运动的过程中,加速度变大D．嫦娥三号在环月段椭圆轨道上P点的速度大于Q点的速度7、(本题9分)如图所示，一质量为M的光滑大圆环，用一细轻杆固定在竖直平面内；套在大环上质量为m的小环，从大环的最高处由静止滑下，滑到大环的最低点的过程中，(重力加速度大小为g)()A．小环滑到大圆环的最低点时处于失重状态B．小环滑到大圆环的最低点时处于超重状态C．此过程中小环的机械能守恒D．小环滑到大环最低点时，大圆环对杆的拉力大于(m＋M)g8、(本题9分)如图所示，轻质弹簧上端固定，下端系一物体．物体在A处时，弹簧处于原长状态．用手托住物体使它从A处缓慢下降，到达B处时手和物体自然分开且物体也不动．此过程中，物体克服手的支持力所做的功为W．不考虑空气阻力，在此过程中（）A ．弹簧弹性势能增加量小于物体重力势能减少量B ．弹簧弹性势能增加量大于物体重力势能减少量C ．物体与弹簧组成的系统机械能增加量为WD ．若将物体从A 处由静止释放，则物体到达B 处时的动能为W9、 (本题9分)如图所示，甲、乙两人静止在光滑的冰面上，甲沿水平方向推了乙一下，结果两人向相反方向滑去．已知甲的质量为45kg ，乙的质量为50kg ．则下列判断正确的是（ ）A ．甲的速率与乙的速率之比为10：9B ．甲的加速度大小与乙的加速度大小之比为9：10C ．甲对乙的冲量大小与乙对甲的冲量大小之比为1：1D ．甲的动能与乙的动能之比为1：110、 (本题9分)如图所示，两个完全相同的小球从水平地面上方同一点O 分别以初速度12v v 、水平抛出，落在地面上的位置分别是A 、B ，O '是O 在地面上的竖直投影，且:1:2O A AB '=，若不计空气阻力，则两小球 ( )A ．初动能之比为1∶3B ．重力对两个小球做功不同C ．重力做功的平均功率相同D ．落地瞬间重力的瞬时功率相同二、实验题11、（4分）如图所示，为“验证碰撞中的动量守恒”的实验装置示意图。
辽宁省本溪市高级中学、盘锦市高级中学2023年高三物理第一学期期末联考模拟试题含解析
辽宁省本溪市高级中学、盘锦市高级中学2023年高三物理第一学期期末联考模拟试题注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、单项选择题：本题共6小题，每小题4分，共24分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1、在2018年亚运会女子跳远决赛中，中国选手许小令获得铜牌。
在某一跳中，她（可看作质点）水平距离可达6.50 m，高达1.625 m。
设她离开地面时的速度方向与水平面的夹角为α，若不计空气阻力，则正切值tanα的倒数等于（）A．0.5 B．1 C．4 D．82、2019年4月10日21点，科学家发布了黑洞人马座A*的照片。
黑洞强大的引力致使以3 108m/s的速度传播的光都不能逃逸。
已知人马座A*的直径为4400万公里，则人马座A*与地球的质量之比约为（）(可能用到的数据有：地球半径6400km；地球的环绕速度为7.9km/s2倍)A．1011B．1012C．1013D．10143、基于人的指纹具有终身不变性和唯一性的特点，发明了指纹识别技术．目前许多国产手机都有指纹解锁功能，常用的指纹识别传感器是电容式传感器，如图所示．指纹的凸起部分叫“嵴”，凹下部分叫“峪”．传感器上有大量面积相同的小极板，当手指贴在传感器上时，这些小极板和正对的皮肤表面部分形成大量的小电容器，这样在嵴处和峪处形成的电容器的电容大小不同．此时传感器给所有的电容器充电后达到某一电压值，然后电容器放电，电容值小的电容器放电较快，根据放电快慢的不同，就可以探测到嵴和峪的位置，从而形成指纹图象数据．根据文中信息，下列说法正确的是( )A ．在峪处形成的电容器电容较大B ．在峪处形成的电容器放电较慢C ．充电后在嵴处形成的电容器的电荷量大D ．潮湿的手指头对指纹识别绝对没有影响4、如图所示，在纸面内半径为R 的圆形区域中充满了垂直于纸面向里、磁感应强度为B 的匀强磁场，一点电荷从图中A 点以速度v 0垂直磁场射入，与半径OA 成30°夹角，当该电荷离开磁场时，速度方向刚好改变了180°，不计电荷的重力，下列说法正确的是( )A ．该点电荷离开磁场时速度方向的反向延长线通过O 点B ．该点电荷的比荷为02v q m BR= C ．该点电荷在磁场中的运动时间为t ＝3R v π D ．该点电荷带正电 5、在空间中水平面MN 的下方存在竖直向下的匀强电场，质量为m 的带电小球由MN 上方的A 点以一定初速度水平抛出，从B 点进入电场，到达C 点时速度方向恰好水平，A 、B 、C 三点在同一直线上，且AB=2BC ，如图所示，由此可知（ ）A ．小球带正电B ．电场力大小为3mgC ．小球从A 到B 与从B 到C 的运动时间相等D ．小球从A 到B 与从B 到C 的速度变化相等6、如图，在研究功与内能改变的关系时，将一小块易燃物放在厚玻璃筒底部，用力向下压活塞，可以将易燃物点燃。
辽宁省本溪市高级中学、盘锦市高级中学2025届化学高二上期末学业水平测试试题含答案
辽宁省本溪市高级中学、盘锦市高级中学2025届化学高二上期末学业水平测试试题含答案注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（每题只有一个选项符合题意）1、pH＝2的A、B两种酸溶液各lmL，分别加水稀释到1000 mL，其溶液的pH与溶液体积(V)的关系如图所示，则下列说法正确的是( )A．A、B两种酸溶液物质的量浓度一定相等B．稀释后A酸溶液的酸性比B酸溶液强C．a＝5时，A是强酸，B是弱酸D．若A、B都是弱酸，则5≥a>22、将1.60gCuSO4固体在高温下加热，得到0.72g红色固体（纯净物，不含S元素），同时有气体X生成，X可能是SO2、SO3、O2中的两种或三种。
下列说法正确的是A．所得红色固体是铜B．将X通入氢氧化钡溶液，若溶液变浑浊，则X中含有SO3C．X的物质的量最少为0.01molD．将X缓慢通过足量NaOH溶液，若溶液增重0.72g，则X中含0.005molO23、臭氧(O3)可用于杀菌消毒，下列有关臭氧的说法正确的是A．臭氧的相对分子质量为32B．臭氧分子由氧气分子构成C．臭氧与氧气互为同分异构体D．臭氧的相对分子质量为48g/mol4、下列属于天然高分子化合物的组合是（）A．聚乙烯、淀粉 B．纤维素、淀粉 C．塑料、纤维素 D．油脂、蛋白质5、常温、常压下，4.8 g碳（石墨）在一定量的氧气中燃烧，反应完成后碳无剩余，共放出100 kJ的热量。
（已知：碳的燃烧热∆H=－394 kJ/mol ；2C(石墨)＋O2(g)═2CO（g）∆H=－221 kJ/mol），则燃烧后的产物是A．CO2B．COC．CO2和CO D．无法确定6、下列事实不能用平衡移动原理解释的是A ．夏天打开啤酒瓶盖后产生大量气泡B ．浓氨水中加入NaOH 固体产生有刺激性气味气体C ．实验室用排饱和食盐水的方法收集氯气D ．压缩H 2和I 2反应的平衡混合气体，气体颜色变深7、常温下，某酸性溶液中只含4NH +、Cl -、H +、OH -四种离子，下列说法正确的是 A ．溶液中离子浓度可能满足： ()()()()4c Cl c H c NH c OH -++->>>B ．该溶液不能由等物质的量浓度、等体积的盐酸和氨水混合而成C ．可由pH=3的盐酸与pH=11的氨水等体积混合而成D ．再通入适量氨气，溶液中离子浓度可能为： ()()()()4c NH c Cl c H c OH +-+->>>8、糖类、油脂、蛋白质都是与生命息息相关的物质。
辽宁省重点高中协作校2017届高三上学期期末考试地理试题 Word版含答案 (1)
第Ⅰ卷（选择题，共70分）考生注意:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分，共100分，考试时间90分钟。
第I 卷1至4页，第II卷5至8页。
考试结束后，将本试题卷和答题卡一并交回。
2.答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
3.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。
4.本试卷主要考试内容:高考内容。
第Ⅰ卷(选择题共44分)一、选择题(本大题共22小题.每小题2分，共44分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
)河南省剩余劳动力赴外省就业主要集中在东部的广东、江苏、浙江、上海和北京五个省市。
2011年河南省农村剩余劳动力省内就业人数出现拐点，省内就业人数首次高于省外就业人数。
据此完成1-2题。
1.造成河南省农村剩余劳动力回流本省的主要原因是（）①沿海产业向内地迁移②农民工年龄偏高③内地就业环境有所改善④农民工受教育程度低A.①②B.③④C.①③D.②④2.河南省农村剩余劳动力回流（）A.提高了河南省的城市化水平B.为河南省经济发展提供人力资源C.减缓东部地区经济增长速度D.缓解河南省农村人口与土地的压力读2014年长江经济带城市群上、中、下游的总人口、城镇人口和GDP对比图，完成3-5题。
3.长江经济带城市群上、中、下游依次递增的是（）①人口规模②城市化水平③人均GDP ④区域面积A. ①②B.①④C.②③D.③④4.滇中、黔中城市群人口规模相对较小的主要自然原因是（）A.气候炎热B.地形崎岖C.地壳活跃D.土壤贫瘠5.关于长江经济带城市群的发展战略重点，对应正确的是（）①综合交通枢纽，科技创新、先进制造业和现代服务业基地②中部地区崛起的重要增长极，承接产业转移的示范区③全球先进制造业和服务业基地，“一带一路”总枢纽④重要经济中心和开放高地，内陆开放和统筹城乡发展示范区A.成渝城市群一④长江中游城市群一②江淮城市群一③长三角城市群一①B.成渝城市群一①长江中游城市群一④江淮城市群一②长三角城市群一③C.成渝城市群一②长江中游城市群一④江淮城市群一③长三角城市群一①D.成渝城市群一④长江中游城市群一①江淮城市群一②长三角城市群一③大连某海产养殖产业在成都投资进行淡水养殖深海鱼项目，室内的养殖箱相互贯通，箱里流动的淡水经过氯化处理，形成和深海一样的生态环境，用以养殖石斑鱼、鲈鱼、龙虾等高档海鲜。
2017-2018学年辽宁省重点协作校(营口市高级中学等)高一下学期期末考试数学试题
2017-2018学年辽宁省重点协作校(营口市高级中学等）高一下学期期末考试数学试题一、单选题1．已知点，，向量，若，则实数的值为（）A. B. C. D.【答案】D【解析】分析：利用向量的坐标公式求出的坐标，利用向量共线的充要条件：坐标交叉相乘相等，列出方程，求出y的值．详解：由题∵，，故选：D．点睛：解决三点共线问题常转化为以三点为始点、终点的两个向量共线，利用向量共线的充要条件找等量关系；两个向量共线的充要条件是：坐标交叉相乘相等．2．在中，角，，所对的边分别为，，，已知，，，则（）A. B. C. D. 或【答案】A【解析】分析：利用正弦定理解三角形，根据大边对大角，即可得解.详解：已知在中，角，，所对的边分别为，，，已知，，，则有正弦定理可得故选A.点睛：本题考查利用正弦定理解三角形，属基础题.3．（题文）林管部门在每年3月12日植树节前，为保证树苗的质量，都会在植树节前对树苗进行检测，现从甲乙两种树苗中抽测了10株树苗的高度，其茎叶图如图.根据茎叶图，下列描述正确的是（）A. 甲树苗的平均高度大于乙树苗的平均高度，且甲种树苗比乙种树长的整齐.B. 甲树苗的平均高度大于乙树苗的平均高度，但乙种树苗比甲种树长的整齐.C. 乙树苗的平均高度大于甲树苗的平均高度，且乙种树苗比甲种树长的整齐.D. 乙树苗的平均高度大于甲树苗的平均高度，但甲种树苗比乙种树长的整齐.【答案】D【解析】解：由茎叶图中的数据，我们可得甲、乙两种树苗抽取的样本高度分别为：甲：19，20，21，23，25，29，31，32，33，37乙：10，10，14，26，27，30，44，46，46，47由已知易得：甲的均值为="(19+20+21+23+25+29+31+32+33+37)" ÷10 =27乙的均值为="(10+10+14+26+27+30+44+46+46+47)" ÷10 =30S甲2＜S乙2故：乙种树苗的平均高度大于甲种树苗的平均高度，甲种树苗比乙种树苗长得整齐．故选D4．已知三角形的三边满足条件，则（）A. B. C. D.【答案】C【解析】分析：根据已知等式，化简整理得．再由余弦定理加以计算，得到，即可得到角的大小．详解：∵，化简得．由余弦定理，得∵A是三角形的内角，∴．故选C.点睛：本题给出三角形的边满足的条件，求角A的大小．考查了等式的化简、用余弦定理解三角形等知识，属于基础题．5．如图所示框图，当时，输出的值为（）A. B. C. D.【答案】C【解析】分析：据框图的流程依次计算程序运行的结果，直到不满足条件条件，确定输出的值详解：第一次运行，，第二次运行，，第三次运行，，第四次运行，退出循环，输出故选C.点睛：本题考查了循环结构的程序框图，根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.6．已知，则（）A. B. C. D.【答案】B【解析】分析：由求出的值，然后利用“除1”将化为的不等式，代入得值即可.详解：，则.故选B.点睛：本题考查两角和的正切公式，考查同角三角函数基本关系式的应用：化简求值．将所求式化成的三角式后再求值是技巧．7．已知的顶点为，，，，则常数的值为（）A. B. C. D.【答案】B【解析】分析：利用向量的数量积公式，即可求常数的值．详解：由题意，∵，∴故选B.点睛：本题考查向量的数量积公式，考查学生的计算能力，比较基础．8．已知1sin 33πα⎛⎫-= ⎪⎝⎭，则sin 26πα⎛⎫-= ⎪⎝⎭（ ） A. 79-B. 79C. 79±D. 29- 【答案】A【解析】由题意可得1cos cos cos 32663ππππααα⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 27sin 2sin 2cos 2cos22cos 16233669ππππππααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=+=+-=-⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，选A.9．利用随机模拟方法计算和所围成图形的面积.首先利用计算机产生两组之间的随机数：（ ），（ ）；令；若共产生了个样本点，其中落在所围图形内的样本点数为，则所围成图形的面积可估计为（ ）A. B. C. D.【答案】B【解析】分析：由题意，计算对应的面积比即可估计所围成图形的面积．详解：由题意又，由个样本点，，其中落在所围成图形内的样本点数为，则 ，如图所示；∴所围成图形的面积可估计为．故选B点睛：本题考查了用模拟实验法求对应面积的比值问题，是基础题． 10． （ ） A. B.C.D.【答案】A【解析】分析：结合诱导公式，和差角公式和切化弦法，可得答案；详解：故答案为1.点睛：本题考查的知识点是三角函数的化简与求值，难度中档．11．已知是的角平分线与边交于点，且，，，则（）A. B. C. D.【答案】D【解析】分析：如图，过点分别作的高线，垂足分别是．过点作于点，由勾股定理可得长度，利用面积法可得，即可得．详解：如图，如图，过点分别作的高线，垂足分别是．∵是的角平分线，过点作于点，∵在直角中，．又∴在直角中，由勾股定理得到即解得 ，又∵在直角中，．故选D.点睛：本题考查了勾股定理、角平分的性质以及含30度角的直角三角形．根据题意作出辅助线，是解题的难点．12．平行四边形ABCD 中， 2AB =， 1AD =， ·1AB AD =-u u u r u u u r，点M 在边CD 上，则·MA MB u u u r u u u r 的最大值为（ ）A. 2B. 221-C. 5D. 31-【答案】A【解析】Q 平行四边形ABCD 中， 2,1,?1AB AD AB AD ===-u u u r u u u r，点P 在边CD 上，1··cos 4,cos ,1202AB AD A A A ∴∠=∴=-∴=o u u u r u u u r ，以A 为原点，以AB 所在的直线为x 轴，以AB 的垂线为y 轴，建立坐标系， ()()130,0,2,0,,22A B D ⎛∴- ⎝⎭,设 3,2M x ⎛⎫ ⎪ ⎪⎝⎭,则1333,,,2,2222x PA x PB x ⎛⎛⎫-≤≤∴=--=-- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r ，()()22331·221444PA PB x x x x x ∴=-+=-+=--u u u r u u u r ，设()()2114f x x =--，因为1,22x ⎡⎤∈-⎢⎥⎣⎦，所以当12x =-时()f x 有最大值2，故答案为2.二、填空题13．（题文）已知单位向量，的夹角为，则__________．【答案】【解析】分析：由题意并且结合平面数量积的运算公式可得|，通过平方即可求解，可得答案．详解：∵单位向量，的夹角为的夹角为，∴，即答案为．点睛：本题主要考查平面向量数量积的运算性质与公式，以及向量的求模公式的应用，属于基础题．14．已知，则__________．【答案】【解析】分析：由题意设将条件代入化简可得从而得到的值．详解：由题意有可得，∴∴ ，故答案为．点睛：本题考查两个向量的加减法的法则，向量的数乘以及其几何意义，得到是解题的难点和关键.15．在锐角三角形中，若，则__________．【答案】【解析】分析：结合三角形关系和式子可推出 ，进而得到，又，可得，即可得解．详解：由已知条件，， ，两边同除以，，又，可得，，则.故答案为：[8，+∞）．点睛：本题考查了三角恒等式的变化技巧，有一定灵活性，属于中档题．16．在平面直角坐标系中，(0,0),(6,8)O P ，将向量OP u u u r 按逆时针旋转34π后得向量OQ u u u r，则点Q 的坐标是 ．【答案】(72,2)-【解析】试题分析：将向量(6,8)OP =u u u r 按逆时针旋转32π后得(8,6)OM =-u u u u r ，则)(72,2)2OQ OP OM =+=-u u u r u u u r u u u u r【考点】本题考查了向量的坐标运算点评：熟练掌握向量的坐标运算是解决此类问题的关键，属基础题三、解答题17．在平面直角坐标系中，已知角终边上一点为.（1）求的值；（2）求的值.【答案】（1）（2）【解析】分析：（1）利用三角函数的定义，可求，进而利用二倍角公式即可得出结论．（2）化简，即可得到结论.详解：（1）设，则，所以，，所以.（2）原式.点睛：本题考查利用三角函数定义，二倍角公式，诱导公式进行化简求值，属基础题. 18．为了解某冷饮店的经营状况，随机记录了该店月的月营业额（单位：万元）与月份的数据，如下表：（1）求关于的回归直线方程；（2）若在这些样本点中任取两点，求恰有一点在回归直线上的概率. 附：回归直线方程中，，.【答案】（1）（2）【解析】分析：（1）根据题意计算平均数与回归系数，写出回归方程；详解：（2）用，分别表示所取的两个样本点所在的月份，则该试验的基本事件用列举法可得包含个基本事件，设“恰有一点在回归直线上”为事件，则包含个基本事件，用古典概型直接求概率即可。